HIV evolutionary genetics

As part of its life cycle, HIV infects a host cell and reverse transcribes its RNA genome into cDNA, which is subsequently integrated into the host cell’s nuclear genetic material. Reverse transcription, mediated by the viral reverse transcriptase, is a low-fidelity process with the potential to accumulate errors at the rate of 10⁻⁵ to 10⁻⁴ per nucleotide site per generation (1). As a consequence of this process and a rapid rate of turnover of productively infected cells (between 140 and 300 generations per year; refs. 2 and 3), the viral population in an infected individual has the potential to reach a relatively high level of genetic diversity, with pairs of homologous viral sequences differing by as much as 15% (4).

Two papers in this issue of the Proceedings address facets of the debate on how HIV genetic variation accumulates in vivo. In a paper that exemplifies a heartening return by HIV researchers to nuts-and-bolts population genetics, Rouzine and Coffin (5) consider the issue of whether HIV genetic variation can best be modeled stochastically or deterministically. It has been estimated that the total number of HIV-infected cells in a human host is between 10⁷ and 10⁸ (6). However, only a portion of infected cells produce viable viral particles that go on to infect other cells. Population size—the number of infected cells, in this case—certainly determines the rate at which genetic variation accumulates; however, it is not the census population size (the raw count of the number of infected cells) that is important but the effective viral population size. In the simplest type of population—one in which size remains constant, reproductive success is not determined by any selective pressure, and the generations are discrete—the number of individuals that have the potential to produce offspring from generation to generation influences the genetic diversity of that population in well understood ways (7, 8). A small population produces a mutation only rarely, and when it does, that mutation is often lost very quickly through stochastic sampling effects (genetic drift). The same stochasticity can also move that variant to displace the wild type completely relatively quickly. When the population is large, mutants are produced far more frequently, but their fixation in the population occurs at a more sedate pace. Real populations seldom fit the assumptions of the ideal population, and population geneticists use the term effective population size (N_e) to denote the number of individuals in an ideal population that has the same magnitude of genetic drift as the natural population in question (8, 9). Rouzine and Coffin note that the effective size of the HIV population in vivo is unknown, although some estimates, derived on the basis of coalescent times in genealogies of samples of sequences, place the value at around 10³ infected cells (3, 10). In fact, some authors (10, 11) have suggested, by virtue of this very low estimated N_e, that HIV evolution should be viewed as a stochastic process: the fixation (or loss) of a variant from the population, even one with a reasonably high selective advantage (or disadvantage), will be determined principally by sampling in much the same manner as selectively neutral variants. If this argument holds true, then deterministic models of evolution that ignore stochastic effects and predict the genetic behavior of the viral swarm as though the population is (infinitely) large are inappropriate.

The notion that viral evolution is a stochastic process may explain, for instance, why some individuals take longer than others to develop resistance to identical antiretroviral drugs (12) or why it is frequently difficult to detect the effect of selection in regions of the HIV genome that one expects to be under heavy selection pressure (13). Although the effective sizes of natural populations are typically lower than their census sizes, the difference between an estimated HIV N_e of 10³ and the HIV census population size in vivo of 10⁷–10⁸ is large enough to be perplexing.

Rouzine and Coffin begin by trying to determine whether HIV evolves as one would expect if the population were large (i.e., deterministically) or small (i.e., stochastically). They note that, because population size is a continuous variable, whether the genetic variation of a population is molded stochastically or deterministically also exists on a continuum. This continuum is segmented: when the population size is less than 1/s, where s is the relative difference in reproductive potential between a mutant and a wild type caused by selection, fixation and loss are caused largely by sampling; when the population size exceeds 1/μ, where μ is the mutation rate, the population can be modeled as though it were infinitely large. When 1/s < N_e < 1/μ, both stochastic and deterministic effects act on the population to a greater or lesser extent depending on whether N_e is closer to one or the other boundary. (With selectively neutral variants, the lower boundary does not exist, and the population is effectively stochastic below 1/μ and deterministic above.) Rouzine and Coffin define a simple yet cunning test that determines where the HIV population sits on this continuum. Their test is based on the following argument. Consider any two sites that sit close to each other on the genome, each site having two variants. For convenience, we shall refer to the selectively advantageous variants at both sites as A and B and the selectively disadvantageous variants as a and b, and we assume that the selective effects across sites are additive. In a large steady-state population (and consequently, under a deterministic regime), mutation will generate haplotypes of the form Ab, aB, and AB, each of which is more fit than ab. Although the population moves inexorably to a fixation of AB, for a large part of the time, all four haplotypes are present in sufficient numbers to be detectable if a sample of sequences is obtained (see simulation results in figure 4 of ref. 5).

What happens when the population size sits somewhere between 1/s and 1/μ? Still confining the discussion to only those sites at which two variants exist, Rouzine and Coffin argue that one of two scenarios must have happened. First, two haplotypes, Ab and aB, are generated by chance; the probability of generating the double-mutant AB is very small when N_e ≪ 1/μ. Both of these haplotypes increase in number until they pass a critical threshold of 1/s (see simulations shown in figure 3a of ref. 5), beyond which their increase in frequency can be predicted deterministically. These haplotypes displace ab from the population and are present in equal proportions until such time that a mutation arises in either Ab or aB that produces AB; note that AB must still cross 1/s before it, too, can increase deterministically. In this scenario, the probability of seeing all four haplotypes in any sample of sequences is very small, because AB is unlikely to appear before ab has been removed from the population. In a second scenario, either Ab or aB is produced first, passes the 1/s threshold, and acquires a second mutation, AB, which also increases beyond 1/s. As with the first scenario, the likelihood of seeing all four haplotypes simultaneously in a sample of sequences is low. Consequently, Rouzine and Coffin argue, if one does indeed see all four haplotypes, one can be reasonably certain that the population is large enough that stochastic effects minimally influence the evolution of the virus.

To test this line of reasoning, Rouzine and Coffin use samples of sequences encoding for HIV protease (pro; the enzyme involved in cleavage of transcribed viral polyproteins) obtained from three infected individuals and sequences of the V3 region of the envelope (env) gene (an immunogenic region that has been shown to be an important determinant of cell tropism). Three of the four pairs of sites in pro and four of six pairs of sites in the V3 region have all four haplotypes. Rouzine and Coffin conclude, therefore, that the HIV population size is at the very least, close to the deterministic boundary. They proceed to derive estimates of N_e by simulation and obtain values that range from 2 × 10⁴ (for the case where the selection coefficient, s, is very small) to 5 × 10⁵. With a mutation rate on the order of 10⁻⁵, this estimate places the deterministic boundary at 100,000 infected cells; thus, the estimated N_es are reasonably close to the boundary or within the deterministic range. Rouzine and Coffin go on to discuss how the assumptions of their model and the simulations can affect their estimates. In addition, they discuss the effects of epistasis (or coselection of both sites), which can act to decrease the frequency of haplotypes Ab and aB, and recombination, which can serve to generate all four haplotypes, even when the population is small. Their arguments are too detailed to restate here; it is sufficient to note that under their scrutiny, these factors do not change their conclusions.

Rouzine and Coffin leave open the possibility that there will be instances when stochastic factors may well be the determinants of HIV evolution. Under highly active antiretroviral therapy, for instance, when the numbers of infected cells drop by two or more orders of magnitude, the HIV population may find itself in the stochastic zone. Similarly, during the bottleneck at transmission or after the initial phase of acute viremia (which occurs within a few weeks of infection), viral populations may evolve stochastically. Also, it is sometimes the case that a deterministic model provides an adequate explanation for the evolution of resistant variants under some therapeutic regimes, whereas with others, stochastic models have greater explanatory power (14). Rouzine and Coffin highlight the fact that evolving populations sit on a continuum between stochasticity and determinism. The recognition of this continuum is itself a major step forward in the debate, because until now, participants in the stochastic–deterministic debate have conceptually polarized the HIV population. The implication here is that researchers could do better than adopt a “one-model-fits-all” approach.

The second paper, written by Leitner and Albert (15), addresses a different issue, although this issue also has an impact on our understanding of the evolutionary genetics of HIV. Is the tempo of HIV molecular evolution clock-like, i.e., do substitutions accumulate in the HIV genome at a regular pace? To establish that a gene or gene fragment evolves in a clock-like fashion, it is necessary to show that, when the molecule evolves independently in different lineages, it does so at the same rate. Leitner and Albert (15) make use of HIV sequences spanning the V3 region of env and the p17 region of the gag gene obtained from nine epidemiologically clustered individuals for whom the history of HIV transmission, including times of infection and sampling, is well documented. Each individual was represented by a single sequence, derived either directly from a pool of amplified viral sequences or by reconstructing a majority-rule consensus after different sequences were obtained. Genetic distances between sequences were calculated in several different ways, including and excluding corrections for multiple substitutions and rate heterogeneity across sites. Estimates of the rate of substitution were obtained by regressing the pairwise distances against known times between sample collections. In addition, other methods, less prone to the nonindependence of pairwise distance measures, were also used. In all cases, there was very good agreement among estimates, with the rates of substitution ranging from 6.6 × 10⁻³ to 7.0 × 10⁻³ per nucleotide site per year for the V3 region and from 6.6 × 10⁻³ to 7.0 × 10⁻³ per site per year for p17.

The molecular clock has been used to support the argument that evolution is predominantly neutral (16). The rate at which selectively neutral mutations become fixed in the population depends only on the rate of mutation, whereas the rate of fixation of a selectively advantageous mutation depends on N_e and s. It has been argued, therefore, that it is unlikely for a variety of substitutions to accumulate in the same molecule at the same rate in independent lineages (where, in the study by Leitner and Albert (15), these correspond to different hosts), because each lineage/host is likely to have different selection regimes and population sizes. Nonetheless, models of evolution that incorporate selection have been constructed that can also show the same rate constancy as neutral models over long time scales (17). In fact, it has been observed that, contrary to what one expects under a neutral and Poisson-directed accumulation of substitutions, the variance of the rate of substitution is often greater than the average rate of substitution (18, 19), leading evolutionary biologists to question whether the molecular clock truly offers support for the neutral theory. Leitner and Albert (15) show by simulation that, for their data, the variance in the rate of substitution between any pair of sequences is not significantly different from that expected if the process is strictly Poisson. They conclude, therefore, that “HIV-1 evolution can be adequately described by a neutral evolutionary model” (15). This conclusion may well be startling to many, because it has been accepted almost as dogma that selection is a major determinant of viral evolution. For instance, for immunogenic regions of the viral genome (V3 is considered one such region), it has been argued that there is ongoing selective pressure imposed by the immune system to acquire substitutions that effectively camouflage the virus, allowing it to evade detection (20). However, if most substitutions are selectively neutral, then what role does the immune system play in shaping viral variation? It is worth noting, at this point, that failure to reject the Poisson model of substitution should not be equated with an acceptance of neutrality, because that remains the null hypothesis in this case. It may be that there are indeed positive and purifying selection pressures acting on V3 and p17, respectively, and failure to detect these is a consequence of the number and length of sequences used. Alternatively, because the genetic distances calculated by Leitner and Albert (15) are effectively averages over all sites, there is the potential to miss site-specific selective effects (21).

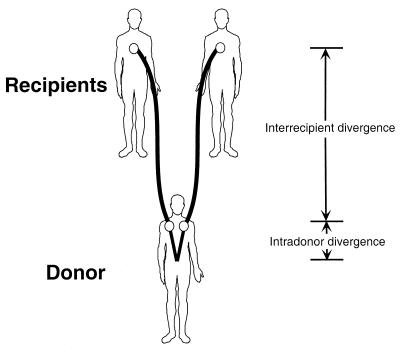
The authors also note that the best-fitting line passing through the points on the distance–time graph does not pass through the origin but intercepts the distance axis at some positive value (0.02 for V3 and 0.004 for p17). They call this quantity “ancestral divergence,” effectively the average distance between pairs of donor sequences at the instant of transmission. As Leitner and Albert (15) point out, this ancestral or intradonor divergence is a function of the HIV N_e in the donor. In an epidemiological context, there is some significance in this value. Some studies have looked at the historical population dynamics of the HIV epidemic or subepidemics by using sequences obtained from different individuals (22, 23). However, the genetic divergence between pairs of such sequences will depend on both the (effective) number of infected individuals in a population and the (effective) number of infected cells within individuals (Fig. 1). If these two numbers are similar, say, on the order of 10⁵ as Rouzine and Coffin estimate, then any epidemiological parameters estimated, e.g., the rate of growth of the number of infected individuals, conceivably may be confounded by processes acting on the viral populations within individuals as well.

Figure 1.

Transmission of two viruses to two recipients from the same donor. Two variants within a donor may differ by as much as 15% (4). This intradonor divergence adds to the genetic divergence of the sampled isolate that accumulates naturally within each recipient or, if the recipient from which the sample is obtained is at the end of a transmission chain, through its continued evolution in each intermediate host. The intradonor variance is a function of N_e in vivo and, potentially, the time since infection.

Mathematical models of HIV population dynamics that couple genetic diversity with viral kinetics have existed in the literature for some time (24, 25). Such models have not been uniformly popular. However, as we begin to understand more about the underlying processes that govern the evolution of HIV, it is likely that we will begin to see a greater degree of integration between population genetic and kinetic models. Thus, we may obtain a more complete picture of the disease course and potentially uncover and/or confirm the existence of a link between HIV variation and disease progression, if indeed such a link exists (with HIV, it is usually wise to end equivocally).