Bayesian design using adult data to augment pediatric trials

Abstract

Background

It can be difficult to conduct pediatric clinical trials because there is often a low incidence of the disease in children, making accrual slow or infeasible. In addition, low mortality and morbidity in this population make it impractical to achieve adequate power. In this case, the only evidence for treatment efficacy comes from adult trials. Since pediatric care providers are accustomed to relying on evidence from adult studies, it is natural to consider borrowing information from adult trials.

Purpose

The goal of this article is to propose a Bayesian approach to the design and analysis of pediatric trials to allow borrowing strength from previous or simultaneous adult trials.

Methods

We apply a hierarchical model for which the efficacy parameter from the adult trial and that of the pediatric trail are considered to be draws from a normal distribution. The choice of (the variance of) this distribution is guided by discussion with medical experts. We show that with this information, one can calculate the sample size required for the pediatric trial. We discuss how inference of these studies in pediatric populations depends on the parameter that captures the similarity of the treatment efficacy in adults compared to children.

Results

The Bayesian approach can substantially increase the power of a pediatric clinical trial (or equivalently decrease the number of subjects required) by formally leveraging the data from the adult trial.

Limitations

Our method relies on obtaining a value for the inter-study variability,, which may be difficult to describe to a clinical investigator.

Conclusions

The Bayesian approach has the potential of making pediatric clinical trials feasible because it has the effect of borrowing strength from adult trials, thus requiring a smaller pediatric trial to show efficacy of a drug in children.

Introduction

Many diseases effect both children and adults, but treatments are often developed and tested only in adults. When there is insufficient information on dose and efficacy in children, pediatricians face the dilemma of extrapolating the evidence from adult clinical trials to a pediatric population or treating children with unproven treatments. Recently there has been pressure on pharmaceutical companies by the US Food and Drug Administration (FDA) and on the academic community by NIH to conduct clinical trials in children. One approach [1] is to conduct studies to establish pediatric dosage, but to infer efficacy from adult trials. There has also been a call to do more efficacy trials in children [2]. However, this is often challenging as diseases can have a low incidence in children and the timing and course of the disease can make the trial infeasible. This issue has arisen for us in the context of designing clinical trials for children in intensive care units (ICU) to test interventions that were developed or are in development for adults.

Since a pediatrician’s observation that a drug is effective in adults increases his/her belief in its effectiveness in children, a natural approach toinference is to make these considerations explicit using Bayesian methods. Trials that ‘borrow strength’ using Bayesian methods are currently being considered by the FDA, although the various ‘draft guidance’ documents do not give explicit suggestions as how to incorporate external information [3]. For the pediatric ICU studies, we want to use adult clinical trial data to generate a prior distribution to be used for the pediatric trial, and describe how to design (find the sample size required) and analyze the results of these studies.

There is a literature on applying Bayesian methods to extrapolate results from trials to populations who were not included in the original trial. This can occur, for example, when one wants to register a drug in a country where it was not tested. In a randomized clinical trial called a ‘bridging’ study, investigators look for similarity in the positive treatment effect [4,5]. Similarly, Bayesian methods can be used to ‘interpolate’ by determining how to estimate treatment effects among subsets of patients studied in a clinical trial. Dixon and Simon [6] propose a method that uses hierarchical models.

The most straightforward way to apply Bayesian methods is to elicit a prior distribution on the treatment effect from medical experts and use this to design and analyze the trial [7]. In a study by Goodman and Sladky in 2005 [8], a prior is used that is based on a meta-analysis with modified mean and variance reflecting the investigator’s beliefs. However, for our pediatric ICU application, we cannot always assume that the adult trials are already completed. In this situation the pediatricians would not have an informed prior belief on the efficacy of the new treatment. Therefore, we would like to design a pediatric trial knowing only the design of the adult trial. This is often preferable as there may be cost savings in doing simultaneous pediatric and adult trials. In addition, simultaneous pediatric and adult trials allow simultaneous approval for both populations and minimizes off-label pediatric use of a drug that was only proven efficacious in adults. On the other hand, doing one study after the other may save costs because if an adult study fails the pediatric study may not be deemed necessary.

One shortcoming of methods for which only one prior is used to determine the posterior of the efficacy parameter is that the report of a clinical trial using these techniques will only be helpful to investigators who have same prior as the authors of the report. However, different pediatricians may develop different prior beliefs about the efficacy of a treatment in children based on viewing the same adult data. Thus it would be useful to have a method that would allow each pediatrician to interpret the data from a pediatric study based on their own prior belief on the relevance of the adult data and the results of one adult study. This would be facilitated by a prior that has only one parameter which can be relatively easily understood.

Two Bayesian methods of borrowing strength from one clinical trial to another are the use of hierarchical models and power priors. The former is described in [9,10] and are widely used while the latter is as an approach [11] where the prior distribution is the likelihood from another trial (the adult trial) raised to a power that measures the extent to which the result applies to the current (pediatric) trial [12]. More specifically, if we let π₀(θ) denote the prior distribution for θ, let D₀ be the adult data, and let L(θ|D) be the likelihood, then we define a discounting parameter, a₀, which weights the adult data relative to the current (pediatric) study as

$$\pi (\theta \mid D_0,a_0)\propto L{(\theta \mid D_0)}^{a_0}{\pi }_0\left(\theta \right)$$

and ranges from one, when the data from an adult is of equivalent value, to zero where no borrowing from adult results is appropriate.

In this article, we will propose a Bayesian approach for formalizing what pediatricians do when they combine the results from large adult trials with the results of smaller pediatric trials to make treatment decisions. We will use a hierarchical model for this, but will show that in our setting, the hierarchical model and power prior methods are equivalent. Thus one can either specify the variation of the efficacy parameters of the adult and pediatric trials or a power parameter which specifies the extent to which the adult trial extrapolates to children. Therefore, the difficult task of having medical experts to elicit a prior is reduced to the specification of one number representing how similar children effects are to the adult effects. From this, we will be able to propose a design for the trial that can be conducted simultaneously or subsequent to the adult trial. The results from the trial can be reported so that interpretation of efficacy can be driven by the prior of the reader. We will apply these methods to guide pediatric study design and analysis in the context of information from adult trials. Our goal is to provide a new way to design pediatric trials, which we hope will encourage the conduct of these trials in a setting that would otherwise be prohibitive to complete.

Methods

We consider a hierarchical model that allows us to incorporate the information from an adult study population into our determination of thedistribution of the parameter for the pediatric population. For this, we will need to specify the parameter of interest, which is the measure of a treatment’s efficacy, and it’s likelihood. This parameter can be any parameter related to a hypothesis that can be tested in both a pediatric study and an adult study. We assume that the parameter estimate is approximately normally distributed. This can either be due to a large enough sample size or as the result of some transformation (such as logarithmic transform) on another parameter. This implies that the likelihood function will be Gaussian. Next, we will need to specify the hierarchical model that allows us to link the information on efficacy from adult and pediatric trials. We denote the parameters from the adult study and the associated pediatric study as β_A and β_P, respectively. We assume that these parameters have a common prior normal distribution with mean μ and variance ν². We assume that μ has a noninformative prior. The specification of ν reflects how much variation we can expect in studies conducted in adults and children. This approach differs from the usual use of hierarchical models where ν is given a prior distribution. We discuss this and other sensitivity issues in section ‘Sensitivity to Assumptions’. We focus on the case where the posterior is asymptotically normal; otherwise the posterior can be simulated using WinBUGS [13].

Evaluating treatment efficacy in children

Let ${\widehat{\beta }}_P$ be the estimate of the treatment effect based on the pediatric data from m_P subjects, and let s_P be its standard error multiplied by $\sqrt{m_P}$. We factor $1∕\sqrt{m_P}$ out of the standard error to facilitate the sample size calculation. For example, in a two sample t-test with equal variance, the treatment effect will have standard error $\sigma \sqrt{4∕m}$ where σ is the standard deviation of the outcome. Thus s=2σ.

Now consider three random variables: β_P, ${\widehat{\beta }}_P$ the maximum likelihood estimate of β_P, and ${\widehat{\beta }}_A$, the maximum likelihood estimate from the adult study. If there is more than one adult study we assume that the ${\widehat{\beta }}_A$ is the parameter estimate from a meta-analysis of all of them. The parameter ν measures the variation between the response of adults and children to a treatment and not the variation expected from study to study within those groups. We will determine a treatment is efficacious if β_P > 0. Let ${\sigma }_{\mu }^2$ be the variance of μ and let $s_A∕\sqrt{m_A}$ be the standard error of ${\widehat{\beta }}_A$, where m_A is the sample size of the adult study. Most clinical trials are large enough so that ${\widehat{\beta }}_A$ and ${\widehat{\beta }}_P$ can be considered normally distributed. This simplification allows us to analyze studies with all types of endpoints using the same method [14,15]. The random variables (${\beta }_P,{\widehat{\beta }}_P,{\widehat{\beta }}_A$) are jointly multivariate normal with mean 0 and variance covariance matrix given by

$$\left[\begin{array}{ccc}\hfill {\sigma }_{\mu }^2+{\nu }^2\hfill & \hfill {\sigma }_{\mu }^2+{\nu }^2\hfill & \hfill {\sigma }_{\mu }^2\hfill \\ \hfill \hfill & \hfill {\sigma }_{\mu }^2+{\nu }^2+s_P^2∕m_P\hfill & \hfill {\sigma }_{\mu }^2\hfill \\ \hfill \hfill & \hfill \hfill & \hfill {\sigma }_{\mu }^2+{\nu }^2+s_A^2∕m_A\hfill \end{array}\right]$$

The posterior distribution of β_P is it’s conditional distribution given ${\widehat{\beta }}_A$ and ${\widehat{\beta }}_P$. We can use standard methods to perform this calculation and then let ${\sigma }_{\mu }^2\to \infty$ to find the posterior of β_P. To simplify the expression let

$$\omega =\frac{s_A^2}{(s_A^2∕m_A)+2{\nu }^2}.$$ (1)

Then the posterior mean of β_P is

$$\frac{{\left[\frac{s_P^2}{m_P}\right]}^{-1}{\widehat{\beta }}_P+{\left[\frac{s_A^2}{\omega }\right]}^{-1}{\widehat{\beta }}_A}{{\left[\frac{s_P^2}{m_P}\right]}^{-1}+{\left[\frac{s_A^2}{\omega }\right]}^{-1}}$$ (2)

and the variance is

$${\left[\frac{m_P}{s_P^2}+\frac{\omega }{s_A^2}\right]}^{-1}.$$ (3)

This number ω in (1) can be thought of as the number of adults that are borrowed from the adult data and used in the analysis of the pediatric data. Our proposed hierarchical model is equivalent to the Bayesian method suggested by Berry [16] for trials of similar medical devices. He suggests that the weight of the prior data be multiplied by a factor to account for uncertainty about the relevance of the prior data to the current problem. That factor is equivalent to ω/m_A. In his examples, he uses a value equal to 0.5, that is he assumes that half of the data from the previous trial can be pooled into the current trial. If ω/m_A = 0.5 then the prior distribution of β_P has mean ${\widehat{\beta }}_A$ and variance $2s_A^2∕m_A$. This would be equivalent to letting ${\nu }^2=0.5s_A^2∕m_A$. Setting ν² to this value would be equivalent to assuming that the between study variation is equal to 1/2 the variation of the maximum likelihood estimate. This would be a reasonable choice of ω or ν² if m_A were originally chosen to be large enough to resolve treatment differences, but not so large as to distinguish between similar studies. This approach is equivalent to a power prior as described in Ibrahim and Chen [11], since taking a normal probability density to the ω/m_A power is equivalent to multiplying the precision by ω/m_A. Thus Ibrahim and Chen’s a₀ is equal to ω/m_A.

What makes the most sense to us is to elicit ν² rather than ω or ω/m_A because ν or ν² is a direct measure of how different adult and pediatric results are expected to be. If the adult trial is large then $\omega \approx s_A^2∕\left(2{\nu }^2\right)$. One can think of ω as the ratio of the information that we have on the difference between adults and children, 1/(2ν²), and the information of one observation in the adult trial, which is $1∕s_A^2$. We note that ω should be interpreted as the effective sample size representing a discounted amount of information borrowed from the adult study. When s_A = s_P, an ω value, say 100, leads to a posterior mean that is the same as that obtained by adding 100 additional patients to the pediatric sample who have a mean effect equalling ${\widehat{\beta }}_A$ and variance equalling $s_A^2$. However in the general situation this equivalence does not hold, and ω should be interpreted in context with s_A, s_P, m, and n as in (1) above. This is another reason why we prefer eliciting to eliciting ω, because the latter tends to be more difficult to interpret.

The posterior distribution of β_P will be asymptotically normal with mean given by (2) and variance given by (3). Thus, letting Φ denote the normal cumulative distribution function, the posterior probability of the null hypothesis that β_P ≤ 0 is

$$\Phi \left(-\frac{{\widehat{\beta }}_P\frac{m_P}{s_P^2}+{\widehat{\beta }}_A\frac{\omega }{S_A^2}}{\sqrt{\frac{m_P}{s_P^2}+\frac{\omega }{s_A^2}}}\right).$$ (4)

where ω is defined in (1) above. In frequentist terms, this is analogous to a one-sided p-value for the test of the null hypothesis β_P ≤ 0 in that small values constitute evidence against the null hypothesis. Since pediatricians may disagree on their prior belief as to the similarity of children and adult effects, we suggest that the data be reported by plotting the probability of the null hypothesis versus. This would allow each pediatrician to use his/her own prior when evaluating the data. For the purpose of FDA approval, it will be necessary to specify these parameters. We discuss this further in the next section in the context of an analysis of a study.

Sample size calculation

The probability of finding a positive result in children will depend on the result we find in adults. To find the sample size n required for the pediatric study, we need to define a Bayesian analogue of power, calculate this ‘power’ for various choices of n and then choose the value of n for which this ‘power’ is 80–90%. Frequentist power is defined as the probability of deciding that a treatment is effective under the assumption that the true difference β is equal to some prespecified clinically meaningful difference. In our calculations we make the assumption that the design of the two studies will be the same so s_A=s_P=s.

Conditional on β_P and β_A, β_P is normal with mean β_P and variance $\frac{s^2}{m_P}$. Using the formula from (4), we can show that the power will be

$$g\left({\beta }_P\right)=\Phi \left(\frac{\frac{-1.96\sqrt{(m_P∕s^2)+(\omega ∕s^2)}-(\omega ∕s^2){\widehat{\beta }}_A}{(m_P∕s^2)}-{\beta }_P}{\sqrt{s^2∕m_P}}\right).$$

This can be simplified to

$$g\left({\beta }_P\right)=\Phi \left(\frac{-1.96\sqrt{m_P+\omega }-(1∕s)(\omega {\widehat{\beta }}_A+m_P{\widehat{\beta }}_P)}{\sqrt{m_P}}\right)$$

where ω is defined in (1) above.

One could get the power by calculating g(β_P) with β_P set to a clinically meaningful alternative hypothesis, and ω calculated using (1) and the that is specified by a clinical expert. This is a frequentist power calculation. It gives the probability of rejecting the null hypothesis, albeit using a Bayesian analysis, under the assumption of a clinically meaningful change. An alternative method to calculate power is to use the prior distribution of β_P. Thus, letting ϕ be the normal density function with mean ${\widehat{\beta }}_A$ and variance s²/ω, the probability of rejecting the null hypothesis given that β_P > 0 (the power), is

$$\frac{{\int }_0^{\infty }g\left(\beta \right)\varphi \left(\beta \right)\text{d}\beta }{{\int }_0^{\infty }\varphi \left(\beta \right)\text{d}\beta }.$$ (5)

This calculation would require numerical integration. Note also that we calculate the probability that the null hypothesis is rejected conditional on β_P > 0. This is because we do not want to reject the null hypothesis if β_P ≤ 0 so we do not include that region in our power calculation. This is similar to the method described in [17]. It is also possible to run Monte Carlo simulations to estimate this quantity.

Application to study design and inference

We now illustrate the use of our methods to both design a trial that would evaluate efficacy in a pediatric population, as well as to analyze and synthesize data available from adult and pediatric trials. In addition, we consider a third example for which adequate trials were conducted in bothpediatric and adult population. This third example is meant to illustrate the interpretation of the parameter ν that must be elicited from a medical expert.

Power and sample size calculations

We use the study of Omega-3 Fatty Acid, Gamma-Linolenic Acid, and Anti-Oxidant Supplementation in the Management of Acute Lung Injury or Acute Respiratory Distress Syndrome in Children (OMEGA) as an example to illustrate the difference between our proposed power calculation and the traditional power calculation based only on one study. As of this writing the adult study is ongoing and a pediatric study using the methods of this article is being proposed.

The parameter of interest is the difference in ventilation free days (VFD) [18] between patients who receive the medical food as opposed to standard feeding. The adult study will accrue 1000 eligible patients and the pediatric study would accrue 200 patients with a treatment: control ratio of 1:1. In the adult study the mean difference in VFD to study day 28 is 2.25 days with a standard deviation of VFD of 10.5.

We estimate the power of the test using the Bayesian method and the power of the test based just on the pediatric study under varying true treatment effects. We use ν = 0.8 and 0.5 and assume that the standard deviation of VFD is equal in adults and children.

Table 1 gives a comparison of the Bayesian power calculation and the traditional power calculation based only on pediatric study.

Table 1.

Comparison of power calculations

Adult effect	True effect in peds	Bayes power ν=0.8 (%)	Bayes power ν=0.5	Traditional (%) power (%)
2.25	1	36	74	10
2.25	2	63	91	27
2.25	3	84	98	52
2.25	4	95	99	77
2.25	5	99	99	92

Clearly, the Bayesian approach of combining the data from the two trials provides more power to detect treatment efficacy even under the more modest assumption that ν = 0.8. Looking at this graphically, Figure 1 gives the relationship of the power of the Bayesian approach to the value of ν (and ω), assuming the true pediatric effect is 1 VFD. This graph illustrates the sensitivity of the power to the value of ν, noting for example that the power of the Bayesian method exceeds 80% when ν < 0.45 and exceeds 90% when ν < 0.38. It is important to understand the effect of this method on Type I error. The frequentist Type I error rate in a one-sided test will be greater than 0.025 when the adult study is positive. This is expected because the adult results are providing information on the pediatric efficacy. One approach to evaluating the impact of the choice of is to consider the inference that would be made if the observed pediatric result were zero or negative and the adult effect were positive. For instance if the pediatric result were zero VFD and adult result were 2.25 from 1000 patients, then from (4) the pediatrician would conclude the pediatric effect significant (Prob(β_P ≤ 0|data, ν) < 0.025) if he/she believes the value of ν was < 0.48. If an investigator believes the value of ν is in this range, then they would only be convinced that the treatment was not of benefit in children if the pediatric result went in the wrong direction or the adult result were equivocal. This suggests that one could try to elicit ν by asking under what situations an investigator would use a drug for children given different results in adults and children.

Figure 1.

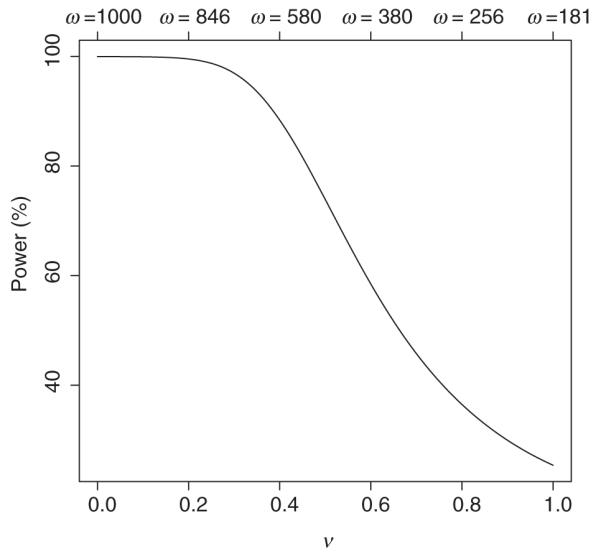
Power of Bayes analysis for varying ν and ω values

Inference

We use a study of the effect of Drotrecogin Alfa to illustrate the effect of ν values on Bayesian inference. In a published report [19], the efficacy of Drotrecogin Alfa in treating severe sepsis was demonstrated in 1690 adult patients (840 in placebo group, 850 in Drotrecogin Alfa group). The 28 day mortality rate was 30.8% in the placebogroup and 24.7% in the treatment group, giving an odds ratio of 1.36. The study found a statistically significant association between Drotrecogin Alfa treatment and mortality.

In a separate study led by Giroir [20], the efficacy of Drotrecogin Alfa was assessed in pediatric patients. A total of 477 patients were included. The 28-day mortality was 17.45% in the placebo arm and 17.15% in the treatment group, with no statistically significant evidence that the treatment was effective in the pediatric population.

We apply Bayesian methods described here to assess the efficacy of Drotrecogin Alfa for pediatric patients using the data from both studies. We calculate the posterior distribution of the log-odds ratio and the associated posterior probability that the null hypothesis is true. We calculate these statistics with values ranging from 0 to 1.

Figure 2 gives the Bayesian posterior probability that the null hypothesis is true Prob(β_P ≤ 0|data, ν) in the pediatric clinical trial under varying values. This probability is an increasing function of and takes values greater than 0.025 when ν > 0.044. This figure could be used for interpretation of the results of the study, as it informs an investigator how to examine the data from that of the pediatric trial within the context of their belief in the relationship between the efficacy in the pediatric versus the adult population.

Figure 2.

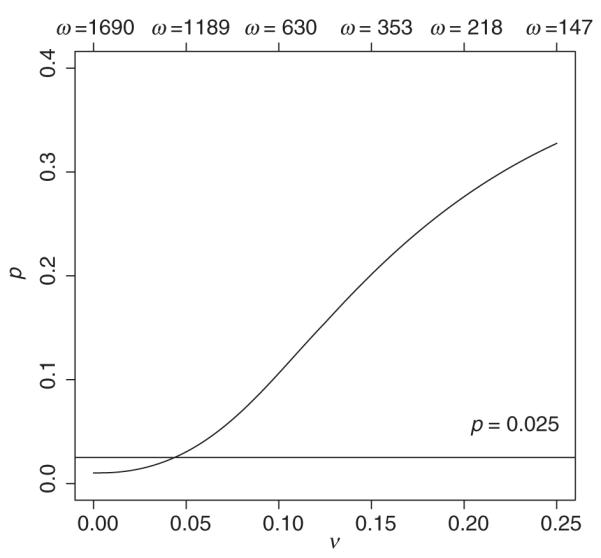
Posterior probability of the null hypothesis being true under a range of ν and ω values

The specification of ν is difficult in this setting because the parameter is the log-odds of mortality which is not intuitive. One way to express the results would be to say that if an investigator were willing to believe a-priori that the true odds ratio in children was between 0.89 and 1.13 ($\text{exp}(\pm 1.96\ast \sqrt{2}\ast 0.044)$) times the true odds ratio in adults, with 95% probability, then their value of ν would be 0.044 and they would see the pediatric trial as ‘just barely significant’, P(β_P > 0|ν = 0.044) = 0.975.

Estimation of ν from clinical trials

There are some diseases and indications that have been carefully studied in sufficiently large clinical trials in both pediatric and adult populations. There are several drugs for treating HIV/AIDS and cancer that have been tested by multi-centered trials groups focused on each of these populations. In addition, there are treatments for symptoms experienced by both populations that have undergone extensive clinical trails, such as for example, analgesic treatments for fever from upper respiratory tract infection (URTI). We consider treatments for fever to obtain an estimate for the parameter ν discussed in this article.

Table 2 summarizes findings from three published papers [21-23] regarding the average temperature reduction effect within 6 h using Ibuprofen or Tylenol (Acetaminophen) on adult and children. We consider both treatments to get our estimate for ν as we can get a better estimate of the parameter by utilizing two or more studies and obtaining a Bayesian estimate that incorporates all sources of variation. This requires an assumption that ν can be drawn from trials that have the same efficacy endpoint (decrease in fever) and the same disease/symptom (URTI). Using Table 2, we can estimate $\nu =\mid {\beta }_A-{\beta }_P\mid ∕\sqrt{2}$. The estimated ν = 0.32 for Ibuprofen and ν = 0.18 for Acetaminophen.

Table 2.

Estimated temperature reduction in adults and children by two drugs

Drug	Adult effect	Pediatric effect
Ibuprofen	1.21°C(n=44)	1.66°C(n=58)
Acetaminophen	0.62°C(n=157)	0.87°C(n=56)

From the publications we obtain estimated $s_A^2∕m_A=0.04$ for Ibuprofen and 0.0078 for Acetaminophen. Applying (1) using these estimates of ν leads to ω/m_A = 0.163 and 0.107, for Ibuprofen and Acetaminophen, respectively. This implies that the adult study sample is counted as equivalent to 16.3 and 10.7% of the original size in a pediatric study under a Bayesian design. Therefore, the effective sample size contribution from the adult Ibuprofen study to the test of efficacy in children would be about 7. In a corresponding Acetaminophen pediatric study, the effectivesample size contributed by the adult trial would be about 16.

Sensitivity to assumptions

In the methods described above we assume a Gaussian likelihood and a Gaussian hierarchical model where is specified rather than having a prior distribution itself. We discuss these assumptions in turn.

We use a Gaussian likelihood because we assume that these methods will mainly be used for clinical trials with relatively large sample size. The advantage of using a Gaussian likelihood and priors is that they allow a closed form expression for all the quantities of interest and they make the interpretation of the method we propose more straightforward. The only common clinical trial situation where this might not work is the analysis of rare adverse events, where a Poisson likelihood or binomial likelihood would be more appropriate.

In order to understand the sensitivity of our assumptions on the prior distribution of β_P, β_A, and ν, consider that when the adult study is complete there will be an induced prior on β_P. This prior will be normal and have a location which is equal to ${\widehat{\beta }}_A$ and a dispersion that is a function of the size of the adult study and the value of. If rather than choosing a value of ν we choose a prior for it, then the effect will be to change the shape of the distribution and it’s dispersion but not it’s location. For instance if we assume that 1/ν² has a prior that is Γ(a, b) then the prior for β_P will have a t-distribution with degrees of freedom and dispersion dependent on (a, b). For most choices of (a, b) there is a corresponding choice of a fixed ν which will usually yield similar inferences. Choosing (a, b) rather than ν adds complexity without adding much in the way of flexibility. The effect of the choice of a normal prior for β_A and β_P is similar to the specification of ν rather than specifying it’s prior. The consequences of the choice of a different distribution will be small compared to the consequences of a different choice of ν.

There would be advantages to using a prior for ν if there were more than one type of ‘adult’. For instance, in bridging studies with multiple countries, the use of a prior distribution for ν allows the hierarchical model to adapt to the observed variation between countries. In that case the prior for the country of interest will depend not only on the mean of the estimates from the other countries but on the observed dispersion of the estimates. It is worth pointing out that in the case of multiple historical studies, some properties discussed in this article, such as the equivalence between using a power prior and using a hierarchical model, no longer hold [7]. In this situation, we would prefer a prior on ν. It is also possible that one would want a prior for β_P that isn’t centered at ${\widehat{\beta }}_A$, but has some offset or multiplicative factor that derives from known differences between children and adults. This can be accommodated with some cost in complexity. We prefer in these cases to try to find a parameterization that naturally makes this correction such as we did with the use of the log-odds as a parameter in example 2.

Discussion

When practical factors limit the investigators’ ability to recruit large samples in a pediatric study, information from the corresponding adult study can be useful for statistical analyses. Our examples suggest that the Bayesian approach can improve the power of statistical inference in pediatric clinical trials. The approach can improve the precision of statistical estimation by reducing the width of the confidence intervals in a pediatric study. Bayesian methods allow for designs with sample sizes smaller than that required in a completely standalone study, which can be prohibitively large. We caution that it is wise to carefully review the design and analyses of an adult study before including it in a Bayesian design and analysis, as the conditions of the trial or the patient population may make this extrapolation inappropriate.

We note that although clinical trials are primarily focused on testing efficacy, they also serve the important function of providing a profile of the side effects and complications of a new therapy. Some side effects in pediatric subjects may be too rare or require too long follow-up to be revealed in a study based on this Bayesian technique. It may be important in such a case to carry out a more careful monitoring of the side effects in a post-marketing surveillance or Phase IV or V trial.

Our proposed techniques could also be used in other situations where one is trying to extend the results of a study to new populations. For instance, pharmaceutical companies often have to decide whether to test an approved drug in a new population, the often-called phase IIIB trial. Using our technique, by leveraging the data from the previous trial, they could get enough data from a relatively small study to decide whether to go on to larger registration trials. This method could also be used in a registration trial itself, although the subjectivity in the choice of might be a problem for regulators.

We have proposed a Bayesian approach for formalizing what pediatricians do when they use results from large adult trials in combination with evidence from pediatric studies to make a decision about whether a treatment should be used to treat children. Our methods can be applied to both design and analysis of trials done in these two populations. Bayesian methods allow a formalization of the belief about the relationship between the outcome of treatment in the two populations, which is a strength in that it translates the discussion to a more quantitative comparison. However, it also represents the challenge of these methods both in communicating the design and analysis with medical colleagues and in determining the correct prior to use. We have tried to respond to this issue by framing the relationship in terms of a single parameter that can be used graphically and descriptively to aid the discussion. It is our hope that this approach may increase the use of Bayesian methods in the arena of pediatric clinical research, which will ultimately increase the chance that pediatric clinical trials will be carried out and reported in way that convinces care-givers and ultimately improves pediatric care.