A Subset-Based Approach Improves Power and Interpretation for the Combined Analysis of Genetic Association Studies of Heterogeneous Traits

Abstract

Pooling genome-wide association studies (GWASs) increases power but also poses methodological challenges because studies are often heterogeneous. For example, combining GWASs of related but distinct traits can provide promising directions for the discovery of loci with small but common pleiotropic effects. Classical approaches for meta-analysis or pooled analysis, however, might not be suitable for such analysis because individual variants are likely to be associated with only a subset of the traits or might demonstrate effects in different directions. We propose a method that exhaustively explores subsets of studies for the presence of true association signals that are in either the same direction or possibly opposite directions. An efficient approximation is used for rapid evaluation of p values. We present two illustrative applications, one for a meta-analysis of separate case-control studies of six distinct cancers and another for pooled analysis of a case-control study of glioma, a class of brain tumors that contains heterogeneous subtypes. Both the applications and additional simulation studies demonstrate that the proposed methods offer improved power and more interpretable results when compared to traditional methods for the analysis of heterogeneous traits. The proposed framework has applications beyond genetic association studies.

Introduction

Meta-analysis offers a powerful tool for combining distinct genome-wide association studies (GWASs). Recent reports^1,2 have yielded additional discoveries when the underlying studies were relatively homogeneous, but major methodological challenges have emerged as the field moves toward combining studies from distinctly different populations and study designs. Most importantly, a new approach is needed for combining existing GWASs of distinct but putatively related traits that can provide insights into pleiotropic effects^2–6 of known susceptibility loci and aid the discovery of novel susceptibility regions affecting multiple traits. Although standard approaches to meta-analysis work well when GWASs are combined so that the average effect of a SNP marker on a single trait can be measured, these methods are not optimal for the analysis of distinct traits for which the effect of individual susceptibility loci manifests only in a specific subset or in different directions for different traits.

Similar statistical issues arise in the analysis of case-control studies in which cases comprise distinct subtypes with heterogeneous genetic architecture. For example, in recent studies of select cancers,^7–9 histologically distinct subtypes exhibit both shared and different genetic susceptibilities. Accordingly, an overall “pooled” case-control analysis reduces the power for detecting susceptibility loci specific to certain subtypes.¹⁰ Restriction of the analysis to individual subtypes improves the power for detecting specific associations but can lose the opportunity for examining how loci associate with more than one subtype. The tradeoff between combining and separating (“lumping” versus “splitting”) attains higher specificity at the cost of a reduction in the sample size. An agnostic approach that preserves the comprehensive perspective with the likely specificity of effects would be better.

In this report, we offer an agnostic approach that generalizes standard fixed-effects meta-analysis by allowing some subset of the studies to have no effect. The method explores all possible subsets of “non-null” studies to identify the strongest association signal and then evaluates the significance of the signal while accounting for multiple tests required by the subset search. We use modern statistical theory for tail-probability approximation to develop a multiple-testing adjustment procedure that can efficiently account for correlation among different test statistics without resorting to computationally expensive resampling techniques. We constructed a one-sided version of this method by limiting the space of hypotheses tested, i.e., by only exploring models in which all non-null studies have effects in the same direction. We further developed a two-sided version of the method to allow non-null studies to have effects in opposite directions. We also provide a more general formulation of the methodology that allows powerful pooled analysis in the context of a single case-control study in which cases can consist of distinct disease subtypes. This permits both case-control and case-case comparisons (among subsets of disease subtypes) to detect the strongest association signals.

We present simulation studies to explore the power of the proposed method in the presence of heterogeneity. The results indicate that the proposed method gains substantial power—sometimes approaching between 100% and 500%—over some of the alternatives. The method also performs well in distinguishing the subsets of associated and unassociated traits for a specific variant.

Two illustrative applications of the method are shown. In the first, we examined secondary effects of established cancer susceptibility SNPs by using summary results of GWASs of six distinct cancers involving a total of 21,473 cases and 25,891 controls. The analysis identified a number of known secondary effects as well as a number of promising novel secondary effects. In another application, we analyzed seven known susceptibility SNPs for glioma (MIM 137800), a form of brain tumor, by using new GWAS data from 1,856 glioma cases and 4,955 controls from the GliomaScan Consortium. Compared with standard case-control analysis, the proposed method, which accounts for subtype heterogeneity, produced much stronger evidence of replication for two of the SNPs (p values decreased by 100- and 10,000-fold, respectively).

We conclude the paper by considering further improvements of the method that could use restricted and/or weighted subset searches in order to explicitly incorporate prior plausibility.

Material and Methods

Subset-Based Meta-Analysis

We describe the methods by assuming that summary-level data are available from individual studies (of possibly heterogeneous traits) that participate in the meta-analysis. Let $\left({\beta }_k,s_k\right),k=1,\mathrm{\dots },K$ denote the estimates of regression parameter and its standard error for a given SNP from each of K different studies. In standard fixed-effect meta-analysis,¹¹ the association for the SNP is tested on the basis of a weighted combination of the Z statistics, $Z_k={\beta }_k/s_k$, of the form $Z_{meta}={\sum }_{k=1}^K{w}_k{Z}_k$, in which $w_k$ is chosen so that $Var\left(Z\right)={\sum }_{k=1}^K{w}_k^2=1$. Under the assumption of a fixed effect of the SNP across all studies, the optimal weights are given by $w_k=\left(1/s_k\right)/\left(1/\sqrt{{\sum }_{k=1}^{K}1/s_k^2}\right)$, which is known to produce a result that is asymptotically equivalent to that of a pooled analysis of the studies.

$$Z_{meta}=\frac{\sum _{k=1}^K{Z}_k/s_k}{\sqrt{1/s_k^2}}$$

If covariate adjustments are similar across studies, then $s_k\propto 1/\sqrt{n_k}$, where $n_k$ is the sample size for the $k^{\text{th}}$ study, and thus, simple weights of the form $w_k=\sqrt{{\pi }_k}$, in which ${\pi }_k=n_k/{\sum }_{k=1}^K{n}_k$, are close to optimal.¹² For case-control studies with unequal numbers of cases and controls, such optimal weights could be defined in terms of an “effective sample size,” which is the harmonic mean of the number of cases and controls. If there are shared subjects among studies, then $Z_{meta}$ should be appropriately standardized so that the covariance between Z statistics across studies (see below) can be accounted for.

For the subset-based meta-analysis, we propose evaluating the evidence of the association for a SNP for any given subset S of the studies on the basis of the Z statistic

$$Z\left(S\right)=\sum _{k\in S}\sqrt{{\pi }_k\left(S\right)}{Z}_k,$$

in which $\pi \left(S\right)=n_k/{\sum }_{k\in S}{n}_k$ denotes the sample size for the $k^{\text{th}}$ study relative to the total sample size for the given subset S. More generally, the weights for the subset-based meta-analysis can be taken proportionally to $1/s_k$ as discussed above. We propose that the overall evidence for the association of the SNP be evaluated on the basis of

$$Z_{\text{max}-\text{meta}}=ma{x}_{S\in \mathit{S}}\left|Z\left(S\right)\right|,$$

i.e., with the use of the maximum (in absolute value) of the subset-specific Z statistics over the class S of all possible $2^K-1$ subsets of the K studies. When K is large, the number of possible subsets grows exponentially. The computation of $Z_{\text{max}-\text{meta}}$, however, can be done rapidly given that the evaluation of each $Z\left(S\right)$ simply involves taking a different weighted sum of precomputed quantities.

Under the null hypothesis of no association for the SNP in any of the individual studies, the vector of test statistics $Z\left(S\right)$ for different values of S should follow a multivariate normal distribution with a mean of zero and unit variance for each component and with covariance between a pair of subsets A and B of the form

$$Cov\left\{Z\left(A\right),Z\left(B\right)\right\}=\sum _{k\in A,B}\sqrt{{\pi }_k\left(A\right)}\sqrt{{\pi }_k\left(B\right)}+\sum _{l\in A\backslash B}\sum _{m\in B\backslash A}\sqrt{{\pi }_l\left(A\right)}\sqrt{{\pi }_m\left(B\right)}Cov\left(Z_l,Z_m\right).$$

If all of the individual studies are independent, i.e., if they don't have any shared subjects between them, then the second term in the above sum disappears. If the individual studies are not independent, it is possible to obtain analytic expressions for covariance terms on the basis of information on shared subjects.¹³ Later in this section, we provide a general formula for such covariance terms for case-control studies when cases or/and controls are shared between certain studies.

Once the multivariate distribution of subset-specific Z statistics is characterized as above, the next task is to obtain the distribution of the maximum. In this report, we exploit some recent theory for tail approximations for multivariate distributions to obtain analytic but sharp upper bounds for the p values of the proposed test statistics. The discrete local maxima (DLM) method¹⁴ gives an accurate way of estimating tail probabilities of a test statistic (e.g., a Z score) that is maximized over a grid. It takes advantage of the local correlation structure of the statistics over neighboring grid points. In our application, the grid points represent different subsets, and two subsets are defined as neighbors if one can be obtained from the other when a single study is added or dropped.

The DLM-based approximate p value for the one-sided test with an observed test statistic $Z_{\text{max}-\text{meta}}=T$ is given by (see Appendix B)

$$P_{\text{DLM}}=\sum _{s\in \mathit{S}}\underset{T}{\overset{\mathrm{\infty }}{\int }}2pr\left(\text{neighboring}\text{subsets}\text{have}\text{absolute}Z\text{score}<z|Z_s=z\right)\varphi \left(z\right)dz,$$

where $\varphi (.)$ denotes the standard normal density and S indexes all possible subsets involved in the maximum. Further invoking the so-called “separability” assumption,¹⁴ which is essentially that the neighboring subsets are conditionally independent conditional given the current subset, the above p value can be approximated by

$${\tilde{P}}_{\text{DLM}}=\sum _{s\in \mathit{S}}\underset{T}{\overset{\mathrm{\infty }}{\int }}2\prod _{k=1}^{K}pr\left(\left|Z_{s\pm k}\right|\text{<}z|Z_s=z\right)\varphi \left(z\right)dz.$$

Separability in this context can be justified by the conservativeness of the above approximation (Appendix D). The conditional probabilities in the last expression can be evaluated with a univariate conditional normal distribution in which covariances between subsets are calculated on the basis of formulae given in the next section. For more details on the derivation and discussion of the assumptions made, see Appendix B. Numerical investigations with the use of simulation studies demonstrate that the above procedure can maintain desired type-I error rates for all of the different subset-based methods considered (Tables S4 and S5, available online).

Two-Sided Tests

To construct a powerful two-sided statistic for the detection of effects in opposite directions, we search for subsets of studies that show the strongest association signals separately in positive and negative directions to obtain $Z_{\max ,+}$ and $Z_{\max ,-}$, respectively. We then aim to combine the two statistics by using a chi-square method. To circumvent the problem of dealing with a complex negative correlation between $\left|Z_{\max ,+}\right|$ and $\left|Z_{\max ,-}\right|$, we first evaluate the p values, namely ${\tilde{P}}_{DLM}^{+}$ and ${\tilde{P}}_{DLM}^{-}$, of the two tests by conditioning on the observed signs of the Z statistics of the individual studies. These conditional p values, which are obtained by a minor modification of the aforementioned DLM method (see Appendix B), can be shown to be distributed independently of one another under the assumption that the individual studies are independent. Thus, they provide a convenient way of combining the association signals with the use of Fisher's method,¹⁵ i.e.,

$$Z_{\max -\text{meta}}^{\left(2\right)}=-2\left[\log {\tilde{P}}_{DLM}^{+}+\log {\tilde{P}}_{DLM}^{-}\right]\text{and}{\tilde{P}}_{DLM}^{\left(2\right)}=P\left({\chi }_4^2>Z_{\max -\text{meta}}^{\left(2\right)}\right).$$

When all the observed association signals are on one side (say positive), we use $Z_{\text{max}-\text{meta}}^{\left(2\right)}=-2\log {\tilde{P}}_{DLM}^{+}$ and ${\tilde{P}}_{DLM}^{\left(2\right)}={\tilde{P}}_{DLM}^{+}$.

Analysis of Case-Control Studies with Heterogeneous Disease Subtypes

We adapt the proposed method to account for heterogeneity among disease subtypes within a single case-control study. We consider two types of subset-based analysis. In one (“case-control”), we compare each subset of the disease subtypes with the fixed control group. In another (“case-complement”), we compare each subset of the disease subtypes with its complementary subset that includes the common control group as well as the other case subtypes. The latter approach is potentially more powerful given that each subset of cases is being compared with a larger pool of “controls.” For either of these analyses, it is possible to characterize the multivariate distribution of Z statistics for all the different subset-based tests, and one can therefore use the procedure described above to assess the significance of the maxima of these subset-based tests. If $Z\left(A\right)$ and $Z\left(B\right)$ denote the Z statistics for the association test for a SNP from case-control studies A and B with an arbitrary amount of overlap between subjects, then, under the null hypothesis of no association and the assumption that there is no covariate adjustment, the correlation between the statistics is given by

$$Corr\left\{Z\left(A\right),Z\left(B\right)\right\}=\sqrt{\frac{n_A^{\left(1\right)}{n}_A^{\left(0\right)}}{N_A}}\sqrt{\frac{n_B^{\left(1\right)}{n}_B^{\left(0\right)}}{N_B}}\left[\frac{n_{AB}^{\left(11\right)}}{n_A^{\left(1\right)}{n}_B^{\left(1\right)}}-\frac{n_{AB}^{\left(10\right)}}{n_A^{\left(1\right)}{n}_B^{\left(0\right)}}-\frac{n_{AB}^{\left(01\right)}}{n_A^{\left(0\right)}{n}_B^{\left(1\right)}}+\frac{n_{AB}^{\left(00\right)}}{n_A^{\left(0\right)}{n}_B^{\left(0\right)}}\right],$$

where $n_A^{\left(1\right)}$, $n_A^{\left(0\right)}$, and $N_A$ are the number of cases, controls, and subjects, respectively, in study A (and in study B with corresponding notation) and $n_{AB}^{\left(ij\right)}$ denotes the number of subjects with different phenotype categories $\left(i,j\right)\in \left(0,1\right)$ who overlap between studies A and B. For example, $n_{AB}^{\left(00\right)}$ denotes the number of shared controls between studies A and B, and $n_{AB}^{\left(10\right)}$ denotes the number of individuals who are treated as cases in study A but as controls in study B. Similar analytic expressions for covariances have been derived previously for special cases.^13,16 Once the correlation structure between the Z scores for case-control or case-complement analysis of disease subtypes is obtained as above, the one-sided-subset search procedure is used, and p values are approximated with the DLM procedure (see Appendix C).

Restricted and Weighted Subset Search

The proposed testing framework can allow restricted and/or weighted subset searches that could incorporate prior plausibility of models. For the analysis of ordered disease subtypes, for example, one might consider subset searches by cumulatively collapsing the subtypes in backward and forward directions. Such restricted analysis can not only improve the power of the detection of overall association by reducing the number of tests compared to an agnostic search but also lead to findings that are easier to interpret. The DLM procedure used for the evaluation of p values extends to such restricted searches with appropriate modifications for the “class of all subsets” and the definition of “neighboring subsets.”

In certain applications, one can incorporate prior knowledge, such as the degree of relatedness among traits, in the proposed analysis by using a weighted hypothesis-testing framework.^17,18

The agnostic subset-based method can be thought of as testing each subset for association while spending equal type I error for all subsets. If certain hypotheses (subsets) are more likely to be true (associated) on the basis of prior knowledge, a natural idea is to spend type I error differentially so that more plausible subsets can be tested with the use of more liberal thresholds. More formally, one can achieve this by defining a weighted test statistic for each subset as

$$T_s=\frac{p_s}{w_s}=\frac{2\left[1-\Phi \left(\left|Z_s\right|\right)\right]}{w_s},$$

where, for each subset s, $\left|Z_s\right|$ is the subset-specific meta-analysis test statistic discussed earlier, $p_s$ is the associated nominal p value, and $w_s$ is a prespecified weight. Now, an overall test statistic for detecting the strongest signal over different subsets and the corresponding p value can be defined as

$$T_{\min }^{\left(w\right)}={\min }_{s\in \mathbf{S}}{T}_s=T_{s_0}\text{and}{p}^{\left(w\right)}=pr\left(T_{\min }^{\left(w\right)}<T_{s_0}|H_0\right),$$

where $s_0=\arg {\min }_{\mathbf{S}}{T}_s$. With the use of the definitions above, the multivariate distribution of the $T_s$'s can be rewritten in terms of the associated Z scores, which have a multivariate normal distribution. Therefore, the p value $p^{\left(w\right)}$ can again be approximated with an appropriate modification of the DLM procedure.

Simulation Studies

We conducted simulation studies to evaluate the type I error and power of the various statistics discussed. In each case-control simulation, the genotype frequencies in the underlying population were assumed to be under a Hardy-Weinberg equilibrium with a minor allele frequency (MAF) of 0.3. We then induced the genotype frequencies for the cases and controls by setting a disease prevalence of 1% and a logistic linear disease model of the form

$$\mathit{log}itpr\left(D=1|G=g\right)=\alpha +\beta g,$$

where β denotes the log-OR (odds ratio) association parameter. We considered two different study settings. In the first (Table 1 and Figure 1), we considered a total of K = 5 or K = 10 independent case-control studies of possibly heterogeneous traits (each study had 2,000 cases and 2,000 controls). For each K, we assumed that a given SNP is associated with the outcome only for a fraction π (up to rounding) of the studies with π = 1/5, 2/5, 3/5, 4/5 or 1. Among studies that contained true associations, the number of studies, T₁, with a positive effect of the SNP was set such that α = T₁/K is either 1 (i.e., all effects are in the same direction) or 3/4 (i.e., some effects are in opposite directions) up to rounding. In the main simulations, we assumed that the magnitude of the effects of a SNP on the associated outcomes was constant (OR = 1.15), and we obtained the effects in opposite directions by simply reversing the sign of the log-OR coefficients. In additional simulations (Table S1 and Figure S1), we allowed heterogeneity in the effect of a SNP on the associated outcomes. In this setting, we allowed the genotype OR among positively associated traits to vary approximately in the range of 1.05 to 1.25 (a mean of 1.15).

Table 1.

Performance of the Subset-Based Test for Detection of the Truly Associated Subset of Traits

(K, T1, T2)	Sensitivity (True Positive Probability)		Specificity (True Negative Probability)
	One-Sided	Two-Sided	One-Sided	Two-Sided
5 traits: 100% positive
(5, 1, 0)	0.920	0.986	0.835	0.500
(5, 2, 0)	0.943	0.943	0.886	0.505
(5, 3, 0)	0.934	0.935	0.921	0.477
(5, 4, 0)	0.924	0.925	0.926	0.412
5 traits: 75% positive
(5, 1, 1)	0.502	0.982	0.883	0.721
(5, 2, 1)	0.621	0.971	0.906	0.745
(5, 3, 1)	0.676	0.950	0.918	0.782
10 traits: 100% positive
(10, 2, 0)	0.942	0.953	0.879	0.563
(10, 3, 0)	0.941	0.944	0.893	0.579
(10, 4, 0)	0.932	0.932	0.914	0.587
(10, 5, 0)	0.926	0.927	0.923	0.573
(10, 6, 0)	0.927	0.927	0.922	0.557
(10, 7, 0)	0.922	0.924	0.933	0.522
10 traits: 75% positive
(10, 1, 1)	0.500	0.978	0.855	0.675
(10, 2, 1)	0.621	0.973	0.877	0.698
(10, 3, 1)	0.672	0.955	0.901	0.739
(10, 3, 2)	0.566	0.934	0.907	0.778
(10, 4, 2)	0.616	0.924	0.915	0.801
(10, 5, 2)	0.656	0.933	0.927	0.825

In each simulation, a total of K = 5 or K = 10 distinct traits are analyzed (each trait has 2,000 cases and 2,000 controls). A variant of MAF = 0.3 is assumed to be associated with a subset of size T (<K) of the traits with an odds ratio of 1.15 (see Table S1 for results under heterogeneity of odds ratios). The “100% positive” sections assume that all of the associations are in the same direction, and the “75% positive” sections assume that 75% of the associations are positive and 25% are negative. The two measures of performance that are shown are (1) sensitivity (the average proportion of associated traits detected) and (2) specificity (the average proportion of null traits discarded). The following abbreviations are used: K, total number of traits analyzed (5 or 10); T₁, number of traits that are truly associated in the positive direction; and T₂, number of traits that are truly associated in the negative direction.

Figure 1.

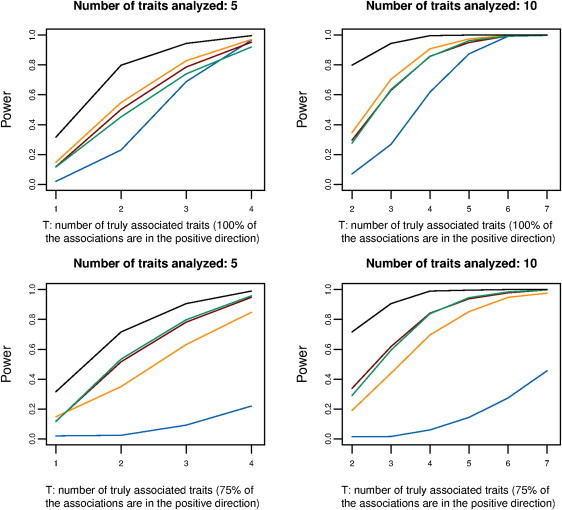
Simulation-Based Power comparison of Alternative Methods for Detecting an Overall Association

In each simulation, it is assumed that a total of five or ten distinct traits are analyzed (for each trait, there are 2,000 cases and 2,000 controls). A variant with a MAF = 0.3 is assumed to be associated with a subset of the traits (the number of such traits is shown on the x axis) and has a fixed OR of 1.15 (see Figure S1 for results under heterogeneity of ORs). The upper panels assume that all of the associations are in the same (positive) direction, and the lower panels assume that 75% of the associations are positive and 25% are negative. In addition to the two-sided (green line) and one-sided (orange line) subset-based tests, power curves are also shown for the overall meta-analysis (blue line), Fisher's combined p value method (a multiple-degree-of-freedom [df] chi-square test) (maroon line), and a “gold-standard” test (black line) that assumes that the subset of non-null traits that are truly associated with the given SNP are known a priori. All powers are shown at an alpha level of 0.001.

In the second setting (Figure 2), we considered a single case-control study with K = 7 distinct case groups (representing disease subtypes). We assumed that the study included a total of 14,000 cases (2,000 subjects in each case group) and a shared control group that contained either N₀ = 14,000 or 3,000 subjects. We allowed the number of disease subtypes, T₁, that are truly associated with a SNP to vary. For each case type, the genotype OR for a SNP was fixed at 1 for unassociated subtypes and at 1.15 for associated subtypes. For both these settings, the type I error (Tables S4 and S5) was estimated at levels 0.05, 0.01, and 0.001 with 1,000, 5,000 and 50,000 simulation replicates, respectively. Power was estimated for levels 0.001 and level 10⁻⁷ (Figure S3) with 500 replicates.

Figure 2.

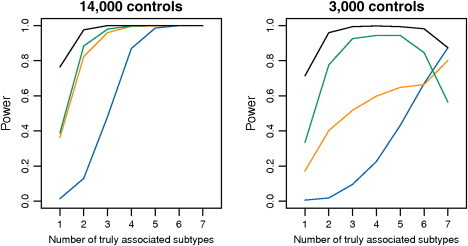
Simulation-Based Power Comparison of Alternative Methods in the Analysis of a Case-Control Study with Heterogeneous Disease Subtypes

Each simulation includes 14,000 cases equally distributed over seven subtypes. The left and right panels correspond to designs with 14,000 and 3,000 controls, respectively. A variant with a MAF of 0.3 is assumed to be associated with a subset of the subtypes (the number of such subtypes is shown on the x axis) and have a fixed OR of 1.15. The power curves for two alternative subset-based tests, “case-control” (orange line) and “case-complement” (green line), are shown along with those for an overall case-control analysis (blue line) and a “gold-standard” (black line) case-complement test that assumes that the subset of associated subtypes is known a priori. All powers are shown at an alpha level of 0.001.

Results

We conducted simulation studies to investigate the power of alternative methods to detect a susceptibility SNP by combining signals across multiple studies of heterogeneous traits. In each simulation, it is assumed that only a subset of the studies (traits) contains true signals (Figure 1). When all of the studies that contain true association signals (i.e., non-null studies) have effects in the same direction (Figure 1, upper panel) and when the number of true studies containing the signal is small relative to the total number of studies included in the analysis, we observe that substantial power is gained by both the one-sided and two-sided tests as well as the multiple-degree-of-freedom (df) chi-square test (Fisher's combined p value method) when they are compared with the standard fixed-effect meta-analysis method. For example, in the simulation setting in which ten studies are included in an analysis but only three contain true association signals, the power for detection of the SNP was 26.8% for the standard meta-analysis and was 70.4% and 63.6% for our proposed one-sided and two-sided tests, respectively. In this scenario, it is noteworthy that the one-sided test gained significant power over both the proposed two-sided and multiple-df chi-square tests. When non-null studies contained association signals in opposite directions, the power loss was more substantial for standard meta-analysis than for the alternatives (Figure 1, lower panel). In this setting, we observe that the proposed two-sided test and the multiple-df chi-square test perform similarly, and both can provide substantial gain in power over the one-sided test by combining association signals from opposite directions. Qualitatively similar behavior was observed for all methods when we allowed for a significant amount of heterogeneity among the ORs within non-null studies in the simulations (Figure S1).

It is instructive to compare the power of the proposed tests with that of the “gold-standard” test, namely one that assumes the true subset of non-null studies to be known a priori. It is evident that there is a significant loss of power for the proposed tests as a result of a multiple-testing penalty associated with comprehensive subset searches. The magnitude of such loss depends on the total number of studies included in the analysis given that the number of subsets to be explored increases exponentially with the number of studies. For example, in the setting of Figure 1, where only three studies contain the true effect, the power of the one-sided test is either 82.8% or 70.4% depending upon whether the studies are evaluated against a total of 5 or 10 studies, respectively. When the correlation between different subset analyses is accounted for, the penalty associated with multiple testing is lower than that associated with a standard Bonferroni procedure (see Figure S2), i.e., multiplication of the p value of the maximal subset by the total number of subsets. It is noteworthy that even after adjustment for a large number of comparisons, the subset-based approach, relative to standard meta-analysis, can yield a major gain in power.

We evaluate how the proposed methods perform in detecting the correct subset of non-null studies (Table 1). Regardless of the ratio of the number of null and non-null studies, the proposed methods can achieve high sensitivity and specificity as a tool for set selection. For example, in the setting of Table 1 in which five out of ten studies contained true association signals in the same direction, the proposed one-sided test had a sensitivity of 92.6% and specificity of 92.7%. In other words, the method on average included 5 × 0.921 = 4.6 of the non-null and 5 × (1−0.927) = 0.37 of the null studies in the detected set of associations. The two-sided test can have higher sensitivity in the presence of true effects in opposite directions, but it can also have lower specificity as it attempts to identify two distinct sets over which the risk of false positives is accumulated. When we allowed for heterogeneity in ORs among the non-null studies (Table S1), as expected on theoretical grounds (see Appendix A), the sensitivities of both methods were reduced, but the specificities remained comparable to those in the absence of heterogeneity.

Simulation studies also illustrate that the subset-based methods can gain power over standard approaches to the analysis of case-control studies when the cases contain etiologically heterogeneous subtypes (Figure 2). For example, in the left panel of Figure 2, when a SNP is assumed to be related to only two of seven subtypes, then the standard case-control analysis has an estimated power of approximately 13% for detecting the association. In contrast, for the same setting, the power of the subset-based analyses was >80%, which is only marginally lower than the “gold standard” test, which assumes that the correct subset is already known. The gain in power of the subset-based analysis over the standard analysis is particularly remarkable given that the former requires multiple-testing adjustment for 2⁷−1 = 127 comparisons. We observe little difference in power between the alternative “case-control” and “case-complement” approaches when the number of controls is similar to the total number of cases in the study (Figure 2, left panel). However, in the alternative setting (Figure 2, right panel), in which the number of controls is significantly smaller than the total number of cases, a substantial power advantage is observed for the “case-complement” approach.

We provide a case study to illustrate the utility of the method in the investigation of an established association of rs2736100, a SNP in the TERT (MIM 187270)-CLPTM1L (MIM 612585) area of chromosomal region 5p15.33, by using data from GWASs of six different cancers that have been reported^6,9,19–22 previously (see Table S2 for details on sample sizes). The TERT-CLPTM1L region is known to be associated with at least seven distinct cancers,^23–25 but rs2736100 (or other strongly correlated SNPs) has been associated with three cancers (lung adenocarcinoma, glioblastoma [MIM 137800], and testicular germ cell tumors [MIM 273300])^7,24–27 as well as idiopathic pulmonary fibrosis²⁸ (MIM 178500) and a form of bone-marrow-failure syndrome dyskeratosis congenita (MIM 613989).^29,30 An analysis of this SNP illustrates the operating characteristics of the method both for evaluating the overall significance of the association and for the selection of the associated subsets. A forest plot (Figure 3) shows that the minor allele for this SNP is positively associated with one cancer, negatively associated with some others, and possibly has no effect on a third group. The standard meta-analysis did not provide significant evidence for an overall association (p = 0.1432). In contrast, the one-sided test detected the cluster of cancers of the kidney (MIM 144700) and lung (MIM 211980) to be negatively associated with the SNP (p = 4.43 × 10⁻⁴). The two-sided search additionally detected pancreatic cancer (MIM 260350) as positively associated, which has been reported previously,^25,31 and increased the significance of the overall association substantially (p = 1.23 × 10⁻⁵).

Figure 3.

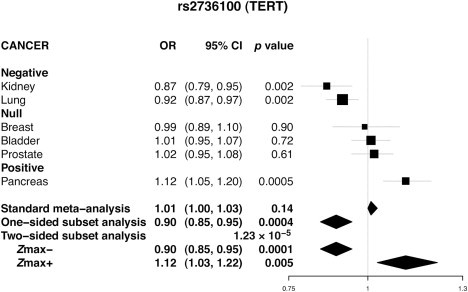
Forest Plot showing the Effect of a TERT SNP across Cancers at Six Different Sites

A two-sided subset-based test found (1) the cluster of kidney and lung cancers to be negatively associated, (2) pancreatic cancer to be positively associated, and (3) the cluster of breast, prostate, and bladder cancers to have no association. The p values for overall association with the use of standard meta-analysis, one-sided, and two-sided subset-based tests are shown along with their respective OR estimates at the bottom of the figure.

Next, we applied our new method to examine secondary effects for 89 previously reported cancer susceptibility SNPs in other GWASs³² by using the data set described above. Here, in the analysis of each SNP, we exclude the primary cancer (if it was present in our data set) for which the locus was reported originally. Our two-sided analysis identified a total of 16 loci that showed statistically significant secondary effects at a nominal level (p < 0.05) (Table 2). A number of SNPs that are in the TERT-CLPTM1L region and that have known effects across multiple cancers achieved strong statistical significance (false discovery rate [FDR]-adjusted p value < 0.05). The region generally showed consistent secondary effects for pancreatic cancer in one direction and for bladder (MIM 109800), lung, and kidney cancers in the opposite direction. In the 8q24 region (rs6983267), a SNP that has previously been identified in GWASs of colon^33,34 and prostate³⁵ (MIM 176807) cancers showed modest secondary effect for breast cancer (MIM 114480) in one direction and for lung, bladder, kidney, and pancreatic cancers in the opposite direction.

Table 2.

Results from Two-Sided Analysis of 89 Established Cancer GWAS Hits Based on Data from Six Cancer Sites^a

Rank	SNP	Original Phenotype(s)	MAF	Chr	Gene Neighborhood	Two-Sided p Value	Significant Phenotype Clustersb		FDR- Adjusted p Value
							Positively Associated	Negatively Associated
1	rs401681	basal cell carcinoma	0.45	5	CLPTM1L	5.99 × 10−8	pancreatic cancer	bladder and lung cancers	5.27 × 10−6
2	rs2736100	brain and lung cancers	0.50	5	TERT	3.61 × 10−4	pancreatic cancer	kidney cancer	1.08 × 10−2
3	rs6457327	non-Hodgkin lymphoma	0.36	6	C6orf15, PSORS1C1, CDSN	3.68 × 10−4	kidney cancer		1.08 × 10−2
4	rs2660753	prostate cancer	0.11	3	LOC285232	3.17 × 10−3		breast and kidney cancers	6.97 × 10−2
5	rs29232	nasopharyngeal cancer	0.36	6	GABBR1, SUMO2P, MOG	6.22 × 10−3		kidney cancer	9.49 × 10−2
6	rs6010620	brain cancer	0.22	20	RTEL1, TNFRSF6B	6.47 × 10−3		bladder cancer	9.49 × 10−2
7	rs10993994	prostate cancer	0.38	10	MSMB	8.62 × 10−3	bladder and kidney cancers		1.08 × 10−1
8	rs6983267	prostate and colorectal cancers	0.50	8	POU5F1B	1.08 × 10−2	breast cancer	bladder, kidney, lung, and pancreatic cancers	1.10 × 10−1
9	rs1051730	lung cancer	0.34	15	CHRNA5, CHRNA3	1.12 × 10−2	bladder and breast cancers		1.10 × 10−1
10	rs505922	pancreatic cancer	0.37	9	ABO	1.31 × 10−2		kidney and lung cancers	1.16 × 10−1
11	rs10411210	colorectal cancer	0.12	19	RHPN2	1.74 × 10−2	bladder cancer		1.39 × 10−1
12	rs258322	melanoma	0.10	16	CDK10, SPATA2L, LOC100128862	1.92 × 10−2	kidney cancer		1.41 × 10−1
13	rs9642880	bladder cancer	0.46	8		2.54 × 10−2	breast and pancreatic cancers		1.72 × 10−1
14	rs4430796	prostate cancer	0.47	17	HNF1B	4.27 × 10−2		lung cancer	2.51 × 10−1
15	rs4779584	colorectal cancer	0.22	15	SCG5, GREM1	4.63 × 10−2		kidney cancer	2.51 × 10−1
16	rs872071	chronic lymphocytic leukemia	0.49	6	IRF4	4.90 × 10−2	kidney cancer		2.51 × 10−1

For each SNP, the primary cancer(s) through which the SNP was originally discovered is (are) excluded, and a two-sided subset search is conducted among the remaining cancers. SNPs significant at a nominal 5% level are shown. The following abbreviations are used: MAF, minor allele frequency; Chr, chromosome; and FDR, false discovery rate (Benjamini-Hochberg procedure).

^aData for this example were obtained from the National Cancer Institute GWASs. See Table S2 for details on sample sizes.

^bThose clusters with a corresponding one-sided p value (i.e., p⁺ or p⁻) less than or close to 0.05.

There was clear evidence of enrichment for secondary effects of known cancer SNPs even after excluding SNPs in the known pleiotropic regions of TERT-CLPTM1L and 8q24. A binomial enrichment test comparing the numbers of observed and expected SNPs below a p value threshold of 0.05 achieved strong statistical significance (p = 9.6 × 10⁻⁵). High statistical significance (FDR-adjusted p value < 0.05) for specific secondary effects is observed for the non-Hodgkin-lymphoma-associated region PSORS1C1 (MIM 613525)-CDSN (MIM 602593) in kidney cancer and for the prostate-cancer-associated SNP rs2660753 (in chromosomal region 3p12) in kidney and breast cancers. Other notable results, although of less significance, include secondary effects of the regions MSMB (MIM 157145), ABO (MIM 110300), and HNF1B (MIM 189907), each of which has been suggested to contribute to multiple cancers or related traits.

Finally, we applied the proposed subtype-analysis approach to investigate the association for seven known glioma susceptibility loci^24,36,37 by using a new GWAS from GliomaScan, a consortium of 18 studies (Table S3). There were 1,856 cases, including those of all primary gliomas and those of a limited number of other neuroepitheliomatous tumors (ICD-O-3 code 9380-9480 and ICD-O-3 9490-9523), and 4,955 glioma-free controls at the time of selection. Detailed morphology and histology codes were requested from all cases when available. On the basis of this information, glioma cases were classified into six subgroups that are expected to be more homogenous because of their histology and behavior. These classifications were GBM (glioblastoma [ICDO-3 9440, 9441]), HGG-AST (other high-grade astrocytoma [ICDO-3 9401]), LGG-AST (low-grade astrocytoma [ICDO-3 9381, 9400, 9411, 9420, 9421, and 9424]), OLIGO (mixed oligoastrocytoma and oligodendroglioma [ICDO-3 9382, 9450, 9451, and 9460]), OTH (other low-grade and high-grade glioma [ICDO-3 9383, 9390-9394, 9470-9473, 9500, 9503, 9505, and 9506]), and UNK (glioma of unknown histology). All analyses were carried out with individual-level data and included adjustment for eigenvectors.

Standard case-control analysis via logistic regression replicated association for three of the regions, TERT, CDKN2BAS (MIM 613149), and RTEL1 (MIM 608833)-TNFRSF6B (MIM 603361), at a genome-wide significance level (p value < 10⁻⁷). Moreover, the analysis also replicated the association for two other SNPs, rs4295627 (chromosomal region 8q24.1) and rs2252586 (EGFR [MIM 131550] locus in chromosomal region 7p11.2), at a Bonferroni-adjusted significance level of 0.05/7 = 0.007. For each of the five SNPs, the new methods that incorporated subtype information replicated the association at a comparable level of significance. However, for two additional SNPs in the chromosomal regions 7p11.2 (EGFR) and 11q23.3 (PHLDB1 [MIM 612834]), the proposed methods provided much stronger evidence of replication, whereas standard analysis failed to replicate association at the significance level of 0.05/7. For rs11979158 (EGFR region), which showed a GBM-specific effect, the p value improved from 1.21 × 10⁻² for overall logistic to 5.85 × 10⁻⁴ and 5.10 × 10⁻⁴ for the subset-based case-control and case-complement analyses, respectively. For SNP rs498872 (PHLDB1 region), which showed effects on all subtypes other than GBM, a dramatic improvement in p value was observed from overall logistic regression (p value = 0.046) to subset-based case-control (p = 4.73 × 10⁻⁵) and case-complement (p = 6.75 × 10⁻⁶) analyses.

Discussion

We present a flexible and powerful approach to studying heterogeneous traits, and this approach can account for subset-specific and bidirectional effects of individual variants. Simulation studies demonstrate the utility of the methods both for the detection of susceptibility loci and for the identification of clusters of traits with shared genetic architecture. An illustrative analysis of secondary effects for known cancer SNPs via the proposed method provides preliminary evidence that pleiotropy across a set of complex phenotypes, such as common cancer sites, might be more common than previously reported.³⁸ Thus, future analyses of existing GWASs across cancer sites will be valuable for obtaining new biological insights and for uncovering novel susceptibility loci.

Subset-based tests that account for phenotypic heterogeneity have been previously proposed for linkage³⁹ and association^40,41 analyses. A challenge for their broader use has been that evaluating the significance of their resulting test statistics can be difficult. In our approach, the simple forms for the test statistics and their correlation structure enable rapid implementation of the method for large-scale studies and the evaluation of small p values that are needed for achieving significance in GWASs. We have used the DLM method to derive an analytic approximation of the p values that we have found to be both computationally and statistically efficient. It is also easy to implement alternative, possibly more exact methods for evaluating p values on the basis of the general formula we provide for the variance-covariance structure of the underlying Gaussian field for which the proposed test statistic is a maximum. In particular, stochastic alternatives such as the R package mvtnorm⁴² and importance sampling⁴³ and parametric-bootstrap and deterministic alternatives such as multiple integration⁴⁴ are available and can be implemented for the use of the analytic variance-covariance formulae we provide.

As one might expect, the greatest gain in power for our method over standard fixed-effect meta-analysis is observed when either a fraction of the studies contain true associations or select studies display effects in opposite directions (Figure 1); these two scenarios are likely for a combined analysis of several heterogeneous traits. Also as expected, there can be a substantial cost when a large fraction of the studies contain association signals and have all effects in the same direction (Figure S3). In that scenario, which might represent the truth for meta-analyses of studies of a single trait across relatively homogeneous populations, subset-based analyses can have lower power than standard meta-analysis. For example, when ten out ten studies had true effects, the power of meta-analysis (the same as “gold standard”) was 87.6%, whereas that of the one-sided subset search was 67% (see Figure S3). The magnitude of this loss increases with the total number of studies analyzed and the associated penalty due to multiple testing. Because the standard meta-analysis and the subset-based approaches have complementary strengths, it might sometimes be prudent to apply both of them to protect against loss of power. One can split the total type I error between the two procedures by using a weighted hypothesis-testing framework.

Both the simulation study (Table 2) and the illustrative example (Table 3) demonstrate that the proposed approach also has a major advantage for the analysis of case-control studies in the presence of subtype-specific effects for susceptibility SNPs. In the analysis of the GliomaScan GWAS, the proposed method convincingly replicated associations for all known susceptibility SNPs, whereas standard case-control analysis provided only weak evidence for some of the same associations. Moreover, a number of recent independent reports,^45–47 which corroborate some of the subtype-specific effects we detected for SNPs rs497756 (in CDKN2BAS in chromosomal region 9p21.3), rs4295627 (in chromosomal region 8q24.1), and rs2736100 (in TERT in chromosomal region 5p15.33), provide additional support for the validity and utility of the method. These results suggest that reanalysis of existing case-control GWASs with the use of disease subtype information can discover additional variants. For study designs with more cases than controls,⁴⁸ we observed that the subset-based case-complement approach that permits both case-case and case-control comparisons can yield substantial power over similar analysis restricted to case-control comparisons. These results have implications for sample-size considerations for future case-control studies with heterogeneous disease subtypes as well for studies in which cases have been scanned in anticipation of comparison to publicly available controls.

Table 3.

Results from Subtype Analysis of Seven Known Glioma SNPs using 6 Histologic Subtypes^a

SNP	Chr	MAF	Gene Neighborhood	Overall Logistic		Subset Search (Case-Control)			Subset Search (Case-Complement)
				p Value	OR [ 95% CI]	p Value	OR [ 95% CI]	Best Subset	p Value	OR [ 95% CI]	Best Subset
rs2736100	5	0.49	TERT	2.78 × 10−10	1.29 [1.19–1.40]	2.44 × 10−10	1.37 [1.24–1.51]	GBM, OLIGO, HGG-AST	7.69 × 10−10	1.33 [1.22–1.46]	GBM, OLIGO, HGG-AST, UNK
rs2252586	7	0.27		1.06 × 10−3	1.16 [1.06–1.26]	3.34 × 10−3	1.21 [1.06–1.36]	GBM, HGG-AST, OLIGO	3.27 × 10−3	1.19 [1.06–1.34]	GBM, HGG-AST, OLIGO, UNK
rs11979158	7	0.19	EGFR	1.02 × 10−2	0.87 [0.78–0.97]	5.85 × 10−4	0.73 [0.61–0.87]	GBM	5.10 × 10−4	0.73 [0.61–0.87]	GBM
rs4295627	8	0.2	LOC100-130376	3.55 × 10−4	1.20 [1.08–1.32]	1.30 × 10−4	1.62 [1.26–2.07]	OLIGO	5.20 × 10−4	1.35 [1.14–1.59]	OLIGO, HGG-AST, OTH, UNK
rs4977756	9	0.42	CDKN2BAS	1.71 × 10−8	1.26 [1.16–1.36]	1.21 × 10−9	1.41 [1.26–1.57]	GBM	1.13 × 10−9	1.34 [1.22–1.47]	LGG-AST, GBM, UNK
rs498872	11	0.31	ARCN1, PHLDB1	4.64 × 10−2	1.09 [1.00–1.19]	4.73 × 10−5	1.35 [1.17–1.56]	LGG-AST, OLIGO, HGG-AST, OTH	6.75 × 10−6	1.33 [1.17–1.50]	LGG-AST, OLIGO, HGG-AST, OTH, UNK
rs6010620	20	0.23	RTEL1, TNFRSF6B	5.44 × 10-13	0.69 [0.62-0.76]	1.78 × 10-11	0.67 [0.60-0.75]	GBM, HGG-AST, LGG-AST, OLIGO	2.59 × 10-11	0.69 [0.62-0.77]	GBM, HGG-AST, LGG-AST, OLIGO, OTH, UNK

The following abbreviations are used: Chr, chromosome; MAF, minor allele frequency; OR, odds ratio; CI, confidence interval; GBM, glioblastoma; OLIGO, mixed oligoastrocytoma and oligodendroglioma; HGG-AST, other high-grade astrocytoma; and UNK, glioma of unknown histology.

^aData for these results were provided by the GliomaScan Consortium (see Table S3 for details of the individual studies).

An alternative class of tests that can be used for meta-analysis of heterogeneous studies is the multiple-df chi-square tests, such as the Fisher's combined p value method.¹⁵ In their simplest form, these tests sum up individual squared association-test statistics or transformed p values over independent studies to obtain an overall signal. Such methods have been used for meta-analysis of linkage studies⁴⁹ and have also been addressed in the context of GWASs.^50,51 Although such methods and some other direction invariant tests⁵² are known to have superior power over standard meta-analysis in the presence of heterogeneity, these methods might lead to difficulty of interpretation because an overall significant association could be driven by arbitrary patterns of effects in individual studies. In meta-analysis of different studies of the same trait, for example, an overall significant association is generally not considered interesting unless the observed effects are in the same direction.

In our main simulation studies, we have compared the power of the proposed methods against that of a multiple-df chi-square test for meta-analysis of independent studies (Figure 1 and Figures S1 and S3). In additional simulations (Figures S4 and S5), we compared our method with two adaptive versions of the chi-square test, namely the adaptive rank truncated product (ARTP)⁵³ and adaptively weighted (AW) statistics.⁵⁴ These two versions also explore subsets of studies for optimization of the underlying statistics. In these comparisons, we found that, in general, the proposed method and all chi-square-type tests can have comparable power for the detection of an overall association in the presence of heterogeneity, although there are specific scenarios in which one method can outperform the other. In principle, chi-square-type tests can also be adapted to take into account directional and ordering constraints and possibly prior weighting for the improvement of the interpretation of the results, but these extensions require further developments. Additional methodological developments are also needed for the application of some of these methods for meta-analysis of correlated studies and analysis of case-control studies with heterogeneous disease subtypes. In some of these methods, however, the evaluation of p values might necessarily require expensive permutation algorithms because analytic approximations similar to those for the proposed methods might not be possible.

A recent study proposed the examination of pleiotropic effects on the basis of the enrichment of p values reaching a specific significance threshold across multiple GWASs of related traits.⁵⁵ Such enrichment methods, although appealing as simple screening tools, do not incorporate the total evidence of association from individual studies. Thus, they are likely to lose power in the presence of studies that might contain significantly stronger or weaker individual association signals than those imposed by a specific p value cutoff. The subset-based approach to meta-analysis has some similarity with a recent method⁵⁶ proposed for combining association signals across multivariate phenotypes on the basis of weighted-sum test statistics in which the weights for individual traits are estimated first on the basis of a held-out “training” dataset. The proposed method assigns 0–1 weights to individual studies depending on their exclusion or inclusion in a particular set and then maximizes the test statistics over all possible such weights to obtain the best association signal with the use of the entire dataset.

A limitation of standard meta-analysis, multiple-df tests, and some of the other methods described above is that they do not readily identify the true subset of traits putatively associated with a specific variant. In a combined analysis of heterogeneous traits, an important aspect of inference is the subset identification that is needed both for the interpretation of results and for replication efforts. Our simulation studies indicate that the proposed method performs well in this regard (Table 1 and Table S1). This capability is also illustrated in an important application in which the proposed method correctly identified signals for additional cancers in well-established multiple-cancer susceptibility regions, such as 8q24 and TERT-CLPTM1L on 5p15.33 (Table 2). We further show that the proposed method can be theoretically motivated on the basis of a likelihood-ratio statistic and is expected to have robust properties for set selection (See Appendix A).

Another major advantage of the proposed method over the aforementioned alternatives is its flexibility to enable improvement of power and interpretation by using restricted and weighted subset searches. As noted earlier, the one-sided test is one form of restricted search that ensures that the overall association is driven by a cluster of studies with effects in the same direction. Similarly, if there is a certain ordering among the disease subtypes, e.g., stages of a cancer or levels of diagnosis for a psychiatric disorder, then the subset search can be easily restricted so that the overall association is not driven by biologically implausible patterns (see Material and Methods). The proposed method can also take into account less restrictive constraints, such as prior knowledge of possible clustering of the traits, by applying continuous weights to subsets. In studies of cancers that occur at different organ sites, for example, a prior grouping or a similarity metric can be defined on the basis of studies of familial aggregation, of second cancers, and of known effects of shared biologic pathways or common environmental exposures such as smoking. A weighted hypothesis-testing framework (see Material and Methods) allows the incorporation of such information as prior weights in such a way that the overall type-I-error rate of the procedure does not depend on the correctness of these weights, and yet power can be gained when the prior information is reasonable.

In conclusion, the proposed subset-based association-testing framework has multiple attractive features for meta-analysis or pooled analysis of heterogeneous studies. The method not only has robust power for the detection of overall association but also is appealing because it leads to readily interpretable results. We provide an analytic approach for the approximation of p values that can be evaluated rapidly in large-scale studies. Furthermore, the generality and flexibility of the framework lend it potential applicability in a wide variety of settings, such as for both meta-analysis of heterogeneous traits and subtype analysis for a single trait. These methods are likely to have other applications within genomics (such as gene-environment interaction and gene-expression studies) and, more generally, even within other contexts involving extensive heterogeneity of effects. The methods proposed here have been implemented in a user-friendly R statistical package called ASSET (association analysis based on subsets).

Appendix A: Properties of $Z_{\text{max}-\text{meta}}$—Equivalence with Likelihood Ratio Test and Consistency as a Variable Selector

Let ${\hat{\beta }}_j$ denote effect-size estimates obtained from independent studies that are possibly heterogeneous, and let ${\sigma }_j^2$ be the corresponding standard errors that can be assumed to be fixed constants for the purposes of this section. Consider the following underlying model for heterogeneity:

$${\hat{\beta }}_j\sim N\left(\beta {\gamma }_j,{\sigma }_j^2\right),{\gamma }_j\in \left\{0,1\right\},j=1,\dots K,$$

where ${\gamma }_j$ is a binary indicator of the $j^{\text{th}}$ study being “non-null.” For any fixed values of the ${\gamma }_j$-s, the MLE (maximum likelihood estimate) of β is simply given by the inverse-variance weighted average

$$\hat{\beta }=\frac{\sum _{j=1}^K{\gamma }_j{\hat{\beta }}_j/{\sigma }_j^2}{\sum _{j=1}^K{\gamma }_j/{\sigma }_j^2}.$$

Because the true ${\gamma }_j$'s are not known, the likelihood needs to be maximized with respect to β and the ${\gamma }_j$'s. The corresponding LRT (likelihood ratio test) can thus be derived as

$${\text{LRT}}_{\left(\beta ,\Gamma \right)}=max\left\{1,ma{x}_{\gamma \ne 0}\frac{{\text{sup}}_{b}L\left({\hat{\beta }}_1,{\hat{\beta }}_2,\dots ,{\hat{\beta }}_K\mathrm{\mid }\beta =b,\Gamma =\gamma \right)}{L\left({\hat{\beta }}_1,{\hat{\beta }}_2,\dots ,{\hat{\beta }}_K\mathrm{\mid }\beta =0,\Gamma =\gamma \right)}\right\}=\text{exp}\left[\frac{Z_{\text{max}-\text{meta}}^2}{2}\right].$$

Next, we show that under the above model, $Z_{\text{max}-\text{meta}}$ is a consistent variable selector in the sense that in large samples, it is guaranteed to be maximized for the true value of $\Gamma ={\gamma }_0$ and will therefore correctly identify the subset of studies that contain true associations. We can write

$$pr\left({\text{argmax}}_{\gamma }Z\left(\hat{\beta },\gamma \right)\ne {\gamma }_0\right)=pr\left(\underset{\gamma \ne {\gamma }_0}{\cup }\left|Z\left(\hat{\beta },\gamma \right)\right|\text{>}\left|Z\left(\hat{\beta },{\gamma }_0\right)\right|\right)\ge \sum _{\gamma \ne {\gamma }_0}pr\left(\left|Z\left(\hat{\beta },\gamma \right)\right|\text{>}\left|Z\left(\hat{\beta },{\gamma }_0\right)\right|\right).$$

Let ${\beta }_i=E\left({\hat{\beta }}_i\right)$ denote the true population value of the effect size for the $i^{\text{th}}$ study. We assume ${\sigma }_i^2={\sigma }^2/n_i$ for some constant ${\sigma }^2$ so that the standard error for each study is inversely proportional to its sample size. We further assume that $n_i=n\times p_i$ so that as the total sample size increases, the relative proportions of sample sizes between studies converge to fixed constants. Let $n_{\gamma }={\sum }_{i\in S_{\gamma }}{n}_i$ denote the total sample size for $S_{\gamma }$. With these notations, it can be easily seen that the vector $\left\{Z\left(\hat{\beta },\gamma \right),Z\left(\hat{\beta },{\gamma }_0\right)\right\}$ converges to a bivariate normal distribution that has a mean vector $\left({\mu }_{\gamma }^{\left(n\right)},{\mu }_{{\gamma }_0}^{\left(n\right)}\right)$, unit variances, and covariance $C^{\left(n\right)}$ given by

$${\mu }_{\gamma }^{\left(n\right)}=\sum _{i\in S_{\gamma }}\frac{n_i}{\sqrt{n_{\gamma }}}\frac{{\beta }_i}{{\sigma }_i}=\sum _{i\in S_{\gamma }\cap S_{{\gamma }_0}}\frac{n_i}{\sqrt{n_{\gamma }}}\frac{{\beta }_i}{\sigma }\text{and}{C}^{\left(n\right)}=\sum _{i\in S_{\gamma }\cap S_{{\gamma }_0}}\frac{n_i}{\sqrt{n_{\gamma }}\sqrt{n_{{\gamma }_0}}}.$$

When all ${\beta }_i$'s are constant $\left(\beta \right)$ for non-null studies, we obtain

$${\mu }_{\gamma }^{\left(n\right)}=\frac{\beta }{\sigma }\frac{n_{\gamma \cap {\gamma }_0}}{\sqrt{n_{\gamma }}},{\mu }_{{\gamma }_0}^{\left(n\right)}=\frac{\beta }{\sigma }\sqrt{n_{{\gamma }_0}},\text{and}{\mu }_{{\gamma }_0}^{\left(n\right)}-{\mu }_{\gamma }^{\left(n\right)}=\frac{\beta }{\sigma }\frac{n_{\gamma \cap {\gamma }_0}}{\sqrt{n_{\gamma }}}\left(\frac{\sqrt{n_{\gamma }}\sqrt{n_{{\gamma }_0}}}{n_{\gamma \cap {\gamma }_0}}-1\right).$$

It can be seen with the Cauchy-Schwartz inequality that

$$\frac{\sqrt{n_{\gamma }}\sqrt{n_{{\gamma }_0}}}{n_{\gamma \cap {\gamma }_0}}\to \theta >1$$

for some constant θ, and ${\mu }_{{\gamma }_0}^{\left(n\right)}-{\mu }_{\gamma }^{\left(n\right)}$ therefore converges to positive or negative infinity according to whether β is positive or negative. Now, given that $Z\left(\hat{\beta },\gamma \right)$ and $Z\left(\hat{\beta },{\gamma }_0\right)$ have finite variances and covariances but the difference in their mean converges to infinity, it can be easily seen that for each $\gamma \ne {\gamma }_0$,

$$pr\left(\left|Z\left(\hat{\beta },\gamma \right)\right|\ge \left|Z\left(\hat{\beta },{\gamma }_0\right)\right|\right)\to 0,\text{and}\text{hence},pr\left({\text{argmax}}_{\gamma }Z\left(\hat{\beta },\gamma \right)={\gamma }_0\right)\to 1.$$

Following the above logic, we can further show that even when the ${\beta }_i$'s are not constant across non-null studies, $Z_{\text{max}-\text{meta}}$ is a conservative variable selector in the sense that for large samples, it will select only non-null studies, but it is not guaranteed to select all of the non-null studies. To see this, we note that, in general, for any given γ, we have ${\mu }_{\gamma }^{\left(n\right)}<{\mu }_{\gamma \cap {\gamma }_0}^{\left(n\right)}$ (in absolute value), and the difference goes to infinity as the sample size increases.

Appendix B: Discrete Local Maxima for Subset-Based Meta-Analysis

To evaluate $pr\left(\left|Z_{max}\right|={\text{max}}_{\gamma }\left|Z\left(S_{\gamma }\right)\right|>T\right)$, the DLM method relies on the observation that the event {$\left|Z\left(S_{\gamma }\right)\right|>T$ for some γ} is contained in the union of the events {$\left|Z\left(S_{\gamma }\right)\right|>T$ and $Z\left(S_{{\gamma }^{\ast }}\right)<Z\left(S_{\gamma }\right)$ for ${\gamma }^{\ast }$ neighbors of γ}. Thus, by applying Bonferroni to these unions of events, one can write

$$pr\left(\left|Z_{max}\right|={\text{max}}_{\gamma }\left|Z\left(S_{\gamma }\right)\right|\text{>}T\right)\ge \sum _{\gamma }pr\left(\left|Z\left(S_{\gamma }\right)\right|\text{>}T\text{and}\text{subset}{S}_{\gamma }\text{is}\text{a}\text{local}-\text{maximum}\text{of}\left|Z\left(S_{\gamma }\right)\right|\right)=p_{\text{DLM}}.$$

Furthermore, by integrating over possible values Z of $Z_{S_{\gamma }}$ and observing that terms corresponding to $Z_{S_{\gamma }}>T$ and $Z_{S_{\gamma }}<-T$ are equal (by symmetry), we get

$$p_{\text{DLM}}=\sum _{\gamma }\underset{T}{\overset{\mathrm{\infty }}{\int }}2pr\left(\left|Z_{S_{{\gamma }^{\ast }}}\right|\text{<}z\text{for}\text{all}\text{neighbors}{\gamma }^{\ast }\text{of}\gamma |Z_{S_{\gamma }}=z\right)\varphi \left(z\right)dz,$$ (Equation B1)

where $\varphi (.)$ is the standard normal density. By simplifying and using the “separability” assumption, we get

$$\begin{array}{c}{\tilde{P}}_{\text{DLM}}=\sum _{s\in \mathbf{S}}\underset{T}{\overset{\mathrm{\infty }}{\int }}2\prod _{k=1}^{K}pr\left(\left|Z_{s,\pm k}\right|\text{<}z\mathrm{\mid }{Z}_s=z\right)\varphi \left(z\right)dz\\ =\sum _{s\in \mathbf{S}}\underset{T}{\overset{\mathrm{\infty }}{\int }}2\prod _{k=1}^{K}pr\left(l_k\left(z\right)<Z_k<u_k\left(z\right)\mathrm{\mid }{Z}_s=z\right)\varphi \left(z\right)dz,\end{array}$$ (Equation B2)

where $Z_{s\pm k}$ denotes the $k^{\text{th}}$ neighbor of the current subset s obtained by adding the $k^{\text{th}}$ study if it is not already included and dropping it otherwise. The bounds $l_k\left(z\right)$ and $u_k\left(z\right)$ are simple linear functions of z and meta-analysis weights (see Appendix D for details). The conditional probabilities in the above expressions can be easily evaluated with a univariate conditional normal CDF (cumulative distribution function) for which the correlation is given by the formula described in the main text. In Appendix D, we show that the separability assumption is conservative when the individual studies are independent.

For the two-sided meta-analysis, we apply the above procedure to calculate the p values for the two conditional one-sided tests,$Z_{\text{max},+}$ and $Z_{\text{max},-}$. The steps for the calculations are analogous to those for the one-sided test except that all of the distributions are evaluated conditionally on the observed signs of the study-specific Z statistics.

Appendix C: Discrete Local Maxima for Subtype Analysis

Let N denote the total number of cases. Let $n_s$ be the number of cases in a subset s of the disease subtypes and g_s be the corresponding sum of genotypes for the $n_s$ subjects. Let $n_k$ be the number of cases with the $k^{\text{th}}$ subtype of the disease. We will denote the estimated minor allele frequency (MAF) of a SNP from all subjects by $\hat{p}$ and denote that from the controls by ${\hat{p}}_0$. It can be shown that in the absence of covariates and under the null hypothesis of no association, the Z scores for “case-control” and “case-complement analysis” for a given subset of disease subtypes s can be asymptotically represented as

$$\begin{array}{c}{Z}_s\approx \frac{g_s-2n_s{\hat{p}}_0}{\sqrt{2n_s^{\prime }p\left(1-p\right)}},\text{where}{n}_s^{\prime }=n_s\left(1+\frac{n_s}{n_0}\right),\text{and}\\ Z_s\approx \frac{g_s-2n_s\hat{p}}{\sqrt{2{\tilde{n}}_{s}p\left(1-p\right)}},\text{where}{\tilde{n}}_s=\frac{n_s\left(N-n_s\right)}{N},\end{array}$$

respectively. With the above representations, it is now easy to relate the Z scores for neighboring subsets with the formula

$$Z_{s\pm k}=\frac{\sqrt{n_s^{\prime }}{Z}_s\pm \sqrt{n_k^{\prime }}{Z}_k}{\sqrt{n_s^{\prime }\pm n_k\left(1\pm \frac{n_k}{n_0}\right)\pm 2\frac{n_s{n}_k}{n_0}}}$$

for case-control analysis and with the formulae

$$Z_{s+k}=\frac{\sqrt{{\tilde{n}}_s}{Z}_s+\sqrt{{\tilde{n}}_k}{Z}_k}{\sqrt{{\tilde{n}}_s+{\tilde{n}}_k-2\frac{n_k{n}_s}{N}}}\text{and}{Z}_{s-k}=\frac{\sqrt{{\tilde{n}}_s}{Z}_s-\sqrt{{\tilde{n}}_k}{Z}_k}{\sqrt{{\tilde{n}}_s-{\tilde{n}}_k+2\frac{n_k\left(n_{s\backslash k}\right)}{N}}}$$

for case-complement analysis. Above, $Z_k=Z_{\left\{k\right\}}$ corresponds to the Z score associated with a single disease subtype k. These representations imply that each $Z_s$ is a linear combination of its constituent $Z_k$'s with positive weights and that $Z_{s\pm k}$'s are conditionally independent given $Z_s$ and ${\hat{p}}_0$ (or $\hat{p}$). It is difficult to prove the conservativeness of the separability assumption for subtype analysis unconditionally. Using the above facts, the argument in Appendix D proves this conservativeness conditionally given ${\hat{p}}_0$ (or $\hat{p}$). Accordingly, one can compute bivariate integrals in Equation B2 by conditioning on a Z score $Z_0$ corresponding to the departure of ${\hat{p}}_0$ (or $\hat{p}$) from the true MAF p. However, in our simulations, we observed that the usual DLM approximation with univariate integrals provided adequate (i.e., conservative) p values for subtype analysis.

Appendix D: Conservativeness of the Separability Assumption

Here, we prove the conservativeness of the “separability” assumption in going from Equation B1 to Equation B2, and hence, the overall conservativeness of the DLM procedure for one-sided or two-sided analysis of heterogeneous traits by using independent studies. These arguments also justify the conservativeness of the separability assumption conditionally on $Z_0$ (defined in Appendix C) for the analysis of heterogeneous subtypes.

Following the notation of Appendices B and C, we note that conditional on $Z_s=z$, the events $\left\{Z_{s\pm k}>-z\right\}$ ($\left\{Z_{s\pm k}>0\right\}$ for a two-sided search) are almost sure events for large Z. Hence, it suffices to show the conservativeness for the probabilities $pr\left\{Z_{s\pm k}<z\forall k\mathrm{\mid }{Z}_s=z\right\}$ ($pr\left\{Z_{s\pm k}<z\forall k\mathrm{\mid }{Z}_s=z,Z_0=z_0\right\}$ for subtype analysis). Note that for both meta-analysis of heterogeneous traits and subtype analysis, the (asymptotic) linearity of the component Z scores implies

$$Z_{s\pm k}=w_s·Z_s\pm w_k·Z_k$$

for some positive weights $w_s$ and $w_k$ depending on sample sizes. Hence, conditional on $Z_s=z$, we can rewrite the events $\left\{Z_{s+k}<z\right\}$ and $\left\{Z_{s-k}<z\right\}$ as $\left\{Z_k<u_k\left(z\right)\right\}$ and $\left\{Z_k>l_k\left(z\right)\right\}$, in which $u_k\left(z\right)=\left(\left(1-w_s\right)z\right)/\left(w_k\right)$ and $l_k\left(z\right)=\left(\left(w_s-1\right)z\right)/\left(w_k\right)$ denote the lower and upper bounds, respectively. Below, we show that given $Z_s=z$, the K events $\left\{Z_{s\pm k}<z\right\}$ are either independent or negatively correlated to each other (conditional on $Z_0=z_0$ in the case of subtype analysis).

Consider the pair of events $\left\{Z_{s-k}<z\right\}$ and $\left\{Z_{s-k^{\prime }}<z\right\}$, which correspond to $Z_k$ and $Z_{k^{\prime }}$, respectively, being dropped from the current subset. These events translate to $\left\{Z_k>l_k\left(z\right)\right\}$ and $\left\{Z_{k^{\prime }}>l_{k^{\prime }}\left(z\right)\right\}$, which are negatively correlated events (because $Z_k$ and $Z_{k^{\prime }}$ are part of the positively weighted linear combination $Z_s$, which is fixed at z). Similarly, the events $\left\{Z_{s+k}<z\right\}$ and $\left\{Z_{s+k^{\prime }}<z\right\}$, corresponding to $Z_k$ and $Z_{k^{\prime }}$, respectively, being added to the current subset translate to $\left\{Z_k<u_k\left(z\right)\right\}$ and $\left\{Z_{k^{\prime }}<u_{k^{\prime }}\left(z\right)\right\}$, respectively. These are independent given that the weighted sum $Z_s=z$ does not involve $Z_k$ and $Z_{k^{\prime }}$. Finally, the events $\left\{Z_{s+k}<z\right\}$ and $\left\{Z_{s-k^{\prime }}<z\right\}$ translate to $\left\{Z_k<u_k\left(z\right)\right\}$ and $\left\{Z_{k^{\prime }}>l_{k^{\prime }}\left(z\right)\right\}$. Again, these are independent given that $Z_s=z$ does not constrain $Z_k$.

Thus, in each case, either independent or negatively correlated events are being separated as a product, which implies that each probability term is being approximated conservatively.

Web Resources

The URLs for data presented herein are as follows:

• Biowulf Linux cluster, http://biowulf.nih.gov

• Online Mendelian Inheritance in Man (OMIM), http://www.omim.org

• R package ASSET, http://dceg.cancer.gov/bb/tools/asset