Time-dependent cross ratio estimation for bivariate failure times

Abstract

In the analysis of bivariate correlated failure time data, it is important to measure the strength of association among the correlated failure times. One commonly used measure is the cross ratio. Motivated by Cox’s partial likelihood idea, we propose a novel parametric cross ratio estimator that is a flexible continuous function of both components of the bivariate survival times. We show that the proposed estimator is consistent and asymptotically normal. Its finite sample performance is examined using simulation studies, and it is applied to the Australian twin data.

1. Introduction

Statistical methods for analysing bivariate correlated failure time data are of increasing interest in many medical investigations. In the analysis of such data, it is important to measure the strength of association among the correlated failure times. Several global dependence measures have been proposed, such as Kendall’s τ and Spearman’s correlation coefficient (Hougaard, 2000, Ch. 4), and the weighted average reciprocal cross ratio (Fan et al., 2000a,b). Local dependence measures have also been proposed. One commonly used measure is the cross ratio, which is formulated as the ratio of two conditional hazard functions and thus measures the relative hazard of one time component conditional on another time component at some time-point and beyond (Kalbfleisch & Prentice, 2002, Ch. 10).

Global measures, though quantitatively simple, are not always desirable because they can mask important features of the data and often do not address scientific questions of interest when the dependence of two event times is time dependent and modelling such dependence is of major interest (Nan et al., 2006). In such settings, the cross ratio function is of particular interest because of its attractive hazard ratio interpretation. Clayton (1978) considered a constant cross ratio that yields an explicit closed-form bivariate survival function, the Clayton copula model. Reparameterizing the Clayton model, Oakes (1982, 1986, 1989) analysed bivariate failure times in the frailty framework, where a common latent frailty variable induces correlation between survival times. Though bivariate distributions induced by frailty models generate a rich subclass of Archimedean distributions, these models provide only restrictive approaches to modelling the time-dependent cross ratio, because in the Archimedean distributions it is completely dictated by the specification of the copula and the marginal distributions. For the Clayton and gamma frailty models, many likelihood-based estimating methods have been developed for parameter estimation, see, e.g., Clayton (1978), Oakes (1986), Shih & Louis (1995), Glidden & Self (1999) and Glidden (2000). Such methods may also be applied to other copula models.

To estimate the cross ratio as a function of time, Nan et al. (2006) partitioned the sample space of the bivariate survival time into rectangular regions with edges parallel to the time axes and assumed that the cross ratio is constant in each rectangular region. A Clayton-type model was established for the joint survival function, and a two-stage likelihood-based method similar to that of Shih & Louis (1995) was used to estimate the piecewise constant cross ratio. In the context of competing risks, Bandeen-Roche & Ning (2008) proposed a nonparametric method for estimating the piecewise constant time-varying cause-specific cross ratio using the binned survival data based on the same partitioning idea for the sample space. Time-varying cross ratios can also be estimated from a copula model. Recently, Li & Lin (2006) and Li et al. (2008) characterized the dependence of bivariate survival data through the correlation coefficient of normally transformed bivariate survival times. Such methods, however, require assumptions of specific copula models for the joint survival function, for which appropriate model checking techniques are lacking.

We are not aware of any method in the literature on estimating the cross ratio as a flexible continuous function of both time components without modelling the joint survival function. The methods of estimating weighted reciprocals of cross ratios proposed by Fan et al. (2000a, 2000b) cannot be applied to the estimation of the cross ratio itself. In this article, we consider a parametric model for the log-transformed cross ratio, a polynomial function of the two time components, for censored bivariate survival data. Other parametric models can also be considered. Since a closed form of the joint survival function is not available for the cross ratio with a general polynomial functional form of times, it is difficult to develop a likelihood-based approach for estimation. Instead we construct an objective function for the cross ratio parameters, which we call the pseudo-partial-likelihood, by mimicking the partial-likelihood of Cox’s proportional hazards model (Cox, 1972). Specifically, we treat whether an event happens at a time-point or beyond along one time axis as a binary covariate and the other time component as the survival outcome variable, and then construct the corresponding partial likelihood function. Such a construction does not need models for either the joint or the marginal survival function, and it is robust against model misspecification. We obtain the parameter estimates by maximizing the pseudo-partial likelihood function. We show that the estimator is consistent and asymptotically normal. The proofs rely heavily on empirical process theory. The proposed methodology is readily extendable to the estimation of an arbitrary cross ratio function using tensor product splines.

2. The cross ratio function

Let (T₁, T₂) be a pair of absolutely continuous correlated failure times. The cross ratio function of T₁ and T₂ (Clayton, 1978; Oakes, 1989) is defined as

$$\theta (t_1,t_2)=\frac{{\lambda }_2(t_2|T_1=t_1)}{{\lambda }_2(t_2|T_1>t_1)}=\frac{{\lambda }_1(t_1|T_2=t_2)}{{\lambda }_1(t_1|T_2>t_2)},$$ (1)

where λ₁ and λ₂ are the conditional hazard functions of T₁ and T₂, respectively. The second equality in (1) can be verified via direct calculation using Bayes’ rule. The two event times T₁ and T₂ are independent if θ(t₁, t₂) = 1, positively correlated if θ (t₁, t₂) > 1, and negatively correlated if θ (t₁, t₂) < 1 (Kalbfleisch & Prentice, 2002). Following Clayton (1978) and Oakes (1982, 1986, 1989), model (1) gives rise to the second-order partial differential equation

$$\frac{{\partial }^{2}h}{\partial t_1\partial t_2}+(\theta -1)\frac{\partial h}{\partial t_1}\frac{\partial h}{\partial t_2}=0,$$ (2)

where h(t₁, t₂) = − log{S(t₁, t₂)} and S(t₁, t₂) is the joint survival function of (T₁, T₂) at (t₁, t₂).

When θ is constant, it can be shown that (2) has a unique solution, the Clayton copula (Clayton, 1978). When θ is piecewise constant on a grid of the sample space of (T₁, T₂), (2) is also solvable (Nan et al., 2006). The solution is similar to the Clayton model within a rectangular region, but with left truncation at the lower left corner of the region, and all the pieces of the joint survival function are interconnected through survival functions on the edges of the grid. Once the analytical form of the joint survival function is available, it becomes possible to develop a likelihood-based approach. For example, Nan et al. (2006) extended the two-stage approach of Shih & Louis (1995) to the estimation of the piecewise constant cross ratio.

On the one hand, obtaining an explicit analytical solution of (2) for an arbitrary cross ratio function is impossible, even when θ is a simple linear function of t₁ and t₂. On the other hand, computing the cross ratio through directly modelling the joint survival function S(t₁, t₂) using, for example, a copula model, may not be desirable because the model assumption can be too strong and rigorous model checking tools are lacking. Instead, we propose a pseudo-partial likelihood approach to estimate the cross ratio θ that is a continuous function of (t₁, t₂). In particular, we consider a parametric model

$$\beta (t_1,t_2;\gamma )=\text{log}\{\theta (t_1,t_2;\gamma )\},$$ (3)

where γ is a finite-dimensional Euclidean parameter. It is straightforward to extend the parametric model to a nonparametric model using tensor product splines. In this article, we focus on the parametric model, because it can approximate a smooth function arbitrarily well in practice and is advantageous in theoretical investigation.

3. The pseudo-partial likelihood method

Consider a pair of correlated continuous failure times (T₁, T₂) that are subject to right censoring by a pair of censoring times (C₁, C₂). Assume censoring times are independent of failure times. Suppose we observe n independent and identically distributed copies of (X₁, X₂, Δ₁, Δ₂), where X₁ = min(T₁, C₁), X₂ = min(T₂, C₂), Δ₁ = I (T₁ ⩽ C₁) and Δ₂ = I (T₂ ⩽ C₂). Here I (·) denotes the indicator function. We further assume that there are no ties among observed times for each of the two time components.

In view of the difficulty in directly solving (2) analytically, in this section we propose a simple pseudo-partial likelihood method motivated by Cox’s partial likelihood idea, treating one time component as the covariate. Using epidemiological terminology, if we treat {j : T_1j = t₁} and {j : T_1j > t₁} as exposure and nonexposure groups respectively, then from the first equality in (1), the cross ratio θ (t₁, t₂) becomes the hazard ratio of T₂ between these two groups. Fix t₁ at X_1i. If X_1i is a censoring time, then the exposure group becomes empty due to the no-tie assumption. Thus we need X_1i to be a failure time, and then the conditional hazard of subject k with X_1k ⩾ t₁ at t₂ = X_2j is simply λ₂(X_2j | X_1j > X_1i) θ (X_1i, X_2j)^{I(X_1k = X_1i)Δ_1i}. By mimicking the partial likelihood idea, we can construct an objective function as follows with t₁ = X_1i

$$\begin{array}{l}\prod _{j=1}^n{\left\{\frac{{\lambda }_2(X_{2j}|X_{1j}>X_{1i})\theta {(X_{1i},X_{2j})}^{I(X_{1j}=X_{1i}){\Delta }_{1i}}}{{\Sigma }_{X_{2k}⩾X_{2j}}I(X_{1k}⩾X_{1i}){\lambda }_2(X_{2j}|X_{1j}>X_{1i})\theta {(X_{1i},X_{2j})}^{I(X_{1k}=X_{1i}){\Delta }_{1i}}}\right\}}^{I(X_{1j}⩾X_{1i}){\Delta }_{2j}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=K_n\prod _{j=1}^n{\left\{\frac{\theta {(X_{1i},X_{2j})}^{I(X_{1j}=X_{1i})}}{{\Sigma }_{X_{2k}⩾X_{2j}}I(X_{1k}⩾X_{1i})\theta {(X_{1i},X_{2j})}^{I(X_{1k}=X_{1i})}}\right\}}^{I(X_{1j}⩾X_{1i}){\Delta }_{2j}{\Delta }_{1i}},\end{array}$$

where $K_n={\prod }_{j=1}^n{\left\{{\sum }_{X_{2k}⩾X_{2j}}I(X_{1k}⩾X_{1i})\right\}}^{I(X_{1j}⩾X_{1i}){\mathrm{\Delta }}_{2j}({\mathrm{\Delta }}_{1i}-1)}$ is a constant independent of θ and can be ignored. In the above objective function, the indicators I (X_1j ⩾ X_1i) in the outer exponent and I (X_1k ⩾ X_1i) in the denominator exclude subjects who do not belong to either the exposure or the nonexposure group. Under the no-tie assumption, we know that there is either one subject or none from the exposure group appearing in the risk set. If one such subject appears, it must satisfy k = i and X_2i ⩾ X_2j, so the denominator becomes N (X_1i, X_2j) − 1 + θ (X_1i, X_2j), where $N(t_1,t_2)={\sum }_{k=1}^{n}I(X_{1k}⩾t_1,X_{2k}⩾t_2)$ denotes the size of the risk set; otherwise, the denominator equals N(X_1i, X_2j). So we can rewrite the above objective function by dropping K_n as

$$\prod _{j=1}^n{\left[\frac{\theta {(X_{1i},X_{2j})}^{I(X_{1j}=X_{1i})}}{\{N(X_{1i},X_{2j})-I(X_{2j}⩽X_{2i})\}+\theta (X_{1i},X_{2j})I(X_{2j}⩽X_{2i})}\right]}^{I(X_{1j}⩾X_{1i}){\mathrm{\Delta }}_{2j}{\mathrm{\Delta }}_{1i}}.$$ (4)

The risk set at an arbitrary pair of times (t₁, t₂) may be empty, giving N(t₁, t₂) = 0. We need to exclude such situations from calculations of the above objective function, or hereafter we assume that N(t₁, t₂) ⩾ 1.

Considering the symmetric structure of the definition of θ (t₁, t₂) determined by the second equality in (1), we can construct the same objective function as (4) by switching the roles of X₁ and X₂. By multiplying (4) with its symmetric construction over all possible ways of creating the exposure and nonexposure groups, i.e. all subjects, we obtain the pseudo-partial likelihood function

$$L_n=\prod _{i=1}^n{L}_i^{(1)}{L}_i^{(2)},$$ (5)

where $L_i^{(1)}$ is given in (4) and

$$L_i^{(2)}=\prod _{j=1}^n{\left\{\frac{\theta {(X_{1j},X_{2i})}^{I(X_{2j}=X_{2i})}}{N(X_{1j},X_{2i})-I(X_{1j}⩽X_{1i})+\theta (X_{1j},X_{2i})I(X_{1j}⩽X_{1i}}\right\}}^{I(X_{2j}⩾X_{2i}){\mathrm{\Delta }}_{1j}{\mathrm{\Delta }}_{2i}}.$$

The maximizer of (5) is called the pseudo-partial likelihood estimator.

To proceed, we replace θ by β through (3) and write l_n = n⁻¹ log L_n. Let β̇_γ (t₁, t₂; γ) = ∂β(t₁, t₂; γ)/∂γ. Differentiating l_n(γ) with respect to γ and assuming no ties among observed times, we obtain the estimating function

$$U_n(\gamma )=\partial l_n(\gamma )/\partial \gamma =U_n^{(1)}(\gamma )-U_n^{(2)}(\gamma )+U_n^{(3)}(\gamma )-U_n^{(4)}(\gamma )$$

for γ where

$$\begin{array}{l}{U}_n^{(1)}(\gamma )=U_n^{(3)}(\gamma )=\frac{1}{n}\sum _{i=1}^n{\mathrm{\Delta }}_{1i}{\mathrm{\Delta }}_{2i}{\dot{\beta }}_{\gamma }(X_{1i},X_{2i};\gamma ),\\ U_n^{(2)}(\gamma )=\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^n\frac{{\mathrm{\Delta }}_{1i}{\mathrm{\Delta }}_{2j}I(X_{1j}⩾X_{1i})I(X_{2j}⩽X_{2i})e^{\beta (X_{1i},X_{2j};\gamma )}}{N(X_{1i},X_{2j})-I(X_{2j}⩽X_{2i})(1-e^{\beta (X_{1i},X_{2j};\gamma )})}{\dot{\beta }}_{\gamma }(X_{1i},X_{2j};\gamma ),\\ U_n^{(4)}(\gamma )=\frac{1}{n}\sum _{i=1}^n\sum _{j=1}^n\frac{{\mathrm{\Delta }}_{1j}{\mathrm{\Delta }}_{2i}I(X_{2j}⩾X_{2i})I(X_{1j}⩽X_{1i})e^{\beta (X_{1j},X_{2i};\gamma )}}{N(X_{1j},X_{2i})-I(X_{1j}⩽X_{1i})(1-e^{\beta (X_{1j},X_{2i};\gamma )})}{\dot{\beta }}_{\gamma }(X_{1j},X_{2i};\gamma ).\end{array}$$

Then an estimator γ̂_n can be obtained by solving the equation U_n(γ) = 0 using the Newton–Raphson algorithm.

4. Asymptotic properties

We consider a polynomial parametric model with finite number of terms for β(t₁, t₂; γ) in (3). In particular, we assume that

$$\beta (t_1,t_2;\gamma )=\sum _{k,l}{\gamma }_{kl}{t}_1^k{t}_2^l=z{(t_1,t_2)}^{\prime }\gamma ,$$ (6)

where γ is the vector of coefficients {γ_kl} and a prime denotes matrix transpose. It is seen that β̇_γ(t₁, t₂, γ) = z (t₁, t₂) is free of γ. We have found that a cubic model with 0 ⩽ k + l ⩽ 3 in (6) often yields satisfactory estimates for smooth cross ratio functions. In this section, we provide asymptotic results for the estimation of γ in (6). Other parametric models, for example the piecewise constant model of Nan et al. (2006), can also be considered and theoretical calculations proceed similarly with modified regularity conditions that guarantee that β(t₁, t₂; γ) and β̇_γ(t₁, t₂, γ) belong to Donsker classes. For model (6) we consider the following regularity conditions.

• Condition 1. The failure times are truncated at (τ₁, τ₂), 0 < τ₁, τ₂ < ∞, such that pr(T₁ > τ₁, C₁ > τ₁, T₂ > τ₂, C₂ > τ₂) > 0.

• Condition 2. The parameter space Γ is a compact set and the true value γ₀ is an interior point of Γ.

• Condition 3. The matrix E{Δ₁Δ₂z(X₁, X₂)^⊗2} is positive definite. Here z^⊗2 = zz′.

Theorem 1. Under Conditions 1–3, the solution of U_n(γ) = 0, denoted by γ̂_n, is a consistent estimator of γ₀.

The proof of Theorem 1 follows two major steps: first we show that U_n(γ) converges to a deterministic function u(γ) uniformly, then we show that u(γ) is a monotone function with a unique root at γ₀. Consistency follows immediately. The calculation heavily involves modern empirical process theory (van der Vaart & Wellner, 1996). We refer to the Appendix and the online Supplementary Material for more details.

Theorem 2. Under Conditions 1–3, n^1/2(γ̂_n − γ₀) converges in distribution to a normal random variable with zero mean and variance I(γ₀)⁻¹ Σ (γ₀)I (γ₀)⁻¹, where I(γ₀) = 2E{Δ₁Δ₂z(X₁, X₂)^⊗2} and Σ(γ₀) is the asymptotic variance of U_n(γ₀), which is determined by (A8) in the Appendix.

The asymptotic normality in Theorem 2 can be obtained by using a Taylor expansion of U_n(γ̂_n) around γ₀. Again the calculation involves empirical process theory; a sketch of the proof is provided in the Appendix with more details in the online Supplementary Material. The asymptotic expression of Σ(γ₀) also leads to a variance estimator of n^1/2(γ̂_n − γ₀), which is given at the end of the Appendix.

5. Numerical examples

5.1. Simulations

We conduct simulations to assess the performance of the proposed method. Directly generating data from a bivariate distribution with a cross ratio function given in (6) is technically formidable because the second-order nonlinear partial differential equation (2) does not have a closed-form solution. Instead, we generate data from a given joint distribution function of (T₁, T₂). Thus our method estimates an approximation of the true cross ratio function.

We generate bivariate failure times from the same Frank family as Fan et al. (2000a, p. 347) and censoring times C₁ and C₂ from a uniform (0, 2.3) distribution, yielding a censoring rate of 40%. The estimated cross ratio is obtained using the cubic polynomial model (6) with 0 ⩽ k + l ⩽ 3 by maximizing the pseudo-partial likelihood function (5) with respect to coefficients γ. Results are averaged over 1000 simulation runs, each with a sample size of 400.

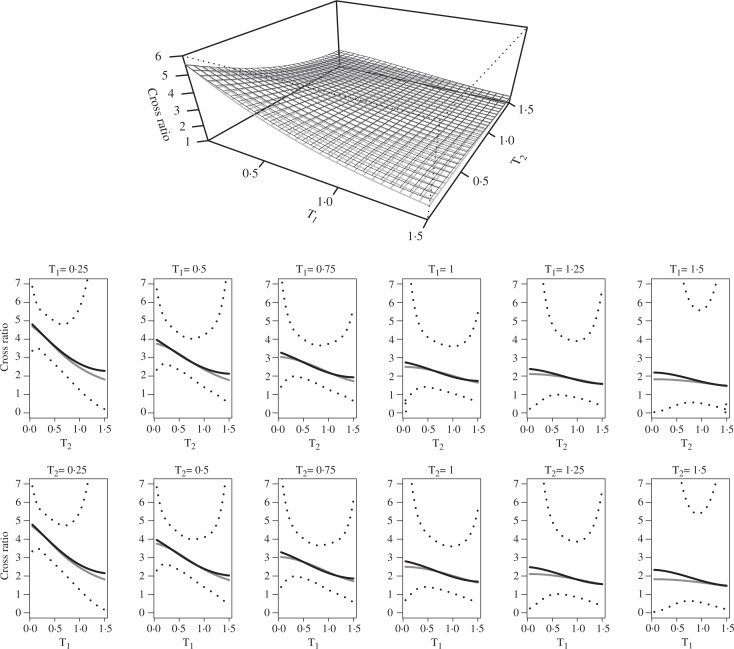
We plot the estimated surface together with the true cross ratio surface in the upper panel of Fig. 1. The lower panel gives the cross ratio as a function of one time component fixing the other time component from t = 0.25 to t = 1.50. Based on the empirical variance of γ̂, we calculate the pointwise confidence bands for β. Then by exponentiating, we obtain pointwise empirical confidence bands for θ. Figure 1 suggests that the proposed method estimates the true cross ratio of the Frank family very well, despite the fact that (6) is only an approximation to the true log cross ratio.

Fig. 1.

Cross ratio for the Frank family. A grey surface or curve is the true cross ratio and a black surface or curve is the estimated cross ratio. Dot curves in the lower panels are empirical pointwise 95% confidence bands.

To check the performance of the proposed variance estimator, we choose nine points based on the quartiles of the observed time distribution, and calculate the empirical standard error and the average of the model-based standard error estimates at each of those points together with the 95% coverage probability. Table 1 shows that the model-based variance estimators work well, with coverage probabilities close to 95% at most surveyed grid points. Bootstrap variance estimators also work well at those points, and are provided in the online Supplementary Material, but are more computationally intensive.

Table 1.

Simulation results for the Frank family

		X2 25%		X2 50%		X2 75%
X1	β	β̂avg (see, sem, cp)	β	β̂avg (see, sem, cp)	β	β̂avg (see, sem, cp)
25%	1.51	1.51 (0.12, 0.13, 96)	1.31	1.33 (0.17, 0.17, 95)	0.98	1.06 (0.35, 0.31, 91)
50%	1.31	1.33 (0.17, 0.17, 96)	1.20	1.19 (0.16, 0.16, 96)	0.94	0.95 (0.24, 0.24, 94)
75%	0.98	1.04 (0.34, 0.31, 92)	0.94	0.94 (0.24, 0.24, 95)	0.79	0.76 (0.27, 0.26, 93)

The points on both margins are the quartiles of the marginal distributions of X₁ and X₂. β, true log cross ratio; β̂_avg, average of the point estimates of β; se_e, empirical standard error; se_m, average of the model based standard error estimates; cp, 95% coverage probability.

We consider an additional simulation study to examine the proposed method for cross ratios close to 1 with a different curvature to the Frank family, which also shows that the proposed method works well. Detailed results are provided in the online Supplementary Material.

To compare the efficiency of the proposed method with the two-stage method of Nan et al. (2006), we adopt the same simulation set-up assuming that the cross ratio θ is piecewise constant over four intervals: θ = 0.9 when t₁ ∈ [0, 0.25), θ = 2.0 when t₁ ∈ [0.25, 0.5), θ = 4.0 when t₁ [0.5, 0.75), and θ = 1.5 when t₁ > 0.75. The data are generated in the same way with the same sample size and number of replications as in Nan et al. (2006). Instead of the polynomial function in (6), we use indicator functions on those four intervals to estimate θ. The comparison results are shown in Table 2. Though the two-stage method is more efficient, the loss in efficiency for our method is minor, especially at the beginning of the follow-up. Our method is not limited to the piecewise constant assumption.

Table 2.

Efficiency comparison

	Two-stage sequential method				Pseudo-partial likelihood method
θ	θ̂avg	see	seb	cpb (%)	θ̂avg	see	seb	cpb (%)	sem	cpm (%)
0.90	0.92	0.12	0.12	93	0.92	0.12	0.12	97	0.12	95
2.00	2.04	0.31	0.29	93	2.04	0.30	0.31	95	0.31	94
4.00	4.09	0.65	0.71	96	4.13	0.76	0.78	96	0.76	97
1.50	1.51	0.25	0.25	94	1.54	0.29	0.31	96	0.33	96

The left panel is taken from Nan et al. (2006). θ̂_avg, point estimate average; se_e, empirical standard error; se_b, average of the bootstrap standard error estimates using 100 bootstrap samples; se_m, average of the model-based standard error estimates; cp_b and cp_m, 95% coverage probabilities using se_b and se_m, respectively.

5.2. The Australian Twin Study

In this section, we present our real data analysis of ages at appendectomy for participating twin pairs in the Australian Twin Study (Duffy et al., 1990). The same data were analysed in Prentice & Hsu (1997) and Fan et al. (2000a,b). Primarily, the Australian Twin Study was conducted to compare monozygotic and dizygotic twins with respect to the strength of dependence in the risk for various diseases between twin pair members, because stronger dependence between monozygotic twin pair members would be indicative of the genetic effect in the risk of disease of interest. Information was collected from twin pairs over the age of 17 on the occurrence, and the age at occurrence of disease-related events, including the occurrence of vermiform appendectomy. Those who did not undergo appendectomy prior to survey, or were suspected of undergoing prophylactic appendectomy, gave rise to right-censored failure times. For simplicity, the study was treated as a simple cohort study of twin pairs. Based on the descriptive analysis of Duffy et al. (1990), females were more likely than males to undergo appendectomy across all ages and birth cohorts. Moreover, monozygotic female twins were found to be more concordant for appendectomy during their lifetime than their dizygotic counterparts. As the sample size for the females is twice as large as that for the males and the zygotic effect is more pronounced, we focus on female twin pairs. By doing so, we also avoid the difficulties of modelling sex differences for the opposite sex dizygotic pairs.

As in Prentice & Hsu (1997), analyses presented here are confined to 1953 female twin pairs with available appendectomy information. The data comprised 1218 monozygotic twin pairs and 735 dizygotic twin pairs. Out of the monozygotic twin pairs, there are 144 pairs in which both twins were appendectomized, 304 pairs in which one twin underwent appendectomy and 770 pairs in which neither twin received the procedure. The corresponding numbers for the dizygotic twin pairs are 63, 208 and 464, respectively.

Since the order of twin one and twin two is arbitrary, we can take advantage of such symmetry to improve the estimation efficiency by using the following model reduced from (6),

$$\beta (t_1,t_2;\gamma )={\gamma }_0+{\gamma }_1(t_1+t_2)+{\gamma }_2(t_1^2+t_2^2)+{\gamma }_3{t}_1{t}_2+{\gamma }_4(t_1^2{t}_2+t_1{t}_2^2)+{\gamma }_5(t_1^3+t_2^3).$$ (7)

We have observed that the analysis without such restriction yields similar results to the restricted analysis. Here we only report the restricted analysis. We conduct separate analyses for monozygotic and dizygotic twins.

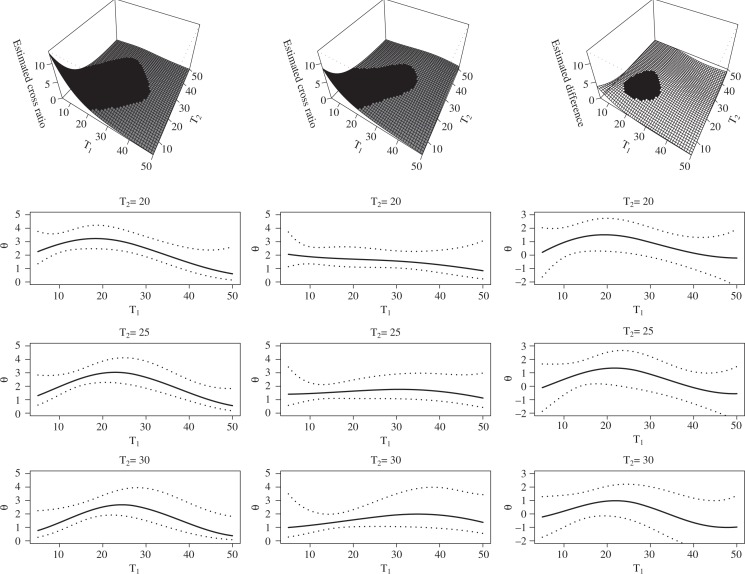
The estimated cross ratio surfaces for both monozygotic and dizygotic twins are plotted in the upper panel of Fig. 2, which also shows the difference between the two estimates. To clearly present the variability of the estimates, in the lower panel of Fig. 2 we also provide the pointwise 95% confidence bands for the estimated cross ratio at three different values of T₂. The confidence bands for the cross ratio differences are obtained from separate analyses of 100 bootstrap samples from the pooled monozygotic and dizygotic data.

Fig. 2.

Estimated cross ratio function for the Australian Twin Study. Left panel: monozygotic twins, middle panel: dizygotic twins, and right panel: the difference between monozygotic twins and dizygotic twins. The shaded areas in the upper left and upper middle plots are regions where the association is statistically significant, and the shaded area in the upper right plot is the region where the difference in the strength of association is significant based on the pointwise confidence bands. In the lower panels, the solid lines represent the cross ratio estimates and dotted lines represent pointwise 95% confidence bands.

Figure 2 suggests that at a younger age the association for appendicitis risk between monozy-gotic twin pair members and dizygotic twins is strong, particularly in monozygotic twins, suggesting a genetic component to the disease. This finding is consistent with Fan et al. (2000a). Also, both monozygotic and dizygotic twin pairs are more likely to undergo appendectomy around the same time. The upper right plot in Fig. 2 identifies the region shaded in black where the difference in the strength of association between monozygotic and dizygotic twins is statistically significant based on the pointwise confidence band. The plots on the upper panel also show that such dependence diminishes over time. This suggests that later in life environmental causes may be more important in the development of the disease. From the pointwise confidence bands, we can see that the association between monozygotic twins is significantly positive in a larger age range. In addition to testing the difference locally, we can also test whether the difference is significant globally. Existing methods assume that the cross ratio is a constant for a global test. Our method, with a more flexible cross ratio surface, can test whether the cross ratio surface is the same for monozygotic twins and dizygotic twins by testing H₀ : γ_mz = γ_dz, where γ_mz and γ_dz denote the coefficients in (7) for monozygotic twins and dizygotic twins respectively. Using a ${\chi }_6^2$ statistic (γ̂_mz − γ̂_dz)^T {vâr(γ̂_mz) + vâr(γ̂_dz)}⁻¹ (γ̂_mz − γ̂_dz), we obtain a p-value of 0.13.

6. Discussion

Nonparametric estimation of the log cross ratio β (t₁, t₂) is of interest, particularly when it is a smooth function of (t₁, t₂), for which the regression spline method using the tensor product splines can be implemented. When the number of knots is fixed, the model is essentially a parametric model and asymptotic properties can be derived in a similar way. If the number of knots is allowed to grow with the sample size, then a different approach needs to be developed for the proofs of asymptotic properties, which is usually challenging. We have assessed the regression spline method in simulations under different combinations of number of knots and degree of smoothness, and observed slightly more variable results, not presented in this article. This may be due to the fact that the cross ratio surface in the simulation setting only changes with time gradually, i.e., it tends to be too flat to apply the regression spline method.

The proposed estimator is based on pseudo-partial likelihood instead of the true likelihood, and thus likely to be inefficient, as illustrated in the simulation study comparing with the two-stage approach of Nan et al. (2006). If we were to construct the true likelihood for an arbitrary cross ratio, we would need to solve h(t₁, t₂) in (2) when θ = θ (t₁, t₂) to obtain the joint distribution F(t₁, t₂). Unfortunately, a closed-form solution does not exist for even the simplest nontrivial functional forms for θ(t₁, t₂), for example, linear functions. Our method is robust because it bypasses modelling the joint and marginal distributions of the bivariate survival times.

Another interesting extension of the proposed approach is to allow the cross ratio to vary with a covariate. Prentice & Hsu (1997) proposed a regression approach for the covariate effect on both the marginal hazard functions and the cross ratio. Their cross ratio, however, is not allowed to depend on time. The comparison of monozygotic and dizygotic twins in the Australian Twin Study presented in Fig. 2 is equivalent to the estimation from an interaction model: β(t₁, t₂, W) = z(t₁, t₂)′ γ₁ + Wz(t₁, t₂)′γ₂, where W is a binary covariate. The most intuitive and straightforward model for the cross ratio with covariates would be β (t₁, t₂, W) = z(t₁, t₂)′ γ+ W′α for a covariate vector W, which looks simpler than the model with interactions. We have found, however, the proposed pseudo-partial likelihood method cannot be directly applied to the estimation of (γ, α). Modifications will be necessary and methods of incorporating covariates into the cross ratio function are under investigation.

Due to the partial likelihood type of construction in (4), the proposed approach can be easily modified to handle left truncation in addition to right censoring. Let (U_1i, U_2i) be the truncation times for subject i, then (4) can be replaced by

$$\prod _{j=1}^n{\left[\frac{\theta {(X_{1i},X_{2j})}^{I(X_{1j}=X_{1i})}}{\{N(X_{1i},X_{2j})-I(U_{2i}⩽X_{2j}⩽X_{2i})\}+\theta (X_{1i},X_{2j})I(U_{2i}⩽X_{2j}⩽X_{2i})}\right]}^{I(X_{1j}⩾X_{1i}⩾U_{1j}){\mathrm{\Delta }}_{2j}{\mathrm{\Delta }}_{1i}},$$

where $N(t_1,t_2)={\sum }_{k=1}^{n}I(X_{1k}⩾t_1⩾U_{1k},X_{2k}⩾t_2⩾U_{2k})$. Additional simulations, not reported in this article, show that such modification works well for left truncated data.

The no-tie assumption is used to construct the objected function. In practice, however, event times may be rounded which yield ties. Commonly used approaches for tied observations in the Cox model can also apply here, e.g. the jittering method that breaks ties by adding tiny random values to observed times.

Supplementary material

The online Supplementary Material contains detailed proofs of Theorems 1 and 2, additional simulations and the bootstrap variance estimates for the simulations reported in Table 1.

Appendix

Sketch of the proof of Theorem 1

Let ( $X_1^{*}$, $X_2^{*}$, ${\mathrm{\Delta }}_1^{*}$, ${\mathrm{\Delta }}_2^{*}$) be an independent copy of (X₁, X₂, Δ₁, Δ₂). Define the deterministic function u(γ) = u⁽¹⁾(γ) − u⁽²⁾(γ) + u⁽³⁾(γ) − u⁽⁴⁾(γ), where

$$\begin{array}{l}{u}^{(1)}(\gamma )=u^{(3)}(\gamma )=E\{{\mathrm{\Delta }}_1{\mathrm{\Delta }}_{2}z(X_1,X_2)\},\\ u^{(2)}(\gamma )=u^{(4)}(\gamma )=E\left[{\mathrm{\Delta }}_1^{*}{\mathrm{\Delta }}_{2}z(X_1^{*},X_2)\frac{I(X_1⩾X_1^{*})I(X_2⩽X_2^{*})\text{exp}\{\beta (X_1^{*},X_2;\gamma )\}}{S_{X_1,X_2}(X_1^{*},X_2)}\right],\end{array}$$

and S_{X1, X2} (·, ·) is the bivariate survival function of the observation time (X₁, X₂). We will first show that $U_n^{(k)}(\gamma )$ converges uniformly to u^(k)(γ) (k = 1, …, 4), then show that u(γ) = 0 has a unique solution at γ₀, and finally show the consistency of γ̂_n that is the solution of U_n(γ) = 0. Due to the symmetric construction, we only need to establish the convergence of $U_n^{(1)}$ and $U_n^{(2)}$.

Following the notation of van der Vaart & Wellner (1996), we use 𝕇_n and 𝕈_n to denote the empirical measures of n independent copies of ( $X_1^{*}$, $X_2^{*}$, ${\Delta }_1^{*}$, ${\Delta }_2^{*}$) and (X₁, X₂, Δ₁, Δ₂) that follow the distributions P and Q, respectively. Although these two samples are identical, i.e. 𝕇_n = 𝕈_n and P = Q, we use different letters to keep the notation tractable for the double summations.

For (6), $U_n^{(1)}(\gamma )={𝕈}_n{\mathrm{\Delta }}_1{\mathrm{\Delta }}_{2}z(X_1,X_2)$ that is free of γ, and Δ₁, Δ₂ and z(X₁, X₂) are all bounded, hence by the law of large numbers, it is trivial to obtain ${\text{sup}}_{\gamma }|U_n^{(1)}-u^{(1)}|=|({𝕈}_n-Q){\mathrm{\Delta }}_1{\mathrm{\Delta }}_{2}z(X_1,X_2)|\to 0$ either almost surely or in probability. Convergence in probability should be adequate here for the proof.

To show the uniform convergence of $U_n^{(2)}(\gamma )$, we first define

$$\begin{array}{l}{g}^{(n)}({\mathrm{\Delta }}_2,X_1,X_2,{\mathrm{\Delta }}_1^{*},X_1^{*},X_2^{*};\gamma )=\frac{{\mathrm{\Delta }}_1^{*}{\mathrm{\Delta }}_{2}z(X_1^{*},X_2)I(X_1⩾X_1^{*})I(X_2⩽X_2^{*})e^{\beta (X_1^{*},X_2;\gamma )}}{n^{-1}\{N(X_1^{*},X_2)-I(X_2⩽X_2^{*})(1-e^{\beta (X_1^{*},X_2;\gamma )})\}},\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\tilde{g}}^{(n)}({\mathrm{\Delta }}_2,X_1,X_2,{\mathrm{\Delta }}_1^{*},X_1^{*},X_2^{*};\gamma )=\frac{{\mathrm{\Delta }}_1^{*}{\mathrm{\Delta }}_{2}z(X_1^{*},X_2)I(X_1⩾X_1^{*})I(X_2⩽X_2^{*})e^{\beta (X_1^{*},X_2;\gamma )}}{S_{X_1,X_2}(X_1^{*},X_2)}.\end{array}$$

The only difference between the two expressions is in the denominators of the two fractions. By fixing ( ${\Delta }_1^{*}$, $X_1^{*}$, $X_2^{*}$) at (δ₁, x₁, x₂), we also define

$$\begin{array}{l}{h}_{{𝕈}_n}^{(n)}({\delta }_1,x_1,x_2;\gamma )={𝕈}_n{g}^{(n)}({\mathrm{\Delta }}_2,X_1,X_2,{\delta }_1,x_1,x_2;\gamma ),\\ \hspace{0.17em}{h}_Q^{(n)}({\delta }_1,x_1,x_2;\gamma )=Q{g}^{(n)}({\mathrm{\Delta }}_2,X_1,X_2,{\delta }_1,x_1,x_2;\gamma ),\hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}{\tilde{h}}_Q({\delta }_1,x_1,x_2;\gamma )=Q\tilde{g}({\mathrm{\Delta }}_2,X_1,X_2,{\delta }_1,x_1,x_2;\gamma ).\end{array}$$

Similarly, fixing (Δ₂, X₁, X₂) at (δ₂, x₁, x₂), define

$$\begin{array}{l}{h}_{{𝕇}_n}^{(n)}({\delta }_2,x_1,x_2;\gamma )={𝕇}_n{g}^{(n)}({\delta }_2,x_1,x_2,{\mathrm{\Delta }}_1^{*},X_1^{*},X_2^{*};\gamma ),\\ h_P^{(n)}({\delta }_2,x_1,x_2;\gamma )=P{g}^{(n)}({\delta }_2,x_1,x_2,{\mathrm{\Delta }}_1^{*},X_1^{*},X_2^{*};\gamma ),\hspace{0.17em}\\ \hspace{0.17em}\hspace{0.17em}{\tilde{h}}_P({\delta }_2,x_1,x_2;\gamma )=P\tilde{g}({\delta }_2,x_1,x_2,{\mathrm{\Delta }}_1^{*},X_1^{*},X_2^{*};\gamma ).\end{array}$$

Then we have $U_n^{(2)}(\gamma )={𝕇}_n{h}_{{𝕈}_n}^{(n)}$ and u⁽²⁾(γ) = Ph̃_Q. It is clear that, under Conditions 1 and 2, the summation and integration are interchangeable, which yields $P{h}_{{𝕈}_n}^{(n)}={𝕈}_n{h}_P^{(n)}$. Thus as Ph̃_Q = PQ_g̃ and $Q{h}_P^{(n)}=QP{g}^{(n)}$, applying the triangle inequality we obtain

$$\begin{array}{ll}\underset{\gamma }{\text{sup}}|U_n^{(2)}-u^{(2)}|\hfill & =\underset{\gamma }{\text{sup}}|{𝕇}_n{h}_{{𝕈}_n}^{(n)}-P{\tilde{h}}_Q|\hfill \\ & ⩽\underset{\gamma }{\text{sup}}|{𝕇}_n{h}_{{𝕈}_n}^{(n)}-P{h}_{{𝕈}_n}^{(n)}|+\underset{\gamma }{\text{sup}}|{𝕈}_n{h}_P^{(n)}-Q{h}_P^{(n)}|+\underset{\omega ,\gamma }{\text{sup}}|g^{(n)}-\tilde{g}|,\hfill \end{array}$$

where ω represents all the arguments of functions g⁽ⁿ⁾ and g̃. For (6), it is straightforward to argue that, under Conditions 1 and 2, functions g⁽ⁿ⁾ and g̃ are Donsker. Then by Theorems 2.10.2 and 2.10.3 in van der Vaart & Wellner (1996), we know that $h_{{𝕈}_n}^{(n)}$ and $h_P^{(n)}$ are Donsker, and hence Glivenko–Cantelli. Thus the first and second terms on the right-hand side of the above inequality converge to zero in probability. The third term converging to zero in probability holds because sup_{t1, t2}|n⁻¹N(t₁, t₂) − S_{X1, X2} (t₁, t₂)| → 0 in probability. Then $U_n^{(2)}(\gamma )$ converges uniformly to u⁽²⁾(γ) in probability. Thus we have shown that U_n(γ) converges uniformly to u(γ) in probability.

To show u(γ₀) = 0, it suffices to show u⁽¹⁾(γ₀) = u⁽²⁾(γ₀). Note that u⁽¹⁾(γ) is in fact free of γ for (6). The uniqueness of γ₀ as the solution of u(γ) = 0 can be proved by showing that (i) the matrix u̇ (γ) ≡ du(γ)/dγ is negative semidefinite for all γ ∈ Γ, and (ii) u̇ (γ) is negative definite at γ₀. We refer to the online Supplementary Material for detailed calculations.

Given the fact that U_n(γ̂_n) = 0 and sup_γ|U_n(γ) − u(γ)| = o_p(1), we have |u(γ̂_n)| = |U_n(γ̂_n) − u(γ̂_n)| ⩽ sup_γ |U_n(γ) − u(γ)| = o_p(1). Since γ₀ is the unique solution to u(γ) = 0, for any fixed ∊ > 0, there exists a δ > 0 such that pr(|γ̂_n − γ₀| > ∊) ⩽ pr(|u(γ̂_n)| > δ). The consistency of γ̂_n follows immediately.

Sketch of the proof of Theorem 2

Define U̇_n(γ) ≡ dU_n(γ)/dγ. By Taylor expansion of U_n(γ̂_n) around γ₀, we have

$$n^{1/2}({\widehat{\gamma }}_n-{\gamma }_0)=-{\dot{U}}_n{(\gamma *)}^{-1}{n}^{1/2}{U}_n({\gamma }_0),$$ (A1)

where γ^* lies between γ̂_n and γ₀. By a similar calculation as in the Appendix showing the uniform consistency of U_n(γ), we can show that sup_γ|U̇_n(γ) − u̇(γ)| = o_p(1). Thus by the consistency of γ̂_n, which implies the consistency of γ^*, and the continuity of u̇ (γ), we obtain U̇_n(γ^*) = u̇(γ₀) + o_p(1), where u̇ (γ₀) = − 2E{Δ₁Δ₂z(X₁, X₂)^⊗2} = −I(γ₀) is invertible by Condition 3. Hence based on the fact that continuity holds for the inverse operator, (A1) can be written as

$$n^{1/2}({\widehat{\gamma }}_n-{\gamma }_0)=I{({\gamma }_0)}^{-1}+o_p(1)n^{1/2}{U}_n({\gamma }_0).$$ (A2)

We now need to find the asymptotic representation of n^1/2 U_n(γ₀). We only check it for $U_n^{(1)}({\gamma }_0)-U_n^{(2)}({\gamma }_0)$. The calculation for $U_n^{(3)}({\gamma }_0)-U_n^{(4)}({\gamma }_0)$ is virtually identical and yields the same asymptotic representation. It is easily seen that

$$n^{1/2}\{U_n^{(1)}({\gamma }_0)-u^{(1)}({\gamma }_0)\}={𝔾}_n\{{\mathrm{\Delta }}_1{\mathrm{\Delta }}_{2}z(X_1,X_2)\},$$ (A3)

where 𝔾_n = n^1/2(𝕇_n − P) = n^1/2 (𝕈_n − Q). We then focus on each term of the following decomposition:

$$n^{1/2}\{U_n^{(2)}({\gamma }_0)-u^{(2)}({\gamma }_0)\}={𝔾}_n(h_{{𝕈}_n}^{(n)})+{𝔾}_n(h_P^{(n)})+n^{1/2}(PQ{g}^{(n)}-PQ\tilde{g}).$$ (A4)

For the first term on the right-hand side of (A4), we have $h_{{𝕈}_n}^{(n)}=(h_{{𝕈}_n}^{(n)}-{\tilde{h}}_{{𝕈}_n})+({\tilde{h}}_{{𝕈}_n}-{\tilde{h}}_Q)+{\tilde{h}}_Q$. It is straightforward to verify that $h_{{𝕈}_n}^{(n)}-{\tilde{h}}_{{𝕈}_n}$ and h̃_𝕈n − h̃_Q converge to zero in variance semimetric. Together with the fact that $h_{{𝕈}_n}^{(n)}$, h̃_𝕈n, and h̃_Q are Donsker, we have

$${𝔾}_n{h}_{{𝕈}_n}^{(n)}={𝔾}_n(h_{{𝕈}_n}^{(n)}-{\tilde{h}}_{{𝕈}_n})+{𝔾}_n({\tilde{h}}_{{𝕈}_n}-{\tilde{h}}_Q)+{𝔾}_n{\tilde{h}}_Q={𝔾}_n{\tilde{h}}_Q+o_p(1).$$ (A5)

For the second term of (A4), we write $h_P^{(n)}=(h_P^{(n)}-{\tilde{h}}_P)+{\tilde{h}}_P$. It can also be verified that $h_P^{(n)}-{\tilde{h}}_P$ converges to zero in variance semimetric. Together with the fact that $h_P^{(n)}$ and h̃_P are Donsker, we obtain that

$${𝔾}_n{h}_P^{(n)}={𝔾}_n(h_P^{(n)}-{\tilde{h}}_P)+{𝔾}_n{\tilde{h}}_P={𝔾}_n{\tilde{h}}_P+o_p(1).$$ (A6)

Now consider the third term on the right-hand side of (A4). Define the function

$$f({\delta }_1,x_1,x_2,{\delta }_2^{*},x_1^{*},x_2^{*})=\frac{{\delta }_1^{*}{\delta }_{2}z(x_1^{*},x_2)I(x_1⩾x_1^{*})I(x_2⩽x_2^{*})e^{\beta (x_1^{*},x_2;{\gamma }_0)}}{{\{S_{X_1,X_2}(x_1^{*},x_2)\}}^2}.$$

By a straightforward calculation, we obtain

$$\begin{array}{ll}{n}^{1/2}(PQ{g}^{(n)}-PQ\tilde{g})=\hfill & -{𝔾}_n\{\int \int I(X_1⩾x_1^{*},X_2⩾x_2)f({\delta }_1,x_1,x_2,{\delta }_2^{*},x_1^{*},x_2^{*})\hfill \\ & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}dP({\delta }_1^{*},{\delta }_2^{*},x_1^{*},x_2^{*})dQ({\delta }_1,{\delta }_2,x_1,x_2)\}+o_p(1).\hfill \end{array}$$ (A7)

Detailed derivation is provided in the Supplementary Material. Then by equations (A3)–(A7), we obtain

$$\begin{array}{ll}{n}^{1/2}{U}_n({\gamma }_0)\hfill & =n^{1/2}\{U_n({\gamma }_0)-u({\gamma }_0)\}\hfill \\ \hfill & =2{𝔾}_n\{{\mathrm{\Delta }}_1{\mathrm{\Delta }}_{2}z(X_1,X_2)-{\tilde{h}}_Q({\mathrm{\Delta }}_1,X_1,X_2;{\gamma }_0)-{\tilde{h}}_P({\mathrm{\Delta }}_2,X_1,X_2;{\gamma }_0)\hfill \\ \hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}+\int \int I(X_1⩾x_1^{*},X_2⩾x_2)f({\delta }_1,x_1,x_2,{\delta }_2^{*},x_1^{*},x_2^{*})\hfill \\ \hfill & \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}dP({\delta }_1^{*},{\delta }_2^{*},x_1^{*},x_2^{*})dQ({\delta }_1,{\delta }_2,x_1,x_2)\}+o_p(1)\hfill \\ \hfill & \to N(0,\Sigma ({\gamma }_0))\hfill \end{array}$$ (A8)

in distribution. Thus from (A2) we obtain the desired asymptotic distribution of n^1/2(γ̂n − γ₀). Replacing h̃_Q (Δ₁, X₁, X₂; γ₀) by $h_{{𝕈}_n}^{(n)}$ (Δ₁, X₁, X₂; γ₀), h̃_P (Δ₂, X₁, X₂; γ₀) by $h_{{𝕇}_n}^{(n)}$ (Δ₂, X₁, X₂; γ₀), dP by d𝕇_n and dQ by d𝕈_n and plugging γ̂_n for γ₀ in (A8), we can estimate Σ(γ₀) via sample variance. Together with either U̇_n(γ̂_n) or 2𝕇_n{Δ₁Δ₂z(X₁, X₂)^⊗2} as an estimator for I(γ₀), we can easily obtain a model-based variance estimator for γ̂_n. We used U̇_n(γ̂_n) in our numerical examples because it is already available in the implementation of the Newton–Raphson algorithm.