The dependence of pyranose ring puckering on anomeric configuration: methyl idopyranosides

Abstract

In the aldohexopyranose idose, the unique presence of three axial ring hydroxyl groups causes considerable conformational flexibility, rendering it challenging to study experimentally and an excellent model for rationalising the relationship between puckering and anomeric configuration. Puckering in methyl α- and β-l-idopyranosides was predicted from kinetically rigorous 10 μs simulations using GLYCAM11 and three explicit water models (TIP3P, TIP4P and TIP4P-EW). In each case, computed pyranose ring three-bond (vicinal) ¹H-¹H spin-couplings (³J_H,H) trended with NMR measurements. These values, calculated puckering exchange rates and free energies were independent of the water model. The α- and β-anomers were ¹C₄ chairs for 85% and >99% of their respective trajectories and underwent ¹C₄→⁴C₁ exchange at rates of 20 μs^-1 and 1 μs^-1. Computed α-anomer ¹C₄↔⁴C₁ puckering rates depended on the exocyclic C6 substituent, comparing hydroxymethyl with carboxyl from previous work. The slower kinetics and restricted pseudorotational profile of the β-anomer were caused by water occupying a cavity bounded by the anomeric 1-O-methyl and the C6 hydroxymethyl groups. This finding rationalises the different methyl α- and β-l-idopyranoside ³J_H,H values. Identifying a relationship between idopyranose anomeric configuration, μs-puckering and water structure facilitates engineering of biologically and commercially important derivatives and underpins deciphering presently elusive structure-function relationships in the glycome.

Introduction

Understanding the conformational dynamics of carbohydrates in aqueous solution is central to rationalising their plethora of bioactivities. This goal promises to enable structure-based design of new medicines and materials, but its realisation remains challenging due to experimental and computational difficulties of probing carbohydrate motions, which occur over a broad range of timescales. Glycosidic linkages librate on nanosecond timescales while pyranose ring conformational exchange (or puckering) and anomerization are microsecond¹ and millisecond timescale phenomena, respectively. The latter process is influenced by the anomeric effect, whose electronic origin remains controversial.²

The methyl l-idopyranosides 1 and 2 (Figure 1) are unique among the simple l-aldohexopyranosides because, in the ¹C₄ chair conformation, they exhibit three axial hydroxyl groups at C2, C3 and C4; all other aldohexopyranosides contain a mixture of axial and equatorial hydroxyl substituents at these sites. The idohexopyranosyl ring configuration is thus associated with considerable conformational heterogeneity in water that depends on anomeric configuration.³ Rationalising this association could help explain structure-function relationships in the wider glycome (starch and cellulose differ only in their linkage stereochemistry), but it would be difficult to explore in sugars with more stable puckering signatures (e.g., glucose).⁴ Idohexopyranoses are important precursors in much needed new approaches to heparan sulphate synthesis.⁵ Furthermore, methyl α-l-idopyranosiduronic acid (α-l-IdoA^- 3, Figure 1), a constituent in heparan and dermatan sulfates and the widely used antithrombic drug heparin,⁶ was recently predicted¹ to undergo microsecond puckering that depends on substituents and epimerization and is crucial to bioactivity (e.g., anticoagulation).⁷

Figure 1.

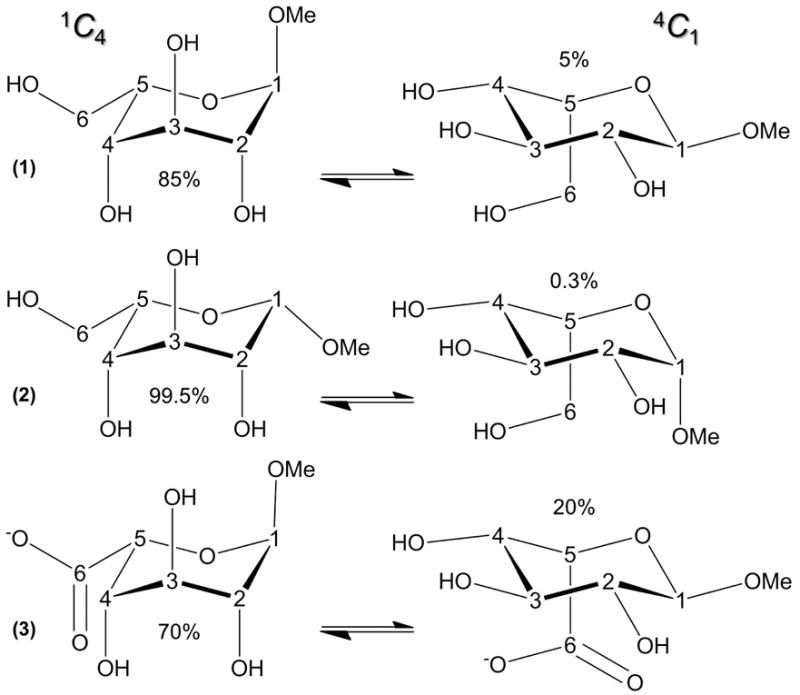
Chair puckers and calculated populations of methyl α- (1) and β- (2) l-idohexopyranosides studied using 10 μs unbiased explicit solvent molecular dynamics and NMR spectroscopy (d-isomers). Structures and computed populations of methyl α-l-idopyranuronate (3), studied previously,¹ are illustrated for comparison.

Prior work has shown that three-bond (vicinal) ¹H-¹H spin-couplings (³J_H,H) differ in the α- and β-d-idopyranoses,³ indicating different conformational equilibria. The distribution of puckers in the α-pyranose may include skew-boats in aqueous solution,³ however, the kinetics of ¹C₄↔⁴C₁ exchange remain unknown. Unfortunately, experimental ³J_H,H values provide no kinetic information, and puckering rates derived from previous non-equilibrium picosecond⁸ ab initio simulations and nanosecond⁹ enhanced sampling molecular dynamics (MD) must be treated with caution since perturbations applied to traverse high (≈8-10 kcal mol^-1) free energy barriers associated with chair-chair interconversion distort the kinetics.¹⁰ In order to better understand puckering dynamics and the effect of C6 substitution in idohexopyranosyl rings and to facilitate exploitation of puckering in structure-based design, we sought to reproduce the experimentally observed dependence of the methyl idopyranoside puckering equilibrium on anomeric configuration using kinetically rigorous microsecond simulations, in which conformational sampling is not artificially enhanced (e.g. by elevated temperature).

Water plays a central role in defining oligosaccharide conformation by influencing glycosidic linkage structure.¹¹ The effect of water and different water models on pyranose ring puckering has not been studied previously using microsecond simulations. The present explicit solvent MD (six 10 μs trajectories) converge aqueous puckering in the methyl l-idopyranosides 1 and 2 for the first time. Comparison of these new data with those from a previous 10 μs simulation of 3 shows that idopyranosyl ring ¹C₄↔⁴C₁ exchange kinetics depend on the C6 substituent structure. Predicted ³J_H,H values in 1 and 2 trended with NMR measurements made on the d isomers of 1 and 2 at 750 MHz. These computed properties, calculated chair-chair exchange rates, and relative free energies were unaffected by the type of water potential used in the simulations, comparing three models often used for biomolecular systems¹²: TIP3P,¹³ TIP4P¹⁴ and TIP4P-EW.¹⁵ The experimentally observed puckering behaviours of 1 and 2 were explained by different water structure around each anomer and not by intramolecular steric interactions.

Methods

Molecular dynamics

Periodic molecular dynamics simulations of charge-neutral methyl α- and β-l-idopyranosides 1 and 2 were extended to 10 μs using NVIDIA graphics processing units and a development version of ACEMD¹⁶ software (2108). Both monosaccharides were modelled using the GLYCAM11 force field (Supporting Information), each was solvated in an explicit water box of equal side length (28 Å) and three solvent potentials were compared: TIP3P,¹³ TIP4P¹⁴ and TIP4P-EW.¹⁵ Following initial conjugate-gradient energy minimisation (1000 steps), each system was heated from 0 to 298K and equilibrated in the NPT ensemble (for 20 ns) prior to 10.25 μs NVT production dynamics, the first 250 ns were discarded and data were recorded at 10 ps intervals. The velocity-Verlet integration algorithm and a hydrogen mass repartitioning scheme allowed a 4 fs time-step without affecting the equilibrium distribution.¹⁷ Hydrogen atoms were constrained using the M-SHAKE algorithm¹⁸ and electrostatic interactions were calculated via the PME method with a grid spacing of 0.9 Å (in the X, Y and Z dimensions). Electrostatic and van der Waals interactions were truncated at 9 Å and a scaling factor of 1.0 was employed for carbohydrate 1-4 interactions,¹⁹ the importance of this term has been addressed recently.²⁰ Gas phase simulations were performed identically; however a cubic box of side length 20 Å and a PME grid spacing of 1.0 Å were used.

Calculation of molecular properties

All molecular properties were computed using the complete 10 μs trajectories (1,000,000 data points). Puckering was quantified using the Cremer-Pople²¹ parameters θ, ϕ and Q, which were derived using the GROMACS²² analysis tool g_puckering. Relative free energies (ΔG) of binned puckers were calculated using the standard relationship ΔG=kTln(p₁/p₂), where k is the Boltzmann constant, T is temperature (289K) and p is probability. Puckers were placed in bins of equal area on the Cremer-Pople sphere (unequal spacing in the azimuthal angle θ and equal spacing in the meridian angle ϕ). To achieve this, linear binned values were divided by sin θ to normalize for the area on the sphere (the circumference at azimuthal angle θ is 2πrsinθ on a sphere of radius r). Rotamer populations were computed as described previously²³ and pyranose ring ¹H-¹H vicinal spin-couplings were calculated using the substituent-adjusted Karplus equations of Altona and Haasnoot²⁴ (see Supporting Information). Radial distribution functions (RDFs) and water densities were derived using the AMBER²⁵ tool ptraj (keywords “radial” and “grid”, respectively). The RDF bin spacing was set to 0.05 Å.

Synthesis of methyl α- and β-d-idopyranosides

d-Idose was prepared by cyanohydrin reduction using d-xylose and KCN as substrates.²⁶ The C2-epimeric products, d-idose and d-gulose, were separated by chromatography on a column (3 cm × 100 cm) containing Dowex 50 × 8 (200-400 mesh) ion-exchange resin in the Ca⁺² form;²⁷ idoses eluted first, followed by gulose. d-Idose was converted into the methyl d-idopyranosides by Fischer glycosidation as described previously.²⁸ After the reaction was complete (∼2 h), the resin catalyst was removed by vacuum filtration, and the methanolic solution was concentrated at 30° C in vacuo to give a syrup. ¹³C NMR of the syrup in ²H₂O showed that it contained idofuranosides and idopyranosides, and the 1,6-anhydro derivative (the glycosidation reaction time was kept to a minimum to reduce the amount of the latter). This syrup was dissolved in a minimal amount of distilled water and the solution was applied to a column (2.5 cm × 100 cm) containing Dowex 1 × 8 (200-400 mesh) ion-exchange resin in the OH form.²⁹ The column was eluted with distilled, decarbonated water, and the effluent was assayed with phenol-sulfuric acid³⁰ to locate the eluting pyranosides. Careful pooling of fractions gave >95% pure samples of methyl α-d-idopyranoside and methyl β-d-idopyranoside as determined by ¹H NMR; the anomers were assigned from their anomeric ¹H NMR signal multiplicities by analogy to those reported for α- and β-d-idopyranoses.³

NMR Spectroscopy

High-resolution ¹H NMR spectra of the methyl α- and β-d-idopyranosides in ²H₂O were obtained at 750 MHz and 25° C. Spectra were collected with 2000-3000 Hz sweep widths and 32K points, and FIDs were zero-filled once before processing with resolution enhancement to improve spectral resolution. Since ¹H spectra of 1 and 2 were not first-order at 750 MHz, the data were simulated using the MacNUTs program (MacNUTs Pro; Acorn NMR Inc.: Livermore, CA) to extract accurate chemical shifts and ³J_H,H values. Reported ¹H chemical shifts (Supporting Information) are accurate to ±0.002 ppm and reported ³J_H,H values (Table 1) are accurate to ±0.2 Hz. The ¹H chemical shifts were referenced to the internal residual HOD signal at 4.8 ppm. ¹³C[¹H] NMR spectra of 1 and 2 were obtained at 150 MHz in ²H₂O and 21° C. Spectra were collected with 8500 Hz sweep widths and 128K points, and FIDs were zero-filled once before processing with resolution enhancement to improve spectral resolution. ¹³C chemical shifts (Supporting Information) were referenced externally to the C1 signal of α-d-[1-¹³C]mannose (95.5 ppm).³¹

Table 1.

Calculated (TIP3P, TIP4P, TIP4P-EW) and experimental (EXPT) ³J_H,H values (Hz) for 1 and 2.

Anomer	3JH,H	TIP3P	TIP4P	TIP4P-EW	EXPT
α	J1,2	2.4	2.6	2.6	4.3
α	J2,3	2.8	3.0	2.9	6.7
α	J3,4	3.1	3.2	3.2	6.1
α	J4,5	1.3	1.6	2.8	3.6
β	J1,2	1.6	1.7	1.7	1.7
β	J2,3	3.0	2.9	2.9	4.1
β	J3,4	3.0	2.9	2.9	4.6
β	J4,5	1.1	1.4	2.8	2.5

Calculated ³J_H,H values were derived from 10 μs trajectories using the substituent-adjusted Karplus equations of Altona and Haasnoot.²⁴ Computed and experimental values correspond to l- and d-forms of the sugars, respectively. Calculated values not trending with the experimental data (where the β-anomer ³J_H,H value was equal to or greater than the α-anomer ³J_H,H value) are bold.

Results and Discussion

Molecular 3D-properties and comparison with experiment

Based on our previous metric for conformational convergence (determined by the average value of cos θ, where θ is the Cremer-Pople²¹ polar angle),¹ the dynamic 3D-ensemble of ring puckers in 1 and 2 approached the simulation average pucker after approximately 5 μs of explicit solvent MD, irrespective of the water model used (see Supporting Information). Puckering convergence took longer than found previously for net charge-neutral explicit solvent simulations of 3, methyl 2-O-sulfo-IdoA (dianion) and methyl β-d-glucuronate (anion),¹ methyl β-d-glucopyranoside, β-d-galactopyranoside, N-acetyl-β-d-galactosaminide, α-d-mannopyranoside and α-l-fucopyranoside,⁴ and five methyl and free α-anomer d-hexosamines²³ (the appropriate number of Na⁺ counterions were used to neutralise the ensembles). Both 1 and 2 underwent ¹C₄↔⁴C₁ transitions with all three water models and their average puckers were independent of the water potential (see Supporting Information). In 1, the average Cremer-Pople²¹ pucker parameters θ, ϕ and Q (see Methods) for ¹C₄ chairs were 169° (±6°), 135° (±70°) and 0.53 (±0.04); in 2, these values were 171 ° (±6°), 195° (±80°) and 0.57 (±0.04), respectively. These results show a larger average value of ϕ in the β-anomer, indicating a shift from puckers in the ²S_O-region (ϕ≈150°) to those in the ¹S₃-region (ϕ ≈210°). The increased Q value in the β-anomer indicates a more chair-like (less flat) pucker relative to the α-anomer. For the ⁴C₁ chairs of 1, the average θ, ϕ and Q values were 12° (±6°), ≈158° (±100°) and 0.54 (±0.04); in 2 these values were 14° (±7°), ≈151° (±55°) and 0.53 (±0.04), respectively. The ⁴C₁ chair thus appears to be less sensitive to anomeric configuration than the ¹C₄ form.

In the ¹C₄ pucker of 1 and 2, all ring vicinal proton-proton pairs are gauche (axial-equatorial or equatorial-equatorial), and therefore relatively small ³J_H,H values are expected (≈1-4 Hz). In the ⁴C₁ chair, ³J_1,2, ³J_2,3 and ³J_3,4 in the α-anomer, and ³J_2,3 and ³J_3,4 in the β-anomer, correspond to trans (diaxial) coupled protons, and thus large couplings are expected (≈10 Hz). Computed ³J_H,H values were in general agreement with these expectations and with prior³ and new experimental data (Table 1) in that couplings for the α-anomer were larger and thus indicative of a greater proportion of ⁴C₁ form in aqueous solution than found for the β-anomer. Three minor exceptions were noted (bold in Table 1): J_2,3 (TIP3P and TIP4P-EW) and J_4,5 (TIP4P-EW), in which the computed ³J_H,H values were either identical in both anomers or at most 0.2 Hz greater in the α-anomer (i.e., within the estimated experimental error of ±0.2 Hz). The computed ³J_H,H values for the α-anomer were all smaller than the corresponding experimental observations (≈2-4Hz). In the β-anomer, the maximum difference between calculated and experimental ³J_H,H values was ±2 Hz. All computed ³J_H,H values were effectively independent of the water model (within 0.2 Hz of each other), except for ³J_4,5, which differed at most by 1.7 Hz. Although the absolute computed and experimental ³J_H,H values for 1 differed by several Hz, the comparisons in Table 1 provide confidence that the force fields reproduced qualitatively the relative differences between the α- and β-l-idopyranoside equilibrium puckering distributions. The NMR data predicts a more balanced ¹C₄:⁴C₁ equilibria than does the MD data (see Supporting Information, two-site models). Improvement of the computed ³J_H,H values for the very finely balanced conformational equilibria of 1 and 2 can be achieved via small corrections to force field parameters.

The computed exocyclic hydroxymethyl rotamer populations in 1 and 2 were similar and unaffected by the water models used (Supporting Information). Using the TIP3P water model, the tg:gt:gg states for the α- and β-l-idopyranoside were populated (±1%) at 17:14:69 and 18:8:75, respectively. The experimental populations for the d isomers, in which the gt and gg states are reversed with respect to the l isomer, were (±5%) 24:0:76 (α-anomer) and 29:4:67 (β-anomer), indicating a slight over-estimation of gt in the simulations and faithful representation of the experimentally observed trend for gg >> tg > gt.

Puckering thermodynamics and kinetics

In the simulations of 1 and 2 using three water models, the ¹C₄ and ⁴C₁ conformers were the two most populated (lowest energy) ring puckers (Figure 2 and Supporting Information). Ratios of ¹C4:⁴C₁ chairs in the a-anomer simulations were 85:5 (TIP3P) and 84:7 (TIP4P) and 84:8 (TIP4P-EW), resulting in computed free energy differences (ΔG) between the two chairs of 1.7 (TIP3P) and 1.4 kcal mol^-1 (TIP4P and TIP4P-EW). For the β-anomer, the ¹C₄:⁴C₁ ratios were 99.5:0.3 (TIP3P), 99.4:0.4 (TIP4P) and 99.8:0.1 (TIP4P-EW) and the computed ΔG values were, respectively, 3.5, 3.3 ad 3.9 kcal mol^-1. In addition to having a higher energy ⁴C₁ pucker, pivotal 3D-intermediates in the β-anomer simulation were predicted to have higher free energies when compared to the corresponding α-anomer puckers (Figure 2 and Supporting Information). For example, the lowest energy non-chair puckers in the α- and β-anomer simulations (for all water models) were B_1,4 and ⁵S₁, respectively, which were ≈2 and ≈4 kcal mol^-1 higher in free energy cf. ¹C₄. In the α-anomer, ⁵S₁, ³S₁, ²S_O and ¹S₃ puckers were ≤ 3 kcal mol^-1 above the ¹C₄ energy. For the β-anomer, the next lowest energy puckers (B_1,4, ^2,5B, ^1,4B and ²S_O) were predicted to be > 5 kcal mol^-1 above the ¹C₄ form.

Figure 2.

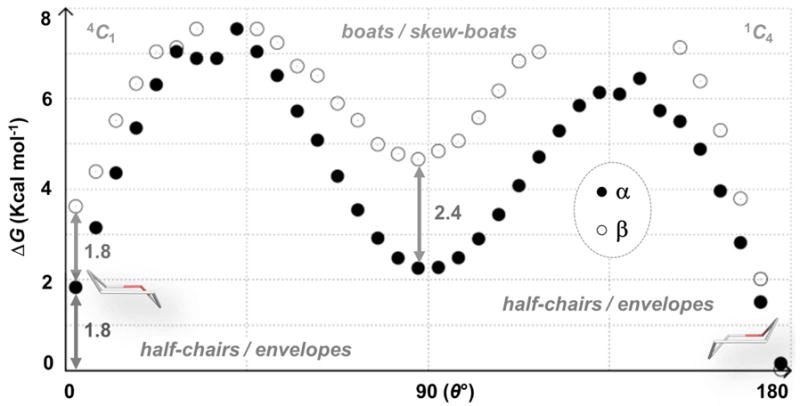
One-dimensional puckering free energy (G) landscapes for 1 and 2 computed from 10 μs explicit solvent (TIP3P) simulations. Free energy differences of ⁴C₁ and equatorial puckers are noted.

Figure 2 footnote: This simplified representation facilitates comparison with other sugars. Computed free energies for all sampled canonical puckers are reported in the Supporting Information.

Computed rates of ¹C₄↔⁴C₁ exchange were also independent of the water potential employed (Table 2). Rates for the forward (¹C₄→⁴C₁) transition were 20 μs^-1 and 1 μs^-1 in the α- and β-anomers, respectively; the backward (⁴C₁→¹C₄) rates were in the range 200-300 μs^-1 in 1 and 150-250 μs^-1 in 2. Our previous simulation of 3 predicted forward and backward rates of 4 μs^-1 and 19 μs^-1, respectively.¹ This comparison suggests that the C6 carboxyl substituent of 3 slows the forward and backward puckering exchange rates by approximately five- and ten-fold, respectively, in idopyranosyl rings.

Table 2.

Calculated rates of exchange (μs^-1) between chair puckers in the six α- and β-l-idopyranose 10 μs simulations.

Anomer	Transition	TIP3P (μs-1)	TIP4P (μs-1)	TIP4P-EW (μs-1)
α	1C4 → 4C1	20.1	19.8	20.4
β	1C4 → 4C1	0.9	0.9	0.7
α	4C1 → 1C4	292.0	200.0	193.0
β	4C1 → 1C4	167.0	149.0	250.0

Puckering itineraries

Currently, it is not possible to quantify μs-timescale puckering itineraries using experiments alone. Kinetically rigorous simulations are the best way to improve our understanding of puckering and to complement the burgeoning field of functional glycomics. Previous density functional theory studies of 1 predicted ¹C₄↔⁴C₁ exchange and that the most likely 3D-itinerary connects the ⁴C₁ chair and the boat B_3,O through the transition-state envelope pucker E₃.³² A recent metadynamics study found the skew-boat and boat puckers ¹S₃, ^OS₂, ^1,4B and B_2,5 to be the lowest energy non-chair 3D-intermediates in α- and β-d-idopyranose.⁹ Our computed puckering free energy landscapes for 1 and 2 were very similar for the TIP3P, TIP4P and TIP4P-EW water models (see Supporting Information). All 38 canonical puckers (chairs, half-chairs, boats, skew-boats and envelope puckers) were populated in the α-anomer simulations. In the β-anomer simulations, all ¹C₄-hemisphere puckers were populated, however, specific half-chair and envelope puckers were not explored, including ⁴C₁-hemisphere ⁴H₃, ⁴E and ⁴H₅ (θ≈30-70° and ϕ≈210-270°) and ¹C₄-hemisphere ¹H_O and ¹E (θ≈100-140° and ϕ≈30-90°) (Figures 3 and 4). Three equatorial puckers, ^3,OB, ^OS₂ and B_2,5 (θ≈70-110° and ϕ≈0/360, 330 and 300°), were also precluded in the β-anomer. By inspection of these 3D-intermediates, the limited pseudorotational profile and reduced number of inter-hemisphere transitions in 2 could not be attributed to intramolecular steric hindrance (e.g., between the bulky anomeric 1-O-methyl and C6 hydroxymethyl groups). This observation implicates water-pyranose interactions as the cause of the experimentally observed different puckering 3D-ensembles of 1 and 2, with which our calculated ³J_H,H values are consistent.

Figure 3.

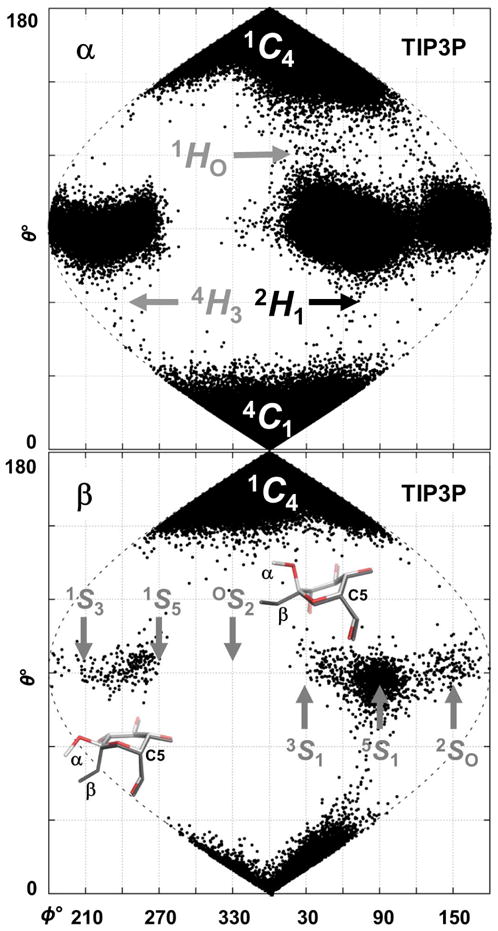
Sinusoidal projection of computed puckering in 1 (top) and 2 (bottom).

Figure 3 footnote: Data are from 10 μs simulations using GLYCAM11 and the TIP3P solvent model. All sampled puckers are shown. Predicted 3D-intermediates linking chair and equatorial puckers in the α-anomer (¹H_O and ⁴H₃) which were precluded in the β-anomer simulation, are indicated in grey (top). Models of these puckers (α- and β-anomers) are shown at their respective positions in puckering space on the β-anomer plot (bottom), in which equatorial skew-boat (S) puckers are labelled above/below their respective positions (grey). By inspection of these overlaid 3D-structures, it is apparent that no intermolecular steric hindrance results from anomerisation. Analogous plots for TIP4P and TIP4P-EW water models are reported in the Supporting Information.

Figure 4.

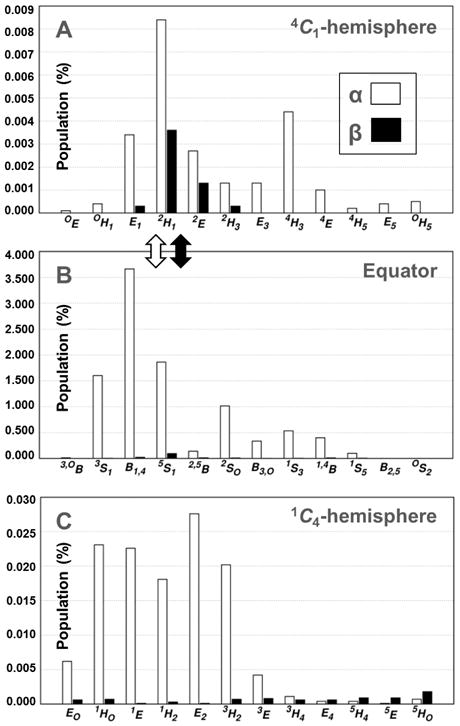
Histograms showing the occupancy of pyranose puckers for (1) and (2) in the ⁴C₁-hemisphere (A), equatorial region (B) and ¹C₄-hemisphere (C) during 10 μs simulations (TIP3P water model).

Figure 4 footnote: The most likely transitions (based on pucker populations) between the equator and the ⁴C₁-hemisphere are denoted by arrows. Multiple conformational itineraries between the equator and the ¹C₄-hemisphere were predicted for (1), e.g., B_1,4 ↔ ¹E.

A role for water mediating idopyranose μs-puckering

Two computed metrics derived from the explicit solvent MD support the hypothesis that the water structure is different around 1 and 2. Firstly, calculated radial distribution functions (RDFs) for hydrogen-bonding interactions between hydroxyl hydrogen and water oxygen atoms differed in the α- and β-l-idopyranose simulations at the O2 and O4 positions. The relatively decreased peak height in the β-l-idopyranose RDFs at 1.8 Å indicates comparatively fewer solute-solvent hydrogen bonding interactions (cf. α-l-idopyranose) in the first hydration shell at both positions (Figure 5). The inequalities observed in the second solvation shell trended similarly and also indicate a different water structure at O2 and O4. Integration of the RDFs in the first shell (1.0 to 2.5 Å) showed the presence of 0.55 and 0.48 water molecules in the α- and β-anomers, respectively. In the second shell (3.0 to 5.0 Å), the respective water occupancy was computed to be and 1.14 and 1.05. No differences were observed in RDFs computed for interactions between water oxygen atoms and hydroxyl hydrogen atoms at the pyranose O3 and O6 positions.

Figure 5.

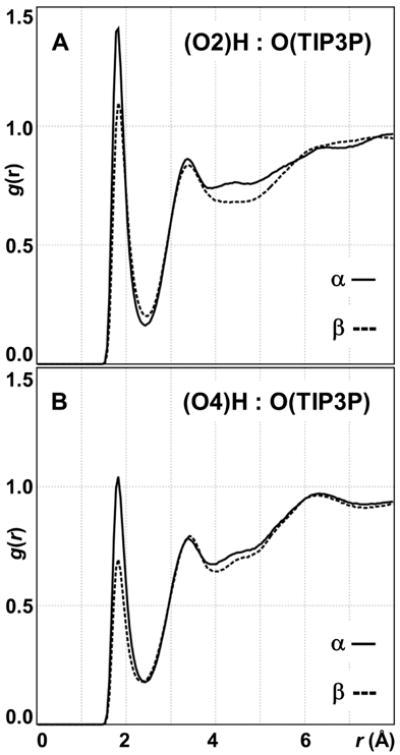
Radial distribution functions for the through-space interaction of TIP3P water oxygen atoms and hydroxyl hydrogen atoms at the α- (1) and β (2) -l-trajectories using the substituentidohexopyranosyl ring positions O2 (A) and O4 (B).

Secondly, the computed water density in close proximity to the solute, over the lifetime of the 10 μs trajectories, was different in the simulations of 1 and 2. Inequalities were observed in the computed water densities using the TIP3P solvent model, with the most significant difference being the greater propensity of water to cluster in the cavity bounded by the anomeric 1-O-methyl substituent and the C6 hydroxymethyl group in the β-anomer, compared to the α-anomer (Figure 6). The explicit solvent simulations therefore suggest that water molecules present within this cavity in the β-l-idopyranoside slow the μs-kinetics of pyranose puckering.

Figure 6.

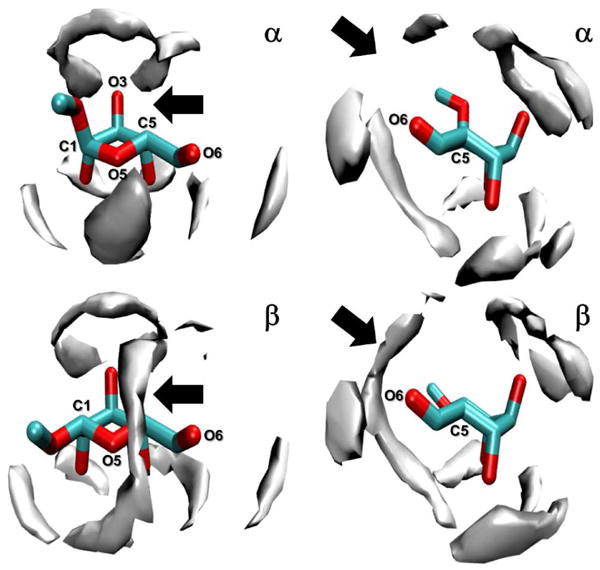
Isosurface representations of computed water densities surrounding 1 and 2 during 10 μs explicit solvent (TIP3P) simulations.

Figure 6 footnote: Two views of each anomer, in the ¹C₄ pucker, are shown. The cavity bounded by the anomeric 1-O-methyl substituent and the C6-hydroxymethyl group is indicated by an arrow.

This hypothesis was further supported by analysis of 10 μs periodic gas phase MD data for 1 and 2. The principal difference from the explicit solvent MD was a three-fold increase in the computed forward ¹C₄→⁴C₁ transition rate in the β-anomer, computed to be 1 μs^-1 in the aqueous MD and 3 μs^-1 in the gas phase (Supporting Information). Calculated α-anomer ¹C₄→⁴C₁ puckering rates were identical in the water and gas phase MD. This finding is consistent with the proposal that water structure causes the slower puckering kinetics of the β-anomer, compared to the α-anomer. Together, these predictions rationalise the smaller measured and calculated ³J_H,H values in the β-anomer (cf. the α-anomer). Mechanistically, the explicit solvent MD findings suggest that water molecules limit the capacity of the β-anomer to adopt the 3D-intermediates ¹H_O and ⁴H₃ highlighted in Figure 3.

Conclusions

Pyranose ring puckering is crucial to carbohydrate-protein interactions and concomitant bioactivity, exemplified by the heparin-antithrombin III interaction,⁷ which initiates anticoagulation. Previous work has shown that pyranose substituents and chiral configurations (epimers) impact μs-puckering kinetics.^{1, 4, 23} To further understand the effects of stereochemical changes on puckering, here we used flexible idopyranosides as a model to explore the dependence of pyranose μs-exchange on anomeric configuration, which is also a key regulator of bioactivity (e.g., glycan-lectin³³ binding).

The aqueous simulations described herein explain the different experimentally observed puckering ensembles in 1 and 2 and reveal intermediate puckers that are less favourable in the β-anomer compared to the α-anomer, in water. Comparison with a previous¹ explicit solvent 10 μs simulation of methyl α-l-idopyranuronate 3 intimated that conversion of the C6 carboxyl group to a hydroxymethyl group in an α-l-idopyranosyl ring significantly increases the forward (¹C₄→⁴C₁) and backward (⁴C₁→¹C₄) puckering exchange rates by five- and ten-fold, respectively. Based on previous work concerning the effect of 1-O-methylation on aqueous monosaccharide μs-puckering,²³ we anticipate that the free reducing idopyranoses will exhibit different puckering 3D-ensembles from those seen in the simulations of 1 and 2. The effect of C6 substitution in the free reducing idopyranoses also remains to be studied.

The present work reaffirms the role of water as a major contributor to carbohydrate 3D-structure,¹¹ suggesting that water determines pucker populations and chair-chair exchange kinetics, and also provides evidence that three- and four-site water models perform similarly with respect to computed μs-puckering 3D-structural, kinetic and thermodynamic properties. It will likewise be informative to test the performance of simpler (e.g., implicit) and more complex (e.g., five-site) water models when such simulations become practical on the timescales required to converge pyranose puckering (≈2-5 μs).^{1, 4, 23} The observation that water structure plays a role in pyranose μs-puckering kinetics can be exploited to help engineer exchange rates and bioactivity. For example, substituents that stabilise potential biologically important puckers in 1, 2, 3 and structurally-related molecules can be studied in silico on μs-timescales and in water, prior to synthesis and biological testing. In this regard, biologically relevant, kinetically rigorous and experimentally validated microsecond simulations, such as those reported here, are an important step towards deciphering glycomic structure-function relationships and rational design of new carbohydrate-based medicines and materials.