Comparative Studies of Microtubule Mechanics with Two Competing Models Suggest Functional Roles of Alternative Tubulin Lateral Interactions

Abstract

The dynamic assembly and disassembly of microtubules and the mechanical properties of these polymers are essential for many key cellular processes. Mathematical and computational modeling, especially coupled mechanochemical modeling, has contributed significantly to our understanding of microtubule dynamics. However, critical discrepancies exist between experimental observations and modeling results that need to be resolved before further progress toward a complete model can be made. Open sheet structures ranging in length from several hundred nanometers to one micron have often been observed at the growing ends of microtubules in in vitro studies. Existing modeling studies predict these sheet structures to be short and rare intermediates of microtubule disassembly rather than important components of the assembly process. Atomic force microscopy (AFM) studies also reveal interesting step-like gaps of the force-indentation curve that cannot yet be explained by existing theoretical models. We have carried out computational studies to compare the mechanical properties of two alternative models: a more conventional model where tubulin dimers are added directly into a microtubule lattice, and one that considers an additional type of tubulin lateral interaction proposed to exist in intermediate sheet structures during the microtubule assembly process. The first model involves a single type of lateral interactions between tubulin subunits, whereas the latter considers a second type that can convert to the canonical lateral contact during microtubule closure into a cylinder. Our analysis shows that only the second model can reproduce the AFM results over a broad parameter range. We propose additional studies using different sizes of AFM tips that would allow to unambiguously distinguish the relative validity of the two models.

Introduction

Microtubules (MTs) are long, hollow cylindrical polymers consisting of ∼13 parallel protofilaments (PF), each formed by the head-to-tail assembly of αβ-tubulin heterodimers. The outer and inner diameters of MTs are ∼25 and 15 nm, respectively, whereas the length can vary from tens of nanometers to tens or even hundreds of micrometers, frequently spanning the whole cell. MTs serve as one of the three major cytoskeletal components in eukaryotic cells, acting as mechanical support for cells and as both the stage and player in many eukaryotic cellular processes, including intracellular transport, cell motility, mitosis, and meiosis.

Understanding the nanomechanical properties and assembly/disassembly dynamics of MT is a fundamental problem, and an active research topic in molecular cell biology and in material science (1–4). MT dynamic instability is known to be a key property for MT function, and a number of protein families interact with MTs to precisely regulate their dynamics and ultimately their function (5,6). MT dynamics regulation has been shown to be of particular biological significance during cell division, as well as of outstanding pharmaceutical value in the treatment of cancer. Many widespread diseases are found to correlate with malfunctioning of MT assembly. For example, Huntington's disease is an autosomal dominant inherited neurodegenerative disease presenting progressive involuntary movements and cognitive changes. Its gene product has been shown to interact with polymerized MT (7). Depolymerization of MTs by toxins such as rotenone disrupts vesicular transport and is found to be related to neurodegenerative diseases such as Parkinson's and Alzheimer's disease. Down syndrome, one kind of severe genetic disease, is known to be caused by chromosome missegregation that may be due to meiotic spindle MT defects or defects in MT-chromosome binding. Therefore, MTs and their associated proteins often serve as therapy targets (8). For instance, Taxol is a broadly used anticancer drug targeting MTs. It disrupts the fast dividing cancer cells by altering MT dynamics. MT-stabilizing drugs are also used in Alzheimer's disease treatment (9,10).

Additionally to their dynamics, the mechanical properties of MTs, e.g., bending resistance and local deformation, are also essential for many MT functions, such as proper spindle assembly and function or the beating of cilia and flagella. Although there have been extensive studies on the responses of MTs to mechanical stress, the nonlinear response of MTs bending, especially buckling, is not fully understood. Moreover, the linear mechanical properties of MTs under various conditions (different binding proteins, different assembly conditions, etc.) are still under debate. For instance, different labs reached different conclusions on whether a pure MT or Taxol-treated MT has higher Young's modulus (3,11–15). Other quantitative measurement can vary as much as two orders of magnitude (see Table S1, which summarizes some published results). Recently, de Pablo et al. (16) and Schaap et al. (17) pushed onto an MT surface using an atomic force microscopy (AFM) tip and measured the indentation distance as a function of the force applied. They observed nonlinear responses, especially backward steps—sudden drops in the force needed to induce further indentation. Interestingly, the process was reversible. Upon removing the AFM tip, the original MT structure was recovered.

From a mathematical modeling perspective, an MT and related tubulin-based polymers are modeled either as continuous manifolds or as interacting discrete objects. For the latter a widely used scheme is to model individual αβ-tubulin heterodimers as rigid bodies interacting through longitudinal and lateral bonds as described in available MT cryo-electron microscopy (cryo-EM) structures. Computational studies with this model (which we will refer to as L1) have had significant success in explaining a number of experimental observations (18–20).

On the other hand, a number of studies indicate that alternative, nonmicrotubular interactions may exist between tubulin subunits (21–23). Wang and Nogales (21) obtained the cryo-EM structure of a tubulin polymer (called ribbon in the remaining discussions) in the presence of GMPCPP and high magnesium at low temperatures (21–23). The ribbon structure, which converts directly into MTs upon raising the temperature, is formed by two types of alternating lateral interactions between PFs: one is indistinguishable from that in MTs, which we call tube bond (notice that we refer to a noncovalent contact as a bond to follow the convention in the field (24)); the other is a different type of interaction, which we call the sheet bond (23,25). In a doublet one particular PF interacts with two PFs simultaneously, with one interaction resembling the tube bond and the other structurally resembling the sheet bond (23,26). Schaap et al. discussed this two-type lateral bond model as a possible explanation to their experimental observations (16,17). Interestingly, we have also previously noticed that residues that participate in the sheet bond are evolutionarily more conserved than those forming the tube bonds (23,27), a fact that suggests that these residues are functionally significant.

We have previously formulated a computational model (referred to here as L2) that considers the two types of lateral interactions during early tubulin assembly stages (23). With stochastic simulations, the model suggests that tubulins can form kinetically trapped intermediate structures with mixed types of the lateral bonds, which eventually convert into the MT structure. These intermediates may correspond to the observed open sheet structures at the growing end of MTs observed by cryo-EM (28,29).

The objective of this study is to determine if a sheet bond is required to explain the mechanical data of Schaap et al. through comparative analysis of the two discrete MT structure models against experimental data. Our hypothesis was that the existence of the sheet bond would have a significant effect on the mechanical properties of MTs, and that the two models may predict qualitatively different behaviors at some extreme conditions. For the L2 model, mechanical stress may transform some of the lateral bonds to sheet bonds locally as it distorts MTs. MTs in vivo are constantly under large mechanical tension (30–32). Without breaking the MT, the mechanism of converting lateral bonds to sheet bonds may release some of the mechanical stress. Consequently, sheet bonds could serve as a temporary alternative interaction between PFs that maintain some stability in the distorted MT. Given the uncertainty of some key parameters, our strategy here was to first develop a mathematical framework capable of describing both types of models, and then examine their predictions within the physically relevant parameter space.

Methods

The model

The size of the system that we are trying to study, together with the lack of high resolution structural information, make molecular dynamics simulations at the atomistic level impractical and unreliable. Instead, we used a coarse-grained modeling framework that treats the assembly of α- and β-tubulins as rigid bodies connected by elastic springs. For better comparison with previous studies, we chose the mathematical structure of our models to resemble as much as possible the work of VanBuren et al. on the L1 model (20) (see Fig. 1). VanBuren et al. modeled tubulin dimers as connected vectors. We expanded the representation concerning two major aspects. First, we treated each monomer as a rigid body and allowed both intra- and interdimer bending motion to be consistent with experimental observations (21,33). Second, each tubulin dimer has spatially distributed lateral interaction sites, similar to the model of Molodtsov et al. (18) but with extra binding sites corresponding to the sheet bonds for the L2 model. Therefore, our model contains more degrees of freedom than those previously described, necessary to fully describe the two sets of tubulin lateral interactions. Fig. 1, a–c, illustrate the basic modes of three-dimensional motion related to both longitudinal and lateral tubulin-tubulin interactions, and the composite sheet-tube bond conversion central to the L2 model.

Figure 1.

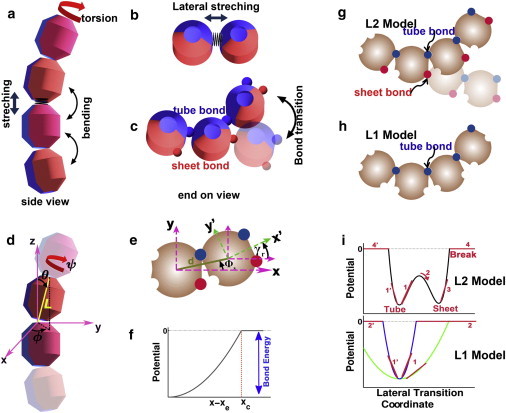
Schematic representation of the physical parameters used in the L1 and L2 models (color online). (a) Basic modes of motion related to longitudinal interactions: interdimer stretching, intra- and interdimer bending, and interdimer torsional motion. (b) Basic modes of motions related to lateral interactions: stretching, translational shift, and torsion. (c) Conversion between two types of lateral bonds that result from the combinations of lateral modes. (d) Four coordinates (L, θ, ϕ, ψ) describe the relative position and orientation between two neighboring monomers. Monomers, each treated as a rigid body, are connected head to tail along the longitudinal direction (protofilament). All energy terms are expressed as functions of these four coordinates. (e) The relative coordinates (d, θ_s, ϕ_r), describing the relative position and orientation between two lateral neighboring monomers, represent the distance and the translational angle between the centers of mass of two monomers, and the reorientation of the monomer internal coordinate system, respectively. These values are derived from the four coordinates in (d). (f) Schematic illustration of the truncated harmonic potential form used, where x_e stands for the equilibrium value in the corresponding dimension, and x_c is the critical value where the interaction becomes zero. (g–h) Schematic comparison between the L2 and L1 models. The former generalizes the latter by adding one more type of lateral interaction (sheet bond in red) in addition to besides the traditional tube bond (in blue). (i) Schematic illustration of the composite double-well (for the L2 model) and single well (for the L1 model) potentials along the lateral bond conversion coordinate. The blue and green curves for the L1 model correspond to stiff and soft tube bonds, respectively. The lateral transition coordinate is defined as an effective coordinate that combines the effects of stretching, shifting and rotating movements.

Fig. 1, d and e, summarize the mathematical terms used in the L1 and L2 models. For each PF, with the assumption that neighboring tubulins are connected head-to-tail, the degrees of freedom for each monomer are reduced to four, with (L, θ, φ, ψ) defining the relative position and orientation of a monomer relative to the previous one on the same PF. Three additional coordinates define the spatial position of the starting (minus) end of the PF relative to the laboratory frame. To facilitate the description, we also define several auxiliary variables using the four basic coordinates. Following VanBuren et al., we define Φ as the angle between the preferred and the actual orientation of the vector representing a monomer. Each monomer has an internal coordinate frame, with the x axis along the connection between the center of mass (COM) and the middle of the two lateral interaction sites on one site, the z axis along the connection between the COM of the α-tubulin and the longitudinal interaction site of the two intradimer tubulins, and the y axis perpendicular to the x-z plane. We then define Φ_s and γ_r to describe the lateral shift and rotation relative to the COM (see Fig. 1 e and Fig. S1).

With the previous mathematical representation, we introduce individual free energy terms to define the longitudinal and lateral interactions between monomers. Longitudinally, there are stretching (changing of L relative to its equilibrium value), bending (changing of Φ), and torsion terms (changing of ψ) (Fig. 1, a and c). Laterally, there are stretching (changing of d), shifting (changing of Φ_s), and rotation terms (changing of γ_r) (Fig. 1, b and e, Fig. S1). To be comparable with the experimental data, especially the elastic properties measured for the MT, the main part of each energy term is represented by a harmonic potential in the form $E=1/2k{\left(x-x_e\right)}^2+E_0$ within a cutoff x_c, a near hard surface interaction when the monomers are very close, and a relaxed tail for x > x_c. Fig. 1 f shows the main (harmonic part) shape of the energy functions. Overall, the energy function has a Lennard-Jones-like potential form in the distance space, where the parameters can be easily input from elastic measurements. For simplicity, we neglect possible cross-terms. The sheet and tube bonds have different equilibrium values of d, Φ_s, and γ_r, respectively. Two monomers can switch between the sheet and tube bonds (see Fig. 1, c and g), with a double-well shaped composite potential along the switching coordinate (as a combination of Φ_s and γ_r, see Fig. 1 i). To obtain the L1 model, one simply sets the sheet bond-related spring constants and E₀ to be zero, resulting in a single-well shaped potential (Fig. 1, h and i). Fig. 1 i shows two such potentials corresponding to a stiff and a soft tube bond, respectively. The total energy (potential of mean force, to be more precise) of the structure is then summed over all the potential function terms.

Numerical methods

All model parameters are listed in Table 1, unless otherwise mentioned. Some of the parameters were estimated from available experimental data, and inherited from the model of VanBuren et al. For parameters lacking experimental data, we varied the values over physically feasible ranges and analyzed the model behavior. We obtained stable conformations by minimizing the total energy of the structure using the Quasi-Newton method and the simplex approach (34). The local minimization algorithms allowed us to obtain metastable structures. To simulate AFM experiments, we first constructed a stable MT form, and then exerted force with a sphere-shaped AFM tip onto the MT wall. At each step, the AFM tip moved a small step (0.2 nm in our simulations) down to the MT wall, and then the stable conformation was obtained by minimizing the total energy, including the hard-sphere interactions between tubulin monomers (modeled as spheres with diameter 4 nm) and the AFM tip. We calculated the force exerted by the tip using the force balance relation. Further details of the model and the numerical procedure can be found in the Supporting Material.

Table 1.

Model parameters

Parameter	Physical interpretation	Value	Estimation method and reference
kland	Spring constant for longitudinal stretching	1.32 GPa · nm	(20) (11–15,47–51) (16,17)
kbend	Spring constant for longitudinal bending	34 kBT/dimer · rad	(20, 52)
ktorsion	Spring constant for longitudinal torsion	10 kBT/dimer · rad2	Model based
klot	Spring constant for lateral stretching	0.8 GPa · nm	(20) (11–15,47–51) (16,17)
kst	Spring constant for tube bond lateral shifting	116 kBT/dimer	(3) (53,54)
kss	Spring constant for sheet bond lateral shifting	10 kBT/dimer	Model based
krt	Spring constant for tube bond lateral rotation	50 kBT/dimer · rad2	Model based
krs	Spring constant for sheet bond lateral rotation	10 kBT/dimer · rad2	Model based
$\Delta G_{long}^o$	Longitudinal bond energy	−20 kBT	(2,24)
$\Delta G_{lat}^o$	Lateral bond energy	Tube bond: −5 kBT	(2,23,24)
		Sheet bond: −3 kBT

All parameters are base values and details on how to get the values can be found in the Supporting Material. Different values used in model estimations are specified in the main text.

Results

The L2 but not L1 model can reproduce the AFM studies on MT wall deformability by force over a broad parameter range

Fig. 2 a schematically describes the AFM experiments of Schaap et al. (16,17,35). The AFM tip pushes onto the surface of a Taxol stabilized MT that has been immobilized on a glass slide. The experiment measures the force-indentation (F-I) curve, that is, the force exerted on the MT wall by the AFM tip versus the induced indentation on the MT wall. The black line in Fig. 2 b reproduces a typical experimental curve. The curve can be divided into four regions: region 1 corresponds to indentations from 0 to the value indicated by the red dashed line shown in Fig. 2 b, where the mechanical response is linear, and the slope of 0.074 ± 17% N/m reflects the effective spring constant of the MT wall; often there is a step-like gap ∼0.6 nm wide that follows region 1, and which we label region 2; (see also Fig. S2 for the definition of a gap); in region 3, the mechanical response is again quasilinear; finally, in region 4 the response is nonlinear, implying that the MT can no longer hold its integral structure.

Figure 2.

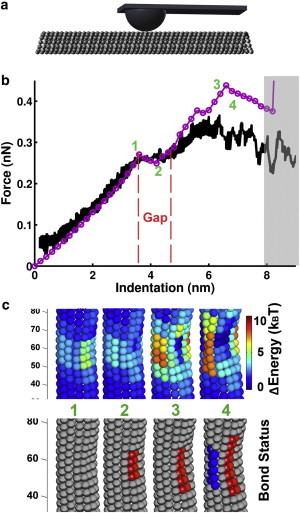
Simulated results using the L2 model for an AFM tip pushing against the microtubule wall. (a) Schematic illustration of the experimental setup with the tip size corresponding to 25 nm. (b) Experimental force-indentation curve (black line) adapted from (17) and the simulated results (purple circles). The black line is averaged over 24 indentation curves from five different experiments. Simulated F-I curve (purple circled line) with a ∼120 nm MT and a tip with radius = 25 nm to be consistent with the experiment. The red dashed lines indicate the gap region between two linear segments present before the nonlinear response. Fitting the first linear region gives a slope ∼0.07 N/m, as compared to the experimental slope of ∼0.074 ± 17% N/m. Within the gray region complicated dynamic processes take place in real systems, which one should not expect the current modeling approach to capture. (c) Sections of the simulated MT conformations under the pressure of the AFM tip, shown at different indentation positions (as numbered in (b)). Upper panel shows local energy plots. Lower panel shows bond type plots: tube bond is gray, sheet bond is red, and blue indicates the break of the lateral bond between adjacent tubulins. All mechanical and energetic values involved are listed in Table 1, unless otherwise indicated.

We first performed computer simulations using the L2 model and mimicking the experimental conditions closely. Fig. 2 b and c, Fig. S3 a and an online supporting movie (Movie S1 of the Supporting Material) show that the L2 model can easily reproduce the gap (region 2 in the curve). As the AFM tip compresses the MT, the tubulin dimers around the contact region are under mechanical stress (step 1 in Fig. 2, b and c), giving the first linear response region of the F-I curve. The stress builds up, until the conversion of some tube bonds into sheet bonds releases some of the stress, and results in the gap (step 2). Further compression leads to a quasilinear response again. The L2 model predicts that during the process, additional sheet-to-tube bond conversion may take place, which may result in even more gaps. This prediction awaits experimental confirmation (step 3). Eventually some lateral bonds break, with some tubulin dimers even dissociating from the MT (step 4). In this region one does not expect that the current energy-based procedure of calculating the force could capture the complicated dynamic process taking place during the AFM experiments (highlighted as gray region in Fig. 2 b). It is also expected that the L2 model would predict slightly delayed rupture events than the L1 model due to the energy relaxation of lateral bond interaction concomitant with a transition from tube bond to sheet bond at some place in the microtubule structure (Fig. 2 c, upper panel).

We can consider these results of the simulation in the context of the double-well shaped potential between two neighboring tubulin dimers shown in Fig. 1 f. A number of tubulins within and near the AFM tip contact region contribute to the observed F-I curves. For the tubulin molecules in direct contact with the AFM tip and their near neighbors, the response corresponds to first being pushed uphill within the tube potential well (labeled 1 in the upper panel of Fig. 1 f), which contributes to region 2 of the F-I curve, and then crossing the barrier and falling to the sheet bond well (labeled 2 in the figure), which results in the gap, and then being pushed uphill again within the sheet bond well (labeled 3 in the figure), which contributes to region 3 of the curve (together with major contributions from other tube bonds). Eventually, some tubulins break their lateral bonds completely (labeled 4 in the figure), leading to complex nonlinear responses (step 4). For those tubulins on the opposite site of the MT with respect to the tubulin-AFM tip contact site, their response in the F-I experiment corresponds to first being pushed uphill within the tube potential well along the 1′ direction, and eventually breaking the bond (labeled 4′ in the figure).

Given the uncertainties of model parameters, we performed a sensitivity analysis for those parameters lacking precise experimental constraints. The upper panel of Fig. 3 a gives the dependence of the linear response slope of the F-I curve, κ, on various parameters. The largest change of κ (±25%) occurs when the two tube bond-related parameters k_st or k_rt vary from half to twofold of the base values. The torsional energy and sheet bond-related spring constants have negligible effects on κ. The results indicate that most of the contribution to the linear response comes from the tube bonds, which constitute the majority within the structure. On the other hand, the lower panel of Fig. 3 a shows that the gap position depends strongly on the tube shift constant k_st as well as on the sheet bond parameters k_ss and k_rs. These results reflect the fact that in the L2 model the gap is due to tube-to-sheet bond conversion, and involves large relative lateral rotations between neighboring tubulins. The two-parameter analyses in Fig. 3, b–d, further show that these parameters affect the MT mechanical properties cooperatively. Accurate experimental measurements may help to constrain these parameters. Fig. 3 d shows the region of k_st and k_rt consistent with the observed gap position and the linear response slope. In summary, the L2 model reproduces the gap behavior over a broad range of parameter values, with the only requirement that the barrier between the sheet and tube bonds is lower than the individual bond energies.

Figure 3.

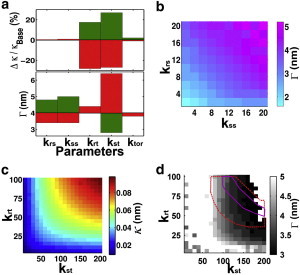
Sensitivity analysis and estimation of the L2 model parameters. (a) Dependence of the slope of the linear force-indentation curve region (κ) and the gap starting position (Γ) on various model parameters, while keeping all others at their base values listed in Table 1. For each parameter, the graphs show relative changes in κ from those for k_base to values of 0.5 k_base (red bars) and 2k_base (green bars). (b) Two-dimensional contour plot of Γ dependence on k_ss (in units of k_BT/dimer) and k_rs (in units of k_BT/dimer/rad²), with all other parameters at base values. (c) Two-dimensional contour plot of κ dependence on k_st (in units of k_BT/dimer) and k_rt (in units of k_BT/dimer/rad²). (d) Two-dimensional contour plot of Γ dependence on k_st and k_rt. The blank area indicates Γ > 5 nm, Γ < 3 nm or no recognizable gap. The region enclosed by dashed lines gives κ = [0.05, 0.85] N/m, and the region enclosed by the solid line gives κ = [0.07, 0.08] N/m.

We performed similar analysis using the L1 model. Fig. S4 (also see Fig. 4) gives some typical F-I curves with the L1 model using different values of the tube bond energy. Interestingly, the L1 model also produces a recognizable gap under certain conditions (see Fig. S4). However, in this case the gap always appears at an indentation around or larger than 5 nm. Furthermore, only a short and barely recognizable quasilinear region follows the gap before a structureless nonlinear region. Additionally, only a very small range of parameters can generate this gap-like behavior, even for these very loose criteria to identify gaps (Fig. S9). These two features persist upon varying parameter values, and are inconsistent with the experimental observations. Close examination of the simulations showed that at the gap the PF pressed by the AFM tip broke some lateral bonds with neighboring PFs without breaking any longitudinal bond (Fig. S4 g) This is one of the mechanisms suggested by Schaap et al. to explain the gap in their experimental curves. The process corresponds to pushing the single-well shaped potentials in the lower panel of Fig. 1 f up first (labeled 1 and 1′ in the figure), and then breaking the bonds (labeled 2 and 2′ in the figure). However, this unzipping mechanism usually initializes breaking of additional lateral bonds, explaining why the F-I curve quickly enters the nonlinear region after a very short quasilinear region.

Figure 4.

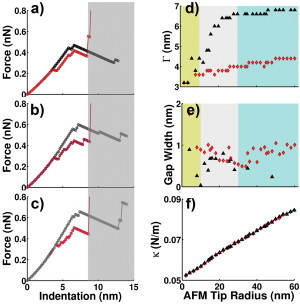
Comparison of the force-indentation curves created by the L1 (black triangle) and L2 (red diamond) models (color online). (a–c) The F-I curves with AFM tip radii of 20, 30, and 40 nm, respectively. The gray area indicates where the experiments and simulations do not correspond to the same conditions. (d–e) The gap position Γ and width as a function of the AFM tip radius R. Yellow region: R = 0 ∼10 nm; gray region: R = 10 ∼30 nm; blue region: R = 30 ∼60 nm. Missing points correspond to nonrecognizable gaps. (f) Calculated slope of the linear region of the F-I curve κ versus the AFM tip radius. All simulations were performed with an MT length of ∼120 nm, and using the parameters listed in Table 1 unless otherwise stated.

Suggested AFM experiments to distinguish between the two models

Although the previous analysis indicates that the L2 model explains the gap in the experimental F-I curves better than the L1 model does, the evidence is not fully conclusive because the latter can also generate the gap with certain choices of parameters. We suggest that one would be able to discriminate between the two models by measuring the F-I curves using AFM tips with different sizes. As shown in Fig. 4, the two models show qualitatively different behaviors. Consistent with what is shown in Fig. 2 and Fig. S4, Fig. 4, a–c, show that both models can generate the gap. However, with tip size increasing from 10 to 30 nm, the L1 model predicts that the gap position increases from ∼4 to > 6 nm, whereas the L2 model predicts roughly an unchanged gap position (see Fig. 4 d). With a large sized tip (30–60 nm), the L2, but not the L1 model predicts a noticeable gap width (see Fig. 4 e). Fig. 4 f shows that both models predict similar, nearly linear dependence of κ on the AFM tip size. Therefore, one cannot distinguish the two models by examining MT behaviors within the linear region, and needs to go beyond.

Suggested experiments to further constrain model parameters

As shown in Fig. 3, accurate measurement of mechanical properties could be used to determine MT model parameters. Here, we present additional modeling studies using the L2 model that could be explored experimentally in the future. Fig. S5 a shows the energy state for a typical long MT with the AFM tip pressing on the middle of the MT wall. The nonzero energy changes on the MT wall are about ± 40 nm apart from the tip center point at an indentation of 7.4 nm (which is just before the MT breaks). This indicates that MT deformation can only propagate ∼40 nm along one direction. This conclusion can also be drawn from Fig. S5, b and c. The F-I curves overlapped in the linear region for MT lengths > 80 nm, for both small and large AFM tips. More detailed analysis (Fig. S5 c) showed that the shorter the MT, the softer the response to the pressing AFM tip. For varying AFM tip radius, the critical lengths at which the boundary effects vanish are predicted to be all around 80 nm. The AFM tip radius changes the response strength of the MT wall (Fig. S5, c and d). The larger the AFM tip, the higher the effective spring constant κ. This effect is due to larger tips having a larger contact surface on the MT wall and thus leading to more tubulin monomers being involved. Note that the change of κ (∼0.04–0.09 N/m, Fig. S5 c) is small despite the large variation in the tip radius β (2–60 nm). This result is consistent with experimental observations (17). Fig. S5, c and e, show that the gap position Γ increases with the tip radius, but decreases with the MT length, and it plateaus at around 50 nm. Again, because a larger tip has a larger contact surface with the MT wall, the force is resisted by more tubulin monomers. Therefore, the monomers tend to have smaller deformations per unit of indentation distance because of the smaller force exerted on them. This effectively delays the transition from tube bond to sheet bond and therefore the gap position Γ. Similarly, a shorter MT is softer, and its lateral bond transition takes place at a larger indentation.

Another set of simulations that could be tested experimentally is to change the position of the AFM tip by moving the tip across the MT (from PF to PF) or along the MT longitudinal direction (along a single PF) (see Fig. S6). MTs are polymers of α- and β-tubulin dimers polymerized head to tail into PFs, about 13 of which associate laterally making the cylinder. Therefore, the MT wall is not smooth but bumpy, both along the longitudinal (z) and even more so the lateral directions (x). We find that the bumps along the PFs do not make observable difference on both linear and quasilinear responses, but those formed between PFs do have effects on both kinds of mechanical responses. The effective spring constant κ changes with the number of protofilaments that interact with the AFM tip when it moves along the x direction. These changes are not observed, in contrast, when the AFM tip moves along the z direction because the interacting PFs remain the same. The Supporting Material provides a detailed discussion.

The L2 model predicts metastable hybrid sheet structures with different curvatures during MT assembly

Fig. 5 gives several examples of structures obtained by minimizing the free energy of the L2 model. There are two structures available experimentally at medium resolution (12–8 Å): the ribbon polymer containing alternating tube and sheet lateral bonds (21), and the MT containing only tube bonds (36). We constrained the parameters of our L2 model by requiring it to reproduce the two structures. The ribbon structure shown in Fig. 5 a contains the correct alternating sheet and tube bonds between PFs. The sheet bond tends to bend out of plane, and the tube bond tends to bend into the plane. Notice that the bending is not exactly perpendicular to the PF axis. The overall structure is thus helical in nature (ribbon-like). The bending angle between monomers along each PF is ∼3.5°, consistent with the experimental value (22). The MT structure shown in Fig. 5 e is energetically the most stable structure. The L2 model also gives a (large) number of additional structures (as those shown in Fig. 5, b–d), which we call hybrid because they are neither pure MT structures nor pure ribbon structures but combinations of some sheet bonds and some tube bonds. Such structures correspond to local minima of the free energy function. Increasing the content of tube bonds has a straightening effect in the structure. Therefore, the presence of hybrid polymers can in principle explain the observed sheet intermediates during the assembly process (29), with the variable curvatures reflecting the amount of initial sheet bonds already converted to tube bonds. To support this proposal, Fig. 5 c shows a polymer with one end closed into a tube, and another end still having the open structure with remnant sheet bonds. Fig. 5 d gives another hybrid structure with branched ends, which resembles more closely what is observed experimentally (29).

Figure 5.

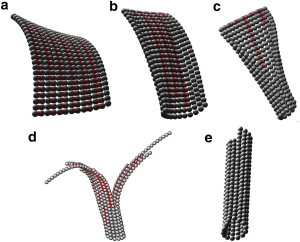
Typical tubulin polymer structures obtained through local free energy minimization of the L2 model starting with different initial conformations (color online). In this figure, a red dotted line corresponds to sheet bonds between two neighboring PFs. (a) Ribbon structure with the two types of lateral bonds alternating between neighboring PFs. (b–d) Hybrid structures with less regular distribution of the lateral bonds. (e) Canonical MT structure.

Discussion and Conclusions

Currently, a widely accepted model assumes that MT assembly is a simple process where individual αβ-tubulin heterodimers add one by one onto the growing end of an MT (37,38). Mathematical modeling using this model (which we will refer to as L1) has had significant success explaining a number of experimental observations. However, there are still unresolved contradictions between experimental observations and computational modeling results based on the L1 model. Following the observation that the fast growth of MTs occurs via the elongation of an outwardly curved sheet-like structure (29), Jánosi et al. (1) and Chretien and et al. (39) performed theoretical studies on the sheet structure using a continuum elastic model and a ball-spring model (40), always assuming only one type of lateral bond. These studies explained the sheet structures with different curvatures as incomplete MTs with different number of PFs. However, one should treat the conclusions from this continuum model studies with some caution. In particular, work did not address how and whether the a priori assumed sheet structure can form under the L1 model. Systematic stochastic modeling studies by VanBuren et al. show that, based on the L1 model, long incomplete structures at the MT growing end are very unlikely to form. Such structures appear both energetically and kinetically unfavorable and are precursors for disassembly rather than assembly (20). This observation is against the proposal of Chrétien and co-workers that the observed long sheets are merely incomplete MTs with the number of protofilaments <13 (29). VanBuren et al. did not examine the dependence of sheet length on tubulin concentration. One would expect in their model weak or inverse dependence, because low tubulin concentrations favor disassembly and, thus, sheet formation according to VanBuren et al. (20). This is in contradiction to the observation that the sheet structures are observed under growth conditions and become longer upon increasing tubulin concentrations (29).

A number of studies indicate that alternative, nonmicrotubular interactions may exist between tubulin subunits during the MT polymerization process in the form of an assembly intermediate. These studies include the visualization by cryo-EM of open sheet structures at the growing end of MTs (28,29,41–43), and the cryo-EM structure of a tubulin polymer (ribbon) proposed to mimic such growth sheets. Because the ribbon structure of Wang and Nogales (21) was obtained under distinct conditions from those normally used for in vitro assembly of MTs, most significantly low temperatures, there has been some skepticism about whether the observed new lateral contact is an artifact without physiological significance.

Therefore, a systematic analysis on this alternative bond type is timely and needed. To shed light on the still remaining issues concerning the structural basis of MT dynamics, and resolve apparent discrepancies between experimental and model observations, we performed coarse-grained modeling studies on the mechanical properties of two classes of competing models of tubulin interactions that assume either one or two types of lateral bonds between neighboring protofilaments. The previously described L1 model (18,20) can explain a significant body of experimental observations. The L2 model presented in this work is an extension of the L1 model. The L2 model incorporates most of the properties of the L1 model, but has been extended to incorporate new structural data and to further reproduce additional experimental results that are not readily accounted for by the latter. Specifically, we analyzed the AFM measurements of Schaap et al. (17) Within the context of the L2 model the experimentally observed gap can be reproduced over a broad range of modeled parameter space and experimental conditions. In this model the gap arises from the tube-to-sheet bond conversion of a small number of tubulins being pushed by the AFM tip. In contrast with the simulation results observed with the L2 model, the previously proposed L1 model reproduces the gap only under a narrow range of experimental conditions. Most importantly, large structural ruptures usually follow the gap, in contradiction with the observed quasilinear response region that follows the gap in the experimental F-I curve. Our analysis leads to predictions concerning the mechanical properties of MT that are experimentally testable. In particular, our analysis indicates that it should be possible to distinguish between the two models and thus ascertain their validity, by measuring the F-I curves using different AFM tip sizes. The type of AFM experiments described by Schaap and colleagues is closely related to the nonequilibrium single molecule pulling experiments that are widely used to study macromolecule properties (44). More quantitative AFM data should make it possible to reconstruct the double well-shaped free energy landscape schematically shown in Fig. 1 i, as previously shown for single molecule data (45). Such reconstruction should allow us to extract the exact value of the free energy difference between the two types of lateral bonds.

The L2 model also predicts that early tubulin assembly intermediates structurally correspond not only to the well-characterized MT lattice, but also to the ribbon polymers obtained by Wang and Nogales (21) and Wang et al. (22), and most importantly, a number of hybrid structures with various contents of the two types of lateral bonds present in the latter. We propose that these hybrid structures may correspond to different stages of the sheet structures with variable curvatures and lengths observed at the end of growing MTs, as those observed by Chretien et al. (29).

It is important to emphasize the need to evaluate competing models against multiple, rather than single experiments. In particular, an acceptable model should reproduce multiple experiments with a single set of parameters. In the doublet microtubule structure present in axonemes, at least one PF must interact with two other PFs simultaneously (26). This is clear evidence of the existence of two types of lateral bonds for tubulin in vivo that needs to be explained by global models of tubulin interactions. Although it is hard to argue that such lateral contacts do directly illustrate what happens during microtubule growth or during the AFM experiments of Schaap et al., they are singularly suggestive of the complex interaction landscape in tubulin polymers. An alternative to the existence of more than one type of lateral contact is that there is a single type of lateral tubulin interaction but involving highly flexible tubulin regions, as illustrated by the flat, single-well potential in Fig. 1 f. However, the elastic mechanical property of an MT, quantified in AFM experiments in the slope of the linear response region, sets the limit to how flexible the interactions within a single potential well can be. The estimated flexibility makes the previously mentioned alternative explanation to the doublet structure unfavorable.

We propose that the existence of the sheet bond affects MT assembly dynamics and its regulation mechanism. A large number of proteins regulate MT assembly and disassembly dynamics in vivo through interaction with tubulin, especially at the plus end of a growing MT (5,6). The sheet bond could provide an alternative binding surface for those proteins to discriminate between the body and the tip of an MT (25).

In summary, although there is not yet enough experimental data to make our studies totally conclusive in discriminating between the tubulin assembly models compared, and thus additional experiments are necessary, our computational studies indicate that further consideration and testing of the proposed L2 model is warranted. In this work, we have focused on the effect of the proposed new type of lateral bond on MT mechanical properties, and made several experimentally testable predictions. Many plus end-tracking proteins (+TIPS) preferentially bind to the growing plus end of an MT (5), and evidence shows that the prototype of these proteins, EB1, can regulate the closure of the sheet growth structure into tubes during the MT assembly process (46). It is obvious that an alternative type of lateral interaction between PFs in growing MT ends would offer a unique landing pad for +TIPS, distinct from the canonical lateral interactions in the body of MTs, and thus could be used for the distinct localization of these factors and as a powerful regulatory tool of MT dynamics. An obvious area of future analysis is to extend the L2 model to study the interaction of +TIPS with dynamic microtubules. We believe that understanding the properties of the sheet bond holds the potential to guide the design of new tubulin-based drugs that regulate microtubule dynamics by uniquely proving that tubulin interface.