Abstract
The physical and biomechanical principles that govern undulatory movement on wet surfaces have important applications in physiology, physics, and engineering. The nematode Caenorhabditis elegans, with its highly stereotypical and functionally distinct sinusoidal locomotory gaits, is an excellent system in which to dissect these properties. Measurements of the main forces governing the C. elegans crawling gait on lubricated surfaces have been scarce, primarily due to difficulties in estimating the physical features at the nematode-gel interface. Using kinematic data and a hydrodynamic model based on lubrication theory, we calculate both the surface drag forces and the nematode's bending force while crawling on the surface of agar gels within a preexisting groove. We find that the normal and tangential surface drag coefficients during crawling are ∼222 and 22, respectively, and the drag coefficient ratio is ∼10. During crawling, the calculated internal bending force is time-periodic and spatially complex, exhibiting a phase lag with respect to the nematode's body bending curvature. This phase lag is largely due to viscous drag forces, which are higher during crawling as compared to swimming in an aqueous buffer solution. The spatial patterns of bending force generated during either swimming or crawling correlate well with previously described gait-specific features of calcium signals in muscle. Further, our analysis indicates that one may be able to control the motility gait of C. elegans by judiciously adjusting the magnitude of the surface drag coefficients.
Introduction
Many undulating organisms including earthworms and nematodes move in environments where surfaces are lubricated by a thin liquid film. Examples include soil dwelling nematodes that are responsible for soil aeration (1) and parasitic nematodes that move inside the small intestine (2). The nematode and model organism Caenorhabditis elegans is of particular interest because it is widely used in biomedical research and usually investigated while crawling on wet agar plates (3–5). Undulatory locomotion on wet surfaces bears important differences with motion on dry surfaces where the texture, structure, and patterns of the organism's outer body and surface play an important role in overcoming dry friction (6–9). On wet surfaces, the thin liquid film formed between the organism's outer body and the surface is known to reduce (dry) friction, and hence facilitates propulsion by providing thrust. However, many questions remain regarding the forces nematodes need to generate to overcome surface drag. Knowledge of such forces is critical for developing accurate dynamic models (10–12), and understanding the nematode's internal muscle activities (13–15). It can also provide insight into the different kinematics and motility gaits (e.g., swimming and crawling) observed in C. elegans studies (10,11,13,16).
Much effort has been devoted to understanding the physical mechanisms by which organisms such as the nematode C. elegans generate thrust and propulsion on lubricated surfaces (5,16–18). Of particular interest is the drag force and its components, acting on the surface of the nematode. Values of surface drag forces are often obtained using resistive force theory (RFT) (5,11,16), born out of studies on undulatory swimming of organisms immersed in a liquid (19–21). In RFT, the components of the drag force normal (Fn) and tangential (Ft) to the nematode's body are assumed to be linearly proportional to the local body speed along normal and tangential directions, respectively. We note that, in the slender body theory, the drag forces are asymptotically proportional to lowest order of local body speeds (22,23). The corresponding drag force coefficients are Cn and Ct. Under this scenario, the anisotropy between the normal and tangential drag coefficients (i.e., Cn ≠ Ct) leads to net motion (24). For C. elegans swimming in fluids, the drag coefficient ratio Cn/Ct is typically in the range of 1.4–2 (10,25,26). In contrast, estimated values of Cn/Ct for nematodes crawling on lubricated surfaces (agar gels) vary by as much as an order of magnitude (5,11,16,18) and can range from 1.5 to 35. As a consequence, it is still challenging to accurately estimate the forces and energy necessary for nematodes to move on wet surfaces.
In this study, we investigate the mechanics of undulatory locomotion on thin liquid films in experiments by using a simple lubrication model. Lubrication models were recently applied to investigate nematode locomotion in granular media (27) and on liquid films (28) in experiments as well as on purely elastic surfaces using a simple theoretical model (18). The experimental investigations estimated the lubrication force to be ∼O(10−7) N (27,28), whereas an elastohydrodynamic model, used to investigate the dynamics of C. elegans on soft surfaces, found drag coefficients values of ∼O(10) and drag coefficient ratios that are rather insensitive to the surface stiffness (18). However, to the best of our knowledge, there are no experimental investigations that are able to estimate the drag forces Fn,t and its components (normal and tangential) as well as the drag coefficients Cn,t of nematodes moving on wet surfaces. Here, we present a methodology to do just that by incorporating kinematic data into a lubrication model. In addition, the nematode's internal bending forces during the crawling gait are estimated by considering the contributions of internal elastic and external viscous (surface) drag forces. Finally, spatial-temporal signals of both kinematics and internal bending forces for crawling nematodes are compared to those for nematodes immersed in a fluid to gain further insight into the mechanisms governing these two motility gaits. The analysis provided here indicates that the adoption of a crawling gait by nematodes appear to be a result of large drag coefficients that characterizes the wet surface rather than the high fluid viscosity. Results show that the spatial and temporal patterns of the internal bending force correlate well with previously described gait-specific features of calcium signals in muscle (13).
Results
Experimental observations, film lubrication, and anisotropic drag forces
C. elegans are transferred and allowed to move freely on the surface of Nematode Growth Medium (NGM) agar plates, which are cultured and prepared using standard methods (see the Supporting Material). After solidifying, a thin liquid film typically forms on top of the agar gel because the water concentration of NGM is relatively high (98% by weight). The crawling motion of the nematodes is captured using video microscopy at 15 frames/s (see Movie S1 in the Supporting Material). A total of 23 worms were used in the subsequent experiments. A snapshot of a single nematode crawling on an agar plate over three bending (undulatory) cycles is shown in Fig. 1 a, in which the red line corresponds to the nematode's body centerline (i.e., the skeleton). Here, the nematode's locomotion is decomposed into normal and tangential directions; the normal direction is defined to be perpendicular to the nematode body length whereas the tangential direction is defined along the nematode body length (Fig. 1 a). The propulsive and drag forces associated with nematode crawling on thin liquid films are analyzed along these two directions.
Figure 1.
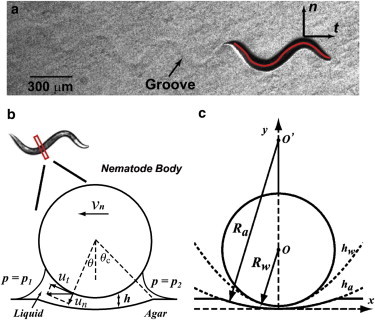
(Color online) (a) The nematode C. elegans crawls on an agar plate. (Red line) Body centerline (skeleton). (Black arrows) Unit normal and tangential vectors n and t along the nematode body. As the nematode proceeds, it leaves behind a groove on the surface. (b) Schematic diagram of nematode cross section during crawling. The fluid pressure on each side is p = p1 and p = p2. Other parameters are defined in the text. (c) The groove shape is assumed as a circular arc with radius Ra. The radius of the nematode is Rw. (Dashed lines) Parabolic curves hw and ha approximating the nematode and groove surface shapes, respectively.
Because the nematode's body length (L ≈ 1 mm) is ∼25 times its body radius (Rw ≈ 40 μm), we consider C. elegans to be a long, slender body. Hence, the analysis (to be discussed below) is restricted to the nematode's two-dimensional cross section (Fig. 1 b). As shown in Fig. 1 a, a groove forms as the nematode moves on the agar surface (17,30). In the normal direction, the nematode slides on the surface against the groove, which is lubricated by a thin liquid film. The shape of this groove is described by a symmetric circular arc-curve of radius Ra with an angular span of 2θc, as shown schematically in Fig. 1, b and c. A typical groove is 1.0-μm deep and 28-μm wide, as measured by optical interferometer (see the Supporting Material). The groove effective radius and angular span are calculated to be Ra = 100 μm and θc = 20°. The height of the liquid film h is defined as the distance between the nematode body and agar surface (Fig. 1 b). For nematodes crawling on wet agar gels, this liquid film has been shown to be very thin such that h ≪ Rw (30). In the following discussion, we study the dynamics of nematodes crawling on a wet surface with a preexisting groove.
Analytical expressions for drag forces during crawling
In the normal direction, the nematode's body and agar surface (i.e., groove) are approximated by two parabolic curves ha = x2/2Ra and hw = h0 + x2/2Rw, respectively (Fig. 1 c). The liquid film thickness is
where h0 is the minimum film thickness. We define a groove shape parameter and a normalized film thickness as and e = h0/C, respectively. The liquid film thickness can then be expressed as h = C(e + X2), where X = x/Rw. Here, the groove spans from the left edge x = −xm to the right edge x = xm, with a width of 2xm = 28 μm (Fig. 1 c). We note that the local curvature of the groove does not play a significant role on locomotion dynamics (see the Supporting Material and Batchelor (31)). Rather, the film thickness h determines the hydrodynamics of lubrication. In other words, within the lubrication region , the flow can be effectively described by the nematode body y = h = (hw – ha) sliding on a flat surface (y = 0).
In the experiments, the nematode's typical normal sliding speed υn is 1 mm/s. On top of the agar plate there exists a thin layer of liquid, which we model as a dilute and purely viscous agarose solution (∼0.15 wt %) (32). The viscosity and density of the solution are μ = 10 mPa·s (33) and ρ = 103 kg/m3. The Reynolds number, defined as is less than 10−2, and the dimensionless gap width δ = h/Ra ≈ 0.01 for a typical lubrication film thickness of h ≈ 1 μm (34). Hence, we may omit terms in O(δ) and O(δRe) in the dimensionless momentum equations (see detailed derivation in the Supporting Material). If we further assume that liquid flow lubricating the nematode's body and the gel are uniform and steady, the governing equations reduce to (see the Supporting Material)
| (1) |
| (2) |
| (3) |
The no-slip boundary conditions on the nematode's body and the agar surface are, respectively (Fig. 1 b),
| (4) |
| (5) |
By solving Eqs. 1–3 along with the boundary conditions, we obtain the following velocity profiles for ux and uy,
| (6) |
| (7) |
Next, we introduce the above equations for the velocity components ux and uy into Eq. 3, and obtain
| (8) |
Equation 8 is the well-known Reynolds equation (see the Supporting Material and Hamrock et al. (34)). Note that in addition to the hydrodynamic equation for lubrication, surface tension enters our analysis through the pressure boundary conditions on each side of the nematode (Fig. 1 b). In principle, surface tension exerts forces both along the gravitational and horizontal (i.e., agar surface) directions. Here, we first consider the case where the meniscus is symmetric and only the component of surface tension acting along the direction of gravity is considered. The effect of asymmetric menisci where surface tension features horizontal force components will be addressed in the subsequent section, where we find that horizontal forces arising from surface tension are small compared to lubrication forces. Hence, the following results derived from considering a symmetric meniscus retain the dominating features of the mechanics of nematode crawling.
The pressure p and its gradient dp/dx can now be computed by rearranging and integrating Eq. 8. The boundary conditions are 1), dp/dx = 0 at θ = θc (x = xm, X = Xm) and 2), at θ = θc (x = xm, X = Xm), where p = p0 = 0 is the reference pressure, and p1 = p2 are the capillary pressures resulting from the surface tension of (symmetric) liquid menisci. The capillary pressure p2(= p1 ≈ −125 Pa) is estimated using the Laplace-Young equation and geometrical considerations (see the Supporting Material). This results in
| (9) |
| (10) |
where
Given the pressure gradient dp/dx, we compute the velocity profiles ux and uy in Eqs. 6 and 7.
The drag forces acting on the nematode are obtained by integrating the fluid viscous stress (τ) over the nematode's body surface, given by y = h = (hw – ha). Note that τ = −pI + 2μD, where p is the hydrodynamic pressure, I is a unit tensor, D is the rate of deformation tensor, and μ (≈10 mPa s) is the fluid viscosity. Then, the drag forces in the normal and tangential directions are given by (see derivations in the Supporting Material)
| (11) |
and
| (12) |
where υt corresponds to the nematode's tangential (crawling) speed, and Fx and Fz are forces per unit length.
We note that the drag force relations obtained above (Eqs. 11 and 12) resemble the form of expressions obtained using RFT (20). Namely, the components of the drag force are linearly proportional to the fluid viscosity (μ) and the nematode's crawling speed (υn and υt), such that Fx,z = μυn,tCn,t, where Cn,t is the drag coefficient and n and t correspond to the normal and tangential directions, respectively (see Fig. 1 a). In Eqs. 11 and 12, the drag coefficients are defined by the expressions in the curly brackets.
The force relations derived above (Eqs. 11 and 12) can provide some useful insight. We note that as the groove surface becomes flatter, i.e., Ra → ∞, the shape parameter increases, and the effective values of Cn and Ct become smaller. That is, the mere presence of a groove increases the drag forces in both normal (x) and tangential (z) directions. Also, the drag coefficient ratio Cn/Ct remains independent of the groove shape parameter C.
Estimating the drag coefficients
The next step consists in calculating the drag coefficient ratio Cn/Ct and its individual components for crawling motion. We begin by noting that, in resistive force theory, the ratio Cn/Ct is related to the nematode's motility kinematics such that its normalized forward speed U/c is given by (5,26,35)
| (13) |
The quantities c, A, and λ correspond to the nematode's wave speed, bending amplitude, and wavelength, respectively. These kinematic quantities are measured in experiments by tracking the nematode's motion on agar plates as shown in Fig. 2. The nematode's motion and its kinematics are investigated using an in-house code (36). The body centroid and the body centerline (i.e., the skeleton) are tracked and presented in Fig. 2, a and b, in the laboratory and nematode's frames, respectively. One can extract relevant kinematic metrics from the body centroids and centerlines such as forward locomotion speed U and body curvature κ (Fig. 2, a and c).
Figure 2.
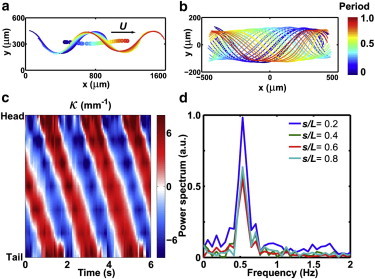
(Color online) The kinematics of C. elegans crawling on an agar plate. Body centerlines (or skeletons) of crawling nematodes in (a) laboratory frame and (b) nematode's frame of reference. The centroids of the skeleton in panel a are color-coded, and tracked to obtain the crawling speed U (see Movie S2 in the Supporting Material). (c) Spatio-temporal contour plot of the nematode's bending curvature κ, which display a traveling wave from head to tail. (d) Fast-Fourier transform of the curvature plot at varied locations of the nematode's body. The nematode's bending frequency is ∼0.5 Hz and independent of position along the body.
The curvature κ is defined as κ(s,t) = dϕ/ds, where ϕ is the angle made by the tangent to the x axis in the laboratory frame at each point along the body centerline, and s is the arc length coordinate spanning the head of the nematode (s = 0) to its tail (s = L). Body curvature is computed from the measured nematode's body centerlines y(s,t), where the curvature κ(s,t) = ∂2y/∂x2 and s ≈ x for small amplitudes. Fig. 2 c shows the experimentally measured spatio-temporal evolution of the nematode's body curvature κ(s,t) for three beating cycles. The periodic diagonal patterns seen in Fig. 2 b show undulatory bending waves propagating from head to tail. The undulating waveforms are characterized by the interval of the periodic patterns and the slope of the diagonal lines. The body bending frequency (f) is obtained from the one-dimensional fast-Fourier transform of the curvature field κ at multiple body positions s/L (Fig. 2 d). A single frequency peak f ≈ 0.5 Hz is found in the Fourier spectrum. This single peak is irrespective of body position and corresponds to a wave speed c = 0.39 mm/s. The wavelength of the undulatory wave is defined as λ = c/f = 0.79 mm. A summary of the experimental results is presented in Table 1 along with a comparison to data for nematodes swimming in buffer solution.
Table 1.
Kinematics for swimming and crawling nematode
| Swimming | Crawling | |
|---|---|---|
| Speed U (mm/s) | 0.38 ± 0.02 | 0.27 ± 0.01 |
| Frequency f (Hz) | 1.99 ± 0.05 | 0.49 ± 0.02 |
| Wavespeed c (mm/s) | 4.27 ± 0.18 | 0.41 ± 0.02 |
| Amplitude A (mm) | 0.26 ± 0.01 | 0.10 ± 0.01 |
| Wavelength λ (mm) | 2.15 ± 0.07 | 0.83 ± 0.02 |
| Shape parameter (λ/A) | 8.23 ± 0.28 | 8.44 ± 0.28 |
| Efficiency (U/c) | 0.09 ± 0.01 | 0.65 ± 0.01 |
By inserting the experimentally measured values of U, λ, A, and c into Eq. 13, we estimate the value of the drag coefficient ratio for crawling nematodes on wet agar surfaces to be ∼Cn/Ct = 9.4 ± 0.6. This value is much larger than for nematodes immersed in Newtonian fluids (Cn/Ct ≈ 2) (10,19,26) and close to the range of values (Cn/Ct ≈ 9–14) found for nematodes crawling on substrates of varying stiffnesses (5).
The individual components of the drag force can be calculated by evaluating the expressions enclosed in the curly brackets of Eqs. 11 and 12. As shown in Fig. 3, the normal and tangential drag coefficients are plotted as functions of the gap width h0. Their ratio Cn/Ct as a function of h0 is shown in the inset. By using the above estimated value of Cn/Ct, we can obtain the value of h0 which is ∼0.86 μm. Here, Rw = 40 μm and Ra = 100 μm are the nematode's body radius and the groove's effective radius, respectively. The maximum value of span length xm is 14 μm. Hence, the values of the normal and tangential drag coefficients yield Cn = 222.0 and Ct = 22.1. To the best of our knowledge, the only other estimates available for Cn and Ct lie in the range of Cn ≈ Ct ≈ 5–40, with Cn/Ct < 2 (18).
Figure 3.
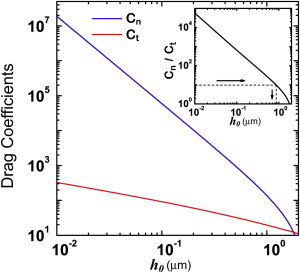
(Color online) The drag coefficients and the drag coefficient ratio (inset) as a function of the gap width h0. The blue (upper) and red (lower) lines are the normal and tangential drag coefficients, respectively. (Inset) The normal and tangential drag coefficient ratio Cn/Ct as a function of h0. (Dashed lines) Estimated drag coefficient ratio Cn/Ct ≈ 9.4, which corresponds to h0 ≈ 0.86 μm.
The effects of surface tension on crawling
The asymmetric menisci between the nematode body and the liquid film imposes forces in the gravitational direction and normal to the nematode body. In the direction of gravity, the lubrication force balances the gravitational force and, more importantly, surface tension (see derivation in the Supporting Material). This surface tension can also leads to forces normal to the nematode body and its motility due to the asymmetric nature of the menisci on either side of the nematode.
To investigate the effect of normal forces due to surface tension on nematode motility, we compare the motility behavior of nematodes crawling on standard NGM agar plates and on agar plates treated with surfactant. We used Tween 20 at its critical micelle concentration of 0.1 g/L to treat the agar plates. The presence of Tween 20 on the liquid film reduces surface tension by 50%, from 71 mN/m to 38 mN/m (37) (see preparation details in the Supporting Material). Fig. 4 shows the comparison of nematode kinematics between the standard NGM plate and Tween 20-treated agar plate; 23 nematodes are used in each experiment. Results for the beating amplitude, wavelength, and shape factor λ/A show little change once surfactant is introduced. The swimming speed, beating frequency, and wave speed decrease by ∼ 10% on Tween-20 agar plates compared to untreated plates even though surface tension is reduced by 50%. These data suggest that surface tension effects on nematode motility on wet agar plates are finite but small (see also the Supporting Material for theoretical estimates) and that propulsion is most likely dominated by viscous lubrication forces. Although the effects of surface tension on C. elegans motility warrant a more in-depth study, here we will focus our efforts on viscous lubrication forces that seem to be the dominant component.
Figure 4.
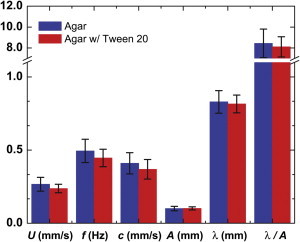
(Color online) Comparison of nematode kinematics between standard NGM plate (blue) and Tween 20-treated agar plates (red). The error bars represent the standard deviations. A total of 23 and 14 worms are recorded and measured on NGM- and Tween 20-treated agar plates, respectively.
The effects of anisotropic drag forces on C. elegans' kinematic efficiency
Traditionally, two main motility gaits (swimming and crawling) are reported depending on whether C. elegans is fully immersed in a liquid or moving on top of a surface. Parameters used to distinguish between these two motility forms have included metrics such as bending frequency f = 1/T, amplitude A, and wavelength λ, where values of such quantities are found to be much lower for crawling than for swimming (10,13). Our kinematic data also show similar trends (Table 1), and we find that the kinematic efficiency defined as U/c is eight-times larger for crawling than for swimming.
There are, however, some interesting similarities between crawling and swimming nematodes. In particular, the shape parameter value defined as λ/A is nearly identical for both crawling and swimming gaits (Table 1). This constant value of λ/A is likely to result from biological constraints on the muscle strain (5). Because U/c is a function of Cn/Ct and λ/A only (see Eq. 13), we infer that the kinematic differences observed between these two motility gaits may be attributed to the different values of the ratio of drag coefficients experienced by C. elegans because λ/A remains nearly constant.
Overall, we find that anisotropic drag forces influence the undulatory locomotion in two aspects, i.e., the energy cost (Eqs. 11 and 12) and the undulation efficiency (Eq. 13). The tangential drag coefficient Ct determines the nematode's required propulsion (mechanical) force and the energy cost because it is responsible for most of the translational resistance to forward motion, whereas the drag coefficient ratio Cn/Ct determines the ratio of the propulsion energy dissipated along both the transversal and longitudinal directions (19).
Calculating the nematode's internal bending force
Bending is required for C. elegans to generate forward thrust. In this section, we calculate the total force necessary to bend the nematode's body using experimental data and knowledge of the drag forces. We compare the calculated nematode bending force patterns between crawling and swimming nematodes. A force balance on the nematode body shows that the bending force needed to overcome resistance arises from two components: one is the elastic resistance due to body bending, while the other is the viscous force distributed along the nematode body. In the limit of small undulating amplitudes, the total muscle bending force at position s = sp can be obtained by summing up the elastic and distributed viscous drag forces acting along the nematode body,
| (14) |
where s = 0 and s = L represent the head and tail of the nematode body, respectively. The unit normal vector of the local body segment is given by . The first term on the right-hand side represents the elastic force required to bend the nematode body, while the second term represents the viscous force due to the liquid film. The bending force is directly related to the local curvature and thus computed at a single point s = sp. In contrast, the viscous forces are distributed along the nematode body and must therefore be integrated from the head (s = 0) to the point s = sp. Altogether, internal muscle actuation must overcome both the elastic and viscous drag forces to sustain undulatory locomotion (see the Supporting Material for details). We note that the linearization approach in the limit of small amplitude displacements is chosen so as to obtain a closed-form analytical solution for the bending forces. This enables us to readily compare the dynamics between swimming and crawling behaviors. To calculate the internal bending forces, we need values of the normal Cn and tangential Ct drag coefficients. For crawling, the analysis presented above leads to Cn = 222 and Ct = 22. For swimming, Lighthill's resistive force theory (RFT) model ((21,26) and see the Supporting Material) leads to Cn = 4.5 and Ct = 2.8.
The total muscle force is decomposed into normal and tangential directions. The tangential component of the force describes the resistance to changes in body length. The normal component of describes the bending force, and it is given by
| (15) |
The magnitude of the internal bending force Fb (s,t) can be determined at any time t and location s along the nematode body by combining experimentally measured nematode speed and bending curvature with individual values of the normal and tangential drag coefficients. To compute the internal elastic contribution, we also need values of the nematode's bending modulus Kb, a material property that is typically difficult to measure. Here, we will use two previously estimated values of Kb, namely Kb = 4.2 × 10−16 N m2 (38) and Kb = 9.5 × 10−14 N m2 (10). The differences in the magnitude of Kb reflect the different assumptions in determining the spatial and temporal form of the nematode's (internal) active bending moment. Fig. 5, a and b, show the magnitude of Fb using Kb = 4.2 × 10−16 N m2 (38) for both crawling and swimming nematodes for three bending cycles. Fig. 5, c and d, show the corresponding magnitude of Fb using Kb = 9.5 × 10−14 N m2 (10). The solid black lines in Fig. 5 correspond to regions where the nematode's curvature κ is zero, and arrows show the directions of the bending waves.
Figure 5.
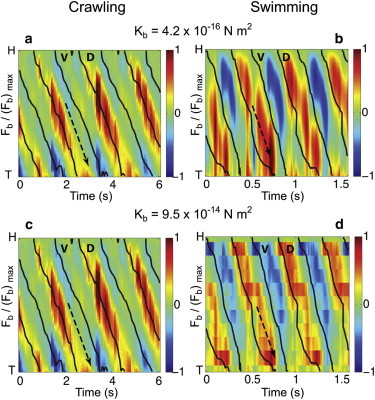
(Color online) Normalized spatio-temporal bending force patterns for crawling (left panel) and swimming (right panel) C. elegans. The bending forces are calculated for (a and b) Kb = 4.19 × 10−16 N m2 (38) and (c and d) Kb = 9.5 × 10−14 N m2 (10). H and T represent the head and tail of the nematode body, respectively. The ventral and dorsal sides are denoted as V and D. (Overlaid black solid lines) Regions where the curvature κ = 0. (Dashed arrows) Directions of the traveling waves.
The bending force patterns presented in Fig. 5 are time-periodic and in general, spatially complex. For swimming nematodes with Kb = 4.2 × 10−16 N m2 (38), the bending force is larger near the head, while most of the bending force is accumulated around the midsection for crawling C. elegans. For both swimming and crawling C. elegans, spatial patterns for the bending force are very similar to previously described gait-specific features of calcium signals in muscle (13). In particular, we note that the larger value for Kb (Fig. 5, c and d) yields larger resistance to nematode bending. As a result, the spatial distribution of Fb is not identical for the two cases. Here, the ventral/dorsal sides are determined by close inspection of the nematode's body. The ventral side is identified as the side where the vulva lies that is characterized by a large opening at the middle of the body. We note that for both gaits, signals for the bending curvature are rather periodic, whereas those for the bending force exhibit unequal strength along ventral and dorsal sides. We hypothesize that this unequal ventral/dorsal bending is most likely the result of an asymmetry in the ventral/dorsal neurological structures (15) (see Fig. 5).
Because the bending force patterns are time-periodic, the data shown Fig. 5, a and b, can be phase-averaged. Fig. 6, a and c, shows the phase-averaged spatial distribution of Fb using the bending modulus values Kb = 4.2 × 10−16 N m2 (38) and Kb = 9.5 × 10−14 N m2 (10) for crawling and swimming nematodes, respectively. Note that the shaded areas in Fig. 6 correspond to standard error of the mean. In general, crawling nematodes generate bending forces Fb that are 40-fold larger than nematodes swimming in an aqueous solution. Using Kb = 4.2 × 10−16 N m2, the peak values of internal bending force for crawling and swimming nematodes are ∼85 nN and 1.8 nN; in the case of Kb = 9.5 × 10−14 N m2, the peak values of internal bending force for crawling and swimming nematodes are ∼89 nN and 3.0 nN. By comparison, a study of C. elegans moving in an array of flexible pillar found bending forces ranging from 200 nN to 1000 nN (39), while another experiment of nematodes crawling in glass beads estimated bending forces of ∼100 nN (27). However, direct measurements of locomotive forces remain scarce due to experimental challenges.
Figure 6.
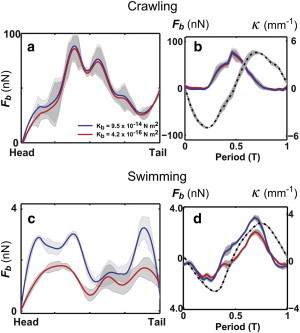
(Color online) Spatial (a and c) and temporal (b and d) patterns of the bending forces Fb for crawling (top panel) and swimming (bottom panel) C. elegans for Kb = 9.5 × 10−14 N m2 (blue) (10) and Kb = 4.19 × 10−16 N m2 (red) (38). (Shaded areas) Mean ± SE. (a and c) The spatial patterns are averaged over five periods. Most of the bending force is located near the head for swimming nematodes and around the body's midsection for crawling nematodes. (b and d) Temporal patterns are obtained at position s/L = 0.55 for both crawling and swimming nematodes. (Dashed lines) Bending curvatures.
The phase-averaged bending force signal is shown as a function of one bending period in Fig. 6, b and d, for crawling and swimming nematodes. The bending force signals are compared to the curvature signals, and measurements are made at s/L = 0.55 for both swimming and crawling. Results are shown for both Kb = 4.2 × 10−16 N m2 (38) and Kb = 9.5 × 10−14 N m2 (10). We find that, for crawling, the bending force and bending curvature signals are not in phase with each other (Fig. 6 b). On the other hand, the force and curvature signals are nearly in phase for swimming nematodes (Fig. 6 d). One possible explanation for the observed phase lag in crawling nematodes is the (much) larger viscous drag forces experienced by nematodes moving on wet surfaces. In the case where little viscous drag is present, the internal bending forces remain nearly in phase with the bending curvatures, as indicated by Eq. 14. In other words, a phase difference between the bending force and curvature is a consequence of enhanced viscous drag forces; the larger the drag forces, the larger the phase difference between the internal bending forces and the bending curvatures.
We can further study the biomechanics of undulatory locomotion by computing the total power during crawling and swimming, respectively. The total power P(t) in locomotion is ultimately consumed by both the endogenous tissue dissipation
and exogenous fluid viscous dissipation
such that
| (16) |
where μ is the fluid viscosity, η is the passive tissue viscosity, and I is the nematode body moment of inertia. In Fig. 7 a, the relative contribution of tissue dissipation to fluid viscous dissipation is investigated by varying the viscosity ratio η/μ up to four decades. Here, the fluid viscosities for swimming and crawling are 1 mPa·s and 10 mPa·s, respectively. The value of passive tissue viscosity η is difficult to measure and only an upper bound of ∼400 Pa·s is available (10). The period-averaged fluid dissipated power Pfluid is 64 pW and 4.5 pW for crawling and swimming nematodes, respectively. Note that the total power dissipation is dominated by the fluid viscosity for values of η/μ smaller than 105 and 104 for crawling and swimming, respectively. Above those values, the power dissipation is dominated by the tissues. In Fig. 7, b and c, we show the normalized powers, i.e., P∗tissue/(= Ptissue/(Ptissue)max) and P∗fluid(= Pfluid/(Pfluid)max), for both crawling and swimming nematodes over one beating cycle, respectively. Both P∗tissue and P∗fluid show phase differences for these two motility gaits, which is caused by different viscous drags (i.e., drag coefficients) and locomotion frequency (C. elegans undulates four times faster during swimming comparing to crawling).
Figure 7.
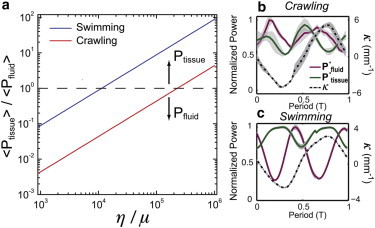
(Color online) Power dissipated by tissue Ptissue and by fluid Pfluid. (a) The ratio of period-averaged powers 〈Ptissue〉/〈Pfluid〉 as a function of viscosity ratio η/μ, where η is tissue passive viscosity and μ is the fluid viscosity. (Dashed line) Situation where total power is dissipated equally through fluid and tissue. (Below the line) Region where Pfluid dominates over Ptissue, and vice versa. (b and c) Temporal patterns of normalized dissipation powers and curvature within one period. (Solid red, green, and dashed black curves) P∗tissue (= Ptissue/(Ptissue)max), P∗fluid(= Pfluid/(Pfluid)max), and bending curvatures, respectively. (Shaded areas) Mean ± SE.
Discussion
Uncoordination (unc) is a very common phenotype among genetic mutations in C. elegans. The affected genes may be expressed in neurons, muscles, or even in other tissues affecting the structures required for coordinated movement (40). For more than 30 years, different unc phenotypes of C. elegans were mostly observed on NGM (agar) plates. Here, we have quantified the biomechanical properties of crawling C. elegans using both experiments and modeling in an effort to provide quantitative tools for motility phenotyping of mutant strains on wet agar gels. The analysis presented above focuses on wild-type C. elegans, although the methods can be easily extended to different nematode strains and other organisms. We coupled kinematic data, such as nematode's speed and body curvature, with a hydrodynamic model to obtain estimates of the (surface) drag forces acting on the C. elegans. Values of the surface drag forces were then used to calculate the nematode's internal (muscle) bending force, which are compared to recent calcium imaging data (13). Results on crawling nematodes are also compared to C. elegans swimming in water-like, buffer solutions to gain insight into the nematode's adaptive motility kinematics across different environments.
Results show that the analytical expressions for the surface drag forces along the normal and tangential directions of the nematode's body (Eqs. 11 and 12) share a similar form to the drag forces expressions obtained using RFT. Equations 11 and 12 indicate that resistance to locomotion can be quantified by the tangential drag coefficient Ct while propulsion efficiency is a strong function of the drag coefficient ratio Cn/Ct. We find here that the drag coefficient ratio Cn/Ct is ∼10 for nematodes moving on wet agar plates (NGM), in agreement with a recent experimental study (5). In similar experiments, Berri et al. (11) reported values of Cn/Ct that are ∼30. This larger value may be due to the amount of moisture and dissolved agar present on top of the plate. On the other hand, a recent theoretical investigation (18) found values of Cn/Ct ≈ 2 that are smaller than ours; a possible source of error may be the use of a purely elastic model that cannot account for plastic deformations (e.g., grooves) on agar surfaces. By considering a thin liquid film between the nematode's body and the agar surface, we are also able to estimate the individual values of the normal and tangential components of the drag forces for crawling nematodes. Using Eqs. 11 and 12 along with kinematic data, we find that Cn = 222.0 and Ct = 22.1 (Fig. 3). For comparison, we note that a recent theoretical analysis estimated Cn and Ct to be of O(10), with a drag coefficient ratio less than 2 (18), which is closer to swimming than for crawling.
In addition, our analysis suggests that modulations in nematode's motility gaits may be a response to the viscous drag force experienced by nematodes (10). This force is given by , where μ is the fluid viscosity, Cn,t are the drag coefficients, is the nematode's velocities, and the subscripts n and t mean normal and tangential. A recent investigation by Fang-Yen et al. (10) showed experimentally that nematode motility gaits can be gradually modulated from swimming to crawling as fluid viscosity μ is increased; that is, nematodes showed swimming-like behavior in low viscosity environments (1 mPa s) and crawling-like behavior in high viscosity environments (104 mPa s). Here, we show that crawling-like behavior can also occur in environments with low viscosity (∼10 mPa s) provided that the magnitude of the drag coefficients (Cn,t) are large. In particular, we find that nematodes exhibit crawling-like behavior on agar plates for normal drag coefficient that is 40-fold larger than that of swimming (Cn ≈ 222 for crawling and Cn ≈ 5 for swimming). Our results suggest that one can control the motility gait of C. elegans by judiciously adjusting the magnitude of the surface drag coefficients in addition to fluid viscosity (10). For example, one can vary the surface geometry by adding patterns or structures.
Knowledge of the individual components of the drag forces allows for calculating the internal bending force of both crawling and swimming nematodes (Fig. 5). We find that the bending force patterns are time-periodic and spatially complex. These patterns provide additional insight into the different motility gaits observed in C. elegans, namely swimming and crawling. The temporal patterns of the bending force, for example, reveal a phase lag with respect to the bending curvature. This phase lag is a measure of the viscous drag force contribution, which is larger for crawling than for nematodes swimming in waterlike buffer solutions. The spatial patterns show that large values of the bending force are concentrated near the head for swimming nematodes, while, for crawling, much of the bending force is concentrated in the nematode's midsection. These calculated spatial patterns correlate rather well with regions of high calcium activity (13).
The analysis and data presented here strongly suggest that although the motility patterns associated with crawling and swimming can be distinguished by distinct kinematics (Fig. 3 and Table 1) and bending force patterns (Fig. 5), changes in the environment's (external) drag coefficient ratio can also contribute to modulations in motility gaits (Eqs. 11 and 12). Further, the analysis is able to capture main biomechanical features of undulatory crawling on lubricated surfaces (agar plates), and it can provide direct estimates of force and power expenditures that are useful for motility phenotyping activities such as in genetic and drug screening applications involving C. elegans.
Acknowledgments
We acknowledge fruitful discussions with S. Jung, A. Brown, David Hu, R. Carpick, G. Wabiszewski, G. Juarez, and N. Keim.
This work was supported by National Science Foundation CAREER grant No. (CBET)-0954084.
Supporting Material
References
- 1.Griffiths B.S. Microbial-feeding nematodes and protozoa in soil: their effects on microbial activity and nitrogen mineralization in decomposition hotspots and the rhizosphere. Plant Soil. 1994;164:25–33. [Google Scholar]
- 2.Olsen O. Dover Publications; Mineola, NY: 1986. Animal Parasites: Their Life Cycles and Ecology. [Google Scholar]
- 3.Brenner S. The genetics of Caenorhabditis elegans. Genetics. 1974;77:71–94. doi: 10.1093/genetics/77.1.71. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Geng W., Cosman P., Schafer W.R. Quantitative classification and natural clustering of Caenorhabditis elegans behavioral phenotypes. Genetics. 2003;165:1117–1126. doi: 10.1093/genetics/165.3.1117. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Karbowski J., Cronin C.J., Sternberg P.W. Conservation rules, their breakdown, and optimality in Caenorhabditis sinusoidal locomotion. J. Theor. Biol. 2006;242:652–669. doi: 10.1016/j.jtbi.2006.04.012. [DOI] [PubMed] [Google Scholar]
- 6.Blair J., Iwasaki T. Optimal gaits for mechanical rectifier systems. IEEE Trans. 2011;56:59–71. [Google Scholar]
- 7.Gray J. The mechanism of locomotion in snakes. J. Exp. Biol. 1946;23:101–120. doi: 10.1242/jeb.23.2.101. [DOI] [PubMed] [Google Scholar]
- 8.Guo Z.V., Mahadevan L. Limbless undulatory propulsion on land. Proc. Natl. Acad. Sci. USA. 2008;105:3179–3184. doi: 10.1073/pnas.0705442105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Hu D.L., Nirody J., Shelley M.J. The mechanics of slithering locomotion. Proc. Natl. Acad. Sci. USA. 2009;106:10081–10085. doi: 10.1073/pnas.0812533106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Fang-Yen C., Wyart M., Samuel A.D. Biomechanical analysis of gait adaptation in the nematode Caenorhabditis elegans. Proc. Natl. Acad. Sci. USA. 2010;107:20323–20328. doi: 10.1073/pnas.1003016107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 11.Berri S., Boyle J.H., Cohen N. Forward locomotion of the nematode C. elegans is achieved through modulation of a single gait. HFSP J. 2009;3:186–193. doi: 10.2976/1.3082260. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Stephens G.J., Bueno de Mesquita M., Bialek W. Emergence of long timescales and stereotyped behaviors in Caenorhabditis elegans. Proc. Natl. Acad. Sci. USA. 2011;108:7286–7289. doi: 10.1073/pnas.1007868108. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Pierce-Shimomura J.T., Chen B.L., McIntire S.L. Genetic analysis of crawling and swimming locomotory patterns in C. elegans. Proc. Natl. Acad. Sci. USA. 2008;105:20982–20987. doi: 10.1073/pnas.0810359105. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 14.Stretton A.O. Anatomy and development of the somatic musculature of the nematode Ascaris. J. Exp. Biol. 1976;64:773–788. doi: 10.1242/jeb.64.3.773. [DOI] [PubMed] [Google Scholar]
- 15.White J.G., Southgate E., Brenner S. The structure of the ventral nerve cord of Caenorhabditis elegans. Philos. Trans. R. Soc. Lond. B Biol. Sci. 1976;275:327–348. doi: 10.1098/rstb.1976.0086. [DOI] [PubMed] [Google Scholar]
- 16.Niebur E., Erdös P. Theory of the locomotion of nematodes: dynamics of undulatory progression on a surface. Biophys. J. 1991;60:1132–1146. doi: 10.1016/S0006-3495(91)82149-X. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Gray J., Lissmann H.W. The locomotion of nematodes. J. Exp. Biol. 1964;41:135–154. doi: 10.1242/jeb.41.1.135. [DOI] [PubMed] [Google Scholar]
- 18.Sauvage P., Argentina M., Di Meglio J.M. An elasto-hydrodynamical model of friction for the locomotion of Caenorhabditis elegans. J. Biomech. 2011;44:1117–1122. doi: 10.1016/j.jbiomech.2011.01.026. [DOI] [PubMed] [Google Scholar]
- 19.Hancock G.J. The self-propulsion of microscopic organisms through liquids. Proc. R. Soc. A. 1953;217:96–121. [Google Scholar]
- 20.Johnson R.E., Brokaw C.J. Flagellar hydrodynamics. A comparison between resistive-force theory and slender-body theory. Biophys. J. 1979;25:113–127. doi: 10.1016/S0006-3495(79)85281-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Lighthill J. Flagellar Hydrodynamics: The John von Neumann Lecture, 1975. SIAM Rev. 1976;18:161–230. [Google Scholar]
- 22.Cox R.G. The motion of long slender bodies in a viscous fluid: Part 1. General theory. J. Fluid Mech. 1970;44:791–810. [Google Scholar]
- 23.Keller J.B., Rubinow S.I. Slender-body theory for slow viscous flow. J. Fluid Mech. 1976;75:705–714. [Google Scholar]
- 24.Lauga E., Powers T.R. The hydrodynamics of swimming microorganisms. Rep. Prog. Phys. 2009;72:096601. [Google Scholar]
- 25.Chattopadhyay S., Wu X.-L. The effect of long-range hydrodynamic interaction on the swimming of a single bacterium. Biophys. J. 2009;96:2023–2028. doi: 10.1016/j.bpj.2008.11.046. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Sznitman J., Shen X., Arratia P.E. Propulsive force measurements and flow behavior of undulatory swimmers at low Reynolds number. Phys. Fluids. 2010;22:121901. [Google Scholar]
- 27.Juarez G., Lu K., Arratia P.E. Motility of small nematodes in wet granular media. Europhys. Lett. 2010;92:44002. [Google Scholar]
- 28.Gart S., Vella D., Jung S. The collective motion of nematodes in a thin liquid layer. Soft Matter. 2011;7:2444–2448. [Google Scholar]
- 29.Reference deleted in proof.
- 30.Wallace H.R. Movement of eelworms. I. The influence of pore size and moisture content of the soil on the migration of larvae of the beet eelworm, Heterodera schachtii schmidt. Ann. Appl. Biol. 1958;46:74–85. [Google Scholar]
- 31.Batchelor G. Cambridge University Press; Cambridge, UK: 2000. An Introduction to Fluid Dynamics. [Google Scholar]
- 32.Zhang R., Turner L., Berg H.C. The upper surface of an Escherichia coli swarm is stationary. Proc. Natl. Acad. Sci. USA. 2010;107:288–290. doi: 10.1073/pnas.0912804107. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 33.Hirata T. Fracturing due to fluid intrusion into viscoelastic materials. Phys. Rev. E. 1998;57:1772–1779. [Google Scholar]
- 34.Hamrock B.J., Schmid S.R., Jacobson B.O. Marcel Dekker; New York: 2004. Fundamentals of Fluid Film Lubrication. [Google Scholar]
- 35.Gray J., Hancock G.J. The propulsion of sea-urchin spermatozoa. J. Exp. Biol. 1955;32:802–814. [Google Scholar]
- 36.Sznitman R., Gupta M., Sznitman J. Multi-environment model estimation for motility analysis of Caenorhabditis elegans. PLoS ONE. 2010;5:e11631. doi: 10.1371/journal.pone.0011631. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 37.Kim C., Hsieh Y.-L. Wetting and absorbency of nonionic surfactant solutions on cotton fabrics. Colloids Surf. A Physicochem. Eng. Asp. 2001;187–188:385–397. [Google Scholar]
- 38.Sznitman J., Purohit P.K., Arratia P.E. Material properties of Caenorhabditis elegans swimming at low Reynolds number. Biophys. J. 2010;98:617–626. doi: 10.1016/j.bpj.2009.11.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 39.Doll J.C., Harjee N., Pruitt B.L. SU-8 force sensing pillar arrays for biological measurements. Lab Chip. 2009;9:1449–1454. doi: 10.1039/b818622g. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 40.Herndon, L., and D. Hall. 2010. Glossary U. In WormAtlas. DOI:10.3908/wormatlas.6.21.
- 41.Eckmann D.M., Cavanagh D.P., Branger A.B. Wetting characteristics of aqueous surfactant-laden drops. J. Colloid Interface Sci. 2001;242:386–394. [Google Scholar]
- 42.Mutwakil M.H., Steele T.J., de Pomerai D.I. Surfactant stimulation of growth in the nematode Caenorhabditis elegans. Enzyme Microb. Technol. 1997;20:462–470. [Google Scholar]
- 43.Gems D., Maizels R.M. An abundantly expressed mucin-like protein from Toxocara canis infective larvae: the precursor of the larval surface coat glycoproteins. Proc. Natl. Acad. Sci. USA. 1996;93:1665–1670. doi: 10.1073/pnas.93.4.1665. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Sharma A., Ruckenstein E. The role of lipid abnormalities, aqueous and mucus deficiencies in the tear film breakup, and implications for tear substitutes and contact lens tolerance. J. Colloid Interface Sci. 1986;111:8–34. [Google Scholar]
- 45.Sauvage, P. 2007. Study of the locomotion of C. elegans movement and mechanical perturbations. PhD thesis. Universite Paris Diderot-Paris 7, Paris, France.
- 46.Hemmer R.M., Donkin S.G., Politz S.M. Altered expression of an L1-specific, O-linked cuticle surface glycoprotein in mutants of the nematode Caenorhabditis elegans. J. Cell Biol. 1991;115:1237–1247. doi: 10.1083/jcb.115.5.1237. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 47.Johnson K.L. Cambridge University Press; Cambridge, UK: 1985. Contact Mechanics. [Google Scholar]
- 48.Camalet S., Jülicher F., Prost J. Self-organized beating and swimming of internally driven filaments. Phys. Rev. Lett. 1999;82:1590–1593. [Google Scholar]
- 49.Wiggins C.H., Riveline D., Goldstein R.E. Trapping and wiggling: elastohydrodynamics of driven microfilaments. Biophys. J. 1998;74:1043–1060. doi: 10.1016/S0006-3495(98)74029-9. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.


