Tonotopic Relationships Reveal the Charge Density Varies along the Lateral Wall of Outer Hair Cells

Abstract

Outer hair cells amplify and improve the frequency selectivity of sound within the mammalian cochlea through a sound-evoked receptor potential that induces an electromechanical response in their lateral wall membrane. We experimentally show that the membrane area and linear membrane capacitance of outer hair cells increases exponentially with the electrically evoked voltage-dependent charge movement ($Q_T$) and peak membrane capacitance ($C_{\mathit{peak}}$). We determine the size of the different functional regions (e.g., lateral wall, synaptic basal pole) of the polarized cells from the tonotopic relationships. We then establish that $Q_T$ and $C_{\mathit{peak}}$ increase with the logarithm of the lateral wall area ($A_{\mathit{LW}}$) and determine from the functions that the charge (σ_LW, pC/μm²) and peak (ρ_LW, pF/μm²) densities vary inversely with $A_{\mathit{LW}}$ (σ_LW = 1.3/A_LW and ρ_LW = 9/$A_{\mathit{LW}}$). This shows contrary to conventional wisdom that σ_LW and ρ_LW are not constant along the length of an individual outer hair cell.

Introduction

Outer hair cells (OHCs) amplify and improve the frequency selectivity of sound within the mammalian cochlea. This amplification is provided in part by the sound-evoked receptor potential (1) that induces an electromechanical response in the lateral wall of an OHC (2). This electromechanical process requires the membrane protein prestin (3). Hearing sensitivity decreases by ∼50 dB in the absence of OHCs (4) and by a similar magnitude when the membrane protein prestin is knocked-out (5).

Mechanical strain produces charge movement in the OHC lateral wall membrane (6). Charge movement is also evoked by changing the transmembrane potential and monitoring the voltage-dependent membrane capacitance (7) (Fig. 1 c). This measurement of the OHC membrane capacitance is routinely used to monitor somatic motility (7) and to determine the specific linear (8–11) and nonlinear (voltage-dependent) capacitances of isolated (7,9–14) or in situ (15) OHCs. The specific linear capacitance is determined by the capacitance of the nonpolar region of the lateral wall membrane. The voltage-dependent capacitance is the result of prestin-associated charge movement within the lateral wall (3).

Figure 1.

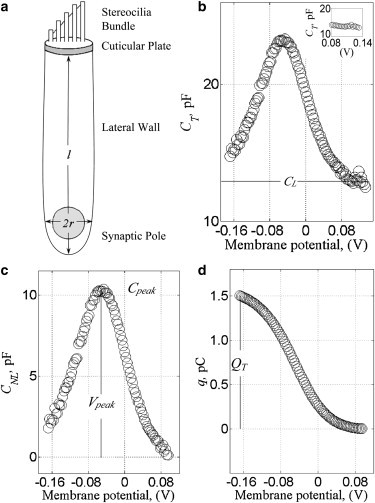
Functional regions and electrical parameters of the OHC. (a) Schematic diagram of an OHC. Plots of (b) membrane capacitance, (c) nonlinear capacitance, and (d) charge as a function of membrane potential for an OHC. (Lines with symbol) Measured electrical and geometrical parameters. (b, inset) The linear capacitance. Data originated from a turn-3 cell obtained from an adult male albino guinea pig (∼16 weeks old). The parameters are C_L, 13.1 pF; V_peak, −0.047 V; C_peak, 10.16 pF; Q_T, 1.5 pC; R_m, 124 MΩ; R_s, 7.2 MΩ; l, 37.3 μm; and A_M, 1,195 μm² (No. 52 albino). The voltage was corrected for the drop across the pipette.

Values of specific linear capacitance for model planar phospholipids bilayers range from 0.0065 to 0.0072 pF/μm² (16–18). Mammalian cells exhibit similar values ranging from 0.005 pF/μm² (19) to 0.01 pF/μm² (20,21). Experimental estimates >0.01 pF/μm² are generally due to inaccurate estimates of membrane area caused by folds and canaliculi, inclusion of voltage-dependent capacitance, or substantial concentration of proteins within membranes (22,23). One approach to determine the specific linear capacitance of a cell with a uniform plasma membrane is to measure the area after unfolding the excess membranous pockets with hydrostatic pressure while simultaneously measuring the membrane electrical admittance (19). This approach is not as useful for cells like the polarized OHC because it has four different functional regions: the stereocilia bundle, the cuticular plate, the lateral wall, and the synaptic basal pole, each of which may have different membrane properties (Fig. 1 a). The microchamber provides an elegant but technically challenging technique to electrically isolate the lateral wall from the other regions of the OHC after which the linear and nonlinear capacitance can be determined (9). We adopt an alternative method that takes advantage of the varying size and spatial arrangement of the OHCs within the organ of Corti. We determine the linear and nonlinear capacitances of the functional regions by experimentally measuring the membrane area and capacitance of a population of OHCs across the cochlea.

Tonotopicity is based upon a topographic map that relates the characteristic frequency to place within the organ of Corti (24,25). The characteristics of OHCs depend upon the position of the cells within the organ of Corti. Shorter OHCs are located in the high-frequency basal region of the cochlea, and longer cells are located in the apical low-frequency region (26). We use these natural variations in the length of OHCs across the guinea pig cochlea to compile relationships among the surface area of the membrane, the magnitude of the linear and nonlinear capacitance and the total voltage-dependent charge where the capacitance is determined with electrical admittance measurements from isolated OHCs under voltage-clamp (27). The functional regions of the OHC can be determined from the relationships, and we show that the voltage-dependent charge movement increases with the logarithm of the area of the lateral wall membrane. These data reveal that the voltage-dependent charge density of the lateral wall varies along the length of individual OHCs.

Material and Methods

Outer hair cell classification

Both albino and tricolor guinea pigs were used in this study and were further categorized based upon sex and sexual maturity. Specifically, adulthood was classified based upon sexual maturity that is ∼4–6 weeks (weight ∼340 g) for females and 3–5 weeks (weight ∼425 g) for male guinea pigs (28). The albinos include 13 adult males (7–40 weeks 475 g to >600 g) and the tricolor guinea pigs include 12 adult males (6–40 weeks >600 g). We also use data obtained from OHCs of prepubertal females (11 albino and five tricolor guinea pigs) to estimate the size of the cuticular plate. Tricolors were bred at Baylor College of Medicine (Houston, TX) where the colony was supplemented with animals from Elm Hill Laboratories (Chelmsford, MA); albinos were purchased from Charles River (Wilmington, MA). The OHCs from both strains were pooled according to age. We did this because we found no difference between the relationships compiled for cells from albinos (turn 1, 2; turn 2, 5; turn 3, 3; and turn 4, 9) compared to tricolors (turn 1, 2; turn 2, 3; turn 3, 3; and turn 4, 17) except for the voltage at peak capacitance, and this comparison of phenotype will be reported in a further communication. In addition, when the data were categorized based upon sex and sexual maturity, we found that the adult male exhibited the most robust relationships. The data obtained from adult females and prepubertal animals will be reported in a further communication. Baylor College of Medicine Animal Care and Use Committee approved the care and use of the guinea pigs.

Outer hair cell isolation

Guinea pigs were euthanatized with carbon dioxide and decapitated. The temporal bones were removed from the skull and both bullae were opened to expose the cochlea. After the otic capsule was removed, the modiolus was cut at the base below the first turn and the four turns were separated from the rest of the temporal bone. Individual turns were then dissected to preserve the structure of the organ of Corti. The cochlear partition of each turn was then incubated in 0.5 mg/mL of trypsin (Sigma-Aldrich, St. Louis, MO) for 5–12 min at room temperature. The OHCs were then isolated by mechanical disturbance of the solution containing each turn with a pipette. All isolation procedures were performed in Ca²⁺-free solution (see below). OHCs were then plated onto the glass bottom of poly-d-lysine-coated microwell petri dishes (MatTek, Ashland, MA). The dish containing the cells was perfused with extracellular solution with a peristaltic pump (model No. RP-1 4 channel pump; Rainin, Oakland, CA) at a constant flow rate of 0.3–0.7 mL/min.

Solutions and pipettes

All chemicals were purchased from Sigma-Aldrich. Dissection solution contained 147 mM NaCl, 5.5 mM KCl, 10 mM HEPES, 2 mM CoCl₂, and 2.5 mM MgCl₂. The intracellular solution contained 140 mM CsCl, 2 mM MgCl₂, 10 mM EGTA, and 10 mM HEPES. The extracellular solution contained 20 mM CsCl, 105 mM NaCl, 10 mM HEPES, 2 mM CoCl₂, 1.5 mM MgCl₂, 2 mM CaCl₂, and 20 mM N(CH₃CH₂)₄Cl. The pH and osmolality were adjusted to 7.2 ± 0.02 and 300 ± 2 mOsm Kg⁻¹ with the addition of CsOH or NaOH (dissection solution) and glucose, respectively. The pipettes were made of fused quartz and pulled with a laser-based puller (Sutter Instrument, Novato, CA) and coated with Sylgard (Dow Corning, Midland, MI) and had resistances between 2 and 6 MΩ.

Whole-cell patch-clamp recordings

Isolated OHCs were imaged with bright-field illumination (oil immersion 100× objective lens on an Axiovert 135 microscope; Zeiss, Oberkochen, Germany). Healthy isolated OHCs were selected within 4 h of death of the animal. Before each experiment an image of the OHC was obtained with a video camera (model No. NC-70x; DAGE-MTI, Michigan City, IN) and this image was projected onto a monitor and recorded on tape with a videocassette recorder (model No. AG-1970, S-VHS; Panasonic, Secaucus, NJ). Because pressure can affect both the linear (19) and the voltage-dependent capacitance (29,30), we controlled the pipette pressure during giga-seal formation and during recordings with a high-speed pressure clamp (HSPC-1; ALA Scientific Instruments, Farmingdale, NY) (31). Giga-seals were formed at the basal pole of an OHC at a pressure of −2.7 ± 1.3 kPa. Once the whole-cell configuration was achieved at −0.060 V, a pressure of 0 to −0.27 ± 0.13 kPa was maintained during the remainder of the recording. Upon giga-seal formation, the pipette capacitance was corrected with the compensation circuitry of the amplifier (Axopatch 200B, Molecular Devices, Sunnyvale, CA), where the transients disappeared into the baseline noise with a root mean square of 0.6 ± 0.02 pA.

In whole-cell mode, the electrical admittance was monitored with a dual frequency sinusoidal stimulus that was added to a DC ramp of 0.3 V/s (−0.18 V to +0.18 V). The stimuli were the sum of two 0.010 V peak-to-peak sine waves at frequency f and 2f where f was 195.3125, 390.625, and 781.25 Hz. To determine the real and imaginary parts of the current, the current was measured every 10 μs and a fast Fourier-transform conducted every 2048, 1024, and 512 records for stimuli at f. This current was first corrected for the inherent phase shifts of the amplifier and then the real and imaginary parts of the electrical admittance were calculated by dividing the complex current by the complex voltage.

The capacitance was calculated from the electrical admittance as described previously (27). Because the measurements of the capacitance depend upon the electrical properties of the cell (e.g., size of cell, conductance, and series resistance), different stimulus frequencies were used for cells from turns 1–4 (27). The lowest f was used for cells from turn 4 whereas the highest f was used for cells from turns 1 and 2. The membrane, (R_m), and series resistances (R_s) were determined when the voltage-dependent capacitance disappeared into the noise floor at ∼0.1 V, where the electrical components of the cell are linear. Only cells that exhibit a R_s < 11 MΩ are included in the analysis. For the limited stimulus frequency range (up to 800 Hz), there are no significant differences in the values of the capacitance.

The DC conductance of the cells was obtained by applying a square-wave of magnitude 0.01 V (voltages of −0.1 to +0.1 V) to the cell. The conductance was calculated from the change in the steady-state part of the measured current relative to the step change in the voltage. There is a voltage drop across the pipette determined by R_s/(R_s+R_m) and this value can be significant in OHCs because they exhibit a high conductance (8,32). This voltage drop will vary for a nonconstant conductance. When the DC conductance of the cell was measured, we corrected for the voltage drop from the membrane resistance measured at DC, and when it was not, we corrected for the voltage drop from the admittance measurements when the electrical components of the cell were linear.

Software written in LabVIEW (Ver. 8.5.1; National Instruments, Austin, TX) controlled the stimuli and data acquisition. The data analysis and statistics were performed with MATLAB (version 7; The MathWorks, Natick, MA). The fits of the data to the two-state Boltzmann were performed with the lsqcurvefit function in the optimization toolbox of MATLAB.

Results

Measurement and definition of electrical parameters

Outer hair cell membrane capacitance, C_T, is a function of three variables—area, A; pressure, P; and voltage, V—and is given by

$$C_T\left(A,P,V\right)=C_L\left(A,P\right)+C_{NL}\left(A_{NL},P,V\right),$$ (1)

where the linear capacitance, C_L, is the capacitance that depends upon the area of the membrane and C_NL is the differential or voltage-dependent capacitance. It largely represents the prestin-associated (3) charge movement, q (7,29), that occurs within an area of the membrane, A_NL, and is described by

$$C_{NL}\left(A_{NL},P,V\right)=\frac{\partial q}{\partial V},$$ (2)

where C_L is determined from the measured C_T at positive potentials (≥0.1 V) when there was no detectable voltage-dependent charge movement and at a constant pipette pressure of 0–0.27 kPa (Fig. 1 b, inset). Specifically, ΔC_T/ΔV, was calculated throughout the recording (Fig. 1 b) with 4–6 consecutive values and the mean linear capacitance (ΔC_T/ΔV = 0), was determined at voltages at and beyond this zero slope. It is the sum of four terms that represents the four different regions of the OHC,

$$C_L\left(A\right)=c_{LW}{A}_{LW}+c_B{A}_B+c_{CP}{A}_{CP}+c_{SB}{A}_{SB},$$ (3)

where c represents the specific linear capacitance and the subscripts represent the region of the cell, namely the lateral wall (c_LW), basolateral region (c_B) (see below for definition), cuticular plate (c_CP), and stereocilia bundle (c_SB). Likewise, A represents the membrane area of the lateral wall (A_LW), basolateral region (A_B), cuticular plate (A_CP), and stereocilia bundle (A_SB). Because P is constant in our experiments it will no longer be included as a variable in the descriptions. See Table S1 in the Supporting Material for an index of abbreviations.

The total length of the cell (l) was measured from the cuticular plate to the basal pole of the cell. The length of bent OHCs was calculated as the sum of segments subdivided to follow the curvature. The width of the cell was measured at the diameter of the nucleus, orthogonal to the long axis of the cell (Fig. 1 a). This membrane area, A_M, was calculated with

$$A_M=2\pi r\left(L+r\right)=2\pi rl,$$ (4)

where 2r is the measured width of the cell and L is the length of the lateral wall. In terms of the different regions of the cell body, A_M is

$$A_M=A_{LW}+A_B$$ (5)

and is a fraction of the total membrane area, A,

$$A=A_{LW}+A_B+A_{CP}+A_{SB}.$$ (6)

C_NL(A_NL, V) was determined with Eq. 1 (Fig. 1 c) after subtracting C_L. The total voltage-dependent charge movement, Q_T (Fig. 1 d) was then calculated by integrating C_NL(A_NL, V) over the membrane voltage range where the charge was not zero {∼0.100 to −0.18 V} with

$$Q_T=\sum _{i=1}^{i=N}{C}_{NL}^i\left(A_{NL},V^i\right)dV,$$ (7)

where dV ∼ 0.003 V and N is the total number of points (between 100 and 200) and the superscript i represents the nonlinear component of the capacitance measured at membrane voltage Vⁱ.

Tonotopic relationships across the cochlea

Plots of Q_T as a function of A_M and C_L are shown in Fig. 2, a and b. The charge increases monotonically with A_M and C_L and saturates at higher values. The relationships are not linear but are readily described by logarithmic functions where A_M and C_L increase exponentially with Q_T (see Table 1, functions 3 and 4). Specifically,

$$Q_T=\alpha \text{ln}{A}_M+\beta ,$$ (8)

where α and β are constants with units of pC (see section S2 in the Supporting Material). When Q_T approaches 0, the area devoid of voltage-dependent charge is obtained from the intersection with the abscissa at 437 ± 70 μm². A value of 428 ± 76 μm² is obtained upon fitting the C_peak to the same logarithmic function in support of the analysis (Table 1, function 6). This analysis cannot differentiate if this area arises from either the synaptic pole or the inferior border of the apical cap or from both regions. We assume (15,33) it arises primarily at the base of the cell (albeit 2.3 times larger than the expected area of the base ∼188 ± 61 μm²) and the voltage-dependent charge is largely confined to the lateral wall. This enables us to equate A_NL ≡ A_LW in Eqs. 2 and 7. The region devoid of voltage-dependent charge from the basal pole to the superior aspect of the nucleus is coined the basolateral region and is represented by A_B in Eqs. 3, 5, and 6. Likewise, the best-fit line to the data in Fig. 2 b intersects the abscissa at 5.2 ± 0.6 pF (Table 1, function 3), and with respect to the C_peak, the value is 5 ± 0.7 pF (Table 1, function 5). This root represents the capacitance of the membrane that is not a part of the lateral wall, C_NLW, and from Eq. 3 it is

$$C_{NLW}=C_{CP}+C_{SB}+C_B.$$ (9)

Figure 2.

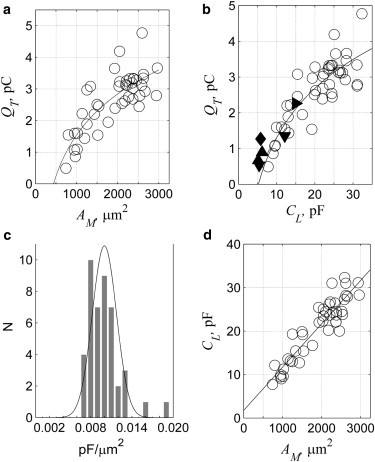
Tonotopic relationships for OHCs from adult male guinea pigs. (a) The area of the basolateral region is determined from the intercept with the abscissa of the logarithmic relationship between Q_T and A_M. (b) The linear capacitance of the nonlateral wall region of the OHC is determined from the intercept with the abscissa of the relationship between Q_T and C_L. (Open circles) Measurements. (Lines) Fits of data to logarithmic functions. Refer to Table 1, functions 3 and 4 for details of the fit. Other symbols represent values for other mammalian species: mice (up-triangle) (12); rat (down-triangle) (15); mice (diamond) (11); and gerbil (right-triangle) (13). (c) The histogram of the specific capacitance on a cell-by-cell basis. (Solid line) Gaussian fit to the data upon removing the two highest values. (d) The specific capacitance of the lateral wall as determined from the slope of C_L versus A_M (refer to Eq. 11a). (Solid line) Linear fit to the data (see Table 1, function 1).

Table 1.

Parameters calculated upon fitting the OHC data to the tonotopic relationships for adult male guinea pigs

	Function	α∗	β	p-Value	AB (μm2)	CNLW (pF)	R2
1.	CL = (α)AM + β	0.010 (0.0007)	1.776 (1.321)	0.186			0.846
		0.0096 (0.0006)†	2.221 (1.120)	0.050			0.789
2.	CL-CSB = (α)(AM) + β	0.0097 (0.0007)	1.527 (1.312)	0.251			0.839
		0.0092 (0.0006)†	2.001 (1.114)	0.077			0.778
3.	QT = (α)ln(CL) + β	1.990 (0.183)	−3.276 (0.5487)	<0.0001		5.17 (0.64)	0.737
	QT = (α)(CL) + β	0.1090 (0.011)	0.370 (0.242)	0.134			0.697
4.	QT = (α)ln(AM) + β	1.871 (0.212)	−11.383 (1.593)	<0.0001	436.8 (70)		0.649
	QT = (α)(AM) + β	0.001 (0.0001)	0.539 (0.276)	0.058			0.603
5.	Cpeak = (α)ln(CL) + β	13.679 (1.455)	−22.036 (4.358)	<0.0001		4.99 (0.74)	0.678
	Cpeak = (α)(CL) + β	0.747 (0.087)	3.043 (1.896)	0.116			0.639
6.	Cpeak = (α)ln(AM) + β	13.025 (1.602)	−78.969 (12.017)	<0.0001	428.0 (76)		0.611
	Cpeak = (α)(AM) + β	0.008 (0.001)	3.920 (2.048)	0.062			0.575

Numbers in parentheses represents standard deviation of the estimates.

^∗All p-values associated with the slope (α) are <0.0001.

^†Grouped data from adult male and prepubertal female guinea pigs.

We now estimate lateral wall capacitance from the above relationships after we determine the capacitance of the bundle that contributes to C_L (34). We do this because, unlike the base and cuticular plate, the number and length of the stereocilia within a bundle varies across the cochlea and among the three rows of OHCs. The number decreases and the length increases from base to apex (35,36). We obtained the length, λ, of the stereocilia as a function of place in the cochlea from electron microscopy data of the guinea pig (35) and the number of stereocilia across the cochlea, n, from the chinchilla (36), and calculated the total membrane area for each row at each position with 2πRλn, where R is the radius of stereocilia at 100 nm (37). We used the n from chinchilla because the number for the guinea pig is not available and the frequency/place map of the chinchilla is close to the guinea pig (38). We converted from place to frequency (24) and frequency to OHC length (26) and calculated A_M with the measured radius of OHC at 5.45 ± 0.8 μm. We find the relationship between A_M and A_SB is linear up to A_M ∼2000 μm², where the slope is 0.07 μm² of A_SB/μm² of A_M. For A_M > 2000 μm², the area of the stereocilia bundle reaches an average constant value of ∼140 μm². We then used the specific capacitance of 0.0075 pF/μm² to calculate the membrane capacitance of the bundle (19,20).

The bundle capacitance is subtracted from the linear capacitance to obtain the relationship of Q_T as a function of C_L – C_SB (data not shown). The best-fit line still exhibits a logarithmic function that intersects the abscissa at a lower value of 4.86 ± 0.7 pF; this value now represents the sum of C_B and C_CP. A similar value of 4.68 ± 0.7 pF is determined from the relationship between C_peak and C_L – C_SB.

Specific capacitance of the lateral wall of OHC

We use Eq. 3 to estimate the capacitance of the lateral wall for each cell after subtracting 4.86 pF and the calculated C_SB for each cell. We determine the area of lateral wall with Eq. 5 after subtracting the basolateral region at 436.8 μm². The specific capacitance is then calculated with

$$c_{LW}=\frac{C_{LW}}{A_{LW}}.$$ (10)

The histogram is shown in Fig. 2 c and exhibits a slight skew toward higher values exhibiting a mean of 0.010 ± 0.002 pF/μm² (see Table S3 within the Supporting Material), and becomes Gaussian (p-value: 0.516) with a mean value of 0.010 ± 0.0017 pF/μm² when the highest values (2) are excluded. We obtain a second estimate of the specific capacitance from the relationships between C_L and A_M (Fig. 2 d). Rearranging Eq. 3 and expressing the area of the lateral wall and basolateral regions in terms of A_M, where we make use of Eq. 5 we find for A_M > A_B that

$$C_L-C_{SB}=c_{CP}{A}_{CP}+c_{LW}{A}_M,$$ (11a)

where a plot of C_L − C_SB versus A_M will exhibit a slope of c_LW. If the basolateral region was electrically isolated from the rest of the OHC, and the capacitance incrementally measured as its area changed, the specific capacitance of the basolateral region, i.e., c_B, could be calculated from the slope with

$$C_L=c_{CP}{A}_{CP}+c_B{A}_M,$$ (11b)

where A_M is the isolated area of the basolateral region. Because the experimental data are dominated by changes in the area of the lateral wall, we obtain a slope of 0.0097 ± 0.0007 pF/μm² from Eq. 11a. The intercept with the ordinate is the capacitance of the cuticular plate at 1.53 ± 1.31 pF (p-value = 0.25) (Table 1, function 2). A more reliable value for C_CP at 2–2.2 pF (p-value 0.05–0.07) is obtained by pooling the data from adult males and prepubertal females (Table 1, functions 1 and 2). C_B is determined upon rearranging Eq. 9, where C_CP ≈ 2.1 pF and c_B is then calculated to be 0.006 pF/μm² (range 0.013–0.002 pF/μm²).

Charge density of the lateral wall of the OHC

Plots of Q_T as a function of A_LW and C_LW are shown in Fig. 3, a and b. The charge increases monotonically with A_LW and C_LW and saturates at higher values. We examined whether these relationships were linear across the cochlea by fitting the data to unconstrained and constrained (intercept = 0) linear models. The latter does fit the data but provides the weakest correlation (R² = 0.4, see Table S2 in Supporting Material). The unconstrained fit is better but results in a significant positive intercept (∼1 pC), which implies there is an area in the lateral wall that exhibits a charge greater than the linear density. Although the data can be fit to a linear relationship, we propose that a more appropriate model, which accounts for this nonuniform distribution of charge, is a logarithmic function. Specifically, we write Q_T in terms of A_LW with

$$Q_T=\alpha \left(\text{ln}{A}_{LW}\right)+\beta ,$$ (12)

where α and β are constants with values 1.3 and −6.7 pC (see Table S2). The charge density of the lateral wall, σ_LW, is obtained from the derivative of Q_T with respect to A_LW, where A_LW = {250,…, 3000} μm², then

$$\begin{array}{c}{\sigma }_{LW}=\frac{\partial Q_T}{\partial A_{LW}}\\ =\frac{\alpha }{A_{LW}}.\end{array}$$ (13)

Substituting the values for α at 1.3 pC into Eq. 13, the magnitude of σ_LW is

$${\sigma }_{LW}=\frac{1.30}{A_{LW}}=\frac{1.30}{2\pi rL}$$ (14)

and is 1.30 pC/C_LW when described in terms of the linear capacitance. Equation 14 shows that the charge density decreases as the length of the lateral wall increases. Because C_peak is a function of Q_T (Fig. 3 c), a similar trend is observed between C_peak and A_LW (Fig. 3 d). We also propose that the best model to describe this relationship is a logarithmic function (see Table S2) with a slope of 9.04 pF/A_LW where the peak density, ρ_LW, is also inversely related to the length of the lateral wall (Fig. 4 b). This inverse relationship between Q_T and A_M is observed in Fig. 2 a. The charge density with respect to the total measured area is 1.87 pC/A_M and the peak charge density is 13 pF/A_M.

Figure 3.

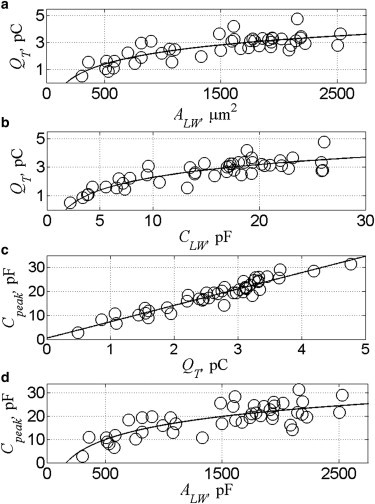
Voltage-dependent charge movement and peak capacitance exhibit nonlinear relationships with respect to the size of the lateral wall. (a) The charge increases with the logarithm of the area (α, 1.300 ± 0.145 pC; β, −6.689 ± 1.040 pC; and R², 0.658) and (b) capacitance of the lateral wall (α, 1.296 ± 0.117 pC; β, −0.7010 ± 0.310 pC; and R², 0.744). (c) The peak capacitance increases linearly with the total charge. (d) The peak capacitance increases with the logarithm of the area of lateral wall (α, 9.045 ± 1.094 pF; β, −46.262 ± 7.867 pF; and R², 0.619). (Circles) Single cell measurements; (lines) fits to logarithmic or linear functions.

Figure 4.

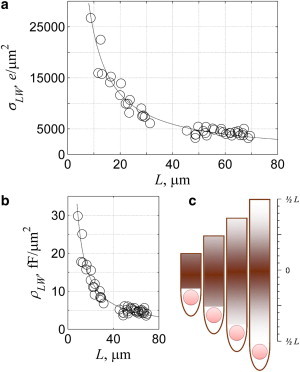
Charge and peak densities are inversely related to the area of the lateral wall for for OHCs obtained from the adult male guinea pig. (a) The charge and (b) peak density shown with respect to the length of the lateral wall. The length of the lateral wall was determined by dividing A_LW by 2πr. (c) Cartoon showing voltage-dependent charge density along the lateral wall where the color-code indicates charge density; maximum in the middle, and decays inversely with area toward the apex and base.

The relationship between C_NL and V is often described by the derivative of the two-state Boltzmann function (3,7,12), where C_peak is

$$C_{peak}=\frac{\nu }{4}{Q}_T,\nu =\frac{ze\delta }{k_{\text{B}}T},$$ (15)

where z is the valence of the charge, e is the charge of the electron, δ is the fraction of the distance traveled across the dielectric, k_B is Boltzmann's constant, and T is temperature. Expressing σ_LW in terms of Eq. 15, then Eq. 14 becomes

$${\sigma }_{LW}\approx \frac{4}{\nu }\frac{9}{A_{LW}}\approx \frac{4{\rho }_{LW}}{\nu },$$ (16)

where we show that ν has a value of 27 V⁻¹ from the relationships (Fig. 3, a and d, and see section S3 in the Supporting Material) or a value of 28 V⁻¹ from the linear slope (7.04 pF/pC, p-value < 0.0001, Fig. 3 c) between C_peak and Q_T. This value for ν is within the range found in the literature (3,12). It is also the same value obtained upon fitting the data from each cell to the two-state Boltzmann (28 ± 4 V⁻¹). The Q_T obtained upon fitting is within 5% of the values obtained by integration (e.g., Fig. 1 d).

A more recent description of the relationship between C_NL and V proposes that the nonlinear capacitance has two components (bell and nonbell) (39). The bell component is described by the two-state Boltzmann and the nonbell when V = V_peak is described by C_NB = ΔC/(1+ ν^-1). From their model and our data (Fig. 3 c) the intercept of the ordinate equals ΔC/2 and is 0.59 ± 0.9 pF with a mean asymmetry of 1.2 pF. When we subtract this mean value from C_peak, we find similar relationships suggesting this asymmetry model cannot explain the nonlinear observations.

Discussion

The first main finding of this work is the voltage-dependent charge density is inversely related to the lateral wall area (Eq. 14) for OHCs from adult males (Fig. 3, a and b). This suggests that σ_LW varies along the length of the OHC lateral wall (Fig. 4 a) whereas most studies assume σ_LW in the lateral wall of OHC is constant (9,12,13,15). The second main finding is that the size of the functional regions of the OHC can be determined by compiling the relationships between the measured geometry and the membrane capacitance across the cochlea.

Determining the functional regions of the OHC

For adult males, the capacitance of the nonlateral wall region is 5.17 ± 0.6 pF (Table 1), which, after subtracting the capacitance of the stereocilia, becomes 4.9 ± 0.7 pF. This value (5.2 pF) is less than the value determined from seven cells (7) with the microchamber technique, i.e., 6.2 pF (9). The discrepancy may arise from the age and sex of the animals used to obtain the cells. When we pooled all the OHC data, regardless of the age and sex of the animal we found a similar value at 6.1 ± 0.6 pF.

We determine the capacitance of this basolateral region to be 2.8 ± 1.7 pF and calculate a mean specific membrane capacitance of 0.0061 pF/μm² and find this value is constant across the cochlea (section S2 in the Supporting Material). The mean membrane capacitance of this region is 1.5-fold greater than the estimate from the microchamber experiments at 1.85 pF (9). We determine the specific linear capacitance of the lateral wall is 0.010 ± 0.002 pF/μm² and find it is constant across the cochlea for cells originating from adult males (Fig. 2, c and d, and see section S1 in the Supporting Material). This is a similar value to that found with a smaller population of cells at 0.008–0.01 pF/μm² for guinea pigs (9), and also comparable to the value of 0.008 pF/μm² determined in mice (11). This value of 0.01 pF/μm² for the OHC lateral wall is twofold more than that observed in secretory cells (19), but the same as initially measured in a variety of cells (20) and more recently found in neurons (21). The density of membrane proteins (and to a lesser extent the concentration of cholesterol) is shown to affect the thickness of eukaryotic cell membranes (22). If the lateral wall membrane has an elevated concentration of prestin molecules and a depleted concentration of cholesterol (relative to the base and apex) (40) then both factors will contribute to increasing the linear specific capacitance resulting in a value close to 1.0 pF/μm relative to 0.005 pF/μm². The total specific capacitance of the lateral wall (linear and nonlinear) depends upon the area and ranges from 15 to 40 fF/μm² (Fig. 4 b), albeit most of the data exhibit a twofold difference in the total specific capacitance at up to 27 fF/μm².

The measurements were conducted close to zero pipette pressure because of the reported effects of pressure on the charge movement in OHCs (29,30). When experiments were conducted without controlling the pipette pressure (16 cells, data not shown), we obtained different values for the slope at 0.005 pF/μm² (compare to Table S3) and intercept at 10.6 pF (Fig. 2 d). A slope of ∼0.01 pF/μm² and a much smaller intercept with the ordinate (1.8 pF) (see Eq. 11a) was obtained when pressure was controlled (p-value > 0.05) (Fig. 2 d). To obtain a statistically reliable estimate of the size of the cuticular plate, we pooled the data from prepubertal females and adult males (see above) and determined a value of ∼2.1 ± 1.1 pF (Table 1, functions 1 and 2). The size of the cuticular plate determined from electron micrographs (41,42) is ∼160 μm² (where A_CP = πr² + (2πr)L_CP and L_CP is the length of the cuticular plate. From this we determine a reasonable mean value of the specific capacitance of the cuticular plate at 0.013 pF/μm². The size and capacitance of the stereocilia bundle is the one region of the OHC that we are unable to determine. Ignoring this contribution results in the same relationships with small but minor changes in the constants derived (Table 1).

The first study to measure the capacitance of the OHC across the cochlea determined a slope of 0.475 pF/μm (8) from a plot of the capacitance versus the OHC length. Eq. 11a shows that the slope is dominated by the lateral wall capacitance for A_M ≫ A_B, where the specific capacitance can be calculated by dividing by 2πr (see Eq. 4). They found the radius of the OHC was 5.5 μm, and we calculate a specific capacitance of 0.0137 pF/μm² with their data. As previously reported, this value was overestimated because the voltage-dependent capacitance was not completely removed (8). A second study that also did not discriminate the C_L from the C_NL, determined a slope of 0.45 pF/μm from which we also calculate a specific capacitance of 0.0137 pF/μm² (14).

In a later study with many more cells (245 cells), the slope was reported to be 0.344 pF/μm and in the same way, we calculate the specific capacitance of 0.00998 pF/μm² (10), which is the same as we find with fewer cells (44 cells) when we calculate the area of each cell. Analyzing our data with respect to l (except we use r: 5.45 ± 0.6 μm), the slope and specific capacitance are 0.292 ± 0.016 pF/μm and 0.0085 ± 0.0014 pF/μm² where the mean value is ∼15% less than we find when we consider the area for each cell (Fig. 2, c and d, and see Table S3). Likewise, in the first study (8) the intercept with the ordinate was found to be 7.73 pF, which (Eq. 11a) should represent the size of the cuticular plate (here we ignore the contribution of 1 pF due to the stereocilia). We find a smaller value for the intercept at 4.13 ± 0.94 pF, which becomes 3.82 ± 0.91 pF when we removed the capacitance of the stereocilia. These values are twofold greater than our measurement for the capacitance of the cuticular plate at ∼2.1 pF.

We conclude an approximate estimate of the linear specific capacitance of the lateral wall is obtained by measuring the length of OHCs and capacitance across the cochlea, provided the nonlinear component is removed. Better estimates are obtained by controlling the pressure and calculating the area for each cell because OHCs tend to become shorter and fatter upon isolation from the animal. To obtain a reasonable estimate for the capacitance of the cuticular plate, it is necessary to control the pipette pressure during the recordings, measure the area (not just the length of the OHC), and record from a large number of cells.

Voltage-dependent charge density of the lateral wall is not constant along the length of an OHC

Early results with the microchamber experiment suggest the charge density within an OHC is approximately constant, as evidenced by the linear relationship of Q_T versus C_L (see Fig. 7 b of Huang and Santos-Sacchi (9)). They assumed that the σ_LW was constant within a cell and this then led to the proposal that σ_LW increases inversely with frequency across the cochlea from 5000 to 46,000 e/μm² from the apex to the base (i.e., the density varies inversely with position but is constant within a cell) (10). We find the relationship between Q_T and C_L when measured across the cochlea (compare to that of an individual cell) is better described with a logarithmic rather than a linear function (Fig. 2 b, Table 1), and the relationships between Q_T and A_M and C_peak and C_L are also logarithmic (Fig. 2 a, Table 1). Indeed, later experimental evidence provided by the same group suggests there are microdomains of varying density in the lateral wall of the OHC (43,44). Specifically, they show greater mechanically induced currents were observed in the middle of the lateral wall membrane relative to the areas distal to the middle (43). Examination of the histogram shows the current decreases 20–30% from either side of the middle of the OHC (Fig. 4 a of Santos-Sacchi and Takahashi (43)). Another report suggested the specific capacitance of the membrane was invariant to cell length and concluded that the charge density was constant across the cochlea (Fig. 7 b of Preyer et al. (14)). However, they did not discriminate between C_L and C_NL or between A_LW and A_NLW. Indeed, we find a similar result when estimating the specific peak capacitance with their method and our data.

More recently, a different group suggested that σ_LW is indeed constant within the lateral wall and across the cochlea at 10,000 e/μm² in the rat (15). This finding is supported by postembedded immunogold labeling of prestin: the concentration of the label is constant from the apex of the cell to the inferior aspect of the nucleus where it declined at the base. They suggest the discrepancy between their data and the earlier work (10) is due to the varying size of the nonlateral wall region at 318 and 207 μm² for low and high frequency cells. Although there may be differences between a rat and guinea pig cochlea, our data are in agreement with Santos-Sacchi et al. (10); the size (hence the linear capacitance) of the base and cuticular plate (excluding a minor contribution from the stereocilia) of the OHCs from the guinea pig are constant for an adult male. We do concur with Mahendrasingam et al. (15) that the nonlateral wall region can vary, but propose the stage of sexual maturity of the animal may be a more plausible cause. Indeed, there is some evidence that sexual maturation affects properties within the central auditory pathways (45,46). Mahendrasingam and colleagues used immature rats (P17) to obtain their measurements; rats typically take ∼50–60 days to reach sexual maturity (47). Evidence that sexual maturity affects membrane properties will be reported in a further communication.

Even though the data can be fit to a linear function (see Table S2), the significant positive nonzero intercept suggests there is a “hot spot” in the lateral wall where the charge is greater than the mean value. We propose that this nonuniformity is better described with a logarithmic function where σ_LW varies inversely with the length. This suggestion is similar to the earlier proposal that the charge density varies inversely with the frequency (Fig. 3 of Santos-Sacchi et al. (10)). However, they assumed that the charge density was uniform within a single cell. When we calculate the charge density on a cell-by-cell basis with the same assumption and plot the values with respect to L (see Fig. S1 in the Supporting Material), we find this relationship is fit equally poorly with a linear, logarithmic, exponential, or reciprocal function. If their assumption is correct that the charge density is constant within a single cell but varied depending upon the position of the cochlea, then the two plots (see Fig. S1, uniform charge density within a cell; Fig. 4 a, no requirement that there is uniform charge density within a cell) should be similar, and there should be a robust relationship between charge density and the reciprocal of the length of the lateral wall. The poor fit exhibited in Fig. S1 compared to Fig. 4 a, suggests that the functions are not the same, implying that the charge density is not uniform within a cell (Fig. 4 a). This is a different conclusion than reported in Santos-Sacchi et al. (10), but is supported by later evidence described by the same group (43,44). Although we are unable to predict the distribution of the charge, based upon the earlier observations (43,44), we suggest the highest voltage-dependent charge density is located in the middle of the lateral wall and decays inversely with A_LW reaching the lowest value at the base and apex of the longest cell (Fig. 4 c). Specifically, there is a maximum density of 27,000 e/μm² for a cell with the lowest lateral wall area (∼300 μm²) and a minimum density of 5000 e/μm² for an A_LW of 2500 μm².

An explanation for the discrepancy between the linear distribution of prestin along the lateral wall (15) and the nonlinear voltage-dependent charge density (Fig. 4) is the permittivity of the membrane becomes lower at the ends relative to the middle of the lateral wall during the charge movement. Indeed, any change within the membrane that results in increased permittivity (i.e., better screening or shielding of charge) should allow for more charge to accumulate. We note the hypothesis that cholesterol being depleted along the lateral wall of an OHC (40) would facilitate charge accumulation. We emphasize the σ_LW reflects the electric field of the lateral membrane, which is not detected by imaging prestin with immunogold particles.

Compiling the natural relationships between the measured geometry and charge (Figs. 2–4) reveals features that are not always apparent when examining average properties at one or two different regions. This is particularly relevant for the cochlea as it is inherently nonlinear. It is well known that the frequency of the sound is related to the position of maximum amplitude on the basilar membrane by an exponential function; the frequency increases exponentially with the distance from the apex of the cochlea. Specifically, f ≈ 10^b/(aln10) (10^ax – 1), where f is frequency and x is the distance from the helicotrema and a and b are constants (25,38). More recently, others describe the cochlea as a logarithmic (48) or Archimedean spiral (49). We find the nonlinear properties of the OHCs also exhibit logarithmic functions (Figs. 2 and 3) and suggest similar functions describe the relationships for other mammalian species. Indeed, a similar nonlinear relationship is implicit in published data (10), although not explicitly discussed (see section S4 in the Supporting Material). In addition, we compare the linear capacitance and total voltage-dependent charge measured for the rat (15), mice (11,12), and gerbil (13), with the guinea pig (Fig. 2 b) and find the values lie within the scatter of our data. This observation is in agreement with the idea that the length of the cell, and hence, the linear capacitance, represents frequency (26), where Q_T or C_peak represents place.

This work allows us to estimate the number of charges moving within the lateral wall under physiological conditions. This is estimated by assuming a median receptor potential of 0.004 V (50) for an OHC from a guinea pig (turn 3, A_LW ∼2000 μm²) and a peak density of 9.04 pF/A_LW (see Table S3); the density would vary from ∼900 e/μm² in the middle to ∼100 e/μm² at the ends of the cell. This estimate tacitly assumes that the membrane potential is close to the potential at maximum gain (voltage at peak capacitance, which is ∼0.062 V for an adult male guinea pig) and this is still not confirmed.

Finally, we predict that the axial displacement (ΔL) and total force (F) would decrease with the inverse of L as found for σ_LW (Fig. 4). This predicts that the force exhibited for a shorter cell would be greater than the force originating from a cell at the apical region and amplification would be greater at the basal region of the cochlea as suggested in Santos-Sacchi et al. (10). Indeed, measurements show the maximum ΔL of an OHC from the basal end of the cochlea is smaller than a cell from the apical end (51) and the axial stiffness decreases monotonically with cell length (52,53). However, this predication is contrary to the evidence that F (hence, charge) is constant with frequency and invariant to cell length (54). The reasons for this are unclear, but the different experimental conditions may contribute. In addition, they report a significant range (3–53 pN/mV) for F whereas we estimate a sevenfold increase in the σ_LW for a short compared to a long OHC. It is possible that their range masked detecting a change in F with cell length.