Predicting Nonspecific Ion Binding Using DelPhi

Abstract

Ions are an important component of the cell and affect the corresponding biological macromolecules either via direct binding or as a screening ion cloud. Although some ion binding is highly specific and frequently associated with the function of the macromolecule, other ions bind to the protein surface nonspecifically, presumably because the electrostatic attraction is strong enough to immobilize them. Here, we test such a scenario and demonstrate that experimentally identified surface-bound ions are located at a potential that facilitates binding, which indicates that the major driving force is the electrostatics. Without taking into consideration geometrical factors and structural fluctuations, we show that ions tend to be bound onto the protein surface at positions with strong potential but with polarity opposite to that of the ion. This observation is used to develop a method that uses a DelPhi-calculated potential map in conjunction with an in-house-developed clustering algorithm to predict nonspecific ion-binding sites. Although this approach distinguishes only the polarity of the ions, and not their chemical nature, it can predict nonspecific binding of positively or negatively charged ions with acceptable accuracy. One can use the predictions in the Poisson-Boltzmann approach by placing explicit ions in the predicted positions, which in turn will reduce the magnitude of the local potential and extend the limits of the Poisson-Boltzmann equation. In addition, one can use this approach to place the desired number of ions before conducting molecular-dynamics simulations to neutralize the net charge of the protein, because it was shown to perform better than standard screened Coulomb canned routines, or to predict ion-binding sites in proteins. This latter is especially true for proteins that are involved in ion transport, because such ions are loosely bound and very difficult to detect experimentally.

Introduction

Proteins form complex three-dimensional (3D) folds that ultimately determine their biological role. At the same time, these 3D structures exist in a water phase in which many different types of ions in turn interact with the macromolecules. As a result, many proteins bind metal ions specifically or nonspecifically as part of the active site or to stabilize the protein structure by creating or maintaining secondary/tertiary structural elements (1–4). In addition, ions are essential components of living organisms. This is especially the case for metal ions, because 70% of all enzymes contain metal ions. Ions are involved in all aspects of physiological response, such as signal transduction (5), regulation of enzyme catalytic activity (6), maintenance of osmotic balance (7), and the general ionic environment (6). These few examples illustrate the importance of ions for almost any biological process.

Metal ions in biological systems can be classified into two types (6): 1), bulk metal ions (Na, K, Mg, and Ca), which constitute 1% of human body weight; and 2), trace metal ions (Fe, Cu, Mn, Zn, Co, Mo, Ti, Va and Ni), which constitute 0.01% of human body weight. Both types of ions can serve as specifically bound entities that contribute to protein function and stability, and as mobile charge carriers in the water phase that enable screening of the electrostatic potential. The former function has been the focus of many investigations, as outlined below, and the latter has been explored mostly by means of Debye-Hückel screening of noninteracting point charges.

The Zn ion is frequently tightly bound to proteins and is considered an essential cofactor for hundreds of enzymes and thousands of metabolic and regulatory proteins, serving two main roles: structural and regulatory (catalytic) (4,8). Structural sites are typically characterized by a zinc-centered tetrahedral coordination in which the metal ion is fully coordinated by four Cys residues via a thiolate group, or His residues usually in combination with Cys, forming zinc finger motifs (9). Structural zinc sites have important implications for the functioning of metalloproteins (10). In catalytic sites, zinc ions participate directly in the catalytic process and generally exhibit a distorted tetrahedral geometry, typically making three bonds to O/N/S atoms and a fourth one to a water molecule, which in turn is frequently an activated nucleophile for the catalytic process (8). Calcium is one of the most important metals in cells because it controls a broad spectrum of vital processes ranging from bone mineralization to cell signaling (11–13). In some extracellular enzymes, occupation of Ca-binding sites involving surface loops leads to enhanced protein stability and provides protection against proteolytic digestion (14). Other enzymes have evolved Ca-binding sites in which the Ca ion plays an electrophilic role in catalytic hydrolysis of substrates (14). Magnesium is also one of the most vital elements of the body. It activates ∼300 enzymes and is involved in regulation of cellular permeability and neuromuscular excitability (15). Half of it is present in the skeleton and the other half is present in enzymes. The concentration is high inside cells but low in blood plasma (6). Magnesium may participate in enzymatic reactions in two ways, by binding to a substrate or a protein (6). Among the noncharged protein ligands that bind Mg, the side chains of Asn/Gln and the backbone carbonyl groups are the most common, followed by the Ser/Thr, His, and Tyr side chains. The preferred coordination number is 6 for Mg (16) and Na (17), 4–6 for Zn (16), and 6–8 for Ca (18).

The above examples illustrate that knowledge of an ion's position is important for understanding various biological reactions. Ion-binding sites in biological macromolecules are typically identified through x-ray crystallography or NMR methods. However, the proper assignment of an ion's position in x-ray structures of proteins is not always trivial. Many ion sites can be easily mislabeled or may be missing entirely from fully refined crystal structures or solution structures of proteins, and must be located through further experiments. For example, identification of Na-binding sites in protein crystals is complicated by the comparable electron densities of this monovalent cation and water (19). Therefore, the development of computational methods that can predict ion-binding sites and complement experimental techniques is of great importance.

There are numerous numerical/computational methods that can be applied to predict the positions of specifically bound ions. The most common methods are based on the coordination numbers of ions (8,18), geometries (20–24), preferences (16,25), and ligands (26–28). A straightforward and computationally fast algorithm is valence screening for metal ions (19,29). This method essentially calculates the valence potential of oxygen atoms within a defined radius along a fine 3D grid laid over a molecular structure to predict potential ion-binding sites. However, this approach requires that the structures be determined with high accuracy (resolution ≥1.5 Å) (1). The most popular geometry-based ion prediction methods are CHED (30) and its variances SeqCHED (31), MetSite (32), and MDB3 and MSDsite (33–37). It was previously pointed out that the environments of metal ions in proteins share common features regardless of the ion type and its precise pattern of ligation to the protein (38). It was shown that the metal ion is coordinated by an inner sphere of hydrophilic groups (containing oxygen, nitrogen, or sulfur atoms) embedded in an outer sphere of hydrophobic groups (containing carbon atoms), giving rise to a center of substantial hydrophobicity contrast (38). Thus, it was proposed that the hydrophobicity contrast function may be useful for locating, characterizing, and designing metal-binding sites in proteins (38).

Other groups of methods are based on energy calculations that account for the combination of both short- and long-range forces to predict the energy of interaction between the ion and the biomolecule. The short-range forces include several components, such as the van der Waals (vdW) force (39), whereas the main component of the long-range forces is electrostatic interactions (40). One of the first attempts to determine energetically favorable binding sites for biologically important macromolecules was implemented in an algorithm called GRID, which calculates the interaction of probes (e.g., water, the methyl group, amine nitrogen, carboxyl oxygen, and hydroxyl) with the protein and makes predictions based on the magnitude of the calculated energy (41). Similarly, another energy-based method, Q-SiteFinder, uses the interaction energy between the protein and a simple vdW probe to locate energetically favorable binding sites (42).

All of these approaches are aimed at predicting specifically bound ions that typically are buried in the biomolecule and are not accessible from the water phase. On the other end of the spectrum are methods that treat the ions as noninteracting mobile point charges present in the surrounding water phase. These approaches are based on either a numerical solution of the Poisson-Boltzmann (PB) equation (43) or the generalized Born (GB) model (44). Although GB-based methods are considered to be the fastest for calculating the electrostatic potential of proteins in solution, methods that use the PB equation are believed to be more accurate (45,46). However, they both can overestimate the screening by not accounting for mutual repulsion between ions of the same polarity and the physical inability to build an extremely high concentration due to volume exclusion effect (finite size of ions) (47–49). To minimize the errors originating from ions (noninteracting point charges) and solution (continuous, homogeneous, and isotropic medium, characterized solely by a scalar, static dielectric constant) approximations, investigators have employed a set of corrections, including alteration of dielectric function (50–53), surface of macromolecule treatment (51,54–56), atomic radius adjustment (44,45), and alternative modifications (44,57).

However, very little has been done to explicitly model ions loosely bound to the protein's surface, which are not part of the ion atmosphere or specifically bound in the protein interior. Such surface-exposed ions can be seen in some experimentally determined 3D structures, providing the opportunity to examine why such ions are bound to the protein surface. Here, we investigated the role of electrostatics in nonspecific surface-bound ions on a set of 529 experimentally determined ion positions involving four types of ions (Ca, Mg, Zn, and Cl), and show that electrostatics is the major driving force for the binding. Using this observation, we developed a method that uses a DelPhi-generated potential map in conjunction with a clustering algorithm to predict ion-binding sites. The method can be used to place explicit ions into PB solvers and thus to extend the limits of the PB approach. In addition, the predictions can be used to place counterions at the beginning of molecular-dynamics (MD) simulations to neutralize the net charge of the corresponding macromolecule, or simply to predict loosely bound ions that experimental techniques cannot easily detect.

Methods

Protein structures with experimentally determined ions

We surveyed the Protein Data Bank (PDB) (58) for x-ray structures containing Mg, Zn, Ca, or Cl ions. We also explored other types of ions, including Na, Cu, Fe, and Mn, but after application of the pruning procedure described in the next section, the corresponding cases were reduced to <15 and therefore we removed those entries from our data set. The resolution was required to be >3 Å to avoid artifacts of structural imperfections. This resulted in a total of 24,455 PDB files, of which 3708 contained Mg, 13,450 contained Ca, 3936 contained Zn, and 3361 contained Cl. Some of these structures had ions bound inside the corresponding protein and others contained ions that were clearly involved in chemical contacts. Such specific ion binding is not the subject of this study, and thus these cases were removed from the data set.

Fixing missing atoms and generation of hydrogen atoms

Some of the structures in the experimental database had structural defects, and thus all of the structures were subjected to the profix program from the JACKAL package (http://wiki.c2b2.columbia.edu/honiglab_public/index.php/Software) developed in Honig's laboratory (59) to add missing atoms and/or sequence fragments. To protonate proteins in the data set (i.e., to generate missing hydrogen atoms), we used TINKER software (pdbxyz and xyzpdb packages) (60) with AMBER force-field parameters (61). Because the study was aimed at surface-bound ions that are not involved in specific interactions, the residue charged states were considered to be standard and no pKa calculations were performed, because surface-exposed titratable groups are typically fully ionized at neural pH. In addition, it was almost impossible to determine the pH of the crystallographic experiment at which the ion positions were obtained. Therefore, to avoid introducing additional ambiguity, all acids and bases were considered ionized.

Pruning the data set to include only nonspecific surface-bound ions

In this study, nonspecifically bound ions are considered to be ions that do not make specific contacts with protein atoms and are accessible from the water phase. The first criterion was applied by requiring that the shortest distance between the ion and specific atoms of the protein be larger than the sum of their vdW radii (this is termed the vdW bond). As discussed in the Introduction, previous studies indicated that Ca and Mg preferably bind to oxygen atoms, whereas Zn is frequently found to bind to nitrogen, and for negatively charged Cl ions, the best binding partners are positively charged hydrogen atoms. The vdW radii were taken from the Cambridge Structural Database (http://www.ccdc.cam.ac.uk/products/csd/radii/) and the above criteria were applied to each ion (the vdW bonds are provided in Table 1). Proteins with ions at a distance shorter than the corresponding vdW bond were deleted from the data set. In addition, in some cases, ions were found quite far away from the protein surface due to the presence of ligands or surfactants in the PDB file (small molecules were deleted from the PDB files because they represent specific binding as well). To avoid such cases, which were a tiny fraction of our data set, we applied an additional criterion to delete any protein having an ion >5 Å away from the closest protein atom.

Table 1.

vdW bond and SASA for tested ions

	Ca	Cl	Mg	Zn
SASA (100%), Å2	151.31	128.68	123.11	97.818
VdW bond, Å	3.52	2.84	3.25	2.94
Typical partner	O	H	O	N

100% SASA relates to the case in which the ion is completely exposed to the solvent molecules.

The second criterion was to select ions that are solvent-exposed and to avoid buried cases. For this purpose, we calculated the solvent-accessible surface area (SASA) for each tested ion in the protein using NACCESS software (http://www.bioinf.manchester.ac.uk/naccess/) (62) and a probe radius of 1.4 Å. The calculations were performed using atomic radii for protein atoms taken from the AMBER force field (61). At the same time, the SASA for isolated ions was also calculated, and these reference values are shown in Table 1 (first row). To reinforce the requirement that ions should be solvent-accessible, we required that in the corresponding protein they retain at least 50% of their accessibility in the free state. At the same time, to avoid unwanted cases of ions being separated from the protein by water shell, we also deleted ions that retained >75% of their free-state accessibility from the data set. As a result, our database comprised 446 proteins in total, including 47, 29, 153, and 224 proteins and 51, 35, 161, and 267 ions for Ca, Zn, Cl, and Mg, respectively (this purged data set and the corresponding PDB files of fixed and protonated proteins structures can be downloaded from http://compbio.clemson.edu/downloadableData.php).

Electrostatic potential calculations

We subjected all proteins in the data set to continuum electrostatic potential calculations using DelPhi (63). The following parameters were used: scale = 1 grid/Å; percentage of protein filling of the cube = 70%; dielectric constant = 2 for the protein and 80 for the solvent; ionic strength = 0.5 M; water probe radius = 1.4 Å; and Stern ion exclusion layer = 2.0 Å (for optimization purposes, the internal dielectric constant and ionic strength were varied). Ions and all heteroatoms were deleted from the corresponding PDB files.

We performed two types of calculations. The first one used the protein structure file in conjunction with the above parameters and the FRC module of DelPhi. The FRC module allows users to output the calculated electrostatic potential at desired point(s) (see the DelPhi manual at http://compbio.clemson.edu/downloadDir/delphi/delphi_manual.pdf). For our purposes, the point at which the potential was collected was the position of the corresponding ion. The coordinates of the ion were taken from the corresponding PDB file. This procedure allowed us to probe the potential at the position of ion without the ion being present in the calculations. For the second type of calculations, we outputted the DelPhi-calculated potential map into a file in CUBE format (http://compbio.clemson.edu/delphi.php). The CUBE potential map provides the electrostatic potential at each grid point within the grid. The difference between these two types of calculations is that the usage of the FRC module requires prior knowledge of the position of the ion and thus is used for testing purposes only, whereas the potential in the CUBE potential map is outputted at each grid point and can be used to make predictions.

Analyzing the potential map and clustering algorithm

A potential map calculated with the above parameters with DelPhi could result in a grid size of hundreds of points or more, which in turn could result in more than a million grid points where the potential is calculated. A direct analysis of such a large array could result in ranking on the top of the list grid points close in space and neglecting other potentially important sites. A particular example is shown in Fig. S1, a and b, in the Supporting Material, in which a case with a sharp potential well is contrasted with another case with a very shallow potential valley. To avoid such cases, we applied a clustering algorithm.

As mentioned above, the CUBE potential map contains the potential at each grid point, including grid points inside the protein. However, our aim in this study was to use the potential map to predict surface-bound ions, and to exclude any ion bound in the protein interior. Therefore, the points analyzed by the potential map were those located on the surface of the protein. A grid point was considered to be at the surface of the protein if the shortest distance between the grid point and the atoms of the protein was larger than the ion-specific vdW bond. At the same time, to avoid predicting ion-binding sites unrealistically far away from the protein surface, we required that the grid point be located within a 5 Å distance from the protein atoms (the cutoff distance is shown with a dashed line in Fig. 1 A). Then these surface grid points were clustered beginning with the point with the smallest X-coordinate and forming a cluster with a radius of 5 Å (Fig. 1 A). Clusters were not intersected. The point with the highest absolute potential was chosen to represent the cluster (Fig. 1, where the representative point for each cluster is shown in black). It can be seen that at this initial clustering, some representative grid points could be quite close to each other (open circles in Fig. 1 B). To avoid such a case, secondary clustering was performed within nonintersecting spheres of 10 Å. For each sphere, we calculated the geometrical center of all representative points within the sphere, and all representative points that happened to be within 5 Å away from this center were merged, leaving the point with largest potential only (Fig. 1 B, where remaining representative points are shown in black). This procedure also resulted in a few cases in which these representative points were still close to each other (Fig. 1 C). Thus, a final purging was performed such that if two representative points were situated within 5 Å from each other, they were merged to the point with the highest absolute potential (Fig. 1 C, solid black circles). Then, all remaining representative points were checked with respect to their accessibility to the water phase. To that end, we explicitly placed ions at each representative point and then applied the procedure for SASA calculation as described in Methods. Only representative points for which the ion retained 50–75% of the maximum SASA typical for the given type of ion were kept in the final representative set of grid points. This was done to ensure that the representative points would be neither too close to the protein surface nor too far away from it, and would be consistent with our selection of experimentally selected ion-binding sites.

Figure 1.

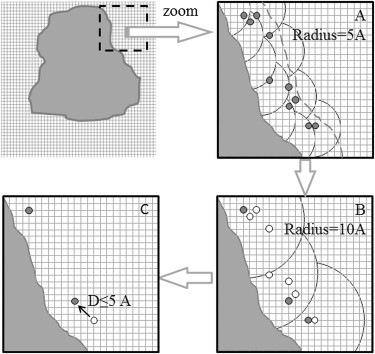
Schematic representation of the clustering algorithm. The left upper panel shows a protein mapped onto a grid. A small region (shown with dashed square) is zoomed and shown in panel A. Large circles symbolize the border of clusters, small open circles represent all points in a cluster, and solid dark circles represent points with the highest absolute potential. In panel A the radius of each cluster was 5 Å (the dashed line shows a cutoff distance of 5 Å away from the protein surface). (B) A more rigorous condition for cluster determination was applied (radius of clustering = 10 Å, and distance between the geometric average of all points in the cluster and farthest to its point in the cluster ≤5 Å. (C) The final step of clustering is to search for all resultant points <5 Å from each other and leave only those with greater absolute potential.

Benchmarking parameters

Dmin

Dmin is defined as the shortest distance between representative grid points and the experimentally determined ion's position.

Rank

The representative grid points for each tested type of ion were sorted in descending order (by absolute value) of the potential (positive for Cl, and negative for Ca, Mg, and Zn). The position of a given point within this list is termed the Rank. Thus, a representative grid point in the third position within the ordered list of N representative points is considered to have Rank = 3.

Receiver operating characteristic curves

We analyzed the ability to predict the experimental ion's position and accuracy of the described method by plotting receiver operating characteristic (ROC) curves. The x axis represents the Rank of the closest representative grid point to the experimentally determined ion position, and the y axis represents the number of successful predictions (true predictions) in percentage of all predictions. Two definitions of true positive prediction were adopted: 1), a prediction is considered to be true if the representative point situated at the shortest distance from the ion experimental position (Dmin) is predicted; and 2), a prediction is considered to be true if the distance between the predicted representative grid point and the actual experimental ion position is <10 Å. We chose this criterion because the parameters of the clustering algorithm result in the shortest distance between representative grid points being ≥10 Å.

Results

Distribution of the potential at the experimentally determined ion positions

For each experimentally determined ion position, we used the FRC procedure of DelPhi (see Methods) to deliver the potential at the ion's position in the absence of the ion. We did this to investigate the role of electrostatic potential in ion binding. Because these ions are not expected to be involved in chemical interactions with the corresponding protein, the driving force should be nonspecific, and naturally the electrostatics is presumed to be a dominant factor. The potentials for each type of ion were collected and found to not follow the normal distribution (Fig. 2). This indicates that ions are situated at positions where the electrostatic potential is not randomly distributed, but rather shows a preference for the presence of ions of a given polarity. It can be seen that the potential collected at the positions of positively charged ions is always negative, whereas the potential at the positions of negatively charged Cl ions is always positive. This observation indicates that both types of ions in our data set are nonspecifically bound ions, and that the electrostatics favors their binding.

Figure 2.

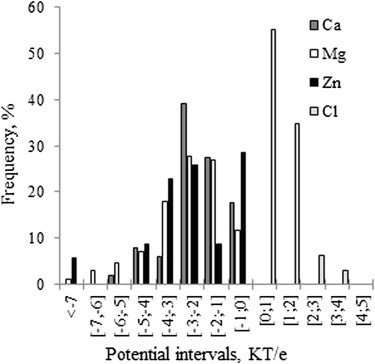
Distribution of the electrostatic potential at experimental ion positions grouped with respect to ion type.

Analysis of the electrostatic potential map

For each protein in the data set, the electrostatic potential map was analyzed and the grid points were clustered as described in Methods. The corresponding representative grid points were ranked by descending absolute value of the potential, so that the point with highest absolute potential had Rank = 1. Depending on the size, shape, and net charge of the investigated protein and in general the distribution of the charges inside it, the corresponding electrostatic potential clustering resulted in a different number of representative grid points. Fig. 3 shows the distribution of the number of representative grid points for each type of ion in the proteins from the examined data set (dark bars). A significant difference is observed among cases involving Ca, Zn, and Mg ions (which has a broad distribution) versus Cl ions (which has a narrow distribution, with a mean of ∼20–30 representative points). This may reflect the differences in the biophysical properties (e.g., number of residues, shape, and charges) of the corresponding proteins in our data set, which hold different types of ions. The same figure (Fig. 3, light bars) shows the Rank distribution of the closest to the actual ion's position representative grid point. It should be clarified that due to the clustering procedure and the GRID algorithm, the representative grid points do not necessary have to match the ion's position. It can be seen that in all cases, for both positively and negatively charged ions, the representative grid point closest to the ion's position is ranked among the top 10 points in 20–60% of the cases (Fig. 3). The best results were obtained for Mg ions, which showed a sharp peak at Rank < 10. These results indicate that the representative point closest to the actual ion's position is within the top 10 representative points with the highest electrostatic potential in ∼60% of the cases in the data set. The results for other types of ions (Ca, Zn, and Cl) are less impressive but still indicate a clear trend that the position of the ion binding is within the vicinity of the strongest electrostatic potential.

Figure 3.

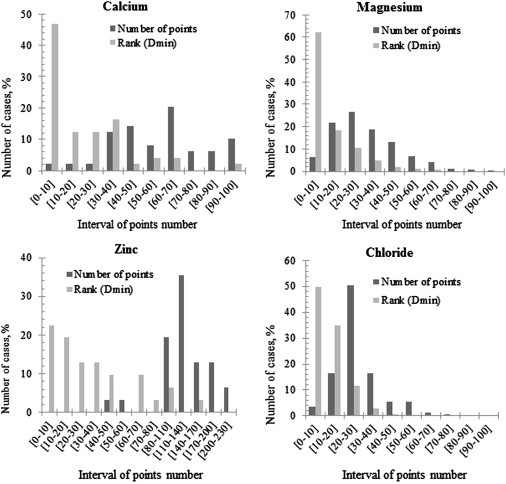
Distribution of all representative grid points found by the clustering method with Rank = 1 (dark bars) and the Rank of the closest representative grid point with respect to the original ion's position (light bars).

To investigate how accurate (in principle) the described method can be in detecting the original position of tested ions, we examined the distribution of the distances of the closest representative grid points. The results are shown in Fig. S2 (light bars). According to our data, in the vast majority of the cases, the representative grid point is located within 10 Å from the actual ion's position that is equal to the uncertainty that is determined by the clustering method. This ensures that the clustering algorithm does not eliminate potentially good representative candidate points. It should be pointed out that although cases with the Zn ion show the worst ranking results (see Fig. 3, light bars), they show the best results in terms of distribution of the closest representative grid point (100%). This indicates that the proximity of the representative grid point to the actual position of an ion is not a crucial factor in the obtained ranking (Fig. 3 and Fig. S2, light bars).

The next question to address was the distribution of the distance between the ion's actual position and the representative grid point with highest absolute value of the potential (Rank = 1; positive for Cl (D(Pmax)) and negative for Ca, Mg, and Zn (D(Pmin)). The results are shown in Fig. S3 (dark bars). It can be seen that the maxima of the corresponding distributions are within 30–40 Å for all types of ions. Replacing the DelPhi calculations with a less computationally demanding screened Coulomb law resulted in much worse predictions, as shown in Fig. S3. In addition, in a small number of cases, the first-ranked representative point is located >80 Å from the actual position of the ion, which may be on the other side of the protein. Some plausible explanations for these prominent failures are presented in Fig. S4, Fig. S5, Fig. S6, and Fig. S7, and it is suggested that the geometry of the surface and the curvature of the potential may contribute to the preference of a given ion to bind at a particular position.

Two parameters of the protocol are the internal dielectric constant of the protein and the ionic strength in the water phase. To test the sensitivity of the method and to find the optimal values of these parameters, we constructed ROC curves (as described in Methods) for each case in our data set, choosing two different values for the parameters (internal dielectric constant = 2 and 4, and ionic strength = 0.15 M and 0.5 M). We generated the ROC curves by varying the Rank, which essentially means varying the number of predictions (Fig. 4). It can be seen that the method is not sensitive to the values of the parameters in the cases of Ca, Cl, and Mg ions, but is quite sensitive in the case of Zn ions. The best results were obtained with internal dielectric constant = 2 and ionic strength = 0.5 M. In terms of percentiles, for 62% of the cases for Mg, 47% of the cases for Ca, 23% of the cases for Zn, and 50% of the cases for Cl based on the experimental data set, the closest representative point was found within the first 10 ranked points. We made similar observations by using the second definition of true predictions (see Methods). The results are shown in Fig. S8.

Figure 4.

ROC curves for Ca, Mg, Zn, and Cl ions containing proteins data set, calculated with respect to different parameters. The first number corresponds to the dielectric constant of the solution, and the second one corresponds to the ionic strength in moles/l. The x axis represents the Rank of the closest representative grid point to the experimentally determined ion position. The y axis is the number of successful predictions (true predictions) in percentage of all predictions. A prediction is considered to be true if the representative point situated at the shortest distance from the ion experimental position (Dmin) is predicted.

Discussion

In this work, we sought to investigate the role of electrostatics in nonspecific surface ion binding. To that end, we created a purged data set to include PDB structures with experimentally determined ions that are located on the protein surface and are not involved in chemical interactions. However, we note that some of these entries may still have ions involved in specific interactions or may be artifacts of the crystallographic procedure. We attempted to delete all ions with crystallographic constants, but not all entries were manually screened for such cases. In addition, it is possible that some other factors, not revealed in the x-ray experiment, could also contribute to the binding. Despite the requirement for relatively high resolution of the structures in the data set, it is still possible that the crystallographic ion position is within fractions of angstroms or more away from its actual position. Therefore, it is plausible that some of the ion positions in our data set are not nonspecifically surface-bound ions. Such ions cannot be predicted by means of electrostatics alone.

It is quite possible that some of the top Rank predicted ion-binding sites are away from the experimental ion's actual position. Examples and analysis of the worst predictions for each type of ions are presented in Fig. S4, Fig. S5, Fig. S6, and Fig. S7, a and b. In all cases, the representative grid point with Rank = 1 had an absolute electrostatic potential much higher than the potential of the experimentally determined ion. This clearly indicates that electrostatic interactions alone cannot predict such cases. We conducted our investigation without using surface curvature, structural flexibility, and other factors that may contribute to the binding. It can be expected that the binding and immobilization of an ion are easier achieve in the cavity point, surrounded by relatively rigid amino acids. However, this would require a different approach that would combine the clustering algorithm with geometrical and structural information. On the other hand, it can be speculated that the predicted ion positions reflect additional possible ion-binding sites that were not revealed in this particular x-ray experiment due to thermal fluctuations, the resolution of the x-ray structure, or other details of the experimental procedure. Thus, some of the “false” predictions may not be false after all.

Conclusions

This study shows that electrostatics plays a dominant role in ion binding, and ions are always situated at a potential opposite to their polarity. Because nonspecific ion binding is electrostatically driven, one can use this observation to extend the limits of PB approaches. It was mentioned that the limitation of the PB method stems from the treatment of ions as mean-field interacting point charges. Obviously, such an assumption will not be valid in the water phase exposed to a strong potential, because it will result in overprediction of an ion's concentration. Such a high potential would occur close to the macromolecule charges, and thus near the macromolecule surface. One can explicitly position an ion in such a surface electrostatic valley and treat it explicitly in the PB calculations. The presence of the ion will greatly reduce the potential, and thus the validity of the PB approach will be retained.

One can use the method presented here in conjunction with a standard MD package to place ions before conducting MD simulations. This would simply require one to know the net charge of the macromolecule (either by performing pKa calculations or assuming standard protonation states) and what type of ion should be placed. Once these are decided, the number of ions (N) that one needs to place is the ratio between the next charge and the valence of the type of ion. Then, one should use the ranking list provided by our procedure and place ions at the top N ranked positions. Because the method accounts for electrostatic interactions only, it supposedly is not sensitive to structural variations and fine details of the structure. Therefore, one does not have to minimize a structure before using it to place the ions.

Our method uses DelPhi in conjunction with a clustering algorithm to predict nonspecifically bound ions on the surface of proteins. Such ions are very difficult to determine experimentally because their mobility is not restricted by special constraints. A typical example is provided by ion transport proteins. It was previously shown that binding a beryllium ion on the surface of HLA class II histocompatibility antigen (ID 3lqz, α-chain) induces the fibrotic lung disorder called chronic beryllium disease (64). Although investigators have proposed several beryllium-binding sites on the basis of experimental investigations, the problem is far from solved. Thus, this approach can be used to predict these positions and guide further experimental investigations.