Axonal transport analysis using Multitemporal Association Tracking

Abstract

Multitemporal Association Tracking (MAT) is a new graph-based method for multitarget tracking in biological applications that reduces the error rate and implementation complexity compared to approaches based on bipartite matching. The data association problem is solved over a window of future detection data using a graph-based cost function that approximates the Bayesian a posteriori association probability. MAT has been applied to hundreds of image sequences, tracking organelle and vesicles to quantify the deficiencies in axonal transport that can accompany neurodegenerative disorders such as Huntington’s Disease and Multiple Sclerosis and to quantify changes in transport in response to therapeutic interventions.

1 Introduction

Defects in axonal organelle transport are correlated with neurodegenerative diseases including Huntington’s, Alzheimer’s and Multiple Sclerosis (MS) (De Vos et al., 2008). In order to precisely evaluate the role of deficiencies in axonal organelle transport in the pathogenesis of these diseases, and also to evaluate the impact of potential therapeutic interventions, reliable methods for quantifying the transport of organelles along the axon under different experimental conditions are required. Fluorescent protein microscopy has made it possible to capture time lapse image sequence data showing the transport of individual organelles along the axon. Manual approaches to analysing such data are tedious and error-prone. There is a pressing need for accurate and reliable automated tools for quantifying axonal organelle transport. We present a new approach to multitarget tracking designed specifically for the high target density and high noise conditions that are typical of image sequence data showing axonal organelle transport. We demonstrate this approach by evaluating organelle transport in wild type compared to Huntington’s disease populations, and also to evaluating the effects of inflammation in the pathogenesis of MS by quantifying axonal organelle transport of hydrogen peroxide treated versus control groups.

Automated tracking in axonal transport sequences is a challenging problem. Although the number of organelles being tracked is similar to other subcellular transport problems, all of the organelles are transported along a thin axon rather than being spread throughout the image domain. This dramatically increases the target density and exacerbates the problems of occlusions, missed detections and low signal-to-noise ratio that are observed in most subcellular transport image sequences. Kymograph projection can circumvent some of these issues, allowing analysis of axonal transport (Haghnia et al., 2007; Ludington and Marshall, 2009). For example, Mukherjee et al. use kymographs to automatically analyse BDNF organelle transport (Mukherjee et al., 2011). Kymographs are an excellent way to visualise axonal organelle transport. However, approaches based on analysing organelle transport directly from kymographs assume a straight 1D axon. Because the axon has curvature and thickness, such approaches introduce systematic measurement error into organelle motion analysis. Tracking organelle transport by extracting motion parameters from the kymograph also discards 2D motion information that may be discriminative. Our approach is to track axonal organelle transport directly on the 2D image sequence data, rather than on the kymograph.

Several other tracking approaches have been proposed for analysing live-cell fluorescence image sequences. Jaqaman et al. use single frame assignment to build organelle track segments in fluorescence microscope image sequences (Jaqaman et al., 2008). These track segments are then linked using a second bipartite matching. The authors have provided a well designed open-source software implementation of this tracking methodology in conjunction with the paper. We compare the performance of this implementation with MAT for simulated organelle data in Section 3.1. Similarly, Broeke et al. quantify organelle transport along neuronal axons using a single-frame assignment tracker applied to fluorescence labelled image sequences (Broeke et al., 2009).

Multitarget tracking has also been posed in a graph-theoretic framework where the detections are treated as vertices of a graph and the edges are possible inter-frame associations. Our approach was inspired by the directed graph formulation presented in Shafique and Shah, where a k-partite hypergraph matching is used to solve for the optimal track cover (Shafique and Shah, 2005). However, edge weights in the graph are generally dependent on other associations in the graph e.g., weights based on velocity, acceleration, etc. The tracking graph changes after every assignment. Thus, their tracking solution required the addition of a greedy heuristic method, a limitation that our approach removes. Berclaz et al. use a k-shortest paths algorithm to approximate the solution to Multiple Hypothesis Tracking (MHT) formulated as an integer programming problem over a Probabilistic Occupancy Map (POM) (Berclaz et al., 2011). As with other MHT approaches, this algorithm requires an accurate statistical model of detection errors, in this case the POM. The motion model of (Berclaz et al., 2011) is limited to edge constraints in the graph, so this approach would likely be inaccurate in high object-density settings. Chenouard et al. propose to use a branch and bound approach to solve the full MHT problem in polynomial time (Chenouard et al., 2009). Their approach is used for tracking Golgi units in live-cell image sequences of Drosophila oocytes. However, branch and bound is not guaranteed to achieve a polynomial time solution to the exponential MHT problem, and their approach still requires statistical modelling of segmentation errors and occlusions.

We have developed a tracking approach called Multitemporal Association Tracking (MAT) that solves the tracking problem across multiple image frames, is robust to segmentation errors and does not require labor-intensive tuning of parameters related to the imaging conditions or culture density. Instead, tracking cost function parameters are established once for the type of object being tracked. MAT works by considering multiple frames of segmentation results simultaneously. MAT searches forward from the current time instance to find all feasible paths based on typical object behaviour and performs the association between paths (rather than detected objects) and the current set of tracks. The association is done at each time instance and uses a minimum spanning tree optimisation (Papadimitriou and Steiglitz, 1998), iteratively assigning the lowest cost, or equivalently highest likelihood, associations between tracks and feasible paths. This is described in detail in Section 2. By minimising this cost function, MAT approximates the Bayesian a posteriori probability estimate for the data association problem (Saerens et al., 2002). The key difference between MAT and other approaches to solving the multitarget tracking problem is in the relaxation of the requirement that a single track can be assigned to at most one detection, or future path in the case of windowed tracking solutions. Allowing multiple tracks to share a single future path matches the nature of the biological problem where organelles can appear to merge, and also greatly reduces the complexity of the tracking solution.

MAT has been applied to image sequences containing phantom data and to the analysis of transport of organelles and vesicles along neuronal axons. MAT has also been used for automated stem-cell tracking and lineaging (Winter et al., 2011) where it achieved a significant improvement in tracking accuracy compared to previous approaches (Cohen et al., 2010). MAT is implemented in C++ and typically requires just a few seconds to track an entire image sequence.

2 Methods

2.1 Multitemporal Association Tracking

Given the set of all detections Y returned by a segmentation routine we partition Y into the subsets Y^t where Y^t is the set of detections in frame t and denote the ith detection in frame t as $Y_i^t$. We construct the graph G with Y as its vertices and let the edges $e_{\mathit{\text{ij}}}^{t_1}=\{Y_i^{t_1},Y_j^{t_2}\}$ of G represent feasible forward-associations of detections in distinct frames t₁ < t₂. Any path τ on the graph G represents a possible object track. Tracking is posed as a combinatorial optimisation problem by assigning to each association a cost, representing the likelihood that an object assumes a given sequence of states, and choosing the set of tracks, ω, so as to optimise some objective function over the edge costs. New tracks are initialised with previously untracked segmentation results. Tracking associations that constitute physically impossible behaviours of the objects are assigned an infinite cost. We extend tracks so as to minimise the track costs for each track in ω.

We denote a partially constructed object track terminating at vertex $Y_i^t\text{ as }{\tau }_i^t$. Similarly an extension of ${\tau }_i^t$ passing through detections $Y_j^{t+1},Y_k^{t+2},\dots ,Y_u^{t+W-1}$ is written ${\rho }_{\mathit{\text{jk}}\dots u}^{t+1}$ and the set of all such feasible extensions is written as ${\rho }_j^{t+1}$ for a constant window size W. The MAT algorithm examines all possible associations of ${\tau }_i^t$ to extensions ${\rho }_j^{t+1}$ and we define extension-to-track association costs

$$c_{\mathit{\text{ij}}}=\underset{{\rho }_j^{t+1}}{\text{min}}\{C({\tau }_i^t,{\rho }_j^{t+1})\}\text{\hspace{1em}for all }i,j.$$ (1)

$C\left({\tau }_i^t,{\rho }_j^{t+1}\right)$ is the cost function encapsulating typical axonal organelle transport behaviour. We define a matching edge in frame t, $c_{\mathit{\text{ij}}}^{*}$, if

$$c_{\mathit{\text{ij}}}^{*}\le c_{\mathit{\text{in}}}\mathit{\text{ and }}{c}_{\mathit{\text{ij}}}^{*}\le c_{\mathit{\text{mj}}}$$ (2)

for all feasible edges $(Y_i^t,Y_n^{t+1})\text{ and }(Y_m^t,Y_j^{t+1})$. The set of assigned edges is then $C^{*}=\left\{c_{\mathit{\text{ij}}}^{*}\right\}$, and tracks are extended by

$${\tau }_n^{t+1}={\tau }_m^t\cup c_{\mathit{\text{mn}}}^{*}\text{ for all }{c}_{\mathit{\text{mn}}}^{*}\in C^{*}.$$ (3)

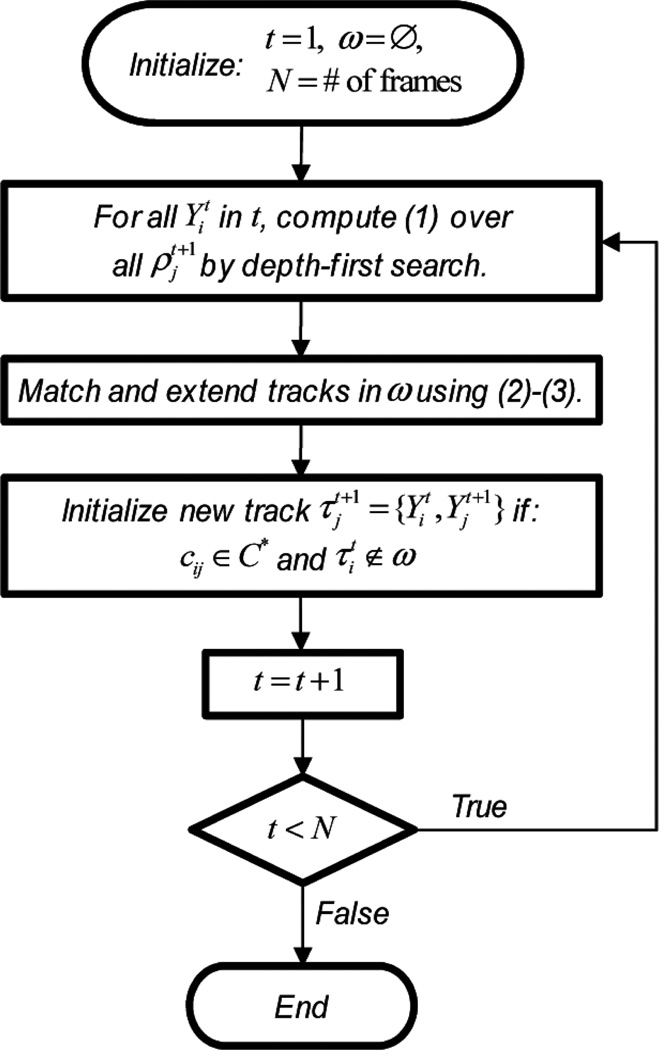
This optimisation approach guarantees a minimum cost for the extended object tracks ${\tau }_n^{t+1}$ within the window size W. This follows directly from equation (2) since any edge with cost $c_{\mathit{\text{mp}}}<c_{\mathit{\text{mn}}}^{*}$ would imply $c_{\mathit{\text{mn}}}^{*}$ does not satisfy equation (2) and thus $c_{\mathit{\text{mn}}}^{*}\notin C^{*}$. Figure 1 shows a flow diagram for the MAT algorithm. Similar to a minimum spanning tree approach (Papadimitriou and Steiglitz, 1998), we always choose the minimum cost edge to extend tracks. One important consideration when using graph-theoretic combinatoric optimisation to analyse multi-target tracking problems is that whenever we extend a track, it changes the costs of other connected edges in the graph, due to the nature of the tracking problem. We must therefore run the algorithm iteratively extending tracks from previously assigned edges and subsequently computing new costs to future track extensions. This approach is similar to belief propagation approaches to the data association problem (Chen et al., 2006). In contrast to Chen et al. (2006), we relax the constraint that detections must be assigned to only one track, allowing a ‘softer’ assignment of tracks to detections.

Figure 1.

Flow diagram for multitemporal association algorithm

In order to analyse organelle transport on the axon we define a cost encapsulating typical organelle behaviour. The axonal transport cost function is modelled as a combination of two aspects, motion cost and appearance cost,

$$C_{\text{axon}}(\tau ,\rho )=C_{\text{length}}(C_{\text{appearance}}(\tau ,\rho )+C_{\text{motion}}(\tau ,\rho )).$$ (4)

We multiply by a length penalty in order to discourage short tracks which will otherwise have lower costs. Axonal transport is accomplished by kinesin proteins that are known to move at a constant velocity. The main component of the motion cost is the coefficient of variation of track velocity.

$$C_{\text{motion}}(\tau )=\{\begin{array}{cc}\sigma \left(|v(\tau )|\right)/\mu \left(|v(\tau )|\right),& \mu \left(|v(\tau )|\right)>1\\ \sigma \left(|v(\tau )|\right),& \mu \left(|v(\tau )|\right)\le 1\end{array},$$ (5)

where μ(|ν(τ)|) and σ(|ν(τ)|) are the mean and standard deviation of instantaneous track speed. This motion cost favours tracks with a constant velocity, encouraging track extensions that adhere to the kinesin protein motion model. Similarly, aside from imaging variations, a given organelle’s appearance should not vary much while being transported. The appearance cost is a coefficient of variation over the track intensities to discourage intensity variation.

$$C_{\text{appearance}}(\tau )=\sigma (I(\tau ))/\mu (I(\tau )).$$ (6)

The appearance and motion cost terms encapsulate the typical behaviour of organelles transported along the axon.

Because the axon is a narrow structure, axonal organelle transport imaging scenarios are very crowded and noisy. As stated previously, this is challenging for a tracker as it creates a large number of false detections and occlusions or missed segmentation errors. MAT uses typical object behaviours rather than statistical models of segmentation errors and occlusions. MAT implicitly handles false detection noise as false detections will not adhere to the object model. Occlusions (merged detections) and missed detections are handled by considering k-frame track extensions of the form ${\rho }_j^{t+\mathrm{k}}$ for k > 1, allowing a track to predict past a missed segmentation or occlusion.

In the case of axonal transport analysis, organelles or vesicles are fluorescently labelled and appear as bright dots or blobs in the microscope image sequences. We use a scaled Otsu threshold (Otsu, 1979) with scale parameter α to identify foreground regions within a radius of the axon centreline. For each foreground region we apply an extended-maxima transform (Soille, 1999) with parameter h to find the local maxima in the blobs. These maxima approximate the organelle centres to be tracked, and the foreground region corresponding to each maximum is defined as the connected-component of the associated organelle. Figure 4(a) shows some segmentation results identifying foreground regions (green dots) and organelle centres (red dots).

Figure 4.

Segmentation of ssNPY organelles, peaks (red) and connected components (green), the blue line is the axonal centreline used to generate the kymograph (a). Kymograph generated from pretreatment ssNPY organelle image sequence; (b). Blur distance constraints projected onto a portion of the kymograph, detections (red), satisfied constraints (yellow), and outside blur constraint (blue) (c). Pretreatment ssNPY tracks overlaid on the kymograph, example track highlighted in red (d). Axon image with arrows pointing to tracked organelles and an example organelle track highlighted and labelled (e) (see online version for colours)

Using MAT as defined above, with windows size (W) of 6 frames, we can find the set of tracks which best adheres to typical organelle transport behaviours. However, assuming on average n detections per frame, we must examine n^W track extensions per frame. Given m frames this leads to a total of mn^W cost evaluations over an entire sequence. The number of extensions is polynomial in n, but clearly can be prohibitive in problems where there is considerable noise or n is large. Generally, a small subset of the extensions represent realistic object behaviours and we wish to gate the set of track extensions such that we only consider this feasible subset. We constrain the instantaneous velocity, acceleration, and blur distance of tracks to find the feasible subset. Organelle velocity is limited to 20 pixels/frame and acceleration is constrained to less than 8 pixels/frame². The blur constraint is derived from the microscope imaging setup. The camera shutter captures photons from the microscope for only the exposure ratio r_exp=Δt_exposure/Δt_frame. A moving organelle will be blurred during exposure. We approximate the blurred organelle by its connected-component and thus the distance between organelle connected-components in adjacent frames should not exceed 1–r_exp times the organelle instantaneous velocity. Figure 4(c) shows blur constraints projected onto a kymograph, yellow lines indicate that the blur constraint is satisfied, blue lines indicate associations which will not be considered because they violate the constraint.

3 Results

3.1 Phantom data

We project our tracking results onto kymographs to qualitatively verify the accuracy of MAT applied to axonal organelles (see e.g., Figure 4(d)). More quantitative verification, however, quickly becomes extremely difficult as there are generally between 40–70 detections per frame and hand verification for just a single organelle in one image sequence can take hours – we are developing automated tools to improve this in the future. In order to make it easier to accurately evaluate and compare tracking performance, we generated phantom data sets with properties similar to axonal transport data. Since the tracker relies on an underlying segmentation to generate the set of detections, the phantom data sets also decouple the evaluation of tracking performance from the segmentation algorithm.

Phantom data generation is initialised by creating a set of detection positions and associated speeds such that the detections are randomly distributed within a radius of a phantom axon. We move each detection following the curvature of the axon at the chosen speed and distance from the centreline. Whenever a track leaves the frame a new track is initialised at one of the ends of the axon. These rules create a set of tracks which maintain a constant velocity. We also specify a percentage of randomly distributed false detections to add to each frame. Figure 2 shows an example frame from the phantom axon data with 100 detections per frame and 60% false detection noise. We can then measure the accuracy of the tracking algorithm under varying amounts of noise as follows. We write an edge association originating from detection Y_m ∈ Y as e_m ∈ Edges, with Edges the set of all associations. We define tracking errors as

$${\mathit{\text{Edges}}}^{\text{err}}=\left\{e_m^{\text{tracked}}|e_m^{\text{tracked}}\ne e_m^{\text{phantom}}\right\}\text{ for all }{Y}_m\in Y.$$ (7)

Figure 2.

Single frame of phantom data. (left) All detections generated within 8-pixels of a phantom axon (blue line). (right) Zoom view showing true objects with organelle centres (red dots) and tails indicating direction and magnitude of velocity. False detections are marked with a magenta ‘x’ (see online version for colours)

This is the set of incorrect associations in the tracking results. We also define a percentage error.

$$\epsilon =\frac{\left|{\mathit{\text{Edges}}}^{\text{err}}\right|}{{|\mathit{\text{Edges}}}^{\text{phantom}}|}$$ (8)

which is simply the count of erroneous associations over the total true associations in the phantom data set.

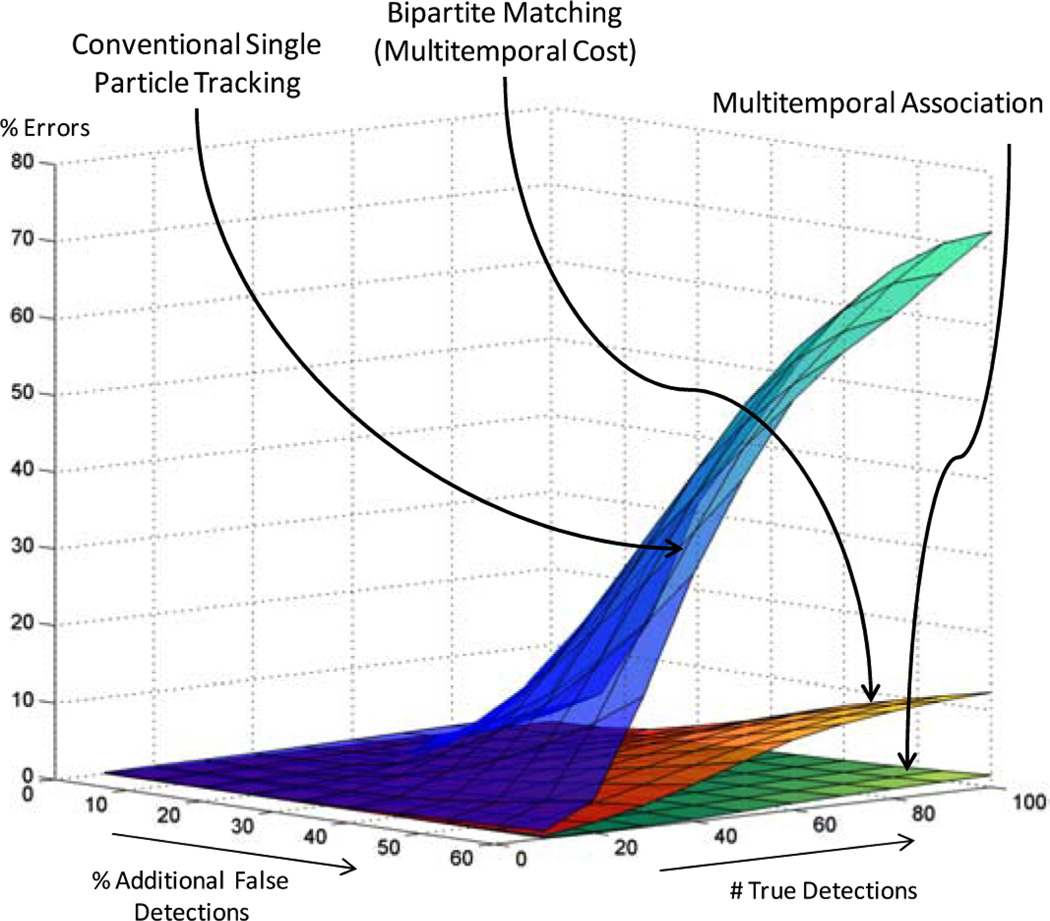
We generated phantom data sets ranging from 10–100 detections per frame and 0–60% false detections per frame. For each combination of false detections and detections per frame we generated 20 data sets resulting in a total of 600 phantom image sequences. For comparison purposes we created a bipartite matching tracker which used exactly the same multitemporal cost function, and the same input data, but applied the Hungarian algorithm (Kuhn, 2005), a standard bipartite matching technique, to associate segmentation results to tracks. We also applied the source implementation of the single particle tracking algorithm from (Jaqaman et al., 2008). This implementation utilises a Kalman filter (Simon, 2006) single frame cost function, which is the appropriate state estimation given that the organelles move at a constant velocity. The search radius for this tracker was set to our maximum velocity gate, and the gap closing parameter was left at the default of 10 frames. No additional parameter tuning was attempted as our interest was in comparing with a generic tracking solution. We applied the three tracking approaches to all 600 simulated image sequences and found the median error rate ε over each of the 20 data sets with the same detections and false detections per frame. As shown in Figure 3, MAT performs significantly better in crowded noisy environments with an error rate of 1.6% compared to 12.4% for the bipartite matching tracker that uses the same multiframe cost function and compared to 72% for the single particle tracking approach in (Jaqaman et al., 2008). Because a single image sequence can have tens or even hundreds of thousands of assignments, this reduction in error rate translates into a very significant improvement in tracking performance. Figure 3 also shows, however, that all the trackers are dependent on the accuracy of the underlying segmentation, i.e., as we increase false detections tracking errors also increase. This highlights the need to improve segmentation as well as tracking in high target-density problems.

Figure 3.

Comparison of error rate for MAT (green surface), a bipartite assignment tracker using axonal transport cost function (orange surface) and a conventional single particle bipartite tracking solution using source code provided by Jaqaman et al. (2008) (blue surface). MAT achieves significantly better performance in the presence of high noise and target densities (see online version for colours)

3.2 Brain Derived Neurotrophic Factor

Deficiencies in Brain Derived Neurotrophic Factor (BDNF) transport have been shown to play a role in several neurodegenerative disorders such as Huntingon’s disease (Gauthier et al., 2004). In order to examine the relationship between BDNF transport and Huntington’s disease, image sequences were captured with the BDNF organelle fluorescently labelled for two populations; a mutant huntingtin protein population and a wild-type population. Image sequences were captured for eight experiments with 10–12 neurons in each experiment. Four of the experimental data sets were made up of wild-type neurons and the other four were comprised of mutant huntingtin neurons. We tracked BDNF transport in 90 image sequences using MAT and calculated instantaneous velocities over all tracks. We collected all velocities by data set and computed empirical probability distributions over the velocities for each data set using a normalised histogram. The probability distributions were compared using the Bhattacharya distance (Theodoridis and Koutroumbas, 2009) to create a pairwise distance matrix over all eight data sets. The Bhattacharya distance has been shown to be an effective measure of separability of probability distribution functions (Comaniciu et al., 2000); it is related to the optimal Bayesian classification error. The distance matrix was analysed with gap spectral clustering (Cohen et al., 2009), a robust computational technique that provides a multiresolution, multidimensional anlaysis of the time sequence data obtained from segmentation and tracking. Gap spectral clustering uses algorithmic statistics (Vitanyi, 2006) to select the most meaningful clustering method for extracting information from the distance matrix. The gap spectral clustering found two groups in the data, however one data set from each group was misclassified for a total classification error of 25%. Table 1 summarises the classification results of the BDNF data sets.

Table 1.

BDNF classification results

Dataset	Movies in dataset	Actual classification	Gap spectral clustering classification
1	9	Wild-type	Group A
2	14	Huntington’s	Group A
3	14	Wild-type	Group A
4	7	Huntington’s	Group B
5	10	Huntington’s	Group B
6	14	Wild-type	Group B
7	12	Huntington’s	Group B
8	10	Wild-type	Group A
	Total movies		Total classification errors
	90		2 (25%)

3.3 Secretory sequence of Neuropeptide Y

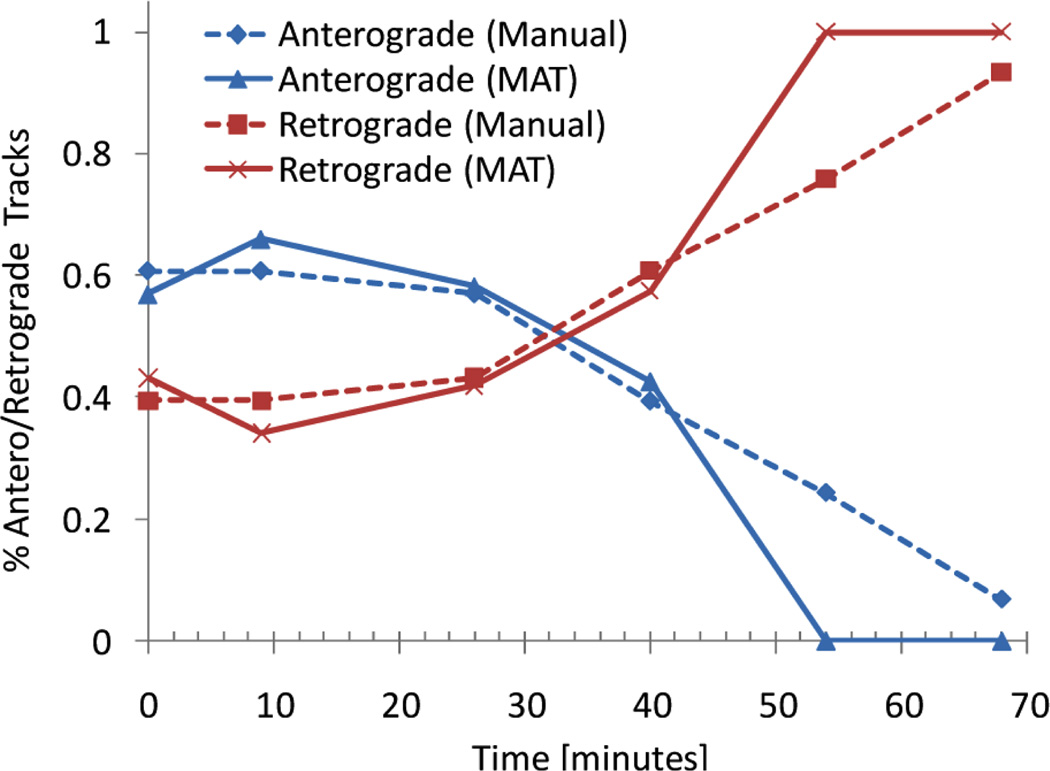
As stated previously, axonal transport defects have been proposed as a mechanism leading to axonal degeneration in several neurodegenerative diseases including MS. Inflammation is an early symptom of MS; quantifying the effects of inflammation on axonal transport is an important step in characterising the pathogenesis of MS. Labelling secretory sequence of Neuropeptide Y (ssNPY) fluorescently marks all Golgi-derived vesicles, in contrast to BDNF labelling which marks BDNF organelles specifically, thus it is a useful marker for examining general axonal vesicle transport. In order to study the effects of inflammation on axonal transport an ssNPY labelled neuron was treated with hydrogen peroxide (H₂O₂), a common in vivo inflammatory mediator. Six image sequences of the labelled neuron were captured before and periodically after the treatment. Though biologically distinct, ssNPY and BDNF labelled image sequences are similar from an image analysis perspective, and in both cases the organelles or vesicles being tracked behave in a similar manner, i.e., they are transported along the axon of a neuron at a piecewise constant velocity by kinesin or dynein motor proteins. Our analysis of the ssNPY vesicles used the same segmentation and axonal transport cost function as the BDNF organelles described previously. Figure 4(d) and (e) shows tracking results projected onto the kymograph and an associated image frame for the ssNPY pre-treatment sequence. It is clear from the kymograph projection that there are still tracking errors which might disrupt downstream analysis. Nonetheless our automated tracking results achieved good concordance with manual analysis of the same data, as shown in Figure 5.

Figure 5.

Manual and automated analysis of the transport of the ssNPY vesicle before and after treatment with H₂O₂ (see online version for colours)

The six movies from this data set show transport along a neuron before and at various times after undergoing H₂O₂ treatment. We applied our tracker to all six movies and collected counts of vesicles moving in the anterograde (toward the distal end of the axon) and retrograde (toward the soma) directions. The transport direction is biologically significant because generally anterograde and retrograde transport are carried out by different proteins. Figure 5 shows a comparison of our results to manual measurements of anterograde and retrograde transport made on a kymograph for the same image data. Both the manual and automated tracking results detected a difference in the effect of the H₂O₂ treatment on anterograde versus retrograde motion. Interestingly, the retrograde transport was impacted differently than anterograde transport, with anterograde transport declining as the fraction of retrograde transport increased.

4 Discussion

Neural axon transport image sequences offer a particularly challenging environment for automated tracking and analysis algorithms. There is a great need for automated tools which perform well on such sequences, as manual analysis of the data is quickly becoming infeasible due to the large number of image sequences being analysed. We have developed a multiframe graph-theoretic tracking algorithm which performs well in noisy, high occlusion environments such as those found in axonal transport image sequences. The MAT algorithm does not require explicit modelling of imaging parameters or object densities but relies only on typical object behaviours modelled by the cost function. This has allowed use of the MAT tracker in the examination of several similar axonal transport problems as well as use in a stem-cell tracking and lineaging application (Winter et al., 2011).

We present preliminary results of application of MAT to the analysis of organelle and vesicle transport along neuronal axons as well as phantom data with similar properties. Analysis on the phantom transport data shows MAT consistently outperforms other bipartite matching trackers with an error rate of about 1.6% compared with 72% for the tracker of Jaqaman et al. (2008). We applied MAT to BDNF organelle transport sequences and were able to use gap spectral clustering to separate the data into mutant-huntingin and wild-type groups with an error rate of 25%. MAT analysis of percentage of retrograde and anterograde transport of Golgi-derived vesicles before and after H₂O₂ treatment agrees with manual analysis, highlighting an interesting difference between the impact of the treatment on retrograde versus anterograde transport.

MAT does have limitations. First, MAT requires a window size (W) image frames be available at the time of tracking. If an application requires the tracks be updated every time a new image frame becomes available, then a hybrid approach combining MAT with other methods would have to be developed. Also, the MAT cost function must be carefully constructed to capture typical behaviour for objects being tracked. Once the cost function is constructed however MAT is applicable to any sequence containing the modelled objects. Finally, though MAT has a very low error rate, e.g., 1.6% on the phantom data, even minor tracking errors in biological image sequences may significantly affect further analysis. We are thus developing editing tools to allow for the correction of segmentation and tracking errors. We have previously developed tools for the validation and editing of stem-cell lineages (Winter et al., 2011) and similar editing tools are in development for axonal transport analysis.

Biographies

Mark R. Winter is a Doctoral student at the University of Wisconsin – Milwaukee (UWM). He studies applications of pattern recognition and inference techniques to the characterization of dynamic biological systems. Mark received baccalaureate degrees in Computer Engineering and Applied Mathematics from the University of Colorado in 2005 and a Master’s degree in Electrical Engineering from UWM in 2010. In the interim he worked in programming and algorithm development for America's Army game and on CT imaging related algorithms for IMTEC.

Cheng Fang received her BS from both Nanjing University and Chinese Pharmaceutical University. She went on to complete an MS in cancer biology from Nanjing University before she came to the United States to pursue her PhD. She received her PhD degree from Pennsylvania State University in 2007. Since then, she has been working in Dr. Gary Banker’s lab in Oregon Health & Science University as a postdoctoral fellow. She is interested in studying axonal transport in neurodegenerative diseases.

Gary Banker is Senior Scientist in the Jungers Center f or Neurosciences Research and Professor of Neurology and Cell Biology at Oregon Health and Science University. Before joining OHSU in 1998, he held faculty positions at Albany Medical College and the University of Virginia School of Medicine. He received his doctorate from the University of California at Irvine in 1973 and completed postdoctoral training at Washington University in St. Louis. His research interests concerns the development and maintenance of neuronal polarity and applications of live-cell imaging in cellular neurobiology.

Badrinath Roysam is currently the Hugh Roy and Lillie Cranz Cullen University Professor at the University of Houston, and Chair of the Electrical and Computer Engineering Department. Until 2010, he was a Professor of Electrical, Computer and Systems Engineering at Rensselaer Polytechnic Institute. He received his doctorate from Washington University in St. Louis in 1989, and Bachelors in Electronics from the Indian Institute of Technology in 1984. His research interests are in the broad area of multi-dimensional image analysis with an emphasis on biological microscopy derived imagery.

Andrew R. Cohen received the BSEE, MSCE, and PhD Degrees from Rensselaer Polytechnic Institute in 1989, 1991, and 2008, respectively. He is currently an Assistant Professor in the Department of Electrical Engineering and Computer Science at the University of Wisconsin, Milwaukee. He was previously employed as a software design engineer in the operating systems group at Microsoft and as a microprocessor product engineer at Intel. His research interests include image sequence analysis, algorithmic information theory, and machine learning and pattern recognition for biological applications.