Abstract
Identifying the risk factors for comorbidity is important in psychiatric research. Empirically, studies have shown that testing multiple, correlated traits simultaneously is more powerful than testing a single trait at a time in association analysis. Furthermore, for complex diseases, especially mental illnesses and behavioral disorders, the traits are often recorded in different scales such as dichotomous, ordinal and quantitative. In the absence of covariates, nonparametric association tests have been developed for multiple complex traits to study comorbidity. However, genetic studies generally contain measurements of some covariates that may affect the relationship between the risk factors of major interest (such as genes) and the outcomes. While it is relatively easy to adjust these covariates in a parametric model for quantitative traits, it is challenging for multiple complex traits with possibly different scales. In this article, we propose a nonparametric test for multiple complex traits that can adjust for covariate effects. The test aims to achieve an optimal scheme of adjustment by using a maximum statistic calculated from multiple adjusted test statistics. We derive the asymptotic null distribution of the maximum test statistic, and also propose a resampling approach, both of which can be used to assess the significance of our test. Simulations are conducted to compare the type I error and power of the nonparametric adjusted test to the unadjusted test and other existing adjusted tests. The empirical results suggest that our proposed test increases the power through adjustment for covariates when there exist environmental effects, and is more robust to model misspecifications than some existing parametric adjusted tests. We further demonstrate the advantage of our test by analyzing a data set on genetics of alcoholism.
Keywords: Comorbidity, Environmental factor, Family-based association test, Maximum test statistic, Multiple traits, Ordinal traits
1 Introduction
The advent of high throughput genotyping technologies has enabled investigators to identify genes that contribute to complex human traits through association analysis (Klein et al. 2005; Arking et al. 2006; Duerr et al. 2006; Chen et al. 2007). Extended from the original transmission/disequilibrium test (TDT) (Spielman, McGinnis, and Ewens 1993), family-based association tests (FBAT) have been developed to assess association between genetic markers and disease status in different study designs including sibships (Spielman and Ewens 1998; Horvath and Laird 1998; Knapp 1999), nuclear families (Weinberg 1999; Lunetta et al. 2000; Rabinowitz and Laird 2000), and general pedigrees (Martin et al. 2000). Moreover, tests have been proposed for quantitative traits (Allison 1997; Rabinowitz 1997), traits with distribution belonging to an exponential family (Liu, Tritcher, and Bull 2002), and ordinal traits (Zhang, Wang, and Ye 2006; Wang, Ye, and Zhang 2006).
The aforementioned methods examine a single trait and hence are not applicable to analyze comorbidity that involves multiple illnesses in the same patient. It is well-documented that comorbidity is a significant issue in studies of mental and behavioral disorders. For example, anxiety and depression often co-occur in the same patient (Li and Burmeister 2009), and sometimes a single patient is addicted to nicotine, alcohol and other substances (Merikangas et al. 1998; True et al. 1999). Furthermore, comprehensive studies have demonstrated that jointly testing correlated traits is more powerful than testing a single trait at a time (Zhu and Zhang 2009). Lange et al. (2003) proposed a multivariate extension of family-based association tests based on generalized estimating equations (FBAT-GEE) to test multiple quantitative traits simultaneously. Considering the fact that many mental disorders are measured in ordinal scales, Zhang, Liu, and Wang (2010) proposed a non-parametric association method to test any hybrid of dichotomous, ordinal, and quantitative traits based on a generalization of Kendall’s tau. However, all these works did not consider covariate effects in their tests.
Environmental factors or covariates, such as gender and age, can be very important in assessing the association between putative risk factors and the outcomes. Failure to account for those covariates can produce misleading bias of the association of interest, or affect the testing power. To accommodate covariates, for example, Wang, Ye, and Zhang (2006) added the environmental factors into the proportional odds logistic model to deal with a single ordinal trait. Unfortunately, it is usually challenging to build a parametric model for multiple complex traits. To resolve this difficulty, we develop a nonparametric method to perform association test for multiple complex traits meanwhile adjusting for covariates.
In contrast with the tests not considering covariates, we test the null hypothesis that there is no association, conditional on the covariates, between marker alleles and any linked locus that influences the traits (Jiang and Zhang 2011). In addition, we extend the U-statistic measuring the genetic association in Zhang, Liu, and Wang (2010) by imposing a weight function on each sample pair in terms of covariates. The weight function is chosen in a way that it increases the contribution of a sample pair to the statistic if they share similar covariate information, but decreases the contribution otherwise. The induced weighted test statistic follows a χ2 distribution under the null hypothesis.
In practice, we do not know the weight function that is optimal in a study. Changing the parameters in the weight function will result in different weights and thus different test statistics. To approximate the optimal weighting scheme, we select a grid of parameters in the weight function, and define the maximum test statistic. The maximum statistic reflects the strongest association measure using different weight functions. To make use of the maximum statistic, we investigate its null distribution and approximate it in an asymptotic way. Moreover, we propose an easy-to-implement resampling approach which can also assess the significance of the maximum statistic.
Through our simulated family-based studies, we demonstrate that our proposed test increases the power of detecting the association for multiple ordinal traits compared to the test that ignores the covariates, when the covariates affect the traits. Not surprisingly, the performance of all methods including ours deteriorates when more of parental genotypes are missing. Compared with existing covariate-adjusted tests, our test is more robust to model misspecifications, even though different settings may be favorable to different methods. To further demonstrate the benefit of our test, we apply it to the data set from the Collaborative Study on the Genetics of Alcoholism (COGA).
2 Nonparametric Test Adjusting for Covariates
Suppose we observe a vector of traits T = (T(1), …, T(p))′, marker genotype M, and a vector of covariates Z = (Z(1), …, Z(l))′ for each of n study subjects. These n subjects may be unrelated in a population-based association study or may belong to nuclear families in a family-based association study. In the latter case, let Mpa represent the observed parental marker genotypes to distinguish from those of the offspring. We should note that we consider one marker locus because most of the association analyses scan the genome with one marker at a time.
2.1 Testing multiple traits without covariates
Zhang, Liu, and Wang (2010) presented a nonparametric association test to detect the association between multiple traits and a genetic marker by using a generalized Kendall’s tau. Their test generalized the FBAT-GEE proposed by Lange et al. (2003) in order to accommodate different types of traits, especially ordinal traits. We briefly review their method before introducing ours.
For individuals i and j, let Ti and Tj be their vectors of traits respectively. Then, a trait kernel is defined as , where function fk(·) is the kernel function. It can be chosen as the identity function for a quantitative or binary trait (Rabinowitz 1997), or the sign function for an ordinal trait (Zhang, Wang, and Ye 2006). Meanwhile, let C be the number of any chosen allele for marker genotype M. It is noteworthy that this method can accommodate any justifiable choice of C. Then, a marker kernel is defined as Dij = Ci − Cj.
A U-statistic is defined as
| (1) |
The association test statistic is , where E0(U) and Var0(U) are the mean and variance of U under the null hypothesis that there is no association between marker alleles and any linked locus that influences the traits T. Illustrated in their work, the test statistic follows an asymptotic χ2 distribution under the null hypothesis.
2.2 Adjusting for covariates
As shown above, Zhang, Liu, and Wang (2010) did not take into account the covariates Z in their association test, which as we discussed in the Introduction, is an important issue. Therefore, our proposed method fills this important gap.
The adjustment is realized by imposing a weight on each pair of samples in the U-statistic (1) according to the information of their covariates, yielding a weighted U-statistic. The weights, denoted by w(Zi, Zj), reflect the relative importance of the pair (i, j) in the statistic attributed to the covariates. Intuitively, the weight function should impose a relatively large weight when Zi is close to Zj, and a relatively small weight when Zi and Zj are far away. That is, we increase the contribution of a sample pair in the testing when they possess similar covariate information.
For convenience, write Z = (Zco′, Zca′)′ with Zco for the continuous covariates and Zca for the categorical covariates. Given that all continuous covariates are standardized, one choice of the weight function w(Zi, Zj) is given by
where Wh(·) is a positive and decreasing function of the Euclidean distance between and depending on a “bandwidth” parameter h, and Wq(·) is also a positive and decreasing function of the “discrete distance” between and depending on another parameter q. In practice, the functions Wh(·) and Wq(·) can be chosen on a case-by-case basis. For example, Chen, Manichaikul, and Rich (2009) gave a choice for w(·) when dealing with the single binary trait in family-based association studies. In the following, we choose Wh(u) = exp(−u2/2h2) with h > 0, and Wq(v) = (1 − q)I(v = 0) + qI(v = 1), with 0 ≤ q ≤ 0.5. To reflect the variation of h and q, we write the weight function as w(Zi, Zj; h, q). Then a weighted U-statistic is given by
| (2) |
2.3 Fixed-(h, q) test statistic
Recall that the usual null hypothesis of a genetic association test is that there is no association between marker alleles and any linked locus that influences the traits (Laird, Horvath, and Xu 2000; Zhang, Liu, and Wang 2010). However, we need to revise this null hypothesis accordingly for a nonparametric test in the presence of covariates. Following Jiang and Zhang (2011), we test that there is no association between marker alleles and any linked locus that influences the traits conditional on the covariates. This null hypothesis was proposed to remove spurious associations caused by the confounding effects from the covariates, as have been demonstrated through simulations in a population-based study (Jiang and Zhang 2011).
To derive the null distribution of the proposed statistic S(h, q), we follow the ideas used in Laird, Horvath, and Xu (2000) and Zhang, Liu, and Wang (2010). In particular, they computed the distribution of the test statistic by treating the offspring genotype as random, and conditioning on all phenotypes and parental genotypes (if available). This conditioning eliminates the need for assumptions about the phenotype distribution, the genetic model and the parental genotype distribution. As a result, the test is robust and less prone to population stratification and ascertainment bias. In our situation, we compute the distribution of S(h, q) by treating the offspring genotype as random, and conditioning on all phenotypes, parental genotypes (if available), and covariates.
Under these settings, we can rewrite the fixed-(h, q) U-statistic S(h, q) as
| (3) |
where . Similar to Theorem 1 in Zhang, Liu, and Wang (2010), the weighted U-statistic S(h, q) has the following asymptotic null distribution conditional on all phenotypes, parental genotypes (if available), and covariates,
| (4) |
if Var0{S(h,q)} has a full rank. In the above formula,
In addition, we can define the fixed-(h, q) test statistic as
| (5) |
which converges to in distribution under the null hypothesis (if Var0{S(h, q)} does not have a full rank, p is replaced with the rank of Var0{S(h, q)}).
The mean and the covariance need to be calculated for . On the one hand, there is no parental genotype information Mpa in a population-based study. Therefore, we can estimate the probability P(C = c|Z = z) using the sample data to approximate the mean and the covariance. On the other hand, similar to the robustness to population admixture of a family-based study, we assume that P(C = c|Mpa, Z = z) = P(C = c|Mpa) whenever parental genotypes are available. This “conditional independence” assumption means that the covariates neither affect nor are affected by the transmission of marker alleles from parents to offspring, which is practically reasonable. Under this assumption, the mean and covariance become and , which can be readily computed using Mendelian laws, or using the method in Rabinowitz and Laird (2000) for more general situations. It is worth mentioning that although this conditional independence assumption reduces the computation complexity, it might result in more false positives if the parental genotypes are not completely observed. We refer to the following sections for experimental results and discussions on this issue.
It is noteworthy that the fixed-(h, q) test statistic becomes the test in Zhang, Liu, and Wang (2010), and the FBAT-GEE proposed by Lange et al. (2003) under the respective, restrictive conditions. Thus, this statistic broadens the scope of genetic association analysis.
2.4 Power calculations
In this subsection, we present an analytical approach to calculating the power of the fixed-(h, q) test. To calculate the power, we need to determine the distribution of the test statistic under the alternative hypothesis.
Let Δμ = μ1 − μ0 ≡ E1{S(h, q)} − E0{S(h, q)}, Σ0 = Var0{S(h, q)}, and Σ1 = Var1{S(h, q)}, where subscripts 0 and 1 indicate for the null and the alternative hypotheses, respectively. It is seen that, under the alternative hypothesis, has approximately a distribution of a weighted sum of independent noncentral random variables as follows,
| (6) |
where e1 ≥ · · · ≥ ep ≥ 0 are the eigenvalues of . and Δμ̃i is the ith component of , where Q is an orthonormal matrix such that .
Using (6), the conditional power
 of
at the significance level α is given by
of
at the significance level α is given by
| (7) |
where is the 100(1 − α)% percentile of a distribution. We refer to the moment-based approach of Liu, Tang, and Zhang (2009) to approximate the distribution of .
To calculate
 by (7), we need to evaluate μ1 and Σ1. In a family-based study,
by (7), we need to evaluate μ1 and Σ1. In a family-based study,
By Bayes’ theorem, we have that
| (8) |
which depends on P(T|C = c, Z) and P(C = c|Mpa), the penetrance and allele frequency in classic genetic epidemiology. They are necessary genetic model parameters in order to compute the power of a test. Once (8) is known from these two parameters, we can evaluate μ0, μ1, Σ0, Σ1 so that
 can be calculated from (7).
can be calculated from (7).
2.5 Maximum-(h, q) test
The fixed-(h, q) test statistic has the virtue of convenience; however, the adjustment through a single weight function is usually not enough due to different possible choices of the parameters h and q. We follow the idea of using the maximum test statistic as commonly used in the literature of nonparametric testing (e.g., Su and Ullah 2009) and genetic applications (e.g., Hoh and Otts 2000). The basic idea is to choose a grid of h and q values, and to maximize the weighted test statistic over those choices. By doing so, we are trying to approximate the optimal weighting scheme, yielding the strongest association measure.
Specifically, let {h1, …, hL1} and {q1, …, qL2} be pre-specified grid points of h and q that provide a reasonable coverage, then define
| (9) |
To investigate the asymptotic null distribution of , we need to derive the asymptotic joint distribution of R = {R(h1, q1), …, R(hL1, qL2)}′ with each R(hl1, ql2) being defined as in (4). Similar to (3), write
where . Then , with Var0D(S) = diag[Var0{S(h1, q1)}, …, Var0{S(hL1, qL2)}] that consists of only the diagonal blocks of Var0(S). In addition, we have the asymptotic distribution of S similar to that of S(h, q),
| (10) |
if Var0(S) has a full rank.
We verify in Theorem 1 that, under mild conditions, the distribution function of under the null hypothesis can be approximated by that of max1≤l1≤L1,1≤l2≤L2||R̃l1l2||2, where with G ~ N(0, IpL1L2). Here, R̃l1l2 denotes the sub-vector of R̃ at the same positions as where R(hl1, ql2) is within R.
Theorem 1
Assume that the eigenvalues of Var0D(S) and Var0(S) are uniformly bounded from both above and below, i.e., there exist two positive numbers c and C such that c ≤ λmin{Var0D(S)} ≤ λmax{Var0D(S)} ≤ C and c ≤ λmin{Var0(S)} ≤ λmax{Var0(S)} ≤ C uniformly for all n, where λmin and λmax denote the smallest and largest eigenvalues respectively. Then for any x ∈ ℝ, as n → ∞,
| (11) |
Notice that the distribution of maxl1l2||R̃l1l2||2 still depends on the sample size n, and hence strictly it is a finite-sample approximation instead of an “asymptotic” distribution. With this approximation in hand, we can use it to assess the significance of our test statistic . Recall that and can be readily evaluated from the sample data (see Section 2.3). Thus, we can evaluate the empirical distribution of maxl1l2||R̃l1l2||2 using Monte Carlo method only for the part G, and use this empirical distribution as the reference null distribution for our test.
2.6 Test using resampling
Instead of using the approximated null distribution as discussed in Section 2.5, we can make use of resampling to assess the significance of . To perform a resampling test, we need to generate a reasonably large number of sample data under the null hypothesis in a way that is consistent with the study design. Recall that our test statistic is calculated conditioning on the phenotypes, the parental genotypes (if available), and the covariates, we will resample the genotype data.
For a population-based study in which the subjects are independent, we can follow the idea of restricted permutation in Yu et al. (2010) to resample the data. When the covariates are all categorical variables, we permute the genotypes in each stratum defined by the covariates. When some covariates are continuous, the restricted permutation can still be used if we categorize them; however, the validity and performance of this approach warrant further investigation. For a family-based study, the situation is slightly different though. Recall that the children’s genotypes were solely determined by their parents’ marker alleles under the null hypothesis (see Section 2.3). Then we can resample the children’s genotype using the method given by Rabinowitz and Laird (2000). Conditional on the minimal sufficient statistic, they provided a unified approach that can assess the conditional distribution of the children’s marker alleles, which is valid with arbitrary patterns of missing marker allele information. Therefore, we resample the children’s marker alleles using that conditional distribution as our null samples.
A resampling test statistic is calculated using a resampled data set in the same way as the test statistic is calculated. To access the p-value of our test, we need to set a reasonably large number M, and calculate M resampling test statistics using M resampled data. The p-value is the proportion of the resampling test statistics that exceed our observed test statistic, that is .
3 Simulation Studies
In this section, we conduct a series of simulation studies that are designed for two specific aims. First, we compare the performance of the tests with and without adjusting for the covariates. Second, we compare our nonparametric covariate-adjusted test with other covariate-adjusted methods.
3.1 Comparison with the unadjusted test
3.1.1 Without confounders
The data sets are generated as follows. First, the parents’ genotypes at trait (with alleles D and d) and marker (with alleles A and a) loci are simultaneously generated according to certain allele frequency and coefficient of linkage disequilibrium δ, which determine haplotype frequencies of AD, Ad, aD and ad. We set the frequencies of both allele D and allele A at 0.3.
When the trait allele is not associated with the marker allele, δ = 0, otherwise δ is chosen to be 0.11. Table 1 provides the details about the haplotype frequencies when δ = 0 and δ = 0.11. After parental genotypes are generated, the offspring genotypes are generated based on parental genotypes and also the genetic distance between the trait and marker loci. During the simulation, the trait and marker loci are assumed to be 1 cM apart.
Table 1.
Haplotype frequencies with P(D) = P(A) = 0.3.
| Haplotype | AD | Ad | aD | ad | |
|---|---|---|---|---|---|
| δ = 0 | Frequency | 0.09 | 0.21 | 0.21 | 0.49 |
| δ = 0.11 | Frequency | 0.20 | 0.10 | 0.10 | 0.60 |
Second, two covariates, one continuous (Zco) and one categorical (Zca), are generated independently for each offspring. For clarity, we let Zco ~ N(1, 2) and P(Zca = 1) = 1 − P(Zca = 0) = 0.7. Notice that neither covariate is a confounder in this setting.
Lastly, conditional on the trait genotype G of the offspring and the covariates Zco and Zca, the bivariate ordinal traits T = (T(1), T(2))′ are generated according to the following random effects proportional odds model
where j = 1, 2. U1 and U2 are random effects generated from (U1, U2)′ ~ N(0, Σ).
We set K1 = 3, K2 = 4, (α1,1, α1,2) = (−0.5, −0.3), (α2,1, α2,2, α2,3) = (−0.5, −0.3, −0.1). In order to examine the behaviors of our proposed method when the covariates are weakly or strongly associated with the traits, we set βco = βca = 0.0, 0.5, 1.0, 1.5, and 2.0, but fix βg = 2.0 and for convenience. It is noteworthy that, as long as the coefficient of linkage disequilibrium δ = 0, the generated samples are under our null hypothesis; otherwise, the generated samples are under the alternative hypothesis.
We implement the maximum-(h, q) asymptotic test (Section 2.5) in our simulation, while we also apply the maximum-(h, q) resampling test (Section 2.6) for the purpose of comparison. In practice, we select the grid of h and q as {C1(C2/C1){l1/(L1−1)}: l1 = 0, …, L1 − 1} and {0.5l2/(L2 − 1): l2 = 0, …, L2 − 1}, respectively, and choose C1 = 0.05, C2 = 10, L1 = 8, and L2 = 5 in all simulations. The simulation results are based on 10,000 replications for the asymptotic test, and 1,000 replications for the resampling test.
The upper part of Table 2 compares the nominal levels of type I error with those estimated empirically from 200, 400 or 600 trios (two parents and one child). It clearly shows that the empirical type I error and the nominal significance level are very close. Subject to random variations, the accuracy is higher when we have more families and/or when the nominal levels are greater.
Table 2.
Type I errors of our proposed maximum-(h, q) asymptotic test.
| Confounder | No. of nuclear families | Missing rate | α = 0.05 | α = 0.01 | α = 0.001 |
|---|---|---|---|---|---|
| No | 200 | N/A | 0.0466 | 0.0090 | 0.0006 |
| 400 | N/A | 0.0512 | 0.0097 | 0.0010 | |
| 600 | N/A | 0.0453 | 0.0111 | 0.0013 | |
|
| |||||
| Yes | 200 | 0.1 | 0.0490 | 0.0086 | 0.0009 |
| 0.2 | 0.0542 | 0.0088 | 0.0012 | ||
| 0.3 | 0.0575 | 0.0098 | 0.0011 | ||
| 400 | 0.1 | 0.0533 | 0.0106 | 0.0009 | |
| 0.2 | 0.0624 | 0.0132 | 0.0013 | ||
| 0.3 | 0.0752 | 0.0167 | 0.0019 | ||
| 600 | 0.1 | 0.0535 | 0.0101 | 0.0011 | |
| 0.2 | 0.0682 | 0.0150 | 0.0013 | ||
| 0.3 | 0.0879 | 0.0210 | 0.0022 | ||
Table 3 compares the power of the covariate-adjusted and unadjusted tests for different covariate effects. From Table 3 we can see that the unadjusted test achieves a slightly higher power than the adjusted test if there is no covariate effect on the traits; the performances of the two tests are comparable if the covariate effects are relatively weak; otherwise the adjusted test outperforms the unadjusted test substantially. For the purpose of comparison, Table 3 also lists the power of maximum-(h, q) resampling test for two nominal levels of significance (0.05 and 0.01) when the number of trios is 200. Clearly, the results from the resampling test resemble those from the asymptotic test.
Table 3.
Power comparison without confounder. : the unadjusted association test in Zhang, Liu, and Wang (2010); : the proposed maximum-(h, q) asymptotic test; : the proposed maximum-(h, q) resampling test.
| No. of trios | α | Method | Covariate effect
|
|||||
|---|---|---|---|---|---|---|---|---|
| 0.0 | 0.5 | 1.0 | 1.5 | 2.0 | ||||
| 200 | 0.05 |
|
0.681 | 0.521 | 0.372 | 0.275 | 0.222 | |
|
|
0.674 | 0.519 | 0.360 | 0.275 | 0.233 | |||
|
|
0.726 | 0.522 | 0.306 | 0.189 | 0.135 | |||
| 0.01 |
|
0.432 | 0.281 | 0.161 | 0.099 | 0.071 | ||
|
|
0.391 | 0.269 | 0.162 | 0.099 | 0.075 | |||
|
|
0.491 | 0.283 | 0.128 | 0.064 | 0.041 | |||
| 0.001 |
|
0.160 | 0.082 | 0.036 | 0.017 | 0.011 | ||
|
|
0.223 | 0.097 | 0.028 | 0.011 | 0.006 | |||
|
| ||||||||
| 400 | 0.05 |
|
0.948 | 0.848 | 0.685 | 0.551 | 0.448 | |
|
|
0.960 | 0.838 | 0.565 | 0.348 | 0.233 | |||
| 0.01 |
|
0.846 | 0.658 | 0.441 | 0.297 | 0.213 | ||
|
|
0.877 | 0.643 | 0.321 | 0.154 | 0.084 | |||
| 0.001 |
|
0.563 | 0.337 | 0.164 | 0.091 | 0.054 | ||
|
|
0.671 | 0.361 | 0.115 | 0.040 | 0.018 | |||
|
| ||||||||
| 600 | 0.05 |
|
0.996 | 0.963 | 0.864 | 0.750 | 0.643 | |
|
|
0.998 | 0.954 | 0.750 | 0.512 | 0.345 | |||
| 0.01 |
|
0.972 | 0.876 | 0.684 | 0.512 | 0.387 | ||
|
|
0.983 | 0.866 | 0.532 | 0.280 | 0.149 | |||
| 0.001 |
|
0.845 | 0.620 | 0.362 | 0.214 | 0.133 | ||
|
|
0.914 | 0.646 | 0.264 | 0.092 | 0.039 | |||
3.1.2 With confounders
The simulation studies in Section 3.1.1 provide a detailed comparison between the covariate-adjusted and unadjusted tests when there does not exist any confounder. To further evaluate the performance of our proposed test with confounders in terms of type I error and power, we conduct more simulations.
The procedure of generating the data is similar to that in Section 3.1.1 except the following. First, we consider families with two children. Second, some of the paternal and maternal marker genotypes (Cf and Cm) are assumed unavailable according to a pre-specified missing rate. Third, for those families with complete parental genotypes, we simulate Zca based on the model logit{P(Zca = 1)} = γf Cf + γmCm; for those families with incomplete parental genotypes, we simulate Zca from the offspring genotype C by using the model logit{P(Zca = 1)} = γC. As a result, the categorical covariate plays the role of a confounder in this setting.
Our focus here is to evaluate how the confounder affects the performance. Thus, we fix βco = βca = 2.0, and βg = 2.0. We set the paternal and maternal genotype missing rate to be equal, and let the rate vary among 0.1, 0.2, and 0.3. We believe this range is practical and reasonable.
The lower part of Table 2 compares the nominal levels of type I error with those estimated empirically from 200, 400 or 600 nuclear families. Our proposed test reasonably controls the false positives when the parental genotype missing rate is about 10%. However, with a higher missing rate, the type I error of our proposed test becomes more inflated, although this phenomenon is not unique to our test.
Table 4 tabulates the power of the covariate-adjusted and unadjusted tests. Clearly, our proposed test outperforms the unadjusted test. However, as noted above, both tests cannot control the type I error rate when parental genotypes are missing at a relatively high rate. Thus, Table 5 presents the power after the type I error rate is empirically adjusted to the nominal level. We should note that this is only feasible in simulation in order to make a fair comparison of power between the methods. A slight change of power can be observed after correcting the type I error. In addition, Table 5 indicates that our proposed test is more powerful than the unadjusted test.
Table 4.
Power comparison with confounder. : the unadjusted association test in Zhang, Liu, and Wang (2010); : the proposed maximum-(h, q) asymptotic test.
| No. of nuclear families | Missing rate | Method | α = 0.05 | α = 0.01 | α = 0.001 | |
|---|---|---|---|---|---|---|
| 200 | 0.1 |
|
0.441 | 0.209 | 0.065 | |
|
|
0.258 | 0.089 | 0.029 | |||
| 0.2 |
|
0.428 | 0.205 | 0.048 | ||
|
|
0.253 | 0.099 | 0.025 | |||
| 0.3 |
|
0.441 | 0.207 | 0.044 | ||
|
|
0.273 | 0.088 | 0.024 | |||
|
| ||||||
| 400 | 0.1 |
|
0.787 | 0.604 | 0.248 | |
|
|
0.468 | 0.265 | 0.075 | |||
| 0.2 |
|
0.791 | 0.600 | 0.218 | ||
|
|
0.508 | 0.279 | 0.073 | |||
| 0.3 |
|
0.798 | 0.600 | 0.234 | ||
|
|
0.518 | 0.292 | 0.075 | |||
|
| ||||||
| 600 | 0.1 |
|
0.933 | 0.804 | 0.490 | |
|
|
0.675 | 0.412 | 0.166 | |||
| 0.2 |
|
0.949 | 0.790 | 0.515 | ||
|
|
0.701 | 0.433 | 0.177 | |||
| 0.3 |
|
0.943 | 0.827 | 0.519 | ||
|
|
0.727 | 0.454 | 0.179 | |||
Table 5.
Adjusted power comparison with confounder. : the unadjusted association test in Zhang, Liu, and Wang (2010); : the proposed maximum-(h, q) asymptotic test.
| No. of nuclear families | Missing rate | Method | α = 0.05 | α = 0.01 | α = 0.001 | |
|---|---|---|---|---|---|---|
| 200 | 0.1 |
|
0.421 | 0.249 | 0.056 | |
|
|
0.257 | 0.098 | 0.021 | |||
| 0.2 |
|
0.379 | 0.212 | 0.084 | ||
|
|
0.235 | 0.112 | 0.037 | |||
| 0.3 |
|
0.402 | 0.219 | 0.060 | ||
|
|
0.253 | 0.105 | 0.047 | |||
|
| ||||||
| 400 | 0.1 |
|
0.796 | 0.613 | 0.471 | |
|
|
0.495 | 0.257 | 0.140 | |||
| 0.2 |
|
0.770 | 0.584 | 0.316 | ||
|
|
0.480 | 0.305 | 0.128 | |||
| 0.3 |
|
0.756 | 0.572 | 0.390 | ||
|
|
0.501 | 0.283 | 0.104 | |||
|
| ||||||
| 600 | 0.1 |
|
0.922 | 0.802 | 0.618 | |
|
|
0.655 | 0.413 | 0.245 | |||
| 0.2 |
|
0.899 | 0.741 | 0.527 | ||
|
|
0.668 | 0.418 | 0.188 | |||
| 0.3 |
|
0.900 | 0.730 | 0.539 | ||
|
|
0.644 | 0.362 | 0.180 | |||
3.2 Comparison with other covariate-adjusted methods
In this subsection, we compare our proposed method with the parametric covariate-adjusted method given by Wang, Ye, and Zhang (2006), as well as the FBAT-GEE (Lange et al. 2003) adjusting for covariates.
As the parametric method in Wang, Ye, and Zhang (2006) deals with a single trait at a time, we apply the Bonferroni correction to test multiple traits. Moreover, to adjust for covariates in FBAT-GEE, as suggested by Lange et al. (2003), we fit a regression model of each trait versus the covariates and then replace the original traits in the FBAT-GEE statistic with their corresponding residuals. Because our traits considered below are ordinal, we use a proportional odds logistic model to compute the residuals for the traits.
Recall that our test only involves a single parameter h for all continuous covariates. To evaluate the effect, we deliberately include two continuous covariates and impose different effects by the two covariates. To further consider model misspecifications, we also include an interaction effect. The two covariates Z1 and Z2 independently follow the distribution of N(1, 2). The quantitative traits Y = (Y (1), Y (2))′ are then generated according to the following model
where (ε1, ε2)′ follows a bivariate normal distribution N(0, Σ).
We can choose different parameter values in this model to examine the performance of the tests under different settings. First, with β1 = 0.16, β2 = 0.64, and β12 = 0, we aim to compare our test with the others when the covariates have different main effects. Second, with β1 = 0, β2 = 0, and β12 = 0.64, the interaction is present in the absence of the main effects, allowing us to examine the robustness of all methods when the model is clearly misspecified. Third, we combine the above parameter choices to set β1 = 0.16, β2 = 0.64, and β12 = 0.64 for a general model including both the main and interaction effects. The other parameters are fixed at μ = 0, βg = 0.8, and .
After the quantitative traits are generated, the ordinal traits T = (T(1), T(2))′ are generated by discretizing Y (1) and Y (2) separately. For clarity, we set the number of categories of T(1) and T(2) to be 3 and 4, while using 50%, 67% sample percentiles to discretize Y (1) and using 33%, 54%, 75% sample percentiles to discretize Y (2).
Since the maximum-(h, q) asymptotic and resampling tests have similar performance according to the previous subsection, we only include the former in the results. All results are based on 10,000 replications. Table 6 depicts the power of the three covariate-adjusted tests. When the covariates have different main effects on the traits, the parametric methods show superiority over our nonparametric method. This could be due to the lack of flexibility of our method caused by a single choice of the parameter h. However, when the parametric model assumptions are violated as in the model including the interaction term, our proposed test is more robust to the model misspecification and substantially outperforms the others. Finally, for the general model including both the main effects and an interaction term, our test still demonstrates an obvious advantage in terms of power, based on the current choice of parameter values. In general, while different settings may be favorable to different methods, our proposed method is more robust to model misspecifications.
Table 6.
Comparisons of three covariate-adjusted methods. : the proposed maximum(h, q) asymptotic test; FBAT-GEE-COV: FBAT-GEE adjusting for covariates (Lange et al. 2003); FBAT-O-COV: the covariate-adjusted test for an ordinal response (Wang, Ye, and Zhang 2006).
| Covariate effects | No. of trios | Method | α = 0.05 | α = 0.01 | α = 0.001 | |
|---|---|---|---|---|---|---|
|
β1 = 0.16 β2 = 0.64 β12 = 0 |
200 |
|
0.396 | 0.179 | 0.040 | |
| FBAT-GEE-COV | 0.541 | 0.297 | 0.101 | |||
| FBAT-O-COV | 0.547 | 0.296 | 0.091 | |||
| 400 |
|
0.729 | 0.485 | 0.194 | ||
| FBAT-GEE-COV | 0.859 | 0.675 | 0.387 | |||
| FBAT-O-COV | 0.854 | 0.654 | 0.345 | |||
| 600 |
|
0.902 | 0.741 | 0.431 | ||
| FBAT-GEE-COV | 0.965 | 0.888 | 0.684 | |||
| FBAT-O-COV | 0.964 | 0.866 | 0.623 | |||
|
| ||||||
|
β1 = 0 β2 = 0 β12 = 0.64 |
200 |
|
0.299 | 0.117 | 0.022 | |
| FBAT-GEE-COV | 0.187 | 0.064 | 0.011 | |||
| FBAT-O-COV | 0.211 | 0.080 | 0.016 | |||
| 400 |
|
0.597 | 0.346 | 0.118 | ||
| FBAT-GEE-COV | 0.345 | 0.159 | 0.040 | |||
| FBAT-O-COV | 0.385 | 0.189 | 0.054 | |||
| 600 |
|
0.807 | 0.594 | 0.285 | ||
| FBAT-GEE-COV | 0.499 | 0.263 | 0.089 | |||
| FBAT-O-COV | 0.547 | 0.308 | 0.110 | |||
|
| ||||||
|
β1 = 0.16 β2 = 0.64 β12 = 0.64 |
200 |
|
0.254 | 0.091 | 0.015 | |
| FBAT-GEE-COV | 0.195 | 0.067 | 0.012 | |||
| FBAT-O-COV | 0.218 | 0.081 | 0.015 | |||
| 400 |
|
0.524 | 0.278 | 0.081 | ||
| FBAT-GEE-COV | 0.362 | 0.164 | 0.046 | |||
| FBAT-O-COV | 0.399 | 0.195 | 0.056 | |||
| 600 |
|
0.740 | 0.509 | 0.227 | ||
| FBAT-GEE-COV | 0.525 | 0.288 | 0.101 | |||
| FBAT-O-COV | 0.565 | 0.326 | 0.119 | |||
4 Application to COGA Data
4.1 Background
The Collaborative Study on the Genetics of Alcoholism (COGA) is a large scale, multi-center family study, which aims to identify susceptible genes for alcohol dependence and alcohol-related phenotypes (Begleiter et al. 1995; Edenberg 2002; Edenberg et al. 2005). The data included 143 families with a total of 1,614 individuals.
Although there are multiple alcohol-related traits available in COGA data, most of linkage and association analyses of alcohol dependence focused on the trait ALDX1 (Alcohol DX-DSM3R+Feighner) only. ALDX1 defines the severity of the alcohol dependence based on the DSM-III-R (American Psychiatric Association 1994) and Feighner criteria (Feighner et al. 1972). This measure was recorded on an ordinal scale with four levels (pure unaffected, never drunk, unaffected with some symptoms, and affected); however, almost all the previous analyses treated ALDX1 as a binary outcome. Following Zhang, Liu, and Wang (2010), we consider three ordinal traits together: (1) ALDX1, (2) MaxDrink (maximum number of drinks in a 24 hour period) with four levels (0–9, 10–19, 20–29, and more than 30 drinks), (3) TimeDrink (spent so much time drinking, had little time for anything else) with 3 levels (“no”, “yes and lasted less than a month”, and “yes and lasted for one month or longer”). As revealed in Zhang, Liu, and Wang (2010), the association signal of ALDX1 was enhanced by jointly analyzing these three traits. However, they did not evaluate whether the environmental factors also contribute to the alcoholism risk, which is an important issue to consider in genetic studies of alcoholism (Edenberg 2002).
4.2 Data analysis
In our data analysis, we consider two covariates: age at interview and sex. We focus on chromosome 7 because (1) several prior studies (Reich et al. 1998; Zhu et al. 2005; Dick et al. 2008) reported very strong suggestions of linkage with susceptibility loci for alcohol dependence on this chromosome; (2) we want to compare our results with those of Zhang, Liu, and Wang (2010). There are a total of 31 microsatellite markers on chromosome 7. We test for association between alcohol dependence and 31 markers one by one using the three traits together, and apply Bonferroni correction to adjust for multiple testing involving 31 markers.
To apply the proposed nonparametric covariate-adjusted test , we follow the same choices of the grid points of h and q as in the simulation. Due to the similarity of using the maximum-(h, q) asymptotic test and the maximum-(h, q) resampling test suggested by our simulation studies, we only provide the results from resampling test for simplicity. As mentioned in Section 2.6, we obtain the resampled data of children’s marker alleles using the approach in Robinowitz and Laird (2000), based on nuclear families as in FBAT (Laird, Horvath, and Xu 20 00). The number of resampling used is 10, 000.
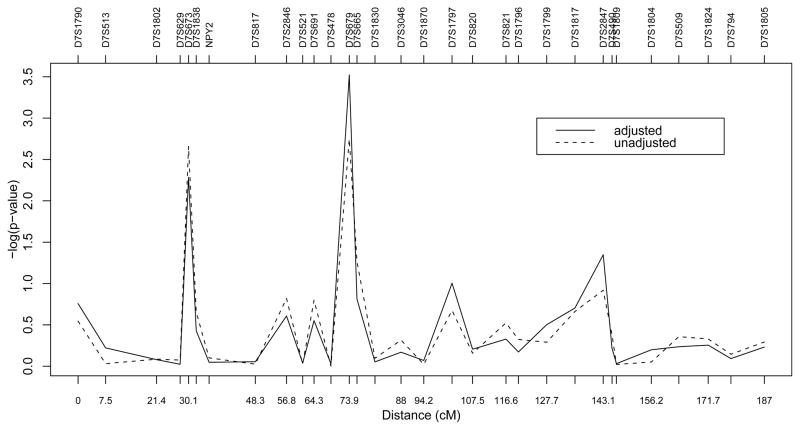
Using the unadjusted test in Zhang, Liu, and Wang (2010), we repeat their calculation in a recent release (version 2.0.3) of FBAT. We find that the smallest p-value is reached at the marker D7S679, as 0.0018, which is almost significant at the overall 0.05 level after the Bonferroni adjustment (αBonferroni = 0.05/31 = 0.0016). Moreover, when we adjust for age at interview and sex, the covariate-adjusted test provides us with a much smaller p-value 0.0003 for the marker D7S679. Thus, adjusting for the covariates reveals a much more significant association between D7S679 and alcohol dependence. This suggests that failure to adjust for covariates might lose the power of detecting significant associations. The distributions of the p-values of the 31 markers for these two tests are shown in Figure 1.
Figure 1.
Log p-values of association tests between alcohol dependence and markers on chromosome 7 using three traits ALDX1, MaxDrink, and TimeDrink together. The solid line represents the proposed covariate-adjusted maximum-(h, q) resampling test and the dash line represents the unadjusted test in Zhang, Liu, and Wang (2010).
5 Discussion
Due to the important role of comorbidity in mental and behavioral research, investigators have begun to pay more and more attention to multiple traits. Based on a generalization of Kendall’s tau, Zhang, Liu, and Wang (2010) proposed a nonparametric test to detect the association between multiple (quantitative and/or ordinal) traits and a genetic marker. In this paper, we have extended their method to accommodate covariates. The null hypothesis and the test statistic are both modified to handle the effects brought by the presence of covariates. Our simulation studies and real data analysis reveal that the power is much enhanced after adjusting for covariates in the association test when the covariate effects on the traits exist. When compared to some existing covariate-adjusted methods such as the FBAT-GEE test, our test could lose some power due to the single choice of the parameter h (or q) for all continuous (or categorical) covariates. Nonetheless, our test is more robust to model misspecifications, and outperforms the other tests when the parametric model assumptions are invalid.
Regarding the confounding effects, we test a null hypothesis of conditional independence as in Jiang and Zhang (2011). They have demonstrated that the spurious association can be alleviated using this null hypothesis in a population-based study. Nonetheless, this current work focuses on the family-based studies, and makes a reasonable assumption that the covariates and offspring genotypes are “conditionally independent” given their parents’ genotypes. This assumption simplifies the computation of our test statistic, and works well when the offspring genotypes are determined by their parents’ genotypes. However, when parental genotypes are not completely observed, our test as well as other existing tests might lead to more false positives (see the simulation results in Section 3.1.2). Therefore, it remains important to improve our test to deal with the situation when there is a relatively high rate of missing parental genotypes.
The fixed-(h, q) test given in Section 2.3 is sensitive to the choice of h and q. To solve this problem, we propose a maximum-(h, q) test over pre-specified grids of h and q. Our simulation results suggest that the power is no longer sensitive to the selection of grids provided that they have a reasonable coverage. Although our proposed maximum-(h, q) test works well in simulation and real data analysis, whether there exist optimal h and q and how to choose the optimal ones are important research topics, because the answers may help us choose different optimal parameters for different covariates. Nonetheless, it is reasonable to conclude from our numerical studies that the maximum-(h, q) test leads to a practically adequate approximation to the performance of the optimal weighting scheme.
We should also point out that although the analytical approach to calculating the power (Section 2.4) establishes a useful framework for power calculations involving multiple traits, there are a number of important issues that warrant thorough and further investigation. For example, as in typical power calculations, one needs to specify an applicable model to describe the penetrance function, especially for multiple ordinal traits, where the correlations among the traits are important. Moreover, selection issues and ascertainment bias are of great importance in genetic studies. Their influence on the power calculations should be considered carefully. Finally, we examined power based on fixed h and q. It is technically challenging to derive the asymptotic distribution of the maximum-(h, q) statistic under the alternative hypothesis. Hence, the power calculation based on optimal h and q remains to be an open question.
Although this work focuses on family studies, it is important to explore the applicability of our method in the broad literature of nonparametric tests for multiple variables.
Appendix: Proof of Theorem 1
Let , where n denotes the sample size throughout the proof. Then , i.e., the probability measures μn ≡ μGn weakly converges to μ ≡ μG. Roughly, our objective is to apply the above weak convergence result to establish the approximation of R by R̃ in distribution. As and are obtained from an identical “transformation” of Gn and G, our objective is intuitively correct. The unique difficulty aries from the fact that the transformation implicitly depends on n. It leads us to pursue our objective uniformly for the transformations.
Formally, let
 be the family of continuous mappings f of x ∈ ℝpL1L2 into ℝL1L2 as follows,
be the family of continuous mappings f of x ∈ ℝpL1L2 into ℝL1L2 as follows,
in which , and (Vnx)l1l2 extracts a sub-vector of Vnx as same as that in Section 2.5.
According to Theorem 3.4 in Rao (1962), if we can verify that (i)
 is compact under uniform convergence on compacta, and (ii) μf−1 has continuous marginal distributions for each f ∈
is compact under uniform convergence on compacta, and (ii) μf−1 has continuous marginal distributions for each f ∈
 , then
, then
| (A.1) |
where the supremum is taken over all sets A of the form A = {x: fl1l2 (x) ≤ al1, l2, l1 = 1, …, L1, l2 = 1, …, L2} with f (x) = {f1,1(x), …, fL1L2 (x)}′ ∈
 and a = (a1,1, …, aL1L2)′ is an arbitrary vector of ℝL1L2.
and a = (a1,1, …, aL1L2)′ is an arbitrary vector of ℝL1L2.
Notice that μn(A) is the joint distribution function of {||R(h1, q1)||2, …, ||R(hL1, qL2)||2}′ and μ(A) is the joint distribution function of (||R̃1,1||2, …, ||R̃L1L2|| 2)′, when the function f associated with A is chosen as the n-th element in
 . So it is readily seen that (A.1) leads to the conclusion (11) in Theorem 1. Therefore, we will verify the above-mentioned conditions (i) and (ii) to prove (A.1) in the following. It is noteworthy that we only need to prove (A.1) restricting both Gn and G in a large enough compact rectangle K of ℝpL1L2. This is because μn ⇒ μ and we can make K big enough such that μn(Kc) < ε and μ(Kc) < ε with n large enough, for any ε > 0.
. So it is readily seen that (A.1) leads to the conclusion (11) in Theorem 1. Therefore, we will verify the above-mentioned conditions (i) and (ii) to prove (A.1) in the following. It is noteworthy that we only need to prove (A.1) restricting both Gn and G in a large enough compact rectangle K of ℝpL1L2. This is because μn ⇒ μ and we can make K big enough such that μn(Kc) < ε and μ(Kc) < ε with n large enough, for any ε > 0.
Condition (i):
 is compact under uniform convergence on compacta. As in Rao (1962), this can be proved by checking the following conditions according to the Ascoli theorem: (a), sup{|f(x)|: x ∈ K, f ∈
is compact under uniform convergence on compacta. As in Rao (1962), this can be proved by checking the following conditions according to the Ascoli theorem: (a), sup{|f(x)|: x ∈ K, f ∈
 } < ∞; (b),
} < ∞; (b),
 is equicontinuous, i.e., for each ε > 0 there exists a δ > 0, as long as x, y ∈ K and ||x − y|| < δ, we have that |f(x) − f(y)| < ε for all f ∈
is equicontinuous, i.e., for each ε > 0 there exists a δ > 0, as long as x, y ∈ K and ||x − y|| < δ, we have that |f(x) − f(y)| < ε for all f ∈
 .
.
For (a), we only need to prove that sup{|fl1,l2 (x)|: x ∈ K, f∈
 } < ∞. This can be seen from
} < ∞. This can be seen from
since , which is uniformly bounded due to the assumptions of Theorem 1 (||M|| denotes the spectral norm of a matrix M).
For (b), we only need to prove that there exists some δ > 0, as long as x, y ∈ K and ||x − y|| < δ, then |fl1l2 (x) − fl1l2(y)| < ε for all n, 1 ≤ l1 ≤ L1 and 1 ≤ l2 ≤ L2. It is seen that
Then condition (b) holds since ||Vn|| and ||x|| are both uniformly bounded.
Condition (ii): μf−1 has continuous marginal distributions for each f ∈
 . For any a ∈ ℝL1L2, we need to prove that μf−1(a) = 0 for any f ∈
. For any a ∈ ℝL1L2, we need to prove that μf−1(a) = 0 for any f ∈
 .
.
where fG is the density function of G. Since the eigenvalues of Vn are uniformly bounded from both above and below due to our assumptions (this can be proved since the eigenvalues of Var0D(S) and Var0(S) are all uniformly bounded from both above and below), we know that there exists a non-degenerate density function of G̃ = VnG as fG̃, then,
Thus, condition (ii) is verified.
Footnotes
This work is supported in part by grant R01DA016750 from the National Institute on Drug Abuse. The COGA data were provided by the Collaborative Study on the Genetics of Alcoholism (U10AA008401). Zhu’s research is also supported by the National Natural Science Foundation of China (grant 11001044) and the Fundamental Research Funds for the Central Universities (grant 09QNJJ001). We thank the editor, an associate editor, and three referees for their constructive comments and suggestions.
References
- Allison DB. Transmission-Disequilibrium Tests for Quantitative Traits. The American Journal of Human Genetics. 1997;60:676–690. [PMC free article] [PubMed] [Google Scholar]
- American Psychiatric Association. Diagnostic and Statistical Manual of Mental Disorders. 4. Washington, DC: American Psychiatric Press; 1994. [Google Scholar]
- Arking DE, Pfeufer A, Post W, Kao WHL, Newton-Cheh C, Ikeda M, West K, Kashuk C, Akyol M, Perz S, Jalilzadeh S, Illig T, Gieger C, Guo C-Y, Larson MG, Wichmann HE, Marbán E, O’Donnell CJ, Hirschhorn JN, Kääb S, Spooner PM, Meitinger T, Chakravarti A. A Common Genetic Variant in the NOS1 Regulator NOS1AP Modulates Cardiac Repolarization. Nature Genetics. 2006;38:644–651. doi: 10.1038/ng1790. [DOI] [PubMed] [Google Scholar]
- Azzalin A, Capitanio A. Statistical Applications of the Multivariate Skew Normal Distribution. Journal of the Royal Statistical Society: Series B. 1999;61:579–602. [Google Scholar]
- Begleiter H, Reich T, Hesselbrock V, Porjesz B, Li TK, Schuckit MA, Edenberg HJ, Rice JP. The Collaborative Study on the Genetics of Alcoholism. Alcohol Health & Research World. 1995;19:228–236. [PMC free article] [PubMed] [Google Scholar]
- Chen W-M, Manichaikul A, Rich SS. A Generalized Family-Based Association Test for Dichotomous Traits. The American Journal of Human Genetics. 2009;85:364–376. doi: 10.1016/j.ajhg.2009.08.003. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen X, Liu C-T, Zhang M, Zhang H. A Forest-Based Approach to Identifying Gene and Gene-Gene Interactions. Proceedings of the National Academy of Sciences of the United States of America. 2007;104:19199–19203. doi: 10.1073/pnas.0709868104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dick DM, Aliev F, Wang JC, Grucza RA, Schuckit M, Kuperman S, Kramer J, Hinrichs A, Bertelsen S, Budde JP, Hesselbrock V, Porjesz B, Edenberg HJ, Bierut LJ, Goate A. Using Dimensional Models of Externalizing Psychopathology to Aid in Gene Identification. Archives of General Psychiatry. 2008;65:310–318. doi: 10.1001/archpsyc.65.3.310. [DOI] [PubMed] [Google Scholar]
- Duerr RH, Taylor KD, Brant SR, Rioux JD, Silverberg MS, Daly MJ, Steinhart AH, Abraham C, Regueiro M, Griffths A, Dassopoulos T, Bitton A, Yang H, Targan S, Datta LW, Kistner EO, Schumm LP, Lee AT, Gregersen PK, Barmada MM, Rotter JI, Nicolae DL, Cho JH. A Genome-Wide Association Study Identifies IL23R as an Inflammatory Bowel Disease Gene. Science. 2006;314:1461–1463. doi: 10.1126/science.1135245. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Edenberg HJ. The Collaborative Study on the Genetics of Alcoholism: An Update. Alcohol Research & Health. 2002;26:214–218. [PMC free article] [PubMed] [Google Scholar]
- Edenberg HJ, Bierut LJ, Boyce P, Cao M, Cawley S, Chiles R, Doheny KF, Hansen M, Hinrichs T, Jones K, Kelleher M, Kennedy GC, Liu G, Marcus G, McBride C, Murray SS, Oliphant A, Pettengill J, Porjesz B, Pugh EW, Rice JP, Rubano T, Shannon S, Steeke R, Tischfield JA, Tsai YY, Zhang C, Begleiter H. Description of the Data from the Collaborative Study on the Genetics of Alcoholism (COGA) and Single-Nucleotide Polymorphism Genotyping for Genetic Analysis Workshop 14. BMC Genetics. 2005;6(Suppl 1):S2. doi: 10.1186/1471-2156-6-S1-S2. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feighner JP, Robins E, Guze SB, Woodruff RA, Jr, Winokur G, Munoz R. Diagnostic Criteria for Use in Psychiatric Research. Archives of General Psychiatry. 1972;26:57–63. doi: 10.1001/archpsyc.1972.01750190059011. [DOI] [PubMed] [Google Scholar]
- Hoh J, Ott J. Scan Statistics to Scan Markers for Susceptibility Genes. Proceedings of the National Academy of Sciences of the United States of America. 2000;97:9615–9617. doi: 10.1073/pnas.170179197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Horvath S, Laird NM. A Discordant-Sibship Test for Disequilibrium and Linkage: No Need for Parental Data. The American Journal of Human Genetics. 1998;63:1886–1897. doi: 10.1086/302137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang Y, Zhang H. Propensity Score-Based Nonparametric Test Revealing Genetic Variants Underlying Bipolar Disorder. Genetic Epidemiology. 2011;35:125–132. doi: 10.1002/gepi.20558. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Klein RJ, Zeiss C, Chew EY, Tsai J-Y, Sackler RS, Haynes C, Henning AK, SanGiovanni JP, Mane SM, Mayne ST, Bracken MB, Ferris FL, Ott J, Barnstable C, Hoh J. Complement Factor H Polymorphism in Age-Related Macular Degeneration. Science. 2005;308:385–389. doi: 10.1126/science.1109557. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Knapp M. Using Exact P Values to Compare the Power between the Reconstruction-Combined Transmission/Disequilibrium Test and the Sib Transmission/Disequilibrium Test. The American Journal of Human Genetics. 1999;65:1208–1210. doi: 10.1086/302591. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lange C, DeMeo DL, Laird NM. Power and Design Considerations for a General Class of Family-Based Association Tests: Quantitative Traits. The American Journal of Human Genetics. 2002;71:1330–1341. doi: 10.1086/344696. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lange C, Laird NM. Power Calculations for a General Class of Family-Based Association Tests: Dichotomous Traits. The American Journal of Human Genetics. 2002;71:575–584. doi: 10.1086/342406. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lange C, Silverman EK, Xu X, Weiss ST, Laird NM. A Multivariate Family-Based Association Test Using Generalized Estimating Equations: FBAT-GEE. Biostatistics. 2003;4:195–206. doi: 10.1093/biostatistics/4.2.195. [DOI] [PubMed] [Google Scholar]
- Laird NM, Horvath S, Xu X. Implementing a Unified Approach to Family-Based Tests of Association. Genetic Epidemiology. 2000;19(Suppl 1):S36–S42. doi: 10.1002/1098-2272(2000)19:1+<::AID-GEPI6>3.0.CO;2-M. [DOI] [PubMed] [Google Scholar]
- Lam KF, Lee YW, Leung TL. Modeling Multivariate Survival Data by a Semiparametric Random Effects Proportional Odds Model. Biometrics. 2002;58:316–323. doi: 10.1111/j.0006-341x.2002.00316.x. [DOI] [PubMed] [Google Scholar]
- Li MD, Burmeister M. New Insights into the Genetics of Addiction. Nature Reviews Genetics. 2009;10:225–231. doi: 10.1038/nrg2536. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu H, Tang Y, Zhang HH. A New Chi-Square Approximation to the Distribution of Non-Negative Definite Quadratic Forms in Non-Central Normal Variables. Computational Statistics & Data Analysis. 2009;53:853–856. [Google Scholar]
- Liu Y, Tritchler D, Bull SB. A Unified Framework for Transmission-Disequilibrium Test Analysis of Discrete and Continuous Traits. Genetic Epidemiology. 2002;22:26–40. doi: 10.1002/gepi.1041. [DOI] [PubMed] [Google Scholar]
- Lunetta KL, Faraone SV, Biederman J, Laird NM. Family-Based Tests of Association and Linkage That Use Unaffected Sibs, Covariates, and Interactions. The American Journal of Human Genetics. 2000;66:605–614. doi: 10.1086/302782. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Martin ER, Monks SA, Warren LL, Kaplan NL. A Test for Linkage and Association in General Pedigrees: The Pedigree Disequilibrium Test. The American Journal of Human Genetics. 2000;67:146–154. doi: 10.1086/302957. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Merikangas KR, Stolar M, Stevens DE, Goulet J, Preisig MA, Fenton B, Zhang H, O’Malley SS, Rounsaville BJ. Familial Transmission of Substance Use Disorders. Archives of General Psychiatry. 1998;55:973–979. doi: 10.1001/archpsyc.55.11.973. [DOI] [PubMed] [Google Scholar]
- Rabinowitz D. A Transmission Disequilibrium Test for Quantitative Trait Loci. Human Heredity. 1997;47:342–350. doi: 10.1159/000154433. [DOI] [PubMed] [Google Scholar]
- Rabinowitz D, Laird NM. A Unified Approach to Adjusting Association Tests for Population Admixture with Arbitrary Pedigree Structure and Arbitrary Missing Marker Information. Human Heredity. 2000;50:211–223. doi: 10.1159/000022918. [DOI] [PubMed] [Google Scholar]
- Rao RR. Relations between Weak and Uniform Convergence of Measures with Applications. The Annals of Mathematical Statistics. 1962;33:659–680. [Google Scholar]
- Reich T, Edenberg HJ, Goate A, Williams JT, Rice JP, Van Eerdewegh P, Foroud T, Hesselbrock V, Schuckit MA, Bucholz K, Porjesz B, Li TK, Conneally PM, Nurnberger JI, Jr, Tischfield JA, Crowe RR, Cloninger CR, Wu W, Shears S, Carr K, Crose C, Willig C, Begleiter H. Genome-Wide Search for Genes Affecting the Risk for Alcohol Dependence. American Journal of Medical Genetics (Neuropsychiatric Genetics) 1998;81:207–215. [PubMed] [Google Scholar]
- Spielman RS, Ewens WJ. A Sibship Test for Linkage in the Presence of Association: The Sib Transmission/Disequilibrium Test. The American Journal of Human Genetics. 1998;62:450–458. doi: 10.1086/301714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spielman RS, McGinnis RE, Ewens WJ. Transmission Test for Linkage Disequilibrium: The Insulin Gene Region and Insulin-dependent Diabetes Mellitus (IDDM) The American Journal of Human Genetics. 1993;52:506–516. [PMC free article] [PubMed] [Google Scholar]
- Su L, Ullah A. Testing Conditional Uncorrelatedness. Journal of Business & Economic Statistics. 2009;27:18–29. [Google Scholar]
- True WR, Heath AC, Scherrer JF, Xian H, Lin N, Eisen SA, Lyons MJ, Goldberg J, Tsuang MT. Interrelationship of Genetic and Environmental Influences on Conduct Disorder and Alcohol and Marijuana Dependence Symptoms. American Journal of Medical Genetics (Neuropsychiatric Genetics) 1999;88:391–397. doi: 10.1002/(sici)1096-8628(19990820)88:4<391::aid-ajmg17>3.0.co;2-l. [DOI] [PubMed] [Google Scholar]
- Wang X, Ye Y, Zhang H. Family-Based Association Tests for Ordinal Traits Adjusting for Covariates. Genetic Epidemiology. 2006;30:728–736. doi: 10.1002/gepi.20184. [DOI] [PubMed] [Google Scholar]
- Weinberg CR. Allowing for Missing Parents in Genetic Studies of Case-Parent Triads. The American Journal of Human Genetics. 1999;64:1186–1193. doi: 10.1086/302337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yu K, Wheeler W, Li Q, Bergen AW, Caporaso N, Chatterjee N, Chen J. A Partially Linear Tree-based Regression Model for Multivariate Outcomes. Biometrics. 2010;66:89–96. doi: 10.1111/j.1541-0420.2009.01235.x. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Liu C-T, Wang X. An Association Test for Multiple Traits Based on the Generalized Kendall’s Tau. Journal of the American Statistical Association. 2010;105:473–481. doi: 10.1198/jasa.2009.ap08387. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhang H, Wang X, Ye Y. Detection of Genes for Ordinal Traits in Nuclear Families and a Unified Approach for Association Studies. Genetics. 2006;172:693–699. doi: 10.1534/genetics.105.049122. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu W, Zhang H. Why Do We Test Multiple Traits in Genetic Association Studies? (with discussion) Journal of the Korean Statistical Society. 2009;38:1–10. doi: 10.1016/j.jkss.2008.10.006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhu X, Cooper R, Kan D, Cao G, Wu X. A Genome-Wide Linkage and Association Study Using COGA Data. BMC Genetics. 2005;6(Suppl 1):S128. doi: 10.1186/1471-2156-6-S1-S128. [DOI] [PMC free article] [PubMed] [Google Scholar]