A novel variational Bayes multiple locus Z-statistic for genome-wide association studies with Bayesian model averaging

Abstract

Motivation: For many complex traits, including height, the majority of variants identified by genome-wide association studies (GWAS) have small effects, leaving a significant proportion of the heritable variation unexplained. Although many penalized multiple regression methodologies have been proposed to increase the power to detect associations for complex genetic architectures, they generally lack mechanisms for false-positive control and diagnostics for model over-fitting. Our methodology is the first penalized multiple regression approach that explicitly controls Type I error rates and provide model over-fitting diagnostics through a novel normally distributed statistic defined for every marker within the GWAS, based on results from a variational Bayes spike regression algorithm.

Results: We compare the performance of our method to the lasso and single marker analysis on simulated data and demonstrate that our approach has superior performance in terms of power and Type I error control. In addition, using the Women's Health Initiative (WHI) SNP Health Association Resource (SHARe) GWAS of African-Americans, we show that our method has power to detect additional novel associations with body height. These findings replicate by reaching a stringent cutoff of marginal association in a larger cohort.

Availability: An R-package, including an implementation of our variational Bayes spike regression (vBsr) algorithm, is available at http://kooperberg.fhcrc.org/soft.html.

Contact: blogsdon@fhcrc.org

Supplementary information: Supplementary data are available at Bioinformatics online.

1 INTRODUCTION

Population-based genome-wide association studies have succeeded in discovering a large number of variants that individually explain a small percentage of heritability for many complex phenotypes. For example, when considering height in Caucasian populations, over 180 loci have been identified (Allen et al., 2010; Weedon et al., 2008), which cumulatively explain 10% of the variation, whereas the total estimated heritable variation is 80–90% (Hirschhorn et al., 2001; Sale et al., 2005). This ‘missing’ or ‘dark’ heritability (Maher, 2008) has many purported causes, including additional highly penetrant or large effect rare alleles (Manolio et al., 2009), epistatic interactions (McCarthy and Hirschhorn, 2008), epigenetic variation (Eichler et al., 2010) or many uncharacterized loci of small effect (Yang et al., 2010). In the case of height, most of the additional loci recently identified are in this latter category, and only reach genome-wide significance in studies with hundreds of thousands of subjects (Allen et al., 2010; Weedon et al., 2008; Yang et al., 2010). In addition, predictive models of height within the Framingham study (Makowsky et al., 2011) have demonstrated that a much larger number of loci are likely contributing to variation in height, though not all of these loci may reach a stringent genome-wide significance threshold. Yang et al. (2010) also showed that the estimated heritability ascribed to height can largely be explained through observed common variants across the genome, where common variants explained 45% of the variation in height within an Australian population of European descent. These studies demonstrate an important challenge that while evidence suggests many common genetic variants driving phenotypic variation exist, our current methodologies and studies are under-powered to map the location of many of these causal variants.

The GWAS approach of testing individual variants for association with phenotype has succeeded in producing replicable associations (McCarthy and Hirschhorn, 2008). This success is largely attributable to both stringent Type I error control after accounting for a large number of tests and the systematic correction for confounding factors such as population stratification (Gibson, 2010; Price et al., 2010). Complex phenotypes, such as body height, with hundreds of genetic associations could in theory benefit from a modeling approach that tests for multiple genetic variants simultaneously. One type of solution to this problem is the use of penalized multiple regression methods. These methods can have greater power to detect genetic associations by including all the genetic variants within the GWAS in the model of association (Carbonetto and Stephens, 2011; He and Lin, 2011; Hoggart et al., 2008; Li et al., 2011; Logsdon et al., 2010; Makowsky et al., 2011; Wu et al., 2009). Penalized regression consists of estimating the additive genotypic effects β=β₁,…,β_m, in a multiple regression model y_i=∑_j^m x_ij β_j+e_i. In this model, y_i is the phenotype, x_ij is the jth genotype, and e_i is the residual error for the ith individual. Penalization of β is necessary to prevent model over-fitting when millions of variants are being tested with only thousands of samples. Although each penalized regression method proposed for GWAS can have greater power than single-marker analysis, none has demonstrated strict control of FWER, thus precluding their broader application in the field.

We propose the first penalized regression methodology, based on the variational Bayes approach of Logsdon et al. (2010), that is capable of directly controlling the family-wise error rate (FWER) through a variant level test statistic, z_vb, that is approximately 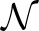(0, 1) distributed under the null hypothesis. Similar to Logsdon et al. (2010) and Carbonetto and Stephens (2011) our variational Bayes spike regression (vBsr) approach treats the genetic effects β as random, with the prior β_j ∼ (1−p_β)I[β=0]+p_βI[β≠0]. This prior can be thought of as a constraint on β similar to best subset selection, with p_β controlling the sparsity of the subset solution. We simplify the models proposed by Logsdon et al. (2010), who propose a three-component mixture, and the approach of Carbonetto and Stephens (2011), who propose a two- component mixture, by using a two-component mixture without the ‘slab’ component (see Supplementary Material for further details). The variant level statistic z_vb is derived based on the results of fitting the vBsr model. We show that when p_β→0 this statistic is asymptotically 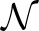(0, 1) under the null hypothesis. We then propose a diagnostic statistic (log(KL)) to determine the size of the vBsr best subset solution (i.e. p_β : p_β>0) such that this empirical distribution is approximately 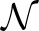(0, 1) for the vast majority of genetic variants within the GWAS. The main assumptions of this approach are that most genetic variants are independent of the phenotype of interest, their empirical distribution under the null hypothesis will be 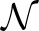(0, 1), and this distribution will be very sensitive to model over-fitting (for example if p_β is tuned to be too large). Given these conservative assumptions, the innovation of this test-statistic is therefore 2-fold. Not only can we demonstrate that it is possible to generate an approximately 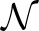(0, 1) distributed test statistic within a multi-locus penalized regression methodology (and therefore have much tighter control of the FWER) but also it is possible to use the data to suitably tune the penalized regression methodology to ensure that this approximation is valid.

1.1 Variational Bayes approximate inference

While variational Bayes approximations were first proposed as mean-field theory in theoretical physics (Parisi, 1988), they have seen a recent resurgence in the field of machine learning (Beal, 2003; Bishop, 2006) by providing tractable approximations to challenging Bayesian inference problems. Consider an arbitrary vector of parameters θ₁,…,θ_J=Θ, a data matrix W, a likelihood function defined as ∏_i^Np(W_i|Θ) and a prior defined as p(Θ). A typical Bayesian inference problem is to identify the posterior distribution of the parameters of interest given the data, p(Θ|W). In practice, this is often analytically or computationally intractable (e.g. exact Markov chain Monte Carlo approaches may not scale well to large datasets), so instead one can fit a model with an approximate distribution Q(Θ|W)=∏_j^J q_j(θ_j|W), by minimizing the Kullback–Leibler (KL) divergence (Kullback and Leibler, 1951) D_KL(Q(Θ|X)||p(Θ|W))= ∫ q(Θ|W) log (q(Θ|W)/p(Θ|W)) dΘ. In addition, the variational Bayes approximation generates a lower bound 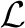(W) of the marginal posterior probability of the data p(W). Further details of variational Bayes methods are provided in the Supplementary Material.

2 METHODS

2.1 GWAS regression models

We compare the relative performance of vBsr with both the popular lasso penalized regression method (Tibshirani, 1996) and standard single variant test statistics for a range of simulated datasets and experimental data. We chose these methods for comparison to demonstrate that vBsr can control Type I error as well as single variant analysis, but under certain circumstances has greater power than either a single variant analysis or the lasso. The lasso was chosen for comparison since previous work indicates it has greater power than single variant tests in GWAS (Wu et al., 2009), but in general suffers from poor Type I error control (Li et al., 2011).

For all the multiple locus methods, we consider the following multiple regression model (with the single variant methods only considering each j-th variant separately)

where y_i is the phenotype, x_ij is the genotype at the j-th locus for m loci, z_ik is the k-th unpenalized covariate for p covariates and e_i is the residual error term, which is assumed to be normally distributed with error variance parameter σ²_e, for the i-th individual. All columns of the genotype matrix X are standardized to have mean zero and variance one. The first column of the covariate matrix Z is always the intercept. For single-marker analyis, we define χ²_sma as the standard score statistic for single variant association for this regression model.

2.2 vBsr model

2.2.1 Fitting the vBsr model

For the vBsr model, we assign an improper ‘spike’ prior to each penalized regression coefficient β_j ∼ (1−p_β)I[β=0]+p_βI[β≠0]. To estimate the posterior distribution of penalized regression coefficients, we use a variational Bayes approximation and minimize the Kullback–Leibler divergence between the factorized approximate posterior distribution ∏_j^m q_βj(β_j|α, σ²_e, p_β, y, X, Z) and the full posterior distribution, p(β₁,…,β_m|α, σ²_e, p_β, y, X, Z). For the vBsr model, the approximate posterior distribution for an arbitrary β_j parameter is (1−p_j)I[β_j=0]+p_j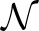(μ_j, σ²_j)I[β_j≠0], with p_j the approximate posterior probability of β_j not being zero, μ_j the approximate posterior mean of the non-zero effect and σ²_j the approximate posterior variance of the non-zero effect. We estimate the error variance parameter σ²_e and unpenalized covariate parameters α₁,…,α_p through maximization of the lower bound 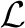(y|σ²_e, α, X, Z)≤p(y|σ²_e, α, X, Z). The full derivations of these updates are provided in the Supplementary Material.

2.2.2 vBsr Z-statistic, z_vb

After fitting the model, we define the vBsr Z-statistic z_vb, for the j-th variant, as z_j=μ_j/σ_j. We show in the Supplementary Material that when p_β→0, this statistic is equivalent to the standard 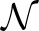(0, 1) distributed score statistic (under the null hypothesis) for a single variant test of association. Alternatively, we want to use this test statistic when there are multiple variants identified as being associated with phenotype when p_β > 0 and z_vb is no longer equivalent to the single variant score statistic. For notational and computational convenience, we define the tuning parameter ℓ₀ = 2log(p_β) − 2log(1−p_β)+log(2π). Given most genetic variants are independent of phenotype, we choose ℓ₀ to ensure the empirical distribution of the z_vb statistic for the vast majority of genetic variants matches the 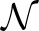(0, 1) distribution as diagnosed based on an estimated Kullback–Leibler divergence, log(KL). See the Supplementary Material for a detailed description of this log(KL) diagnostic statistic.

2.2.3 Bayesian model averaging

If the genotypes are correlated, we run the algorithm multiple times with different initial conditions specified by random permutations of the ordering of the updates of the β_j parameters. This allows us to identify multiple local maxima of the lower bound 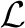(y|σ²_e, α, X, Z) where each maximum can correspond to a different sparse subset of genotypes identified as being in the model (i.e. genotypes with posterior probabilities p_j >> 0). We then reduce the model uncertainty associated with identifying many different sparse models by producing a Bayesian model averaged Z-statistic 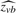, for the j-th genotype, 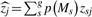, with 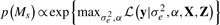, for g unique local maxima. Further details are presented in the Supplementary Material.

2.3 Lasso regression

The lasso solution to the regression equation is

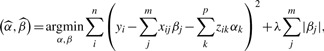for some choice of penalty parameter λ. We use the path solution to the lasso that is solved with the R package glmnet (Friedman et al., 2010), where the log-likelihood is defined as: ℓ(β)=−1/2(n(log(2πσ²)+1)+2), with n being the observed sample size, and σ²=∑_i(y_i−∑_jx_ijβ_j−∑_k^p z_ikα_k)²/n and the corresponding Akaike's information criterion (AIC) and Bayesian information criterion (BIC) are lasso_aic=−2ℓ(β)+2|β|, lasso_bic=−2ℓ(β)+log(n)|β|, with justification of the choice of degrees of freedom |β| as described in Zou et al. (2007). The default settings are used for glmnet, with a path length of 1000. In addition, 10-fold cross-validation is also performed using the glmnet package and the penalty parameter with the minimum mean-squared error is chosen for analysis of the entire dataset.

2.4 Simulations

We simulated haploid genotype data for 10 000 independent genotypes sampled from a Bernoulli distribution with frequency parameter varying between 0.1 and 0.5. Since all simulated genetic architectures were additive, the use of haploid genotypes as opposed to diploid genotypes did not appear to have an effect on any of the results we observed. Sample sizes of 500, 1000 and 2000 were simulated. We first performed null simulations to demonstrate Type I error control by testing null phenotypes (with error variance parameters chosen as in the non-null simulations). Next, we performed non-null simulations to test both Type I error control and power, by simulating genetic architectures with 50 independent loci randomly sampled from the 10 000 independent genotypes. The genetic effects for this model were sampled from a standard normal distribution and the heritability was fixed at 0.5 or 0.9. For each sample size and overall heritability, 1000 replicate phenotype datasets were generated with the same genotypes, while re-sampling the location and magnitude of the genotypic effects. For each phenotype, replicate vBsr was only run once since the lower bound tends to only have one maximum when the genotypes are independent. Finally, we analyzed simulated phenotype data with genetic architectures generated using correlated genotypes. For the correlated genotype data, we used the first 10 000 genotypes on Chromosome 1 within the SHARe dataset, where we randomly split the data into disjoint sets of 500, 1000 and 2000 individuals. For these correlated genotypes, we found that the lower bound had more local maxima, so we ran 60 random restarts of the vBsr algorithm for each replicate analysis. For the simulations with correlated genotypes, the lasso was excluded because of its poor FWER control (as shown in Table 1).

Table 1.

The family-wise error rates and expected number of false positives per replicate analysis, FWER (E[FP]), for a simulation of 10⁴ independent genotypes, with 50 causal variants and 1000 replicates

Simulation	zvba	zvbb	χ2sma	lassoaic	lassobic	lassocv
h2=0.0,n=500	0.063 (0.068)	0.062 (0.066)	0.057 (0.059)	1.00 (>500)	1.00 (>500)	0.518 (10.38)
h2=0.0,n=1000	0.048 (0.050)	0.053 (0.055)	0.044 (0.046)	1.00 (>1000)	0.033 (2.977)	0.498 (8.97)
h2=0.0,n=2000	0.050 (0.051)	0.056 (0.057)	0.049 (0.050)	1.00 (>2000)	0.023 (0.027)	0.506 (7.98)
h2=0.5,n=500	0.046 (0.047)	0.042 (0.042)	0.055 (0.056)	1.00 (>500)	0.993 (>500)	1.00 (99.71)
h2=0.5,n=1000	0.048 (0.048)	0.040 (0.040)	0.048 (0.049)	1.00 (>1000)	0.925 (4.910)	1.00 (155.8)
h2=0.5,n=2000	0.040 (0.040)	0.052 (0.053)	0.051 (0.052)	1.00 (>2000)	0.982 (7.297)	1.00 (188.5)
h2=0.9,n=500	0.051 (0.054)	0.048 (0.050)	0.057 (0.059)	1.00 (>500)	1.00 (162.4)	1.00 (221.7)
h2=0.9,n=1000	0.045 (0.045)	0.051 (0.052)	0.051 (0.051)	1.00 (>1000)	1.00 (18.90)	1.00 (248.1)
h2=0.9,n=2000	0.054 (0.055)	0.051 (0.051)	0.063 (0.063)	1.00 (>2000)	1.00 (15.41)	1.00 (248.8)

The phenotypes in the h²=0.0 simulations were generated under the null model. The z_vb and χ²_sma statistics are controlled to have a FWER of 0.05, whereas the choice of size of the lasso solution is determined by either AIC, BIC or 10-fold cross-validation. The FWER is computed over the null markers.

^a Results for ℓ₀ chosen based on the minimum value of the KL diagnostic statistic along the path.

^b Results for ℓ₀ chosen based on the expected value of the KL diagnostic statistic (as determined by Monte Carlo simulations) along the path.

2.5 Analysis of SHARe data

The WHI SHARe genotype data were collected using the Human SNP Array 6.0 (Affymetrix, Santa Clara, CA, http://www.affymetrix.com) genotype platform, for 8515 self-identified African-American women who consented to have their DNA analyzed. Individuals were filtered based on failed genotyping, call rate <95% or sex/ethnicity discrepancy. Among related individuals, only the subject with the highest call rate was retained. Body height was measured at baseline in centimeters, using wall mounted stadiometers. Height measurements below the 1-st percentile and above the 99-th percentile were truncated as per request of the Fred Hutchinson Cancer Research Center Institutional Review Board, to maintain anonymity. Further details of the quality control of the genotype data are presented in Carty et al. (2011), and study protocols and additional details of the WHI cohort are presented elsewhere (The Women's Health Initiative Study Group, 1998). Some details that are different from the previous analyses of these data include imputing the sporadic missing data to the empirical mean of the observed genotypes, and filtering to 5% minor allele frequency. In addition, as opposed to the analysis published in Carty et al. (2011), the 47 individuals without height data from the first visit were excluded. These differences were-implemented to make our analysis more conservative than the analysis of Carty et al. (2011) to strengthen our confidence in the penalized regression methodologies. For the analysis of the SHARe height data, we performed a marginal pre-screening (using the first four principal components and age as covariates) with a P-value cutoff of 10⁻³. This left 1579 markers (out of an original 772 202 which passed the quality control filters and 5% minor allele frequency filter). We performed a marginal pre-screening to decrease the analysis time for the vBsr method to hours instead of days on a workstation with a twelve core Intel Xeon processor. The vBsr algorithm was run with 1000 restarts, to ensure a high-quality model could be identified across the lower bound surface.

3 RESULTS

3.1 Simulation results

Simulation results for our method in comparison to standard single-marker analysis as well as three different methods for the choice of the penalty parameter (λ) for model selection with the lasso based on AIC, BIC and 10-fold cross-validation are shown in Table 1. The simulation results depicted in this table were for genetic markers that were simulated independently of one another. We see for the null simulations in Table 1 that the Type I error rates can be explicitly controlled for both single-marker analysis and the z_vb statistic using two conservative strategies for choosing the penalty parameter (either based on the minimum KL diagnostic statistic, or the expected KL diagnostic statistic, see Section 2 for details), while only the choice of model size through BIC for the lasso maintains the Type I error even marginally. As expected, the choice of penalty parameter for the lasso based on AIC tends to always choose a large over-fit model in these null simulations, whereas cross-validation does a decent job of controlling the model size, but does not explicitly enforce extreme sparsity, all of which are consistent with previously observed results on model selection criterion for AIC, BIC and cross-validation (Chen and Chen, 2008). Importantly, cross-validation is intended to minimize the prediction error of the lasso model rather than to select genome-wide significant predictors, thus it is not surprising that cross-validation selects a larger model.

For the non-null simulations depicted in Table 1, we still see that the FWER can be controlled for both the z_vb and χ²_sma statistics, but the criteria for choosing the size of the lasso solution perform even worse than in the null simulations. Of all the methods for choosing the size of the lasso solution, BIC does the best, but it still contains an average of 4.91 false positives per replicate analysis (for h²=0.5, n=1000). These results suggest that the lasso is sensitive to weak sampling correlations between true and false positives when n<<m.

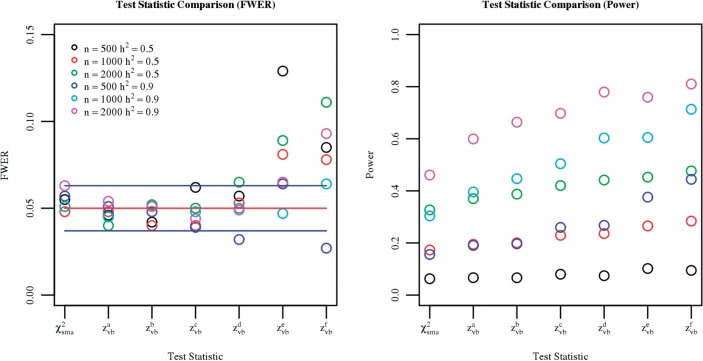
We considered six different strategies for choosing the model size based on the penalty parameter ℓ₀ in the penalized regression model, with the most conservative strategies being either choosing the ℓ₀ with the smallest KL diagnostic statistic or the ℓ₀ with the largest KL statistic less than its expected value of log(KL) based on empirical simulations (z_vb^a and z_vb^b, respectively). The four more liberal strategies were to consider the largest KL statistics less than the minimum plus one (z_vb^c) or two (z_vb^e) standard errors of log(KL), and the same for the expected value of log(KL) (z_vb^d and z_vb^f, respectively). The left panel of Figure 1 depicts the FWER starting with single-marker analysis on the far left, then comparing these six different strategies for choosing model size starting with the most conservative z_vb^a and ending with the most liberal z_vb^f, for the six different non-null simulations. The right panel of Figure 1 depicts power for this same set of test statistics. The more conservative strategies show excellent control of FWER, though have a more modest increase in power over single-marker analysis. Alternatively, the more liberal strategies show a slight deviation from the exact control of FWER but have greater power.

Fig. 1.

The family-wise error rate (FWER) and power for six different strategies for choosing the model size associated with the z_vb statistic, and for single-marker analysis (χ²_sma) for simulations of 10⁴ independent genotypes with differing sample sizes and heritabilities. For the FWER, the red horizontal line shows a FWER of 0.05 and the blue horizontal lines show the 95% CIs for controlling FWER to 0.05. The six different strategies are: choice based on minimum of KL diagnostic statistic (z_vb^a), expectation of the diagnostic statistic (z_vb^b), minimum plus one standard error (z_vb^c), expectation plus one standard error (z_vb^d), minimum plus two standard errors (z_vb^e) and expectation plus two standard errors (z_vb^f)

Even when the model size is constrained to fix the ratio of the number of true positives to false positives, the z_vb statistic can have greater power than the lasso, as shown in the precision-recall curves in Supplementary Figure S1 with the liberal choice of log(KL) based on the expected value plus two standard errors, z_vb^f. Precision (true-discovery rate) is defined as tp/tp+fp and recall (power) is defined as tp/tp+fn, for the total number of true positives (tp), false positives (fp) and false negatives (fn) at a given cutoff of the test statistics for z_vb or χ²_sma, or a given penalty parameter λ for the lasso across 100 replicate simulations. This appears to be especially true for smaller sample sizes with more signal (i.e. greater total heritability). Supplementary Figure S1 also demonstrates that both vBsr and the lasso can outperform single-marker analysis in terms of power and false-discovery rates. In addition, we explored similar simulations with non-independent markers, with results described in the Supplementary Results and shown in Supplementary Figures S2 and S3, where vBsr has superior control of FWER and superior power compared with single-marker analysis for high heritability simulations. We also inspected the Quantile–Quantile plots for the different test statistic strategies, also discussed in the Supplementary Results and shown in Supplementary Figure S4.

3.2 SHARe analysis results

We investigate the relative performance of the z_vb statistic when compared with single-marker analysis and the lasso in terms of the percentage of genotypes that replicated (with a single-locus test) when considering an independent cohort(s). First, none of the model size selection procedures produced meaningful results above and beyond marginal screening to P_sma < 10⁻³ for the lasso (AIC chose a model with 1089 out of 1579 pre-screened features, BIC chose the null model and CV chose a model with 1049 out of 1579 pre-screened features), therefore we did not further investigate that approach. The percentage of loci identified at an estimated false-discovery rate of 10% (assuming 10⁶ features) that were replicated when considering an independent cohort [as described in Carty et al. (2011) for height] was 50% (5/10) with the vBsr approach, as opposed to 33.3 (3/9)% for the single-marker analysis approach. The estimated false-discovery rate was determined as in Benjamini and Hochberg (1995). Notably, for height there is sufficient signal such that the z_vb statistic identifies an additional two loci beyond the marginal test that were replicated in Carty et al. (2011) in an independent cohort. A complete comparison of the results of Carty et al. (2011) and the z_vb statistic is shown in Table 2.

Table 2.

Summary of vBsr results at 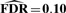for body height

SNP	Gene	Chr	Positiona	Pvb	Psma	Psmab	Prep
rs2121450	Intergenic	2	23094986	6.22×10−8	1.16×10−5	7.08×10−6	3.57×10−4
rs2011603	LCORL	4	17634582	1.50×10−9	2.99×10−9	6.52×10−9	2.71×10−10
rs10027658	Intergenic	4	85011302	4.30×10−7	2.14×10−6	5.43×10−6	6.72×10−4
rs1359312	COL22A1	8	140076725	7.13×10−7	2.87×10−6	3.92×10−6	1.45×10−1
rs606452	SERPINH1	11	74953826	4.43×10−7	3.15×10−6	3.47×10−6	1.56×10−9
rs7968682	HMGA2	12	64658147	5.66×10−7	1.01×10−5	5.49×10−6	4.22×10−10
rs565042	NGFR	17	44932838	8.72×10−8	1.30×10−7	1.09×10−7	5.22×10−5
rs11867328	PSMD12	17	62776578	3.26×10−8	2.36×10−8	1.76×10−8	2.31×10−6
rs7239949c	DYM	18	44872826	9.68×10−8	1.65×10−7	1.62×10−7	8.14×10−7
rs12393627	ARSE	X	2895723	1.21×10−8	1.05×10−6	1.45×10−6	4.96×10−12

This table compares the P-values computed using the z_vb statistic (P_vb) and single-marker analysis (P_sma), for body height using the SHARe GWAS data as described in Section 2, with the single-marker analysis P-values (P_sma^b) and replication P-values (P_rep) reported by Carty et al. (2011). Bold rows represent loci that were replicated based on Carty et al. (2011).

^a The chromosome positions are for build 36 of the human genome.

^b Analysis of (Carty et al., 2011) excluded missing genotypes and contains a slightly different subset of the WHI SHARe samples, therefore the P-values are not exactly the same between analyses.

^c While this specific locus did not replicate, it was in linkage disequilibrium with a locus (rs1787200) that did replicate with P_rep=7.37×10⁻¹⁰. The R² within the SHARe samples analyzed in this article between these two loci is 0.28.

Specifically, both the vBsr approach and the single-marker analysis approach identify the SNPs rs2011603 on Chromosome 4 (LCORL), rs13292627 on Chromosome X (ARSE) and rs7239949 on Chromosome 18 (DYM) that all replicated in the meta-analysis of Carty et al. (2011). (Locus rs7239949 did not replicate itself, but was in strong linkage disequilibrium with locus rs1787200 that did replicate.) In addition, the vBsr approach identified two additional associations with rs606452 on Chromosome 11 (SERPINH1) and rs7968682 on Chromosome 12 (HMGA2) that also replicated in Carty et al. (2011), that were not chosen by SMA with an estimated 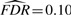. Both single-marker analysis and the vBsr approach identified rs11867328 on Chromosome 17 as being genome-wide significant, though this result was not replicated in the meta-analysis of Carty et al. (2011). Similarly, the association at rs565042 in the nerve growth factor receptor (NGFR) gene did not replicate.

To illustrate the vBsr path solution, we show the estimates of the expected regression coefficients in Figure 2 along the path of ℓ₀. Around ℓ₀=−13 many genetic markers start to enter the model, where likely most of these are false positives. Figure 2 also shows where each choice of model size lies on the ℓ₀ path. The most conservative strategy of z_vb^a identifies very few features, whereas the more liberal strategy of z_vb^d incorporates a large number of features, of which many are likely false positives. In this case z_vb^b lies on the cusp before too many false positives enter the model and degrade the quality of the distributional assumption of the test statistic.

Fig. 2.

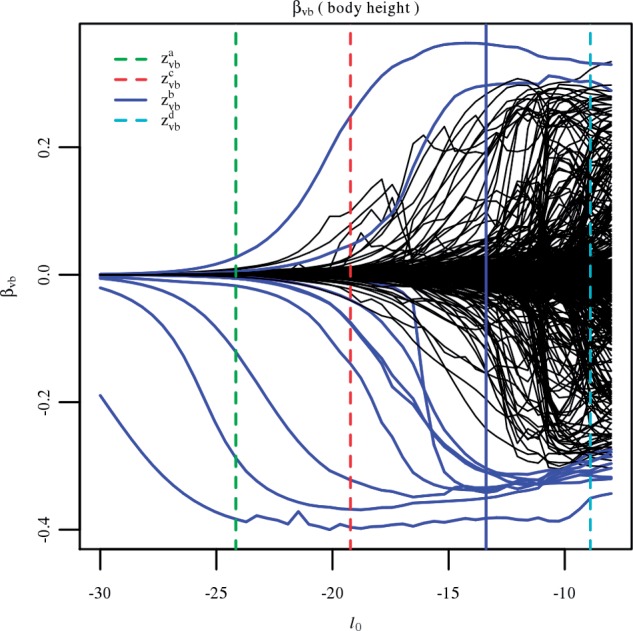
The estimated expected regression coefficients as a function of the penalty parameter ℓ₀ for the analysis of height. As the penalty parameter increases in magnitude, the size of the model increases until it becomes over-fit. The position in the path for the four different strategies is shown with the vertical bars, with the chosen strategy (z_vb^b) in blue. The features that were significant for z_vb^b at 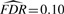are also shown in blue along the entire path

We also show the Q–Q plots for both z_vb and our single-marker analysis in Supplementary Figure S5. For this analysis, we choose ℓ₀=−13.39 specifically such that the Q–Q plot appeared null in the 10⁻³ < P_vb < 10⁻⁴ region, (this corresponded to the strategy associated with the z_vb^b statistic) where P_vb is the P-value associated with the z_vb^b statistic. The P_vb statistic only becomes inflated when P_vb < 10⁻⁴, indicating there exists a value of the model complexity parameter ℓ₀ such that the distributional assumption of the z_vb test statistic is valid for the majority of markers except for the tail cases. Our simulations supported this observation, as shown in the bottom left panel of Supplementary Figure S4, where the distribution of the z_vb^b statistic for the null variants almost perfectly matches its expected distribution. Notably, the Q–Q plots for the z_vb^b statistic look closer to the null assumption than the corresponding SMA Q–Q plots. We found in other simulations (not shown) that the marginal pre-screening had very little effect on the FWER control of the vBsr approach and resulted in a mild loss in power when the phenotype was very heritable or the sample sizes were very large. Although it would be possible to run the entire dataset with the vBsr approach, the identified solution mostly contained variants that were nominally significant (i.e. P_sma < 10⁻⁵), indicating it would be unlikely that any additional associations would arise as genome-wide significant.

4 DISCUSSION

The z_vb test statistic provides three major practical advantages over either single-marker analysis or alternative multiple locus penalized regression approaches in the GWAS setting. First, as demonstrated through both simulations (as shown in Fig. 1; Supplementary Figs S1 and S3), and the analysis of the WHI SHARe GWAS of height (shown in Table 2), this statistic has greater power to detect additional replicable loci beyond those that are identifiable by either a standard single-marker analysis or the lasso, given the phenotype is highly heritable or the sample size is sufficiently large. In addition, while the increase in power was modest over the single-marker analyses in terms of replicated associations, we also see that the two associations vBsr identified on Chromosome 17 had statistically significant correlations with the two replicated hits on Chromosome 17 (the R² between rs11658329, the replicated association and rs11867328, the vBsr association was 0.044, P < 10⁻¹⁶, and the R² between rs1549519, the replicated association and rs565042, the vBsr association, was 0.066, P < 10⁻¹⁶). Although the physical distance between these associations is large, because of the weak statistical dependence vBsr still identifies a signal.

Second, the main innovation of the z_vb statistic is that it is possible to tune vBsr such that it is approximately 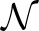(0, 1) distributed under the null hypothesis. This means that, unlike other penalized regression methodologies, it is possible to directly control either the FWER or FDR. Other multiple locus penalized regression procedures often rely on cross-validation, or information criterion such as AIC or BIC to choose the appropriate model size and magnitude of their penalty (Chen and Chen, 2008), which will not necessarily control the Type I error to an arbitrary level (as shown in Table 1 for the lasso). We demonstrated the Type I error control capability of our method through a wide range of simulations, of either the null model for independent genotypes, the null features in a non-null model with independent genotypes (as in Table 1), or even in a non-null model with linkage disequilibrium among genotypes (as in Supplementary Fig. S2).

Third, while a few authors have proposed a choice of penalty parameter within penalized regression methods to asymptotically bound the type I error (Hoggart et al., 2008), our approach is unique, in that we demonstrate a data-driven choice of the penalty parameter ℓ₀. The penalty parameter ℓ₀ (or alternatively p_β) is an appropriate tuning parameter because it directly determines the evidence necessary for a given genetic variant to be included in the model by controlling the scale of the posterior probability of inclusion, p_j, for all genetic variants. The posterior probability of inclusion for a given variant is an essential aspect of the vBsr model since it determines the effect of a given genetic variant on the overall model through the expectation E[β_j]=p_j μ_j, where p_j→0 implies the variant is not in the model and p_j→1 implies the variant is in the model and effectively unpenalized. In general, we always choose ℓ₀ such that the empirical distribution of the z_vb statistic matches very closely to the expected 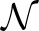(0, 1) null distribution for the vast majority of genetic features (i.e. up to the 99-th percentile for simulations, or between the 99.9-th and 99.99-th percentiles in the dataanalysis), within the study (as shown in Supplementary Figs S4 and S5). Therefore not only can we control the Type I error to an arbitrary level, but also, we do not necessarily rely on an asymptotic argument for the choice of ℓ₀ to ensure the validity of our choice of penalty parameter.

Finally, the vBsr methodology incorporates additional general features beyond the choice of penalty parameters which are unique and distinguish it from alternative penalized regression methodologies (Fan and Li, 2001; Hoggart et al., 2008; Li et al., 2011; Wu et al., 2009; Zhang, 2010) including other ‘spike-and-slab’ approaches (Yen, 2011). This includes the use of Bayesian model averaging to regularize over uncertainty in the space of identified models. In addition, there is theoretical evidence that ‘spike-and-slab’ penalized regression approaches do not suffer from the possible model selection inconsistency of the lasso, given highly correlated predictors (Yen, 2011; Zhao and Yu, 2006). We see the practical consequences of this fact for m>>n datasets where the Type I error rates for the lasso seem to be driven by random correlations between causal and null features (as shown in Table 1), even among independently sampled genetic features. Finally, by defining a test-statistic which is approximated by a 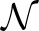(0, 1) distribution for every genotype in the dataset, it is possible to diagnose confounding population structure as is common with single-marker analysis, but challenging with other penalized regression methods.

5 CONCLUSION

Our vBsr methodology is a novel approach for identifying additional replicable loci within genome-wide association studies that directly addresses the limitations of other penalized multiple regression methodologies. Specifically, the data-driven choice of penalty to ensure the validity of the distribution of the test statistic and the use of a penalty with attractive theoretical model selection properties make this a robust and practical tool for the GWAS practitioner interested in identifying additional replicable associations for complex phenotypes with rich genetic architectures.