Noise spatial nonuniformity and the impact of statistical image reconstruction in CT myocardial perfusion imaging

Abstract

Purpose: To achieve high temporal resolution in CT myocardial perfusion imaging (MPI), images are often reconstructed using filtered backprojection (FBP) algorithms from data acquired within a short-scan angular range. However, the variation in the central angle from one time frame to the next in gated short scans has been shown to create detrimental partial scan artifacts when performing quantitative MPI measurements. This study has two main purposes. (1) To demonstrate the existence of a distinct detrimental effect in short-scan FBP, i.e., the introduction of a nonuniform spatial image noise distribution; this nonuniformity can lead to unexpectedly high image noise and streaking artifacts, which may affect CT MPI quantification. (2) To demonstrate that statistical image reconstruction (SIR) algorithms can be a potential solution to address the nonuniform spatial noise distribution problem and can also lead to radiation dose reduction in the context of CT MPI.

Methods: Projection datasets from a numerically simulated perfusion phantom and an in vivo animal myocardial perfusion CT scan were used in this study. In the numerical phantom, multiple realizations of Poisson noise were added to projection data at each time frame to investigate the spatial distribution of noise. Images from all datasets were reconstructed using both FBP and SIR reconstruction algorithms. To quantify the spatial distribution of noise, the mean and standard deviation were measured in several regions of interest (ROIs) and analyzed across time frames. In the in vivo study, two low-dose scans at tube currents of 25 and 50 mA were reconstructed using FBP and SIR. Quantitative perfusion metrics, namely, the normalized upslope (NUS), myocardial blood volume (MBV), and first moment transit time (FMT), were measured for two ROIs and compared to reference values obtained from a high-dose scan performed at 500 mA.

Results: Images reconstructed using FBP showed a highly nonuniform spatial distribution of noise. This spatial nonuniformity led to large fluctuations in the temporal direction. In the numerical phantom study, the level of noise was shown to vary by as much as 87% within a given image, and as much as 110% between different time frames for a ROI far from isocenter. The spatially nonuniform noise pattern was shown to correlate with the source trajectory and the object structure. In contrast, images reconstructed using SIR showed a highly uniform spatial distribution of noise, leading to smaller unexpected noise fluctuations in the temporal direction when a short scan angular range was used. In the numerical phantom study, the noise varied by less than 37% within a given image, and by less than 20% between different time frames. Also, the noise standard deviation in SIR images was on average half of that of FBP images. In the in vivo studies, the deviation observed between quantitative perfusion metrics measured from low-dose scans and high-dose scans was mitigated when SIR was used instead of FBP to reconstruct images.

Conclusions: (1) Images reconstructed using FBP suffered from nonuniform spatial noise levels. This nonuniformity is another manifestation of the detrimental effects caused by short-scan reconstruction in CT MPI. (2) Images reconstructed using SIR had a much lower and more uniform noise level and thus can be used as a potential solution to address the FBP nonuniformity. (3) Given the improvement in the accuracy of the perfusion metrics when using SIR, it may be desirable to use a statistical reconstruction framework to perform low-dose dynamic CT MPI.

INTRODUCTION

Cardiovascular disease is the leading cause of death in the world. One of its manifestations in the heart, coronary artery disease (CAD), often results in acute myocardial infarction (MI) or angina pectoris. In past decades, the morbidity and mortality from CAD has been reduced in part due to the development of revascularization therapy.^{1, 2} However, if the ischemic region extends beyond certain limits, or if a coronary stenosis is not hemodynamically significant, percutaneous coronary intervention (PCI) offers minimal improvements in outcomes. Myocardial perfusion imaging (MPI) often enables a noninvasive assessment³ of CAD prior to PCI, which is desirable for patient selection.⁴ The simultaneously high temporal and spatial resolution of multi-detector computed tomography (MDCT) makes this modality a prime candidate for MPI.^{5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20, 21, 22, 23} The method can also offer CT angiography (CTA) simultaneously with MPI,^{16, 24} enabling an assessment of both coronary anatomy and function from a single scan. This is another compelling advantage of CT MPI in the clinical environment. However, several existing issues impede the application of CT MPI in practice. Technical issues remain to be overcome in CT MPI in order to achieve quantitative perfusion measurements. Furthermore, radiation dose is an important concern due to repeated CT scans over the same anatomical region.

In CT MPI, many time frames are acquired while an iodinated contrast agent is administered through intravenous injection. To mitigate cardiac motion artifacts that may obscure the definition of the myocardium, cardiac CT images are often reconstructed from a selected set of projection view angles to comprise a so-called short-scan angular range, viz., 180° plus the fan-beam angle. The reconstructed image series can then be analyzed to yield quantitative measurements of myocardial perfusion such as the myocardial blood flow (MBF), myocardial blood volume (MBV), and mean transit time (MTT).^{25, 26} However, the selected projection data must be acquired within the same relatively static cardiac phase, which is often selected at the end of diastole.^{27, 28, 29} Due to the need for a high temporal resolution, rapid sequential scanning is necessary, and empirically, the start angle of the short-scan range is generally not constant between time frames. Indeed, the nonsynchronicity between the gantry rotation and the cardiac contraction causes a shift in the short-scan central angle over the duration of the entire MPI data acquisition. This variation has been shown to lead to partial scan artifacts (PSA), which significantly compromise the accuracy of quantitative MPI.^{30, 31, 32, 33} Recently, variations in beam hardening and scatter distribution have been suggested as potential causes for PSA and corresponding correction methods have been proposed.^{30, 31, 32, 33}

In addition to the PSA effects, which often compromise quantitative capability in CT MPI, radiation dose is another serious concern. Admittedly, the ionizing radiation dose imparted to patients during a dynamic perfusion scan can be high because of the long scan time required to properly sample the contrast enhancement curve.^{34, 35} Alternative acquisition schemes have recently been proposed to reduce radiation doses in CT MPI.^{36, 37, 38, 39} However, these methods often invoke the use of projection view angle undersampling and thus require hardware modifications of the scanner. A more typical strategy consists of minimizing the dose by reducing the tube current during the scan. However, this leads to fewer photons reaching the detector and, consequently, to a lower signal-to-noise ratio (SNR). Images reconstructed using filtered backprojection (FBP) from low mAs projection datasets have high noise levels. A possible method to mitigate the noise is to use a statistical image reconstruction (SIR) (Refs. ^{40, 41, 42}) method. This strategy does not require a modification of the scanner hardware. It has a great potential for clinical use despite the fact that the image reconstruction time for a single image volume remains long.

In this paper, in addition to the known partial scan artifacts, we demonstrate a new challenge for quantitative CT MPI measurements: spatial noise nonuniformity. This effect may result in unexpectedly high image noise regions and streaking artifacts being present in some time frames, particularly in low-tube current studies. Specifically, in images reconstructed using FBP, the noise spatial distribution depends on the source trajectory from frame-to-frame and on the structure of the object being imaged. When multiple realizations of noise are generated for a given time frame, and the resulting values in each pixel are compared across noise realizations, a strong gradient in the noise standard deviation can be observed across the entire image. Moreover, this spatial distribution of noise tends to fluctuate from frame-to-frame depending on the source trajectory relative to the object being imaged. Consequently, a region which had a low noise for a certain rotation range can have a much greater noise level once a shift has occurred. This effect can have serious consequences in CT MPI measurements. A scan protocol designed to minimize the ionizing radiation received by the patient should aim at maintaining a high enough SNR to enable quantitative evaluation of the MBF. However, due to spatial variations in the noise level, a tube current deemed adequate for a given short-scan central angle can result in an inadequate noise level, as the source trajectory varies from frame-to-frame. The accuracy of perfusion measurements could therefore be reduced. Furthermore, when the tube current is reduced to very low levels, noise streaks are often observed in images. While the presence of these streaks depends mostly on high attenuation structures in the object, their orientation and severity depends also on the scan central angle. These effects could be particularly significant if one attempts to obtain a quantitative perfusion map.

We demonstrate here that the spatial noise nonuniformity can be significantly mitigated provided that a SIR scheme is used.⁴³ In the SIR framework, the expected noise present in the projection data is integrated into the image reconstruction process. This method mitigates the structured gradient observed in the noise distribution of FBP images, as well as variations in noise level between time frames. Specifically, projection data are weighted by the reciprocal of their noise variance to penalize their contributions in the final reconstructed image. As a result, the structured noise distribution of images reconstructed with FBP is mitigated when using SIR. Furthermore, when using the FBP algorithm, a distance weighting is needed in the backprojection operation. In contrast, no such distance-dependent weighting factor is required in the SIR framework. The absence of this factor results in a noise distribution without a strong view angle dependence at a given time frame. It thus reduces the potential impact of shifts in source trajectory between different time frames. As a result SIR provides a potential cure for the noise spatial nonuniformity in CT MPI observed when the conventional FBP reconstruction is used.

The layout of the paper is as follows. In Sec. 2, we briefly review the FBP algorithm and discuss how the short-scan FBP image reconstruction leads to a nonuniformity in the spatial noise distribution. In Sec. 3, the SIR algorithm that is suggested to alleviate the problem is presented. The projection datasets used in this study are presented in Sec. 4. The results are given in Sec. 5 and the discussion and conclusions are in Sec. 6.

FILTERED BACKPROJECTION

The short-scan FBP formula used to reconstruct image f(x, y) from fan-beam projection dataset g(β, γ) is the following:^{44, 45}

$$\begin{array}{ccc}\hfill f(x,y)& =& \frac{-1}{2{\pi }^2}{\int }_{{\beta }_0}^{{\beta }_0+\pi +{\gamma }_m}d\beta \frac{R}{L{(x,y,\beta )}^2}{\int }_{-{\gamma }_m/2}^{{\gamma }_m/2}d\gamma w(\beta ,\gamma )\hfill \\ & & \times \cos \left(\gamma \right)H_{\mathrm{ramp}}{\left[\sin (\gamma -{\gamma }_0)\right]}_g(\beta ,\gamma ),\hfill \end{array}$$ (1)

where L(x, y, β) the distance between the image point (x, y) and x-ray focal spot position (R cos β, R sin β) and is calculated as follows:

$$\begin{array}{c}\hfill L(x,y,\beta )=\sqrt{{(x-R\cos \beta )}^2+{(y-R\sin \beta )}^2}.\end{array}$$

The initial angle γ₀ is used to denote the detector element position through the following equation:

$$\begin{array}{c}\hfill \cos {\gamma }_0=\frac{R-x\cos \beta -y\sin \beta }{L(x,y,\beta )}.\end{array}$$

R is the x-ray source to isocenter distance, β₀ is the initial angular gantry position, γ_m is the full fan angle, and w(β, γ) is a weight necessary to account for redundancy from doubly measured projections.⁴⁶H_ramp is the ramp filter kernel.

Due to the use of the distance weight L(x, y, β), it is well known that the noise distribution in FBP image reconstruction is not uniform.^{47, 48, 49, 50, 51} Indeed, the filtered projection data are multiplied by a weight inversely proportional to the square of the distance between the source and the image point. If a projection datum is contaminated by a high level of noise, then the image voxels along the corresponding ray will also suffer from a high noise level or even streaks in extreme cases. However, not all the voxels along the ray will be subject to the same increase. The ones closest to the source will suffer more due to the distance term, which increases the relative weight given to its noisy datum. For the full-scan angular range, this distance weighting factor will result in a higher noise level at the periphery of the image, but a lower noise level near the center. For a short-scan range, the view angle distribution is not symmetric. We thus expect that the voxels closest to the source will generally display a higher noise level.

In the context of CT MPI, the left ventricle (LV) and the right ventricle (RV) are transiently filled with blood containing a high concentration of iodinated contrast agent. This high x-ray attenuation medium is expected to result in a higher noise level in the associated projections. Based on the previous discussion, the noise level is also expected to increase in a particular myocardial region when the short-scan range results in a reduced average distance between that region and the source.

STATISTICAL IMAGE RECONSTRUCTION

In contrast with the FBP algorithm, the SIR framework is based on maximum a posteriori estimation. In this framework, the image is reconstructed by solving the following optimization problem:^{40, 41, 42}

$$\begin{array}{c}\hfill \widehat{\mathbf{f}}=\underset{\mathbf{f}}{\arg \max }P(\mathbf{f},\mathbf{g}),\end{array}$$ (2)

where P(f, g) is the joint probability of having an image f with a measured the projection dataset g. It can be shown that, for transmission tomography,^{40, 41, 42, 52} this probability can be approximately maximized by solving

$$\begin{array}{c}\hfill \widehat{\mathbf{f}}=\underset{\mathbf{f}}{\arg \min }[{(\mathbf{Af}-\mathbf{g})}^{\mathrm{T}}\mathbf{D}(\mathbf{Af}-\mathbf{g})+\lambda J\left(\mathbf{f}\right)],\end{array}$$ (3)

where A is a model of the forward projection operation, the matrix D = diag(d₁, d₂, …) is diagonal and its elements are that of vector d. d contains the reciprocal variance of the corresponding projection data, d_k = σ_gk⁻². The variance of a given measurement can be obtained from the corresponding projection data,

$$\begin{array}{c}\hfill {\sigma }_{g_k}^2\cong \frac{1}{I_k{e}^{-g_k}},\end{array}$$ (4)

where I_k is the incident fluence without an object present. In other words, the variance of a projection datum is equal to the inverse of the number of counts registered by the corresponding detector element. The function J(f) is a regularizing term. In the work presented here, the total variation⁵³ (TV) is used as a regularizer.⁵² To focus the investigation to the effect of the data consistency term, the regularization parameter λ is set to a low level. This measure also avoided the reconstruction of images with the overly smooth texture often associated with images obtained via TV minimization. An in-depth investigation of the behavior of the algorithm with respect to variations in λ is desirable but out of the scope of this paper. The nonlinear conjugate gradient method is used to solve the SIR minimization problem.⁵⁴

METHODS AND MATERIALS

Numerically simulated dataset

The first projection dataset used in this study was generated numerically. Contrast arrival and washout in the LV and then in the myocardium were simulated. Regions of healthy and infarcted cardiac muscles were simulated to have different contrast enhancement dynamics. The infarct zone had a slower enhancement with lower amplitude when compared to the healthy tissue. The parameters pertaining to the simulation are given in Table 1. A heart rate (HR) of 60 bpm would have resulted in perfect synchronicity with the gantry rotation. The short-scan range would have been constant between different time frames. The perturbation by 2 bpm generated a 20°-shift in the scan range between each time frame. This enabled the systematic evaluation of the effect of various gantry rotation ranges. The x-ray beam was simulated to be monochromatic in this study to avoid beam hardening as a confounding factor. Scatter distribution was not considered in this study either.

Table 1.

Numerical simulation parameters.

Parameter	Value
Scan time	50 s
Number of time frames	50
Gantry rotation period	0.5 s
Time sampling period	1 s
Number of view angles (short scan)	668
Fan angle	54.9°
Short-scan gantry angular range	234.9°
Heart rate (HR)	62 bpm
Photon fluence	106 photons/detector element

Poisson noise was added to each projection datum with an incident flux of 10⁶ photons per detector element. This value was selected to obtain an image noise level similar to that of a low-tube current CT scan. The flux was assumed to be constant across all detector elements, i.e., I_k = I₀ ∀ k ∈ [1, N_aN_c] where I₀ is the incident flux, N_a is the number of view angles, and N_c is the number of detector elements. The noise was simulated using a pseudorandom number generator, namely, the poissrnd command in the numerical software package MATLAB (MathWorks, Natick, MA).

All scans were reconstructed using FBP with a Shepp-Logan filter at a voxel dimension of (1 mm)². The same voxel size was used for SIR reconstructions.

In order to evaluate the noise standard deviation at various voxels in the image, a Monte Carlo simulation was conducted. Fifty noise realizations were generated for the projection dataset at each time frame. Each projection dataset was reconstructed using FBP and SIR. The standard deviation was estimated for each voxel, thus yielding a map of the noise level for each time frame. The standard deviation at voxel i was calculated using the following formula:

$$\begin{array}{c}\hfill {\sigma }_i=\sqrt{\frac{1}{N_{ins}-1}\sum _{n=1}^{Nins}{(f_{i,n}-{\overline{f}}_i)}^2},\end{array}$$ (5)

where

$$\begin{array}{c}\hfill {\overline{f}}_i=\frac{1}{N_{ins}}\sum _{n=1}^{Nins}{f}_{i,n}.\end{array}$$ (6)

The summations are over the various instances of the noise. N_ins is the number of noise realizations. N_ins = 50 in this study. These maps are used to compare the spatial uniformity of the noise for each algorithm.

In vivo porcine dataset

The other datasets used in this study were in vivo myocardial perfusion scans of a 59 kg male swine. The study was approved by the Institutional Animal Care and User Committee (IACUC) at the University of Wisconsin-Madison. The acquisition was done on a GE Discovery CT scanner (GE Healthcare, Waukesha, WI). The scan parameters are given in Table 2. For each acquisition, a total of 53 ml of iodixanol contrast agent with 320 mg of iodine/ml (Visipaque 320, GE Healthcare, Waukesha, WI) followed by 85 ml of saline solution was injected at a rate of 10 ml/s via an 8 Fr pigtail catheter positioned in the vena cava. The animal was under mechanical ventilation, which was suspended at the end of expiration during scanning. The scans were performed in cine mode and started before the beginning of the injection. The time delay was slightly different between various scans. In order to match the temporal range between the different scans, some of the initial and final time frames were not used in the perfusion analysis.

Table 2.

In vivo dataset parameters.

Parameter	Scan 1	Scan 2	Scan 3
Scan time	50 s	50 s	50 s
Gantry rotation period	0.4 s	0.4 s	0.4 s
Average time sampling period	0.86 s	0.89 s	1.00 s
Number of view angles (short scan)	642	642	642
Fan angle	54.9°	54.9°	54.9°
Short-scan gantry angular range	234.9°	234.9°	234.9°
Mean heart rate (HR)	69 bpm	67 bpm	60 bpm
Tube potential	120 kVp	120 kVp	120 kVp
Tube current	25 mA	50 mA	500 mA

As outlined in the discussion of SIR, the statistical weights from matrix D can be determined based on the counts recorded by the detector. In this case, counts data were obtained from the manufacturer of the scanner used for the study. To evaluate whether the effect varied with noise level, scans at three tube current settings were acquired: 25 mA, 50 mA, and 500 mA. A 30-min waiting period was observed between the different scans to allow for contrast agent clearance. Images reconstructed from the 500 mA scan had a high SNR and were used as a reference. All scans were reconstructed using FBP with a Shepp-Logan filter at voxel dimension of (1.25 mm)³. The same dimension was used for the SIR reconstructions. The slice thickness was set to 1.25 mm.

The noise standard deviation was measured within ROIs for the in vivo dataset. In that case, the formula used was the following:

$$\begin{array}{c}\hfill {\sigma }_{\mathrm{ROI}}=\sqrt{\frac{1}{N_{\mathrm{ROI}}-1}\sum _{i\in \mathrm{ROI}}{(f_i-{\overline{f}}_{\mathrm{ROI}})}^2},\end{array}$$ (7)

where the summation is over different voxels. N_ROI is the number of voxels in the ROI, ${\overline{f}}_{\mathrm{ROI}}$ is the mean voxel value in the ROI. Note that the measurements obtained using this definition might be influenced by the local noise correlation. This must be kept in mind when evaluating the results.

Reconstruction algorithms implementation

Both FBP and SIR were implemented using the C++ programming language using the Intel Integrated Performance Primitives libraries (Intel Corporation, Santa Clara, CA). The programs were executed on a workstation equipped with a Core 2 Quad CPU Q6700 at 2.66 GHz (Intel Corporation) and 8 GB of RAM. The calculations were performed using 32 bits floating point arithmetic. The implementation of the FBP algorithm was done in house. The manufacturer's implementation was not used to ensure full control on the reconstruction parameters.

The computation time of FBP was on average 30 s, while that of SIR was 8 min. 120 conjugate gradient iterations were applied to minimize the SIR objective function. Note that the execution was fully sequential. FBP, as well as the forward- and backward-projection operations used in SIR can also be implemented using general purpose graphical processing units (GPU) programming languages; these architectures enable speed up by more than 100-fold. Even using such an implementation, FBP remains more computationally efficient.

Quantitative perfusion metrics

In order to evaluate the effect of reconstruction algorithms on quantitative perfusion metrics, three quantities were measured from the time attenuation curves measured in various ROIs from the in vivo dataset. These metrics are the normalized upslope (NUS), the MBV, and the first moment transit time (FMT).

The NUS has been shown to correlate well with myocardial blood flow.²⁶ However, it is a relative metric. It is defined as the slope of the time attenuation curve (TAC) in a particular region (m_ROI) divided by the slope of the TAC in the left ventricle (m_LV). In this study, both slopes were measured for time points recorded between the arrival of the contrast agent in the LV and the peak attenuation subsequently observed. A linear least-square fitting procedure was applied to yield the slopes. Formally, the NUS is defined as

$$\begin{array}{c}\hfill \mathrm{NUS}=\frac{m_{\mathrm{ROI}}}{m_{\mathrm{LV}}}.\end{array}$$ (8)

The MBV quantifies the amount of blood having flowed through a volume of interest during a particular period of time. It is measured in units of ml of blood per 100 g of tissue. It is defined as the time integral of the TAC from a given ROI (c_ROI(t)) normalized by the time integral of the TAC in an artery. In this paper, the arterial TAC was measured in the left ventricle (c_LV(t)). The formal definition is as follows:⁵⁵

$$\begin{array}{c}\hfill \mathrm{MBV}=\frac{{\int }_0^T(c_{\mathrm{ROI}}\left(t\right)-c_{\mathrm{ROI},0})dt}{{\int }_0^T(c_{\mathrm{LV}}\left(t\right)-c_{\mathrm{LV},0})dt}{V}_{\mathrm{voxel}}{N}_{\mathrm{voxel}},\end{array}$$ (9)

where V_voxel is the volume of a voxel and N_voxel is the number of voxels in 100 g of tissue. We assumed a tissue density of 1.05 g/ml. In this study, the lower bound of the integral was defined as the time point when the contrast agent is first detected in the left ventricle. c_ROI,0 and c_LV,0 are average attenuation coefficients in the time frames preceding the contrast arrival for the ROI TAC and arterial TAC, respectively.

The FMT provides a relative measure of the transit time of blood in the tissue. It has units of seconds. The formal definition is as follows:⁵⁶

$$\begin{array}{c}\hfill \mathrm{FMT}=\frac{{\int }_0^T(c_{\mathrm{ROI}}\left(t\right)-c_{\mathrm{ROI},0})tdt}{{\int }_0^T(c_{\mathrm{ROI}}\left(t\right)-c_{\mathrm{ROI},0})dt}.\end{array}$$ (10)

The goal of the evaluation presented in this paper is to compare the relative accuracy of various algorithms, not to quantify perfusion in an absolute manner. This explains why simple perfusion metrics that did not require a deconvolution of the TAC were selected.

RESULTS

Numerically simulated dataset

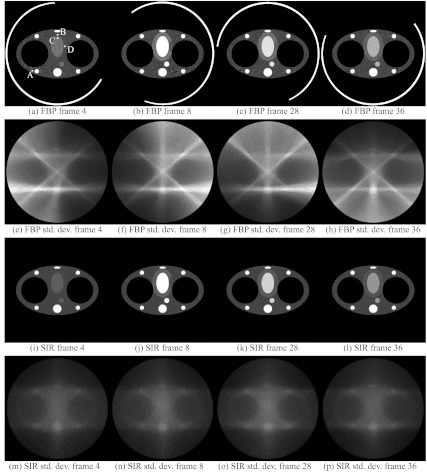
Reconstructions generated using FBP and SIR for four time frames with different short-scan gantry central angles are presented in Fig. 1. Maps of the standard deviation were obtained using the described Monte Carlo method. For each time frame, the source angular range is symbolized by a line segment. As expected from the discussion presented in Sec. 2, the noise level in each FBP images was generally higher for voxels closer to the source trajectory. Qualitatively, it is observed that the images reconstructed using SIR have a more uniform and lower noise spatial distribution with minimal temporal dependence.

Figure 1.

Reconstructions of the numerical phantom at different time frames. (a)–(d) Phantoms were reconstructed using FBP. (e)–(h)Maps of the standard deviation in the FBP reconstruction. (i)–(l) Phantoms were reconstructed using SIR. (m)–(p) The standard deviation maps calculated from SIR reconstructions. The noise is generally more uniform and of lower level in SIR images than in FBP reconstructions. The noise in SIR images has a negligible dependence on the source trajectory. The line segments superposed on the FBP reconstructions represent the short-scan source trajectory. The ROIs in (a) were used for the measurement of enhancement curves (Fig. 2). The display range was set to [0, 0.03] mm⁻¹ for the reconstructions.

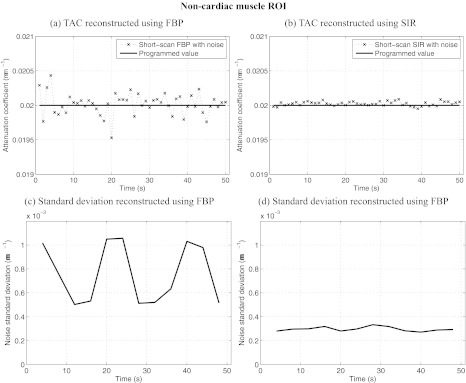
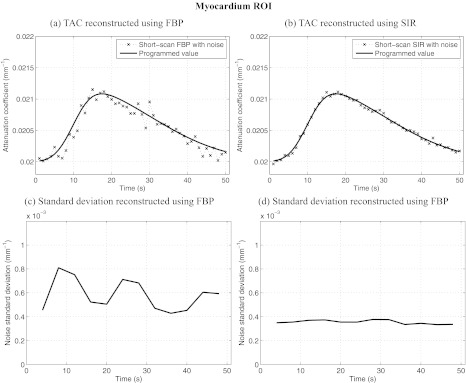
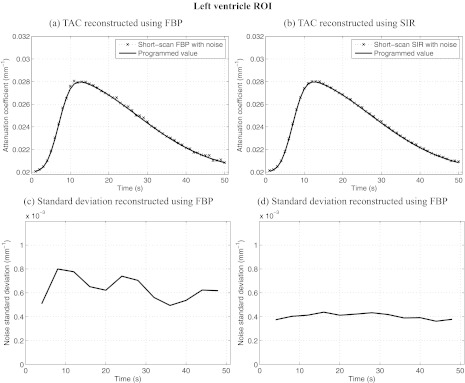
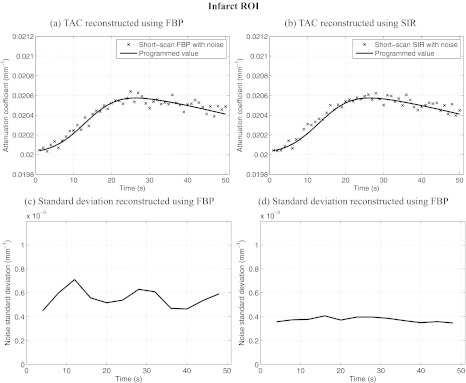
ROIs were selected in various dynamic regions of the phantom and are illustrated in Fig. 1a. All ROIs were 4 × 4 voxels in dimension. The mean attenuation coefficient and the mean noise standard deviation were measured within each ROI for all time frames. Figures 2345 show results of ROI measurements performed respectively in noncardiac muscle, healthy myocardium, the left ventricle, and the infarct region of the myocardium. As expected, changes in the noise level are accompanied by changes in the level of fluctuations observed in the plot of the ROI mean value. ROIs closer to the edge of the object show a more pronounced nonuniformity effect than those closer to isocenter. This behavior is expected since the distance weight shows a large amount of variation between view angles for points farther from isocenter. In particular, the infarct was located near isocenter, which mitigated the variation in the noise level observed in that region. Note that while the heart is typically in the center of the chest, the anterior section is usually far from isocenter. It is thus expected that an infarct situated in the anterior region could have been subjected to a greater relative variation in noise level.

Figure 2.

Dynamic contrast enhancement curves in the noncardiac muscle ROI [A in Fig. 1a]. Also plotted is the relative noise standard deviation as a function of time in the same region. Notice that the level of noise-induced fluctuations in the enhacement curved match the trend observed in the relative noise standard deviation plots. SIR offers less temporal variations in noise and a lower level than FBP. The noise level simulated an incident fluence of 10⁶ photons/detector element.

Figure 3.

Dynamic contrast enhancement curves in the myocardium ROI [B in Fig. 1a]. Also plotted is the relative noise standard deviation as a function of time in the same region. Notice that the level of noise-induced fluctuations in the enhacement curved match the trend observed in the relative noise standard deviation plots. SIR offers less temporal variations in noise and a lower level than FBP. The noise level simulated an incident fluence of 10⁶ photons/detector element.

Figure 4.

Dynamic contrast enhancement curves in the left ventricle ROI [C in Fig. 1a]. Also plotted is the relative noise standard deviation as a function of time in the same region. Notice that the level of noise-induced fluctuations in the enhacement curved match the trend observed in the relative noise standard deviation plots. SIR offers less temporal variations in noise and a lower level than FBP. The noise level simulated an incident fluence of 10⁶ photons/detector element.

Figure 5.

Dynamic contrast enhancement curves in the infarct ROI [D in Fig. 1a]. Also plotted is the relative noise standard deviation as a function of time in the same region. Notice that the level of noise-induced fluctuations in the enhacement curved match the trend observed in the relative noise standard deviation plots. SIR offers less temporal variations in noise and a lower level than FBP. The noise level simulated an incident fluence of 10⁶ photons/detector element.

The noise level varies by up to 110% in the case of ROI D for images reconstructed using FBP. When using SIR, the level varies by a maximum of 20% for the same ROI. The maximal variation is measured as: 2(σ_max − σ_min)/(σ_max + σ_min) × 100%, where σ_max and σ_min are the maximum and minimum noise standard deviations. Furthermore, the variation in the noise level of FBP images is correlated with changes in the short-scan central angle. Indeed, the range is shifted by 20° between each time frame. After 18 s, the scan range had shifted by a full 360° and was back at its initial position. An 18-s periodic oscillation was observed clearly on all FBP noise standard deviation plots. Such an oscillation was not observed on the SIR dynamic curves. Finally, the average noise level over all time frames was 4.50 × 10⁻⁴ mm⁻¹ for FBP reconstructions while it was 2.27 × 10⁻⁴ mm⁻¹ for SIR images. SIR thus reduced the noise level by half.

In summary, based on the results of numerical simulations, high magnitude fluctuations were observed in the noise level both within a particular image and between different time frames. SIR mitigated the spatial variations in the noise level. SIR also reduced the noise level considerably.

In vivo porcine dataset

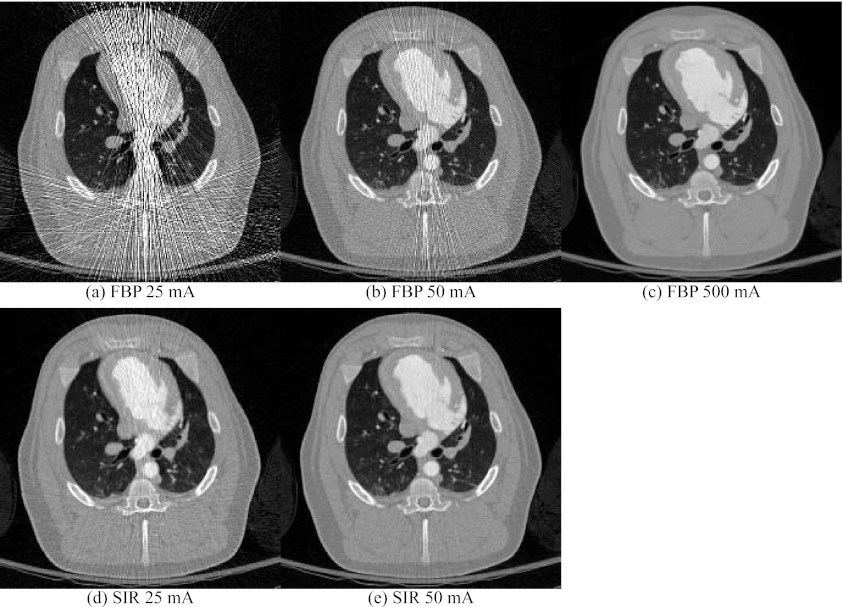
Images were reconstructed using FBP and SIR for all time frames of the porcine projection datasets at 25 and 50 mA. The 500 mA dataset was only processed using FBP. Images reconstructed at the peak contrast concentration in the left ventricle are shown in Fig. 6. It is possible to notice high noise regions within images reconstructed using FBP at 25 and 50 mA. These are caused by projections with low counts. A variation in the noise levels was also observed between different time frames due to both changes in the scan central angle and in the structure of the object following contrast agent injection. When SIR is used, these high noise projections received a low weight in the reconstruction and their deleterious effect on the image is mitigated. One can thus notice a higher SNR in images reconstructed using SIR.

Figure 6.

Reconstructions of the in vivo porcine datasets at different tube currents. The images were reconstructed using FBP and SIR. The display range was [−1000, 900] HU.

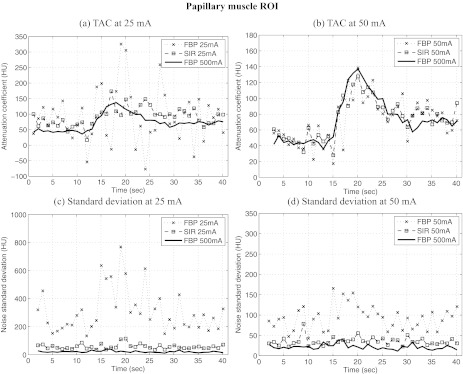
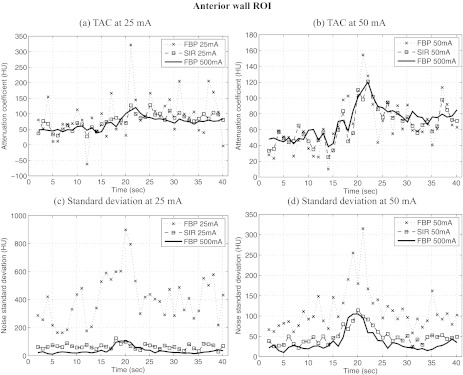
TACs were measured in two different ROIs in the image shown in Fig. 7; the first was located near the papillary muscle (PM), while the second was positioned in the anterior wall (AW) of the left ventricle. Both ROIs had a dimension of 5 × 3 voxels. TACs measured in the PM ROI are shown in Fig. 8 and those from the AW ROI are shown in Fig. 9. One can notice that stochastic fluctuations observed in the TAC measured from images reconstructed using FBP are mitigated in SIR reconstructions. The latter curves also show less divergence from the reference TAC measured from the 500 mA dataset. However, one must note that the scans at different tube current were acquired at 30-min intervals. This implies that physiological changes may have occurred in the animal, which may explain some of the divergence observed.

Figure 7.

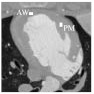
Definition of the regions of interest (ROI) used for the perfusion metric measurements. PM was located near the papillary muscle, while AW was situated in the anterior wall of the myocardium. Both ROIs were 3 × 5 voxels. The display range for this image was [−1000, 900] HU.

Figure 8.

Time attenuation curves (TAC) measured from reconstructions of the in vivo porcine datasets at different tube currents (a, b) and the standard deviation at different time frames (c, d). Images were reconstructed using FBP and SIR. The ROI were the measurements were performed was located in the papillary muscle, PM in Fig. 7. Note that in order to optimize the visualization of the data, the range of attenuation coefficient shown is not constant between the different plots. Also, some divergence from the 500 mA curves might be explained by the fact that a different scan was acquired for each tube current setting.

Figure 9.

Time attenuation curves (TAC) measured from reconstructions of the in vivo porcine datasets at different tube currents. The images were reconstructed using FBP and SIR. Two ROIs were used for the measurements; their location is shown above. Note that in order to optimize the visualization of the data, the range of attenuation coefficient shown is not constant between the different plots. Also, some divergence from the 500 mA curves might be explained by the fact that a different scan was acquired for each tube current setting.

Figures 89 also show the standard deviation between voxels contained in each ROI for each dataset. One can notice that the fluctuations in the TAC were accompanied by an elevation in the standard deviation for the same ROI. This seems to suggest that the fluctuations were stochastic in nature. This is further supported by the fact that the SIR algorithm mitigated the standard deviation to a large extent. As it was observed for the numerical study, the variation in the noise level between different time frames was mitigated using SIR. Furthermore, one may notice the presence of a transient increase in the standard deviation concomitant with the arrival of contrast agent in the ventricles. This increase in noise level was due to the increase in attenuation during that period.

The perfusion metrics defined in Sec. 4D were computed for each dataset reconstructed using both FBP and SIR. The results are presented in Table 3. In all cases, images reconstructed using SIR agreed more closely with the values obtained from the 500 mA reference dataset. The only exception is the NUS at 50 mA, for which the FBP value diverged by 1% from the 500 mA and the SIR NUS diverged by 4%. However, these deviations were very low, which could mean that the difference between these measurements was not statistically significant. Note also that the PM ROI had a relatively low standard deviation for the 50 mA dataset [Fig. 8d]. This may explain the limited improvement observed using SIR in that case.

Table 3.

Quantitative metrics of myocardial perfusion measured in images reconstruction using FBP and SIR in the anterior myocardial wall (AW) and in the papillary muscle (PM) as defined in Fig. 7. Each measurement (f) is presented with the percent deviation from the values calculated from the 500 mA scan (f_ref), |f – f_ref|/f_ref × 100% in parenthesis. Note that some divergence from the reference might be explained by the fact that a different scan was acquired for each tube current setting.

		NUS		MBV (ml/100 g)		FMT (s)
Tube current (mA)	Algorithm	PM ROI	AW ROI	PM ROI	AW ROI	PM ROI	AW ROI
25	FBP	0.351 (90%)	0.196 (83%)	11.7 (47%)	18.3 (31%)	2.72 (62%)	9.76 (4%)
	SIR	0.149 (20%)	0.096 (10%)	17.6 (20%)	15.4 (10%)	8.18 (3%)	9.59 (3%)
50	FBP	0.187 (1%)	0.159 (49%)	14.1 (36%)	16.6 (19%)	9.39 (18%)	8.40 (10%)
	SIR	0.178 (4%)	0.129 (21%)	16.4 (25%)	12.8 (9%)	8.67 (9%)	9.52 (2%)
500 (reference)	FBP	0.185	0.107	22.0	14.0	7.96	9.35

In summary, the conclusions reached using the numerical phantom experiments were further supported using the animal dataset acquired in vivo. In particular, the spatial variation in the noise level and the noise level itself were mitigated using SIR. Furthermore, some evidence was shown suggesting that SIR may improve the precision of quantitative perfusion measurements performed using low-tube current myocardial perfusion scans.

DISCUSSION AND CONCLUSIONS

Limitations and future work

The numerical simulations have some limitations. The x-ray beam was simulated to be monochromatic and scatter radiation was not included. This implies that the mechanisms creating PSA described in the literature, namely, variations in beam hardening and scatter, were not simulated. While this could be perceived as a limitation, the restriction to noise-related fluctuations enabled us to isolate their effect. It would be interesting in future work to determine the fluence level for which noise nonuniformities create fluctuations of the same magnitude as other mechanisms.

Limitations were also present in the study of the in vivo dataset. In particular, separate scans were acquired at different tube currents and were separated by a waiting period to allow contrast clearance. This means that potential physiological changes in the animal could have occurred. These changes could have resulted in some deviation in the perfusion parameters calculated. The results should be interpreted accordingly. Furthermore, only one animal was used in this study. In order to establish the statistical significance of the improvement in the precision and/or accuracy of the perfusion metrics observed using SIR, it would be desirable to perform a larger-scale study with multiple subjects. Also, it is possible that the anatomical differences between the animal model used in this study and human patients lead to slightly different noise nonuniformity behavior. An evaluation in a clinical human dataset might shed some light on this issue in the future.

A few other areas would deserve further investigations in the future. In the context of quantitative MPI, it would be interesting to evaluate to which extent, if any, PSA correction algorithms suggested in the literature^{30, 31, 32, 33} can suppress noise nonuniformity induced fluctuations.

As demonstrated in this paper, the SIR framework can be used to mitigate the demonstrated noise spatial nonuniformity and can be used to reduce radiation dose levels. However, as described in Sec. 4C, the computation time for SIR is still substantially longer than that of FBP despite the use of new computational architecture such as GPU. Computation time is particularly concerning for CT MPI studies since many time frames need to be reconstructed.

The results from the in vivo study demonstrated that in the very low-tube current regime, noise spatial nonuniformity can manifest itself in the form of streaks. While caused by a stochastic process―Poisson distributed and electronic noise in this case—, these streaks caused a systematic error in some regions of the image. Since the orientation and severity of the streaks vary depending on the starting and ending view angles, this error depends at least in part on the scan central angle. Furthermore, it cannot be easily corrected by spatial averaging due to the high spatial correlation of the streaks. In this case, the fluctuations in the attenuation coefficient could show a similar effect to that observed when partial scan artifacts are present.

Conclusions

Images reconstructed using FBP from short-scan, fan-beam projections suffer from nonuniform spatial noise distributions, which tend to fluctuate from frame-to-frame in CT myocardial perfusion imaging. This nonuniform noise distribution is another mechanism that contributes to source trajectory dependent and frame-to-frame variations in MPI. It was shown that when SIR was used, the images had a lower and more uniform noise level in a given time frame, which led to fewer fluctuations in noise level across time frames. The deviation observed between quantitative perfusion metrics measured from low-dose scans and high-dose scans was mitigated when SIR was used instead of FBP to reconstruct images. Since dynamic MPI requires an accurate and predictable evaluation of the contrast dynamics, it may be desirable to use a statistical reconstruction framework for low-dose quantitative CT myocardial perfusion imaging.