Direct reciprocity in structured populations

Abstract

Reciprocity and repeated games have been at the center of attention when studying the evolution of human cooperation. Direct reciprocity is considered to be a powerful mechanism for the evolution of cooperation, and it is generally assumed that it can lead to high levels of cooperation. Here we explore an open-ended, infinite strategy space, where every strategy that can be encoded by a finite state automaton is a possible mutant. Surprisingly, we find that direct reciprocity alone does not lead to high levels of cooperation. Instead we observe perpetual oscillations between cooperation and defection, with defection being substantially more frequent than cooperation. The reason for this is that “indirect invasions” remove equilibrium strategies: every strategy has neutral mutants, which in turn can be invaded by other strategies. However, reciprocity is not the only way to promote cooperation. Another mechanism for the evolution of cooperation, which has received as much attention, is assortment because of population structure. Here we develop a theory that allows us to study the synergistic interaction between direct reciprocity and assortment. This framework is particularly well suited for understanding human interactions, which are typically repeated and occur in relatively fluid but not unstructured populations. We show that if repeated games are combined with only a small amount of assortment, then natural selection favors the behavior typically observed among humans: high levels of cooperation implemented using conditional strategies.

The problem of cooperation in its simplest and most challenging form is captured by the Prisoners’ Dilemma. Two people can choose between cooperation and defection. If both cooperate, they get more than if both defect, but if one defects and the other cooperates, the defector gets the highest payoff and the cooperator gets the lowest. In the one-shot Prisoners’ Dilemma, it is in each person’s interest to defect, even though both would be better off had they cooperated. This game illustrates the tension between private and common interest.

However, people often cooperate in social dilemmas. Explaining this apparent paradox has been a major focus of research across fields for decades. Two important explanations for the evolution of cooperation that have emerged are reciprocity (1–19) and population structure (20–32). If individuals find themselves in a repeated Prisoner’s Dilemma—rather than a one-shot version—then there are Nash equilibria where both players cooperate under the threat of retaliation in future rounds (1–19). The existence of such equilibria is a cornerstone result in economics (1–3), and the evolution of cooperation in repeated games is of shared interest for biology (4–10), economics (11–14), psychology (15), and sociology (16), with applications that range from antitrust laws (17) to sticklebacks (18), although it has been argued that firm empirical support in nonhuman animal societies is rare (19).

Population structure is equally important. If individuals are more likely to interact with others playing the same strategy, then cooperation can evolve even in one-shot Prisoner’s Dilemmas, because then cooperators not only give, but also receive more cooperation than defectors (20–32). There are a host of different population structures and update rules that can cause the necessary assortment (28, 31). Whether thought of in terms of kin selection (20, 25, 26), group selection (24, 27, 32), both (29), or neither (30, 31), population structure can allow for the evolution of cooperative behavior that would not evolve in a well-mixed population. Assortment can, but does not have to be genetic, as for example in coevolutionary models based on cultural group selection (32).

In this article, we consider the interaction of these two mechanisms: direct reciprocity and population structure. We begin by re-examining the ability of direct reciprocity to promote cooperation in unstructured populations. Previous studies tend to consider strategies that only condition on the previous period (8–10) or use static equilibrium concepts that focus on infinitely many repetitions (11, 12). Although useful for analytical tractability, both of these approaches could potentially bias the results. Thus, we explore evolutionary dynamics that allow for an open-ended, infinite strategy space, and look at games where subsequent repetitions occur with a fixed probability δ.

To do so, we perform computer simulations where strategies are implemented using finite state automata (see Fig. 1 for examples), and compliment these simulations with analytical results, which are completely general and apply to all possible deterministic strategies. Our simulations contain a mutation procedure that guarantees that every finite state automaton can be reached from every other finite state automaton through a sequence of mutations. Thus, every strategy that can be encoded by a finite state automaton is a possible mutant. The mutants that emerge at a given time depend on the current state of the population: close-by mutants, requiring only one or two mutations, are more likely to arise than far away mutants, requiring many mutations.

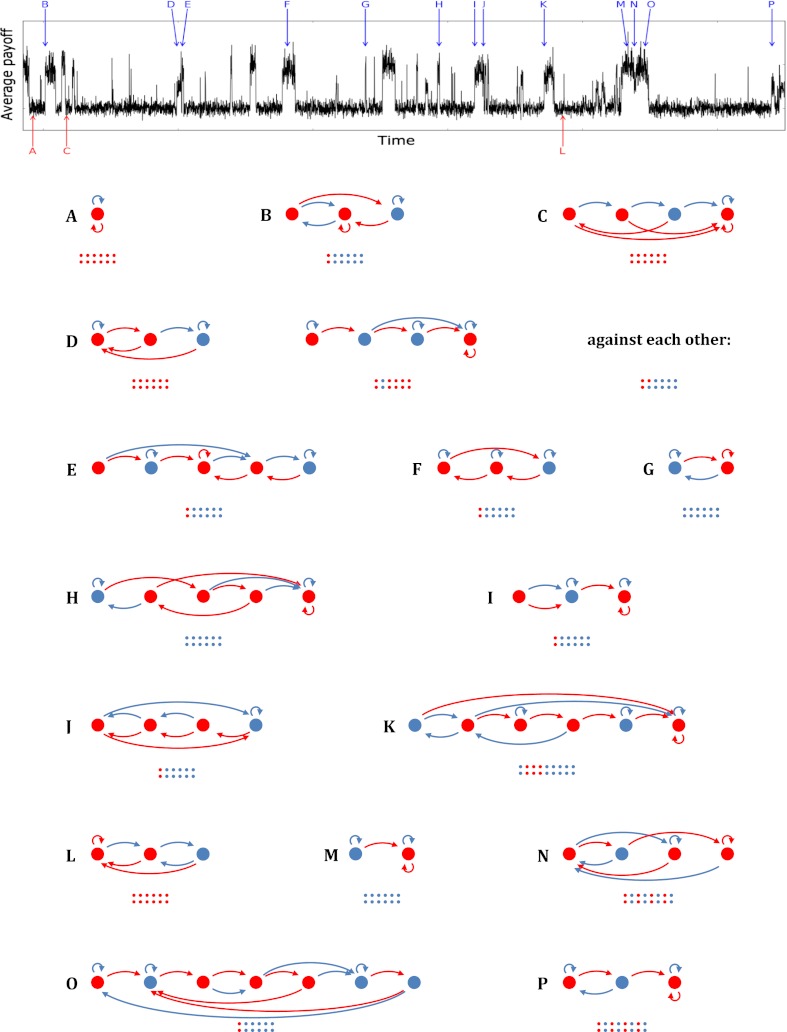
Fig. 1.

Examples of equilibrium strategies observed during a simulation run. The top part of the figure depicts the average payoff during a part of a simulation run with continuation probability 0.85. The payoffs in the stage game are 2 for both players if they both cooperate, 1 for both if they both defect, and 3 for the defector and 0 for the cooperator if one defects and the other cooperates. These payoffs imply a benefit-to-cost ratio of b/c = 2. Because the game lengths are stochastic, there is variation in average payoff, even when the population makeup is constant. The different payoff plateaus indicate the population visiting different equilibria with different levels of cooperation and hence different expected average payoffs. Examples of equilibrium strategies, indicated by letters A through P, are also shown in the following way. The circles are the states and their colors indicate what this strategy plays when in that state; a blue circle means that the strategy will cooperate and a red one means that it will defect. The arrows reflect to which state this strategy goes, depending on the action played by its opponent; the blue arrows indicate where it goes if its opponent cooperates, the red ones where it goes if its opponent defects. The strategies all start in the leftmost state. The small colored dots indicate what the first few moves are if the strategy plays against itself, and in a mixture (case D) also what the two strategies play when they meet each other. The strategies vary widely in the ways in which they are reciprocal, the extent to which they are forgiving, the presence or absence of handshakes they use before they start cooperating, and the level of cooperation. The strategies shown here are discussed in greater detail in the SI Appendix.

Our computer program can, in principle, explore the whole space of deterministic strategies encoded by finite state automata. Fig. 1 shows that the population regularly transitions in and out of cooperation and gives a sample of the equilibrium strategies, with different degrees of cooperation, that surface temporarily. The variety of equilibria shows that evolution does explore a host of different possibilities for equilibrium behavior, and that it is as creative in constructing equilibria as it is in undermining them.

Based on previous analyses of repeated games, one might expect evolution to lead to high levels of cooperation for relatively small b/c ratios in our simulations, provided the continuation probability δ is reasonably large. However, this is not what we find. To understand why, we have to consider indirect invasions (33).

In a well-mixed population, the strategy Tit-for-Tat (TFT) can easily resist a direct invasion of ALLD (always choosing to defect, regardless) because ALLD performs badly in a population of TFT players, provided that the continuation probability δ is large enough. The strategy ALLC (unconditional cooperation), however, can serve as a springboard for ALLD and thereby disrupt cooperation. ALLC is a neutral mutant of TFT: when meeting themselves and each other, both strategies always cooperate, and hence they earn identical payoffs. Thus, ALLC can become more abundant in a population of TFT players through neutral drift. When this process occurs, ALLD can then invade by exploiting ALLC. Unconditional cooperation is therefore cooperation’s worst enemy (10).

Indirect invasions do not only destroy cooperation; they can also establish cooperation (for examples see the SI Appendix). If the population size is not too small, those indirect invasions in and out of cooperation come to dominate the dynamics in the population (34).

We can show that no strategy is ever robust against indirect invasions; there are always indirect paths out of equilibrium (34). Our simulations also suggest that in a well-mixed population, paths out of cooperation are more likely than paths into cooperation. Even for relatively high continuation probabilities, evolution consistently leads only to moderate levels of cooperation when averaged over time (unless the benefit-to-cost ratio of cooperation is very high) (see also SI Appendix, Fig. S5).

How, then, can we achieve high levels of cooperation? We find that adding a small amount of population structure increases the average level of cooperation substantially if games are repeated. The interaction between repetition and population structure is of primary importance, especially for humans, who tend to play games with many repetitions and who live in fluid, but not totally unstructured populations (35–40).

To explore the effect of introducing population structure, we no longer have individuals meet entirely at random. Instead, a player with strategy S is matched with an opponent that also uses strategy S with probability α + (1 – α)x_S, where x_S is the frequency of strategy S in the population, and α is a parameter that can vary continuously between 0 and 1. With this matching process, the assortment parameter α is the probability for a rare mutant to meet a player that has the same strategy (21, 29, 41, 42).

If δ = 0, we are back in the one-shot version of the game. If α = 0, we study evolution in the unstructured (well-mixed) population. Thus, the settings where only one of the two mechanisms is present are included as special cases in our framework.

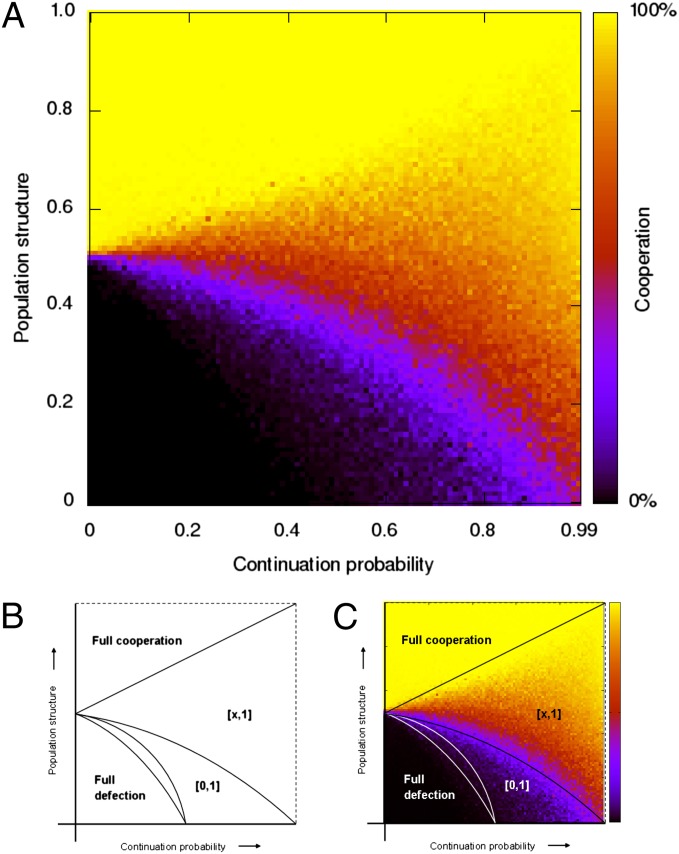
Fig. 2 shows how assortment and repetition together affect the average level of cooperation in our simulations. If there is no repetition, δ = 0, we find a sharp threshold for the evolution of cooperation. If there is some repetition, δ > 0, we find a more gradual rise in the average level of cooperation as assortment α increases. In the lower right region of Fig. 2, where repetition is high and assortment is low (but nonzero), we find behavior similar to what is observed in humans: the average level of cooperation is high, and the strategies are based on conditional cooperation (14, 43–46). In contrast, when assortment is high and repetition is low we observe the evolution of ALLC, which is rare among humans.

Fig. 2.

Simulation results and theoretical prediction with repetition as well as assortment. (A) Every pixel represents a run of 500,000 generations, where every individual in every generation plays a repeated game once. The population size is 200 and the benefit-to-cost ratio is b/c = 2. The continuation probability δ (horizontal axis) indicates the probability with which a subsequent repetition of the stage game between the two players occurs. Therefore, a high continuation probability means that in expectation the game is repeated a large number of times and a continuation probability of 0 implies that the game is played exactly once. On the vertical axis we have a parameter α for the assortment introduced by population structure, which equals the probability with which a rare mutant meets another individual playing the same strategy, and that can also be interpreted as relatedness (21, 29, 41, 42). This parameter being 0 would reflect random matching. If it is 1, then every individual always interacts with another individual playing the same strategy. Both parameters—continuation probability δ and assortment α—are varied in steps of 0.01, which makes 10,100 runs in total. (B and C) A theoretical analysis with an unrestricted strategy space explains what we find in the simulations. This analysis divides the parameter space into five regions, as described in the main text (see the SI Appendix for a detailed analysis and a further subdivision). The border between regions 3 and 4 is an especially important phase transition, because above that line, fully defecting strategies no longer are equilibria. In the lower-right corner, where continuation probability is close to 1, adding only a little bit of population structure moves us across that border.

To gain a deeper understanding of these simulation results, we now turn to analytical calculations. For the stage game of the repeated game we consider the following payoff matrix.

	Cooperate	Defect
Cooperate	b – c	– c
Defect	b	0

Our analytical results are derived without restricting the strategy space and by considering both direct and indirect invasions (see the SI Appendix for calculation details). The analytical results are therefore even more general than the simulation results. The simulations allow for all strategies that can be represented by finite automata (a large, countably infinite set of strategies where the mutation procedure specifies which mutations are more or less likely to occur). The analytical treatment, on the other hand, considers and allows for all possible strategies. Thus, the analytical results are completely general and independent of any assumptions about specific mutation procedures.

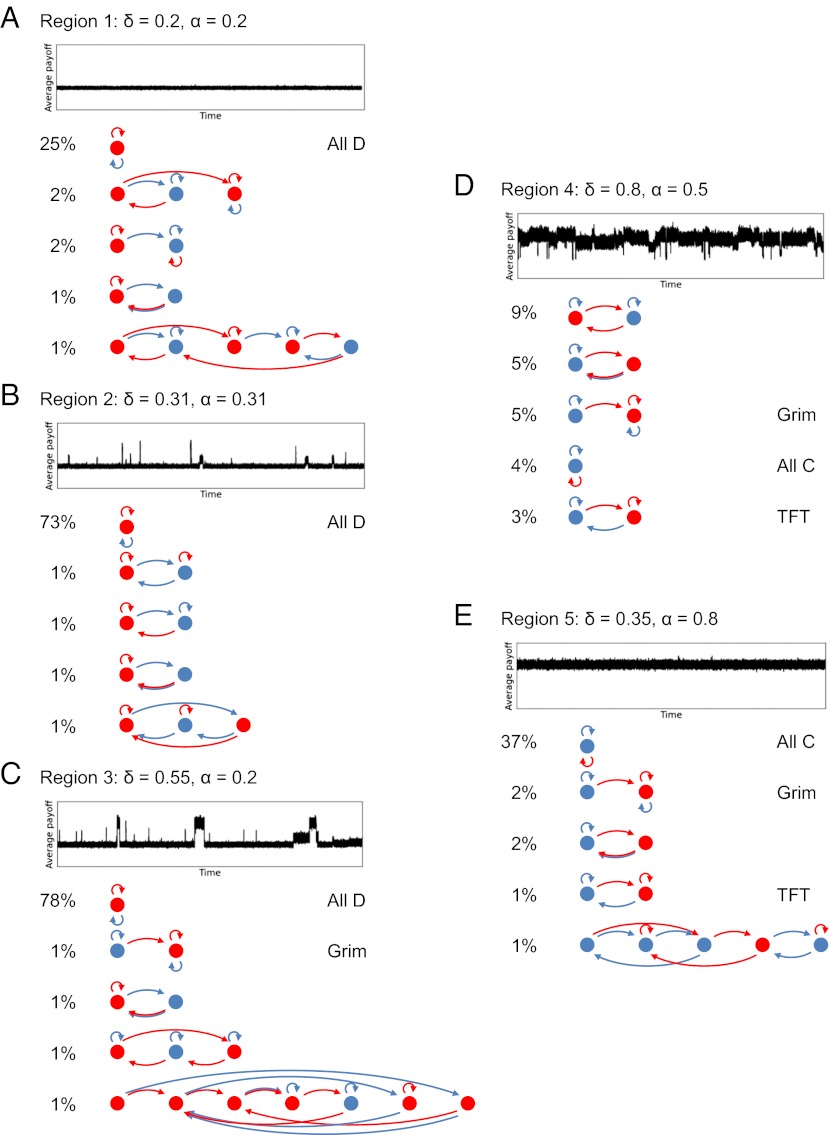
We find that the parameter space, which is given by the unit square spanned by α and δ, can be divided into five main regions (Fig. 2B). We refer to the lower left corner, containing δ = 0, α = 0, as region 1, and number the remaining regions 2–5, proceeding counter clockwise around the pivot (δ, α) = (0, c/b). To discuss these regions we introduce the cooperativity of a strategy, defined as the average frequency of cooperation a strategy achieves when playing against another individual using the same strategy. Cooperativity is a number between 0 and 1: fully defecting strategies, such as ALLD, have cooperativity 0, and fully cooperative strategies, such as ALLC or TFT (without noise), have cooperativity 1. In Fig. 3, we show representative simulation outcomes for parameter values in the center of each region.

Fig. 3.

Runs and top five strategies from the five regions. Each panel (A–E) shows simulation results using a (δ, α) pair taken from the center of the corresponding region of Fig. 2. In each panel, the average payoff over time is shown, as well the five most frequently observed strategies. If any of the strategies have an established name, it is also given. The simulation runs confirm the dynamic behavior the theoretical analysis suggests. In region 1 (A) we only see fully defecting equilibria; all strategies in the top five—and actually almost all strategies observed—always defect when playing against themselves. In region 2 (B) we observe that indirect invasions get the population away from full defection sometimes, but direct or indirect invasions bring it back to full defection relatively quickly. In region 3 (C) we observe different equilibria, ranging from fully defecting to fully cooperative. In region 4 (D) we observe high levels of cooperation, and although cooperative equilibria are regularly invaded indirectly, cooperation is always re-established swiftly. Furthermore, most of the cooperative strategies we observe are conditional. In region 5 (E) we observe full cooperation, and strategies that always cooperate against themselves. By far the most common strategy is ALLC, which cooperates unconditionally. Note that the top five also contain disequilibrium strategies. Strategies 2, 3 and 4 in the top five of region 2 are neutral mutants to the most frequent strategy there (ALLD), and ALLC, which came in fourth in region 4, is a neutral mutant to all fully cooperative equilibrium strategies.

In regions 1 and 2, where both α and δ are less than c/b, all equilibrium strategies have cooperativity 0. In region 1, ALLD can directly invade every nonequilibrium strategy. In region 2 ALLD no longer directly invades all nonequilibrium strategies, but for every strategy with cooperativity larger than 0, there is at least one strategy that can directly invade. The fact that these direct invaders exist, however, does not prevent the population from spending some time in cooperative states. In our simulations, direct invasions out of cooperation are relatively rare, possibly because direct invaders are hard to find by mutation. Instead, cooperative states are more often left by indirect invasions.

In region 3 there exist equilibrium strategies for levels of cooperativity ranging from 0 to 1. In the simulations, we observe the population going from equilibrium to equilibrium via indirect invasions. The population spends time in states ranging from fully cooperative to completely uncooperative. As α and δ increase, indirect invasions that increase cooperation become more likely and indirect invasions that decrease cooperation become less likely; therefore the average level of cooperativity increases.

In region 4 there still exist equilibrium strategies for different levels of cooperativity, but fully defecting strategies are no longer equilibria. All equilibria are at least somewhat cooperative. Indirect invasions by fully defecting strategies are possible, and they do occur, but they result in relatively short-lived excursions into fully defecting disequilibrium states, which can be directly invaded by strategies with positive cooperativity. As a result, cooperativity is high across much of region 4. In particular, reciprocal cooperative strategies, which condition their cooperation on past play, are common, for example TFT and Grim.

Finally, in region 5 all equilibrium strategies have maximum cooperativity, and ALLC can directly invade every strategy that is not fully cooperative. It is disadvantageous to defect regardless of the other’s behavior. Therefore, not only is cooperativity high, but specifically unconditional cooperation (ALLC) is the most common cooperative strategy by a wide margin.

The five regions are separated by four curves, which are calculated in the SI Appendix. One remarkable finding is the following. If assortment is sufficiently high, α > c/b, then introducing repetition (choosing δ > 0) can be bad for cooperation. The intuition behind this finding is that reciprocity not only protects cooperative strategies from direct invasions by defecting ones, but also shields somewhat cooperative strategies from direct invasion by more cooperative strategies. (Details are in the SI Appendix, along with an explanation how repetition can facilitate indirect invasions into ALLC for large enough δ. See also ref. 47 and references therein for games other than the Prisoner’s Dilemma in which repetition can be bad, even without population structure). If we move horizontally through the parameter space, starting in region 5 and increasing the continuation probability, average cooperativity in the simulations therefore first decreases (Fig. 2). Later, cooperativity goes back up again. The reason for this result is that equilibrium strategies can start with “handshakes,” which require one or more mutual defections before they begin to cooperate with themselves (see strategies B, E, F, I, J, K, and O in Fig. 1). The loss of cooperativity for any given handshake decreases if the expected length of the repeated game increases, because the handshake then becomes a relatively small fraction of total play. That effect is only partly offset by the fact that an increase in continuation probability also allows for equilibria with longer handshakes.

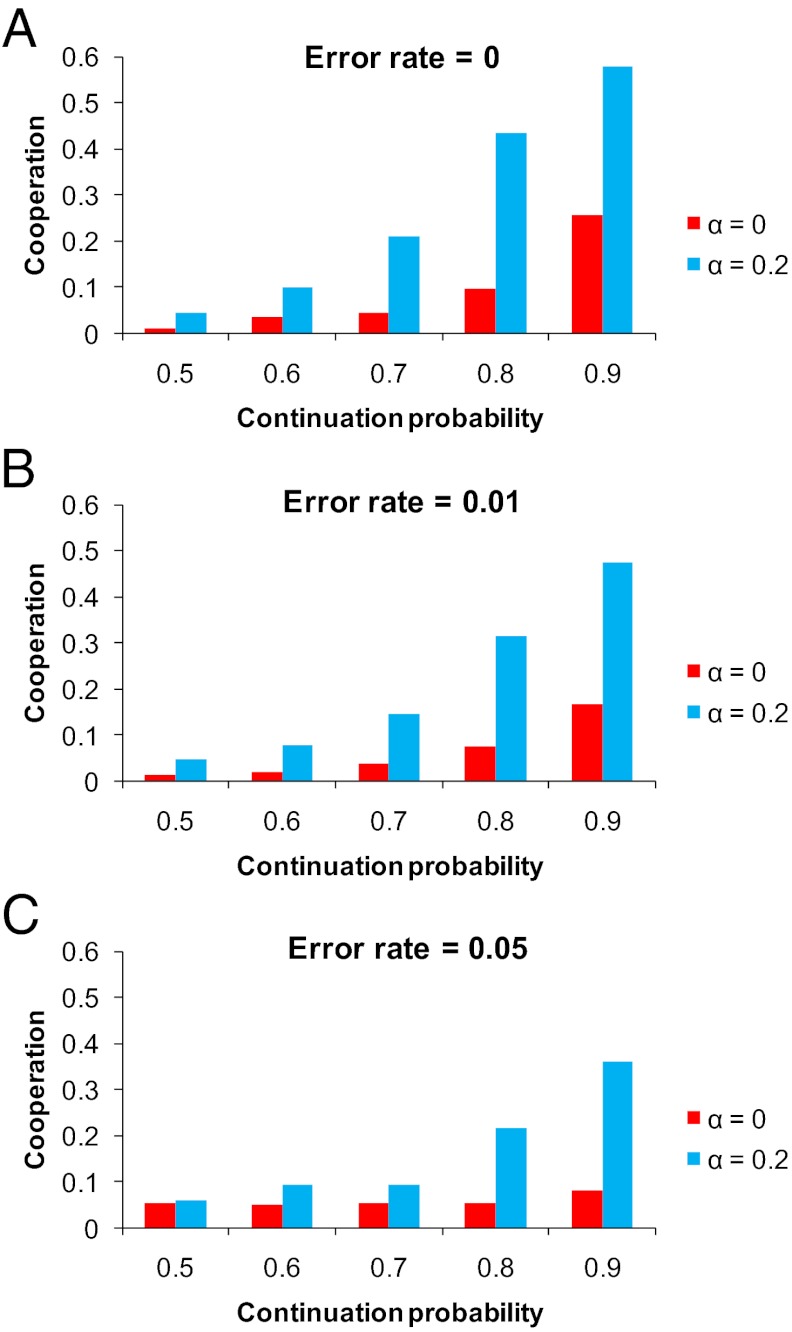
In our simulations, individuals do not make mistakes; they both perceive the other’s action and execute their own strategy with perfect accuracy. Mistakes, however, are very relevant for repeated games (11, 44, 45, 48–50). Therefore, we also ran simulations with errors for a selection of parameter combinations to check the robustness of our results. In those runs, every time a player chooses an action, C or D, there is some chance that the opposite move occurs. Fig. 4 compares error-free simulations with those that have a 1% and 5% error rate. We find that our conclusions are robust with respect to errors: it is the interaction between repetition and structure that yields high cooperation. Another classic extension is to include complexity costs (12, 48). In addition, here one can reasonably expect that the simulation results will be very similar as long as complexity costs are sufficiently small.

Fig. 4.

Simulation results with and without noise. (A–C) The simulations shown in Figs. 1–3 have no errors; individuals observe the actions of their opponent with perfect accuracy, and make no mistakes in executing their own actions. That is of course a stylized setting, and it is more reasonable to assume that in reality errors do occur (11, 44, 45, 48–50). For five values of δ and two values of α we therefore repeat our simulations, but now with errors; once with an execution error of 1% per move, and once with an execution error of 5% per move. With errors, even ALLD against itself sometimes plays C, so the benchmark of no cooperation becomes the error rate, rather than 0. Errors decrease the evolution of cooperation somewhat, but the results do not change qualitatively. If anything, the effect of the combination of repetition and population structure is more pronounced; at an error rate of 5% both mechanisms have only a very small effect by themselves, but together make a big difference at sizable continuation probabilities.

In summary, we have shown that repetition alone is not enough to support high levels of cooperation, but that repetition together with a small amount of population structure can lead to the evolution of cooperation. In particular, in the parameter region where repetition is common and assortment is small but nonzero, we find a high prevalence of conditionally cooperative strategies. These findings are noteworthy because human interactions are typically repeated and occur in the context of population structure. Moreover, experimental studies show that humans are highly cooperative in repeated games and use conditional strategies (14, 43–46). Thus, our results seem to paint an accurate picture of cooperation among humans. Summarizing, one can say that one possible recipe for human cooperation may have been “a strong dose of repetition and a pinch of population structure.”