Ideal glass transitions by random pinning

Abstract

We study the effect of freezing the positions of a fraction c of particles from an equilibrium configuration of a supercooled liquid at a temperature T. We show that within the random first-order transition theory pinning particles leads to an ideal glass transition for a critical fraction c = c_K(T) even for moderate supercooling; e.g., close to the Mode-Coupling transition temperature. First we derive the phase diagram in the T - c plane by mean field approximations. Then, by applying a real-space renormalization group method, we obtain the critical properties for |c - c_K(T)| → 0, in particular the divergence of length and time scales, which are dominated by two zero-temperature fixed points. We also show that for c = c_K(T) the typical distance between frozen particles is related to the static point-to-set length scale of the unconstrained liquid. We discuss what are the main differences when particles are frozen in other geometries and not from an equilibrium configuration. Finally, we explain why the glass transition induced by freezing particles provides a new and very promising avenue of research to probe the glassy state and ascertain, or disprove, the validity of the theories of the glass transition.

Almost any liquid shows an impressive growth of the relaxation time when supercooled below the melting point: indeed typical time scales increase from picoseconds to hours in a rather restricted temperature window. This increase is so steep that below a certain temperature, T_g, it is not possible to equilibrate the system, which then freezes in an amorphous solid, called glass (1). Although T_g is not a critical temperature and only indicates a cross-over point, a recurrent question in the literature is whether a true thermodynamic phase transition to an ideal glass state takes place (at a temperature T_K < T_g). The answer to this question would provide an explanation for the fast growth of the relaxation time and several other phenomena observed experimentally. Nevertheless, other scenarios based on purely dynamical transitions at zero (or finite) temperature or even no transition at all, might also provide alternative explanations (2, 3). In contrast with usual critical phenomena, the study of the glass transition is hampered by the much more severe slowing down of the dynamics. Recent work on growing length scales (4) suggests that even if a transition is present the corresponding critical length that can be observed in experiments is not larger than a few interparticle distances, meaning that experimental systems can be equilibrated only rather far from the putative transition point. This fact makes it quite difficult to prove (or disprove) the existence of the transition and also to contrast theories solely on the basis of their critical properties. Here we propose a way to bypass these problems: we show that an ideal glass transition^† can be induced by a suitable random perturbation even for moderate supercooling. Moreover, we show that the induced ideal glass phase can be accessed and sampled easily. Contrary to the usual situation, where the existence (or the absence) of the ideal glass transition can only be advocated on the basis of doubtful extrapolations, one can now approach it from both ends. As a consequence, determining whether there is indeed a true transition becomes feasible by using the usual machinery of standard phase transitions, in particular finite-size scaling. A crucial point is that this “high-temperature” ideal glass transition is expected within the Random First-Order Transition (RFOT) (5) theory only. Thus, the study of this phenomenon should lead to very sharp tests allowing to ascertain the validity of the theory or disprove it.

The random perturbation we focus on consists in freezing the positions of a fraction c of particles of an equilibrated configuration. This kind of procedure, first performed in ref. 6, has been used to test the mosaic picture of the RFOT theory (7, 8), show the existence of medium range amorphous order (9), and study the growth of a static length (9, 10), called point-to-set (11). Several different geometries of frozen particles have been studied recently. The most remarkable finding was obtained when the positions of all particles behind two parallel walls are frozen (12) and when particles are pinned at random with a concentration c (12–15). In both these cases the relaxation time increases very fast when the fraction of frozen particles is increased or the distance between the two walls is diminished, even at temperatures close to the onset of glassy dynamics. The increase is so dramatic that it was claimed it could correspond to a true divergence (12, 13, 15).

Here we show that, within the RFOT approach, a divergence is indeed expected and related to an ideal glass transition. We first present phenomenological arguments supporting the presence of this phenomenon. We then theoretically derive the existence of this transition and its critical properties and discuss the growth of length and time scales by several methods. Random pinning is a source of quenched disorder; as such it plays an important role in determining the lower critical dimension (equal to two for randomly pinned particles and three for the two walls case) and leads to very unusual finite-size effects. We conclude proposing several ways to study these ideal glass transitions induced by freezing particles and discussing the main reasons that make such studies feasible, in contrast with the usual case of the low-temperature ideal glass transition.

General Arguments

As stressed previously, our results only hold within the RFOT theory, which explains the static and dynamic properties of supercooled liquids in terms of the competition between the surface tension Υ and the configurational entropy density s_c(T). The former is a measure of the extra free-energy cost paid when two different amorphous phases are in contact through a common surface. The latter quantifies the multiplicity of amorphous phases in which the liquid can freeze. In mean field models and approximate computations (16) applied to finite dimensional liquids, s_c is found to vanish at a finite temperature T_K. On a length scale l (in spatial dimension d) the configurational entropy and surface tension respectively scale as Ts_cl^d and Υl^θ (with θ ≤ d - 1). In consequence, on length scales smaller than l_PS = (Υ/Ts_c)^1/(d-θ); i.e., the so-called Point-to-Set (PS) length scale, it is preferable for the system to develop amorphous order, localizing in a given amorphous phase. Instead, for l > l_PS, it is better to break the amorphous order, pay the extra free-energy cost and gain entropy. This mechanism gives rise to the so-called mosaic state envisioned as an assembly of patches of length l_PS (5, 8): a kind of microphase separated state where the number of phases is actually huge (proportional to 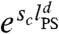). The relaxation time scale of this phase is obtained assuming activated dynamic scaling; i.e., 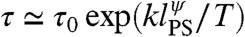, where k is a liquid-dependent constant and τ₀ a microscopic time scale. For certain values of the exponents ψ and θ advocated in the literature (5, 17), the arguments above allow one to obtain a derivation of the Adam-Gibbs law (18) and of the super-Arrhenius behavior characteristic of glass formers. Recently, instantons computations partially confirmed this scenario: the existence of l_PS and its scaling with Ts_c were obtained analytically in (19–24).

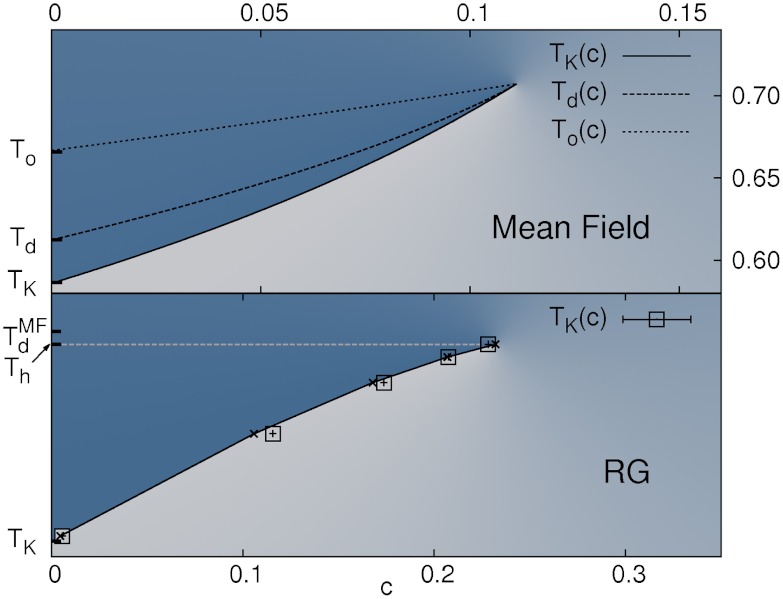
What are the consequences, within the RFOT theory, of freezing at random the positions of a fraction c of particles of an equilibrated configuration? Freezing actually means blocking the particle positions. The remaining particles then evolve in this frozen background. For this constrained liquid both the number of possible amorphous phases and the extra free-energy cost of the interfaces between them, Υ(T,c), change with c. The effect on the interface free-energy cost is subdominant with respect to the configurational entropy variation. The multiplicity of amorphous phases clearly is less than that of the unconstrained system. By pinning a particle one reduces the possible low free-energy configurations of the surrounding ones and, hence, diminishes the configurational entropy density by an amount Y (not to be confused with Υ). Thus, at least for small c, one finds s_c(T,c) ≃ s_c(T) - cY(T). Generically, one expects s_c(T,c) to be a monotonously decreasing function of c, eventually vanishing for a critical fraction of frozen particles c_K(T) ≃ s_c(T)/Y(T) < 1 [at variance, Y(T) is a microscopic configurational entropy loss and is not expected to vanish even at high temperature]. Repeating the previous argument about the competition between configurational entropy and surface free-energy cost, one then finds that the configurations of the constrained liquid are organized in a mosaic with larger tiles: the point-to-set length, l_PS(T,c) = (Υ(T,c)/s_c(T,c))^1/(d-θ), increases as a function of c - c_K and diverges at the point c_K(T) at which s_c(T,c) becomes zero. Concomitantly, the relaxation time, obtained by the relation τ ≃ τ₀ exp[kl_PS(T,c)^ψ/T], diverges too. For c > c_K the system is in an equilibrium amorphous glass phase. In this regime the relaxation time is finite because the pinning field is so strong that the system has nowhere to go: typically sampled configurations are confined to the neighborhood of the initial configuration from which particles were pinned. The condition s_c(T,c_K(T)) = 0, or equivalently s_c(T_K(c),c) = 0, defines a line of ideal glass transitions. The starting point of the transition line, at c = 0, coincides with the ideal glass transition of the unperturbed liquid; the endpoint corresponds to the value of c at which the glass transition line meets the onset temperature line T_o(c), which is defined by the equation Υ(T_o(c),c) = 0 (23, 24). In the top box of Fig. 1 we plot the phase diagram obtained by mean field theory and discussed in more detail later. By going beyond mean field and by taking into account the effect of the quenched disorder induced by the pinned particles, Υ(T,c) gets renormalized with respect to its mean field value. As a consequence, the endpoint of the critical line is depressed to a lower temperature T_h, see bottom box of Fig. 1. The value of T_h depends on the ratio T_d/T_K: we find that T_h/T_d increases when T_d/T_K decreases. In conclusion, ideal glass transitions can be induced at temperatures between T_K and T_h by increasing the fraction of frozen particles in the system^‡. The case corresponding to freezing all particles in the system except those between two infinite flat walls at distance d is similar and will be discussed at the end of the paper. We end this section with two important remarks on the newly found glass transitions. First, pinning particles can be considered as a very nonlinear way to probe the supercooled liquid state. In consequence, the existence of a glass transition for c = c_K(T) reveals the presence of a new characteristic static length scale l_K(T) for the unconstrained liquid. This length scale corresponds to the critical mean distance between frozen particles: 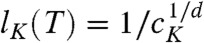. Because c_K(T) ∝ s_c(T), the new static length scale, l_K, is expected to diverge at T = T_K. Interestingly, the divergence is milder than the one of 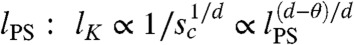. The second very important issue is that, as we shall discuss later, the phase diagram of Fig. 1 is not expected within any theoretical approach other than the RFOT one. In particular the concurrence of several peculiar phenomena discussed in the following sections (like the jump in the order parameter; i.e., the overlap distribution, the nonmonotonous behavior of the relaxation time, and its dramatic growth in proximity of the transition line) can be only explained by RFOT theory. Thus, the phenomena discussed in this work should allow one to test glass transition theories in a very stringent way. One could wonder why showing the existence of ideal glass transition as a function of c is not as difficult as to show it as a function of temperature. In the usual case the main problem is that the low-temperature phase is not known. In the frozen-particle case, this is not the case! Actually, the configuration 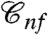of the nonfrozen particles just after freezing out the others is automatically an equilibrium configuration for the pinned system (6, 23, 25), even for c > c_K. In this regime the nonfrozen particles just vibrate within the ideal glass state, which corresponds to 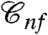and a lump of configurations around it. In consequence, one can now approach the transition from both ends (instead of making extrapolations from high temperature) and show whether there is indeed a transition, study its critical properties, etc. We postpone a more detailed discussion to the end of the paper. In the following we present theoretical arguments to corroborate the previous phenomenological ones.

Fig. 1.

Top box: Phase diagram for the p = 3-spin disordered model 24. The continuous line corresponds to ideal glass transitions taking place at T_K(c). The two dotted lines (from top to bottom) correspond respectively to the onset temperature T_o(c) and the mode coupling critical temperatures T_d(c). Bottom Panel: Phase diagram obtained by the renormalization group approach for T_d/T_K ≃ 1.4 (corresponding schematically to OTP). The variable on the x-axis is proportional to the concentration of pinned particles. The squares are the results obtained by RG for the ideal glass transition line T_K(c). The continuous line corresponds to the phenomenological result c_K ∝ s_c/Y. The endpoint of the transition line takes place at a temperature T_h < T_d in contrast to the mean field case.

Phase Diagram and Mean Field Theory

An easy way to study within mean field theory the effect of freezing degrees of freedom is to focus on the Random Energy Model (REM) (27) (see ref. 28 for a similar computation). The REM is the simplest mean field model displaying an entropy vanishing transition (1) à la Kauzmann and it is often used to understand some aspects of supercooled liquids. The REM is a spin model in which the energies of the configurations are independent and identically distributed (i.i.d.) Gaussian random variables of variance N, where N is the number of spins (such a scaling is needed to obtain a correct thermodynamic limit). The number of configurations with energies between E and E + dE reads 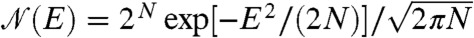. The equilibrium energy is given by the condition 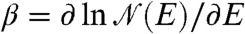; i.e., β = -E_eq(β)/N. The entropy S is simply equal to 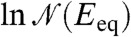. The model has a transition at the temperature 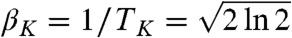at which S(E_eq) vanishes. For T < T_K the energy as a function of temperature does not vary any longer. Now, take a high temperature equilibrium configuration α and freeze a fraction c of its spins. We call this set 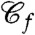. 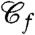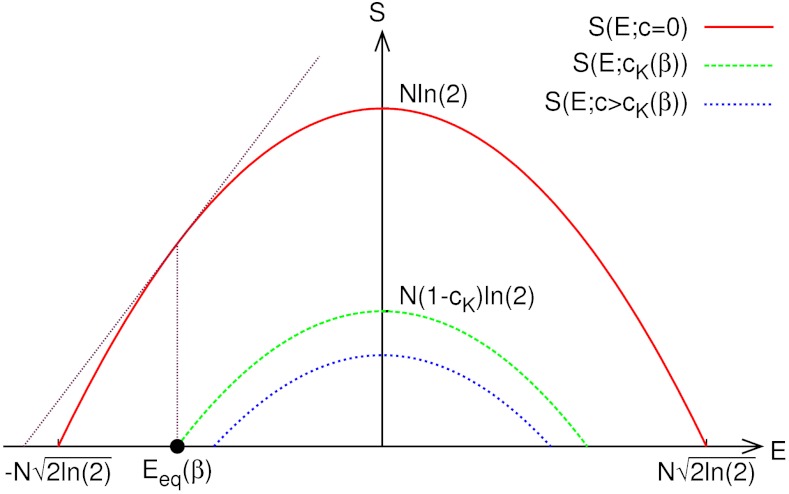In order to study the thermodynamics of the nonfrozen spins, one has to sum over all configurations having the spins in in the same state than in α. The energies of these configurations are also i.i.d. Gaussian variables. As a consequence, one can repeat the previous analysis except that now the number of possible configurations is reduced from 2^N to 2^N(1-c). Thus the energy distribution reads: 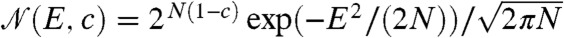. The relationship -E_eq(β)/N = β remains valid but the total entropy is reduced by a factor -Nc ln 2; i.e., S(E,c) = S(E,0) - Nc ln 2, see Fig. 2. Moreover, the overlap, 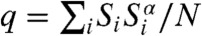, between a typical spin configuration and the reference one is equal to c. At the value c_K = S(E_eq,0)/(N ln 2) there is an entropy-vanishing transition. For c > c_K the system is frozen in the configuration α (q = 1) because all the other ones have an energy that is higher and determined by S(E,c) = 0, see Fig. 2. In consequence the behavior of the overlap distribution, which plays the role of order parameter, is different from usual 1-Replica Symmetry Breaking (RSB) transitions (29): the glass phase is characterized by only one peak at q = 1. The analysis of this simple model confirms our previous assumptions: the configurational entropy per spin is indeed reduced by a factor -Yc, here Y = β²/[2(1 - c)], and, at variance with the case of the REM without pinned spins, the low-temperature ideal glass is known: it is the high-temperature configuration α.

Fig. 2.

Configurational entropy for the REM as a function of E for c = 0,c = c_K,c > c_K (from top to bottom). The equilibrium energy is stuck at the value E_eq(β). For c < c_K the partition function is dominated by configurations with energy E_eq(β) (the straight line has a slope β). For c > c_K the partition function is dominated by the contribution from the reference configuration; higher states lead to a subleading contribution.

An extension of the same analysis to models that display also a dynamical glass transition, akin to the Mode-Coupling Theory (MCT) transition, gives interesting additional information. Following ref. 31 we expect that because this transition is due to the emergence of metastable states, by freezing particles one blocks unstable relaxation modes and transforms unstable states in stable ones, thus raising the MCT transition temperature with respect to its c = 0 value T_d. This picture is only valid up to the temperature, T_o(c), where Υ(c,T) vanishes. We have analyzed the dynamics and the statics of the spherical p-spin model [details will be presented in a forthcoming paper, see also ref. 33] and found that indeed T_d and T_K are shifted upward by freezing particles. The lines T_d(c) and T_K(c) join at the point at which both transitions disappear, see the phase diagram for the p = 3 spin model in the top box of Fig. 1.

Critical Properties and Renormalization Group Analysis

In order to go beyond mean field theory and obtain the divergence of length and time scales one has to take into account nonperturbative fluctuations. To this aim we use the approach recently developed in ref. 33 and generalize it to the case of pinned particles. The analysis is quite cumbersome. In the following we shall only discuss the physical scenario that emerges from our computations; technical details will be presented elsewhere, see also SI Text. Let us first informally review a few important points related to the RFOT theory and the RG analysis of ref. 33. The order parameter of RFOT is the global overlap 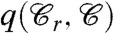between a reference equilibrium configuration, 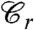, and another equilibrium one, 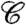, that is constrained to be equal to 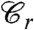on the boundary of the sample. An overlap equal to zero (or, depending on the normalization, to a trivial small value of liquid phase) is characteristic of the liquid phase for which boundary conditions has no effect on the bulk behavior. When the overlap q becomes different from zero long-range amorphous order sets in: the system is in the ideal glass phase, frozen in the same amorphous structure to which 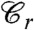belongs. Thus, the discontinuous jump of the global overlap 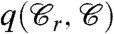is the signature of the ideal glass transition. This transition is driven by the decrease of the configurational entropy, which plays the role of an ordering field favoring the zero overlap—liquid—phase. Including, in a renormalization group sense, nonperturbative fluctuations over the length scale l one finds (33) that the renormalized liquid is characterized by a configurational entropy s_c(l) and a term Y(l), akin to a surface tension in the replica field theory formulation. The latter is related to the surface configurational entropy loss between high and low overlap regions^§ . The scaling with l of the terms s_c(l) and Y(l) is s_cl^d and Yl^d-1 for l ≪ l_PS, where the values of s_c and Y are obtained from mean field theory. For l≫l_PS one instead obtains (33) Y(l) → 0. Correspondingly, amorphous order cannot be stabilized above l_PS because Y(l) becomes much smaller than s_c(l), hence, even by fixing the overlap to one on the boundary of a closed region of size l≫l_PS the system thermodynamically prefers to remain in the low overlap state inside this region^¶. At the transition, when s_c vanishes, the point-to-set length diverges.

How does the scenario depicted above change when one pins particles at random? By doing that, one forces the local overlap to a high value in microscopic regions which are Poisson-distributed inside the sample. Close to all these regions, the system is subjected to an extra field of the order of Y, favoring the high-overlap state. This field opposes the global entropic driving force, which instead favors the low overlap state. In consequence, it is easy to grasp that by increasing the fraction of pinned particles one can induce a transition toward the high overlap state before the configurational entropy of the unconstrained system vanishes, as found within mean field theory. The RG analysis becomes more complicated than the one for c = 0 because the local field induced by pinning particles is located in random positions. Because of this quenched disorder, Y(l) and s_c(l) become random variables and one has to follow the RG flow of their probability law. We have generalized the analysis of ref. 33 to this case and found that the flow is qualitatively identical to the one of the zero-temperature Random Field Ising model in an external field H: Y and s_c respectively play the role of the coupling J and the external field H, whereas c determines the strength of the disorder (the larger is c, the stronger is the disorder) (32).

Let us first describe and discuss our results for temperatures slightly above T_K. In this case, by increasing c toward its critical value we find results very similar to the ones obtained approaching T_K at c = 0 because upon renormalization the variances of Y(l) and s_c(l) become much smaller than the averages. Thus, the random variables Y(l) and s_c(l) are just characterized by their means as in the c = 0 case. The averages surface tension and the average configurational entropy are found to increase as 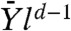and 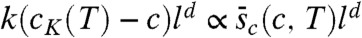respectively. 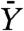and k depend on T and c and are of the order of one, whereas 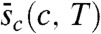is the average configurational entropy density for a given value of c and T; it goes to zero linearly at c_K(T). The length for which Y(l) becomes of the order of s_c(l) is the point-to-set length, l_PS(c,T), for the pinned system (which is much larger than the one for the unconstrained liquid). For l≫l_PS one finds (32) that Y(l) → 0 and hence one cannot stabilize amorphous states. The scaling of l_PS with (c_K(T) - c) is the usual one:

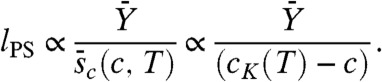As already discussed in ref. 33, the physical picture resulting from the RG analysis is that the renormalized system on the point-to-set length scale is like a liquid at its “onset temperature”. The difference with a normal liquid is the typical value of the free-energy contributions, which respectively are of the order of 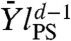and 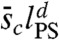, both very large compared to the temperature. This fact suggests that the typical relaxation time follows an Arrhenius law and, therefore, a generalized Vogel-Fulcher-Tamman relation (29) where the divergence of relaxation time is associated to the vanishing of the configurational entropy:

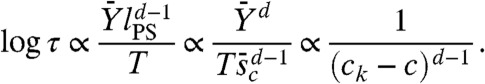Important differences with the c = 0, T = T_K case emerge when varying c at higher temperatures above T_K. Physically, the main consequence of fixing a higher reference temperature is to increase the value of the configurational entropy of the unconstrained liquid. Hence, the fraction of pinned particles needed to counterbalance this effect and to induce the transition increases, see Fig. 1. By doing so the disorder increases too. We find that above a certain temperature, T_h, disorder fluctuations induced by pinned particles are so strong to make the glass transition disappear. We studied the RG flow approaching T_h. We found that the glass transition line ends in a second order transition point and that the long-distance physics is given by the RFIM zero-temperature critical fixed point. This conclusion could be expected (34) on the basis of the results of ref. 35. In this case, Y(l) and s_c(l) remains fluctuating random variables upon renormalization. Calling ν the correlation length exponent for the RFIM [and using the standard notation for the other exponents (36)], for T < T_h, we find that only for l_PS≫1/(T_h - T)^ν the usual scaling laws discussed above are obtained. Instead, for l_PS ≪ 1/(T_h - T)^ν, one finds: 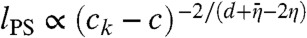and 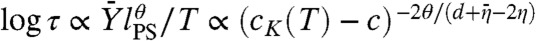. Because in d = 3 the exponent θ is very close to 1.5 and 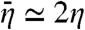, the relaxation time is expected to grow in this regime almost according to the Vogel-Fulcher-Tamman law but with respect to the variable c_K(T) - c instead of T - T_K; i.e., log τ ∝ (c_K(T) - c)^-1. A final important outcome of the RG analysis concerns the T - c phase diagram. In particular we find that the phenomenological law c_K(T) ∝ s_c(T)/Y(T) is quite well obeyed for T < T_h and that the temperature T_h corresponding to the endpoint of the critical line is depressed with respect to its mean field value T_o. The phase diagram in the lower box^|| of Fig. 1 corresponds to T_d/T_K ≃ 1.4, a value typical of fragile liquids like OTP (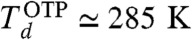, 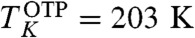) (19, 21). In this case T_h is very close to T_d: T_h ≃ 280 K. Within our approximate treatment the decrease of T_h with respect to T_o depends on the ratio of the mode coupling temperature to the Kauzmann temperature. We found that smaller values of T_d/T_K lead to an increase of T_h/T_d, that can reach values larger than one.

Other Ways of Freezing Particles and the Role of Disorder

Pinning particles at random in space introduces a lot of quenched disorder and, hence, leads to a substantial decrease of the endpoint of the c_K(T) line. In order to reduce this effect, one can pin the particles closest to an ordered template; e.g., a periodic one. This procedure leaves as source of quenched disorder, the fluctuations of the reference equilibrium configuration only (35, 37). In this case we expect similar results, the only change being the precise form of c_K(T) and the value of T_h, which is expected to be higher. Another case considered in the literature (12) corresponds to freezing all particles outside two walls at distance ℓ. Following the Kac analysis of Franz (23), one finds qualitatively the mean field phase diagram of the top box of Fig. 1, where now ℓ is the control parameter playing the role of c^-1. The transition takes place at a value of ℓ proportional to the point-to-set length of the unconstrained system**. The effect of disorder is not taken into account in the Kac analysis. Because the positions of the particles pinned beyond the walls are random, the constraint on the coarse-grained overlap is not homogeneous close to the walls and lead to an effective quenched disorder. Applying our RG treatment to the two wall case and including the effect of disorder, one would find results similar to the previous ones but with d → d - 1. This result has two important consequences. First, as for randomly frozen particles, the mean field phase diagram is modified: the endpoint of the critical glass transition line takes place at a temperature less than the onset temperature computed by mean field or Kac-like techniques. Second, because the system inside the two walls is d - 1 dimensional, the lower critical dimension is higher than the one expected in the case of randomly frozen particles. No first-order transition takes place in two dimensions for the Ising model in presence of quenched randomness (38). Because within our framework glass transitions are related to the first order phase transitions of the RFIM, we conclude that glass transitions can be only induced in systems with dimensions equal to four or higher in the case of two walls. Instead, in the case of randomly pinned particles, also three dimensional systems display glass transitions when c is increased.

The final case we shall discuss corresponds to particles that are frozen not from an equilibrium configuration but instead completely at random; i.e., from an infinite-temperature configuration. This procedure is akin to studying liquids in presence of external quenched randomness (39), a case relevant for porous media (25). Because the quenched disorder is not tailored to an equilibrium configuration at temperature T, we do expect qualitative changes. Indeed, the works (25, 39) find a phase diagram qualitatively similar to the one of the p-spin spherical model in an external magnetic field: above a certain fraction c the glass transition becomes continuous (the Edwards-Anderson parameter has no discontinuous jump) but does not disappear; moreover, the glass phase for c > c_K cannot be reached from high temperature without crossing a transition line, contrary to what is shown in Fig. 1. We shall discuss our phase diagram in more detail in the following.

Glass Transitions Induced by Random Freezing: Novelties, Consequences, and Numerical Verifications

The most striking feature of the phase diagram shown in Fig. 1 is that it is possible to follow a path that connects the liquid and the glass phase without crossing any phase transition, as for the liquid-gas phase transition^†† (see ref. 24 for more details). In fact, at high T or large c long-range amorphous order cannot be present because thermal fluctuations or disorder strength are too strong. The system is therefore in a pinned liquid state that changes smoothly from the high T-low c region to the low T-high c one. A crucial consequence is that one does not have to equilibrate the system on impossibly large time scales or to solve a daunting optimization problem in order to reach the ideal glass. In practice, one has just to equilibrate an unpinned system and then pin a fraction c > c_K of particles. Because immediately after pinning the system is still at equilibrium one can then sample dynamically the ideal glass state, which should be relatively fast because the relaxation time corresponds just to the equilibration inside an amorphous state. Actually, the behavior for c > c_K is quite unusual; in this regime a single amorphous state has free energy lower than all the other ones, even taking into account their configurational entropy. Therefore, on the basis of the usual RFOT arguments one expects a finite PS length and a finite relaxation time for c↓c_K ^‡‡. Because of this fact, one should be able to perform much more detailed investigations of the glass transition. In particular, the belief that it is impossible to prove (or disprove) the existence of the ideal glass transition because the time scale for equilibration diverges so rapidly maybe ill founded. For instance, the RFIM also has a transition with activated dynamic scaling and despite numerical difficulties several properties of the transition have been obtained by numerical simulations. The main difference between the transition of unconstrained supercooled liquids and the RFIM’s one is that for the former the low temperature phase—the ideal glass—is not known. This circumstance prevents one from approaching the glass transition from both ends, from devising clever algorithms to equilibrate the systems, etc. In the case of frozen particles, the low temperature phase is well known. Thus, one can endeavor to demonstrate the existence of the ideal glass transition by applying standard statistical physics techniques. Ideally, one could first study the transition at a finite temperature well above T_K, at a finite c_K(T). This investigation should already lead to major results. Afterwards, by decreasing the temperature, one could measure the c_K(T) line and show, at least by extrapolations, the existence of the ideal glass transition for usual, unconstrained, supercooled liquids. Even though not impossible, numerical verifications will be very challenging (work is underway by L. Berthier and W. Kob). We think that one should start first by studying finite-size scaling. If there is indeed a transition, the averaged probability distribution function of the overlap with the reference configuration should behave as in first order phase transitions: a single peak at small (large) overlap below (above) c_K in the thermodynamic limit^§§. Only at c_K, a two peak structure should be present. The corresponding finite size scaling is expected to be similar to the one of first order phase transitions in presence of quenched randomness, see e.g., (42).

Conclusions

In this work, motivated by the numerical results (12–15) we have studied the effect of pinning particles of an equilibrated supercooled liquid configuration. We have focused on geometries such that the number of unfrozen particles is infinite. In these settings, pinning can lead to a true phase transition and not just a cross-over like in refs. 8, 9. Indeed, we have shown that pinning leads to a decrease of the configurational entropy and, within the RFOT theory, to an ideal glass transition when the confinement parameter c is increased, even for relatively high temperatures, e.g., close to the Mode-Coupling transition temperature. The relaxation time scale^¶¶ is infinite along the c_K(T) line and finite everywhere else, in particular for c > c_K(T). Although in the latter regime motion of single particles can be quite slow, as it is in a crystal, we predict that if properly equilibrated the system should show a nonmonotonous behavior of the relaxation time as a function of c for T < T_h.

Pinning particles may be expected to generically slow down the dynamics whatever is the correct underlying theory [RFOT theory, facilitation theories (2), frustration limited domains (3), etc.]. However, the nonmonotonous behavior of the relaxation time and the concomitant thermodynamic phase transition are expected within RFOT only***, thus opening the way to new and crucial tests of glass transition theories. For example, in the case of kinetically constrained models (KCM), we expect that by increasing c above a critical value c_d one can induce a dynamical glass transition, nonetheless this would not be accompanied by a thermodynamic one. Moreover, the kinetic constraint can be violated in reality. Thus, the dynamically arrested phase and the related dynamical transition (if any) would be spurious and the dynamics above c_d would proceed via alternative unknown relaxation mechanisms, which should lead to a physical behavior quite different from the one expected within RFOT. A detailed study of the effect of pinning particles from the dynamical facilitation point of view would be worthwhile. A first step in this direction has been done very recently in ref. 43. It was observed that the pinning particles procedure leads to a peaked behavior of the relaxation time as a function of c. However, approaching the peak concentration, 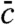, the relaxation time does not show a steep increase, furthermore at 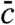only a thermodynamic cross-over, not a phase transition, takes place—a phenomenology highly different from the one expected within the RFOT theory. On the contrary, as noticed in the introduction, the simulation results (13, 14), in particular the recent ones (12, 15), do show a dramatic increase of the relaxation time even for weak pinning. This observation is in complete agreement with our predictions. In order to fully validate (or disprove) our scenario, studies focusing also on intermediate and strong pinning are needed. We notice that our approach shares important similarities with two other approaches: the one of Franz and Parisi (44), consisting in biasing the thermodynamics by favoring configurations having a high overlap with an equilibrium one; and the one of Garrahan, Chandler and coworkers (46), consisting in biasing the dynamics by favoring dynamical trajectories with low dynamical activity. The mean field result analysis of the former leads to a phase diagram that is indeed comparable to ours (the bias strength playing the role of c). Some numerical simulations of three dimensional liquids provide promising results in favor of this similarity also for real liquids (41, 44). Theoretical analysis of KCMs and numerical simulation of glass-forming liquids (46, 47) show that also in Garrahan and Chandler approach one finds a phase diagram similar to the one in Fig. 1. There are however important fundamental differences in this case. The main one is that the phase transition taking place at c_K(T) and shown in Fig. 1 exists within the RFOT theory only, contrary to the dynamical transition studied in refs. 46, 47 that takes place in facilitation-based models but also in those described by the RFOT theory (see ref. 48).

We end this paper by stressing once again that the ideal glass phase can be obtained easily in the case of randomly pinned particles. Hence, if a transition indeed takes place at c_K, it can be very likely studied thoroughly, in particular by finite-size scaling. Studies can be performed in supercooled liquids by numerical simulations and also on colloids by experiments using optical trapping. Because we find that the critical properties for c_K - c → 0⁺ and T > T_K are the same ones as those of the ideal glass transition when T → T_K for c = 0, studying the effect of freezing particles appears to be a new and promising way to understand the glass transition of supercooled liquids.