Entropy-Based Information Gain Approaches to Detect and to Characterize Gene-Gene and Gene-Environment Interactions/Correlations of Complex Diseases

Abstract

For complex diseases, the relationship between genotypes, environment factors and phenotype is usually complex and nonlinear. Our understanding of the genetic architecture of diseases has considerably increased over the last years. However, both conceptually and methodologically, detecting gene-gene and gene-environment interactions remains a challenge, despite the existence of a number of efficient methods. One method that offers great promises but has not yet been widely applied to genomic data is the entropy-based approach of information theory. In this paper we first develop entropy-based test statistics to identify 2-way and higher order gene-gene and gene-environment interactions. We then apply these methods to a bladder cancer data set and thereby test their power and identify strengths and weaknesses. For two-way interactions, we propose an information-gain approach based on mutual information. For three-ways and higher order interactions, an interaction-information-gain approach is used. In both case we develop one-dimensional test statistics to analyze sparse data. Compared to the naive chi-square test, the test statistics we develop have similar or higher power and is robust. Applying it to the bladder cancer data set allowed to investigate the complex interactions between DNA repair gene SNPs, smoking status, and bladder cancer susceptibility. Although not yet widely applied, entropy-based approaches appear as a useful tool for detecting gene-gene and gene-environment interactions. The test statistics we develop add to a growing body methodologies that will gradually shed light on the complex architecture of common diseases.

Introduction

Complex diseases result from mutual interactions between genetic variants and environmental factors and our understanding of their genetic architecture has considerably grown over the last decades. In recent years, there has been great enthusiasm to detect and to characterize gene-gene and gene-environment interactions of complex diseases using genome data [Mahdi et al., 2009; Moore and Williams, 2009; van-der-Woude et al., 2010; Wan et al., 2010; Zhang and Liu, 2007]. However, despite considerable effort, identifying and characterizing susceptibility genes of common complex human diseases and their network of interactions remains a great challenge. The challenge is both conceptual and technical: conceptually, it is not always clear how to define the interactions. There are two different arguments about gene-gene and gene-environment interactions: (1) statistical interaction, (2) biological interaction. Technically, traditional statistical approaches may not be useful because of the complexity and nonlinearity between complex traits and genetic, environment factors.

In traditional statistical models, i.e., linear models and generalized linear models such as logistic regressions, the genetic and environmental effects are decomposed into main and interaction effects [Fisher, 1918]. The statistical interactions are deviations from the main effects and don’t make sense unless the main effect is significant. Moreover, the traditional statistical models may not work for high dimension sparse data. For instance, logistic regression models including interaction terms can fail to converge when some cells contain few individuals [Andrew et al., 2006]. Yet, one advantage of traditional statistical models is that the related theory is very mature and user-friendly softwares are available. For instance, variance partitioning and ANOVA are standard procedure in SAS for data analysis and model selection.

Biological interactions, on the other hand, happen at the cellular level and result from physical interactions between biomolecules such as DNA, RNA and proteins [Moore and Willams, 2009; Bateson, 1909; Bateson, 2002]. The biological gene-gene and gene-environment interaction is the interdependence between genetic and environmental factors and may cause complex diseases. In complex diseases, the relationship between genotypes, environmental factors and disease phenotypes is usually complex and nonlinear. Thus, biological interaction makes sense and it is valid in describing the complicated relation between genetic, environmental factors and disease phenotypes. In the absence of main effects, the biological gene-gene and gene-environment interactions may exist and can be important [Frankel and Schork, 1996]. However, the related theory to detect and to characterize the biological gene-gene and gene-environment interactions is not well-developed. There is a need to develop powerful methods and user-friendly softwares to identify and to interpret the complex genetic architecture of complex traits.

By using multiple genetic markers and environmental factors in analysis, it is usually a high-dimensional problem. For instance, assume we have two single nucleotide polymorphism (SNP) markers. Each of the two SNP has 3 genotypes, and then there are 9 genotype combinations if we consider the two SNPs simultaneously. If we add one environmental factor which has 2 categories, e.g., smoking vs non-smoking, there are 2 × 9 = 18 genotype-environment combinations if we consider the two SNPs and the environmental factor simultaneously. Hence, one needs to handle the high-dimensional data.

In the multifactor dimensionality reduction (MDR) procedure, high dimensional genetic data are collapsed into a single dimensional variable allowing for such data to be analyzed [Hahn et al., 2003; Lou et al., 2007; Ritchie et al., 2001, 2003a, 2003b, 2004; Velez et al., 2007]. MDR is a non-parametric procedure that makes no assumption about the relationship between the phenotypes, the genetic, and the environmental factors. Since there was no alternative and powerful procedure, Andrew et al. [2006] ran logistic regression models to test three way interaction to replicate the findings of MDR. Unfortunately, the logistic regression models failed to converge due to the sparse nature of bladder cancer data. Thus, it is not only interesting but also necessary and important to develop novel statistical methods to detect and to characterize the complex biological gene-gene and gene-environment interactions of complex traits.

The traditional statistical models can not properly fit the nonlinear relationship between genotypes, environment factors and disease phenotypes in the absence of main effects. It may not be able and useful to model biological interactions. For the bladder cancer data of Andrew et al. [2006], the main effects of genetic polymorphisms were not observed and it is unclear if logistic regressions may fit the data well. The failure of convergence may be due to invalidness of the logistic regression model itself.

It is well-known that information theory based on entropy function is widely used to study nonlinear problems and complex system. The entropy function is a nonlinear transformation of interested variables. The entropy is commonly used in information theory to measure the uncertainty of random variables. The entropy-based approach is likely to be very useful to study the nonlinear relationship between genotypes, environment factors and phenotypes and to interpret the gene-gene and gene-environment interactions of complex diseases [Dong et al., 2008; Kang et al., 2008; Nothnagel et al., 2002]. In this article, we develop entropy-based approaches to detect and to characterize gene-gene and gene-environment interactions of complex diseases.

We start with the definition of entropy for genetic markers and environmental factors. Then, 2-way mutual information and information gain (IG) are introduced to describe gene-gene and gene-environment interactions. One idea of this article is to reduce high dimensional data to be a one-dimensional variable, and then to construct a χ²-distribution statistic to test gene-gene interaction of complex diseases. We considered two di-allelic markers A and B in a case-control design. By using the information gain function, we reduce the 9-dimensional genotype combinations of the two markers to be a one-dimensional variable to construct the information gain based test T_IG. The method can be applied to test 2-way gene-environment interaction by treating the levels of environment factor as genotypes of a marker, i.e., one marker is replaced by the environment factor.

To generalize the 2-way methods to handle multiple K-way cases, K ≥ 3, we need to distinguish two different concepts in information theory: interaction information and total correlation information (TCI). In 2-way case, the two concepts are the same. However, they are different in multiple K-way cases, K ≥ 3. Roughly, the interaction information among multiple factors is the amount of information that is common to all the factors. The total correlation information, however, describes the total amount of dependence among all the factors. The K-way total correlation information can be decomposed into a summation of all lower and same order k-way interaction information, 2 ≤ k ≤ K [Jakulin, 2005].

We generalize the 2-way methods to detect and to characterize multiple K-way gene-gene and gene-environment interactions and correlations, K ≥ 3. For multiple K-way interactions, the K-way interaction information is proposed to extend the 2-way mutual information. For multiple K-way correlations, total correlation information is used. Correspondingly, the interaction information gain (IIG) and total correlation information gain (TCIG) can be defined as one-dimensional variables for case-control data. Thus, high-dimensional genetic data are collapsed as one-dimension variables via the information gains. Using the one-dimensional variables, test statistics are constructed which are ${\chi }_1^2$-distributed. Compared with the naive χ² test statistics which usually have high degrees of freedom, the proposed information gain tests are easy to implement. In addition, the naive χ² tests are not always implementable due to sparse nature of high dimension genetic data.

Simulation study is performed to evaluate the robustness of the proposed test statistics by type I error rate calculations. Power analysis is carried out to show the usefulness of the proposed methods. The method is applied to bladder cancer data to explore gene-gene and gene-environment interactions and correlations of SNPs and smoking status with the disease. We use the bladder cancer data to show a forward selection procedure for the final model selection, and the procedure can be applied to the study of other complex traits.

Methods

In information theory, entropy measures the uncertainty associated with a random variable or a random system [Shannon, 1948]. The entropy H(X) of a discrete random variable X is defined by

$$H(X)=-\text{E}[logP(X)]=-\sum _{x\in \mathcal{X}}p(x)logp(x),$$ (1)

where p(x) = P(X = x), x ∈ , is the probability mass function of the random variable X, and 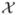is a finite set (e.g., {1, 2, ···, n}) or an enumerable infinite set (e.g., {1, 2, ···}) [Cover and Thomas, 2006]. The log is to the base 2. By definition, 0 log 0 = 0. The higher the entropy H(X), the the higher the uncertainty we may predict the outcome about the variable X. The concept of the Shannon entropy has been used to select interesting combinations of polymorphisms for evaluating and for visualizing the information gain, which in turn allows for the detection of gene-gene and gene-environment interactions [Jakulin, 2005; Jakulin and Bratko, 2003, 2004; Jakulin et al., 2003; Moore et al., 2006; Wu et al., 2009].

Genotype and Environment-Based Entropy

For a case-control study design, we denote the disease status of an individual by D, and attribute the value D = 0 to healthy individuals (control) and the value D = 1 to affected ones (case). For explanation purposes, let us consider two di-allelic markers A and B (e.g., SNPs) and an environmental exposure E. Let us denote the alleles of markers A and B by A, a and B, b, respectively, and code the environmental factor E as E = 0, 1, 2 (e.g., non smoking, < 35 pack years, ≥ 35 pack years). There are three genotypes at marker A (AA, Aa, aa) and three genotypes at marker B (BB, Bb, bb). For convenience, we call each of the genotypes G_A at marker A and G_B at marker B by the number of A and B alleles present. That is,

$$G_A=\{\begin{array}{ll}2\hfill & AA\hfill \\ 1\hfill & Aa\hfill \\ 0\hfill & aa\hfill \end{array}\text{and}{G}_B=\{\begin{array}{ll}2\hfill & BB\hfill \\ 1\hfill & Bb\hfill \\ 0\hfill & bb\hfill \end{array}.$$ (2)

In the literature, genetic markers and environmental factors are treated as attributes [Jakulin and Bratko, 2003; Jakulin et al., 2003]. Using the entropy definition (1), we can define the entropy H(A) of marker A in the general population and the conditional entropy H(A|D) in the affected population as

$$\begin{array}{l}H(A)=-\sum _{i=0}^{2}P(G_A=i)logP(G_A=i),\\ H(A\mid D)=-\sum _{i=0}^{2}P(G_A=i\mid D=1)logP(G_A=i\mid D=1).\end{array}$$ (3)

Similarly, we may define the entropy H(B) of marker B in the general population and the conditional entropy H(B|D) in the affected population. For the environmental factor E, its entropy H(E) in the general population and its conditional entropy H(E|D) in the affected population can be defined, accordingly. When the markers A and B are combined, the entropy H(A, B) in the general population and the conditional entropy H(A, B|D) in the affected population are:

$$\begin{array}{l}H(A,B)=-\sum _{i=0}^2\sum _{j=0}^{2}P(G_A=i,G_B=j)logP(G_A=i,G_B=j),\\ H(A,B\mid D)=-\sum _{i=0}^2\sum _{j=0}^{2}P(G_A=i,G_B=j\mid D=1)logP(G_A=i,G_B=j\mid D=1).\end{array}$$ (4)

Similarly, when one marker (e.g., A) and the environmental factor E are combined, the entropy H(A, E) in the general population and the conditional entropy H(A, E|D) in the affected population are:

$$\begin{array}{l}H(A,E)=-\sum _{i=0}^2\sum _{e=0}^{2}P(G_A=i,E=e)logP(G_A=i,E=e),\\ H(A,E\mid D)=-\sum _{i=0}^2\sum _{e=0}^{2}P(G_A=i,E=e\mid D=1)logP(G_A=i,E=e\mid D=1).\end{array}$$ (5)

The entropy H(B, E) in the general population and the conditional entropy H(B, E|D) in the affected population can be defined in a similar manner. When both markers and the environmental factor are combined, the entropy H(A, B, E) in the general population and the conditional entropy H(A, B, E|D) in the affected population are:

$$\begin{array}{l}H(A,B,E)=-\sum _{i=0}^2\sum _{j=0}^2\sum _{e=0}^{2}P(G_A=i,G_B=j,E=e)logP(G_A=i,G_B=j,E=e),\\ H(A,B,E\mid D)=-\sum _{i=0}^2\sum _{j=0}^2\sum _{e=0}^{2}P(G_A=i,G_B=j,E=e\mid D=1)logP(G_A=i,G_B=j,E=e\mid D=1).\end{array}$$ (6)

2-Way Mutual Information and Information Gain

The mutual information measures the interaction between two markers. In the general population, the mutual information of markers A and B, I(A, B), is defined as [Shannon, 1948; Cover and Thomas, 2006]

$$\begin{array}{l}I(A,B)=H(A)+H(B)-H(A,B)\\ =\sum _{i=0}^2\sum _{j=0}^{2}P(G_A=i,G_B=j)log\frac{P(G_A=i,G_B=j)}{P(G_A=i)P(G_B=j)}.\end{array}$$ (7)

For the two markers A and B, I(A, B) ≥ 0, and I(A, B) = 0 if and only if G_A and G_B are independent (i.e., P(G_A = i, G_B = j) = P(G_A = i)P(G_B = j), p28 of Cover and Thomas [2006]).

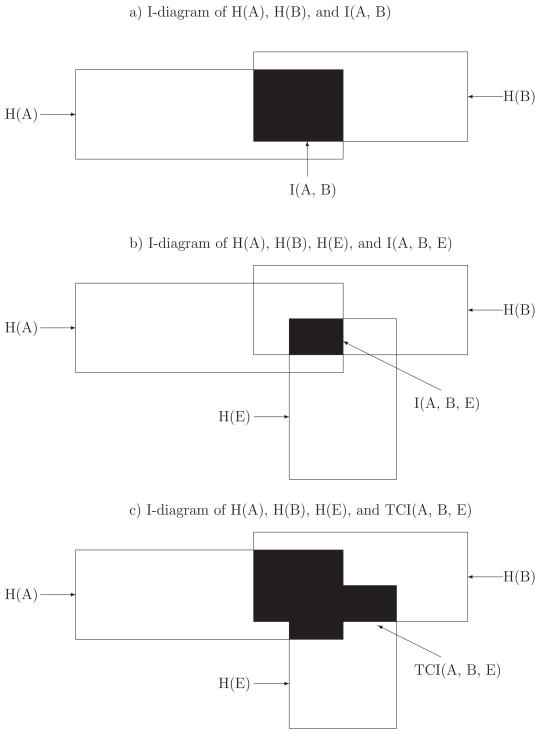
Figure 1a) shows an I-diagram of H(A), H(B) and I(A, B), and it is equivalent to a Venn diagram in set theory [Chanda et al., 2007; McGill, 1954; Yeung, 1991]. The left and right rectangles illustrate the magnitude of H(A) and H(B), respectively, and their overlap, colored in black, corresponds to the magnitude of the I(A, B). In the affected population, the mutual information of markers A and B is defined as

Figure 1.

a) The I-diagram of entropies H(A), H(B), and 2-way mutual information I(A, B); b) The I-diagram of entropies H(A), H(B), H(E), and 3-way interaction information I(A, B, E); c) The I-diagram of entropies H(A), H(B), H(E), and 3-way total correlation information TCI(A, B, E).

$$\begin{array}{l}I(A,B\mid D)=H(A\mid D)+H(B\mid D)-H(A,B\mid D)\\ =\sum _{i=0}^2\sum _{j=0}^{2}P(G_A=i,G_B=j\mid D=1)log\frac{P(G_A=i,G_B=j\mid D=1)}{P(G_A=i\mid D=1)P(G_B=j\mid D=1)}.\end{array}$$ (8)

I(A, B|D) measures the interaction between markers A and B given the disease. For the two markers A and B, I(A, B|D) ≥ 0, and I(A, B|D) = 0 if and only if G_A and G_B are conditionally independent given the disease (i.e., P(G_A = i, G_B = j|D = 1) = P(G_A = i|D = 1)P(G_B = j|D = 1)).

The information gain of markers A and B in the presence of a disease can be defined as the difference between the mutual information in the affected population and that in the general population [Jakulin and Bratko, 2003, 2004; Jakulin et al., 2003; McGill, 1954; Moore et al., 2006]

$$IG(AB\mid D)=I(A,B\mid D)-I(A,B).$$ (9)

If the disease and the two markers are independent (i.e., P(G_A = i, G_B = j|D = 1) = P(G_A = i, G_B = j)), then I(A, B|D) = I(A, B) and the information gain IG(AB|D) is equal to 0. In that case, the interaction between markers A and B does not contribute to predicting disease risk. Hence, we can determine whether the gene-gene interaction between markers A and B predicts disease status by testing if the difference between estimates of mutual information is zero. Based on this rationale, we can build test statistics for practical applications.

For marker A or B and environmental factor E, the mutual information and the conditional mutual information can be defined as above. The information gain of marker A and environmental factor E in the presence of a disease can be defined as the difference IG(AE|D) = I(A, E|D) − I(A, E). If the information gain is null, i.e., IG(AE|D = 0), the marker A and the environmental factor E are independent of the disease status and the interaction between A and E does not predict disease status. Likewise, if the marker B and the environmental factor E are independent of the disease status D, then there is no information gain (i.e., IG(BE|D) = I(B, E|D)−I(B, E) = 0) and the interaction between B and E does not predict disease status.

3-Way Interaction Information and Total Correlation Information

The information gains IG(AB|D), IG(AE|D), and IG(BE|D) represent 2-way interaction gains of two attributes given a disease. If we consider the three attributes A, B and E simultaneously, we can define the 3-way interaction information gain and the total correlation information as follows [Chanda et al., 2007; Han, 1980; McGill, 1954; Watanabe, 1960; Yeung, 1991]. In the general population, the 3-way interaction information of markers A and B and environmental factor E is defined as [Cover and Thomas, 2006, p49].

$$I(A,B,E)=-H(A)-H(B)-H(E)+H(A,B)+H(A,E)+H(B,E)-H(A,B,E).$$

The 3-way interaction information I(A, B, E) contains interactions that can not be explained by the 2-way mutual information I(A, B), I(A, E), and I(B, E). It represents the gain or loss of information by adding one attribute to a pair of attributes. Hence, the 3-way interaction information among attributes A, B and E can be understood as the amount of information that is common to all the attributes, but not present in any subset. The interaction information can be negative or positive.

Figure 1b) shows an I-diagram of H(A), H(B), H(E), and I(A, B, E) for two markers A and B and an environmental factor E [Chanda et al., 2007; McGill, 1954; Yeung-1991]. In Figure 1b), the black region corresponds to the magnitude of the I(A, B, E). Compared to Figure 1a), Figure 1b) includes an additional rectangle corresponding to the magnitude of H(E). If one attribute (e.g., the environmental factor E) is independent of two dependent attributes (e.g., the markers A and B), the interaction information I(A, B, E) will be 0. This is because P(G_A = i, G_B = j, E = e) = P(G_A = i, G_B = j)P(E = e) implies P(G_A = i, E = e) = P(G_A = i)P(E = e) and P(G_B = j, E = e) = P(G_B = j)P(E = e), and thus I(A, B, E) = 0. If all three attributes are independent, the interaction information I(A, B, E) is of course equal to 0. Hence, I(A, B, E) is an interaction among all three attributes.

The total correlation information is defined as the difference between the joint entropy H(A, B, E) and the three individual entropies H(A), H(B) and H(E), i.e.,

$$\begin{array}{l}\mathit{TCI}(A,B,E)=H(A)+H(B)+H(E)-H(A,B,E)\\ =I(A,B)+I(A,E)+I(B,E)+I(A,B,E).\end{array}$$ (10)

The total correlation information describes the total amount of dependence among the three attributes A, B and E. It is always positive, or zero if and only if all the three attributes are independent, i.e., P(G_A = i, G_B = j, E = e) = P(G_A = i)P(G_B = j)P(E = e). It will be different from zero even if only one pair of attributes are dependent. For instance, it is non-zero if the genetic markers A and B are independent of the environmental factor E but A and B are dependent or in linkage disequilibrium. Figure 1c) shows an I-diagram of H(A), H(B), H(E), and TCI(A, B, E) for two markers A and B and an environmental factor E [Chanda et al., 2007; McGill, 1954; Yeung-1991].

The second equality of relation (10) shows that the total correlation information TCI(A, B, E) is equal to the summation of all 2-way mutual information I(A, B), I(A, E), I(B, E), and 3-way interaction information I(A, B, E). Thus, the 2-way mutual information and the 3-way interaction information can be seen as a decomposition of a 3-way dependency into a sum of 2-way and 3-way interactions [Jakulin, 2005]. The existence of 3-way correlations (i.e., TCI(A, B, E) ≠ 0)) indicates the existence of some 2-way or 3-way interactions. On the other hand, the existence of 2-way or 3-way interactions can lead to 3-way correlations.

In the disease population, the 3-way interaction information I(A, B, E|D) and total correlation information TCI(A, B, E|D) of markers A and B and environmental factor E are defined as

$$\begin{array}{l}I(A,B,E\mid D)=-H(A\mid D)-H(B\mid D)-H(E\mid D)+H(A,B\mid D)+H(A,E\mid D)+H(B,E\mid D)-H(A,B,E\mid D),\\ \mathit{TCI}(A,B,E\mid D)=H(A\mid D)+H(B\mid D)+H(E\mid D)-H(A,B,E\mid D).\end{array}$$

The interaction information gain IIG(ABE|D) and the total correlation information gain TCIG(ABE|D) of markers A and B and environmental factor E in the presence of a disease can be defined as the differences [Jakulin and Bratko, 2003, 2004; Jakulin et al., 2003; McGill, 1954; Moore et al., 2006]

$$\begin{array}{l}\mathit{IIG}(\mathit{ABE}\mid D)=I(A,B,E\mid D)-I(A,B,E),\\ \mathit{TCIG}(\mathit{ABE}\mid D)=\mathit{TCI}(A,B,E\mid D)-\mathit{TCI}(A,B,E).\end{array}$$ (11)

If the disease is independent of the two markers and the environmental factor E, I(A, B, E|D) = I(A, B, E) and the information gain IIG(ABE|D) is equal to 0. Similarly, TCI(A, B, E|D) = TCI(A, B, E) and the total correlation information gain TCIG(ABE|D) is equal to 0. Hence, we can test for the existence of gene-gene and gene-environment interactions or correlations between the disease and two markers A and B and the environmental factor E by testing if IIG(ABE|D) and TCIG(ABE|D) are zero. Based on this rationale, we can build test statistics for practical applications.

K-Way Interaction Information and Total Correlation Information

Suppose that we are interested in interactions or correlations between the disease and an arbitrary number K of attributes = (A₁, ···, A_K), which can be genetic markers or environmental factors. For simplicity, we assume that each A_i can take three values 0, 1, or 2. For a vector of realization a⃗ = (a₁, ···, a_K) of = (A₁, ···, A_K), we denote the joint probabilities as P_a⃗ = P(A₁ = a₁, ···, A_K = a_K) = P_a1···aK in the general population and as Q_a⃗ = P(A₁ = a₁, ···, A_K = a_K|D = 1) = Q_a1···aK in the affected population. Based on the joint probabilities, we can define the entropies H( ) = H(A₁, ···, A_K) = −Σ_a⃗ P_a⃗log P_a⃗ and H( | D) = H(A₁, ···, A_K | D) = −Σ_a⃗ Q_a⃗ log Q_a⃗.

For a subset 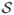= (A_i1, A_i2, ···, A_in) ⊆ = (A₁, A₂, ···, A_K), we can define the related entropies H( 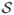) and H( 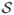| D) in a similar manner. Here ⊆ means that 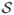is a subset of and it can be equal to = (A₁, A₂, ···, A_K). For a realization s⃗ of 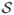= (A_i1, A_i2, ···, A_in), the marginal probabilities are denoted as P_s⃗ and Q_s⃗. For individual attributes A₁, ···, A_K, the marginal probabilities and entropies are denoted as P_{a1, ···, ·,} ···, P_·,···,aK, H(A₁), ···, H(A_K), Q_a1,···,·, ···, Q_·,···,aK, H(A₁ | D), ···, and H(A_K | D). For a subset 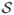, let us denote | 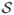| = |(A_i1, A_i2, ···, A_in)| = n, i.e., the number of attributes of 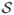. The K-way interaction information can be defined as [McGill, 1954; Han, 1980; Yeung, 1991]

$$\begin{array}{l}I(\mathcal{A})=I(A_1,A_2,\cdots ,A_K)=-\sum _{\mathcal{S}\subseteq \mathcal{A}}{(-1)}^{\mid \mathcal{A}\mid -\mid \mathcal{S}\mid }H(\mathcal{S}),\\ I(\mathcal{A}\mid D)=I(A_1,A_2,\cdots ,A_K\mid D)=-\sum _{\mathcal{S}\subseteq \mathcal{A}}{(-1)}^{\mid \mathcal{A}\mid -\mid \mathcal{S}\mid }H(\mathcal{S}\mid D).\end{array}$$

The K-way interaction information gain is defined as IIG( | D) = I( | D) − I( ).

In the general population, the K-way total correlation information is defined as the difference between the summation of the individual entropies H(A₁), ···, H(A_K) and the joint entropy H( ) [Jakulin, 2005; Watanabe, 1960; Chanda et al., 2007], i.e.,

$$\begin{array}{l}\mathit{TCI}(\mathcal{A})=H(A_1)+\cdots +H(A_K)-H(A_1,\cdots ,A_K)\\ =\sum _{\mathcal{S}\subseteq \mathcal{A},\mid \mathcal{S}\mid \ge 2}I(\mathcal{S}).\end{array}$$ (12)

The total correlation information TCI( ) is the total amount of dependence among all the attributes = (A₁, ···, A_K). As the second equality in relation (12) shows, the total correlation information TCI( ) is equal to the summation of all interaction information I( 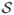) including 2-way mutual information, 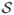⊆ . Thus, the interaction information can be seen as a decomposition of a K-way dependency into a sum of k-way interactions, k ≤ K [Jakulin, 2005]. The existence of K-way correlations indicates the existence of some k-way interactions, k ≤ K. On the other hand, the existence of low order k-way interactions can lead to high order K-way correlations.

In the affected population, the K-way total correlation information is defined as the difference between the summation of the individual entropies H(A₁ | D), ···, H(A_K | D)) and the joint entropy H( | D)), i.e.,

$$\mathit{TCI}(\mathcal{A}\mid D)=H(A_1\mid D)+\cdots +H(A_K\mid D)-H(A_1,\cdots ,A_K\mid D).$$

The K-way total correlation information gain is defined as TCIG( | D) = TCI( | D) − TCI( ). If the disease is independent of the attributes, the interaction information gain IIG( | D) is equal to 0 and similarly, the total correlation information gain TCIG( | D) is equal to 0. The test statistics can be built accordingly to test the interaction or correlation between the disease and the attributes = (A₁, A₂, ···, A_K).

Test Statistics Based on the 2-Way Mutual Information Gain

Based on the above discussion about 2-way mutual information and information gain, we can construct test statistics to detect gene-gene and gene-environment interactions. In what follows, we discuss only the construction of a test statistic to detect a gene-gene interaction between markers A and B. The same procedure can be applied to construct a test statistic to detect a gene-environment interaction between marker A (or B) and environmental factor E.

Consider a case-control design with M controls from an unaffected population and N cases from an affected population. Assume that each individual in the sample is typed at both markers A and B. Let us denote by X_ij the count of controls whose genotypes are (G_A = i, G_B = j), and by Y_ij he count of cases whose genotypes are (G_A = i, G_B = j), i, j = 0, 1, 2. The test statistics can be built based on the column vectors X = (X₀₀, X₀₁, X₀₂, X₁₀, X₁₁, X₁₂, X₂₀, X₂₁)^τ and Y = (Y₀₀, Y₀₁, Y₀₂, Y₁₀, Y₁₁, Y₁₂, Y₂₀, Y₂₁)^τ. Hereafter, the superscript τ denotes the transpose of a vector or a matrix. To remove redundancies, X₂₂ is not included in X, and Y₂₂ is not included in Y. Before defining our test statistics, let us introduce some notations.

In the general population, we denote the joint genotype probabilities for markers A and B by P_ij = P(G_A = i, G_B = j). For the affected population, we denote the joint conditional genotype probabilities for markers A and B by Q_ij = P(G_A = i, G_B = j|D = 1). One can see that P_ij and Q_ij both sum to 1 and that some parameters are redundant. Let us denote P = (P₀₀, P₀₁, P₀₂, P₁₀, P₁₁, P₁₂, P₂₀, P₂₁)^τ and Q = (Q₀₀, Q₀₁, Q₀₂, Q₁₀, Q₁₁, Q₁₂, Q₂₀, Q₂₁)^τ. Both the column counting vector $\left(\begin{array}{c}X\\ X_{22}\end{array}\right)$ and the column counting vector $\left(\begin{array}{c}Y\\ Y_{22}\end{array}\right)$ follow a multinomial distribution. The mean vectors of X and Y are MP and NQ, respectively, and the variance-covariance matrix of X and Y are M[diag (P) − PP^τ] and N[diag (Q) − QQ^τ], respectively. In the following, let us denote Σ = diag (P) − PP^τ and Σ_D = diag (Q) − QQ^τ.

The sample mean X̄ = X/M serves as the estimate of P and the sample mean Ȳ = Y/N serves as the estimate of Q. Assume that the sample sizes M and N are large enough that the large sample theory applies. By the multivariate central limit theorem of large sample theory, $\sqrt{M}\left[\overline{X}-P\right]$ can be approximated by a multivariate normal distribution with a zero mean vector and a variance-covariance matrix Σ [Lehmann, 1983, Theorem 5.1.8, p343]. Similarly, $\sqrt{N}\left[\overline{Y}-Q\right]$ can be approximated by a multivariate normal distribution with a zero mean vector and a variance-covariance matrix Σ_D.

Now, let us define

$$f_{ij}=P_{ij}log\frac{P_{ij}}{P_{i·}{P}_{·j}},g_{ij}=Q_{ij}log\frac{Q_{ij}}{Q_{i·}{Q}_{·j}},$$

where $P_{i·}={\sum }_{j=0}^2{P}_{ij},P_{·j}={\sum }_{i=0}^2{P}_{ij},Q_{i·}={\sum }_{j=0}^2{Q}_{ij}$ and $Q_{·j}={\sum }_{i=0}^2{Q}_{ij}$. Let $f=I(A,B)={\sum }_{i=0}^2{\sum }_{j=0}^2{f}_{ij}$ and $g=I(A,B\mid D)={\sum }_{i=0}^2{\sum }_{j=0}^2{g}_{ij}$. Then, the information gain can be expressed as

$$IG(AB\mid D)=g-f=\sum _{i=0}^2\sum _{j=0}^2{g}_{ij}-\sum _{i=0}^2\sum _{j=0}^2{f}_{ij}.$$

We denote the partial derivatives of functions f and g as $\frac{\partial f}{\partial P}$ and $\frac{\partial g}{\partial Q}$, which are column vectors. The elements of $\frac{\partial f}{\partial P}$ and $\frac{\partial g}{\partial Q}$ are given in the Appendix A as

$$\begin{array}{l}\frac{\partial f}{\partial P_{ij}}=log\frac{P_{ij}}{P_{i·}{P}_{·j}}-log\frac{P_{22}}{P_{2·}{P}_{·2}},\\ \frac{\partial g}{\partial Q_{ij}}=log\frac{Q_{ij}}{Q_{i·}{Q}_{·j}}-log\frac{Q_{22}}{Q_{2·}{Q}_{·2}}.\end{array}$$ (13)

We further denote $\mathrm{\Lambda }={\left[\frac{\partial f}{\partial P}\right]}^{\tau }\mathrm{\sum }\frac{\partial f}{\partial P}/M+{\left[\frac{\partial g}{\partial Q}\right]}^{\tau }{\mathrm{\sum }}_D\frac{\partial g}{\partial Q}/N$.

We denote the estimate of P_ij as P̂_ij = X_ij/M and the estimate of Q_ij as Q̂_ij = Y_ij/N. Similarly, we denote the estimates of other parameters as ${\widehat{P}}_{i·}={\sum }_{j=0}^2{\widehat{P}}_{ij}$, etc. Then, the estimates f̂, Λ̂, and ĝ of f, Λ, and g can be calculated by replacing P_ij and Q_ij using P̂_ij and Q̂_ij.

Based on the large sample theory, $\sqrt{M}(\widehat{f}-f)$ tends to a normal distribution with a zero mean and a variance ${\left[\frac{\partial f}{\partial P}\right]}^{\tau }\mathrm{\sum }\frac{\partial f}{\partial P}$. Similarly, $\sqrt{N}(\widehat{g}-g)$ tends to a normal distribution with a zero mean and a variance ${\left[\frac{\partial g}{\partial Q}\right]}^{\tau }{\mathrm{\sum }}_D\frac{\partial g}{\partial Q}$ [Lehmann, 1983, Theorem 2.5.3, p112]. Note that f = I(A, B) = I(A, B|D) = g under the null hypothesis of independence between the disease and the two markers A and B, and so ĝ − f̂ = (ĝ − g) − (f̂ − f) tends to a normal distribution with a zero mean and a variance Λ. With these discussions in mind, the statistical tests can be constructed as

$$\begin{array}{l}{T}_{IG}={(\widehat{g}-\widehat{f})}^2/\widehat{\mathrm{\Lambda }},\\ T={\left(\widehat{P}-\widehat{Q}\right)}^{\tau }{\left(\frac{\widehat{\mathrm{\sum }}}{M}+\frac{{\widehat{\mathrm{\sum }}}_D}{N}\right)}^{-1}\left(\widehat{P}-\widehat{Q}\right).\end{array}$$ (14)

The test T_IG is based on the information gain IG(AB | D). The test T is a naive χ²-distributed statistic, which is based on the 2 by 8 contingency table to compare the counts of case and controls for genotype combinations of markers A and B. Under the null hypothesis that the two markers are independent of the disease, the test T_IG is centrally ${\chi }_1^2$-distributed with 1 degree of freedom and the test T is centrally ${\chi }_8^2$-distributed with 8 degrees of freedom. Under the alternative hypothesis that the disease and the two markers are not independent, the test T_IG is non-centrally ${\chi }_1^2$-distributed with a non-centrality parameter λ_IG = (g − f)²/Λ and the test T is non-centrally ${\chi }_8^2$-distributed with a non-centrality parameter ${\lambda }_T={(P-Q)}^{\tau }{\left(\frac{\mathrm{\sum }}{M}+\frac{{\mathrm{\sum }}_D}{N}\right)}^{-1}(P-Q)$.

The statistics T_IG and T are overall test statistics to test the association between the markers A and B and the disease. If the markers are associated with the disease (i.e., the markers are not independent of the disease), we need to know which genotypes are associated with the disease. For genotype (G_A = i, G_B = j), we can test if it is associated with the disease using one of the two following tests

$$\begin{array}{l}{T}_{E,ij}=\frac{{({\widehat{g}}_{ij}-{\widehat{f}}_{ij})}^2}{{\widehat{\mathrm{\Lambda }}}_{ij}},\\ T_{ij}=\frac{{({\widehat{P}}_{ij}-{\widehat{Q}}_{ij})}^2}{\widehat{\text{Var}}({\widehat{P}}_{ij}-{\widehat{Q}}_{ij})},\end{array}$$ (15)

where Λ̂_ij is the estimate of Λ_ij and $\widehat{\text{Var}}({\widehat{P}}_{ij}-{\widehat{Q}}_{ij})$ is the estimate of Var(P̂_ij − Q̂_ij). The estimates Λ̂_ij and $\widehat{\text{Var}}({\widehat{P}}_{ij}-{\widehat{Q}}_{ij})$ are given by

$$\begin{array}{l}{\mathrm{\Lambda }}_{ij}=\frac{{\left[\frac{\partial f_{ij}}{\partial P}\right]}^{\tau }\mathrm{\sum }\frac{\partial f_{ij}}{\partial P}}{M}+\frac{{\left[\frac{\partial g_{ij}}{\partial Q}\right]}^{\tau }{\mathrm{\sum }}_D\frac{\partial g_{ij}}{\partial Q}}{N},\\ \text{Var}({\widehat{P}}_{ij}-{\widehat{Q}}_{ij})=\frac{P_{ij}(1-P_{ij})}{M}+\frac{Q_{ij}(1-Q_{ij})}{N}.\end{array}$$

The test T_ij compares the difference P̂_ij − Q̂_ij of the proportions of cases and controls with genotype (G_A = i, G_B = j), and the test T_E,ij is based on the difference f̂_ij − ĝ_ij. If genotype (G_A = i, G_B = j) is strongly associated with the disease, the differences P̂_ij − Q̂_ij and f̂_ij − ĝ_ij tend to be different from 0 and significant results are likely to be found using the tests T_ij and/or T_E,ij.

Under the null hypothesis that the disease and the genotype (G_A = i, G_B = j) are independent, the test T_E,ij and T_ij are centrally ${\chi }_1^2$-distributed. Under the alternative hypothesis that the disease and the genotype (G_A = i, G_B = j) are not independent, the test T_E,ij and T_ij are non-centrally ${\chi }_1^2$-distributed with non-centrality parameters λ_E,ij = (g_ij − f_ij)²/Λ_ij and λ_ij = (P_ij − Q_ij)²/Var(P̂_ij − Q̂_ij), respectively.

Test Statistics Based on the 3-Way Interaction Information Gain and Total Correlation Information Gain

Again, consider a case-control design with M controls from an unaffected population and N cases from an affected population. Let us denote by X_ije the count of controls whose genotypes are (G_A = i, G_B = j, E = e) and by Y_ije the count of cases whose genotypes are (G_A = i, G_B = j, E = e), i, j, e = 0, 1, 2. The test statistics can be built based on two column vectors X and Y, where X includes all X_ije except X₂₂₂, and Y includes all Y_ije except Y₂₂₂ to remove the redundancy.

In the general population, we denote the joint genotype probabilities for markers A and B and environmental factor E by P_ije = P(G_A = i, G_B = j, E = e). In the affected population, we denote the joint conditional genotype probabilities by Q_ije = P(G_A = i, G_B = j, E = e|D = 1). Let us denote a column vector P which includes all P_ije except P₂₂₂ and we denote a column vector Q which includes all Q_ije except Q₂₂₂. The column counting vectors $\left(\begin{array}{c}X\\ X_{222}\end{array}\right)$ and $\left(\begin{array}{c}Y\\ Y_{222}\end{array}\right)$ follow the multinomial distributions $\left(M,\left(\begin{array}{c}P\\ P_{222}\end{array}\right)\right)$ and $\left(N,\left(\begin{array}{c}Q\\ Q_{222}\end{array}\right)\right)$, respectively. The mean vector of X̄ = X/M is P and that of Ȳ = Y/N is Q. The variance-covariance matrices of X and Y are MΣ and NΣ_D, respectively, where Σ = diag (P) − PP^τ and Σ_D = diag (Q) − QQ^τ. As before, we assume that the sample sizes M and N are large enough for the large sample theory to apply. Based on the multivariate central limit theorem, $\sqrt{M}\left[\overline{X}-P\right]$ and $\sqrt{N}\left[\overline{Y}-Q\right]$ tend to a multivariate normal distribution with a zero mean vector and variance-covariance matrices Σ and Σ_D, respectively [Lehmann 1983, Theorem 5.1.8, p343].

Denote $P_{i··}={\sum }_{j=0}^2{\sum }_{e=0}^2{P}_{\mathit{ije}},P_{·j·}={\sum }_{i=0}^2{\sum }_{e=0}^2{P}_{\mathit{ije}},P_{··e}={\sum }_{i=0}^2{\sum }_{j=0}^2{P}_{\mathit{ije}}$. Similarly, Q_i··, Q_·j·, and Q_··e can be defined in a similar manner. Now, let us define

$$f_{\mathit{ije}}=P_{\mathit{ije}}log\frac{P_{\mathit{ije}}}{P_{i··}{P}_{·j·}{P}_{··e}},g_{\mathit{ije}}=Q_{\mathit{ije}}log\frac{Q_{\mathit{ije}}}{Q_{i··}{Q}_{·j·}{Q}_{··e}},$$

If $f=\mathit{TCI}(A,B,E)={\sum }_{i=0}^2{\sum }_{j=0}^2{\sum }_{e=0}^2{f}_{\mathit{ije}}$ and $g=\mathit{TCI}(A,B,E\mid D)={\sum }_{i=0}^2{\sum }_{j=0}^2{\sum }_{e=0}^2{g}_{\mathit{ije}}$, the total correlation information gain can be expressed as

$$\mathit{TCIG}(\mathit{ABE}\mid D)=g-f=\sum _{i=0}^2\sum _{j=0}^2\sum _0^2{g}_{\mathit{ije}}-\sum _{i=0}^2\sum _{j=0}^2\sum _{e=0}^2{f}_{\mathit{ije}}.$$

We denote the partial derivatives of functions f and g as $\frac{\partial f}{\partial P}$ and $\frac{\partial g}{\partial Q}$, which are column vectors. The elements of $\frac{\partial f}{\partial P}$ and $\frac{\partial g}{\partial Q}$ are given in the Supplementary Materials Appendix A as

$$\begin{array}{l}\frac{\partial f}{\partial P_{\mathit{ije}}}=log\frac{P_{\mathit{ije}}}{P_{i··}{P}_{·j·}{P}_{··e}}-log\frac{P_{222}}{P_{2··}{P}_{·2·}{P}_{··2}},\\ \frac{\partial g}{\partial Q_{\mathit{ije}}}=log\frac{Q_{\mathit{ije}}}{Q_{i··}{Q}_{·j·}{Q}_{··e}}-log\frac{Q_{222}}{Q_{2··}{Q}_{·2·}{Q}_{··2}}.\end{array}$$ (16)

Here, $\mathrm{\Lambda }={\left[\frac{\partial f}{\partial P}\right]}^{\tau }\mathrm{\sum }\frac{\partial f}{\partial P}/M+{\left[\frac{\partial g}{\partial Q}\right]}^{\tau }{\mathrm{\sum }}_D\frac{\partial g}{\partial Q}/N$.

To build a 3-way interaction information gain based test statistic, we denote $P_{ij·}={\sum }_{e=0}^2{P}_{\mathit{ije}},P_{·je}={\sum }_{i=0}^2{P}_{\mathit{ije}},P_{i·e}={\sum }_{j=0}^2{P}_{\mathit{ije}}$; and we define Q_ij·, Q_·je and Q_i·e in a similar manner. Let us define

$$h_{\mathit{ije}}=P_{\mathit{ije}}log\frac{P_{\mathit{ije}}{P}_{i··}{P}_{·j·}{P}_{··e}}{P_{ij·}{P}_{·je}{P}_{i·e}},{\ell }_{\mathit{ije}}=Q_{\mathit{ije}}log\frac{Q_{\mathit{ije}}{Q}_{i··}{Q}_{·j·}{Q}_{··e}}{Q_{ij·}{Q}_{·je}{Q}_{i·e}},$$

If $h=I(A,B,E)={\sum }_{i=0}^2{\sum }_{j=0}^2{\sum }_{e=0}^2{h}_{\mathit{ije}}$ and $\ell =I(A,B,E\mid D)={\sum }_{i=0}^2{\sum }_{j=0}^2{\sum }_{e=0}^2{\ell }_{\mathit{ije}}$, the 3-way interaction information gain of markers A and B and environmental factor E can be expressed as

$$\mathit{IIG}(\mathit{ABE}\mid D)=\ell -h=\sum _{i=0}^2\sum _{j=0}^2\sum _0^2{\ell }_{\mathit{ije}}-\sum _{i=0}^2\sum _{j=0}^2\sum _{e=0}^2{h}_{\mathit{ije}}.$$

We denote the partial derivatives of functions h and ℓ as $\frac{\partial h}{\partial P}$ and $\frac{\partial \ell }{\partial Q}$, which are column vectors. The elements of $\frac{\partial h}{\partial P}$ and $\frac{\partial \ell }{\partial Q}$ are given in the Supplementary Materials Appendix B as

$$\begin{array}{l}\frac{\partial h}{\partial P_{\mathit{ije}}}=log\frac{P_{\mathit{ije}}{P}_{i··}{P}_{·j·}{P}_{··e}}{P_{ij·}{P}_{i·e}{P}_{·je}}-log\frac{P_{222}{P}_{2··}{P}_{·2·}{P}_{··2}}{P_{22·}{P}_{2·2}{P}_{·22}},\\ \frac{\partial \ell }{\partial Q_{\mathit{ije}}}=log\frac{Q_{\mathit{ije}}{Q}_{i··}{Q}_{·j·}{Q}_{··e}}{Q_{ij·}{Q}_{i·e}{Q}_{·je}}-log\frac{Q_{222}{Q}_{2··}{Q}_{·2·}{Q}_{··2}}{Q_{22·}{Q}_{2·2}{Q}_{·22}}.\end{array}$$ (17)

Here, $\mathrm{\Gamma }={\left[\frac{\partial h}{\partial P}\right]}^{\tau }\mathrm{\sum }\frac{\partial h}{\partial P}/M+{\left[\frac{\partial \ell }{\partial Q}\right]}^{\tau }{\mathrm{\sum }}_D\frac{\partial \ell }{\partial Q}/N$.

We denote the estimate of P_ije and Q_ije as P̂_ije = X_ije/M and Q̂_ije = Y_ije/N, respectively. Similarly, we denote the estimates of other parameters as ${\widehat{P}}_{i··}={\sum }_{j=0}^2{\sum }_{e=0}^2{\widehat{P}}_{\mathit{ije}}$, etc. Then, the estimates f̂, ĝ, ĥ, ℓ̂, Λ̂, and Γ̂ of f, g, h, ℓ, Λ, and Γ can be calculated by replacing P_ije and Q_ije using P̂_ije and Q̂_ije. The statistical tests to test the correlations and interactions between markers A and B, environmental factor E and the disease can be constructed by

$$\begin{array}{l}{T}_{\mathit{TCIG}}={(\widehat{g}-\widehat{f})}^2/\widehat{\mathrm{\Lambda }},\\ T_{\mathit{IIG}}={(\widehat{h}-\widehat{\ell })}^2/\widehat{\mathrm{\Gamma }}.\end{array}$$ (18)

The test T_TCIG is based on the total correlation information gain TCIG(ABE|D) and can be used to test for the existence of 3-way correlations. The test T_IIG, on the other hand, is based on the 3-way interaction information gain IIG(ABE|D) and can be used to test for the existence of 3-way interactions. Under the null hypothesis that the two markers A and B, and the environmental factor E are independent of the disease, the test statistics T_TCIG and T_IIG are centrally ${\chi }_1^2$-distributed. Under the alternative hypothesis that the two markers and the environmental factor are not independent of the disease, the test statistics T_TCIG and T_IIG are non-centrally ${\chi }_1^2$-distributed with non-centrality parameters λ_TCIG = (g − f)²/Λ and λ_IIG = (h − ℓ)²/Γ, respectively.

Test Statistics Based on the K-Way Interaction Information Gain and Total Correlation Information Gain

Given a case-control sample with M controls and N cases, we are going to construct test statistics to test K-way interactions between K attributes A₁, ···, A_K. Hereafter, |s⃗| is the number of elements in a vector s⃗. The approach is similar to the one we used for lower-order interactions. Let us denote

$$\begin{array}{l}\mathit{TCIG}(\mathcal{A}\mid D)=g-f=\sum _{a_1=0}^2\cdots \sum _{a_K=0}^2[g_{a_1\cdots a_K}-f_{a_1\cdots a_K}],\\ g_{a_1\cdots a_K}=Q_{a_1\cdots a_K}log\frac{Q_{a_1\cdots a_K}}{{\prod }_{\begin{array}{c}\overrightarrow{s}\subset (a_1,\cdots ,a_K)\\ \mid \overrightarrow{s}\mid =1\end{array}}{Q}_{\overrightarrow{s}}},\\ f_{a_1\cdots a_K}=P_{a_1\cdots a_K}log\frac{P_{a_1\cdots a_K}}{{\prod }_{\begin{array}{c}\overrightarrow{s}\subset (a_1,\cdots ,a_K)\\ \mid \overrightarrow{s}\mid =1\end{array}}{P}_{\overrightarrow{s}}},\end{array}$$

where ${\prod }_{\begin{array}{c}\overrightarrow{s}\subset (a_1,\cdots ,a_K)\\ \mid \overrightarrow{s}\mid =1\end{array}}{Q}_{\overrightarrow{s}}=Q_{a_1,\cdots ,·}\cdots Q_{·,\cdots ,a_K}$ is the product of all individual marginal probabilities of A₁, ···, A_K in the affected population and ${\prod }_{\begin{array}{c}\overrightarrow{s}\subset (a_1,\cdots ,a_K)\\ \mid \overrightarrow{s}\mid =1\end{array}}{P}_{\overrightarrow{s}}=P_{a_1,\cdots ,·}\cdots P_{·,\cdots ,a_K}$ is the product of all individual marginal probabilities of A₁, ···, A_K in the general population. We denote the partial derivatives of functions f and g as $\frac{\partial f}{\partial P}$ and $\frac{\partial g}{\partial Q}$, which are column vectors. The elements of $\frac{\partial f}{\partial P}$ and $\frac{\partial g}{\partial Q}$ are given as

$$\begin{array}{l}\frac{\partial f}{\partial P_{a_1\cdots a_K}}=log\frac{P_{a_1\cdots a_K}}{P_{a_1,\cdots ,·}\cdots P_{·,\cdots ,a_K}}-log\frac{P_{2\cdots 2}}{P_{2,\cdots ,·}\cdots P_{·,\cdots ,2}},\\ \frac{\partial g}{\partial Q_{a_1\cdots a_K}}=log\frac{Q_{a_1\cdots a_K}}{Q_{a_1,\cdots ,·}\cdots Q_{·,\cdots ,a_K}}-log\frac{Q_{2\cdots 2}}{Q_{2,\cdots ,·}\cdots Q_{·,\cdots ,2}},\end{array}$$ (19)

which can be proven along the vein of relation (16) in Supplementary Materials Appendix C. We define $\mathrm{\Lambda }={\left[\frac{\partial f}{\partial P}\right]}^{\tau }\mathrm{\sum }\frac{\partial f}{\partial P}/M+{\left[\frac{\partial g}{\partial Q}\right]}^{\tau }{\mathrm{\sum }}_D\frac{\partial g}{\partial Q}/N$, where P is a column vector including all P_a1···aK except P_2···2, Σ = diag (P)−PP^τ, Q is a column vector including all Q_a1···aK except Q_2···2, and Σ_D = diag (Q) −QQ^τ.

Similarly, let us denote

$$\begin{array}{l}\mathit{IIG}(\mathcal{A}\mid D)=\ell -h=\sum _{a_1=0}^2\cdots \sum _{a_K=0}^2[{\ell }_{a_1\cdots a_K}-h_{a_1\cdots a_K}],\\ {\ell }_{a_1\cdots a_K}=Q_{a_1\cdots a_K}log\frac{Q_{a_1\cdots a_K}{\prod }_{\begin{array}{c}\overrightarrow{s}\subset (a_1,\cdots ,a_K)\\ {\mid (a_1,\cdots ,a_K)\backslash \overrightarrow{s}\mid }_{\mathit{mod}(2)}=0\end{array}}{Q}_{\overrightarrow{s}}}{{\prod }_{\begin{array}{c}\overrightarrow{s}\subset (a_1,\cdots ,a_K)\\ {\mid (a_1,\cdots ,a_K)\backslash \overrightarrow{s}\mid }_{\mathit{mod}(2)}=1\end{array}}{Q}_{\overrightarrow{s}}},\\ h_{a_1\cdots a_K}=P_{a_1\cdots a_K}log\frac{P_{a_1\cdots a_K}{\prod }_{\begin{array}{c}\overrightarrow{s}\subset (a_1,\cdots ,a_K)\\ {\mid (a_1,\cdots ,a_K)\backslash \overrightarrow{s}\mid }_{\mathit{mod}(2)}=0\end{array}}{P}_{\overrightarrow{s}}}{{\prod }_{\begin{array}{c}\overrightarrow{s}\subset (a_1,\cdots ,a_K)\\ {\mid (a_1,\cdots ,a_K)\backslash \overrightarrow{s}\mid }_{\mathit{mod}(2)}=1\end{array}}{P}_{\overrightarrow{s}}},\end{array}$$

where |(a₁, ···, a_K)\s⃗|_mod(2) = 0 means that the subset (a₁, ···, a_K)\s⃗ contains an even number of elements, and |(a₁, ···, a_K)\s⃗|_mod(2) = 1 means that the subset (a₁, ···, a_K)\s⃗ contains an odd number of elements. Moreover, the product ${\prod }_{\begin{array}{c}\overrightarrow{s}\subset (a_1,\cdots ,a_K)\\ {\mid (a_1,\cdots ,a_K)\backslash \overrightarrow{s}\mid }_{\mathit{mod}(2)}=0\end{array}}{Q}_{\overrightarrow{s}}$ does not contain Q_a1,···,aK since s⃗ ⊂ (a₁, ···, a_K) means that s⃗ is a real subset of (a₁, ···, a_K) [i.e., s⃗ ≠ (a₁, ···, a_K)]. The same logic applies to the other products. We denote the partial derivatives of functions ℓ and h as $\frac{\partial f}{\partial P}$ and $\frac{\partial \ell }{\partial Q}$, which are column vectors. The elements of $\frac{\partial h}{\partial P}$ and $\frac{\partial \ell }{\partial Q}$ are given as

$$\begin{array}{l}\frac{\partial h}{\partial P_{a_1\cdots a_K}}=log\frac{P_{a_1\cdots a_K}{\prod }_{\begin{array}{c}\overrightarrow{s}\subset (a_1,\cdots ,a_K)\\ {\mid (a_1,\cdots ,a_K)\backslash \overrightarrow{s}\mid }_{\mathit{mod}(2)}=0\end{array}}{P}_{\overrightarrow{s}}}{{\prod }_{\begin{array}{c}\overrightarrow{s}\subset (a_1,\cdots ,a_K)\\ {\mid (a_1,\cdots ,a_K)\backslash \overrightarrow{s}\mid }_{\mathit{mod}(2)}=1\end{array}}{P}_{\overrightarrow{s}}}-log\frac{P_{2\cdots 2}{\prod }_{\begin{array}{c}\overrightarrow{s}\subset (2,\cdots ,2)\\ {\mid (2,\cdots ,2)\backslash \overrightarrow{s}\mid }_{\mathit{mod}(2)}=0\end{array}}{P}_{\overrightarrow{s}}}{{\prod }_{\begin{array}{c}\overrightarrow{s}\subset (2,\cdots ,2)\\ {\mid (2,\cdots ,2)\backslash \overrightarrow{s}\mid }_{\mathit{mod}(2)}=1\end{array}}{P}_{\overrightarrow{s}}},\\ \frac{\partial \ell }{\partial Q_{a_1\cdots a_K}}=log\frac{Q_{a_1\cdots a_K}{\prod }_{\begin{array}{c}\overrightarrow{s}\subset (a_1,\cdots ,a_K)\\ {\mid (a_1,\cdots ,a_K)\backslash \overrightarrow{s}\mid }_{\mathit{mod}(2)}=0\end{array}}{Q}_{\overrightarrow{s}}}{{\prod }_{\begin{array}{c}\overrightarrow{s}\subset (a_1,\cdots ,a_K)\\ {\mid (a_1,\cdots ,a_K)\backslash \overrightarrow{s}\mid }_{\mathit{mod}(2)}=1\end{array}}{Q}_{\overrightarrow{s}}}-log\frac{Q_{2\cdots 2}{\prod }_{\begin{array}{c}\overrightarrow{s}\subset (2,\cdots ,2)\\ {\mid (2,\cdots ,2)\backslash \overrightarrow{s}\mid }_{\mathit{mod}(2)}=0\end{array}}{Q}_{\overrightarrow{s}}}{{\prod }_{\begin{array}{c}\overrightarrow{s}\subset (2,\cdots ,2)\\ \mid (2,\cdots ,2)\backslash \overrightarrow{s}{\mid }_{\mathit{mod}(2)}=1\end{array}}{Q}_{\overrightarrow{s}}},\end{array}$$ (20)

which can be proven along the vein of relation (17) in Supplementary Materials Appendix C. Here, $\mathrm{\Gamma }={\left[\frac{\partial h}{\partial P}\right]}^{\tau }\mathrm{\sum }\frac{\partial h}{\partial P}/M+{\left[\frac{\partial \ell }{\partial Q}\right]}^{\tau }{\mathrm{\sum }}_D\frac{\partial \ell }{\partial Q}/N$. To test for the existence of K-way interactions and correlations between the disease and the attributes A₁, ···, A_K, the ${\chi }_1^2$-distributed test statistics can be constructed as T_TCIG = (ĝ − f̂)²/Λ̂ and T_IIG = (ĥ − ℓ̂)²/Γ̂, respectively.

Association Test Statistics based on 1-way Entropy Loss

Suppose that we are interested in testing for the existence of an association between an attribute and a disease in a case-control study. The entropy of the attribute can be used as the basis to construct test statistics. The attribute here can be a single marker or an environment factor. In addition, if two or more markers are in strong linkage disequilibrium and their haplotype data are available, the haplotype data can be treated as an attribute. Here we use marker A as the attribute. It is well-known that the entropy is maximized when a system reaches its equilibrium state. In the one locus case, the equilibrium state refers to the Hardy-Weinberg equilibrium. Since the assumption of Hardy-Weinberg equilibrium is likely to be true in the general population, the entropy H(A) can reach the maximum. In the affected population, the assumption of Hardy-Weinberg equilibrium may not be true and the conditional entropy H(A|D) may decrease. The entropy loss of marker A in the presence of a disease can be defined as follows:

$$EL(A\mid D)=H(A)-H(A\mid D).$$ (21)

If the disease and marker A are independent, H(A|D) = H(A). Then the entropy loss EL(A|D) is equal to 0. Hence, we can test for the existence of an association between marker A and a disease by testing if the entropy loss is zero. Based on this rationale, we can build test statistics for practical applications.

In the general population, we denote the genotype probabilities for marker A by P_i = P(G_A = i). In the affected population, we denote the conditional genotype probabilities for marker A by Q_i = P(G_A = i|D = 1). Here P = (P₀, P₁)^τ, and Q = (Q₀, Q₁)^τ. The entropy loss can be expressed as

$$EL(A\mid D)=H(A)-H(A\mid D)=\sum _{i=0}^2{P}_{i}log{P}_i-\sum _{i=0}^2{Q}_{i}log{Q}_i.$$

We denote the partial derivatives of the entropy functions H(A) and H(A|D) as the column vectors $\frac{\partial H(A)}{\partial P}$ and $\frac{\partial H(A\mid D)}{\partial Q}$. We can show that the elements of $\frac{\partial H(A)}{\partial P}$ and $\frac{\partial H(A\mid D)}{\partial Q}$ are given by

$$\begin{array}{l}\frac{\partial H(A)}{\partial P_i}=log{P}_i-log{P}_2,\\ \frac{\partial H(A\mid D)}{\partial Q_i}=log{Q}_i-log{Q}_2.\end{array}$$ (22)

For a case-control design with M controls and N cases, let us denote by X_i the count of controls whose genotypes are (G_A = i) and by Y_i the count of cases whose genotypes are (G_A = i), i, = 0, 1, 2. We denote the estimates of P_i and Q_i as P̂_i = X_i/M and Q̂_i = Y_i/N. Then, the estimates Ĥ(A), Ω̂, and Ĥ (A|D) of H(A), Ω, and H(A|D) can be calculated by replacing P_i and Q_i using P̂_i and Q̂_i. Here $\mathrm{\Omega }={\left[\frac{\partial H(A)}{\partial P}\right]}^{\tau }\mathrm{\sum }\frac{\partial H(A)}{\partial P}/M+{\left[\frac{\partial H(A\mid D)}{\partial Q}\right]}^{\tau }{\mathrm{\sum }}_D\frac{\partial H(A\mid D)}{\partial Q}/N$, where Σ = diag (P) − PP^τ and Σ_D = diag (Q) − QQ^τ. The entropy loss-based statistics to test for the existence of an association between marker A and a disease can be constructed by

$$T_{EL}={\left(\widehat{H}(A)-\widehat{H}(A\mid D)\right)}^2/\widehat{\mathrm{\Omega }}.$$

Under the null hypothesis, T_EL is centrally ${\chi }_1^2$-distributed. Under the alternative hypothesis, T_EL is non-centrally ${\chi }_1^2$-distributed with a non-centrality parameter λ_EL = (H(A) − H(A|D))²/Ω.

Results

In this section, we apply the proposed methods to the bladder cancer data of Andrew et al. [2006] to search for interactions between the disease and the genetic variants and smoking factor. Then, we investigate the robustness of the proposed test statistics by type I error rate calculation, using the joint genotype frequencies of the bladder cancer data. We perform power analysis using the analytical non-centrality parameters of 2-way tests under a few interaction models taken from the literature [Moore et al., 2002; Ritchie et al., 2003a].

Application to Bladder Cancer Data

The bladder cancer data of Andrew et al. [2006] consists of 355 cases and 559 controls. The genotype data of 7 SNPs are available, i.e., three SNPs (APE1 148, XRCC1 399, and XRCC1 194) belong to the BER pathway, one (XRCC3 241) belongs to the DSB pathway, and the remaining three (XPC PAT, XPD 751, and XPD 312) belong to the NER pathway. In addition to the bladder cancer status, the following information about each individual is also available: gender, age, and smoking status given in pack years (e.g., non smoking, < 35 pack years, ≥ 35 pack years).

In the MDR analysis of Andrew et al. [2006], the combination of XPD 751 and XPD 312 was the best two-factor model, which was confirmed by the interaction dendrogram and logistic regression analysis. The three-factor model added Pack-years of smoking to XPD 751 and XPD 312 was the most accurate model, which however was not confirmed by the interaction dendrogram or logistic regression analysis (the logistic regression model failed to converge).

We applied the proposed methods to the bladder cancer data of Andrew et al. [2006], and the results are presented in Table 1. For 2-way interaction, we confirmed the result of Andrew et al. [2006]. The combination of XPD 751 and XPD 312 was the only significant SNP combination detected by our 2-way mutual information gain test statistic (T_IG = 51.62, p-value = 6.75e-13), and none of the rest two-factor combinations provided significant result by T_IG. By adding each of the remaining 5 SNPs and Pack years, the 3-way total correlation information gain test statistic T_TCIG provided a significant result (p-value ≤ 2.67e-9). However, the 3-way interaction information gain test statistic T_IIG provided no significant result for any of the three-factor combinations of XPD 751, XPD 312, and one for the remaining 5 SNPs and Pack years (p-value ≥ 0.23).

Table 1.

Results of the 2-way test statistic T_IG and the 3-way test statistics T_IIG and T_TCIG of the bladder cancer data of Andrew et al. [2006].

No. of Factors	SNPs	Test	P-value
2-way interaction	Xpd_751, Xpd_312*	TIG = 51.62	6.75e-13
	XRCC1_194, XPC PAT#	TIG = 2.47	0.12
3-way interaction and 3-way correlation	Xpd_751, Xpd_312, APE1 148	TTCIG = 44.54	2.49e-11
		TIIG = 0.19	0.66
	Xpd_751, Xpd_312, XPC PAT	TTCIG = 43.87	3.51e-11
		TIIG = 0.12	0.73
	Xpd_751, Xpd_312, Pack_years	TTCIG = 40.93	1.58e-10
		TIIG = 0.11	0.74
	Xpd_751, Xpd_312, XRCC3_241	TTCIG = 40.20	2.29e-10
		TIIG = 0.12	0.73
	Xpd_751, Xpd_312, XRCC1_399	TTCIG = 39.90	2.68e-10
		TIIG = 1.46	0.23
	Xpd_751, Xpd_312, XRCC1_194	TTCIG = 35.41	2.67e-9
		TIIG = 0.30	0.58
	Xpd_751, XRCC1_194, XRCC3_241	TTCIG = 5.67	0.02
		TIIG = 1.80	0.18
	XRCC1_399, XRCC1_194, XRCC3_241	TTCIG = 3.67	0.06
		TIIG = 4.25	0.04†
	XPC PAT, XRCC1_194, Pack_years	TTCIG = 3.97	0.05
		TIIG = 0.21	0.65

^*- the most significant result of T_IG;

^#- the second most significant result of T_IG;

^†- the only significant result of 3-way interaction information gain test statistic T_IIG at 5% significance level.

The only significant result provided by the 3-way interaction information gain test statistic T_IIG at 5% significance level came from the combination of XRCC1 399, XRCC1 194, and XRCC3 241 (T_IIG = 4.25, p-value = 0.04). However, the result was hardly significant when we adjusted for multiple comparisons, using the Bonferroni procedure for example, which suggested that there is no 3-way interaction combination based on our analysis. The very significant results provided by the 3-way total correlation information gain test statistic T_TCIG (Table 1) were most likely due to the 2-way combination of XPD 751 and XPD 312.

Type I Error Rates

Using the joint SNP genotype frequencies of bladder cancer data, we performed simulations to evaluate the type I error rates of 2-way information gain based test statistic T_IG and 3-way test statistics T_IIG and T_TCIG, and the results are presented in Table 2. Each empirical type I error rate in Table 2 was calculated based on 100,000 simulations. That is, we simulated 100,000 random samples of N = M = 100, 150, 200, 250, 300, 400, 500, 600, 700 cases and controls, respectively. These sample sizes were used consistently for all error rate calculations. In each sample, M and N were generated according to the multinomial distributions (M, P) and (N, Q), respectively. Here P = Q are the joint genotype frequencies estimated from the bladder cancer data. For instance, the joint genotype frequencies of the combination of Xpd 751 and Xpd 312 is P = Q = (156, 42, 15, 60, 193, 19, 5, 33, 36)^τ/(156 + 42 + 15 + 60 + 193 + 19 + 5 + 33 + 36) = (156, 42, 15, 60, 193, 19, 5, 33, 36)^τ/559, which was used to generate simulation data to calculate the empirical type I error rates of the 2-way test statistic T_IG. In Table D.1 of the Supplementary Materials Appendix D, we present the SNP combinations and their joint genotype frequencies used in the calculations of empirical type I error rates of T_IG, T_IIG, and T_TCIG.

Table 2.

Type I error rates of 2-way test statistic T_IG and 3-way test statistics T_IIG and T_TCIG based on the joint genotype frequencies of bladder cancer data at nominal levels α = 0.01 and α = 0.05. Each of the entries is based on 100, 000 simulations. Pack_years is used as a SNP in simulating its three category genotypes.

α	Test	SNPs used to generate Joint Genotype Frequency	Sample Sizes M = N
			100	150	200	250	300	400	500	600	700
0.01	TIG	Xpd_751, Xpd_312	0.01499	0.01357	0.01200	0.01184	0.01157	0.01070	0.01094	0.01130	0.01039
	TTCIG	Xpd_751, Xpd_312, APE1 148	0.01701	0.01570	0.01434	0.01382	0.01297	0.01262	0.01159	0.01194	0.01122
		Xpd_751, Xpd_312, XPC PAT	0.01886	0.01568	0.01321	0.01280	0.01208	0.01154	0.01058	0.01051	0.01060
		Xpd_751, Xpd_312, Pack_years	0.01888	0.01572	0.01468	0.01366	0.01235	0.01249	0.01223	0.01112	0.01063
		Xpd_751, Xpd_312, XRCC3_241	0.01636	0.01484	0.01289	0.01244	0.01175	0.01176	0.01099	0.01074	0.01059
		Xpd_751, Xpd_312, XRCC1_399	0.01751	0.01454	0.01340	0.01212	0.01234	0.01153	0.01098	0.01168	0.01058
		Xpd_751, Xpd_312, XRCC1_194	0.01418	0.01259	0.01212	0.01203	0.01031	0.01041	0.01027	0.00971	0.01001
	TIIG	APE1, XRCC1_399, XRCC1_194	0.00948	0.00976	0.00908	0.00857	0.0079	0.00743	0.00752	0.00795	0.00753
		Xpd_751, Xpd_312, XRCC1_194	0.00808	0.00961	0.01057	0.01133	0.01092	0.01053	0.00950	0.00924	0.00843
		XRCC3_241, APE1, XRCC1_194	0.00939	0.00733	0.00648	0.00665	0.00677	0.00663	0.00794	0.00848	0.00889
		XRCC3_241, APE1, XRCC1_399	0.00871	0.00797	0.00784	0.00744	0.00818	0.00735	0.00752	0.00782	0.00786
		XRCC3_241, XRCC1_399, XRCC1_194	0.0119	0.01005	0.00887	0.00848	0.00796	0.00762	0.00852	0.00820	0.00845
0.05	TIG	Xpd_751, Xpd_312	0.06148	0.05813	0.05510	0.05575	0.05316	0.05288	0.05173	0.05097	0.05091
	TTCIG	Xpd_751, Xpd_312, APE1 148	0.06852	0.06355	0.06171	0.05974	0.05776	0.0548	0.05584	0.05373	0.05356
		Xpd_751, Xpd_312, XPC PAT	0.06886	0.06400	0.05987	0.05697	0.05601	0.05478	0.05337	0.05043	0.05220
		Xpd_751, Xpd_312, Pack_years	0.07143	0.06579	0.06289	0.06016	0.05851	0.05541	0.05494	0.05439	0.05311
		Xpd_751, Xpd_312, XRCC3_241	0.06608	0.06200	0.05898	0.05620	0.05451	0.05326	0.05137	0.05281	0.05057
		Xpd_751, Xpd_312, XRCC1_399	0.06594	0.06303	0.05968	0.05701	0.05519	0.05466	0.05297	0.05234	0.05223
		Xpd_751, Xpd_312, XRCC1_194	0.05857	0.05689	0.05453	0.05403	0.05321	0.05059	0.05109	0.04992	0.05136
	TIIG	APE1, XRCC1_399, XRCC1_194	0.0573	0.05309	0.05025	0.0463	0.04481	0.04352	0.04516	0.04511	0.04674
		Xpd_751, Xpd_312, XRCC1_194	0.04551	0.04972	0.05394	0.05424	0.05379	0.05187	0.04912	0.04636	0.04599
		XRCC3_241, APE1, XRCC1_194	0.05195	0.04382	0.04132	0.04125	0.04072	0.04327	0.04446	0.04600	0.04696
		XRCC3_241, APE1, XRCC1_399	0.04834	0.04498	0.04412	0.04328	0.04369	0.04312	0.04446	0.04379	0.04317
		XRCC3_241, XRCC1_399, XRCC1_194	0.06258	0.05403	0.04737	0.04526	0.04456	0.04447	0.04672	0.04736	0.04800

We assumed P = Q in our simulation to calculate the type I error rates, i.e., the disease status D is independent of genetic/environmental factors. We calculated an empirical test value for each sample. The empirical type I error rates at nominal levels α = 0.01 and α = 0.05 are reported in Table 2 and represent the proportions of the test values calculated for the 100,000 samples, that exceed the 99-th and 95-th percentiles of the ${\chi }_1^2$-distribution. Because the disease status D is independent of genetic or environmental factors, the empirical type I error rates reported in Table 2 can be thought as false positives.

We then calculated 9 empirical type I error rates for each combination of genotype frequencies, i.e., As the combination of SNPs Xpd 751 and Xpd 312 was the only one to provide very significant T_IG value (Table 1), we calculated the type I error rate only for this combination. To calculate the empirical type I error rate for T_TCIG, we added one of the remaining five SNPs or pack year to Xpd 751 and Xpd 312 and calculated the joint SNP genotype frequencies. This resulted in six combinations of three factors or attributes, i.e., Xpd 751 and Xpd 312 plus one SNP or Pack years. These six combinations provided very significant results of total correlation between the bladder cancer and the three attributes (Table 1). The results of Table 2 show that the empirical type I error rates of 2-way test statistic T_IG and 3-way test statistic T_TCIG are around the nominal level α = 0.01 or α = 0.05 when the sample sizes M = N ≥ 300. Therefore, the test statistics T_IG and T_TCIG are reasonably conservative and robust. The very significant results of T_IG and T_TCIG in Table 1 were most likely from the strong interaction between the bladder cancer and the two SNPs Xpd 751 and Xpd 312.

In our simulation to calculate the entries of Table 2, the null hypothesis of T_IG was that the disease status D is independent of genetic markers A = Xpd 751 and B = Xpd 312, i.e., Q_ij = P(G_A = i, G_B = j|D = 1) = P(G_A = i, G_B = j) = P_ij, but that the genotypes of SNPs A and B are not independent from each other. The null hypothesis of T_TCIG in turn was that Q_ije = P(G_A = i, G_B = j, E = e|D = 1) = P(G_A = i, G_B = j, E = e) = P_ije, i.e., the disease status D is independent of both genetic and environmental factors, but pair-wise and three-way dependences between genetic and environmental factors are allowed. Actually, the genotypes of SNPs Xpd 751 and Xpd 312 are strongly dependent of each other (Pearson χ² = 256.83, p-value < 0.00005). In addition, Xpd 751 and Xpd 312 are in strong linkage disequilibrium. Therefore, the simulated data were generated under the null hypothesis of either T_IG or T_TCIG since the two SNPs, Xpd 751 and Xpd 312, are correlated to each other. The empirical type I error rates of tests T_IG and T_TCIG reported in Table 2 were around the nominal levels, and the two tests were reasonably robust.

To calculate the empirical type I error rates of the interaction information gain-based test statistic T_IIG, we chose the three SNP combinations which were significantly correlated to each other. In the case of three SNPs A, B, and C, significantly correlated means that the four null hypotheses

$$\begin{array}{l}{H}_1:P(G_A,G_B,G_C)=P(G_A,G_B)P(G_C),\\ H_2:P(G_A,G_B,G_C)=P(G_A)P(G_B,G_C),\\ H_3:P(G_A,G_B,G_C)=P(G_B)P(G_A,G_C),\\ H_4:P(G_A,G_B,G_C)=P(G_A)P(G_B)P(G_C),\end{array}$$

are all unlikely to be true. We used the Pearson χ² test to choose the three SNP combinations. In Table D.2 of the Supplementary Materials Appendix D, we present the three attribute combinations of theses SNPs. Utilizing the joint genotype frequencies of the three SNP combinations in Table D.2 of the Supplementary Materials, we performed simulations to calculate the empirical type I error rates for the 3-way test statistic T_IIG. Since each of the three SNP combinations was selected based on the existence of significant correlations between these SNPs, the simulated data were likely to be generated under the null hypothesis of T_IIG, i.e., I(A, B, C|D) = I(A, B, C). The empirical type I error rates of the 3–way test statistic T_IIG reported in Table 2 were generally slightly lower than the nominal levels, which suggests that the test T_IIG is conservative and robust. The test T_IIG was more conservative than the test T_TCIG since the the former was constructed to detect the 3-way or higher order interactions and the the latter was constructed to detect the correlations. The existence of 2-way or 3-way interactions implies 3-way correlations, but 3-way correlations are not necessarily due to 3-way interactions.

In Table E.1 of the Supplementary Materials Appendix E, we present the type I error rates of 1-way entropy loss test statistic T_EL. The test statistic T_EL is reasonably robust and conservative.

Power Comparison

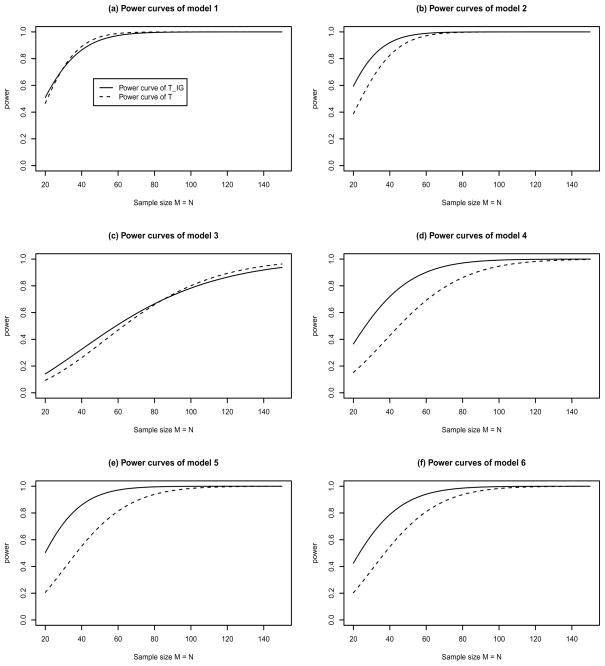
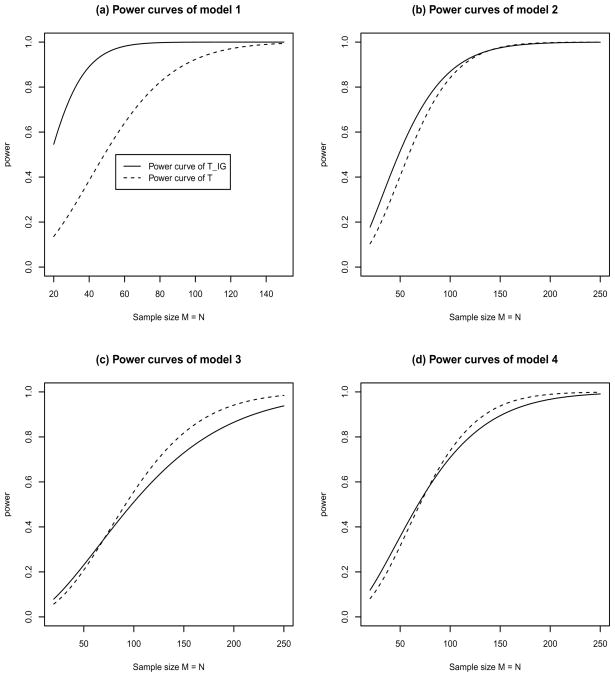
After evaluating the robustness of the test statistic T_IG by type I error rate calculation, we performed power calculations for the information gain based test T_IG and the naive test T. We were mainly concerned with the performance of the test statistic T_IG for nonlinear interactions and in the absence of main effect. To achieve the goal, six models of two-locus penetrance functions and allele frequencies were taken from Moore et al. [2002], Figures 5–10, and the penetrance functions and allele frequencies are presented in Table 3. Similarly, four models were taken from Ritchie et al. [2003a], Figure 2, and the related parameters are presented in Table 4.

Table 3.

Six models of two-locus penetrance functions and allele frequencies taken from Moore et al. [2002], Figures 5–10.

(a) Model 1, PA = PB = 0.5
	BB	Bb	bb
AA	0.083	0.076	0.964
Aa	0.056	0.508	0.085
aa	0.977	0.098	0.062

(b) Model 2, PA = PB = 0.5
	BB	Bb	bb
AA	0.094	0.905	0.097
Aa	0.967	0.097	0.937
aa	0.027	0.990	0.080

(c) Model 3, PA = PB = 0.5
	BB	Bb	bb
AA	0.967	0.314	0.137
Aa	0.313	0.312	0.742
aa	0.129	0.779	0.075

(d) Model 4, PA = PB = 0.5
	BB	Bb	bb
AA	0.967	0.139	0.799
Aa	0.057	0.655	0.627
aa	0.974	0.544	0.019

(e) Model 5, PA = PB = 0.5
	BB	Bb	bb
AA	0.017	0.451	0.711
Aa	0.520	0.571	0.039
aa	0.640	0.053	0.949

(f) Model 6, PA = PB = 0.5
	BB	Bb	bb
AA	0.954	0.256	0.360
Aa	0.010	0.731	0.300
aa	0.801	0.093	0.808

Figure 2.

The power curves of test statistics T_IG and T at a significance level α = 0.01 for the six models of Table 3.

Table 4.

Four models of two-locus penetrance functions and allele frequencies taken from Ritchie et al. [2003a], Figure 2.

(a) Model 1, PA = PB = 0.25
	BB	Bb	bb
AA	.08	.07	.05
Aa	.10	0	.10
aa	.03	.10	.04

(b) Model 2, PA = PB = 0.25
	BB	Bb	bb
AA	0	.01	.09
Aa	.04	.01	.08
aa	.07	.09	.03

(c) Model 3, PA = PB = 0.1
	BB	Bb	bb
AA	.07	.05	.02
Aa	.05	.09	.01
aa	.02	.01	.03

(d) Model 4, PA = PB = 0.1
	BB	Bb	bb
AA	.09	.001	.02
Aa	.08	.07	.005
aa	.003	.007	.02

To make a comparison, we calculated the theoretical power curves of both test statistics T_IG and T based on their non-centrality parameters λ_TIG, and λ_T, and the results are plotted in Figures 2 and 3, respectively. Generally, the power of the information gain-based test T_IG was similar to or higher than that of a naive test T. For models 2 and 4–6 in Table 3 and model 1–2 in Table 4, the power curves of T_IG were higher than those of T. For the other models, the power was similar. Hence, in terms of power, the information gain-based test T_IG performed equally well or better.

Figure 3.

The power curves of test statistics T_IG and T at a significance level α = 0.01 for the four models of Table 4.

By construction, high dimension data are collapsed to build ${\chi }_1^2$-distributed test T_IG which is based on a one-dimension variable. However, the test T is based on genotype frequency comparison of high dimension data and it is ${\chi }_8^2$-distributed. The information of high dimension data is condensed in T_IG. The degrees of freedom of T is 8 and so it is less powerful than T_IG which has only 1 degree of freedom. Intuitively, the reduction of degrees of freedom leads to high power for the test statistic T_IG.

Discussion

In this paper, we propose information gain based test statistics to detect and to characterize gene-gene and gene-environment interactions of complex diseases. For 2-way interaction, an information gain based approach is proposed using mutual information. The information gain in the presence of disease is defined as a one-dimensional variable through mutual information and entropy function of genetic markers, i.e., IG(AB | D) = I(A, B|D)−I(A, B). Based on the one-dimensional information gain, a test statistic T_IG is constructed and is showed to be ${\chi }_1^2$-distributed. As equation (14) shows, the information gain based test T_IG does not involve matrix inverse calculation which facilitates the implementation in practical applications because it is based on the normalization of a one-dimensional random variable ĝ − f̂ = Î(A, B|D) − Î (A, B). However, the calculation of the naive test T involves matrix inverse calculation and it is almost impossible to use it for sparse data as in our simulation calculation of empirical type I error rates. One can calculate the generalized inverse of matrix to implement the naive test T, and then its degrees of freedom changes from dataset to dataset. By power comparison, we clearly showed that the naive test T does not have an advantage over the information gain test T_IG.

In Wu et al. [2009], a mutual information based approach was proposed to construct a statistic to test 2-way gene-environment interaction by using a multi-dimensional vector. Under the null hypothesis of independence of the genetic marker and the environmental factor, the test statistic was showed to be a ${\chi }_2^2$-distributed variable with 2 degrees of freedom [Wu et al., 2009]. Some of the theoretical justification in our discussion such as mutual information is similar to that of Wu et al. [2009]. However, our way to construct the test statistic T_IG is different. In addition, our test statistic T_IG is ${\chi }_1^2$-distributed no matter under the null hypothesis of independence of disease status and genetic and environmental factors or under the alternative hypothesis. Under the null hypothesis, T_IG is centrally ${\chi }_1^2$-distributed. Under the alternative hypothesis, the T_IG is non-centrally ${\chi }_1^2$-distributed.

The methods are generalized to test high order K-way interactions and correlations of genetic markers and environmental factors, K ≥ 3. Two approaches are proposed: (1) an interaction information gain based approach, and (2) a total correlation information gain based approach. Such as the 2-way case, the interaction information gain and total correlation information gain are defined as one-dimensional variables. The related ${\chi }_1^2$-distributed test statistics T_IIG and T_TCIG are constructed to test higher order interactions and total correlations, respectively. The test statistic T_IIG is based on interaction information gain and it can test K-way interactions, K ≥ 3. The test statistic T_TCIG, however, is based on total correlation information gain and it can test K-way correlations, K ≥ 3. One may want to notice that correlation can be treated as the interaction in 2-way case, but they are not the same for high order K-way cases, K ≥ 3.

The power analysis of high order K-way cases, K ≥ 3, is not carried out in this article. Our problem is that we can not find appropriate models of high order K-way interaction such as those of 2-way cases. It would be interesting to explore some high order K-way interaction models first. Then, it will make more sense to calculate the theoretical power of the high order interaction models and make comparison with the simulated results. To our understanding, the area is still very new and a lot of work still need to be done to understand the high order interactions. The current paper is just a starting point. We will continue our research and report our results to scientific community in the future.

The proposed method was applied to bladder cancer data of Andrew et al. [2006]. We confirmed the significant result of 2-way interaction combination of XPD 751 and XPD 312 in Andrew et al. [2006]. However, we found that there was no significant result of 3-way interaction combinations for the bladder cancer data after adjusting for multiple tests. In the meantime, significant 3-way correlations were found which were basically from the 2-way interaction combination of XPD 751 and XPD 312.

In practice, one can use forward procedure to detect the interactions using test statistics T_IG and T_IIG. As the first step, one can test 2-way interactions by T_IG first. In the presence of 2-way interactions, one can search for evidence of 3-way and higher order interactions by T_IIG. If there are multiple genetic markers, the proposed method can be used to construct genet network to interpret the relation among the markers and environmental factors with the disease. Our analysis of the bladder cancer data provides an example of the procedure. Similarly, one can use test statistics T_IG and T_TCIG to detect the correlations, but the high order correlations may be actually from low order interactions.

One advantage of the proposed method is that it collapses high-dimensional genetic and environment data into a single dimension, and this makes it possible to build test statistic for high-dimensional sparse data to detect and to characterize gene-gene and gene-environment interactions and correlations. For instance, there are 27 genotype combinations if we consider 3 di-allelic markers. By using 3-way interaction information gain and total correlation information gain of the three markers, we may reduce the 27-dimensional data to be one-dimensional variables to construct the three-way information gain based test statistics. The principle applies to high order K-way interactions and correlations.

To our knowledge, there is no much research about gene-gene and gene-environment interactions using entropy-based approaches, although investigators are paying more and more attention to the research [Dong et al., 2008; Kang et a., 2008; Moore et al., 2006; Wu et al., 2009; Chanda et al., 2007]. It is a new and an interesting area which deserves more attention and investigation. In this article, we make no assumption about population history. It is unclear which kind of impact would appear in the presence of population structure, genotyping error, missing genotypes, phenocopy, and genetic heterogeneity. It would be interesting and important to systematically investigate the issues in the future study. So far, we focus on qualitative trait of complex trait, i.e., either with disease or no disease. It would be interesting to extend the method for quantitative traits. Besides, new methods and models need to be developed to analyze other data type such as sibling and nuclear family [Lou et al., 2008; Martin et al., 2006]. These can be exciting areas for future investigation.

Appendix A Proof of Relation (13)

A.1 The Subscripts ij Do Not Contain 2

Notice

$$\begin{array}{l}\frac{\partial f_{00}}{\partial P_{00}}=\frac{\partial }{\partial P_{00}}\left[P_{00}log\frac{P_{00}}{P_{0·}{P}_{·0}}\right]=log\frac{P_{00}}{P_{0·}{P}_{·0}}+\left[1-\frac{P_{00}}{P_{0·}}-\frac{P_{00}}{P_{·0}}\right]loge,\\ \frac{\partial f_{01}}{\partial P_{00}}=\frac{\partial }{\partial P_{00}}\left[P_{01}log\frac{P_{01}}{P_{0·}{P}_{·1}}\right]=-\frac{P_{01}}{P_{0·}}loge,\\ \frac{\partial f_{10}}{\partial P_{00}}=\frac{\partial }{\partial P_{00}}\left[P_{10}log\frac{P_{10}}{P_{1·}{P}_{·0}}\right]=-\frac{P_{10}}{P_{·0}}loge,\\ \frac{\partial f_{11}}{\partial P_{00}}=\frac{\partial }{\partial P_{00}}\left[P_{11}log\frac{P_{00}}{P_{1·}{P}_{·1}}\right]=0.\end{array}$$

In addition, we have

$$\begin{array}{l}\frac{\partial f_{02}}{\partial P_{00}}=\frac{\partial }{\partial P_{00}}\left[P_{02}log\frac{P_{02}}{P_{0·}{P}_{·2}}\right]=\left[-\frac{P_{02}}{P_{0·}}+\frac{P_{02}}{P_{·2}}\right]loge,\\ \frac{\partial f_{12}}{\partial P_{00}}=\frac{\partial }{\partial P_{00}}\left[P_{12}log\frac{P_{12}}{P_{1·}{P}_{·2}}\right]=\frac{P_{12}}{P_{·2}}loge,\\ \frac{\partial f_{20}}{\partial P_{00}}=\frac{\partial }{\partial P_{00}}\left[P_{20}log\frac{P_{20}}{P_{2·}{P}_{·0}}\right]=\left[\frac{P_{20}}{P_{2·}}-\frac{P_{20}}{P_{·0}}\right]loge,\\ \frac{\partial f_{21}}{\partial P_{00}}=\frac{\partial }{\partial P_{00}}\left[P_{21}log\frac{P_{21}}{P_{2·}{P}_{·1}}\right]=\frac{P_{21}}{P_{2·}}loge.\end{array}$$

Moreover, we have

$$\frac{\partial f_{22}}{\partial P_{00}}=\frac{\partial }{\partial P_{00}}\left[P_{22}log\frac{P_{22}}{P_{2·}{P}_{·2}}\right]=-log\frac{P_{22}}{P_{2·}{P}_{·2}}+\left[-1+\frac{P_{22}}{P_{2·}}+\frac{P_{22}}{P_{·2}}\right]loge.$$

Therefore, we have

$$\frac{\partial f}{\partial P_{00}}=\sum _{i=0}^2\sum _{j=0}^2\frac{\partial f_{ij}}{\partial P_{00}}=log\frac{P_{00}}{P_{0·}{P}_{·0}}-log\frac{P_{22}}{P_{2·}{P}_{·2}}.$$

Similarly, we have for i, j = 0, 1

$$\frac{\partial f}{\partial P_{ij}}=log\frac{P_{ij}}{P_{i·}{P}_{·j}}-log\frac{P_{22}}{P_{2·}{P}_{·2}}.$$

A.2 The Subscripts ij Contain One 2

Notice

$$\begin{array}{l}\frac{\partial f_{00}}{\partial P_{20}}=\frac{\partial }{\partial P_{20}}\left[P_{00}log\frac{P_{00}}{P_{0·}{P}_{·0}}\right]=-\frac{P_{00}}{P_{·0}}loge,\\ \frac{\partial f_{01}}{\partial P_{20}}=\frac{\partial }{\partial P_{20}}\left[P_{01}log\frac{P_{01}}{P_{0·}{P}_{·1}}\right]=0,\\ \frac{\partial f_{02}}{\partial P_{20}}=\frac{\partial }{\partial P_{20}}\left[P_{02}log\frac{P_{02}}{P_{0·}{P}_{·2}}\right]=\frac{P_{02}}{P_{·2}}loge,\\ \frac{\partial f_{10}}{\partial P_{20}}=\frac{\partial }{\partial P_{20}}\left[P_{10}log\frac{P_{10}}{P_{1·}{P}_{·0}}\right]=-\frac{P_{10}}{P_{·0}}loge,\\ \frac{\partial f_{11}}{\partial P_{20}}=\frac{\partial }{\partial P_{20}}\left[P_{11}log\frac{P_{11}}{P_{1·}{P}_{·1}}\right]=0,\\ \frac{\partial f_{12}}{\partial P_{20}}=\frac{\partial }{\partial P_{20}}\left[P_{12}log\frac{P_{12}}{P_{1·}{P}_{·2}}\right]=\frac{P_{12}}{P_{·2}}loge,\\ \frac{\partial f_{20}}{\partial P_{20}}=\frac{\partial }{\partial P_{20}}\left[P_{20}log\frac{P_{20}}{P_{2·}{P}_{·0}}\right]=log\frac{P_{20}}{P_{2·}{P}_{·0}}+\left[1-\frac{P_{20}}{P_{·0}}\right]loge,\\ \frac{\partial f_{21}}{\partial P_{20}}=\frac{\partial }{\partial P_{20}}\left[P_{21}log\frac{P_{21}}{P_{2·}{P}_{·1}}\right]=0,\\ \frac{\partial f_{22}}{\partial P_{20}}=\frac{\partial }{\partial P_{20}}\left[P_{22}log\frac{P_{22}}{P_{2·}{P}_{·2}}\right]=-log\frac{P_{22}}{P_{2·}{P}_{·2}}+\left[-1+\frac{P_{22}}{P_{·2}}\right]loge.\end{array}$$

Therefore, we have

$$\frac{\partial f}{\partial P_{20}}=log\frac{P_{20}}{P_{2·}{P}_{·0}}-log\frac{P_{22}}{P_{2·}{P}_{·2}}.$$

Similarly, we have for i, j = 0, 1

$$\begin{array}{l}\frac{\partial f}{\partial P_{i2}}=log\frac{P_{i2}}{P_{i·}{P}_{·2}}-log\frac{P_{22}}{P_{2·}{P}_{·2}},\\ \frac{\partial f}{\partial P_{2j}}=log\frac{P_{2j}}{P_{2·}{P}_{·j}}-log\frac{P_{22}}{P_{2·}{P}_{·2}}.\end{array}$$