Group Testing for Case Identification with Correlated Responses

Summary

This article examines group testing procedures where units within a group (or pool) may be correlated. The expected number of tests per unit (i.e., efficiency) of hierarchical- and matrix-based procedures is derived based on a class of models of exchangeable binary random variables. The effect on efficiency of the arrangement of correlated units within pools is then examined. In general, when correlated units are arranged in the same pool, the expected number of tests per unit decreases, sometimes substantially, relative to arrangements that ignore information about correlation.

1. Introduction

Group testing is a method used to reduce the average number of tests needed to identify cases of a disease in a population. The first use of group testing was proposed by Dorfman (1943). Dorfman proposed pooling blood samples of groups of men inducted into the military, and testing the combined samples for antigens to identify the presence of syphilis. If the combined samples tested negative for the antigens, the men were declared syphilis free with only one test. Otherwise, samples from each man were tested individually. Specimen pooling or group testing has been applied to screening for various infectious diseases and has also found broader application in many other areas (see Kim et al., 2007, and references therein). Group testing can also be used to reduce the average number of tests needed to estimate the prevalence of a disease, but this article focuses on case identification.

Dorfman’s two-stage procedure has been generalized to three or more stages. If the initial (or “master”) pool tests positive, the specimens may be pooled into smaller nonoverlapping subpools. If a subpool tests positive, individuals can be tested, or subpools can be divided further into smaller nonoverlapping subpools nested within the previous subpool. This is known as a hierarchical procedure (Johnson, Kotz, and Wu, 1991). Another common group testing algorithm is an array-based procedure (Phatarfod and Sudbury, 1994). In the simplest scenario, a group of n² units (specimens) is arranged into an n × n matrix, and pools of size n are constructed from units in each row or column. The 2n row and column pools are then tested, and positive units are identified by testing the units at the intersections of positive row and column pools.

Prior research regarding group testing procedures typically assumes individual units are independent. This assumption may not be reasonable in certain situations. For example, in the infectious disease setting, responses to a screening test may be positively correlated for individuals from the same geographical area or the same household. A second example arises in HIV vaccine development, where group testing methods are used to detect T-cell responses to specific epitopes induced by a candidate vaccine (Malhotra et al., 2007a, 2007b; Yan et al., 2007). T-cell responses to one or more peptides are identified by using ELISpot, intracellular cytokine staining, or other assays. Li et al. (2006) developed a potential T-cell epitope peptide set designed to contain epitopes found in commonly circulating strains of HIV. The peptide set is made of 15-mer peptides, some of which overlap by 10 or more amino acids. It is reasonable to expect T-cell responses from the same individual to be correlated for overlapping peptides. Indeed, Malhotra et al. (2007a) observed that T cells of HIV infected individuals can recognize multiple peptides containing variants of the same epitope. Roederer and Koup (2003) evaluated possible group testing procedures for this setting using Monte Carlo simulation, but did not consider that T-cell responses may be correlated. Below we show that accounting for this correlation when using group testing for case identification can reduce the average number of tests needed to identify all peptides that elicit a T-cell response.

Some group testing models allow for the probability a unit tests positive (the “prevalence”) to vary between units. Typically these models assume individual responses are independent conditional on the unit-specific prevalence (e.g., see Bilder, Tebbs, and Chen, 2010). The unit-specific prevalences will not generally be known but in some settings may be estimated with reasonable accuracy and precision based on observed covariates. In the absence of knowledge of the unit-specific prevalences, heterogeneity in the prevalences can induce correlation between units. Below we consider an approach to modeling correlation that does not require (i) (estimates of) unit-specific prevalence or (ii) assuming conditional independence.

2. Preliminaries

Suppose that a unit is either positive or negative with respect to some binary trait. For example, the unit could represent an individual with or without disease, or a peptide to which T cells respond or do not respond. Also suppose there is a test that attempts (perhaps with error) to classify units or pools of units as positive or negative, where a pool is considered positive if at least one unit in the pool is positive. The efficiency of a group testing procedure is defined as the expected number of tests per unit required to classify all units as either positive or negative. To evaluate the efficiency, one must calculate the probabilities that pools of units do not have any positive responses. These calculations require knowledge about correlation among units within each pool. Suppose there are n units total which can be partitioned into l clusters of size m and the following assumption holds:

Assumption 1

Units in different clusters are independent, and the joint distribution of the true classification of units in the same cluster is the same for all clusters.

Without loss of generality, let X̃ = (X₁, …, X_m) be a vector of binary random variables representing the true classification of units in a particular cluster, where X_i = 1 if unit i in that cluster is positive, and X_i = 0 otherwise. Let $\dot{X}={\sum }_{i=1}^m{X}_i$, let x̃ be a possible realization of X̃, and let ẋ be the sum of the values of x̃. Let $\stackrel{\sim }{X}\prime =\left(X_1^{\prime },\dots ,X_{m\prime }^{\prime }\right)$ be a subvector of any m′ elements of X̃ where m′ ∈ {1, …, m} and let $\dot{X}\prime ={{\sum }_{i=1}^{m\prime }X}_i^{\prime }$. Deriving the efficiency of a group testing procedure requires assumptions about the distribution of X̃. A class of models for X̃ is defined below by Assumptions 2 and 3 below via the factorization pr(X̃ = x̃) = pr(Ẋ = ẋ)pr(X̃ = x̃ ∣ Ẋ = ẋ).

Assumption 2

Units within a cluster are exchangeable in the sense that

$$\mathrm{pr}((X_1,X_2,\dots ,X_m)=\stackrel{\sim }{x})=\mathrm{pr}((X_{\gamma 1},X_{\gamma 2},\dots ,X_{\mathit{\gamma m}})=\stackrel{\sim }{x}),$$

for any permutation (γ₁, γ₂, … , γ_m) of the set of integers {1, 2, …, m}.

Because the X_i’s are binary, Assumption 2 implies $\mathrm{pr}\left(\stackrel{\sim }{X}=\stackrel{\sim }{x}\mid \dot{X}=\dot{x}\right)={\left(\begin{array}{c}m\\ \dot{x}\end{array}\right)}^{-1}$ for ẋ = 0, …, m, so the distribution of X̃ is fully identified by the distribution of Ẋ.

Assumption 3

The distribution of Ẋ can be expressed as a mixture of binomial distributions such that for ẋ = 0, …, m

$$\mathrm{pr}\left(\dot{X}=\dot{x}\right)=E_{\pi }\left\{\left(\begin{array}{c}m\\ \dot{x}\end{array}\right){\pi }^{\dot{x}}{(1-\pi )}^{m-\dot{x}}\right\},$$ (1)

where $E_{\pi }\left\{g\left(\pi \right)\right\}={\mathit{\int }}_0^{1}g(\pi )\mathit{dF}(\pi )$ for any function g, and π is a random variable with support [0, 1] and cumulative distribution function F.

Note there are connections between Assumption 3 and de Finetti’s Theorem. In particular, if the cluster X̃ can be viewed as a subset of an infinite sequence of exchangeable binary random variables, then Assumption 3 and Lemma 2, below, follow immediately from de Finetti’s Theorem (de Finetti, 1975). In settings motivating this work, such as the epitope mapping studies, the focus is on clusters of finite size, in which case (1) does not hold in general. Nonetheless, (1) is not a particularly strong assumption in settings where X̃ can be viewed as subset of a finite sequence of exchangeable binary random variables of length k ≥ m, for in that case the distribution of Ẋ can be approximated by a mixture of binomial random variables with error going to zero at rate k⁻¹ (Diaconis, 1977). For example, in epitope mapping studies, a set of m exchangeable peptides might be envisaged as a subset of a larger set of k exchangeable peptides.

The lemmas below establish certain properties about the family of distributions under Assumptions 2 and 3 that are used in evaluating the efficiencies derived in Sections 3 and 4. Let E(X_i) = p be the probability that any unit i is positive and let cor(X_i, X_j) = σ be the pairwise correlation between any two units i and j for i ≠ j. We refer to p as the prevalence. Lemma 1 shows that any distribution of exchangeable binary random variables approaches a known limiting distribution as σ approaches one. Lemma 2 shows that the distribution of a subset of units from an exchangeable cluster where (1) holds is of the same form as the distribution of the units in the cluster. By specifying a distribution for π where the first and second moments are p and σ p (1 − p) + p², respectively, the distribution of a vector of exchangeable binary random variables with specified marginal means and pairwise correlations is defined by Lemma 3. Proofs of the lemmas are given in the Web Appendix A.

Lemma 1

Under Assumption 2, as σ approaches 1 the distribution of Ẋ converges to a two-point distribution, where pr(Ẋ = 0) → 1 − p and pr(Ẋ = m) → p.

Lemma 2

Under Assumptions 2 and 3, the distribution of Ẋ′ is a mixture of binomial distributions of the same form as Ẋ, such that

$$\mathrm{pr}\left(\dot{X}\prime =\dot{x}\prime \right)=E_{\pi }\left\{\left(\begin{array}{c}m\prime \\ \dot{x}\prime \end{array}\right){\pi }^{\dot{x}\prime }{(1-\pi )}^{m\prime -\dot{x}\prime }\right\}$$ (2)

for ẋ′ = 1, …, m′.

Lemma 3

Under Assumptions 2 and 3, if E(π) = p and E(π²) = σ p(1 − p) + p², then E(X_i) = p for all i and cor(X_i, X_j) = σ for all i ≠ j.

The models defined by Assumption 3 can be viewed as random effect models where units within the same cluster are positive with (unknown) probability π, with π varying between clusters according to distribution F. In the sequel, three particular models are considered to examine how the efficiencies of group testing procedures are affected by correlated responses. The first is a beta-binomial model where π has a beta distribution with mean p and variance σ p(1 − p). The second model is from Madsen (1993) who described multiple distributions that can be used to model exchangeable binary data. One of those models can be constructed by letting π = p with probability 1 − σ, π = 0 with probability σ(1 − p), and π = 1 with probability σp; this will be referred to as the Madsen model. This model can be thought of as arising from a situation where there are two types of clusters: one type where units are independent, and another type where units all perfectly correlated and behave exactly the same, either all positive or all negative. In both types of clusters, the probability of a particular unit being positive is p. A cluster is of the first type with probability 1 − σ and is of the second type otherwise. A third model, described in Morel and Neerchal (1997), can be constructed by letting $\pi =p+(1-p)\sqrt{\sigma }$ with probability p and $\pi =p-p\sqrt{\sigma }$ with probability 1 − p. In the comparisons described below, the Morel–Neerchal model tended to yield efficiencies between the beta-binomial and Madsen models (results not shown).

The efficiency derivations in Sections 3 and 4 below rely on the following additional notation and assumptions. Let q₀ = 1 and q_m′ = pr(Ẋ′ = 0) denote the probability that m′ units from the same cluster are negative for m′ ∈ {1, …, m}. For the three models above q₁ = 1 − p and q_m′ is given by (2) with ẋ′ = 0. Let T denote the number of tests required by a particular group testing procedure to classify n units as positive or negative. To allow for test error (i.e., false positive or false negative test results), assume pools with at least one positive unit test positive with probability S_e and that pools with no positive units test negative with probability S_p; we refer to S_e and S_p as test sensitivity and specificity. The special case of no test error corresponds to S_e = S_p = 1. Web Appendix B provides further details regarding assumptions about test error.

3. Hierarchical Procedures

3.1 Notation and Efficiency of General Hierarchical Procedures

Consider a hierarchical procedure where n₁ = n units are combined to form a master pool. In the first stage, the master pool is tested, and if it tests positive, w₂ nonoverlapping pools of n₂ units are each tested in the second stage. In a two-stage procedure, n₂ = 1 and each unit in a master pool that tests positive is tested individually. In a general h stage procedure, for each pool that tests positive in stage s − 1, n_{s −1}/n_s nonoverlapping pools of n_s units are tested. There are a total of w_s = n₁/n_s pools that could be tested at stage s if all of the pools in the previous stages test positive. At the hth stage each pool is made up of individual units, so n_h = 1. The total number of tests T = T₁ + … + T_h, where T_s is a random variable representing the number of tests at stage s. The efficiency of a hierarchical procedure is $E(T)/n_1={\sum }_{s=1}^{h}E(T_s)/n_1$. The master pool is always tested, so E(T₁) is always one.

Let $V_{\mathit{si}}^T=1$ if the ith pool in the sth stage has at least one truly positive unit, and 0 otherwise. For a particular arrangement of clusters, let m_sik be the number of units from cluster k in pool i of stage s for k = 1, …, l. In general,

$$\mathrm{pr}\left(V_{\mathit{si}}^T=1\right)=1-\prod _{k=1}^l{q}_{m_{\mathit{sik}}},$$ (3)

is the probability that pool i in stage s is truly positive. Let V_si = 1 if the ith pool in the sth stage tests positive and let V_si = 0 otherwise (i.e., if the pool tests negative or is not tested). For s > 1, $E(T_s)=(w_s/w_{s-1}){\sum }_{i=1}^{w_{s-1}}\mathrm{pr}(V_{(s-1)i}=1)$ which can be evaluated by noting

$$\mathrm{pr}\left(V_{1i}=1\right)=S_e\mathrm{pr}\left(V_{1i}^T=1\right)+\left(1-S_p\right)\mathrm{pr}\left(V_{1i}^T=0\right),$$ (4)

and for s > 1

$$\mathrm{pr}\left(V_{\mathit{si}}=1\right)=\sum _{v=0}^1{S}_e^v{\left(1-S_p\right)}^{(1-v)}\mathrm{pr}\left(V_{(s-1)i_{s-1}}=1\mid V_{\mathit{si}}^T=v\right)\times \mathrm{pr}\left(V_{\mathit{si}}^T=v\right),$$ (5)

where in general, for t < s, i_t denotes the pool in stage t containing the units from pool i in stage s. Equation (5) can be evaluated using the following results:

$$\mathrm{pr}\left(V_{1i_1}=1\mid V_{2i}^T=v\right)=\{\begin{array}{ll}\sum _{u=0}^1{S}_e^u{(1-S_p)}^{1-u}\mathrm{pr}\left(V_{1i_1}^T=u\mid V_{2i}^T=0\right)& \mathrm{if}v=0\\ S_e& \mathrm{if}v=1\end{array}$$

and for s > 2

$$\mathrm{pr}\left(V_{(s-1)i_{s-1}}=1\mid V_{\mathit{si}}^T=v\right)=\{\begin{array}{ll}\sum _{u=0}^1\left\{S_e^u{\left(1-S_p\right)}^{1-u}\mathrm{pr}\left(V_{(s-1)i_{s-1}}^T=u\mid V_{\mathit{si}}^T=0\right)\times \mathrm{pr}\left(V_{(s-2)i_{s-2}}=1\mid V_{(s-1)i_{s-1}}^T=u\right)\right\}& \mathrm{if}v=0\\ S_e\mathrm{pr}\left(V_{(s-2)i_{s-2}}=1\mid V_{(s-1)i_{s-1}}^T=1\right)& \mathrm{if}v=1\end{array}$$

where $\mathrm{pr}\left(V_{(s-1)i_{s-1}}^T=0\mid V_{\mathit{si}}^T=0\right)=\mathrm{pr}\left(V_{(s-1)i_{s-1}}^T=0\right)/\mathrm{pr}\left(V_{\mathit{si}}^T=0\right)$ and $\mathrm{pr}\left(V_{(s-1)i_{s-1}}^T=1\mid V_{\mathit{si}}^T=0\right)=1-\mathrm{pr}\left(V_{(s-1)i_{s-1}}^T=0\mid V_{\mathit{si}}^T=0\right)$ for s > 1.

To determine the efficiency of a particular hierarchical procedure, (4) and (5) are evaluated based on the arrangement of clusters. For the cluster arrangements considered in Sections 3.2 and 3.3 below and for any arrangement where the units are independent, the efficiency calculation is simplified because pr(V_si = 1) is the same for all i and therefore E(T_s) = w_s pr(V_(s−1)i = 1). Johnson et al. (1991) derive the efficiency for a hierarchical procedure with independent units where sensitivity and specificity can depend on the stage. If units are independent, $E(T)/n_1={\sum }_{s=1}^{h}E\left(T_s\right)/n_1={\sum }_{s=1}^h{w}_s\mathrm{pr}\left(V_{(s-1)i}=1\right)/n_1$ is equivalent to their equation (6.19) when sensitivity and specificity are constant for all stages.

3.2 Nested Hierarchical Arrangement

Suppose clusters of size m are arranged such that all units from the same cluster are in the same pool for stages 1 to h′ − 1. Also, suppose for stages h′ to h, all units in the same pool are members of the same cluster. That is, m_sik = m or 0 for s < h′, and m_sik = n_s or 0 for s ≥ h′ where h′ ∈ {2, 3, …, h}. Figure 1a shows an example of an h = 3 stage procedure where m = 6, n₁ = 12, n₂ = 3, and the numbers 1 and 2 denote cluster membership. At stage 2, all six units from the same cluster cannot fit in pools of size 3, but all units in the same pool are from the same cluster, so h′ = 2. Call this a nested hierarchical arrangement. By (3), if 1 < s ≤ h′ then $\mathrm{pr}\left(V_{(s-1)i}^T=1\right)=1-q_m^{n_{s-1}/m}$ for all i, and if h′ < s ≤ h then $\mathrm{pr}\left(V_{(s-1)i}^T=1\right)=1-q_{n_{s-1}}$ for all i.

Figure 1.

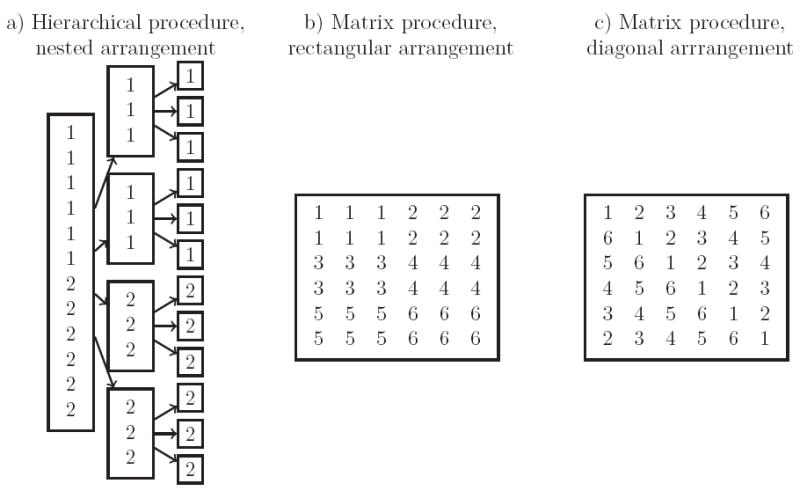
Illustrations of the construction hierarchical and matrix procedures.

3.3 Random Hierarchical Arrangement

Suppose units are arranged in a way that is independent of their cluster membership. Let M̃_si· be the random vector of length l of the number of units from each cluster 1, …, l in pool i in stage s. Let each possible arrangement of the n₁ units have the same probability, so M̃_si· has a multivariate hypergeometric distribution such that

$$\mathrm{pr}\left({\stackrel{\sim }{M}}_{\mathit{si}·}={\stackrel{\sim }{m}}_{\mathit{si}·t}\right)={\left(\begin{array}{c}{n}_1\\ n_s\end{array}\right)}^{-1}\prod _{k=1}^l\left(\begin{array}{c}m\\ m_{\mathit{s\; i\; k\; t}}\end{array}\right),$$ (6)

where m̃_{si ·t} = (m_si1t, …, m_silt) is the tth possible value of M̃_si· for $t=1,\dots ,\left(\begin{array}{c}{n}_1\\ n_s\end{array}\right)$. Then

$$\mathrm{pr}\left(V_{(s-1)i}^T=0\mid {\stackrel{\sim }{M}}_{(s-1)i·}={\stackrel{\sim }{m}}_{(s-1)i·t}\right)=\prod _{k=1}^l{q}_{m_{(s-1)\mathit{i\; k\; t}}},$$ (7)

and therefore

$$\mathrm{pr}\left(V_{(s-1)i}^T=1\right)=1-{\left(\begin{array}{c}{n}_1\\ n_{s-1}\end{array}\right)}^{-1}\sum _{t=1}^{\left(\begin{array}{c}{n}_1\\ n_{s-1}\end{array}\right)}\left\{\prod _{k=1}^l{q}_{m_{(s-1)\mathit{i\; k\; t}}}\left(\begin{array}{c}m\\ m_{(s-1)\mathit{i\; k\; t}}\end{array}\right)\right\}.$$ (8)

When n₁ is large, the number of possible arrangements $\left(\begin{array}{c}{n}_1\\ n_{s-1}\end{array}\right)$ becomes very large, and the exact calculation for (8) is computationally difficult. Monte Carlo simulation can be used to approximate (8). First values of M̃_(s−1)i· are repeatedly sampled from a multivariate hypergeometric distribution according to (6). Then the conditional probability (7) is evaluated for each sample. Finally, one minus the sample mean of the conditional probabilities will approximate (8).

3.4 Comparison of Hierarchical Arrangements

For a two-stage hierarchical procedure with a nested arrangement, if S_e = S_p = 1, the expected number of tests is E(T) = 1 + E(T₂), where $E\left(T_2\right)=w_2\left(1-q_m^{n_1/m}\right)$. If σ = 0 then $q_m=q_1^m$ and the efficiency for all models equals $E(T)/n_1=n_1^{-1}+1-q_1^{n_1}$ as in Dorfman (1943). Figure 2 illustrates the efficiency of a two-stage hierarchical procedure for the beta-binomial and Madsen models for different values of σ as a function of m when S_e = S_p = 1. For large clusters the expected tests per unit is reduced substantially as σ increases. When σ = 0.99, the efficiencies for both models are almost identical, which is consistent with Lemma 1. See Web Figures 1 and 2 for similar results when S_e and S_p are less than 1.

Figure 2.

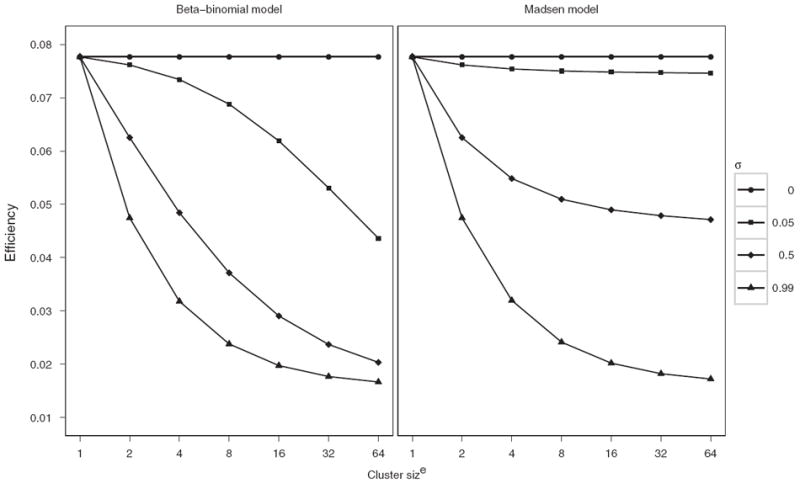
Efficiencies for a two-stage hierarchical procedure where S_e = S_p = 1, n₁ = 64 and p = 0.001 by cluster size m, pairwise correlation σ, and model.

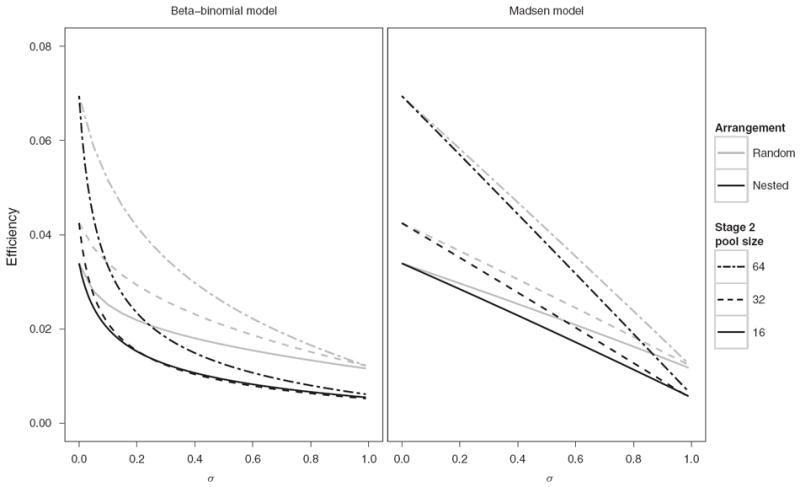
For a three-stage hierarchical procedure with a nested arrangement where all units from the same cluster fit into the same pool in stages 1 and 2 (i.e., h′ = 3) and S_e = S_p = 1, the expected number of tests for stage 2 has the same form as in the two-stage procedure above. Similarly, the expected number of tests for the third stage is $E\left(T_3\right)=w_3\left(1-q_m^{n_2/m}\right)$ so $E(T)=1+w_2\left(1-q_m^{n_1/m}\right)+w_3\left(1-q_m^{n_2/m}\right)$. Figure 3 compares the efficiencies of three-stage hierarchical nested and random arrangements by stage two pool size, n₂, as a function of σ. Efficiencies for the random arrangements were obtained by Monte Carlo simulation. In all cases in Figure 3 the nested arrangements have better efficiency than random arrangements for σ > 0. Similar results when S_e and S_p are less than 1 are given in Web Figures 3 and 4.

Figure 3.

Efficiencies for three-stage hierarchical procedures where S_e = S_p = 1, n₁ = 256, p = 0.001, and m = 32 by pairwise correlation σ, stage two pool size n₂, arrangement, and model.

4. Matrix Procedures

4.1 Notation and Efficiency of General Matrix Procedures

Consider a matrix-based procedure where n = rc units are arranged in a matrix with r rows and c columns. First, r row pools and c column pools are tested. If any rows and columns test positive, then units at the intersections of positive rows and columns are tested. Let Y_ij be 1 if the unit in the ith row and the jth column is truly positive and 0 otherwise, let $R_i^T=\max \left(Y_{i1},\mathrm{\dots },Y_{\mathit{ic}}\right)$, and let $C_j^T=\max \left(Y_{1j},\mathrm{\dots },Y_{\mathit{rj}}\right)$ for i = 1, …, r and j = 1, …, c. Let R_i and C_j denote the observed responses for the tests corresponding to the ith row and the jth column, respectively. If sensitivity or specificity is not one, some columns might test positive while all rows test negative, or the opposite. If this occurs, assume no further tests are carried out such that the unit at the intersection of row i and column j is tested only if R_i = C_j = 1. This is the procedure used in Precopio et al. (2008). In general, for an r × c matrix, the expected number of tests equals

$$E(T)=r+c+\sum _{i=1}^r\sum _{j=1}^c\mathrm{pr}\left(R_i=C_j=1\right).$$ (9)

Let m_i·k be the number of units from cluster k in row i; let m_·jk be the number of units from cluster k in column j; and let m_ijk be the number of units from cluster k in either row i or column j. Then (9) can be evaluated by noting

$$\begin{array}{l}\mathrm{pr}\left(R_i=C_j=1\right)\\ =\sum _{u,v=0}^1\mathrm{pr}\left(R_i=C_j=1\mid R_i^T=u,C_j^T=v\right)\mathrm{pr}\left(R_i^T=u,C_j^T=v\right)\\ =\sum _{u,v=0}^1{S}_e^{u+v}{\left(1-S_p\right)}^{2-u-v}\mathrm{pr}\left(R_i^T=u,C_j^T=v\right),\end{array}$$ (10)

where

$$\mathrm{pr}\left(R_i^T=u,C_j^T=v\right)=\{\begin{array}{cc}1-\left\{\mathrm{pr}\left(R_i^T=0\right)+\mathrm{pr}\left(C_j^T=0\right)-\mathrm{pr}\left(R_i^T=C_j^T=0\right)\right\}\hfill & \hfill \mathrm{if}u=v=1\\ \mathrm{pr}\left(C_i^T=0\right)-\mathrm{pr}\left(R_i^T=C_j^T=0\right)\hfill & \hfill \mathrm{if}u=1,v=0\\ \mathrm{pr}\left(R_i^T=0\right)-\mathrm{pr}\left(R_i^T=C_j^T=0\right)\hfill & \hfill \mathrm{if}u=0,v=1\\ \mathrm{pr}\left(R_i^T=C_j^T=0\right)\hfill & \hfill \mathrm{if}u=v=0,\end{array}$$

and

$$\begin{array}{c}\mathrm{pr}\left(R_i^T=0\right)=\prod _{k=1}^l{q}_{m_{i·k}},\mathrm{pr}\left(C_j^T=0\right)=\prod _{k=1}^l{q}_{m_{·\mathit{j\; k}}},\\ \mathrm{and\; pr}\left(R_i^T=C_j^T=0\right)=\prod _{k=1}^l{q}_{m_{\mathit{i\; j\; k}}}.\end{array}$$ (11)

Let m̃_i·· = (m_{i ·1}, …, m_{i ·l}), let m̃_·j· = (m_{·j 1}, …, m_{·j l}), and let m̃_{i j ·} = (m_{i j 1}, …, m_{i j l}). If the ordered values of m̃_{i ··} and m̃_i′·· are equal, the ordered values of m̃_·j· and m̃_·j′· are equal, and the ordered values of m̃_{i j·} and m̃_i′j′· are equal for all i ≠ i′ and j ≠ j′, then pr(R_i = C_j = 1) is the same for all i and j, and (9) reduces to

$$E(T)=r+c+\mathit{rc}\mathrm{pr}\left(R_i=C_j=1\right).$$ (12)

If S_e = S_p = 1 and all units are independent, then σ = 0 and the expected tests per unit is $E\left(T\right)/n=c^{-1}+r^{-1}+1-\left(q_1^c+q_1^r-q_1^{r+c-1}\right)$ as in Phatarfod and Sudbury (1994).

4.2 Rectangular Arrangement

In a rectangular arrangement, clusters of m units are arranged in submatrices of dimension r′ × c′ so m = r′ c′. These submatrices are arranged in a matrix of dimensions r × c. The number of rows r is assumed to be divisible by r′ and the number of columns c is assumed to be divisible by c′. Figure 1b shows an example of a 6 × 6 matrix procedure where m = 6, r′ = 2, and c′ = 3. Again, the numbers in the figure represent cluster membership. In a rectangular arrangement, clusters are arranged in a way that (12) holds, and $\mathrm{pr}\left(R_i^T=0\right)=q_{c\prime }^{c/c\prime }$, $\mathrm{pr}\left(C_j^T=0\right)=q_{r\prime }^{r/r\prime }$, and $\mathrm{pr}\left(R_i^T=C_j^T=0\right)=q_{\left(c\prime +r\prime -1\right)}{q}_{c\prime }^{c/c\prime -1}{q}_{r\prime }^{r/r\prime -1}$. If S_e = S_p = 1,

$$E(T)=r+c+\mathit{rc}\left\{1-\left(q_{c\prime }^{c/c\prime }+q_{r\prime }^{r/r\prime }-q_{(c\prime +r\prime -1)}{q}_{c\prime }^{c/c\prime -1}{q}_{r\prime }^{r/r\prime -1}\right)\right\}.$$

4.3 Diagonal Arrangement

In a diagonal arrangement, assume r = c = m. Clusters of size m are arranged on diagonals of a matrix such that each row and each column have exactly one unit from each cluster. More precisely, for any i ∈ {1, …, r − 1} and j ∈ {1, …, c − 1}, the responses Y_ij and Y_{(i+1)(j +1)} will correspond to units from the same cluster in a diagonal arrangement. See Figure 1c for an example where r = c = m = 6. Clusters can wrap such that the last unit in a row of the matrix is a member of the same cluster as the first unit in the next row of the matrix. In this arrangement, clusters are arranged in a way that (12) hold and $\mathrm{pr}\left(R_i^T=0\right)=q_1^r$, $\mathrm{pr}\left(C_j^T=0\right)=q_1^r$, and $\mathrm{pr}\left(R_i^T=C_j^T=0\right)=q_1{q}_2^{r-1}$. If S_e = S_p = 1,

$$E(T)=2r+r^2\left\{1-\left(2q_1^r-q_1{q}_2^{r-1}\right)\right\}.$$

4.4 Random Arrangement

Now consider the case where units are arranged in a matrix randomly in a way that is independent of cluster membership. Let M̃_i·· be the random vector of the number of units from each cluster 1, …, l in row i, let M̃_·j· be the random vector of the number of units from each cluster 1, …, l in column j, and let M̃_{i j ·} be the random vector of the number of units from each cluster 1, …, l in either row i or column j. Each possible arrangement of n units has the same probability, so M̃_{i ··} has a multivariate hypergeometric distribution such that

$$\mathrm{pr}\left({\stackrel{\sim }{M}}_{i··}={\stackrel{\sim }{m}}_{i··t}\right)={\left(\begin{array}{c}n\\ c\end{array}\right)}^{-1}\prod _{k=1}^l\left(\begin{array}{c}m\\ m_{i·\mathit{k\; t}}\end{array}\right),$$

where m̃_{i ··t} = (m_{i ·1t}, …, m_{i ·l t}) is the tth possible vector of values of m̃_{i ··t}, $t=1,\dots ,\left(\begin{array}{c}n\\ c\end{array}\right)$.

From (11) it follows that $\mathrm{pr}\left(R_i^T=0\mid {\stackrel{\sim }{M}}_{i··t}={\stackrel{\sim }{m}}_{i··t}\right)={\prod }_{k=1}^l{q}_{m_{i·\mathit{k\; t}}}$, implying

$$\mathrm{pr}\left(R_i^T=0\right)={\left(\begin{array}{c}n\\ c\end{array}\right)}^{-1}\sum _{t=1}^{\left(\begin{array}{c}n\\ c\end{array}\right)}\left\{\prod _{k=1}^l{q}_{m_{i·\mathit{k\; t}}}\left(\begin{array}{c}m\\ m_{i·\mathit{k\; t}}\end{array}\right)\right\}.$$

Additionally, $\mathrm{pr}\left(C_j^T=0\right)$ and $\mathrm{pr}\left(R_i^T=C_j^T=0\right)$ can be calculated in an analogous way. Similar to calculating $\mathrm{pr}\left(V_{(s-1)i}^T=1\right)$ in a randomly arranged hierarchical procedure, calculating $\mathrm{pr}\left(R_i^T=0\right)$, $\mathrm{pr}\left(C_j^T=0\right)$, and $\mathrm{pr}\left(R_i^T=C_j^T=0\right)$ becomes computationally infeasible as n increases, and Monte Carlo simulation can be used to approximate each of these probabilities. The efficiency, E(T)/n, can then be calculated by (10) and (12).

4.5 Comparison of Matrix Arrangements

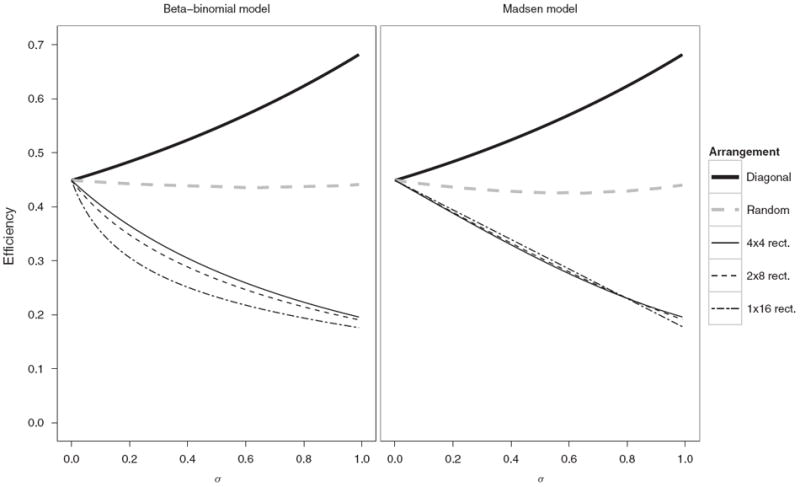
Figure 4 shows the expected tests per unit for a square matrix of size 16 × 16 with clusters of size 16 for different rectangular arrangements, a diagonal arrangement, and a random arrangement, where S_e = S_p = 1. Efficiencies for the random arrangement were obtained by Monte Carlo simulation. For rectangular arrangements, the expected number of tests per unit decreases as σ increases. For the beta-binomial model, the expected tests per unit is lowest when clusters are arranged in a row, and the expected tests per unit increases as the arrangement of clusters moves from a single row to a 4 × 4 square. For the Madsen model, the rectangular arrangements perform about the same. Intuitively, a diagonal arrangement will perform worse than a rectangular arrangement, because positive responses in the same cluster will be in different rows and columns, and therefore more individual testing will be required. This intuition is supported by Figure 4, where the diagonal arrangement performs much worse than the other arrangements as σ increases. In the diagonal arrangement, the most units from the same cluster that are tested together is two. The joint distribution for a cluster of size two is fully specified by the first and second moments, so the efficiency for the diagonal arrangement is the same for both models. The efficiency for the randomly arrangement is worse than the rectangular arrangements, but better than the diagonal arrangement in this case. Similar results when S_e and S_p are less than 1 are given in Web Figures 5 and 6.

Figure 4.

Efficiencies for a 16 × 16 matrix procedure where p = 0.05, S_e = S_p = 1 and clusters are of size m = 16 by arrangement, pairwise correlation σ, and model.

5. Application

Malhotra et al. (2007a) used a 9 × 10 matrix procedure to evaluate T-cell responses to 90 peptides. The matrix algorithm was used to test for peptide responses for each of 23 subjects in the study, so there were a total of 2030 T-cell responses to classify. The peptides were made up of 15 amino acids, with some pairs of peptides overlapping by 10 or more amino acids. To illustrate the potential gain in efficiency when clusters are arranged strategically for group testing, we consider the efficiency of the 9 × 10 matrix procedure for different possible peptide arrangements. Assume the 90 peptides can be partitioned into groups of size 5 or 10 such that T-cell responses to each group of peptides form an exchangeable cluster with positive pairwise correlations. Such clusters might be formed by grouping peptides coded by the same gene (e.g., nef) or grouping peptides with similar amino acid sequences. From Figure 2A of Malhotra et al. (2007a), there were a total of 151 positive responses to the set of 90 peptides for all subjects. Therefore suppose for this illustration the probability of a positive T-cell responses is 0.07 (i.e., ≈ 151/2030).

Figure 5 shows the efficiency of the 9 × 10 matrix procedure if the clusters are in a rectangular arrangement compared to a random arrangement when S_e = S_p = 1. Efficiencies for the random arrangements were obtained by Monte Carlo simulation. For the rectangular arrangements, the clusters of size 5 are arranged in submatrices of size 1 × 5 and the clusters of size 10 are arranged in submatrices of size 1 × 10. For both of these cluster sizes, the rectangular arrangements have a substantial gain in efficiency over the random arrangements. For example, at σ = 0.4 for m = 5, the efficiency for the rectangular arrangement is 0.39 versus 0.48 for the random arrangement from the beta-binomial model, resulting in 0.09 fewer tests per peptide on average. For each of the 23 subjects, 90 peptides are evaluated, so there is a potential savings of about 186 tests by strategically arranging peptides within a matrix. In the presence of test error similar but slightly less savings would be expected (Web Figures 7 and 8). Malhotra et al. (2007a) only examined peptides associated with the Nef gene, but other studies evaluate a much larger number of peptides across the HIV genome (Russell et al., 2003; Koup et al., 2010). For such large scale studies, the savings from a strategic arrangement of peptides can be substantial.

Figure 5.

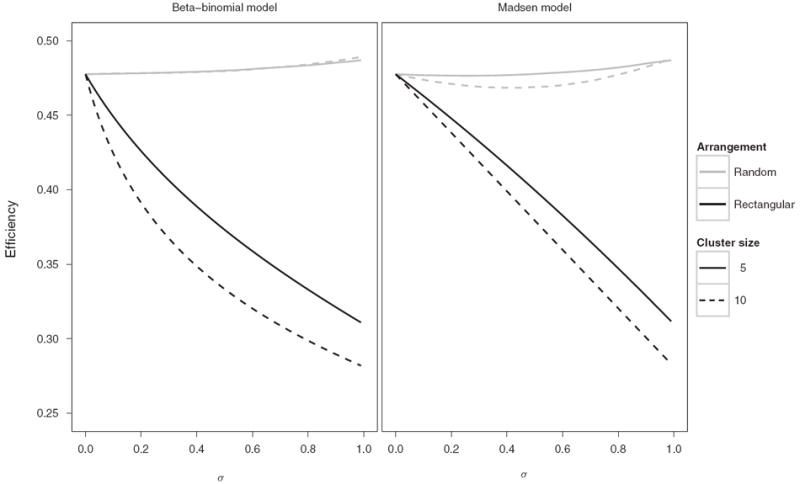
Efficiencies for a 9 × 10 matrix procedure where p = 0.07, S_e = S_p = 1 by pairwise correlation σ, cluster size m, arrangement, and model.

6. Discussion

This article provides closed form expressions for hierarchicaland matrix-based group testing procedures when units within clusters are correlated. These results allow investigation into the effect of correlation and the arrangement of clusters on a procedure’s efficiency. For the three models of exchangeable binary random variables considered, we found that if units from the same cluster are tested together, then the efficiency of a particular procedure can be improved, sometimes substantially, relative to random arrangements, which ignore information about cluster membership.

The feasibility of incorporating information on correlation into the design of particular group testing studies will depend on the setting. In the epitope mapping example, pools of peptides are typically constructed in a single or few large batches. Then epitope mapping studies are conducted by repeating a standard deconvolution algorithm over various sets of specimens (one at a time), e.g., individual sera from participants in an HIV vaccine trial. Because the peptide pools are constructed in batches ahead of time, information on correlation between peptides can easily be utilized when deciding which peptides to combine into pools. Correlation estimates can be obtained through prior experiments in similar settings, public databases (Taylor and Flower, 2007) or prediction models for T-cell epitopes (Lin et al., 2008). In infectious disease screening applications, individual level covariate information can be incorporated into pooling algorithms to improve efficiency (e.g., see Bilder et al., 2010). In such settings where individual level covariates are used to design the pooling algorithm it should be feasible to account for correlation between individuals as well. To facilitate such designs, an R package gtcorr, available at http://cran.r-project.org/, has been developed, which calculates the efficiencies of hierarchical and matrix group testing procedures for the beta-binomial, Madsen, and Morel–Neerchal cluster models.

Throughout this article clusters were assumed to be of equal size with the same distribution (Assumption 1), contain exchangeable units (Assumption 2), and have a distribution within a particular class (Assumption 3). Assumption 1 is helpful for ease of presentation but in fact the efficiency derivations in Sections 3.1 and 4.1 are sufficiently general that this assumption is not required. For instance, (9)-(11) can be used to evaluate the efficiency of any matrix algorithm with varying cluster sizes and different prevalences between clusters. To account for cluster-specific prevalences, the terms q_{mi ·k}, q_{m·j k}, and q_{mi j k} in (11) should be computed using (2) for ẋ′ = 0 and π equal to the prevalence for cluster k. The R package gtcorr allows for clusters of various size and different prevalences between clusters. As discussed in Section 2, Assumption 3 is not a particularly strong assumption. In future research, models that do not assume exchangeable units within clusters (Assumption 2) could be considered. Some empirical investigation regarding violations of Assumption 2 is given in Web Appendix C. These results demonstrate that efficiency estimates obtained when incorrectly assuming an exchangeable correlation structure may be fairly accurate in some settings.