Stepping, strain gating, and an unexpected force-velocity curve for multiple-motor based transport

Summary

Background

Intra-cellular transport via processive Kinesin, Dynein and Myosin molecular motors plays an important role in maintaining cell structure and function. In many cases, cargos move distances longer than expected for single motors; there is significant evidence that this increased travel is in part due to multiple motors working together to move the cargos. While we understand single motors experimentally and theoretically, our understanding of multiple motors working together is less developed.

Results

We theoretically investigate how multiple Kinesin motors function. Our model includes stochastic fluctuations of each motor as it proceeds through its enzymatic cycle. Motors dynamically influence each other and function in the presence of thermal noise and viscosity. We test the theory via comparison with the experimentally observed distribution of step sizes for two motors moving a cargo, and by predicting slightly sub-additive stalling force for two motors relative to one. In the presence of load, our predictions for travel distances and mean velocities are different from the steady-state model: with high motor-motor coupling, we predict a form of strain-gating, where—due to the underlying motor’s dynamics—the motors share load unevenly, leading to increased mean travel distance of the multiple-motor system under load. Surprisingly, we predict that in the presence of small load, two motor cargos move slightly slower than do single-motor cargos. A companion paper confirms this prediction in vivo.

Conclusions

When only a few motors are active, fluctuations and unequal load sharing between motors can result in significant alterations of ensemble function.

Introduction

Directed movement of cargos along MTs is a key component of transport within a cell. Numerous studies suggest that cargos in vivo are moved by more than one microtubule-based motor[1] but relatively little is known about the combined function of multiple motors. Our past experimental work established that multiple kinesin motors can move cargos long distances, and that the force required to stall a bead moved on average by 2 kinesins was slightly less than double the force required to stall a bead moved by a single kinesin[2]. However, we would like more insight into how the motors work together: how do they step, how do they influence each other, how do they respond to an external force that opposes their motion (load), and how is their ensemble function affected by the combination of thermal noise and viscosity?

Molecular motors are stochastic enzymes; in the small-N limit, fluctuations need not average out. To investigate how multiple interacting motors function, and whether fluctuations are important, we developed a Monte Carlo formalism extending a previous description of a single kinesin motor (See supplement in [3]).

While not relevant for an existing steady-state model [4], a key issue for the Monte Carlo simulation is the compliance of the linkage which connects the motor heads to the cargo (Fig. 1). In principle, the magnitude of this linkage stiffness could vary significantly in vivo because it includes multiple sources of compliance that could exist linking the two motors, including stretching of the motors themselves, stretching of any scaffold proteins linking the motors to the cargo, and deformation/stretching of the cargo itself. The strength of the coupling between the motors (set by linkage stiffness) determines how information is propagated between them. We find that coupling strength plays a significant role in determining the ensemble’s function—for weak coupling, fluctuations are not well communicated, and the system’s performance approaches the steady-state model. In contrast, when stronger (likely realistic) coupling coefficients are used, the system’s performance is quite different.

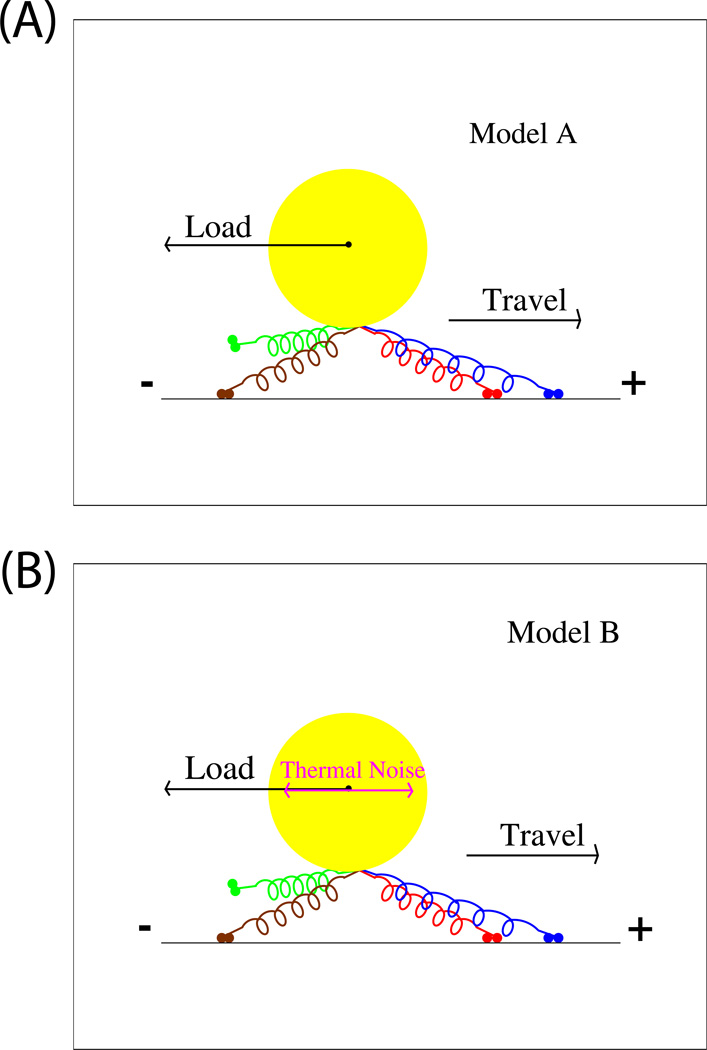
Figure 1. Diagram of Models A (A) and Model B (B).

The cargo (yellow circle) is attached to 4 motors (colored ‘springs’ with two small blobs at their end, indicating the motors’ heads). The motors can attach and detach to the microtubule (black line). In the case shown, while there are N=4 motors attached to the cargo, there are only n=3 engaged motors, because the green motor is not bound to the microtubule. While dynamics determine the instantaneous number of engaged motors n, depending on the simulation, there is an initial choice of N between 1 and 4 motors. N does not vary once a simulation starts. The main difference between Model A (upper panel) and B (lower panel) is that Model B includes thermal noise providing ‘kicks’ in random directions, and the viscosity of the medium. Details of each model are provided in the supplement.

Results

General Procedure

We start with a model of single-kinesin motors that reproduces the existing[5] single-molecule measurements (see supplement text, and Figures S1 and S2). Motors could be placed randomly anywhere on a model cargo or could be placed together (clustered) at a single spot. We chose the latter geometry, based both on in vivo work indicating this is likely the way motors are arranged on physiological cargos [6], and on the desire to compare with an existing theoretical description that implicitly uses such a geometry[4]. We put N=2, 3 or 4 motors on the cargo at a single spot (Fig. 1) and allow the motors to bind to the microtubule stochastically with a probability based on their ‘on-rate’. Simulations typically start with a single motor attached to the microtubule. The motor(s) then walk along the microtubule, with each motor progressing through its kinetic cycle. Individual motors have a probability of detaching from the microtubule at each step, and conversely, at each time step unattached motors can reattach. The cargo continues along the microtubule, instantaneously driven by a number n of engaged motors (n is less than or equal to N, and is updated at every simulation step in accord with the motors’ dynamics), until the simulation ends, or n=0 indicating all motors have fallen off the microtubule.

Each motor attaches only to the bead and the microtubule; there is no direct motor-motor interaction. However, motors can influence each other through the bead. For instance, a stationary motor (Fig. 1, brown motor) can exert a backward force on a moving motor (blue motor) through the cargo. The magnitude of such effects is determined by the linkage stiffness. If motors are flexible and easily extended, the moving motor(s) advance with relatively little opposition; if the motors are stiff, the unmoving motor can in principle significantly inhibit motion. In practice, each motor is modeled as a spring of natural length l which exerts a restoring force only when stretched beyond l. The spring (motor) has no compressional rigidity i.e. it buckles without resistance when compressed. This leads to strong or weak coupling among motors, for high or low linkage stiffness, respectively.

The experimental readout for transport (both in vivo and in vitro) is the position of the cargo, not the locations of individual motor heads on the microtubule. Therefore, the position of the cargo must be calculated at each step of our simulation, taking into account the motors’ positions and spring constants, and any externally applied load. We considered two related models, Models A and B (Fig. 1). Both include the stochastic nature of the motors’ enzymatic cycles and their coupling, but the more general model (Fig 1, Model B, lower panel) also incorporates the effects of thermal noise and viscosity of the medium on the cargo’s motion. Both models are one-dimensional, so that forces, velocities, and displacements are along the direction of the microtubule. The models are complementary: Model B is more realistic, and used for specific predictions, but the simplicity of Model A provides additional insight into the underlying factors leading to the deviations in system performance found in our models in comparison to continuum descriptions of motion [4]. Details of both models’ implementation are provided in the supplement. In contrast to the continuum theory, these models make no assumption about equal load-sharing. We find that the motors’ dynamics themselves frequently result in unequal load sharing, and in load-induced coordination.

Prediction of step-size distributions

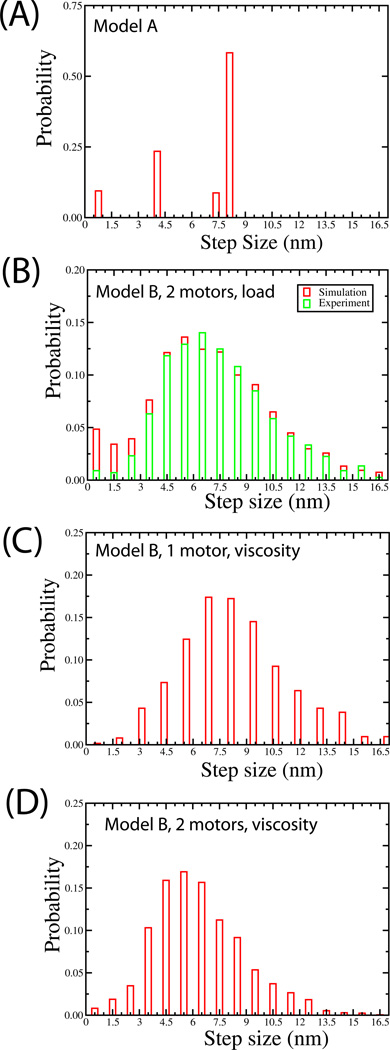
Individual kinesin heads move in 16 nm advances[7], resulting in 8 nm advances of the motor’s center of mass[8]. However, it is not well understood how a cargo’s center of mass advances when moved by two or more motors: do motors synchronize, moving the cargo in increments of 8 nm, or do they function independently, so that the center of mass moves in 4 nm steps? This question is relevant for interpreting in vivo studies that observed 8 nm steps[9, 10]: could these steps reflect transport driven by multiple motors, or when 8 nm steps occur, do they reflect only single-motor function? Model A predicts that under a low to medium load (~3 pN), the cargo’s center of mass should almost all of the time advance in 8 nm steps (Fig. 2A). This reflects two features. First, the force-velocity curve of individual motors is insensitive to load at low load (Supplement, Fig S1A), so the motors need not share load—although the forward motor supports most of the load, it advances at approximately the same rate as the rear motor, so the motors’ microtubule attachment locations can be well separated (supplement, Fig. S5). Thus, applied load is supported by the forward motor, and this motor determines the cargo’s position: when it steps by 8 nm, the cargo advances 8 nm; the rear motor advance does not effect the cargo’s position. However, this prediction is inconsistent with experimental data[11]—cargos driven by single kinesin motors do advance in 8 nm increments but this is not the case for cargos in buffer driven predominantly by two motors (see experimental data in Fig 2B).

Figure 2. Predicted motions of the center of mass of the cargo.

(A) Predicted distribution of steps-wise advances of the cargo, resulting from two motors moving a cargo under low load, according to the dynamics of model A (B) Predicted distribution of steps-wise advances of the cargo, resulting from two motors moving a cargo under low load, according to the dynamics of model B. Here the cargo’s motion was simulated, according to model B, and then the resulting displacement records were analyzed exactly as for experimental data, using the step-distribution method previously investigated [11]. The distribution of detected steps (red histogram bars) are compared to previous experimental data (green bars) from [11]. (C) Predicted distribution of steps-wise advances of the cargo, resulting from a single motor moving a 0.5 μm cargo under no load, but in the presence of a viscosity ~100 that of water (viscosity of water=0.001 Pa-S), according to the dynamics of model B. (D) The same as (C), but for 2 motors. The parameter values are k_on = 2 × 10⁶ M⁻¹•sec⁻¹, and k_cat = 105 sec⁻¹ (see Equation 1 in supplement), K_{0 off}=55 sec⁻¹ and d_l=1.6nm (See Supplement Equation 2.4), [ATP]=3mM and B=0.029 µM (See supplement, Equation 3), A=107 and δ_l=1.3nm (Supplement Equation 4) and F_o = 5 pN. These parameters except F_o are same used in Supplement Figures S1 and S2 which fit extremely well to the experimentally measured single molecule data. The overall length of each motor l is chosen to be l=110 nm with compliance k=0.32 pN/nm. The ‘on’ rate (P_a) for each motor was assumed to be 5 s⁻¹ and the rate of detachment under a load equal to or higher than stall F₀ is P_back=2 s⁻¹. These parameter values are used throughout the manuscript unless indicated otherwise; F_o = 5 pN (used in the simulation here) is a ‘tunable’ parameter, and is chosen to match our experiments; there are no other free parameters.

Importantly, Model A neglects Brownian noise: in the absence of such noise, applied load moves back the cargo’s center of mass, and its position is determined predominantly by the forward motor. However, when Brownian noise is present, thermal fluctuations allow the cargo to sample enough positions that it “sees” the rear motor. In this case, the cargos’ position reflects applied force and both motors’ locations. Model B includes such effects, and agrees well with experiment (Fig. 2B) except for small steps (0–1.5 nm). Unlike the experimental analysis [11], we did not join closely spaced steps after using the step detection algorithm on the simulated data, because we had a priori knowledge of the number of steps in the record. Such joining suppresses small steps, likely accounting for the decrease in small steps in the experimental record relative to the theoretical data (Fig. 2B).

For this comparison of theory and experiment, there were essentially no free parameters. While Model B correctly predicts the cargo’s displacements and Model A does not, this does not necessarily imply that the activity of the individual motors themselves are different in the two models. In fact, the distribution of distances between the locations of where the two motors bind to the microtubule is quite similar in the two models (Supplement, Fig S5, compare A vs B). Thus, much of the difference in predicted step distributions between the two models likely reflects the effect of Brownian noise on our “indicator” of motor function—the position of the cargo—rather than differences in motor activity itself.

Having experimentally confirmed Model B by predicting the experimental distribution of step sizes, we investigated the important but less experimentally tractable situation of transport in cells where the effective cytosolic viscosity could be many times that of water. In principle at very high viscosities, the cargo’s thermal motions might be slow enough that it would not “see” the rearward motor, and so the cargo’s motion would then show step-like advances of ~8 nm, as predicted by Model A. We investigated this issue using Model B, where we applied no external load, but assumed a spherical (0.5 micron diameter) cargo moving through a solution with viscosity ~100X that of water (consistent with the maximum viscosity likely in the cytosol (Shubeita et al, submitted)). For a cargo driven by a single kinesin, we predict 8 nm steps (Fig 2C). For a cargo moved by two kinesins under the same conditions, the distribution of detected step sizes in simulated data (Fig 2D) is similar to that in buffer under low load (Fig 2B), suggesting that high viscosity of the cytosol by itself is unlikely to result in 8 nm steps for cargos moved by two motors. At higher values of viscosity (~1000X water), it becomes difficult to detect clean steps, since the step rise time is slowed, but to the extent that we detect them, we observe the same type of behavior as in Fig 2D (not shown). Thus, the observed 8 nm steps in vivo likely reflect either cargos moved by single motors, or cargos moved by two unsynchronized motors each undergoing 16 nm steps [10, 12], or reflect some synchronization of motors that occurs in vivo but not in vitro.

Testing the theory: 2-motor stalling forces

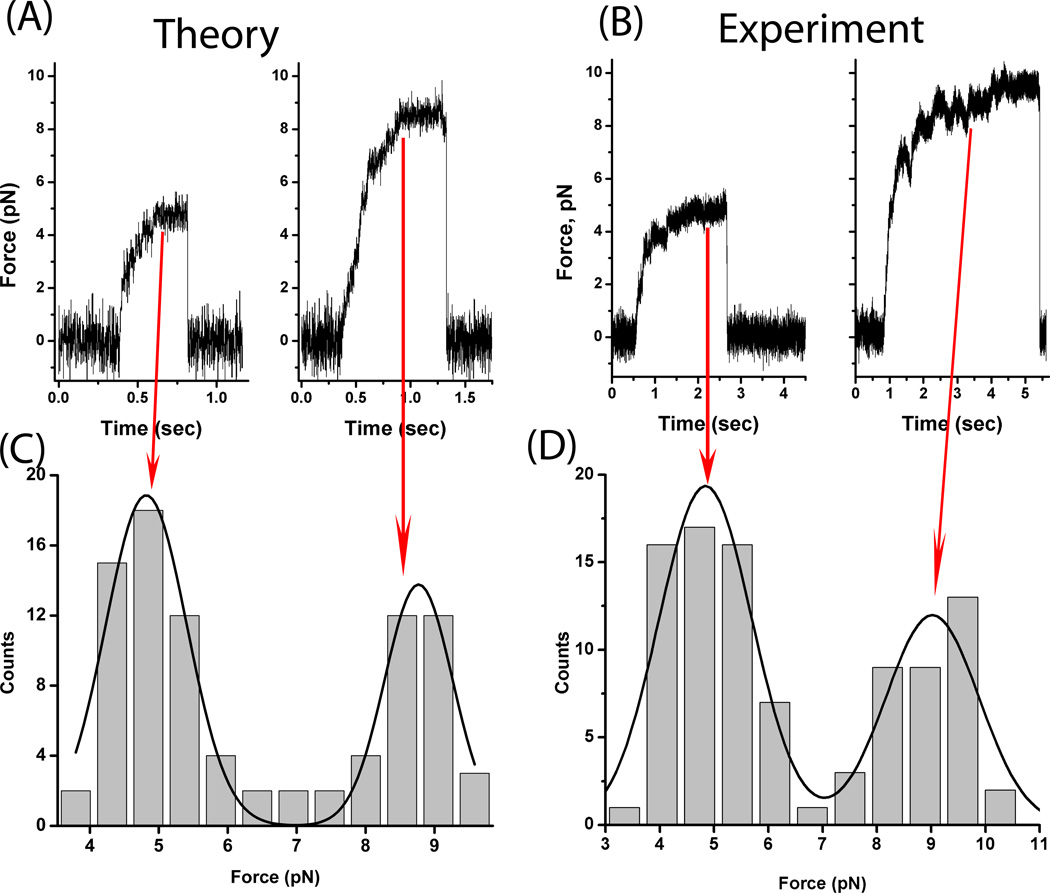
We also tested our model by predicting the force required to stall a cargo moved by two versus one motor. The unitary stall force is a free parameter; to compare with our experiments we set the one-motor stall force to be 4.8 pN. The other adjustable parameter is the motor ‘on’ rate (chosen to be 5/sec); this affects the observed number of one-motor events vs two motor events (not shown). The compliance can significantly affect how the motors work together (see below), but is not a free parameter—the relevant value (used here) was experimentally determined to be 0.32 pN/nm for single kinesin-1 motors in vitro[13]. With this choice of values, we then did in silico experiments: simulations were done for 2-motor beads moving in an optical trap of appropriate stiffness, according to the dynamics of Model B. Such simulations generated simulated stalling-force records of bead displacement as a function of time, which by eye resembled similar traces from actual experiments (Fig 3A,B). Such simulated traces were analyzed using the same criteria to detect and quantify stalls as for experimental data. The histogram of detected stall forces (Fig 3C,D) shows two distinct peaks (Fig. 3C) centered at 4.82 ± 0.05 pN and 8.77± 0.07 pN, while for the experimental data (Fig 3D) the peaks are centered around 4.8 ± 0.1 pN and 9.0± 0.2 pN. Since the one-motor stall is a tunable parameter in our model, for theory-vs-experiment comparison we use the two-motor to one-motor stall force ratio. We theoretically predict a ratio of 1.820 ± 0.025; the experimental ratio for kinesin-1 motors is 1.875 ± 0.066. Thus, the simulations and experiments are consistent.

Figure 3. Predicted distributions of stall forces for cargos moved by one and two motors.

Examples of traces of the cargo’s motion as it moves in an optical trap, for simulated cargos moving according to the dynamics of Model B (A), or actual beads moved by purified kinesin motors in vitro (B). In each case, the left trace is a ‘one-motor’ stall, while the right trace is a ‘two-motor’ stall. By eye, the simulated and experimental stalls appear quite similar. Multiple such traces, both simulated and experimental, were taken and analyzed according to our standard procedure [2] to yield the distribution of stalls predicted by model B (C) or experimentally observed (D). The only free parameter for the theory was the magnitude of the one-motor stall, which was tuned to yield observed stalls at approximately 4.8 pN (to match the experimentally determined one-motor stalls). For the theory, the fits of the gaussians (C) yield peak locations of 4.82 ± 0.05 pN and 8.77± 0.07 pN. For the experiments (D) the peaks are at 4.8 ± 0.1 pN and 9.0± 0.2 pN. With the exception of F_o ( = 2.8 pN), the parameter values are same as used in Figure 2.

The best way to compare theory and experiment is to perform data analysis identically (as above), but this is impossible with the continuum theory, which describes only the steady-state average behavior of the motors. The challenge is to predict what is actually measurable: a “stall” occurs when the mean velocity is zero, so it is tempting to use the theories’ force-velocity curves (e.g. Fig 6A–C) to predict the force at which the mean velocity is zero. However such a force is frequently experimentally unobservable because the mean travel becomes minimal before such a force is achieved. For instance both the continuum theory and our Model B, predict that for two ~6-pN stall motors, the velocity goes to zero at 12 pN of externally applied load (Fig 6B and C, red curves), but the theories also predict that the mean travel becomes ~1 step of the motors at 8.8 pN (continuum, dotted red curve, Fig 4B) or 10.4 pN Model B, solid red curve, Fig 4B). Following a suggestion in [4], we use the theoretical force-persistence curves (see next section) to identify the approximate location of the stalls, by determining the force for which a cargo’s mean travel distance goes to ~8 nm (one step). Using our simulations, we evaluate how well this approach approximates the in silico experiments above.

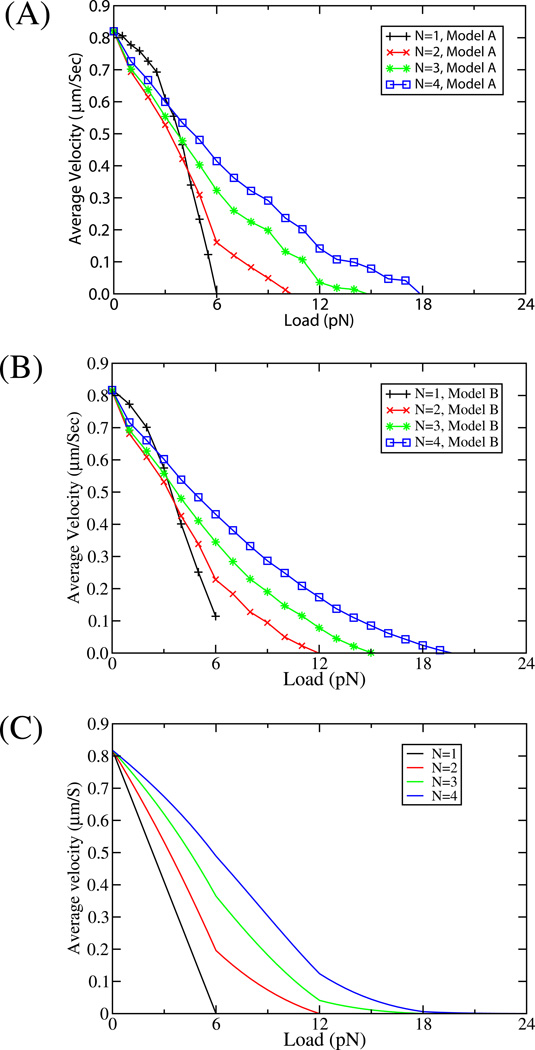
Figure 6. Force-Velocity curves.

Predicted force velocity curves from our multiple motor model for N=1, 2, 3 and 4 motors from Model A (A ) and Model B (B), assuming a linkage stiffness of 0.32 pN/nm, and an ‘on’ rate of Pa=5 s⁻¹. The parameter values and initial conditions are same as in Figure 4A. The average velocity was calculated using the velocities calculated over a time window of 0.5 sec in the steady state. (C) The force velocity curves from the steady-state (SS) model, also assuming an ‘on’ rate of 5 s⁻¹, a single-motor stall force of 6 pN and identical single motor velocities. The parameter values chosen for SS model are v=0.818 µm/s, π_ad=5 s⁻¹, ε_n=1 s⁻¹,F_d = 3 pN and F_s = 6 pN (see supplement equations (7)–(8) and (10)–(12)).

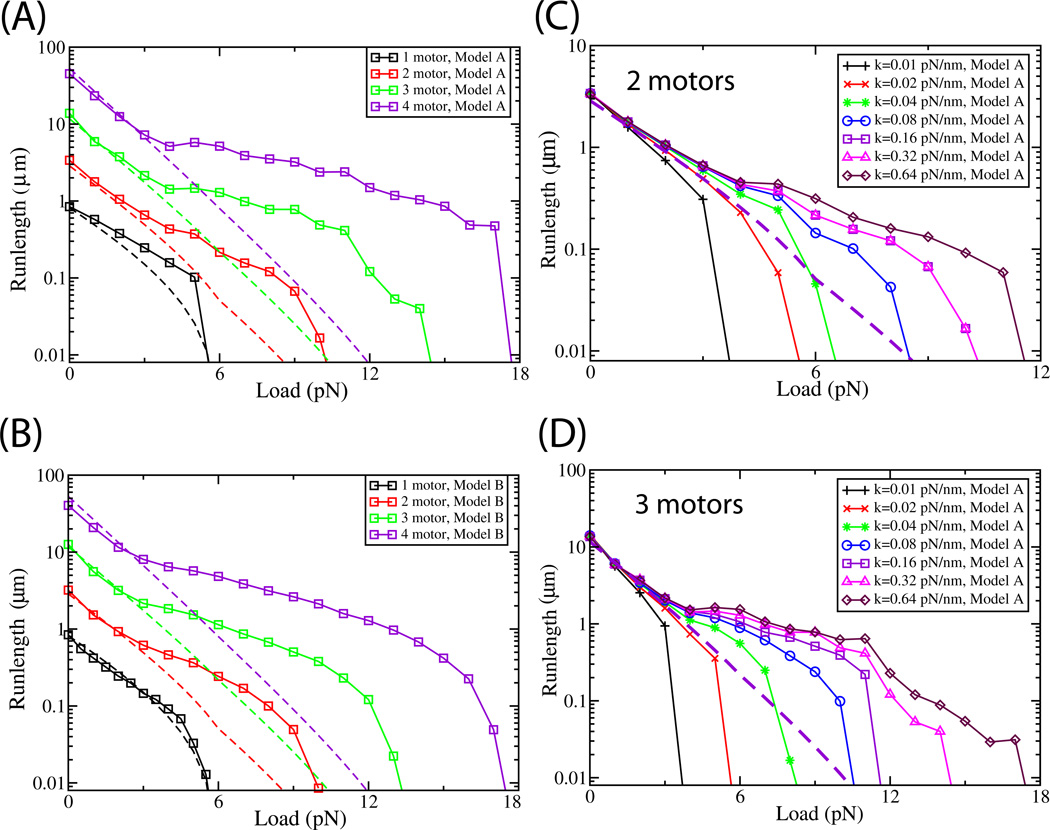
Figure 4. Force-Persistence curves for cargos.

For comparison with the continuum theory[4], simulations were done for motors with a single-motor stall tuned to ~5.7 pN. All models assumed and ‘on’ rate of 5 s⁻¹ and an identical single motor unloaded velocity. A and B: The linkage stiffness was fixed (0.32 pN/nm), but there were different total number of attached motors (N). Curves shown are the predicted mean travel distance of 1, 2, 3, and 4 motors under different degrees of opposing force, moving according to Model A (A) or Model B (B). The dotted line reflects the predicted curve from the Steady State model (SS) of Klumpp et al[4].The Monte Carlo simulations (MC) started with the initial condition of all motors initially attached to microtubule. The parameters chosen for Monte Carlo Simulations of Model A and Model B are same as in Figure 2 except F₀ which was tuned to stall of ~5.7 pN; F₀=6 pN and F₀= 5.1 pN for models A and B, respectively. The parameter values chosen for SS model are v=0.818 µm/s, π_ad=5 s⁻¹, ε_n=1 s⁻¹,F_d = 3 pN and F_s = 6 pN (see supplement equations (9)–(12)). C and D: Force-Persistence curves for cargos at different values of linkage stiffness, for 2 (C) and 3 (D) motors moving according to Model A. The dotted black line is the prediction of the SS model[4], for the same parameters as Fig. 4A (chosen to achieve agreement for the one-motor curve), for 2 motors (A) and three motors (B). All parameters chosen for the MC simulation of Model A are same as in Figure 4A, except for different k values as indicated. The MC initial conditions were the same as 4A, and the steady state models’ parameter values were also as in 4A. The related plot for Model B is found in the supplement, Fig. S7. For 4A–D, the velocity of single motor for SS model was chosen to be 0.818 µm/s to match the single-motor Monte Carlo simulation.

One complication for this comparison is that the kinetic properties of individual motors must be tuned differently, depending on whether we aim to observe the mean one motor stall at 4.8 pN via either of the two approaches. From a practical point of view the difference is irrelevant because the ratio of the two-motor to one-motor stall is approximately constant, independent of the absolute value of the one-motor stall. If we tune the one-motor stall to be 4.8 pN (according to the mean travel distance criteria), the approximate location of the 2-motor stall is predicted to be 8.5 pN (see supplement, Fig. S4), or a 2-motor to 1-motor ratio of 1.77 ± 0.03. In absolute terms, the value of 8.5 is about 0.27 pN less than the peak location determined above using the in silico approach, reflecting roughly a 3% error in determining the theoretical stall value from the two different methods. Using this fast method to compare Model B with experiments thus yields a theoretical prediction that is off by approximately 0.5 pN, or 5.5%. In contrast, after tuning the continuum model parameters [4] to have a 1-motor stall of 4.8 pN, the 2-motor stall is predicted to be 7.4 pN, low by 1.6 pN or 17.8% relative to experiments (Sup. Fig. S4, dotted red line). The continuum theory thus predicts a 2-motor to 1-motor ratio of 1.54 ± 0.04, in contrast to our predicted ratio of 1.77 ± 0.03, and the experimentally measured ratio of ~1.87.

The Force-Persistence curve

Molecular motors are cargo transporters, so it is important to characterize how far and how fast they transport a cargo, and how this is affected by opposition to motion (applied load or viscous drag). For single motors, these effects are summarized by the Force-Processivity (supplement, Fig S1C and D and S2B) and Force-Velocity (supplement, Fig. S1A and S1B, and S2A) relationship which measure the motor’s average travel distance and velocity as a function of applied load (force opposing the motor’s advance). We extended these ideas to characterize how multiple motors move cargos. We consider individually processive motors, making this very different from previous work on linkage stiffness effects on ensembles of single-headed non-processive motors[14]. We first determined the Force-Persistence curves for cargos carrying N= 2, 3, and 4 motors (Fig. 4A,B). The coupling between the motors significantly affects the ensemble performance (Fig. 4C,D), so the Force-Persistence relationship for a given N is not unique, but is a function of motor stiffness. In the simulations below (Fig. 4A,B), we assume the individual motor stiffness to be 0.32 pN/nm, the in vitro[13] stiffness of a kinesin-1 motor.

At no load, the predicted run lengths from either Model A or B (Fig 4A and B, symbols and solid lines) are quantitatively in good agreement with the previous[4] steady-state description (Fig 4, dotted lines of same color), for N=1, 2, 3 and 4 motors. However, the predictions diverge (compare solid and dotted lines of the same color) from the continuum model when the motors function under load (Fig 4A,B).

When load is present, the magnitude of the coupling between motors (determined by the spring constant k characterizing the compliance of the linkage, see Fig. 1) has large ramifications on system behavior. As the stiffness of the linkage between the motor heads and the cargo increased, so did average cargo travel under constant load (Fig. 4C and 4D for cargos with 2 and 3 motors respectively; similar curves for Model B are found in the supplement, Fig. S7). Two effects present in these models but not in continuum models account for these observations. First, for a low-stiffness linkage, when one motor detaches, the applied load supported by the remaining motor stretches the linkage, resulting in load-induced backward motion of the cargos’ center of mass. Second, when the motors have high-stiffness linkages, under high load they dynamically alternate between stepping and supporting load. Each of these effects is discussed below.

Impaired function at low stiffness due to stretching the linkage

Cargos with low stiffness motors on average travel shorter distances under load. When one motor detaches, the applied load supported by the remaining attached motors stretches their linkages, and produces a backward displacement of the cargo’s center of mass; the higher the stiffness k, the less linkage stretching, and the less backward travel (Supplement, Fig. S8A). Interestingly, the motors most likely to detach are the “vanguard”, i.e. those that are farthest along the microtubule and that bear the most load. When such a motor detaches and the cargo moves backward, the unengaged motors likely reattach behind the original “vanguard” location. Indeed, our modeling predicts that the more the cargo’s center of mass moves back, the less likely it is to successfully return to its pre-detachment position (Supplement, Fig S8B).

Improved function at high stiffness due to dynamic Strain Gating

The backward motion of the cargo due to the stretching linkage, combined with the failure to recover after detachment, explains the impaired performance relative to the steady-state model. What accounts for the improved performance at high stiffness? Consider (e.g) two engaged motors with high spring constants, with a backward load of F applied to the cargo. When one motor advances ahead of the other by 8 nm or more, it supports significantly more than F/2 of the applied load (in the limit of an infinitely stiff linkage it supports the entire load F). We hypothesize that this leads to strain-gating: when a motor is ahead, it supports a high load, but is unlikely to step (the applied load decreases its velocity, i.e. decreases the mean stepping rate). In contrast, the rear motor is under low load (most load is supported by the forward motor), and thus steps faster, catching up with the forward motor. When both motors are at the same position, they are equally likely to step, and one steps against F/2. Thus, a typical scenario for two stiff engaged motors under high total load F is that every other step is against a load less than F/2, so relative to a continuum model where the motors always share load equally, the mean force that a given motor steps against is reduced. Note that “strain-gaiting” as used here differs from the previous use describing inter-molecular interactions between kinesin heads (see supplement).

We tested this hypothesized strain gating in a number of ways. First, for a two-motor cargo (with 5.8 pN stall motors, as in Fig 4A,B) moved against 9 pN of externally applied load, we used Model A to directly observe the sequence of forces that were stepped against (Fig. 5A). For strain-gating we expect an alteration of forces, with a step against F/2, then one against a lower force, then against F/2, etc. This sequence of stepping (Fig. 5A) was observed. For lower stiffness cases (e.g. k=0.08 pN/nm), where strain gating is not expected, each step should occur at approximately at F/2. This too was observed (Fig. 5A), and steps against a force of more than F/2 were sometimes observed, corresponding to the forward motor stepping repeatedly. Such steps are not present when perfect strain gating occurs (k=0.64 pN/nm, Fig 5A, red curve) because the forward motor does not step. For a relatively high, but still intermediate stiffness (k=0.32 pN/nm) strain gating occurs but is not perfect, so although most of the time the F/2, lower than F/2, sequence occurs, occasionally a step occurs at larger than F/2.

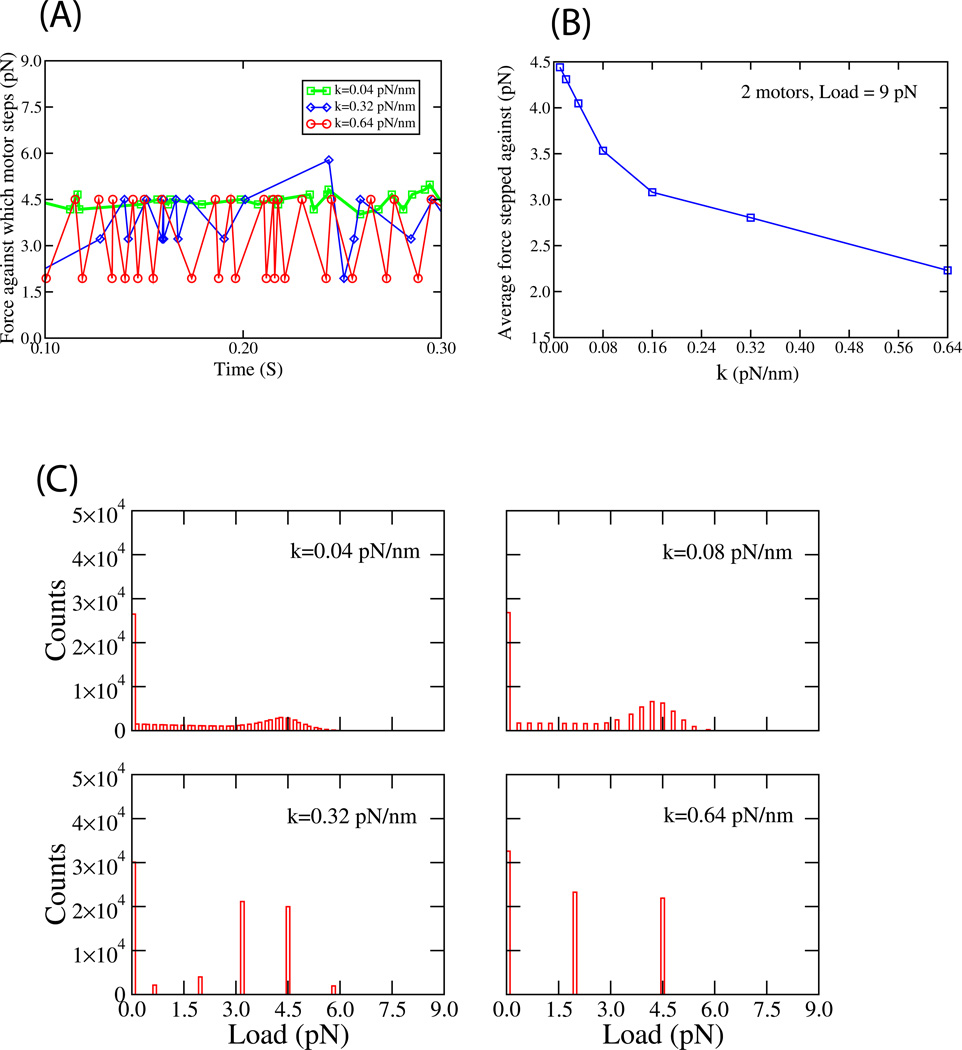
Figure 5. Strain Gating explored for a cargo moved by a maximum of N=2 motors.

(A) A trace of forces against which motors step, for different values of k, when the cargo experiences an applied load of 9 pN. The simulation was started with initial condition that both motors are attached randomly to the microtubule and simulation was stopped when one of the motors detached. (B) The average force that a motor attached to the cargo steps against in model A, when the cargo experiences 9 pN of externally applied load, as a function of the stiffness of the linkage connecting the motors to the cargo. Initial and final conditions are identical to Figure 5A. The related curve for Model B is in the supplement, Fig. S10. (C) The distribution of forces the motors stepped against when a load of 9 pN was applied to the cargo. The 4 panels show the distribution for steps for motors linked to the cargo by different spring constants. Initial conditions identical to Figure 5A. All parameters chosen for MC simulations in Fig. 5 are same as in Figure 4C.

The example traces (Fig 5A) are supported by the overall distribution of forces stepped against, for two motors moving a cargo against 9 pN of externally applied load (Fig. 5C). In the low-stiffness case (k=0.04 and k=0.08 pN/nm, top two panels) the forces stepped against are clustered around F/2 (i.e. 4.5 pN). In the high-stiffness case, there are two peaks reflecting steps of the rear motor (at less than F/2), and either of the motors (against F/2) when they are side-by-side, and sharing load equally. In all panels, the steps against low loads (less than about 1.5 pN) can be ignored because they reflect a transient case where one of the motors has detached, and then reattached significantly behind its initial position, so that it feels little force after it re-attaches, until it approaches its original position.

The benefit from strain gating depends on the linkage stiffness—for both k=0.32 and k=0.64, the typical ‘high load’ advance occurs at F/2, but the force that the rear motor steps at is lower for k=0.64 (peak is at ~1.8 pN, Fig 5C, bottom right) than for k=0.32 (peak is at ~3.1 pN, Fig 5C, bottom left) because in the higher stiffness case the forward motor supports more of the load. Thus, we expect that the ‘average’ force that a motor steps against will decrease, as a function of the linkage stiffness, as the forward motor supports increasing amounts of load, but does not step against them. This is observed in our simulations for both models (Fig. 5B and supplemental Fig. S10). A consequence of this decreased load should be to improve mean cargo travel, because a single motor’s processivity is a function of the load it steps against. This was observed (compare our predicted transport to the continuum model that assumes equal load sharing, Fig 4A,B).

Another consequence of applying high load/strain gating is to induce clustering of the motors on the microtubule. At high load, when the forward motor supports significant load, its enzymatic cycle is slowed (see force-velocity relationship for a single motor in Supp. Fig 1A, 2A, [5]), resulting in the rearward motor(s) catching up. Thus, as the load increases, the average distance between the forward motor and rearward motor decreases. This is observed in both our models (Supplement Fig. S5A and supplement Fig S5B). Thus, the “vanguard” motor in this case is unlikely to be far ahead of the rearward motor and if it were to detach then the foremost microtubule attachment point would not move back appreciably nor would the linkage stretch much. The net result is negligible rearward excursions of the cargo due to motor detachment. Note however that strain gating and the associated clustering happens only at high stiffness; for lower stiffness linkages, the motors do not cluster in the same way (Supplement Fig. S6A and S6B).

We discussed strain gating in the simplest case of two motors, but the uneven load-sharing between motors, combined with preferential stepping of the unloaded motors, occurs when more motors are present as well, and leads to improved performance under load when the motors are coupled to the cargo via stiff linkages; this was observed for 3 motors as well (Fig 4D and supplemental Fig. S7B).

The Force-Velocity curve

We turn now to the velocity behavior of a cargo carrying N=2, 3, or 4 motors, as a function of applied load or viscosity. Both models provide similar curves (Fig 6A and B), which differ from the force velocity curves predicted from the steady-state model (Fig. 6C), particularly in the low-force regime (i.e. at an applied load less than or equal to the stall force of a single motor). For the steady-state model (Fig 6C), whenever load is applied the velocity for cargos moved by multiple motors is higher than for cargos moved by a single motor (as more motors share the load, the load per motor drops and motor velocity goes up). In contrast, our model predicts that at low loads, the velocity is more sensitive to load than in the single-motor case (black curve). This was unexpected since one motor is always attached (our simulations end when all motors detach).

We hypothesized that this unexpected dependence of velocity on load occurred due to detachment of some motors from the microtubule. To test this idea, we modified our simulation and did not allow motors to detach. Then, our result agrees with what is expected when motors share load equally all the time (Supplement, Fig. S11), and where the applied load does not affect the mean number of engaged motors—the 2, 3 and 4 motor force-velocity curves simply involve rescaling the×axis by F/2, F/3 and F/4 respectively, to reflect the lower load per motor.

What does motor detachment do? Consider two initially engaged motors. If they move together and share the load, we know (from the “no detachment allowed” simulation) that they will move faster than a single motor. If one motor detaches, the remaining motor will still not go slower than single motor. This logic also applies for more than two motors initially engaged, and it therefore appeared unlikely that the velocity sensitivity at low load resulted simply from changes in the mean number of engaged motors. Rather, we hypothesized that reduced velocity reflected backward motions of the center of mass of the cargo following a “vanguard” motor detachment, a mechanism discussed above (see also supplement, Fig. S8), and illustrated in a cartoon (Fig. 7C). Further discussion of this general mechanism is found in the supplement.

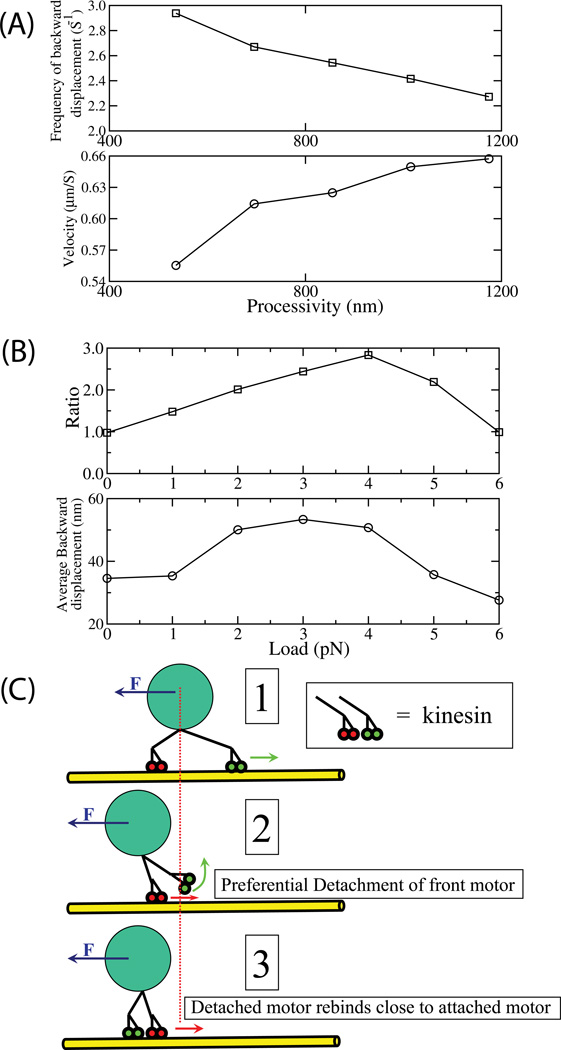
Figure 7. Load-induced symmetry breaking results in altered mean velocity at low loads.

(A) Rate of backward displacements of the cargo, as a function of single-motor processivity (upper panel), and mean cargo velocity as a function of processivity of a single motor (lower panel) for N=2 for applied load of 2 pN. Processivity was calculated using equation (6) (supplement) for different values of parameter A. The values of parameter A used in the simulation to change the effective singlemotor processivity are 67, 87, 107, 127 and 147. Other parameter values are same as in Figure 4A. The simulation was started with the initial condition that both motors are attached randomly to the microtubule.

(B) Ratio of forward to rearward motor detachment events as a function of load (upper panel) and magnitude of backward displacements (after detachment of the forward motor) as a function of load (lower panel) for N=2 motors, linked to the cargo via a 0.32 pN/nm linkage. A ratio of 1 indicates equal probability of detachment of the forward vs rearward motor; ratios higher than 1 indicate the forward motor is more likely to detach than the rearward motor. The parameter values are the same as in Figure 4A. The simulation was started with the initial condition that both motors are attached randomly to the microtubule. The forcevelocity relationship presented in Fig 6(A and B) includes this effect. Note in particular that up to an externally applied load of ~4.5 pN (~3/4 max stall for one motor), the 2-motor mean velocity is below the one motor mean velocity (see Fig 6A and B, intersection of Red and Black curves). When a motor detaches, and subsequently re-attaches, the location of re-attachment is determined randomly, but constrained to be within 110 nm of the cargo, reflecting the motor’s length.

(C) Cartoon of the sequence of events resulting in small backward displacements of the cargo’s center of mass. Initially, in (1) both motors are attached to the microtubule (yellow). Because the load is low, the motors are not clustered, so the location of the cargo’s center of mass (dotted red line) is determined predominantly by the forward motor (green) which balances the externally applied load (F, indicated by blue arrow). Due to the load supported by the forward motor, its processivity is decreased relative to the backward motor, and it has a higher probability of detaching (see ratio, top panel, Fig 7B). Thus, when one of the two motors detaches, it is more likely to be the forward motor, which results in backward motion of the cargo’s center of mass (2), as the externally applied load F is now supported by the only remaining attached motor (in red). However, because the cargo is held close to the microtubule by the bound motor (in red) the detached motor (in green) now has the opportunity to rebind to the microtubule. When it does (3) the distribution of its new binding locations is determined by the cargo’s current center of mass, so that in general, the rebinding of the motor occurs behind its previous attachment location. This completes the cycle, resulting in a small backward motion (Fig 7B, lower panel) of the cargo’s center of mass. Obviously, the more frequent such cycles of detachment/backward motion (determined by a combination of load, and the single-motor processivity, Fig 7A and B), the more effect there is on mean cargo velocity.

From this hypothesis, emerge two predictions. First, there should now be a link between single-motor processivity, and mean cargo velocity. The frequency of the rearward travels of the cargo, caused by detachment of the forward motor, should be determined by the motor’s processivity: larger processivity (i.e. lower “off rate”) should lead to decreased frequency of backward travels (Fig. 7A, top) and thus higher average velocity (Fig. 7A, bottom). Second, increasing load (up to a point) should increasingly favor backward-motions relative to forward motions (due to more likely detachment of the forward motor). We looked at the ratio of forward motor to rearward motor detachments (Fig. 7B), and found that this was true: at no load, the ratio was 1, indicating equal probability of detachment of the ‘forward’ versus ‘backward’ motor, but at a higher load (~4 pN), the forward motor was approximately 3 times as likely to detach. Note that the assumption of equal load sharing made in the steady-state model also prevents this load-induced symmetry breaking (also see supplement). These rearward motions and corresponding decreases in net cargo velocity are predominantly a low-load effect, for two reasons. First, high load slows down the motors and encourages clustering (Supplement Fig. 5), so that the magnitude of backward displacements goes down with high load (Fig. 7B, Bottom panel). Second at higher loads, the motors start to share load, so the relative difference in probability of the forward versus backward motor detaching is much less (Fig. 7B, Top panel).

Because the velocity change is due to symmetry breaking, i.e. the fact that under low load the forward motor supports most of the load, and thus has a higher probability of detaching, we also expect this effect when motion is opposed by viscous drag (e.g. the cytosol). Model B enabled us to investigate this hypothesis. Over a range of viscosities likely found in the cell, we predict that two kinesin motors should move a cargo approximately 6% more slowly than should one (Fig. S12B). This is based on using single-molecule parameters measured in vitro, and has no adjustable parameters. Concurrent with the development of this theory, in vivo experiments were performed (see submitted manuscript by Shubeita et al) comparing lipid droplet motility in wildtype vs mutant Drosophila embryos, where the mutation decreased the number of engaged kinesin motors moving lipid droplets. Consistent with the theoretical prediction, when we quantified the mean droplet velocity, we found that droplets moved by fewer (likely ~1) motor moved ~5.5% faster than those moved by more (likely ~2) motors. While the magnitude of the effect is relatively small, due to our automated tracking and analysis, the effect is well outside our uncertainty (p= 1.37 ×10⁻², two-sided t-test). Based on in vivo stalling force measurements, we had already hypothesized that the in vivo change was from ~2 to ~1 engaged motors; the theory supports this interpretation, since the predicted increase in velocity due to a decrease in the number of engaged motors only occurs for a change from two motor-to-one motor transport. Thus, the theory provides a consistent explanation for the effect of changes in motor number on in vivo velocity, at least for the case of lipid droplets (see additional discussion and Fig. S13).

Materials and Methods

We started with a single-motor model for kinesin, displaying Michaelis-Menten kinetics, following the work of [5]. We extended [5] and the subsequently published Monte Carlo model of kinesin [3] to include detachment kinetics of single motors. Complete details of our single-motor model are described in the supplement including how it is implemented in a Monte Carlo simulation; there we show that it reproduces known single-molecule in vitro experiments.

The Monte Carlo model for multiple motors is an extension of the single-molecule model; the main issue is the geometry for how the motors are attached to the cargo (see Fig. 1). Our multiple motor model includes the appropriate detachment kinetics when the motor is under super-stall (a force larger than it can move against) as experimentally measured [13]. Further, based on recent work([15] and M. Lang, personal communication), it assumes that a forward load does not affect kinesin’s velocity, but does decrease its processivity similar to the effect of a backward-directed force of the same magnitude. Exactly how the simulation is done is discussed in detail in the supplement.

The steady-state model described was presented by Klumpp et al[4] and complete details can be found in that manuscript, though we have a brief discussion of the relevant parts in our supplement.

Discussion

Strain gating, and velocity sensitivity to load

It is important to understand how multiple motors function together, because a variety of studies in vivo suggest that cargos are frequently driven by more than one motor[6], and recent work[6] suggests that regulation of the number of engaged motors could be one important route for regulating transport. Here, we addressed theoretically how two-motor transport differs from one-or three motor transport. Key predictions of our model agree well with experimental data.

Our model(s) reproduce known single-molecule experimental data (see supplemental figures 1 and 2). They include stochastic single-molecule behavior, as well as thermal fluctuations of the cargo, since in many systems involving small numbers of interacting molecules, such fluctuations contribute materially to the overall function of the ensemble. In vivo such fluctuations could be important, since molecular motors are stochastic enzymes, and the N=2, 3, or 4 motors studied here (and likely driving cargo transport in vivo [6]) are in a small-N limit. By including such single-molecule fluctuations, our models differ from a previous steady-state model[4]. As a first experimental validation of our model, we showed that it correctly predicts the experimentally observed distribution of step sizes of the cargo’s center of mass, for a cargo moved by 2 motors (Fig. 2). We also correctly predict the slight sub-additivity of motor stalling forces (Fig. 3), where the two-motor to one motor stalling force ratio is ~1.82. For instance, for motors with a single-motor stall of ~5.7 pN (Fig. 4B, black curve), we predict the two-motor stall to be ~ 10.4 pN (Fig. 4B, red curve), yielding a ratio of 1.82, consistent with in vitro experiments (see above). For the continuum model, using the same criteria, the published prediction for the two-motor stall is ~ 8.8 pN [4] (see also red dotted line, Fig 4B), yielding a ratio of 1.54, quite different from the experimental observations in vitro.

Relative to the steady-state model, our model predicts quite different ensemble function: improved ability of multiple motors to transport cargos under large load, and also more sensitivity of the cargo’s velocity to small externally applied loads. Both of these effects directly relate to fluctuations. The velocity sensitivity at low load results from load-induced symmetry breaking, where increased likelihood of detachment of the front motor results in brief backward motions of the cargo’s center of mass (Fig 7B and C). The predicted decrease in mean velocity of cargos moved by two versus one kinesin was observed experimentally in vivo (Shubeita et al, submitted). The velocity sensitivity is a small-n effect: as the number of engaged motors grows, more motors are likely to be in the “vanguard”, so even at low loads, cargo fall-backs will become smaller and load sharing will increase. The net result is that for cargos driven by a high number of motors, we expect no measurable reduction in velocity (relative to single motor velocity) at any load. Indeed, it has already been shown experimentally that in vitro, if very strong drag is not present, there is no correlation between velocity and motor number [16].

These effects were discovered through our study of kinesin, but in retrospect they depend only on relatively generic features of molecular motors. For instance, two fundamental properties give rise to strain gating: first, it requires a relatively stiff motor-cargo linkage, so that when the motor steps forward by a single step, the forward motor ends up supporting a good deal more than F/2, and second, it requires a generally decreasing force-velocity relationship, so that when the (front) motor is under significant load (relative to the rear motor) it moves through its mechanochemical cycle more slowly, thus allowing the lightly loaded (rear) motor to step first, and catch up. While strain gating will occur under these conditions, the extent that it improves the mean travel of the ensemble will depend on the exact nature of the motor’s force-processivity curve—the more difference there is between the high and low load travel distances, the more improvement that results.

The velocity sensitivity at low load is also generic to any motor whose processivity decreases with load. The effect occurs simply due to symmetry breaking: the forward motor feels more load, and therefore is more likely to detach. While the magnitude of the effect will depend on a variety of factors, in practice in vivo we see a similar velocity effect for cargos moved by one vezsus two dynein motors as well (see Shubeita et al, submitted).

In vivo ramifications

These studies have four implications with regard to transport processes in cells. The first is for cargos whose motion changes frequently with time, for instance bi-directionally moving cargos such as virus particles, lipid droplets, mitochondria, and melanophores[17, 18]. In such cargos, the direction of transport changes every second or so. If motion starts by engaging a single motor, much of the motion will be non-steady state; if they start with a single motor engaged, a large percentage of such cargos would be expected to fall off the microtubule before reaching steady state (see Supplemental Fig. S14, and discussion). Thus, in vivo it might be useful to have some method of ensuring that the cargos remain attached to the microtubules long enough to reach steady state. It is intriguing to speculate that this is one of the roles of proteins like dynactin that provide an independent tether between the microtubule and the cargo.

The second observation is that the mean travel distance of the ensemble is significantly affected by the assumed on rate (below, and not shown). For example, under no load the mean travel distance for two motors is ~3.4 µm if the ‘on’ rate is 5 sec⁻¹, but is only ~2.1 µm with a 2 sec⁻¹ on rate. Thus, for cargos driven by multiple motors, any mechanism able to tune the on rate could have strong effects on mean transport. Such mechanisms could in principle involve posttranslational modifications of the motors themselves, as well as modifications of the microtubules [19, 20] or microtubule associated proteins [2, 21] that affect the on rate.

The third observation is that the ensemble function is significantly improved if the motors are tightly coupled. Membranes are somewhat flexible, so if the motors are randomly attached to the membrane-bound cargo with some membrane between them, the effective compliance of the system will be quite large, and the motors will not cooperate well. For optimal performance (e.g. to achieve good transport under load), our theoretical results suggest that it is important for motors to be clustered together at a single point on the cargo, and potentially bound to each other via stiff protein linkages. Such clustering has been seen in a number of EM studies[6], though the molecular events leading to such arrangements are currently unknown.

Fourth, over the range of cytosolic drag conditions likely relevant for transport in cells, the effect of changing the number of engaged motors on overall cargo velocity is very different from what is commonly expected (Fig. S12). Since it is currently widely believed that due to viscous drag, more motors will move cargos faster, and the detected 8 nm steps in vivo suggest that many cargos are indeed moved by ~1 motor (see above), these theoretical results based on an experimentally validated theory should have significant implications for interpretation of past and future in vivo experiments.

Conclusion

We investigated the function of two or more kinesin motors under load, and found that the system’s performance was strongly affected by the way the motors were linked to the cargo. This suggests that future studies in vivo may need to pay careful attention to motor organization, as alteration of such organization could play an unappreciated role in determining overall function of the transport system.