Abstract
The relationship between performance and ability is a central concern in the social sciences: Are the most successful much more able than others, and are failures unskilled? Prior research has shown that noise and self-reinforcing dynamics make performance unpredictable and lead to a weak association between ability and performance. Here we show that the same mechanisms that generate unpredictability imply that extreme performances can be relatively uninformative about ability. As a result, the highest performers may not have the highest expected ability and should not be imitated or praised. We show that whether higher performance indicates higher ability depends on whether extreme performance could be achieved by skill or requires luck.
Keywords: regression to the mean, randomness, social learning, performance evaluation, ecological rationality
Extreme performance attracts people’s attention. People tend to believe the most successful are the most skillful and that failures lack skill (1, 2). A tendency to imitate the most successful has also been argued to be a basic universal trait that is shaped by evolution and promotes adaptiveness (3, 4). However, is success necessarily an indication of skill and worthy of praise and imitation and failure an indication of lack of skill?
Clearly, observed performance is not always a reliable indicator of skill. Chance events outside the control of individuals often influence performance (5–7). Moreover, such chance events rarely average out over time. Instead, due to “rich-get-richer” dynamics and “Matthew effects” (8), success usually breeds success and failure breeds failure. For example, individuals with early success might be given more resources and instruction, or consumers may favor products with a high market share (9, 10). Prior research has shown how such processes can amplify chance events and produce a weak association between performance and ability (11–13), leading to a distribution of outcomes that is both unpredictable and highly unequal (14). In such settings, extreme success and failure are, at best, only weak signals of skill. The highest performers may be more able than others and the lowest performers less able than others, but one should not expect their skill level to be very far from the mean (15).
These prior contributions show that performance and skill may be weakly associated due to noise and rich-get-richer dynamics, but they do not challenge the idea that higher performers are likely more skilled and worthy of imitation. Even if the highest performers are only marginally more skilled than others, it makes sense to imitate them. In this paper, we show that noise and rich-get-richer dynamics can have more counterintuitive implications that go beyond the conventional understanding of regression to the mean. Noise and rich-get-richer dynamics not only introduce unpredictability but also change how much one can learn from extreme performances and whether higher performance indicates higher skill. In particular, we show that when noise and rich-get-richer dynamics can strongly influence performance, extreme performances can be relatively uninformative about skill. As a result, higher performance may not indicate higher skill. The highest performers may not be the most skilled and the lowest performers may not be the least skilled. The implication is that one should not imitate the highest performers nor dismiss the worst performers. More generally, we show that whether higher performance indicates higher skill depends on whether extreme performance could be achieved by skill or requires luck.
The intuition behind our results is that an extreme performance may be more informative about the level of noise and the strength of rich-get-richer dynamics than about skill. People often have to infer the degree of skill from performance without knowing the extent to which performance is subject to noise or the extent to which past performance influences future performance. Extreme performance indicates that the level of noise is high and that past performance strongly influences future performance, because extreme performances are more likely then. In settings with high levels of noise and when past performance strongly influences future performance, however, observed performance is a less reliable indicator of skill because chance events and early success strongly influence performance. Because extreme performances are less informative about skill levels than moderate levels of performance, a rational person should regress more to the mean when observing extreme performances, implying that the association between performance and ability can be nonmonotonic.
We develop two models to formalize this intuition. The first model assumes that current performance depends on skill but also on past performance and evaluators are uncertain about how much past performance matters. The second model assumes that performance depends on skill and noise and evaluators are uncertain about the extent to which noise matters. For both models, we show that higher performance does not indicate higher skill if luck is essential to achieving extreme performance. On the other hand, when luck is unlikely to result in extreme performance, we show that extreme performances, high or low, can be especially informative about skill.
The implication of our models contradicts descriptive studies about how people evaluate performances: People tend to believe that higher performance indicates higher skill. We show, however, that even when this assumption is faulty, people may have little opportunity or incentive to correct this assumption, as predictions based on such an assumption can be very accurate and may even outperform a correct model when information is scarce. Although it leads to accurate predictions on average, widespread use of this heuristic to identify whom to learn from can lead to diffusion of very risky behavior, and “nudges” (16) may be necessary to help people resist the temptation to praise, blame, or learn from extreme performers. In the following, we show how our conclusion follows from two simple models and discuss the descriptive and normative implications of our findings.
Model 1: Extreme Performance Indicates Strong Rich-Get-Richer Dynamics
One reason why extreme performance may not be a reliable indicator of skill is that an extreme performance indicates especially strong rich-get-richer dynamics. To formalize this, we develop a model in which success depends on skill but also on past success and where evaluators are uncertain about how much past performance matters.
Consider a game with 50 rounds, with each round being a success or a failure. The goal is to obtain as many “successes” as possible. Individuals differ in their skill levels: Some individuals have a higher probability of obtaining success in any given round. In addition to skill, we also assume that outcomes in consecutive rounds are dependent. The probability of succeeding increases if the previous outcome was a success. Specifically, after a success, the probability of success in the next period is ci (1 − wi) + wi, whereas it is only 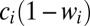 after a failure. In the first period, the probability of success is ci. Here, ci ∈ (0,1) is the skill of individual i, and wi ∈ (0,1) represents the extent to which success probabilities depend on the previous outcome. wi would be high in industries where consumers want to buy the currently most popular product (due to network externalities, for example) and in careers where early success brings resources, training, and visibility that increase future success (9, 10). The level of dependency, wi, is not the same for every player—some players are in contexts where dependency is relatively strong. We also assume that the level of dependence is not fully known to outside observers. It is often difficult to estimate the extent to which success depends on past success rather than on superior skill, especially when few data are available and when past success operates through difficult-to-observe processes such as consumer loyalty. Thus, it may not be clear to an observer whether a streak of successes is due to exceptional skills or to strong dependencies combined with the good fortune of being successful initially. Witness, for example, the debate about whether Microsoft’s success is due to their early lead or to superior quality (17).
after a failure. In the first period, the probability of success is ci. Here, ci ∈ (0,1) is the skill of individual i, and wi ∈ (0,1) represents the extent to which success probabilities depend on the previous outcome. wi would be high in industries where consumers want to buy the currently most popular product (due to network externalities, for example) and in careers where early success brings resources, training, and visibility that increase future success (9, 10). The level of dependency, wi, is not the same for every player—some players are in contexts where dependency is relatively strong. We also assume that the level of dependence is not fully known to outside observers. It is often difficult to estimate the extent to which success depends on past success rather than on superior skill, especially when few data are available and when past success operates through difficult-to-observe processes such as consumer loyalty. Thus, it may not be clear to an observer whether a streak of successes is due to exceptional skills or to strong dependencies combined with the good fortune of being successful initially. Witness, for example, the debate about whether Microsoft’s success is due to their early lead or to superior quality (17).
We simulated this game with 5 million players. Each player has a different value of ci (drawn from a beta distribution with parameters 10,10; the beta distribution is a flexible distribution and also a common choice for modeling heterogeneity in success probabilities) and wi (drawn from a uniform distribution; i.e., a beta distribution with parameters 1,1). These assumptions about the distributions of skill and dependencies imply that the distribution of dependency (wi) is less concentrated around 0.5 than the distribution of skills (ci). Thus, extreme values are more likely for wi than for ci.
Based on the simulated data, we can examine how average skill levels (ci) vary with the number of successes obtained. Intuitively, one might expect that players who achieved the most successes are the most impressive and have the highest value of ci. However, as Fig. 1 shows, the association between success and skill level is nonmonotonic. The average value of skill reaches a maximum at about 40 successes out of 50 and then starts to decline. Players who achieved exceptional performance, that is, successes in 50 rounds, have an average value of skill lower than those with 40 successes. Stated differently, the most successful players are not the most impressive. Rather, moderately successful players are the most impressive ones. A similar pattern is observed for very low levels of success: The players with the lowest levels of success are not the least impressive.
Fig. 1.
The average value of ci for players who obtained different numbers of successes in 50 rounds. Based on 5 million simulations.
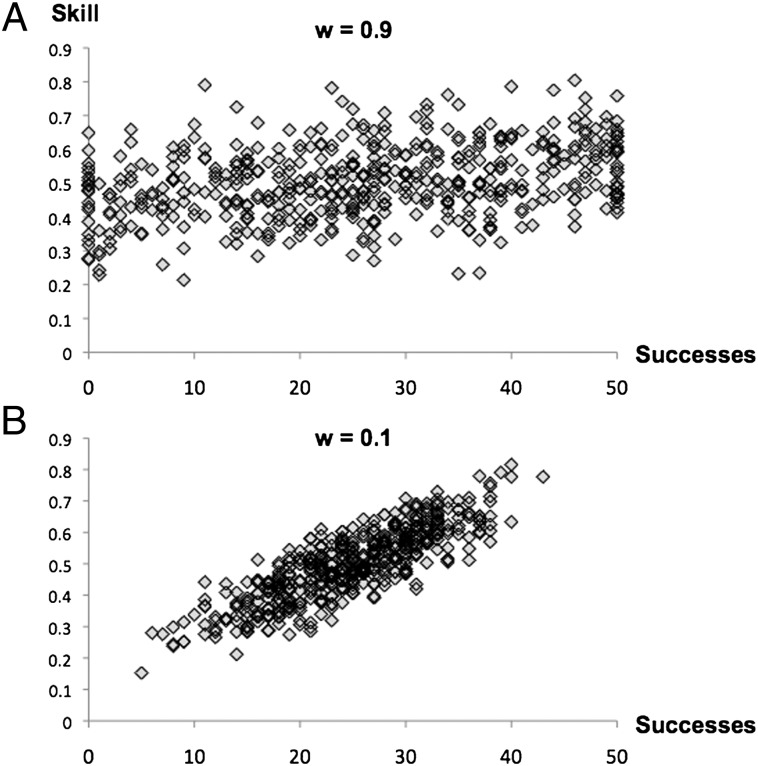
The explanation for this result is that an extreme performance indicates that the level of dependency was strong (wi high): Extreme outcomes are more likely then. When wi is high, however, performance is less informative about skill, because outcomes are substantially influenced by chance events. Chance events can substantially influence outcomes when wi is high, because initial outcomes then strongly influence subsequent outcomes and players with low levels of skill who get lucky initially may have many successes. Similarly, players with high levels of skill could get unlucky initially and may have many failures. As a result, the association between skill levels and eventual outcomes will be weak when wi is high. For example, the correlation between skill and success is only 0.37 when wi = 0.9 (Fig. 2A). Thus, when dependency is strong, achieving extreme performance is a less informative indicator of skill. Nevertheless, strong dependency implies that extreme outcomes are more likely compared with when dependency is weak.
Fig. 2.
Illustration of the association between skill and the number of successes obtained in 50 rounds for strong and weak dependence. (A) wi = 0.9. (B) wi = 0.1. Each figure is based on 1,000 simulations.
In settings when dependency is weak, skill matters more and chance events less in determining the outcome. For example, the correlation between skill and success is 0.82 when wi = 0.1 (Fig. 2B). Because skills matter more in determining outcomes, outcomes are also more informative about skill levels. In particular, obtaining 50 consecutive successes (or failures), when dependency is weak, is a reliable indicator of high (or low) skill, because it is very unlikely that a player without very high (or low) skill would obtain such an extreme result. However, as Fig. 2B illustrates, exceptional performance is less likely when dependency is weak compared with when it is strong.
Overall, our basic result emerges, because an extreme performance indicates that it was achieved in a context in which chance events can substantially influence outcomes, and performance is then an unreliable indicator of skill. For example, achieving 50 successes out of 50 rounds indicates that the degree of dependency must have been very high, and in such settings achieving exceptional performance is not so impressive.
This nonmonotonic association between success and skill emerges only when wi is less concentrated around 0.5 than ci is, namely when extreme values are more likely for wi than for ci. The intuition is that when very high values of dependency are more likely than very high values of skill, extreme results are likely due to a high value of wi rather than a high value of ci. When wi is more concentrated around 0.5 than ci (for example, when wi is a known constant), expected skill is increasing in the number of successes.
Model 2: Extreme Performance Indicates Extreme Noise
Another reason why extreme performance may not be a reliable indicator of skill is that an extreme performance indicates that performance is subject to an especially high level of noise. To illustrate this, we now consider a static model in which performance depends on skill and “luck” and evaluators are uncertain about the impact of luck. Consistent with standard models in social science that examine how noise influences performance (12, 18), we assume that performance is a linear combination of skill (ui) and “noise” (ei) (or luck): 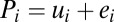 . The task for the evaluator is to infer the expected level of skill from the observed performance:
. The task for the evaluator is to infer the expected level of skill from the observed performance: 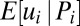 .
.
Our model is similar to standard models, with the exception that we introduce heterogeneity in both skill and noise. Heterogeneity in noise is consistent with the idea introduced in model 1: Some individuals are in contexts where noise matters a lot (when wi is high in model 1), and others are in contexts where noise matters relatively less. A simple way to model such heterogeneity in noise is to assume that the noise distribution is normal with mean zero but that the standard deviation (SD) is not equal for all agents but may differ. Note that such heterogeneity can be interpreted as uncertainty about the noise distribution: Evaluators are not sure about the levels of noise in the system (e.g., the level of risk taken). We introduce uncertainty about the skill distribution in a similar way: We assume that the skill distribution is normal with mean zero but that the SD is not equal for all agents but may differ.
We assume the SDs of both skill and noise distributions are independently drawn from gamma distributions, a flexible and commonly used distribution. The gamma distribution is specified using two parameters, a and b. We assume that the SD of the noise distribution is drawn from a gamma distribution with a = n and b = 1/n. Similarly, the SD of the skill distribution is drawn from a gamma distribution with a = s and b = 1/s. The values of n and s regulate the relative heterogeneity in (or uncertainty about) the skill and noise distributions. The expected SD for both the skill and the noise term is 1, whereas the variances in the SD are 1/n and 1/s. When n or s goes to infinity, the SD becomes clustered around 1, approximating the case when the SD is known.
Heterogeneity implies that the aggregate distributions of both skill and noise will have fatter tails than a normal distribution. Whether the skill or the noise distribution is fatter, and thus more likely to generate extreme values but less likely to generate intermediary values, is regulated by the parameters s and n. Whenever s < n there is more heterogeneity in the skill distribution, which implies that extreme values of ui are more likely but intermediary values less likely than for ei. Conversely, whenever n < s there is more heterogeneity in the noise distribution, and extreme values of ei are more likely but intermediary values less likely than for ui.
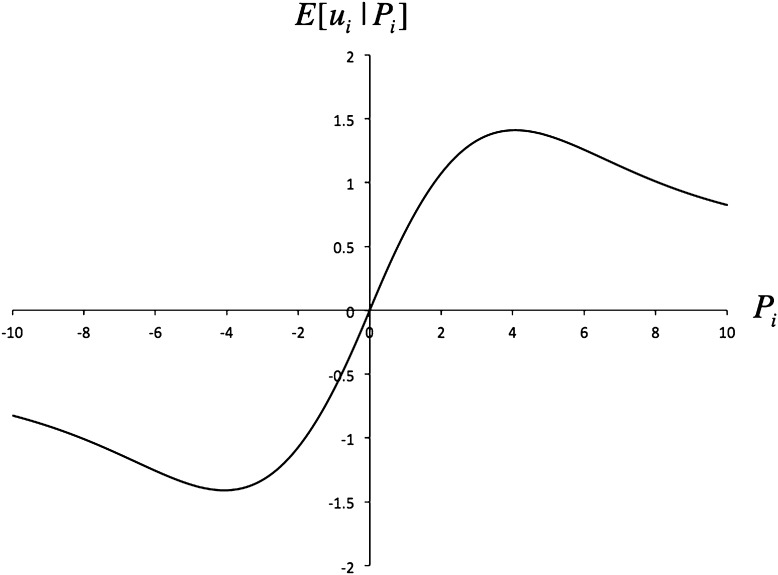
Our model implies a general condition on when a nonmonotonic pattern between performance and skill emerges: Whenever n < s, and there is more heterogeneity in the noise distribution, then expected skill, 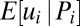 , is not an increasing but a nonmonotonic function of the observed performance, Pi. Fig. 3 provides an illustration for the case when n = 1 and s = 5 (see SI Text for how this is derived). As shown, the highest performers do not have the highest expected skill, nor do the lowest performers have the lowest expected skill.
, is not an increasing but a nonmonotonic function of the observed performance, Pi. Fig. 3 provides an illustration for the case when n = 1 and s = 5 (see SI Text for how this is derived). As shown, the highest performers do not have the highest expected skill, nor do the lowest performers have the lowest expected skill.
Fig. 3.
How expected degree of skill, E[ui|Pi], varies with performance when there is heterogeneity in both the skill and noise distribution but the noise distribution is more fat-tailed (based on numerical integration, for the case when n = 1 and s = 5).
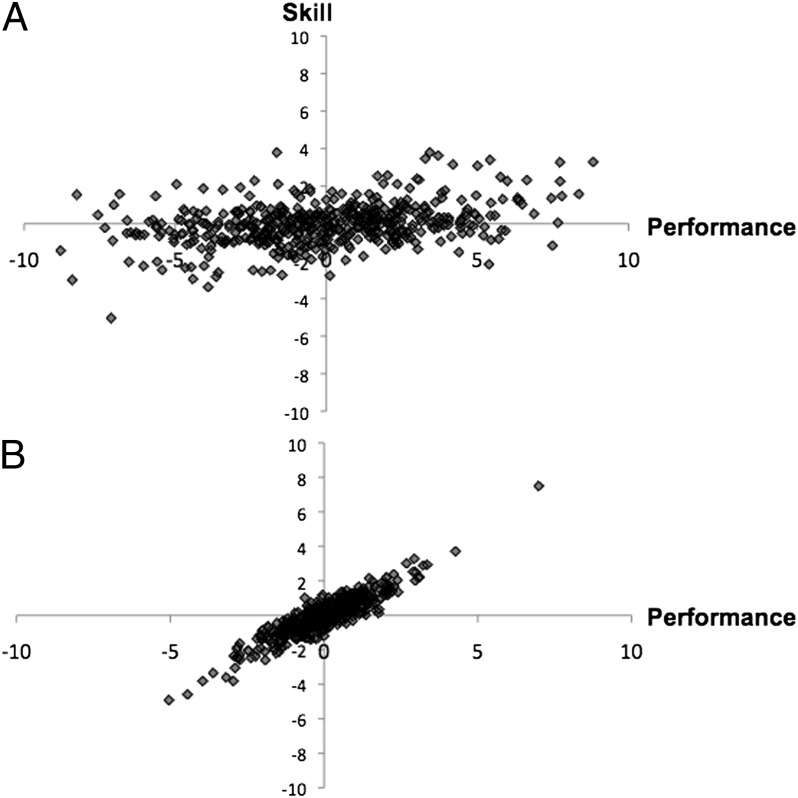
To explain why, note that when n < s, there is more variability in and uncertainty about the SD of the noise term. In this case, an extreme performance indicates that the SD of the noise term was high, because extreme performances are more likely then. If the SD of the noise term is high, however, then an observer should not update his or her estimate of the skill level much, because observations are unreliable and less informative about skill. For example, if the SD of the noise term was equal to 3, extreme levels of performance would be relatively likely but the association between skill and performance would be weak (the correlation between skill and performance is only 0.34; Fig. 4A). Less extreme levels of performance indicate that the SD of the noise term was smaller and that performance is a more reliable signal of skill. For example, if the SD of the noise term was equal to 0.5, extreme levels of performance would be relatively less likely and the association between skill and performance would be strong (the correlation is 0.91; Fig. 4B). The reason for the decline in 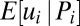 for high values of Pi is thus that very high levels of performance are less informative about skill than lower levels of performance.
for high values of Pi is thus that very high levels of performance are less informative about skill than lower levels of performance.
Fig. 4.
Illustration of the association between skill and performance when the SD of the noise term is high and low. (A) The SD of the noise term is 3. (B) The SD of the noise term is 0.5. Each figure is based on 1,000 simulations.
Although Fig. 3 only shows one illustration, for two particular values of n and s, we have found the same basic result whenever n < s for all combinations of the values of n and s that we have tried. Moreover, we conjecture that this result holds whenever 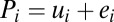 and the noise distribution has fatter tails, that is, when extreme values of ei are more likely but intermediary values less likely than for ui. [Formally, let G and F be the cumulative distribution functions of ui and ei. Suppose G and F are independent, symmetric, and have mean zero. F is more fat-tailed than G if there exists a value
and the noise distribution has fatter tails, that is, when extreme values of ei are more likely but intermediary values less likely than for ui. [Formally, let G and F be the cumulative distribution functions of ui and ei. Suppose G and F are independent, symmetric, and have mean zero. F is more fat-tailed than G if there exists a value 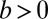 such that for
such that for 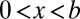 ,
, 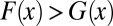 , but
, but 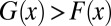 for
for 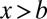 .] If this condition holds, intermediary values of Pi are compatible with a high value of ui and a low value of ei, but an extreme value of Pi indicates that
.] If this condition holds, intermediary values of Pi are compatible with a high value of ui and a low value of ei, but an extreme value of Pi indicates that 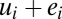 is dominated by ei.
is dominated by ei.
Whenever 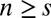 , higher performance indicates higher skill. When n = s, expected skill increases linearly with observed performance (in fact,
, higher performance indicates higher skill. When n = s, expected skill increases linearly with observed performance (in fact, 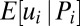 = 0.5 Pi; see SI Text for a proof). When n > s,
= 0.5 Pi; see SI Text for a proof). When n > s,  increases at a higher rate for extreme (high or low) levels of performance. The reason is that extreme levels of performance are especially informative about skill, because an extreme performance is most likely due to a high value of ui. It follows that when n > s, the highest performers are especially good models of imitation and the lowest performers are especially worthy of blame. The model thus shows that whether one should imitate the highest performers depends on the setting and, in particular, the tail properties of the distributions of skill and noise.
increases at a higher rate for extreme (high or low) levels of performance. The reason is that extreme levels of performance are especially informative about skill, because an extreme performance is most likely due to a high value of ui. It follows that when n > s, the highest performers are especially good models of imitation and the lowest performers are especially worthy of blame. The model thus shows that whether one should imitate the highest performers depends on the setting and, in particular, the tail properties of the distributions of skill and noise.
Summary
Our two models show that it is not obvious that higher performance indicates higher skill. Higher performance can indicate lower skill. We showed how this conclusion holds even in simple modifications of well-known models: Model 1 added heterogeneity to a model of self-reinforcing performance, and model 2 added heterogeneity to the standard model of performance as a linear combination of skill and noise. Both our models show that higher performance may not indicate higher skill when extreme values of skill are relatively unlikely (extreme values of ci or ui are less likely than extreme values of wi or ei), and even high levels of skill are unlikely to lead to extreme performance.
When is this scope condition satisfied? We believe it can be satisfied in competitive domains in which performance can be substantially influenced by chance events and even relatively unskilled agents can achieve high performance. Imitation and selection in competitive domains can substantially reduce the heterogeneity of agents (6). Chance events can substantially influence performance when performance depends on forecasts of future events (as in trading) and subjective judgments [by superiors (5)], especially when judgments are influenced by the judgments of others (14). In addition, when performance depends on past performance, errors and chance events may not average out (19) but may be amplified through rich-get-richer dynamics and multiplicative random processes that often generate fat-tailed distributions (11, 20). In these settings, individual performances can differ by several orders of magnitude, whereas the skill distribution is likely less widely dispersed (9) and variations in the upper and lower tails of performance depend more on luck (due to substantial noise or chance events amplified by rich-get-richer dynamics) than on skill.
In other settings, extreme performance is unlikely to be due to luck. Skills may vary substantially whereas chance events can only have a limited impact, such as in a marathon race where both amateurs and professionals compete (amateurs of low skill are very unlikely to beat professionals). In such settings, performance is a good indicator of skill and, as our second model shows, extreme performance may be especially informative.
Our framework assumes that evaluators are uncertain about the noise level or the level of dependency. This is realistic in many settings where actors can choose the level of risk or dependency and evaluators cannot observe the choice. Our results would not hold for evaluators who have detailed information about the setting. Nor would they hold when the individual being evaluated can inform evaluators about the setting, perhaps by taking a costly action to signal that the setting was one with little noise and weak dependency.
Implications
Our model shows how a rational agent, whose inferences follow Bayes’ rule, should infer skill from performance. Given the difficulties that people have in using Bayes’ rule (21), one can ask whether people are able to follow the prescriptions of our model. Do people understand that an extreme performance may signal unreliability and luck? If not, what are the consequences?
To examine how people infer skill from performance, we ran experiments in which participants predicted skill levels based on data on observed performance levels (see SI Text for how the experiments were conducted). Participants in these experiments had ample time to learn the nonmonotonic relationship between ability and performance. The results show that despite clear feedback and incentives to be accurate, 69 out of 119 participants never predicted higher performers to be less skilled than those with moderately high performance. In other words, a majority of participants assumed the most successful were the most skilled and thus mistook luck for skill.
Why do people misinterpret extreme performance, and what are the consequences? We suggest that people misinterpret extreme performance partly because they rely on the assumption that higher performers are more skilled. Relying on such an assumption is not irrational. Rather, it is often true. Perhaps more interesting, even when this assumption is false, a model built on this assumption may outperform a correct model that allows for nonmonotonicity. We use a simulation model to illustrate this point (see SI Text for more information). In the simulation, we examined whether a third-degree polynomial model or a linear model predicted skill levels more accurately based on a sample of performance–skill pairs. The simulation assumed that the association between performance and skill was nonmonotonic (as in Fig. 3). In every period of the simulation, the performance of an individual with unknown skill was observed and the task was to predict her skill. After the prediction, the skill was revealed. Although a third-degree polynomial model can better fit the performance–skill association, the linear model made more accurate predictions for small sample sizes. For example, suppose only four observations were available, that is, four performance–skill pairs. In this case, the linear model made predictions closer to the actual value of skill than the third-degree polynomial model 76% of the time (based on 1 million simulations). Only if 20 or more observations were available was the third-degree polynomial model more likely than the linear model to make accurate predictions.
The intuition for this result is related to the bias–variance dilemma (22): Fitting a third-degree polynomial introduces variance that degrades predictive accuracy. Because people often have to evaluate performances relying on small samples (23), using a linear model as a frugal heuristic may be ecologically rational (24, 25). Even in settings when the extreme performance is not a reliable indicator of skill, decision makers may be served well by initially assuming that performance indicates skill. Moreover, unless large samples are available, people will also have little opportunity to detect that their assumption is incorrect.
Although the assumption that higher performers are more skilled leads to accurate predictions on average, assuming that extreme performances indicate extreme skill can lead to undesirable consequences if people rely on this assumption for identifying outliers especially worthy of praise and blame.
Consider blame for failures. People often attribute catastrophes to the leader in charge, but a catastrophe might be more informative about the character of the system that experienced failure than about the leader’s ability. Complex systems in which components are tightly coupled are sensitive to chance events and external shocks. As a result, extreme failures are more likely for such systems than for systems in which components are loosely coupled. A catastrophe indicates that the underlying system is complex and failure-prone, and in such cases firing the leader might be misguided. Moderate failures could provide more reliable evidence of low ability.
Consider, next, learning from successes. Imitating the practices of successful others has been argued to be an universal trait and beneficial for society (3). Our model also implies that imitating others with high, but not exceptional, performance is likely to be beneficial, whereas imitating exceptional performance could be detrimental. As our models show, the highest performers may both be less skilled and use methods with higher levels of risk. When exceptional performance is due to self-reinforcing processes and initial success, the exceptional performers may continue to perform well but imitators will likely be disappointed (26), because they can at best only replicate the practices, and thus the skill levels, of the high performers, but not their initial good fortune.
More generally, our results suggest a different perspective on when imitating top performers is beneficial for society. On the one hand, when an extreme performance is unlikely unless an agent is lucky, the highest performers might not be the most skilled. Nevertheless, imitation may be largely beneficial if people recognize that the highest performer is not the best or when they are only aware of a few others so the best observed performance is not exceptional. In a society where exceptional performers are highly visible, however, and their practices are covered in business magazines, imitation of the best may not increase skill levels as much but will lead to the diffusion of more risky practices that generate a variable outcome at the societal level (14). On the other hand, when extreme performance requires extreme levels of skill, imitation of and knowledge of the best performers can be especially beneficial, because extreme performances are especially informative.
Finally, consider rewards. The highest performers often receive the highest rewards in organizations. Our results suggest that one should suspect that extremely high performance could be due to excessive risk taking rather than prudent strategy and exceptional skill. Imitation of such highly rewarded performers may further diffuse such risky practices. Moreover, high rewards for exceptional performance may tempt other people to deliberately take risks or to cheat because they are unlikely to achieve extreme performance otherwise [as happened in Barings Bank (27)]. This observation may be relevant for the recurrent financial crises: Rewards for exceptional performance might have led to diffusion of risky practices that eventually resulted in very poor returns. To avoid this, reward systems would need to be redesigned to reflect not just actual performance but also the level of risk (due to leverage but also to focus on products or markets with strong self-reinforcing dynamics). More important, because a nonmonotonic relationship between performance and skill is counterintuitive and a reward system that reflects this relationship may not be perceived as fair, nudges may need to be developed to help people resist the temptation to praise or blame extreme performers.
Supplementary Material
Acknowledgments
We thank Pamela Sammons, Stefan Scholtes, Daniel Ralph, Daniel Levinthal, Anne Miner, Daniel Read, and Thomas Powell for discussions; Lance Bai and Cheeven Tsai for technical assistance; three anonymous reviewers and the editor for their constructive comments; and Jesus College, Saïd Business School at the University of Oxford, and The Saïd Foundation for financial support.
Footnotes
The authors declare no conflict of interest.
*This Direct Submission article had a prearranged editor.
This article contains supporting information online at www.pnas.org/lookup/suppl/doi:10.1073/pnas.1116048109/-/DCSupplemental.
References
- 1.Baron J, Hershey JC. Outcome bias in decision evaluation. J Pers Soc Psychol. 1988;54(4):569–579. doi: 10.1037//0022-3514.54.4.569. [DOI] [PubMed] [Google Scholar]
- 2.Gilbert DT, Malone PS. The correspondence bias. Psychol Bull. 1995;117(1):21–38. doi: 10.1037/0033-2909.117.1.21. [DOI] [PubMed] [Google Scholar]
- 3.Richerson PJ, Boyd R. Not by Genes Alone: How Culture Transformed Human Evolution. Chicago: Univ of Chicago Press; 2005. [Google Scholar]
- 4.Rogers AR. Does biology constrain culture? Am Anthropol. 1988;90(4):819–831. [Google Scholar]
- 5.Thorngate W, Dawes R, Foddy M. Judging Merit. New York, NY: Psychology Press; 2008. [Google Scholar]
- 6.March JC, March JG. Almost random careers: The Wisconsin school superintendency, 1940–1972. Adm Sci Q. 1977;22(3):377–409. [Google Scholar]
- 7.Musch J, Grondin S. Unequal competition as an impediment to personal development: A review of the relative age effect in sport. Dev Rev. 2001;21(2):147–167. [Google Scholar]
- 8.Merton RK. The Matthew effect in science: The reward and communication systems of science are considered. Science. 1968;159(3810):56–63. [PubMed] [Google Scholar]
- 9.Frank R, Cook P. The Winner-Take-All Society. New York: Free Press; 1995. [Google Scholar]
- 10.DiPrete TA, Eirich GM. Cumulative advantage as a mechanism for inequality: A review of theoretical and empirical developments. Annu Rev Sociol. 2006;32:271–297. [Google Scholar]
- 11.Barabasi AL, Albert R. Emergence of scaling in random networks. Science. 1999;286:509–512. doi: 10.1126/science.286.5439.509. [DOI] [PubMed] [Google Scholar]
- 12.Lynn FB, Podolny JM, Tao L. A sociological (de)construction of the relationship between status and quality. Am J Sociol. 2009;115(3):755–804. [Google Scholar]
- 13.Arthur WB. Competing technologies, increasing returns, and lock-in by historical events. Econ J. 1989;99(394):116–131. [Google Scholar]
- 14.Salganik MJ, Dodds PS, Watts DJ. Experimental study of inequality and unpredictability in an artificial cultural market. Science. 2006;311:854–856. doi: 10.1126/science.1121066. [DOI] [PubMed] [Google Scholar]
- 15.Galton F. Hereditary stature. Nature. 1886;33:296–298. [Google Scholar]
- 16.Thaler RH, Sunstein CR. Nudge: Improving Decisions About Health, Wealth, and Happiness. New Haven, CT: Yale Univ Press; 2008. [Google Scholar]
- 17.Tellis G, Yin E, Niraj R. Does quality win? Network effects versus quality in high-tech markets. J Mark Res. 2009;46(2):135–149. [Google Scholar]
- 18.Harrison JR, March JG. Decision making and postdecision surprises. Adm Sci Q. 1984;29(1):26–42. [Google Scholar]
- 19.Denrell J. Random walks and sustained competitive advantage. Manage Sci. 2004;50(7):922–934. [Google Scholar]
- 20.Simon HA. On a class of skew distribution functions. Biometrika. 1955;42(3/4):425–440. [Google Scholar]
- 21.Gigerenzer G. Rationality for Mortals: How People Cope with Uncertainty. New York: Oxford Univ Press; 2008. [Google Scholar]
- 22.Geman S, Bienenstock E, Doursat R. Neural networks and the bias/variance dilemma. Neural Comput. 1992;4(1):1–58. [Google Scholar]
- 23.March JG, Sproull LS, Tamuz M. Learning from samples of one or fewer. Organ Sci. 1991;2(1):1–13. doi: 10.1136/qhc.12.6.465. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Dawes RM. The robust beauty of improper linear models in decision making. Am Psychol. 1979;34(7):571–582. [Google Scholar]
- 25.Gigerenzer G, Brighton H. Homo heuristicus: Why biased minds make better inferences. Top Cogn Sci. 2009;1(1):107–143. doi: 10.1111/j.1756-8765.2008.01006.x. [DOI] [PubMed] [Google Scholar]
- 26.Strang D, Macy MW. In search of excellence: Fads, success stories, and adaptive emulation. Am J Sociol. 2001;107(1):147–182. [Google Scholar]
- 27.Fay S. The Collapse of Barings. New York: W. W. Norton; 1997. [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.