Genome-wide Efficient Mixed Model Analysis for Association Studies

Abstract

Linear mixed models have attracted considerable recent attention as a powerful and effective tool for accounting for population stratification and relatedness in genetic association tests. However, existing methods for exact computation of standard test statistics are computationally impractical for even moderate-sized genome-wide association studies. To deal with this several approximate methods have been proposed. Here, we present an efficient exact method that makes these approximations unnecessary in many settings. This method is roughly n times faster than the widely-used exact method EMMA, where n is the sample size, making exact genome-wide association analysis computationally practical for large numbers of individuals.

INTRODUCTION

There is an increasing interest in using linear mixed models (LMMs, also known as mixed linear models, or MLMs) to test for association in genome-wide association studies (GWAS), because of their demonstrated effectiveness in accounting for relatedness among samples and in controlling for population stratification and other confounding factors^1–7. However, these models present substantial computational challenges. For example, at the time this work was submitted for publication, the most efficient algorithm for computing (effectively) exact association test statistics (either the Wald test or the likelihood ratio test), implemented in the Efficient Mixed Model Association (EMMA) software³, had a per-SNP computational time that increases with the cube of the number of individuals (n). As a result, a medium size GWAS with a few thousand individuals and half a million SNPs would take years of CPU time to analyze^1,7. (While this paper was in review, Lippert et al (2011)⁸ also published an efficient algorithm for this model, implemented in software FaST-LMM; the relationship between this algorithm and ours is discussed later.)

Several approximation methods have been proposed to make genome-wide analysis using linear mixed models possible. Probably the simplest and fastest of these approximations, GRAMMAR (Genome-wide Rapid Association using Mixed Model And Regression), implemented in the software GenABEL⁹, first estimates the residuals from the LMM under the null model, and then treats these residuals as phenotypes for further genome-wide analysis by a standard linear model¹⁰. This substantially reduces per-SNP computation time, making it linear in the number of individuals. More recently two more-sophisticated approximate approaches have been suggested. Zhang et al⁷ use P3D (Population Parameters Previously Determined) which avoids repeatedly estimating variance components when performing each test by simply using the pre-estimated variance components from the null model; their method is implemented in the software TASSEL. Kang et al¹ also avoid repeatedly estimating variance components by a slightly different strategy, which keeps the heritability estimated from the null model fixed when testing individual SNPs. Their approach is implemented in the software EMMAX (EMMA eXpedited). (This approximation, and related ideas, was also considered by previous authors, including^10,11.) Both these last two approximations have per-SNP computation time that increases quadratically with the number of individuals, which makes them practical, on a single desktop computer, for GWAS involving thousands of individuals.

Although in some settings the approximate methods described above provide results almost identical to those of the exact method^1,7, this is not guaranteed in general, and in practice it is hard to know how accurate the approximations will be without running an exact calculation. One possible consequence of inaccuracy in the approximation could be a reduction in power compared with exact methods. For these reasons, the ability to perform exact calculations remains of interest. Here, we present a new, more efficient, method for exact calculations that provides numerically identical results to EMMA (i.e. exact Wald or likelihood ratio test statistics) but is roughly n times faster (computation time per SNP, when using the usual genome-wide relatedness matrix, is quadratic in the number of individuals, with run time similar to EMMAX). This makes exact calculations feasible for large GWAS, obviating the need for approximate methods in most common settings.

RESULTS

The method and its computational complexity is described and derived in detail in the Online Methods section. Briefly, the method requires complete or imputed genotype data^12,13 for all SNPs, and involves only one eigen-decomposition of the relatedness matrix at the beginning (computational complexity O(n³)). For each SNP tested, it effectively replaces the expensive additional eigen-decomposition step in EMMA with one matrix and vector multiplication (computational complexity O(n²)). After this, like EMMA, each iteration of the following optimization step requires cheap operations (complexity O(n)) to evaluate both first and second derivatives of the target functions. We refer to our method as Genome-wide Efficient Mixed Model Association (GEMMA) because it builds on EMMA and facilitates its genome-wide application.

We illustrate our method and compare the analysis results with the exact method EMMA and the approximation methods EMMAX and GRAMMAR, using two examples, a mouse GWAS for high-density lipoprotein cholesterol (HDL-C) levels from the Hybrid Mouse Diversity Panel (HMDP)¹⁴ and a human GWAS for Crohn's disease from the Wellcome Trust Case Control Consortium (WTCCC)¹⁵. The size of this second study makes it computationally impractical to analyze with EMMA³. Table 1 summarizes the computational complexity for the four methods along with CPU time for the two data sets on a single desktop CPU. Table 1 also includes results for the recently-published FaST-LMM⁸, which can produce identical p values to EMMA and GEMMA in the same time complexity as GEMMA; see below for further discussion. As expected GEMMA is comparable in speed with EMMAX, completing the larger (WTCCC) example in under 4 hours.

Table 1.

Performance of different methods for GWAS with the linear mixed model. All computing were performed on a single core of an Intel Xeon L5420 2.50 GHz CPU. The time for the EMMA method is projected from a selection of 10,000 and 100 genetic markers in the HMDP data set and WTCCC data set, respectively. Note that EMMA is implemented in R while others are implemented in C. A C implementation of EMMA could be a few times faster. p is the number of genetic markers, n is the number of individuals, m is the number of strains (equal to n for human studies), c is the number of covariates (fixed effects) in addition to the genotypes. t₁ and t₂ are the number of optimization iterations required, for Brent's method (super-linear rate of convergence) and the Newton--Raphson method (quadratic rate of convergence) respectively. Note that t₂ is expected to be smaller than t₁.

Methods		Time Complexitya	Computing Time
			HDL-Cb	Crohn's Diseasec
Exact Methods	GEMMA	O(mn2+cn2+pn2+pt2c2n)	33 minutes	3.3 hours
	EMMA	O(mn2+pmn2+pt2n)	~ 9 days	~ 27 years
	FaST-LMMd	O(mn2+cn2+pn2+pt1c2n)	6.8 hours	6.2 hours
Approximate Methods	EMMAX	O(mn2+t2n+pn2)	44 minutes	6.4 hours
	GRAMMAR	O(mn2+t2n+pn)	1.6 minutes	12 minutes

^aComplexities are given assuming the usual genome-wide relatedness matrix, which has rank n. In the current implementation of various methods except EMMA, the first terms are actually n³, but it would be straightforward to make them mn² in principle.

^bm=99, n=681 and p=1,885,197 for HDL-C.

^cm=n=4686 and p=442,001 for Crohn's disease.

^dThese results are for the algorithm in FaST-LMM that uses the standard full-rank relatedness matrix, which produces p values that are identical to GEMMA and EMMA. See main text for further discussion.

To verify the correctness of our algorithm and implementation we first validate it by comparing p values calculated by GEMMA with those from EMMA on a subset of SNPs from both data sets. For all SNPs examined the p values from the two methods match exactly (Wald test results shown in Figure 1a and 1b; Likelihood ratio test not shown).

Figure 1.

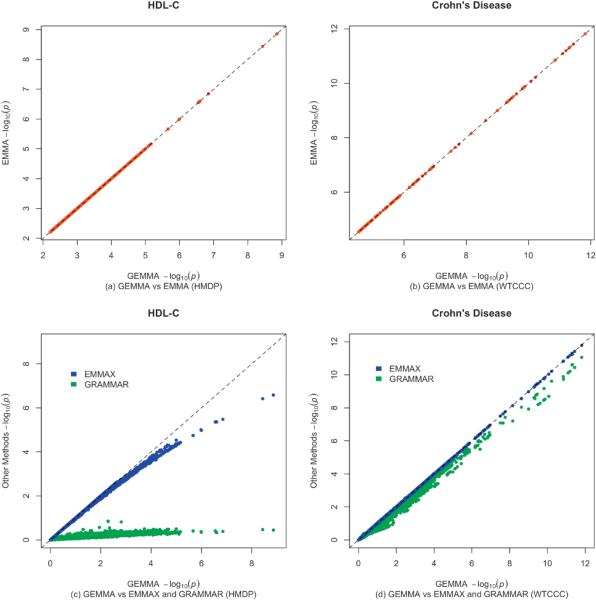
Comparison of -log₁₀ p values obtained from GEMMA with those from EMMA (a, b), and EMMAX and GRAMMAR (c, d). In (a) and (b) the p values are shown for the top 10,000 markers and top 100 markers respectively. In (c) and (d) the p values are shown for all markers (1.9 million and 442k respectively).

Since GEMMA provides exact computations in essentially the same time as EMMAX, the accuracy of the approximations in EMMAX and other methods may seem moot. However, in some settings, and specifically for mixed models with more than one random effect (variance component), the computational trick used by GEMMA does not apply, and approximations along the lines of EMMAX may remain necessary. For this reason the accuracy of different approximation methods remains of some potential interest, and so we present a comparison between the (Wald test) p values from GEMMA, EMMAX and GRAMMAR, genome-wide, on both the HMDP and WTCCC data sets above.

The HMDP GWAS represents a situation where approximation methods such as EMMAX or GRAMMAR may yield inaccurate test statistics. In particular, because individuals in the data set are closely related, and the strongly associated SNPs contribute to a significant proportion of phenotypic variation in HDL-C¹³, using estimates of variance components or fitted residuals from the null model for testing may be expected to yield conservative p values, leading to a potential loss of power. Our empirical comparison (Figure 1c) confirms this: in this case, approximation by EMMAX leads to systematic and appreciable underestimation of the most significant p values (almost two orders of magnitude), while approximation by GRAMMAR leads to dramatic underestimation of all p values. Indeed, in contrast to the exact p values, no p values generated by EMMAX are significant at the conventional 0.05 level after Bonferroni correction, and no p values generated by GRAMMAR are significant even before Bonferroni correction. The fact that the exact p values for the most significant results are substantially more significant than the approximate p values from EMMAX suggests that, in this type of setting, the exact p values may produce a more powerful test; simulation results confirm this (Supplementary Fig. 1).

In contrast, the WTCCC example represents a very different situation where the approximations may be expected to yield accurate test statistics. This is because there is relatively little population stratification in these data (the individuals are all from the UK, and the relatedness matrix is approximately diagonal), and the effect sizes of the most strongly associated SNPs for Crohn's disease are small compared with the effect sizes in the HMDP data above¹⁴. Both conditions favor the approximation assumptions in EMMAX and GRAMMAR. Empirical comparisons (Figure 1d) show that, for this particular data set, the p values from EMMAX differ negligibly from the exact values. However, the p values from GRAMMAR still depart notably from the exact values.

Taken together, the above results confirm that approximation by EMMAX is appreciably more accurate than GRAMMAR, even in cases, such as the WTCCC data, where the sample structure is subtle. The comparisons also demonstrate that the accuracy of the EMMAX approximation can vary from case to case. Consequently, the potential gain in power from doing exact vs approximate tests will also vary among datasets. For the HMDP data, the potential gain in power from the exact calculations appears considerable, and this is confirmed by simulations (Supplementary Fig. 1). For the WTCCC Crohn's disease data the power gain is negligible, and as noted in ref¹ only a small gain in power is generally expected at SNPs with small effect size. Of course, one nice feature of being able to do the exact tests is that it obviates the need to consider which approximations work best under what circumstances, or to consider ways in which the approximations could be improved. We also note that the computational tricks employed here also apply to other settings, including the combined “variable selection plus random effects” model that has been widely studied for phenotype and breeding value prediction¹⁶, but which, without the trick used here, is computationally challenging to fit.

DISCUSSION

In summary, we have presented an efficient method for computing exact values of standard test statistics in linear mixed models. This method is comparable in speed with approximation methods such as EMMAX while yielding exact test statistics. Using two examples we illustrate our method, and show that the approximation methods can yield inaccurate p values when the sample structure is strong and/or when the marker effect size is large. We also find that the approximation by EMMAX is more accurate than the approximation by GRAMMAR genome-wide (a comparison made possible only by the availability of an efficient exact method).

While this work was in review, Lippert et al⁸ also published an efficient method for computing likelihoods for LMMs that, like our method, requires only one singular value decomposition of the relatedness matrix. They use this method, in combination with Brent's optimization algorithm, to produce an algorithm for computing exact test statistics with effectively the same computational complexity as GEMMA: O(mn²+cn²+pn²+ptc²n), as in Table 1. (Lippert et al⁸ also suggest a further innovation, using a low-rank relatedness matrix in place of the usual relatedness matrix computed from all SNPs genome-wide, that produces an algorithm that is linear in n, and so feasible for very large GWAS samples containing more than 100,000 individuals; however changing the relatedness matrix in this way changes the resulting p values appreciably, and in this sense this linear complexity algorithm is not directly comparable with either GEMMA or EMMA; see below for further discussion.) The main additional contribution of our work here beyond that in Lippert et al is that we provide, and make use of, efficient methods for evaluation of not only the likelihood, but also both its first and second derivatives. This allows us to make use of the Newton--Raphson optimization method, which has better theoretical convergence properties than Brent's algorithm (quadratic, vs super-linear), potentially reducing per-SNP computation time by reducing the number of iterations required for convergence, t. The practical effect of this is expected to depend on the sample size n. Examining the theoretical computational complexity, if p is large (and we assume the simplest case with no additional covariates, so c=1) then the per-SNP complexity of the algorithms is O(nw² + tn). Thus if n is large then the n² term will dominate and the number of iterations will have only a small effect of computation time; if n is moderate then the number of iterations may play a more important role. Consistent with this, we found GEMMA to be 12 times faster than the Lippert et al algorithm, implemented in FaST-LMM, for the smaller HMDP dataset (33 minutes vs 6.8 hours), but only 2 times faster for the WTCCC data (3.3 hours vs 6.2 hours). It is possible that implementational issues, which are important but conceptually less fundamental, also contribute to this difference in speed. Besides this difference in speed, which might be considered a minor issue, by providing efficient methods to compute derivatives our work here lays the foundations for similar efficient analyses for LMMs with multivariate phenotypes¹⁷, where multidimensional optimization is required and evaluating the target functions alone is unlikely to suffice.

Here we have focused on computations using the usual relatedness matrix, computed from all SNPs genome-wide, whose rank, r, is typically equal to the number of individuals n. However, as noted by Lippert et al⁸, if a lower-rank relatedness matrix is used then this reduces computing time (computational complexity of the singular value decomposition can scale with nr²) and in some cases memory requirements (e.g. Lippert et al.⁸ suggest using a relatedness matrix based on only a few thousand SNPs; this has the nice property that required singular value decompositions can be done without computing the n by n relatedness matrix itself). Using the usual full-rank relatedness matrix, our current implementation of GEMMA can handle approximately 23,000 individuals on a machine with 64 Gb memory (in double precision); using a lower-rank relatedness matrix, much larger problems could be tackled. However, we note that changing the relatedness matrix can produce much larger changes in p values than, for example, the differences between EMMAX and exact calculations (e.g. Supplementary Fig. 2), and for both the HMDP and WTCCC data using a lower-rank relatedness matrix seems to compromise the ability of the LMM to control for sample structure (Supplementary Table 1). Thus choice of relatedness matrix could affect statistical efficiency (both power, and correct control of type I error due to stratification or relatedness) as well as computational efficiency. Interestingly, statistical and computational considerations may not necessarily conflict: for example,⁷ suggest that use of compressed MLM, which yields a lower-rank relatedness matrix by clustering individuals, can both reduce computation and increase power compared with the full-rank matrix. The general question of which low-rank relatedness matrices produce the best combination of computational and statistical performance seems to be an interesting avenue for further study.

URLs

Our method is implemented in software GEMMA, freely available at http://stephenslab.uchicago.edu/software.html.