Conservation of complex knotting and slipknotting patterns in proteins

Abstract

While analyzing all available protein structures for the presence of knots and slipknots, we detected a strict conservation of complex knotting patterns within and between several protein families despite their large sequence divergence. Because protein folding pathways leading to knotted native protein structures are slower and less efficient than those leading to unknotted proteins with similar size and sequence, the strict conservation of the knotting patterns indicates an important physiological role of knots and slipknots in these proteins. Although little is known about the functional role of knots, recent studies have demonstrated a protein-stabilizing ability of knots and slipknots. Some of the conserved knotting patterns occur in proteins forming transmembrane channels where the slipknot loop seems to strap together the transmembrane helices forming the channel.

There are increasing numbers of known proteins that form linear open knots in their native folded structure (1, 2). In general, knots in proteins are orders of magnitude less frequent than would be expected for random polymers with similar length, compactness, and flexibility (3). In principle, the polypeptide chains folding into knotted native protein structures encounter more kinetic difficulties than unknotted proteins (4–12). Therefore, it is believed that knotted protein structures were, in part, eliminated during evolution because proteins that fold slowly and/or nonreproducibly should be evolutionarily disadvantageous for the hosting organisms. Nevertheless, there are several families of proteins that reproducibly form simple knots, complex knots, and slipknots (1, 2). In these proteins, the disadvantage of less efficient folding may be balanced by a functional advantage connected with the presence of these knots. Numerous experimental (13–16) and theoretical (17–27) studies have been devoted to understanding the precise nature of the structural and functional advantages created by the presence of these knots in protein backbones. It has been proposed that in some cases the protein knots and slipknots provide a stabilizing function that can act by holding together certain protein domains (4). In the majority of cases, however, one is unable to determine the precise structural and functional advantages provided by the presence of knots.

To shed light on the function and formation of protein knots, we performed a thorough characterization of knotting within protein structures deposited in the Protein Data Bank (PDB) (28) by creating a precise mapping of the position and size of the knotted and slipknotted domains and knot tails (1, 2). We identified the types of knots that are formed by the backbone of the entire polypeptide chain and also by all continuous backbone portions of a given protein (1, 2). To characterize the knotting of proteins with linear backbones, one needs to set aside the orthodox rule of knot theory that states that all linear chains are unknotted because, by a continuous deformation, one can always disentangle even highly entangled linear chain into one that follows a straight line. Of course, the characterization of the knotting within the protein structures makes sense only if one considers fixed configurations, in this case proteins in their native folded structures. Then they may be treated as frozen and thus unable to undergo any deformation.

Several papers have described various interesting closure procedures to capture the knot type of the native structure of a protein or a subchain of a closed chain (1, 3, 29–33). In general, the strategy is to ensure that the closure procedure does not affect the inherent entanglement in the analyzed protein chain or subchain. Unfortunately, this approach works well only for some of the possible linear configurations. In other cases, the resulting knot type is not uniquely determined by the geometry of the linear fragment but is strongly affected by parameters of the specific closure algorithm. Another strategy for characterizing the knotting of linear fragments is to keep the ends of the linear fragment fixed in space and to “simplify” the chain by a triangle elimination method or some other chain shortening procedure that avoids intersegmental passages (29, 34). When the shortening procedure has exhausted all simplifications on a protein configuration, one usually obtains configurations with the ends protruding from the entangled portion. It is then easy to connect the ends without passing through the entangled portion. However, the shortening method applied to the same starting configuration can result in different knot types depending on the order of the shortening moves (30). Because the order of the shortening moves is not determined by the actual configuration but depends on arbitrarily chosen parameters, this method also is confronted with the problem that the linear chains do not totally determine the knot type of the frozen chain.

Limitations in these single closure methods stimulated interest in probabilistic methods of defining the most likely knot type of linear chains with a given geometry (1, 3, 30). One relatively simple, unbiased method consists of placing the analyzed linear chain near the center of a large sphere and closing it by adding to each end one long segment connecting it with the same, randomly chosen point on the enclosing sphere. When this procedure is repeated many times, one obtains a spectrum of knots determined by the given linear fragment (30). Knot types that are dominant (i.e., the knot type occurring most frequently) in the resulting spectrum can be considered as characterizing the knotting of the linear fragment (1, 3, 30). In our characterization of the knotting with the protein structures, we apply a uniform closure procedure inspired by Millett et al. (30).

In addition to analyzing the complete polypeptide chains, we also analyzed all continuous subchains to detect knots and slipknots (2). By identifying the knot type of each subchain, we are able to locate the cores of the knots—i.e., the minimal portions of the protein backbones that form a given knot type.

Classification of Knotting in Protein Structures

We analyzed 74,223 structures submitted to the PDB through April 2011 and determined their global and local knotting. In this large set of structures, we found 398 knotted and 222 slipknotted proteins including 64 different carbonic anhydrases sequences. We divided all proteins with knots and slipknots according to the complexity of their knotting. Table 1 lists representative protein family members with complex knotting, whereas the tables in the SI Appendix (see SI Appendix, Tables S1 and S2) list those with simple knotting.

Table 1.

Complex knotting patterns in proteins and their conservation

Motif	Family	Protein/PDB	Source
	α-haloacid dehalogenase	DehI/3bjx	Arthrobacter sideroc aspulatus
	ubiquitin C-terminal hydrolase	UCHL1/3irt	Human
		UCHL3/1xd3	Human
		UCHL3/2wdt [n]	P. falciparum
		UCHL5/3a7sa [n]	Human
		Yuh1/1cmxb	Yeast
	SNF	LeuT(Aa)/2a65	Aquifex aeolicus
	NCS1	Mhp1/2jlo [n]	M. liquefaciens
	AA-permease	ApcT/3gia [n]	Methanocaldococcus
		AdiC/3l1la [n]	E. coli
		AdiC/3ncy [n]	Salmonella
	SSF	vSGLT/3dh4 [n]	Vibrio parahaemolyticus
	BCCT	BetP/2wita [n]	Brevibacterium
		PmCaiT/2wsw [n]	Proteus
		EcCaiT/2wsx [n]	E. coli
	KARI	KARI/1yve	Spinach
		KARI/1yrl	E. coli
		KARI/3fr8 [n]	Rice
	PHY	bphP/3c2w	Pseudomonas
		cph1/2vea	Synechocystis
	PHY	bphP/1ztu	Deinococcus
		bhyB2/2ool	R. palustris
	Cloacin	ColE7/2axca [n]	E. coli
		protein B/1rh1a [n]	E. coli
	S-pyocin	ColE3/1jch [n]	E. coli

Simple motifs are shown in the SI Appendix (see SI Appendix, Tables S1 and S2), respectively, for knotted and slipknotted proteins. The letters K and S followed by knot type notations indicate whether the entire polypeptide chain of a given protein forms a knot (K) or a slipknot (S), respectively, and the knot types formed by the subchains of a given protein. The pictograms show specific knotting patterns observed for the respective protein families (Pfam classification, ref. 35) as illustrated in Figs. 2–5. Respective protein names, their PDB code, and host species are indicated. An [n] indicates proteins whose knotted pattern are established in this study.

The paths of native polypeptide chains are complex. Even using modern computer graphics of protein structures, it is difficult to detect whether a given protein forms a knot and where the knot is located simply by looking at the structure. For this reason, it has been useful to develop ways to visualize the knotting landscape of protein structures in the form of a matrix (2, 36) in which every entry represents the knot type of a different subchain of the native polypeptide chain.

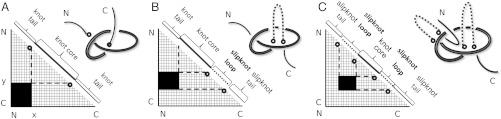
Each entry in the matrix indicates knotting in the subchain starting with the amino acid position indicated on the horizontal axis and ending with the amino acid position indicated on the vertical axis (see Fig. 1). Therefore, the entry in the lower left corner reports the knotting of the entire polypeptide chain in its folded configuration. Entries approaching the diagonal correspond to shorter and shorter subchains.

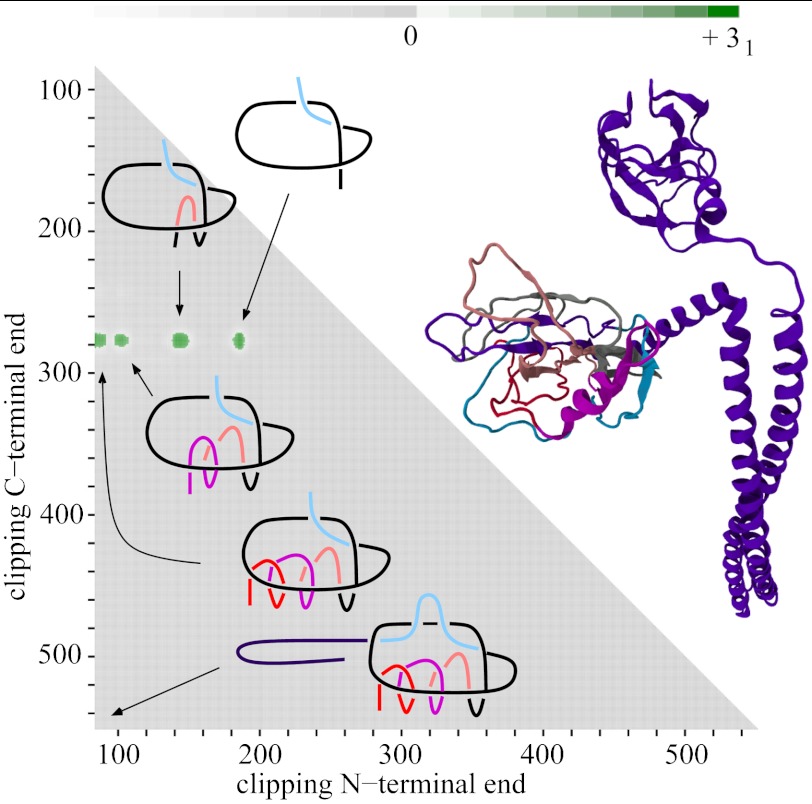
Fig. 1.

Matrix presentations of protein knotting. Each entry in the matrix indicates the knot type formed by one continuous subchain by its shading (Fig. 1) or color (Figs. 2–5). In each case, the subchain starts with the N-terminal amino acid at position x and ends with the C-terminal amino acid at position y, indicated on the horizontal and vertical axes, respectively. Equivalently, this subchain can be interpreted as a part of the diagonal, delimited by the corresponding coordinates x and y, where the entire diagonal corresponds to the entire polypeptide chain. (A) A case of a knotted protein. Notice that the entry in the lower left-hand corner, which corresponds to the entire protein, is shaded; this indicates that the corresponding chain or subchain is knotted. The knot core is defined as the shortest subchain that still forms a knot (see the thickened part of the protein in the sketch above). The two remaining parts of the chain form knot tails, and their length is conveniently represented along the diagonal. Subchains that do not include at least short bits of both knot tails do not form knots and therefore the matrix entries corresponding to these subchains are not shaded. (B and C) Cases of protein slipknots. Notice that in the case of slipknots the entire protein is unknotted (the element in the lower corner is white) but as one (B) or both termini (C) are trimmed to some extent, the remaining fragment forms a trefoil knot, denoted 3₁ in Table 1 and SI Appendix, Table S2, and the corresponding matrix entries are therefore darkened in the matrix. Schematic drawings of the polypeptide chains forming trefoil knots and slipknots illustrate which parts of the polypeptide chains constitute the knot cores (thickened), the knot and slipknot tails (solid line), and the slipknot loops (dashed line).

The identity and strength of the knotting character of each subchain is reported by employing distinct shaded color schemes for each knot type in Figs. 2–5. The schematic presentation in Fig. 1A illustrates the case in which the entire protein forms a 3₁ knot. In such a case, entries at or close to the lower left-hand corner show that the entire protein and subchains encompassing nearly the entire protein form a 3₁ knot. Moving up and/or to the right within the matrix, we eventually reach entries that indicate the unknotted character of the corresponding subchains. If the removal of only a few amino acids from the N or C terminus is sufficient to unknot the fragment, the knot is considered shallow. The entry closest to the diagonal of the matrix that indicates a knotted state in the corresponding subchain gives the size of the knotted core—i.e., the shortest portion of the chain that still forms the given knot type.

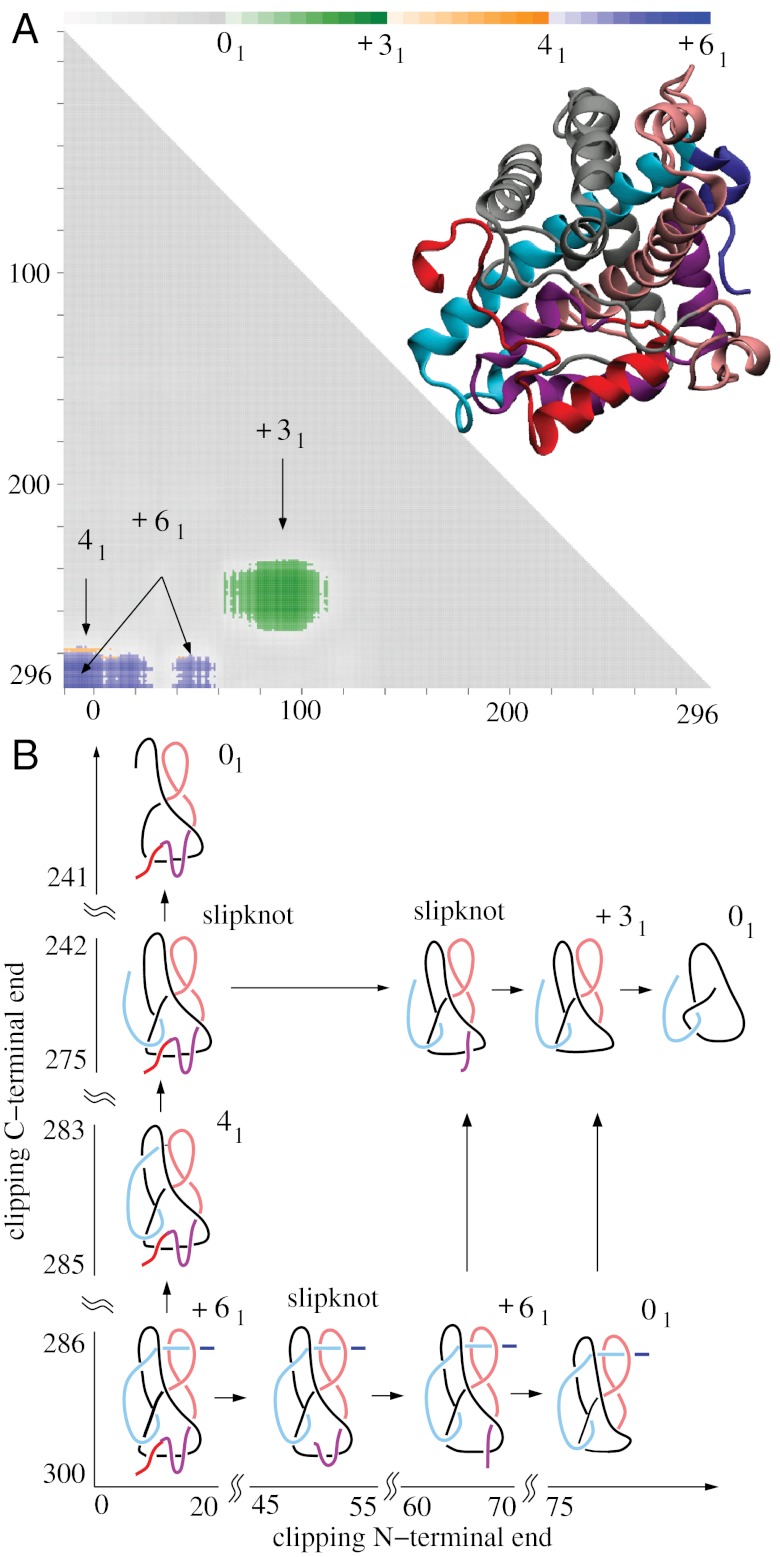
Fig. 2.

The DehI protein forms the Stevedore’s knot as a whole but some of its subchains form 4₁ and 3₁ knots or form Stevedore’s and trefoil slipknots. (A) Matrix presentation of the DehI knotting. The color scale shows the dominant knot type formed by a given subchain and the frequency (shown via the color opacity) of its formation. The color bar above a matrix presents the corresponding frequencies at 10%, 20%, …, 100%. Notice the narrow territory of 4₁ knots above the territory of the Stevedore’s knot. (B) Schematic drawing explaining how the progressive clipping of the C and/or N terminus from the entire polypeptide chain with Stevedore’s knot leads to subchains forming 4₁ and 3₁ knots or Stevedore’s and trefoil slipknots.

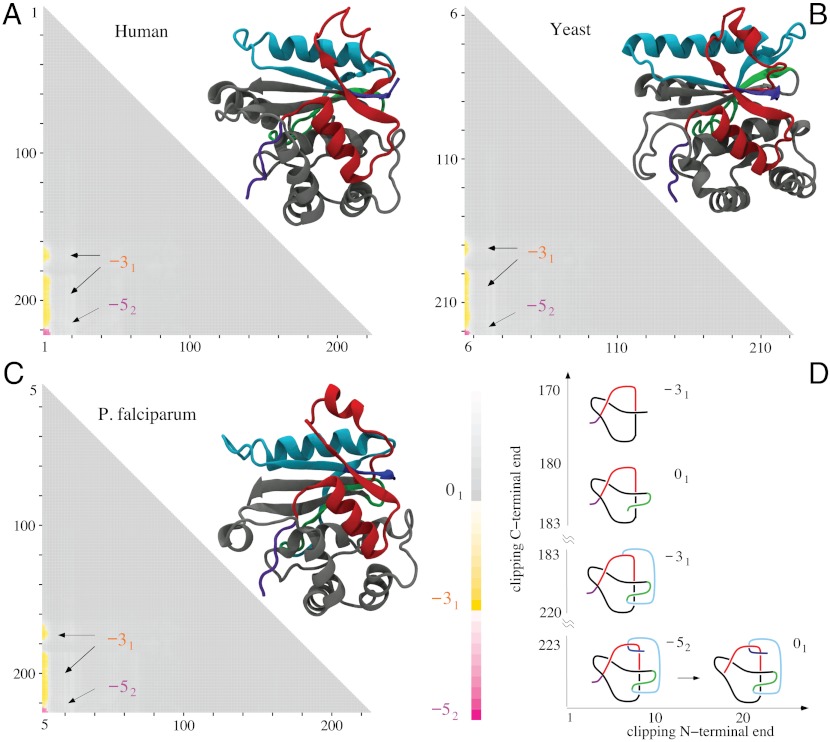
Fig. 3.

Molecular structures and matrix presentation for ubiquitin C-terminal hydrolases from (A) human, (B) yeast, and (C) P. falciparum plasmodium cells form the same knotting motif, K5₂3₁3₁. Notice that in all three cases the proteins form 5₂ knots with nearly the same sizes and positions with respect to a linear map of their polypeptide chains. In all cases, the 5₂ knot is unknotted by removing a few amino acids from the N terminus, whereas removing a similar number of amino acids from its C terminus transforms the remaining portion of the protein into a 3₁ knot. (D) Schematic drawings reflecting the overall structure of ubiquitin C-terminal hydrolases explain how the 5₂ knot is converted into an unknot or 3₁ knot depending which end is trimmed.

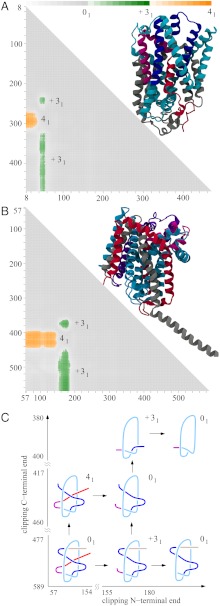
Fig. 4.

LeuT(Aa) and BetP proteins conserve the same knotting notations K3₁4₁3₁ and similar knotting fingerprints despite large sequence divergence. (A and B) The molecular structure and matrix presentation of LeuT(Aa) and BetP knotting. Notice that the matrices have a similar pattern of knots and slipknots. The protein LeuT(Aa) matrix resembles the BetP matrix with 60 aa removed. (C) The schematic drawing reflects the overall structure of the LeuTAa and BetP proteins and shows how clipping the C terminus and/or N terminus (termini) from the entire polypeptide chains (with global unknotted knotting) leads to the formation of subchains that form 4₁ and 3₁ knots.

Fig. 5.

The structure and knotting of Colicin E3, zigzag motif (S3₁3₁3₁3₁). The molecular structure and schematic drawing of Colicin E3 show that the entire protein is unknotted. However, the matrix representation reveals slipknots producing four distinct 3₁ territories on the matrix. Schematic drawings of the protein structure explain how this row of slipknots is created upon polypeptide chain clipping.

Another situation is shown in Fig. 1 B and C, which represent slipknot configurations. In those cases, the entire protein is unknotted but it contains at least one subchain forming a nontrivial knot (for example, this is the case of a shoelace bow). Slipknots in unknotted proteins can be recognized when the entries at or near the lower left-hand corner report an unknotted state but, as one or both ends are trimmed (moving up and/or to the right in the matrix), a knotted subchain is formed.

Table 1 lists the observed knotted and slipknotted proteins in decreasing order of their knotting complexity. In their knotting notation, we list all dominant knot types formed by their various subchains, ordered by length from longest to shortest. For example, the notation K6₁6₁4₁3₁ indicates that the various subchains form 6₁, 4₁, and 3₁ knots. The letter K indicates that the entire protein is knotted. The double presence of the 6₁ knot means that, in the matrix representation of the protein knotting, there are two disjoint “territories” that form a 6₁ knot (see Fig. 2). The notation S3₁3₁3₁3₁ indicates that the entire protein chain forms a slipknot (denoted by S) with four disjoint 3₁ territories in the matrix presentation of the protein (see Fig. 5). Table 1 also shows the names of the protein families to which a given knotted protein belongs, the corresponding PDB access codes, and whether the knotted character of a given protein was established in this study. In several cases, listed in the table and indicated with ^a and ^b, the structure determination was not complete, resulting in an uncertainty concerning the position of some fragments. For our analysis, we replaced missing fragments with a straight line if the missing peptide could be placed in the vicinity of the straight line without clashing with the rest of the chain, indicated by ^a. In one case (1cmx), indicated by ^b, the missing peptide had to follow an arc to avoid a steric clash with the rest of the determined protein structure. The path of this arc was chosen based on the structure of homologous proteins with better resolved crystals.

Knotting Fingerprints of Proteins with Complex Knot Types

Stevedore’s Protein Knot.

The most complex protein knot currently known is formed by the backbone of α-haloacid dehalogenase DehI (27). DehI is a bacterial enzyme hydrolyzing carbon–halogen bonds and is therefore capable of biodegrading environmental pollutants such as herbicides and pesticides (37). The crystal structure of DehI has been known since 2008 (37) but it was only in 2010 that its Stevedore’s knot (6₁ in knot tables) structure was recognized (27). Fig. 2 shows the results of the knotting analysis of all linear subchains within the crystal structure of DehI. The elementary square in the lower left-hand corner with coordinates (1,310), shows that the entire protein forms the 6₁ knot. However, when smaller subchains are considered, these form 4₁ (figure-eight) and 3₁ knots. It may seem surprising that subchains of a protein, which as a whole forms the 6₁ knot, can result in the formation of other nontrivial knot types.

Therefore, let us explain how this knotting pattern occurs. Fig. 2B shows, in schematic form, the essential geometric features of the entire DehI protein backbone and its relevant subchains. Drawings representing the protein subchains resulting from progressively clipping the C terminus are placed above the entire protein in positions that indicate the corresponding protein subchains in the matrix presented in Fig. 2A. The first of these drawings shows that as the C terminus of DehI is clipped progressively, one reaches a point where the remaining C-terminal part no longer pierces the internal loop (indicated by pink in Fig. 2B). Closures of such fragments result in the formation of 4₁ knots. Further clipping of the C terminus results in fragments that no longer pierce the second internal loop (indicated by black in Fig. 2B). The resulting protein fragment forms an unknot but this fragment in fact is a trefoil slipknot, which can be converted to a real trefoil knot by some clipping of its N terminus (see the 3₁ knot in Fig. 2B). The uppermost left drawing presents a protein fragment that, as a result of further C-terminal clipping, is no longer a slipknot because it does not contain any subchains forming nontrivial knots.

The subchains presented to the right of the entire DehI chain illustrate the knotting consequences of progressively clipping the N terminus. We can see that, as the N terminus gets shorter, it retracts first through an imaginary surface spanning the internal loop (indicated by black in Fig. 2B). The placement of the “current” N terminus on that side of the internal loop causes these subchains to form unknots. Interestingly, a further shortening of N termini brings the current N terminus on the original side of the imaginary surface spanning the same internal loop and reestablishes the original knotting of the Stevedore’s knot. This transformation demonstrates that the subchain was in fact a slipknot containing the Stevedore’s knot. The observed direct passages from the Stevedore’s knot to the unknot and then back to the Stevedore’s knot again, upon further shortening of the protein chain, are consistent with the fact that the Stevedore’s knot has unknotting number equal to one (36, 38). Therefore, a slight shortening of the chain can be sufficient to change the resulting knotting, for example from the Stevedore’s knot to the unknot and vice versa. Further clipping of the N terminus converts the resulting fragment to an unknot that contains a trefoil slipknot, which is revealed as a 3₁ knot upon clipping of its C terminus. This conversion is reflected by moving up in the matrix presented in Fig. 2. Continued clipping of N terminus chains, while maintaining the original C terminus, causes the resulting geometries of these chains to become too simple to form nontrivial knots.

Fig. 2A shows that by removing (or adding) one amino acid residue to the protein fragment, the resulting fragment changes from the Stevedore’s knot to the 4₁ knot, from the Stevedore’s knot to the unknot, from the 4₁ knot to the unknot, and from the 3₁ knot to the unknot. Interestingly, these four pairs of knots are strand passage distance one from each other (38–40), which means that, by a single intersegmental strand passage, it is possible to pass from one knot to the other. In fact, as a given protein subchain with a complex geometry is progressively clipped, one can select a perspective from which one can observe a switch from the majority of closures occurring “above” some part of the chain to the majority of closures occurring “below” that part of the chain. This phenomena is conceptually analogous to one intersegmental passage. In the protein configurations analyzed here, we have observed that neighboring knot territories, marked with different colors in the matrices presented in Fig. 2, are formed by pairs of knots that are strand passage distance one from each other. In Fig. 2, we also see that to pass from 6₁ to 3₁ or from the 4₁ knot to 3₁ one needs to pass through the territory of a different knot type (the unknot in this case). Again, this is consistent with the strand passage distance being two between these two pairs of knots (38–40).

The pattern formed by matrix entries identifying knot types formed by all subchains of an analyzed protein, such as this formed in Fig. 2A, constitutes a very complete characterization of protein knotting. Therefore, we propose to call such patterns “knotting fingerprints” of proteins. The biological significance of the complex knotting of the DehI protein is not yet known. Other proteins with similar catalytic activity have not yet been crystallized and therefore, it is not known whether this complex knotting is evolutionarily conserved.

The 5₂ Protein Knot

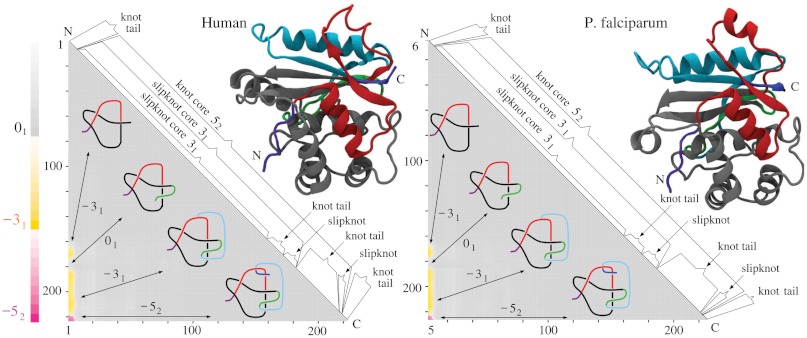
The second most complex knot observed in proteins is the knot 5₂. This knot was originally detected in two functionally related proteins but originating from human and yeast cells (4). Both proteins belong to ubiquitin C-terminal hydrolases, and their function is to rescue ubiquitin, a small protein that marks and directs other proteins for destruction within supramolecular protein complexes known as proteosomes. The ubiquitin marking is a physiological process by which the concentration of various proteins in eukaryotic cells is regulated not only on the level of their synthesis but also on the level of their degradation. The ubiquitin tag directs a protein to be passed into the narrow channel of the proteasome, where it is then digested into short polypeptides. It would be very costly for cells to digest ubiquitin with each protein marked for destruction, which is why ubiquitin is removed from proteins destined for degradation just before they enter proteasomes. This removal is performed by ubiquitin C-terminal hydrolase. It has been proposed that the knotted structure of ubiquitin C-terminal hydrolase protects this enzyme from accidental entrance into the narrow channel of proteosomes (4). Fig. 3 shows the results of our knotting analysis of ubiquitin C-terminal hydrolases isolated from (i) human, (ii) yeast, and (iii) plasmodium cells. We can see that all three proteins not only form the same knot type but also their knotting fingerprints are very similar. In each case, it suffices to clip off several amino acids from the N terminus to completely unknot the protein. Clipping from C terminus is more interesting because, after clipping just a few amino acids, the remaining subchains form 3₁ knots. A further clipping produces first a slipknot and then again a 3₁ knot, which after further clipping turns to an unknot. Fig. 3D, showing essential geometric features of all three ubiquitin C-terminal hydrolases, illustrates how a progressive clipping of the polypeptide chain forming the 5₂ knot can lead to the formation of a 3₁ knot when one end is clipped and to the creation of an unknot when the other end is clipped.

The direct passage from 5₂ to the unknot is consistent with the fact that the 5₂ knot has unknotting number equal to one. The nearly perfect conservation of knotting fingerprints in ubiquitin C-terminal hydrolases from such evolutionary distant organisms as yeast, plasmodium, and human is even more remarkable if one considers that human and yeast proteins have 32% of sequence identity (41, 42), yeast and plasmodium 28%, and plasmodium and human (UCHL5) 25% (all combinations are shown Table 2).

Table 2.

Sequence identity between proteins with K5₂3₁3₁

Name/name	Source/source	PDB/PDB	ID%
UCHL3/UCHL1	human/human	1xd3/3irt	55
UCHL3/UCHL3	human/Plasmodium	1xd3/2wdt	37
UCHL3/UCHL5	human/human	1xd3/3a7s	30
UCHL3/Yuh1	human/yeast	1xd3/1cmx	32
UCHL3/UCHL1	Plasmodium/human	2wdt/3irt	34
UCHL3/UCHL5	Plasmodium/human	2wdt/3a7s	25
UCHL3/Yuh1	Plasmodium/yeast	2wdt/1cmz	28
UCHL5/Yuh1	human/yeast	3a7s/1cmz	25

Coupled Figure-Eight Trefoil Slipknot Motif.

An interesting knotting motif consisting of coupled figure-eight trefoil slipknots was originally observed by King et al. (2) in the case of the transmembrane protein LeuT(Aa), a bacterial homolog of neurotransmitter transporters. Our knotting analysis of the PDB entries reveals that many transmembrane proteins with transporter functions have this knotting motif (see Table 3).

Table 3.

Sequence identity between proteins with the S3₁4₁3₁ motif

Name/name	Source/source	PDB/PDB	ID%
SNF/NCS1	Aquifex/M. liquefaciens	2a65/2jlo	11
SNF/AA	-/Methanocaldococcus	-/3gia	9
SNF/-	-/E. coli	-/3l1l	12
SNF/-	-/Salmonella	-/3ncy	11
SNF/SSF	-/Vibrio	-/3dh4	9
SNF/BCCT	-/Corynebacterium	-/2wit	12
SNF/BCCT	-/Proteus mirabilis	-/2wsw	11
SNF/BCCT	-/E. coli	-/2wsx	11
NCS1/AA	M. liquefaciens/Methanocaldococcus	2jlo/3gia	9
NCS1/-	-/E. coli	-/3l1l	11
NCS1/-	-/Salmonella	-/3ncy	12
NCS1/SSF	-/Vibrio parahaemolyticus	-/3dh4	12
NCS1/BCCT	-/Corynebacterium	-/2wit	8
NCS1/BCCT	-/Proteus mirabilis	-/2wsw	9
NCS1/BCCT	-/E. coli	-/2wsx	10
SSF/AA	Vibrio/Methanocaldococcus	3dh4/3gia	11
SSF/-	-/E. coli	-/3l1l	9
SSF/-	-/Salmonella	-/3ncy	6
SSF/BCCT	-/Corynebacterium	-/2wit	11
SSF/BCCT	-/Proteus mirabilis	-/2wsw	10
SSF/BCCT	-/E. coli	-/2wsx	12
BCCT/AA	Corynebacterium/Methanocaldococcus	2wit/3gia	11
BCCT/-	Proteus mirabilis/-	2wsw/-	9
BCCT/-	E. coli/-	2wsx/-	9
BCCT/AA	Corynebacterium/E. coli	2wit/3l1l	9
BCCT/-	Proteus mirabilis/-	2wsw/-	11
BCCT/-	E. coli/-	2wsx/-	9
BCCT/AA	Corynebacterium/Salmonella	2wit/3ncy	8
BCCT/-	Proteus mirabilis/-	2wsw/-	10
BCCT/-	E. coli/-	2wsx/-	8
BCCT/BCCT	Proteus mirabilis/E. coli	2wsw/2wsx	89
BCCT/BCCT	Proteus mirabilis/Corynebacterium	2wsw/2wit	25
AA/AA	Methanocaldococcus/E. coli	3gia/3l1l	18
AA/AA	Methanocaldococcus/Salmonella	3gia/3ncy	16
AA/AA	E. coli/Salmonella	3l1l/3ncy	82

Fig. 4 A and B present our knotting analysis of the LeuTAa and BetP proteins. The matrix presentations show that the entire proteins are slipknots (i.e., the entire chains form unknots), but contain distinct subchains that form 4₁ and 3₁ knots. Fig. 4C shows the essential geometric features of these proteins. This figure shows how the truncation of the N terminus creates subchains forming 3₁ knots and how the truncation of the C terminus creates fragments forming 4₁ knots. Interestingly, one must clip both ends of the fragment forming the 4₁ knot to convert it to a fragment that forms the 3₁ knot. The schematic drawings in Fig. 4C also explain why extending the C-terminal portion of the protein forming the 3₁ fragment leads first to slipknotted fragments and only later reestablishes the 3₁ knot. Fig. 4 A and B show that, to pass from the 4₁ knot territory to a 3₁ knot territory, one must pass through an unknot territory. This behavior is consistent with the fact that the 3₁ and 4₁ knots are strand passage distance two from each other.

Our analysis of the PDB entries reveals that this complex knotting is conserved across different families of transmembrane proteins and across widely divergent microbes (see Table 3). All of these proteins are membrane cotransport proteins. They share a five-helix inverted repeat motif, which has recently emerged as one of the largest structural classes of secondary active transporters. The similarity between these proteins is shown in Table 3, whereas explanations of abbreviated names of corresponding protein families are listed in the SI Appendix. All of these newly characterized slipknot-forming proteins share less than 23% similarity and less than 12% identity to other members of the SNF family. The lowest sequence identity, 6%, is observed between SSF (Vibrio parahaemolyticus) and AA-permease (Salmonella), based on ref. 42. The fact that all of these proteins show very similar knotting fingerprints despite their large sequence divergence suggests that this particular knotting offers an evolutionary advantage. A number of papers have shown that the formation of knots and slipknots increases protein stability (7, 12) because there are protein subchains that embrace other subchains in a stable manner. In this context, one is tempted to speculate that, in case of transporter proteins forming a transmembrane channel, the channel may be held together more tightly when α-helices forming it are strapped together by a slipknot loop embracing several of the helices.

Zigzag Trefoil Slipknots.

An interesting knotting fingerprint consisting of a horizontal row of 3₁ islands is visible in Fig. 5. We observed this fingerprint in several bactoriocin proteins that belong to two different protein families: Cloacins and S-Pyocins. Cloacins and S-Pyocins are bacterial toxins that are released by some bacteria and enter other bacterial cells via membrane translocation (see Table 4 for the sequence identity for proteins in this class). Fig. 5 illustrates the connection between structure and knotting in the case of Colicin E3. The entire protein chain is unknotted. However if approximately 260 amino acids are clipped from the C terminus, the remaining fragment forms a 3₁ knot. If this protein fragment is then progressively clipped from its N terminus, one observes several fragments in which 3₁ knots appear, disappear, and reappear. Drawings presenting the essential geometric features of Colicin E3 help to explain how this behavior occurs. When the current C terminus and N terminus find themselves on the same side of the imaginary surface spanning the large loop running around the helically arranged C-terminal portion, the segments are unknotted. However, if the current C terminus and N terminus find themselves on opposite sides of our imaginary surface, then the segments form 3₁ knots. By visualizing the geometric reasons for this sequential disappearance and reappearance of 3₁ knots, we named this knotting motif a zigzag trefoil slipknot. This motif arises as a consequence of the large loop embracing other parts of the structure. One could expect such an arrangement to stabilize the relevant parts of the protein molecule.

Table 4.

Sequence identity between proteins with zigzag motif, S3₁3₁3₁3₁

Name/name	PDB/PDB	ID%
ColE7/ColE7	2axc/2bau	62
CoLE7/protein B	2axc/1rh1	24
ColE7/ColE3	2axc/1jch	29
Protein B/ColE7	1rh1/2bau	20
Protein B/ColE3	1rh1/1jch	10
ColE3/ColE7	1jch/2bau	68

Knotting Fingerprint of Proteins with Simple Knot Types

There is a relatively large group of proteins that can be classified as 3₁ knots or which show the presence of a single 3₁ slipknot region in their backbones. The knotting notation of these proteins would then be simply K3₁ or S3₁, respectively. When one looks closely at their knotting fingerprints, we see that these proteins separate into clearly distinct groups (see SI Appendix, Tables S1 and S2). As might be expected, knotted proteins belonging to the same family show similar knotting fingerprints, whereas proteins belonging to different families vary greatly in their knotting fingerprints despite the fact that they have the same overall knotting notation. The strong conservation of the knotting fingerprint, despite significant sequence variance within the individual families of proteins containing simple knots and slipknots, indicates that these relatively simple knotting motifs carry an important functional advantage that has been maintained during their evolution.

The Borders of Knotted Domains Coincide with the Position of Conserved Hinge Sites, Which Are Important for Folding of Knotted Proteins

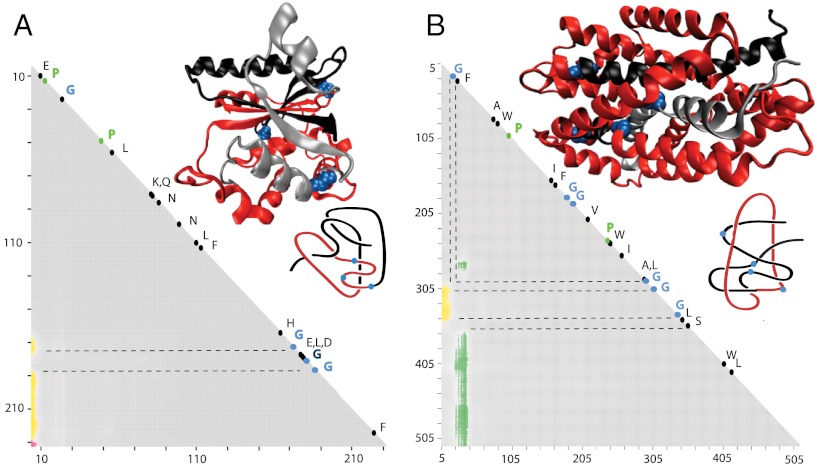
To understand how knotting fingerprints can be conserved in related knotted proteins with largely diverging sequences, we investigated the location of conserved amino acids in these proteins. We are interested especially in understanding which structural elements correspond to the regions of the knotting fingerprints where a small change in the length of the analyzed subchain leads to the formation of unknots, whereas a further length change leads to the formation of the original knot type or of another knot type. In Fig. 6, these regions of the knotting fingerprints and the corresponding portions of polypeptide chain are marked with dashed lines.

Fig. 6.

Sequence conservation in related proteins with complex knotting fingerprints. (A) Ubiquitin C-terminal hydrolase (knot notation K5₂3₁3₁). (B) Five families of proteins with knotting notation S3₁4₁3₁ (see Table 1). The positions of the protein regions where varying the length of the analyzed subchain leads to a passage from a knot to the unknot and then again to a knot are indicated with dashed lines. These regions show strong sequence conservation with a high proportion of conserved glycines. The placement of these glycines can be seen in the molecular structures of representative proteins belonging to the analyzed groups (Yuh1 and LeuT for A and B, respectively) and also on the schematic drawings.

First, we analyzed the location of strictly conserved amino acids in five proteins from the family of ubiquitin C-terminal hydrolases, all of which have the same knotting notation K5₂3₁3₁ (see Table 1). Three of these proteins are of human origin, one is from yeast, and one is from Plasmodium falciparum (see Table 1). Fig. 6A shows the location of all 19 strictly conserved amino acids in these five proteins (the alignment was done using the program Muscle with manual adjustments; ref. 43) and how their position relates to the knotting fingerprint of yeast ubiquitin C-terminal hydrolase. One 15 amino acid long protein region (marked by two dashed lines in Fig. 6A) is highly conserved as it groups six strictly conserved amino acids. This amino acid grouping is the region in which changing the length of the analyzed polypeptide chain leads to a passage from a 3₁ knot to an unknot and again to a 3₁ knot. Among these six conserved amino acids are three glycines, which are known to preferentially locate in protein hinge sites (44). Indeed, an inspection of secondary structure plots of C-terminal hydrolases (http://www.rcsb.org/pdb/explore/remediatedSequence.do?structureId=1cmx) reveals that these three glycines are located in protein regions with high potential flexibility.

Subsequently, we analyzed the sequence conservation within the proteins with the next most complex knotting notation—i.e., S3₁4₁3₁ (see Table 1). Because very similar knotting fingerprints were observed within five protein families (SNF, NCS1, AA-permease, SSF, and BCCT), we compared protein sequences of all nine proteins from these families for which the structure is known. Because the sequence conservation of proteins from different families is generally low, we consider as “highly conserved” those amino acids that were present at least six times in a given position within the aligned sequences of the nine proteins. Fig. 6B shows the location of all the amino acids that fulfilled these criteria. In the case of proteins with the knotting notation S3₁4₁3₁ there are three protein regions where changing the length of the analyzed subchains leads to unknotting, whereas a further length change produces a knotted state (these regions are marked by dashed lines on Fig. 6B). Whereas the entire N-terminal portion is necessary to form a 4₁ slipknot, trimming about 25 amino acids from the N-terminus precludes the formation of any knotted structures. A further trimming allows the formation of 3₁ knots. Interestingly, in the narrow interval transitioning from the 4₁ knot to the unknot and then to the 3₁ knot, we observe one of the highly conserved glycines. In the C-terminal halves of these proteins there are two approximately 20 amino acid long regions where changes in the analyzed subchain length result in a change from the 3₁ knot to the unknot and then to the 4₁ knot (or vice versa). In one of these regions, we observe two highly conserved glycines, whereas the second region contained one highly conserved glycine. An inspection of the secondary structure plots (http://www.rcsb.org/pdb/explore/remediatedSequence.do?structureId=2A65) reveal that at least three out of four of the highly conserved glycines can be involved in hinge formation.

For other proteins with complex knotting signatures, the number of related proteins that have been crystallized is too small for a meaningful analysis of sequence conservation. Our analysis of sequence conservation in proteins with very similar knotting fingerprints reveals that glycines were most frequently represented among conserved amino acids (10 out of 31, see Fig. 6). This very high proportion of conserved glycines may seem surprising because the majority of conserved glycines are located in regions that are likely to serve as hinge sites, which in general are known to have a low sequence conservation (44). However, as the folding of proteins forming knots and slipknots is more complex than that of proteins with trivial knotting, it is likely that hinges involved in their folding may need special properties that require much stricter sequence conservation. In fact, an earlier study that used coarse grained molecular modeling to follow the folding of knotted proteins showed that sharp turns involving glycines and prolines are instrumental in correctly folding knotted proteins (5).

Discussion

Our comprehensive analysis of proteins with complex knotting shows that not only is the overall knot type formed by these proteins conserved but also the precise relative positions of the protein segments forming the knot, which as such determine knotting fingerprints of the knotted proteins. This knotting conservation persists despite significant sequence divergence within the respective protein families. Interestingly, the strongest sequence conservation is observed in protein regions that are likely to serve as hinges during the folding of knotted proteins. Protein hinges or flexible joints regions are generally known to show very poor sequence conservation among proteins belonging to the same family but we observed an opposite trend for related knotted proteins. The instrumental role of hinges or flexible joints in the folding of knotted proteins was noted in earlier studies (27). Our observation of high sequence conservation within hinges in knotted proteins indicates that these hinges have some special properties that are crucial for efficient folding. Further studies will be needed to elucidate the role of these conserved hinges in the process of folding knotted proteins.

We have discovered two previously unknown families of knotted proteins and five families of proteins with slipknots (see Table 1 and SI Appendix, Tables S1 and S2). To our knowledge, this brings the number of distinct protein families where the native backbone can be thought of as forming a knot to 18, and the number of distinct protein folds with slipknots to 17. In the five families of proteins that form transmembrane transporting channels, the slipknot loops seem to strap together several of transmembrane α-helices. This architecture may stabilize the channels during their transporter and symporter action. It is known that, for entropic reasons, knots in random walks have the tendency to form tight-knotted domains (31, 45). It is therefore possible that some pathways of protein knotting may preferentially form tight protein knots. Furthermore, territories of distinct knot types in direct contact in the matrix representations were knot types that were strand passage distance one from each other, something that had not been recognized to date. Because descriptors such as knot types are more global than the geometrical descriptors used to determine fold types, our analysis reveals an additional level of functional significance in protein structures.

Materials and Methods

The PDB dataset (28), as of April 16, 2011, contained 74,223 entries. From the resulting dataset, we retained all proteins with chain length more than 45 aa. In addition to previous studies (4, 25), we accepted chains with more than 1,000 aa and sequences with some missing C^α coordinates. In the case of protein structures with unresolved parts, we “inserted” the missing portions by modeling the structure or by adding a straight line connection. In the modeling procedure, the proteins missing segments shorter than 10 aa were reconstructed based on ref. 46. However, cases such as UCHL1, when 23 C^α atoms were unresolved, were modeled based on sequence similarity or geometrical similarity using software (47). In cases where the missing portions could be connected unambiguously by a straight line (without introducing a steric clash with the rest of structures), we simply added such a line segment. This procedure resulted in a total of 42,389 protein chains. The longest chain in our dataset has 1,223 aa.

As a first step in identifying knots and slipknots in the dataset of 42,389 proteins, we applied the Koniaris–Muthukumar–Taylor algorithm (34). This dataset was further evaluated, as described below, in order to detect only correctly knotted and slipknotted proteins. We computed the knot distribution for each subchain of each protein as follows: For each protein subchain, we create 100 closed knots by connecting the endpoints of the subchain to 100 points on a large sphere. This sphere is centered at the center of mass of the entire protein’s C^α atoms and the radius is 100 times the greatest distance from the center of mass to any C^α atom. Although previous papers had used random points on the sphere, individual samples from random distributions are rarely uniform. Thus, we used software (http://members.ozemail.com.au/~llan/mpol.html) to generate a (nearly) uniform set of 100 points on a unit sphere, and then rescaled them to be points on the large sphere.

For each of the 100 closed knots formed per subchain, we computed the HOMFLYPT polynomial (48, 49) using the Ewing–Millett program (50) to determine the knot type. Although the HOMFLYPT polynomial cannot separate all knot types (i.e., there are different knot types with the same HOMFLYPT polynomial), the knot types found in proteins (to date) have been quite simple, so the HOMFLYPT polynomial does not misclassify knot types. We then compute the percentage of the closures forming each knot type and classify the knot type of the subchain, indicated by the color of the square, to be the knot type with the highest percentage.