Anomalous diffusion and dynamical correlation between the side chains and the main chain of proteins in their native state

Abstract

Structural fluctuations of a protein are essential for a protein to function and fold. By using molecular dynamics (MD) simulations of the model α/β protein VA3 in its native state, the coupling between the main-chain (MC) motions [represented by coarse-grained dihedral angles (CGDAs) γ_n based on four successive C^α atoms (n - 1, n, n + 1, n + 2) along the amino acid sequence] and its side-chain (SC) motions [represented by CGDAs δ_n formed by the virtual bond joining two consecutive C^α atoms (n, n + 1) and the bonds joining these C^α atoms to their respective C^β atoms] was analyzed. The motions of SCs (δ_n) and MC (γ_n) over time occur on similar free-energy profiles and were found to be subdiffusive. The fluctuations of the SCs (δ_n) and those of the MC (γ_n) are generally poorly correlated on a ps time-scale with a correlation increasing with time to reach a maximum value at about 10 ns. This maximum value is close to the correlation between the δ_n(t) and γ_n(t) time-series extracted from the entire duration of the MD runs (400 ns) and varies significantly along the amino acid sequence. High correlations between the SC and MC motions [δ(t) and γ(t) time-series] were found only in flexible regions of the protein for a few residues which contribute the most to the slowest collective modes of the molecule. These results are a possible indication of the role of the flexible regions of proteins for the biological function and folding.

The motions of the side chains and of the backbone of a protein are coupled to each other in protein folding. The removal of the nonpolar side chains from the solvent in protein folding orients the backbone locally (1), and the formation of the backbone hydrogen bonds between residues in the secondary structures induces displacements of their side chains. Therefore, in order to understand protein folding, it is necessary to understand how the motions of the side chains are propagated to the backbone and vice versa. As a prerequisite, it is necessary to understand how the motions of the side chains are coupled to those of the main chain in the native state of a protein. To address this question, five 80 ns all-atom molecular dynamics (MD) simulations of a 46-residue α/β model protein VA3 (PDB: 1ED0) (2) in its native state were analyzed. Protein VA3 was chosen here because it is highly homologous to the well-studied protein crambin, but unlike crambin (3), it is soluble in water (2).

To express the correlation between the main-chain and the side-chain motions quantitatively, two coarse-grained dihedral angles (CGDAs) were defined for each residue n (Fig. S1A). The angles characterizing the fluctuations of the main chain are the CGDAs γ_n (4–6) formed by the virtual bonds joining four consecutive C^α atoms (n - 1, n, n + 1 and n + 2) along the amino acid sequence with 2 ≤ n ≤ N - 2 and N being the number of residues (Fig. S1A). The angles γ_n are coordinates used to describe large changes of protein conformation (7) and are part of coarse-grained models of proteins (8, 9). The angles characterizing the fluctuations of the side chains are defined by the CGDAs δ_n (1 ≤ n ≤ N - 1) formed by the virtual bond joining two consecutive C^α atoms (n, n + 1) and the bonds joining these C^α atoms to their respective C^β atoms (Fig. S1A). For the residue glycine, the side-chain H atom was defined as a pseudo-C^β atom.

To monitor the fluctuations of the side chains, the displacements of the C^β atoms (and pseudo C^β in glycine) of the residues were chosen because they are the atoms of the side chains nearest to the backbone atoms. Consequently, their motions should be strongly related to those of the main chain. Assuming rigid covalent bonds, this coupling can be understood as follows. Because the C^α(n) atom is an sp³-hybridized atom, motion of the C^α(n)─C^β(n) bond of residue n (modifying the CGDA δ_n) induces the displacements of the N(n)–C^α(n) and C^α(n)–C^′(n) backbone bonds (C′ and N atoms are defined in Fig. S1A). Because of the rigidity of the peptide plane and the partial double bond character of the C^′(n-1)─N(n) and C^′(n)─N(n + 1) bonds, the motion of the C^α(n)─C^β(n) bond propagates at least to residues n - 1 and n + 1 (modifying the CGDA γ_n). The coupling between the motions of the C^α─C^β bonds and those of the amide and carbonyl bonds of the backbone also depend on the bond-length and bond-angle deformations, on the noncovalent interactions between the atoms, on the nature of the residue, and on the interactions of the protein with the solvent. Therefore, the magnitude of the correlation between the side-chain motions (measured here by δ_n) and the main-chain motions (measured here by γ_n) should vary along the amino acid sequence.

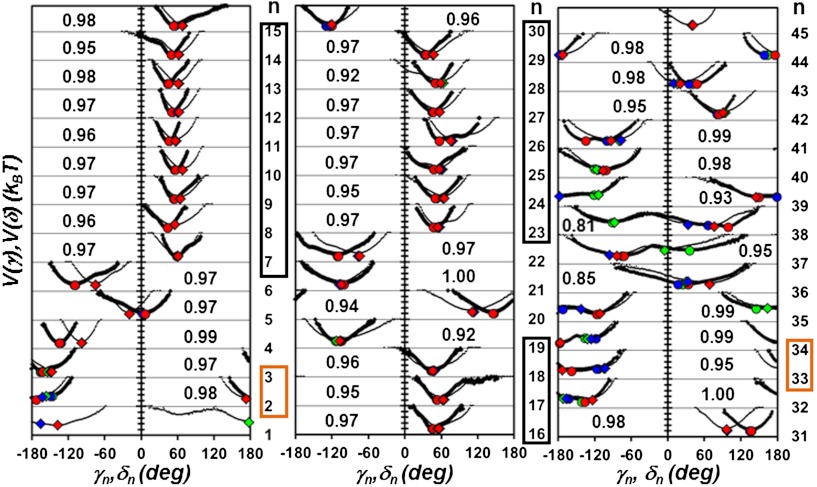
In order to quantify and to understand the coupling between the side chains and the main chain of a protein in its native state, the effective 1-D free-energy profiles (FEPs) V(δ_n) and V(γ_n) (5, 6) along the amino acid sequence of the model protein VA3 (Fig. 1) were first compared. The FEPs were computed over the whole MD runs by using V(δ_n) = -kT ln[P(δ_n)] and V(γ_n) = -kT ln[P(γ_n)], where k and T = 300 K are the Boltzmann constant and temperature, respectively, and P(δ_n) and P(γ_n) are the probability distribution functions (PDFs) of each CGDA δ_n and γ_n (5, 6). As shown in Fig. S2, the FEPs V(δ_n) and V(γ_n) of each residue n were found to be highly correlated [the standard correlation coefficient R (10) averaged along the amino acid sequence is 0.90; see Results section]. This result, as expected, reflects the local constraints imposed by the sp³ hybridization of the C^α atoms on the δ_n and γ_n motions.

Fig. 1.

Effective FEPs V(γ_n) (thick lines) and V(δ_n) (thin lines) computed from MD along the primary sequence (γ_n, n = 2 to 44 and δ_n, n = 1 to 45). The FEPs computed from the five concatenated MD runs (400 ns) are shown. Residues n located in a helix are in a black box and residues located in a β-sheet are in an orange box. For each residue n, the number in the inset is the value of the similarity index h between the FEPs V(γ_n) and V(δ_n) defined in the Results section: Comparison of the FEPs of the CGDAs. The circles and the diamonds represent respectively the maxima of the distributions of the angles γ_n and δ_n computed in each of the three states defined on the free-energy surface of the principal components PC₁/PC₂ defined in the Discussion section: Main-chain motions, side-chain motions and collective modes. The state 1 is indicated by a red symbol, the state 2 is indicated by a blue symbol and the state 3 is indicated by a green symbol.

The similarity between the equilibrium properties V(δ_n) and V(γ_n) does not imply that each point of these FEPs is explored at the same time; i.e., this comparison does not provide any information about the possible dynamical coupling between δ_n and γ_n. To examine the dynamical correlation, the analogy between the fluctuations over time of a dihedral angle; for example γ_n, and Brownian motion on a unit circle (5, 6) (Fig. S1B) is exploited. Since each dihedral angle is coupled to a huge number of microscopic degrees of freedom, its temporal evolution is a stochastic process. The time-evolution of each γ_n(t) [or δ_n(t)] extracted from each MD run is interpreted as the random walk of a fictitious particle on a unit circle; the particle makes a random angular jump of amplitude Δγ_n(t) = γ_n(t + δt) - γ_n(t) [or Δδ_n(t) = δ_n(t + δt) - δ_n(t)], at each time step δt for which the MD run is recorded (δt = 1 ps in refs. 5 and 6 and in the present work). The mechanism of transport of the particle along the circle, due to random fluctuating torques, is characterized by its Mean-Square-Displacement (MSD) and Rotational Correlation Functions (RCFs) (6). The RCFs associated with γ_n are related to the position u_n(t) of the fictitious particle on the circle where u_n(t) = { cos[γ_n(t)], sin[γ_n(t)]} (Fig. S1B). For circular geometry, the RCFs are defined (6, 11) as

[1]

where T_l(x_n) is a Tchebychev polynomial of order l (11). In the present work, the second-order RCFs, T₂(x) = 2x² - 1, were analyzed [results for T₁(x) = x contain similar information (6)]. In Eq. 1, x_n ≡ u_n(t^′)•u_n(t^′ + t) is the cosine of the angular displacement Δγ_n of u_n between t^′ and t^′ + t, and T_l is averaged over all possible initial orientations (at all times t^′). The RCFs of δ_n are defined similarly by Eq. 1 in which the vector u_n(t) = { cos[δ_n(t)], sin[δ_n(t)]}.

It was previously established that the MSD of the random walker, associated with the temporal fluctuations of each γ_n, is a power law of time: MSD(t) = 2D_αt^α, with a diffusion constant D_α and an exponent α < 0.4 depending on n (5, 6). As shown in ref. 6, the RCFs associated with u_n decay as stretched exponentials (SEs): C_l,n(t) = exp(-l²D_αt^α) (6). The quantity 2D_α is the variance of the distribution of the random angular jumps Δγ_n(t) of the random walker, and the exponent α is related to the speed of the diffusion (6). An exponent α < 1 corresponds to a subdiffusive regime (12–15) previously observed in fluorescence experiments (16) and in MD simulations (5, 6, 17–19) of proteins. The subdiffusion means that the random walker has a memory of its past (13). In other words, the random torques which push the walker back and forth on the circle are correlated in time (16).

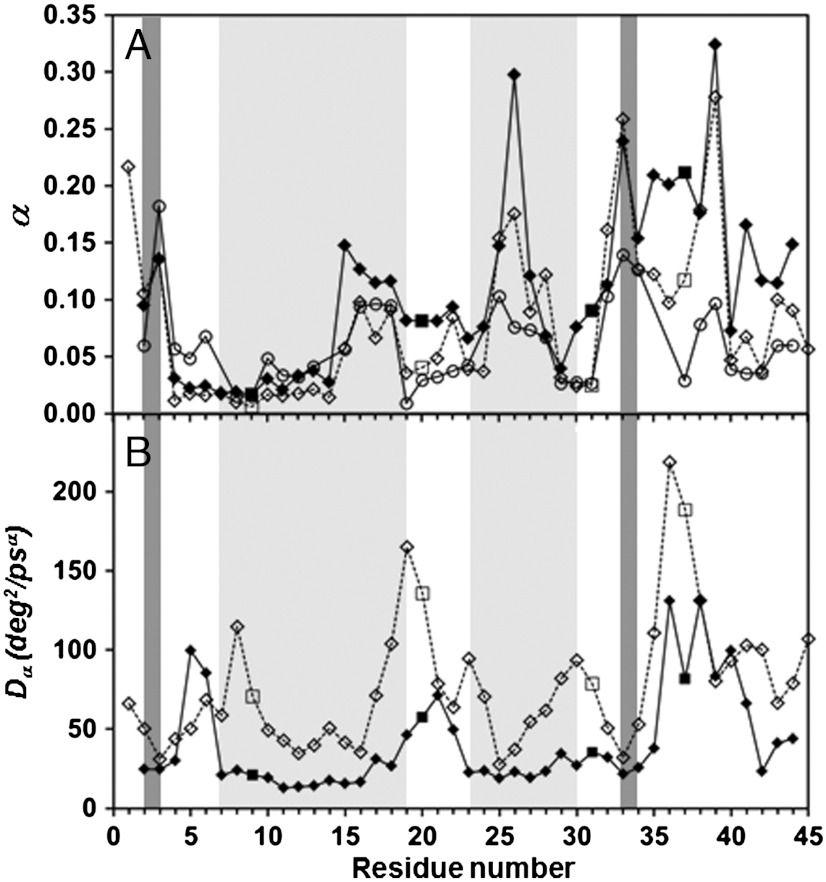
It is found here that the side-chain motions, characterized by δ_n, are also subdiffusive. The RCFs of δ_n computed from MD runs (Eq. 1, l = 2) decay as an SE, i.e., C_2,n(t) = exp(-4D_αt^α) (Fig. S3), with α and D_α varying along the amino acid sequence (Fig. 2). The side chains and the main chain diffuse in quite a similar way: the correlation coefficient R computed between the exponents α of the RCFs of the γ_n and those of the RCFs of the δ_n angles, averaged along the amino acid sequence of VA3, is R = 0.87. The correlation coefficient R computed between the diffusion constants D_α of the RCFs of these CGDAs, averaged along the amino acid sequence of VA3, is R = 0.55.

Fig. 2.

Comparison of the exponents α (A) and diffusion constants D_α (B) of the angles γ_n (filled diamonds and squares for Gly residues) and δ_n (empty diamonds and squares for Gly residues) extracted from the fits of the RCFs T₂ up to 1 ns by using a stretched exponential, exp(-4D_αt^α) along the amino acid sequence of VA3. Results for MD run 1 are shown. The α-helices and β-sheets are indicated by light gray and dark gray stripes, respectively. The empty circles in (A) represent the exponents β computed from R_n(M) for the MD run 1 (see Discussion: Correlation between the CGDA trajectories and steps).

The FEPs (Fig. 1) and the parameters characterizing the diffusion on these FEPs (Fig. 2) are quite similar for the side chains (δ_n) and the main chain (γ_n). One could conclude naively that the two random walkers, moving on a circle and representing the temporal fluctuations of γ_n and δ_n, respectively (Fig. S1B), are most likely making steps in the same direction at the same time. Consequently, one could expect that the time series γ_n(t) and δ_n(t) extracted from the MD runs (named here, in short, these time series γ_n(t) and δ_n(t) trajectories) should be highly correlated. To express this correlation of the motions between the side chain and the backbone at residue n quantitatively, the coefficient R between the steps that the walkers are performing on the δ_n and γ_n circles (Fig. S1B) is computed in the five MD runs. For each MD run, the correlation coefficient R between the steps of the walkers, averaged over the amino acid sequence, is not very high and varied widely between residues (R_avg = 0.42, R_min = 0.1 for n = 3 (CYS), and R_max = 0.63 for n = 36 (SER) in MD run 1 for example). On the contrary, the correlation between the γ_n(t) and δ_n(t) trajectories, computed over 80 ns for each of the five MD runs and averaged over the amino acid sequence, is quite high, but also varies significantly between residues (R_avg = 0.68, R_min = 0.33 for n = 7 (THR), and R_max = 0.99 for n = 38 (SER) in MD run 1, for example). In fact, it was found that trajectories of the side chains [δ_n(t)] and of the main-chain [γ_n(t)] are highly correlated (R ∼ 1) only for a few residues n along the sequence. It is demonstrated here that the correlation between the side-chain and main-chain motions around a residue n depends on its location and not on its nature.

The question arises as to whether residues with a high correlation between the motions of their side chains (δ_n) and of the main chain (γ_n), which are scattered along the amino acid sequence of the protein, also have motions that are coupled to each other through space. To answer this question, a dihedral principal component analysis (dPCA) of the trajectories of the CGDAs (20) was carried out. The dPCA facilitates a projection of the dihedral-angle coordinates of a protein on a few relevant coordinates along which the FEPs and the collective modes of the protein can be analyzed (20–22). By using dPCA, it is demonstrated that the trajectories of the side chains [δ_n(t)] follow those of the main chain [γ_n(t)] (i.e., R ∼ 1) for the residues which contribute the most to the slowest modes of the protein. This conclusion is particularly interesting because the slowest modes of a protein are the ones important for its biological function (23–27). Because the slowest modes of a protein in its native state are the easiest to excite thermally, they should also play a role in the early events of the thermal unfolding of a protein.

Results

Comparison of the FEPs of the CGDAs (Fig. 1).

The minima of the FEPs, V(δ_n) and V(γ_n), are in good agreement with the values of the CGDAs computed from the NMR-derived structures (2) and x-ray structures (PDB: 1OKH) (28) (Fig. S4). The largest deviations compared with the experimental data were found for δ₁, δ₃, δ₂₈, δ₃₅, γ₃₆, γ₃₇, γ₃₈, and γ₄₂ (compared with NMR), and for γ₆, γ₃₅, γ₃₇, γ₃₈, δ₃₈, γ₄₂, and δ₄₂ (compared with X-ray); the CGDAs at n = 1, 35–38 are the angles which are significantly different in the NMR and x-ray structures (Fig. S4). The potentials in helices (Fig. 1) are found to be rather harmonic (except n = 15, 25, 26) with a minimum approximately 50° for V(γ_n) and approximately 60° for V(δ_n), as expected for a canonical right-handed α-helix [for an α-helix (ϕ = -57°, ψ = -47°), γ = 52° and δ = 70°]. The potentials of residues in the antiparallel β-sheet have a minimum close to ± 180° as for a canonical β-sheet [for a antiparallel β-sheet (ϕ = -139°, ψ = 135°), γ = δ = 178°]. Several CGDAs γ_n and δ_n for n = 26, 34, 35, 37, 38, 39, 41 move on a multiple-minima potential; they are located in loops/turns except for n = 26 and 34 (6). In addition, the N-terminal potential V(δ₁) has two minima. As shown in Fig. 1, the FEP of each CGDA δ_n is quite similar to the FEP of the corresponding angle γ_n: the anharmonic potentials with single or multiple minima were found for the same n. In order to quantify the similarity between V(δ_n) and V(γ_n) along the amino acid sequence, these two potentials were aligned on their deepest minimum for each value of n (Fig. S2). The correlation coefficient R (10) between the aligned FEPs and an index of similarity h between the corresponding PDFs were computed. The index h varies between 1 (similar) and 0 (dissimilar). The index h was adapted from ref. 29 and is defined in the SI Text: Calculation of the Pearson Correlation Coefficient R and Similarity Index h for the FEPs. Whereas the coefficient R (10) measures the similarity of the shapes of two functions (a function scaled by a constant factor is perfectly correlated to itself), h rather measures their absolute similarity (29). Because of the definition of h (SI Text), the low values of the PDFs (the less statistically relevant data extracted from MD corresponding to the highest values of the potentials) have a small weight in the computation of the similarity. The FEPs were found to be highly correlated [R ∼ 0.8–1.0 (Fig. S2), except n = 3 (R = 0.65)] and their PDFs highly similar [h ∼ 1 (Fig. 1), except n = 36 (h = 0.85) and n = 38 (h = 0.81)].

Comparison of the RCFs of the CGDAs.

All the RCFs 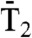of the 43 angles γ_n (6) and of the 44 angles δ_n of VA3 were computed up to 1 ns by using Eq. 1 as in ref. 6. The RCFs are converged on this time-scale (6). Three typical RCFs found for the CGDAs δ_n are identified and are represented in Fig. S3 for the MD run 1 [representative of all runs (6)]. As for the CGDAs γ_n (6), the RCFs are grouped into three types corresponding to three types of FEP V(δ_n) (all shown in Fig. S4). As shown in Fig. S3, the RCF of the CGDA δ_n converges in a few ps to a value close to 1 for a stiff harmonic FEP (as for δ₁₁) (first type) or to a value between 0.7 and 0.9 for a wide or anharmonic single-minimum FEP (as for δ₂₀) (second type), and does not converge on a time-scale of 1 ns for a multiple-minima FEP (as for δ₃₉) (third type). As for the CGDAs of the main chain (6), the RCFs of the CGDAs of the side chains are also extremely well represented by a SE, 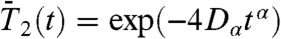(dashed line in Fig. S3).

Typical results for the parameters [α, D_α] of the SE fitted on the RCFs up to 1 ns are shown in Fig. 2 for the MD run 1 for each CGDA γ_n and δ_n. The exponent α, measuring the speed of the spread of the PDF of the CGDA with the time elapsed (6), varies in an extremely similar manner along the amino acid sequence for the CGDAs γ_n and δ_n (correlation coefficient R = 0.87). The exponent α associated with side-chain diffusion is the largest for a multiple-minima V(δ_n) potential (n = 1, 26, 33 and 39, Fig. 2A and Fig. S4) and the lowest for strongly harmonic potentials located in the secondary structures (for example, n = 11, Fig. 2A and Fig. S4), as observed previously for the diffusion of the main chain (6). The exponent α is smaller for δ_n than γ_n for most of the residues n (Fig. 2A), which means (13, 14) that the successive jumps of the side chains (δ_n) are more correlated than the segmental motions of the main chain (γ_n) for these residues. Fig. 2 demonstrates that both the side-chain and the main-chain motions correspond to subdiffusion (α < 1) (13). The smallest diffusion constants of the side-chain and main-chain CGDAs are found in helices (Fig. 2B). Except for n = 5 and 6, the diffusion constant D_α (Fig. 2B) is larger for the side-chain motions than for the main-chain motions, indicating that the side chains are making larger angular displacements than the main chain, which is more constrained. The highest diffusion constants D_α correspond to the CGDAs δ_n located at n = 8, 19, and 36 (they involve the motions of Gly9, Gly20 and Gly37).

Dynamical Correlation Between the Main-Chain (γ_n) and Side-Chain (δ_n) Motions.

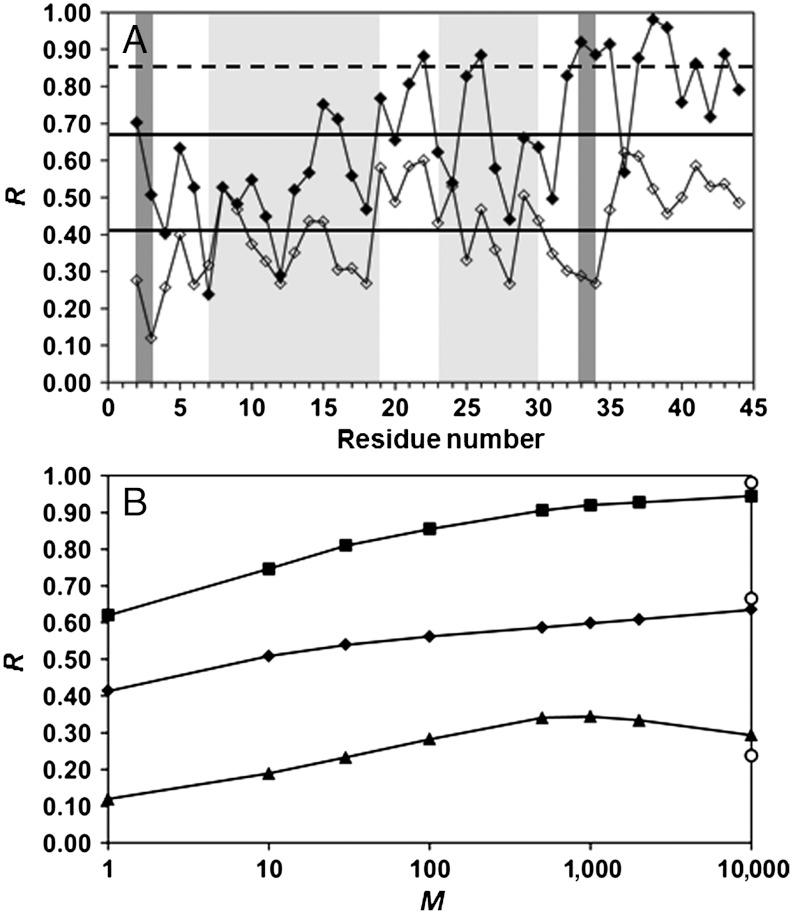
The CGDAs of the main chain and of the side chains diffuse in a similar way (the values of α and D_α of their RCFs are similar) and on very similar FEPs (h between their FEPs is very high). Based on the definition of δ_n and γ_n (Fig. S1) and on the sp³ hybridization of the C^α atom (see Introduction), one could imagine that each δ_n angle follows the motion of the corresponding γ_n angle in the course of time, and that both CGDAs thus explore the same region of their respective FEPs at the same time. In order to test this hypothesis, the correlation coefficient R between the time series of the angular steps Δγ_n(t) and Δδ_n(t) extracted every ps from the MD runs (see Introduction), was computed for each value of n (see Eq. S1). The results are represented in Fig. 3A. The value of R calculated between the time series Δγ_n(t) and Δδ_n(t) varies from R_min = 0.12 (n = 3, CYS) to R_max = 0.62 (n = 36, SER) with a low average value R_avg = 0.41 (the standard deviation σ computed over the amino acid sequence is 0.12). By contrast with these results, the average correlation coefficient R computed between the γ_n(t) and δ_n(t) trajectories is rather high: R_avg = 0.67 (Fig. 3A), but also varies widely along the primary sequence: R_min = 0.24 (n = 7, THR) and R_max = 0.98 (n = 38, SER) (σ computed over the amino acid sequence is 0.19). The coefficients R computed between the δ_n(t) and γ_n(t) trajectories and the Δγ_n(t) and Δδ_n(t) time series follow the same trends qualitatively along the amino acid sequence with exceptions; for example, between n = 32 and 34 (Fig. 3A). Regions of the protein, for which R computed between the δ_n(t) and γ_n(t) trajectories is larger than R_avg + σ (shown by a dashed line in Fig. 3A), are located in loops (except n = 26, 33, and 34). One concludes that the angular steps Δγ_n(t) and Δδ_n(t) are poorly correlated compared with the trajectories δ_n(t) and γ_n(t), which are highly correlated only for few residues.

Fig. 3.

(A) Comparison of the correlation coefficient R between the trajectories γ_n(t) and δ_n(t) (filled symbols) and between the steps Δγ_n(t) and Δδ_n(t) (empty symbols) along the amino acid sequence of VA3. The α-helices and β-sheets are indicated by light gray and dark gray stripes, respectively. The full horizontal lines represent R averaged over the primary sequence (R_avg) for the steps (lowest) and for the trajectories (highest). The dashed line represents the value R_avg + σ = 0.85 for the trajectories. (B) Maximum (squares), average (diamonds), and minimum (triangles) values over the amino acid sequence of the correlation coefficient R_n(M) between the displacements Δγ_n(t; M) and Δδ_n(t; M) as function of the logarithm of the number M of steps. The value of R_n(M) was computed for M equals to 1, 10, 30, 100, 500, 1,000, 2,000, and 10,000. The values of R_max, R_avg and R_min computed between the γ_n(t) and δ_n(t) trajectories are shown for comparison (circles) at M = 10,000. All calculations were performed from the five MD runs (over 400 ns).

Discussion

Correlation Between the CGDA Trajectories and Steps.

How can the correlation coefficient between the CGDA trajectories (0.24 < R < 0.98) be significantly higher than the correlation coefficient (0.12 < R < 0.67) between the coarse-grained angular steps computed every ps (in particular, the values of R between n = 32 and 34 between the CGDA trajectories are larger by about 0.6 than the values of R computed between the CGDA steps; see Fig. 3A)? The values of δ_n(t) and γ_n(t) at time t are respectively the result of the sum of successive random steps Δδ_n(τ) and Δγ_n(τ) from time τ = 0 up to time t. If the correlation R is higher for the CGDA trajectories δ_n(t) and γ_n(t) than for the steps Δδ_n(t) and Δγ_n(t) computed at same time t, it would mean that the correlation coefficient between the trajectories increases as they are carrying out more steps. In other words, they are following the same “average” trajectories as time progresses. To test this hypothesis, two new sets of random steps Δγ_n(t; M) = γ_n(t + Mδt) - γ_n(t) and Δδ_n(t; M) = δ_n(t + Mδt) - δ_n(t) (δt = 1 ps) were generated from the MD runs for each value of M = 10, 30, 100, 500, 1,000, 2,000, 10,000, and each value of n represented in Fig. 3 (see SI Text: Calculation of the Pearson Correlation Coefficient R for the Dihedral Angular Steps for details). The time series Δδ_n(t) and Δγ_n(t) discussed in the Results section (R between these time series is shown in Fig. 3A) are, by definition, equal to Δγ_n(t; 1) and Δδ_n(t; 1). The data Δγ_n(t; M ≠ 1) [Δδ_n(t; M ≠ 1)] correspond to a new time series for which each step (every ps) is in fact the displacement of the angle γ_n [δ_n] between t-M and t ps. The values of R computed between Δγ_n(t; M) and Δδ_n(t; M) increase with M and converge to the values of R computed independently between the γ_n(t) and δ_n(t) trajectories [the variations of R_n(M) are shown for R_n(M)_avg, R_n(M)_min and R_n(M)_max in Fig. 3B and for each value of n in Fig. S5]. The convergence of R_n(M) is reached at M = 10 ns for all residues n, with small deviations between R_n(10 ns) and R computed between the trajectories for n = 2, 8, 9, 19, 25, 32–36 (Fig. S5). The slope of R_n(M) varies along the amino acid sequence (Fig. S5); for example, R_n(M) reaches a plateau at M = 30 ps for n = 9 and only at M = 10,000 for n = 27. As shown by Eq. S3 in the SI Text, 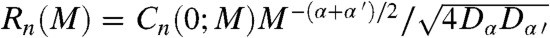, where the cross-correlation function C(0; M) is given by 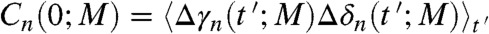with α and α^′ being the exponents of the time in the power-law MSDs of the CGDA γ_n and δ_n, respectively (5, 6). The average 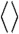is taken over all times t^′ in the whole MD run. It is worth noting that the exponents of the MSD were shown to be close to those of the RCFs given in Fig. 2 (6). For most of the residues (except n = 7, 14, 24, 35, 36), R_n(M) was found here to be approximated by a power-law of time: R_n(M) ∼ M^β. The exponent β was computed from a fit of R_n(M) by a power-law up to M = 1,000, for each residue n for which the power-law was found to be a good approximation. The approximate relation β ≈ α^′ ≈ α was found for most of the residues along the primary sequence (Fig. 2 and Fig. S5). This qualitative relation can be explained as follows. The most subdiffusive CGDA (low exponents in Fig. 2) are the CGDAs for which the RCFs, which involve the correlation between the steps [Eq. 1], converge quickly (< 1 ns) to a constant (for example, n = 11 and 20 in Fig. S3). For these CGDAs, the correlation coefficient between the steps Δγ_n(t^′; M) and Δδ_n(t^′; M) [C_n(0)] also converges to a constant quickly (small β, Fig. 2 and Fig. S5). In the opposite way, the less subdiffusive CGDAs (large exponents in Fig. 2) are those for which the RCFs do not converge to a constant in the ns time-scale (for example, n = 39 in Fig. S3). For these CGDAs, the correlation coefficient between the steps Δγ_n(t^′; M) and Δδ_n(t^′; M) [C_n(0)] does not converge to a plateau in the ns time-scale (high β, Fig. 2 and Fig. S5).

Main-Chain and Side-Chain Motions, Anharmonic FEPs, and Mean-Square-Fluctuations (MSF) of the CGDAs.

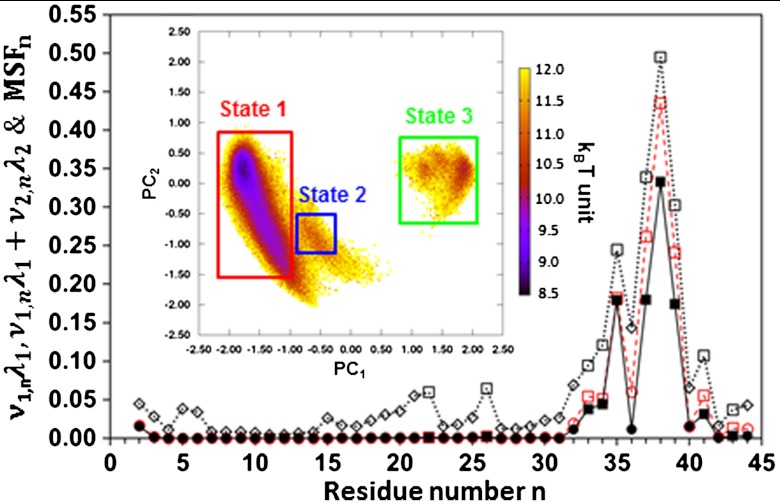
Why does the correlation coefficient R between the trajectories of the side chains [δ_n(t)] and of the main chain [γ_n(t)] vary so widely along the amino acid sequence (Fig. 3A)? The correlation coefficient does not depend on the nature of the residues. For example, the rotations of the side chains around the C^α atoms of the virtual bonds CYS4-PRO5 and CYS40-PRO41 correspond to different values of R: R = 0.4 (n = 4) and R = 0.76 (n = 40) (Fig. 3A). In fact, the correlation coefficient between the CGDA trajectories is very high (R > R + σ = 0.85) only for a few residues: n = 22, 26, 33–35, 37–39, 41, and 43. The FEPs of these highly correlated regions correspond either to wide single-minimum FEPs (n = 22, 33, 43) or multiple-minima FEPs (n = 26, 34, 35, 37–39, and 41) (Fig. 1). Wide FEPs correspond to values of R above the average; for example, n = 21 (R = 0.81) or n = 40 (R = 0.76). They therefore correspond to regions of large structural fluctuations of the protein (“flexible” regions), as demonstrated in Fig. 4 where we show the MSF of each vector u_n = { cos[γ_n(t)], sin[γ_n(t)]} (MSF_n) along the amino acid sequence (see SI Text: The Dihedral Principal Component Analysis). The motions of the main chain (γ_n) and of the side chains (δ_n) are less constrained in the flexible regions than in the rigid regions of the protein. This explains why the main chain can follow, on average, the side-chain motions and vice versa in these flexible regions. The correlation between the trajectories γ_n(t) and δ_n(t) is very low (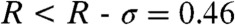) for a few residues (n = 4, 7, 9, 11, 12, 18 and 28), which are all located in a helix (except 4) and have low MSF_n (Fig. 4). Because the motions of the main chain are generally strongly restricted by the amide hydrogen bonds in a helix (the FEPs are stiff harmonic potentials as for n = 12 in Fig. 1), the main chain cannot follow the motion of the side chain, on average, in regions of low structural fluctuations of the protein.

Fig. 4.

Contribution of mode 1 (λ₁ν_1,n, filled diamonds and squares and full lines) to the MSF, contribution of modes 1 and 2 (λ₁ν_1,n + λ₂ν_2,n, red empty circles and red squares and red dashed lines) to the MSF, and MSF (empty symbols and dotted lines) along the amino acid sequence of VA3. CGDAs with multiple-minima potentials (Fig. 1) are shown by squares. The inset represents a color map of the FEL built from the principal components of modes 1 and 2 (PC1 and PC2). Three structural states 1 (red), 2 (blue), and 3 (green) were defined by the three rectangular regions in the FEL. All calculations were performed from the five MD runs (over 400 ns) by applying dPCA to the vectors u_n(t) = { cos[γ_n(t)], sin[γ_n(t)]}.

Main-Chain Motions, Side-Chain Motions, and Collective Modes.

The CGDA structural fluctuations MSF_n can be decomposed into collective modes by using dPCA (20–22). The modes have “frequencies” and directions corresponding to the eigenvalues and eigenvectors of the covariance matrix of the vectors u_n (20) (see SI Text: The Dihedral Principal Component Analysis). The modes with the largest eigenvalues λ_k (named slow modes) correspond to the modes which contribute the most to the structural fluctuations of the protein. The contribution of each CGDA n to a mode k is the so-called influence ν_k,n, and the (20–22).

As the highest correlation coefficients between the δ_n(t) and γ_n(t) trajectories were observed for residues n with high MSF_n (Fig. 4), one wonders if these residues contribute to the same slow collective modes. To answer this question, dPCA was applied to the vectors u_n(t) = { cos[γ_n(t)], sin[γ_n(t)]}. Only the two slowest modes with the largest eigenvalues λ₁ and λ₂ which contribute 37% and 13%, respectively, to the total MSF of the protein (i.e., the sum over n of the MSF_n) were considered. The other modes make much smaller contributions to the total MSF (for example, modes 3 and 4 contribute 7% and 3%, respectively).

In mode 1, the CGDAs γ_n contributing to the MSF_n (as λ₁υ_1,n) are located at n = 2, n = 32–41 as shown in Fig. 4; there are also small contributions at n = 25 and 26 which are hardly visible. The CGDAs n for which the trajectories γ_n(t) and δ_n(t) are highly correlated (R > R_avg + σ = 0.85), namely n = 22, 26, 32–35, 37–39, 41, and 43, are, remarkably, also those which contribute to the slowest mode (except n = 22, 26, and 43). The highest correlation coefficient between the motions of the side chains and of the main chain was found for n = 38 (Fig. 3A), which corresponds to the residue for which the amplitude of the CGDA γ_n is maximum in the slowest modes 1 (Fig. 4) and for which the FEP has the largest activation barrier (Fig. 1). Interestingly, mode 1 at n = 36 has a low amplitude (Fig. 4) compared with the other residues in the loop in which it is located. Similarly, the correlation coefficient between the side-chain and main-chain trajectories at n = 36 is low compared with the correlation coefficients of the other residues in the loop 34–44 (Fig. 3A).

The contribution of the first two modes to the MSF_n of the vectors u_n(t) is λ₁υ_1,n + λ₂υ_2,n and is also shown in Fig. 4. The most important contributions of mode 2 to the MSF occur for n = 32 to 39 and 41 to 44 (Fig. 4). Most of the CGDAs contributing either to mode 1 or mode 2 move on multiple-minima FEPs (Fig. 1), namely n = 34, 35, 37, 38, 39, and 41, and on wide anharmonic FEPs for n = 2, 32, 33, 36, 43, and 44. Thus, it is expected that modes 1 and 2 should correspond to jumps between the different substates of the multiple-minima FEPs along the amino acid sequence (Fig. 1). To test this hypothesis, the 2-D projection of the free-energy-landscape (FEL) of the protein along the directions of the eigenvectors of modes 1 and 2 (20–22) was calculated. The projections of the trajectories of the vectors u_n(t) extracted from the MD runs along the eigenvectors of modes 1 and 2 are the principal components PC₁(t) and PC₂(t), respectively (20–22) (SI Text). From the 2-D PDFs of PC₁ and PC₂ computed from the MD runs, the potential V_1,2 = -kT ln[P(PC₁,PC₂)], shown in the inset of Fig. 4, was calculated. This energy surface can be divided schematically into three basins, states 1, 2, and 3 in Fig. 4. In each basin, the most probable structure of VA3 in the concatenated MD runs was selected, and its CGDAs γ and δ were computed along the amino acid sequence and placed on the 1-D potentials shown in Fig. 1. This projection of the collective PC energy basins on a sequence of 1-D potentials is a powerful approach to interpret the protein dynamics and folding (30). State 1 in Fig. 4 corresponds to the deepest minima of the FEPs V(δ_n) and V(γ_n). The metastable substates of the FEPs V(δ_n) and V(γ_n) for n = 34, 35, 37, 38, 39, and 41 are occupied in state 2. State 3 is an intermediate state with a displacement of the dihedral angles from their most stable positions on the FEPs towards state 2 for n = 1, 2, 32–39, 41, 43, and 44. There is, therefore, large motion of loop 35–44 coupled to a motion of δ₁. The whole motion is represented in Fig. S6 A and B. State 1 is stabilized by two amide backbone hydrogen bonds between Lys1 and Gly37 and between Gly37 and Thr39 (Fig. S6C). The displacement of the loop towards states 2 and 3 is due to the breaking of these two hydrogen bonds (Fig. S6 D and E). In this particular protein, the fluctuations of the long Lys side chain of the N-terminal residue induce the fluctuations of the main chain and of the side chains of a loop located in the C-terminal part. Because the loops and the N and C-terminal parts are more flexible, the side-chain motions and main-chain motions are strongly correlated in this collective motion. This collective motion could contribute to the biological function of VA3, which is still poorly understood (31).

Conclusions

The FEPs of the main-chain and of the side-chain CGDAs are remarkably similar along the primary sequence of the VA3 protein (Fig. 1). It is demonstrated that the side-chain motions (δ_n) are subdiffusive with stretched exponential RCFs (Fig. S3), like the main-chain motions (γ_n) (6). The side chains diffuse slower than the main chain (i.e., the exponent α is smaller) on their FEPs with a larger diffusion constant (Fig. 2). The fluctuations of the coarse-grained steps Δγ_n(t) and Δδ_n(t) (recorded every ps from the MD runs) were poorly correlated on average along the amino acid sequence (Fig. 3A). The correlation coefficient between the displacements of the CGDA γ_n and δ_n after a time t increases with t and converges to the correlation coefficient between the γ_n(t) and δ_n(t) trajectories. The increase of the correlation coefficient of the fluctuations between the displacements of the CGDAs is faster for those which are more subdiffusive (more correlated to their past). In spite of that, the CGDAs γ_n and δ_n move on very similar FEPs along the entire primary sequence of the protein, and the correlation coefficient between their trajectories varies widely along the amino acid sequence (Fig. 3). The highest correlation between the γ_n(t) and δ_n(t) trajectories occurs for residues n located in the most flexible regions of the protein, where the FEPs are generally multiple-minima. In addition, the highest correlated trajectories γ_n(t) and δ_n(t) correspond to residues n which contribute to the slowest collective mode of the protein. This explains the heterogeneity of the correlation coefficient R between the trajectories of the CGDAs along the primary sequence (Fig. 3A). In the particular case of VA3, the side chain of the N-terminal part of the protein hence is coupled to the motion of a loop in the nearby C-terminal part. In these modes, the side chains and main chain follow each other on average in the course of time. The slow collective motions are important for the biological functions of proteins and could play a role in protein folding. Indeed, in an unfolded protein, most of the regions of the protein are flexible and, from our findings, it can be expected that the side-chain motions and the main-chain motions of these regions should follow each other on average. When part of the protein is locked (folded), the residues involved cease to contribute to collective modes and the side chains cease to follow the main chain motion. The implications for the protein entropy and protein folding of this change in the correlation between the side-chain motions and the main-chain motion, when part of the protein is folded, is beyond the scope of the present study but it is worth pursuing in the future.

Methods

Five all atom MD simulations of VA3 in explicit water each of a duration of 80 ns, were carried out previously (6). Details of all MD simulations were given in ref. 6. In the present work, these five MD runs were joined to each other to form a long (400 ns) single MD run. The calculations performed from the five joined MD runs and each MD run are similar (see SI Text: Comparison Between Calculations Performed Over 400 ns (Five MD Runs) and Over 80 ns (for Each MD Run)). The correlation coefficient R was computed according to the standard formula (10), taking care of the periodicity of the angle variables (ref. 5 and SI Text: Calculation of the Pearson Correlation Coefficient R for the Dihedral Angular Steps). The similarity index h defined in theSI Text, and adapted from ref. 29, was applied to the aligned PDFs of the CGDAs. The dPCA was applied to the covariance matrix of the vectors u_n(t) of γ_n. For the CGDAs γ_n, there are 43 modes, each mode k contributing to the MSF_n by λ_kv_k,n (19–21) (see SI Text: The Dihedral Principal Component Analysis. The dPCA was also applied to the covariance matrix of the vectors u_n(t) = { cos[δ_n(t)], sin[δ_n(t)]}. The results were similar to those discussed for the modes of the CGDAs γ_n. The main difference is that δ₃₃ has a larger contribution to the slowest mode 1 (Fig. S7) than γ₃₃ (Fig. 4). More details about the methods and amino acid sequence of VA3 can be found in the SI Text.