Generation of laser-induced cavitation bubbles with a digital hologram

Abstract

We demonstrate a method using a spatial light modulator (SLM) to generate arbitrary 2-D spatial configurations of laser induced cavitation bubbles. The SLM acts as a phase hologram that controls the light distribution in the focal plane of a microscope objective. We generate cavitation bubbles over an area of 380x380 μm² with a 20x microscope objective through absorption of the pulsed laser light in a liquid ink solution. We demonstrate the ability to accurately position up to 34 micrometer sized bubbles using laser energies of 56 μJ.

1. Introduction

Object trapping [1,2], material ablation, and cavitation bubbles generation [3] are standard applications of strongly focused laser light. Laser-beam traps using continuous irradiation have been realized to guide and confine a broad range of objects, from cold atom clouds [4] to cells [1], polystyrene particles [2], and even stabilized gas bubbles [5]. In contrast, when pulsed laser beams are focused inside liquids and the intensities are above a certain threshold, explosive vaporization of the liquid can result from the rapid energy deposition achieved either through stress confinement [6] or through optical breakdown [7]. Such processes result in the formation of a cavitation bubble. The bubble initially undergoes an expansion phase where the pressure and temperature of its interior fall and after some time the bubble attains a maximum volume. The bubble then undergoes a collapse phase due to the pressure imbalance between the surrounding liquid and the bubble interior. The time between the maximum bubble expansion and collapsed state is termed Rayleigh collapse time [8,9]. For bubbles that consist mainly of vapor and which collapse due to atmospheric pressure, the collapse time is given by T_c≈0.1R_max (s/m), where R_max is the maximum bubble radius. Thus, bubbles of 10 μm have a collapse time of about 1 μs. The rapid fluid flow during the bubble expansion and collapse has been used to lyse [10], porate [11] and manipulate both adherent and non-adherent cells. Also, these cavitation bubbles have been combined with microfluidic chips as tools to control and to induce high Reynolds number flow that can be used to mix [12] and pump [13] fluids as well as to manipulate cells [14,15].

In this work we explore a technique to generate micrometer sized bubbles using a digital hologram. Holographic gratings have been used as beam shaping tools, and have been very successful in the creation of arrays of focused spots [16]. So far, most of the studies have been in the direction of laser trapping and the creation of complex optical traps [17–21]. Digital holograms can be formed by spatial light modulators (SLM) which are liquid crystal displays where the phase of an incident beam changes as a function of the voltage applied to the individual pixels on the display. The desired intensity pattern is recovered at the focus of a spherical lens (Fourier transform). Computer controlled SLMs offer the flexibility over static holograms that the phase picture can be changed easily at video refresh rates (50 Hz and above). To our knowledge SLMs have not been used to create bubbles, yet in 1979 Hentschel and Lauterborn pioneered the generation of bubbles with digital holograms using a computer calculated transmission grating made by spin-coated photo resist deposited on a glass substrate [22].

2. Experimental setup

The experimental setup is depicted in Fig. 1. It consists of the laser source, the SLM, optical components, and an inverted microscope to generate and image the bubbles.

Fig. 1.

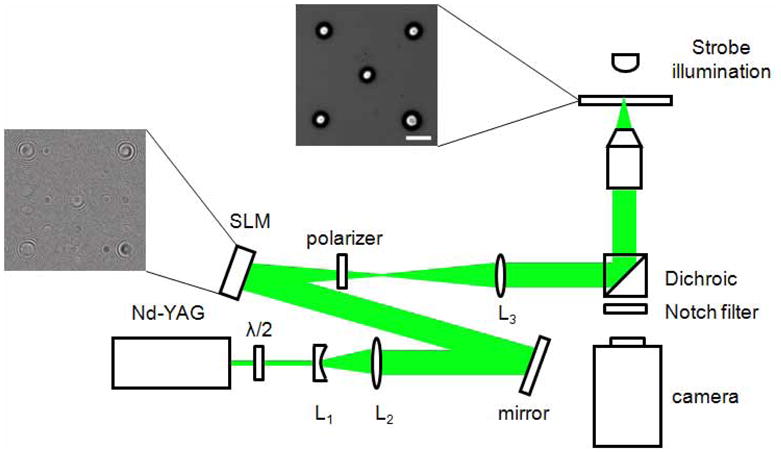
Experimental setup: The Nd:YAG laser generates a single pulse at 532 nm for a duration of 6ns. Using a few optical components (see text) arbitrary configurations of laser foci can be generated. At each laser focus a cavitation bubble is generated. The frame left of the spatial light modulator (SLM) displays the superposition of a Fresnel hologram and the hologram for the ‘five on a dice’ pattern. When focused into a small amount of light absorbing liquid five cavitation bubbles are generated which are illuminated with a homebuilt strobe consisting of a high power light emitting diode (LED) and a current amplifier.

2.1 Laser

Single pulses (6 ns, 532 nm) from a frequency-doubled Nd:YAG laser (Orion, New Wave Research, Fremont, CA) are used to create the bubbles. The linear polarization of the laser beam is rotated by a half wave plate, since the phase modulation provided by the reflective SLM depends on the polarization state of the incident light. The beam is then expanded by a telescope formed by lenses L₁ (f= −30 mm) and L₂ (f=400 mm) to fill the active area of the SLM (Fig. 1). The energy of the laser pulse is controlled by changing the Q-switch delay. The pulse-to-pulse variation of the laser energy is about ±5%. The pulse energy incident on the SLM varied between 260 to 335 μJ.

2.2 Spatial Light Modulator (SLM)

The SLM (model LC-R-2500, Holoeye Photonics AG, Berlin, Germany) has a resolution of 1024x768 pixels with square pixel size of 19 μm length. The total area of the digital hologram is 19.5x14.6 mm². It is a twisted nematic liquid crystal modulator that, depending on the polarization state of the incident beam, allows for almost phase-only modulation [23].

The hologram is calculated using an iterative Fourier transform algorithm with the software provided by the manufacturer (Holoeye software version 2.2). Additionally, this hologram is combined with a lens phase [24] to separate the zero-order undiffracted portion of the light reflected by the SLM. Thus, the lens phase is added to the hologram phase and the result is sent to the SLM. A linear polarizer is used as an analyzer to reduce the undesired higher order diffraction components of the beam reflected/emitted by the SLM. The energy diffracted by the array is about 33% of the incident energy on the SLM, furthermore, the linear polarizer (analyzer) attenuates this diffracted portion of the beam by 50%. Thus the laser pulse energies used to form the patterns range from 44 to 56 μJ. Figure 1 depicts a part of the hologram that results in the bubble pattern at the focal plane of the microscope lens.

The lens L₃ (f=250 mm) collimates and images the hologram into the back aperture of a microscope objective (20x, NA=0.75, Olympus, Singapore) that is integrated within an inverted microscope platform (IX-71, Olympus, Singapore). The SLM is used to project a ‘five on a dice’ pattern at the focal plane of the objective that results in the generation of 5 individual bubbles.

2.3 Illumination and imaging

To image the fast process of bubble expansion and collapse we use strobe illumination, in which a high power light emitting diode (LED, model P7, Seoul Semiconductor, Seoul, South Korea) is triggered together with the laser. The current through the LED is 4–5 A at 40 V. The bubble is imaged at different stages by changing the time delay between the laser trigger and the diode illumination. The high reproducibility of the experiment provided for an extremely consistent bubble dynamics. The image exposure is given by the 0.6 μs duration of the LED strobe.

The LED illumination propagates through the dichroic mirror of the microscope and pictures the bubbles on the sensor of a sensitive CCD camera (Sensicam QE double shutter, PCO AG, Kehlheim, Germany). A notch filter is used to block the 532 nm laser light from reaching the camera.

2.4 Sample volume

Cavitation bubbles are created a few micrometers above microscope cover slides (number one, 130–170 μm thickness) in a thin liquid film. In the reported experiments our irradiation conditions achieve stress confinement in a green laser light absorbing liquid. We found that blue refill ink used for inkjet printers is nicely suited as it contains few impurities and is inexpensive [25].

The upper right frame in Fig. 1 depicts 5 bubbles in the ‘five on a die’ pattern 1μs after the laser pulse (the scale bar is 100 μm). This picture demonstrates that a single laser pulse can be used to create separate bubbles over a large spatial field. In the case shown, the maximum bubble separation is 380 μm which spans almost the entire field of view of the 20x microscope objective.

3. Results and discussions

3.1 Cavitation bubble configurations

We will now give a few examples of SLM generated bubble configurations. Figure 2 left shows a bubble pattern of 9 bubbles arranged on a square pattern pictured 1.2 μs after laser irradiation. The center of each bubble appears bright because the light can pass here with little refraction into the microscope objective. The rim of the bubbles is pictured slightly blurred because of the limited focal depth of the imaging system and the exposure time of 0.6 μs. The bubbles expand to a maximum radius of R_max=50 μm, corresponding to an average radial growth velocity of about 40 m/s. To show the potential of this new technique, a pattern with 16 bubbles is shown in Fig. 2 right. This different bubble pattern is achieved simply by displaying a different hologram on the SLM and delivering another laser pulse. Given a laser with a sufficiently high repetition rate, the formation of different bubble patterns would be limited by the video frame rate of the SLM (70 Hz). Some differences in the bubble sizes and shapes visible in Fig. 2(b) are worth noting. In particular the central four bubbles are smaller in size than the bubbles on the periphery. Moreover, the peripheral bubbles have a pronounced size deviation. It is very likely that bubble-bubble interactions [26] are responsible for the smaller central bubbles because each of these bubbles experience the pressure field from 8 neighboring bubbles during expansion. By contrast the bubbles on the periphery have only 3 or 5 neighbors. Since the pressure acting on a bubble is the superposition of the pressure radiated from each bubble scaled with distance 1/r, it is expected that the central bubbles would expand less. However, this reasoning doesn’t explain why the lower right bubble is smaller than the bubble just above of it or to its left. Here, we believe that the intensity distribution of our laser source is important. The intensity distribution of flash lamp-pumped Nd:YAG lasers are not flat, top-hat, or a simple Gaussian but possess high-order TEM modes. These modes are convoluted with the hologram and will lead to nonuniform intensity fluctuations in the Fourier-plane of the microscope objective. Although not shown, we expect that we can account for these weaker foci by modifying their “contrast” from which adapted phase holograms are calculated or by spatially filtering the laser beam.

Fig. 2.

(a). Array of 9 expanding bubbles (E=44 μJ) imaged at 1.2μs after generation; and (b) 16 expanding bubbles 1.2 us after generation (E=56 μJ). The length of the scale bar is 100 μm.

The versatility of our method is demonstrated by writing bubbly letters in liquid. Here, we chose for the acronym “NTU” standing for Nanyang Technological University. The bubble configuration consists of 34 foci, see Fig. 3. Additionally, we show the dynamics of the bubble cluster expanding and collapsing within less than 10 μs. Due to the closer proximity of the bubbles, strong bubble-bubble interaction is observed as early as 1.2 μs following the bubble generation. This can be seen notably by the bubble splitting at the upper left part of letter ‘N’ and at the lower corners of the letter ‘U’. The bubble clusters reaches a maximum expansion around t=3 μs; yet, some of the more isolated bubbles are already shrinking. It is a common feature in cavitation clusters that bubbles with the lowest number of neighbors collapse first. The collapse of the cluster is depicted at t=5 μs. Supporting our previous statement, the collapse proceeds from areas of lowest bubble densities which is for this particular bubble pattern from above and below. Some of the bubbles exhibit some motion blurring which indicates the rapidity of the collapse. We also note that no coalescence between bubbles has been observed in the three configurations presented here.

Fig. 3.

NTU logo consisting of 34 cavitation bubbles 1.2 μs, 3 μs and 5 μs after the laser pulse (E=56 μJ). The length of the scale bar is 100 μm.

3.2 Application

We envision two important applications of the digital hologram for laser generated bubbles. First, the positioning of bubbles and the easy control of the bubble size with a SLM allows the generation of rapid and precisely actuated liquid flows on small scales. For example it can be used to produce high Reynolds number flows to overcome viscous surface forces and accelerate small amounts of liquids. Ohl’s and Venugopalan’s groups have both shown the utility of cavitation bubbles for mixing [27, 12] and pumping [13] fluids or to rupture plasma membranes of cells in microfluidic devices [14]. The use of the digital hologram allows these manipulations to be performed at different locations without scanning the microfluidic chip or the laser beam. This simplifies the experimental setup and allows fluid to be actuated by light and computers only; without any need for mechanical valves, wired connections, scanning mirrors, or position stages with micrometer resolution.

The second important application is the generation of spatial configurations of cavitation bubbles for current fluid dynamics research. Bremond et al. [26] demonstrated a nanofabrication technique by which an arbitrary configuration of hydrophobic holes on a flat substrate is etched. After submerging this surface in a liquid, bubbles are trapped in these holes and act as cavitation nuclei when the surface is exposed to a tensile wave. This technique has shown great potential to study bubble-bubble interaction, cluster dynamics, and the validity of different numerical schemes. Yet, the complex and costly process of etching holes is greatly simplified by adapting our new technique. It is likely that the investigation of topics such as bubble coalescence, energy focusing in cavitation clusters, and the deformation of shelled vesicles or cells with an impulsive force can be aided greatly by the use of holographic generated cavitation bubbles as opposed to using nanofabrication techniques.

4. Summary

Arbitrary configurations of laser induced cavitation bubbles can be generated using a digital holograms produced by a spatial light modulator. We report on bubble patterns generated from 9, 16, 34 foci each leading to the formation of a distinct bubble. The lifetime of the bubble reaching a maximum radius between 20 μm to 50 μm is less than 5 μs. These rapid bubble dynamics can produce rapid fluid actuation with average velocities of up to 50 m/s. This new method to generate multiple cavitation bubbles in arbitrary 2-D spatial configurations opens up novel possibilities in microfluidic and cavitation research, e.g. for lab-on-chip applications and to study cavitation cluster dynamics.