Abstract
Evolution at high mutation rates is minimally affected by six processes: mutation-selection balance, error catastrophes, Muller’s Ratchet, robustness and compensatory evolution, and clonal interference. Including all of these processes in a tractable, analytical model is difficult, but they can be captured in simulations that utilize realistic genotype-phenotype-fitness maps, as done here by modeling RNA folding. Subjecting finite, asexual populations to a range of mutation rates revealed simple criteria that predict when particular evolutionary processes are important. Populations were initiated with a genotype encoding the most fit phenotype. When purifying selection was strong relative to mutation, the initial genotype was replaced by one more mutationally robust, and the maximally fit phenotype was maintained in a mutation-selection balance where the deleterious mutation rate determined mean fitness. With weaker purifying selection, the most fit genotypes were lost. Although loss of the best genotype was ongoing and might have led to a progressive fitness decline, continual compensatory evolution led to an approximate fitness equilibration. Per total genomic mutation rate, mean fitness was similar for strong and weak purifying selection. These results represent a first step at separating interactions between evolutionary processes at high mutation rate, but additional theory is needed to interpret some outcomes.
Keywords: Muller’s Ratchet, Compensatory Evolution, Evolution of Robustness, Mutation-Selection Balance, Clonal Interference
Introduction
Populations with high mutation rates (such as RNA viruses) are affected by multiple evolutionary processes, and understanding the relative importance of these processes is challenging (Drake and Holland, 1999). For a population starting at high fitness, the net effect of a high mutation rate should be detrimental simply because most mutations are deleterious, and the population will accumulate deleterious mutations faster than selection can purge them. Furthermore, some well known processes exacerbate the fitness decline from a high mutation rate, at least in finite populations: stochastic fixation of deleterious mutations and Muller’s Ratchet (Muller, 1964; Charlesworth et al., 1993; Gordo and Charlesworth, 2000). Yet there are also processes that offset the decline: adaptive and compensatory evolution (Poon and Otto, 2000; Wilke et al., 2003), error catastrophes (Eigen, 1971; Wilke, 2005) and evolution of robustness (van Nimwegen et al., 1999; Wilke, 2001). Finally, the rate of any adaptive evolution can be slowed from clonal interference (Gerrish and Lenski, 1998; de Visser et al., 1999; Miralles et al., 1999). The challenge is to discover generalities in populations that are potentially subject to all of these processes simultaneously.
A convenient ‘null model’ for the effect of a high mutation rate is mutation-selection balance (Haldane, 1927). Deterministically, population mean fitness (W̅) in asexual populations is expected to equilibrate at a value determined only by the deleterious mutation rate:
| (1) |
where Ud is the genome-wide deleterious mutation rate and a ‘hat’ indicates equilibrium (Kimura and Maruyama, 1966). For brevity, we will denote this as the ‘KM’ equilibrium, after the authors. An appealing property of this equilibrium is its independence of the fitness effects and interactions among mutations in asexual populations. The model is limited in ignoring stochastic processes, ignoring beneficial mutations, ignoring recombination, and greatly limiting the fitness landscape. With so many limitations, does the KM equilibrium offer a reasonable approximation to equilibrium fitness in a real population? The utility of the KM fitness equilibrium is its emancipation from many parameters otherwise measured with difficulty, so even if the equilibrium is often inaccurate, it may help delineate when other processes are important.
This study uses simulation to explore the interplay of evolutionary processes at high mutation rates in finite asexual populations. Most basically, we ask when and if mutation-load theory predicts the fitness equilibrium, and if it fails, why and under what conditions. The simulation model attempts to include realism by allowing the population to evolve within a complex fitness landscape, that of RNA secondary structure. Therefore, many evolutionary properties can change over the course of a simulation run, and the outcomes are not simple consequences of constraints imposed for convenience of analysis.
Methods
Evolutionary Simulations
Populations were usually limited to 1000 individuals reproducing asexually in discrete, non-overlapping generations, although some simulations used a smaller population size (N = 100). Individuals were characterized by a single phenotype that was specified completely by genotype. Following models used in previous RNA studies (Wilke, 2001; Cowperthwaite et al., 2006), an individual’s genome consisted of an 99 base ‘RNA molecule’ (bases A,C,G,U) subjected to mutation prior to reproduction. An individual’s phenotype was merely its shape - its genome in a folded state - and fitness was assigned according to the similarity of its genome’s shape to a target shape, as elaborated next.
Genome shape was the minimum free energy fold of its genome, assigned by the Vienna RNA package (Hofacker et al., 1994). This procedure yielded a single secondary structure, SG, for genome G. Fitness, W(G), was a linear function of the difference between SG and the target shape, ST:
| (2) |
H(SG, ST) simply counts the number of differences in structural notation between SG and ST (Hamming distance). The severity of the decline in fitness is determined by the strength parameter γ, which here was 0.15 for steep landscapes, 0.025 for shallow landscapes, and 0.06 for intermediate landscapes. This fitness function assumes a single, optimal shape, but as will be noted below, there are many genomes that fold into any single shape. It would be desirable to consider an even shallower landscape, but much lower values of γ result in an extremely flat landscape such that randomly chosen sequences have fitness of similar magnitude to wild type.
The function H(SG, ST) relies on a particular notational representation of secondary structure. In this notation, a folded molecule is represented unambiguously as a linear string of dots and parentheses, with dots representing unpaired bases and parentheses representing paired bases. For example, an 8-base molecule folded symmetrically with a 4-base loop and 2-base stem is represented as ((…․)). The minimum difference between two non-identical folds is thus two, even though the difference may result from a single base difference. Conversely, a single base difference can result in many structural differences.
This model is loosely motivated by the general finding that RNA secondary structure is highly conserved for many noncoding RNAs such as tRNA and ribosomal RNA (Doudna, 2000; Meer et al., 2010). At the same time, we do not pretend that our model captures any biological system. The property that is most appealing is a fitness landscape in which many different biological properties can evolve.
In prior simulation studies, population size has been held constant (Wilke, 2001; Cowperthwaite et al., 2006). Here the maximum population size was fixed but minimum size was not, allowing extinction. A parent of genotype G has relative fitness W(G) and absolute fitness 5W(G), where the number 5 was chosen arbitrarily as the largest possible (average) number of offspring—for a genotype that folded into the target shape. The individual’s actual number of offspring was then drawn from a Poisson distribution with mean 5W(G). With the possibility of 5 offspring per parent, for a sufficiently large number of parents, the number of offspring in the population could exceed the maximum population size. When this happened, offspring were pruned by random choice without replacement until the maximum allowable population size was attained. All offspring chosen to make up the next generation subsequently underwent a round of mutation. Each position in an offspring genome mutated to a different base with probability U/L, where L = 99 is the sequence length and U is the genomic mutation rate; all base substitutions were equally likely. For a given run, populations were subjected to one of the following genomic mutation rates:
0.05, 0.12, 0.20, 0.29, 0.38, 0.49, 0.60, 0.73, 0.88, 1.1, 1.3, 1.6, 1.9, 2.6, 4.6.
Initial populations were isogenic, with all individuals consisting of a genotype that folded into the optimal shape. This founding, ‘optimal’ genotype was designed using the ViennaRNA function RNAinverse (Hofacker et al., 1994). Mutation and selection altered this initial state, and populations rapidly converged to an approximate fitness equilibrium by 1000 generations, although most runs were carried out to 5000 generations to ensure that quasi-equilibrium had been attained. In several cases, replicate simulations using the same fitness function and target shape were initiated with different genotypes that folded into the optimal shape. These replicates converged to indistinguishable fitness equilibria.
Programing was done using a combination of the Python and Cython (Behnel et al., 2011) programming languages. The source code is located at http://wilke.openwetware.org/Software.html.
Neutral networks in the fitness landscape
One consequence of our genotype-phenotype landscape is a high level of redundancy for each secondary structure. Even secondary structures with complex series of stems and loops have many RNA sequences that will fold as that shape. We estimated the size of the neutral network for the target shape as ≈ 1.2 × 1041 using the NN get size program (Jörg et al., 2008). Even though large, this number is relatively small compared to the total number of unique genotypes for a 99-mer, 499 = 4 × 1059. Thus, our target shape has a large neutral network that still contains relatively few genotypes overall.
Two parameterizations of the realized deleterious mutation rate
The KM model assumes a specific fitness landscape: a single genotype of maximal fitness, and all non-neutral mutations are deleterious. Thus once a genotype has acquired a deleterious mutation, there is no way for its descendants to recover maximal fitness. The equilibrium in (1) applies only as long as the best genotype is maintained.
The KM equilibrium strictly applies to an infinite population, but it provides an expected equilibrium value for finite populations. Calculation of this equilibrium requires knowledge of the deleterious mutation rate. In our simulations, the total genomic mutation rate was fixed, but the fraction of all mutations that were deleterious depended on the genotype. For any genotype, i, it is feasible to exhaustively determine the fraction of all possible single mutations that are deleterious, di. Thus, the deleterious mutation rate for genotype i is diU. The deleterious mutation rate in the KM equilibrium is specifically the deleterious rate of the most fit (mutation-free) genotypes (referred to as the most fit phenotype, since our model allows multiple genotypes with the same fold and thus same fitness). So the relevant deleterious mutation rate is the total mutation rate U times the deleterious fraction of all mutations in the best genomes, Db:
| (3) |
for all existing genotypes j ∈ B that fold into the optimal phenotype, and pj is the frequency of genotype j in the population.
In the simulations, it is easy to identify and measure the best genotypes. This task is challenging in an actual population, where it would be necessary to screen all individuals to identify the most fit and specifically measure their deleterious mutation rates. It is thus useful to determine the accuracy of the KM formula when parameterized with the population average deleterious mutation rate for all n genotypes in the population, Dn:
| (4) |
where . There are thus two forms of the KM equilibrium to test,
| (5) |
| (6) |
Muller’s ratchet
Muller’s Ratchet is a stochastic process that depends on population size, deleterious mutation rate, and effect size of a mutation (Muller, 1964; Charlesworth et al., 1993; Gordo and Charlesworth, 2000). The basic principle is that the best phenotype class will be lost by chance when its expected absolute numbers are low and when, in the absence of recombination and back mutation, it cannot be regenerated. Once the best phenotype class is lost, the next-best phenotype class can be lost by the same process, and so on. The process has the potential to cause extinction, and in the absence of offsetting (compensatory) evolution or a slowdown in the rate of the ratchet, extinction should occur in our simulations.
The critical quantity in the ratchet is the expected number of individuals in the best phenotype class (n0). With a deleterious mutation rate of Ud, a population size of N, and all deleterious mutations with fitness effect s, Haigh (1978) showed that the number retained in the best class at equilibrium was approximately
| (7) |
and the ratchet is expected to operate when n0 is on the order of 10 or less (Maynard Smith, 1978). This formula is not immediately applicable to our model because different deleterious mutations can have different effects, i.e., s is variable. One suggestion is to substitute the harmonic mean of s (s̅), which we apply here (Orr, 2000).
Results
All simulations were initiated with the entire population consisting of a genotype of maximal fitness. From this starting point, all mutations were deleterious or neutral in the immediate generation. This type of landscape satisfies the basic assumptions of the KM model, although our model does allow population parameters to evolve, whereas the KM model does not. If the KM equilibrium is general, it should apply to equilibrium fitness in these populations whenever the best genotype is maintained. The KM equilibrium may be expected to fail if the best genotype is lost, but in such cases, we may ask whether the observed equilibrium lies above or below KM and by how much.
Steep and shallow fitness landscapes
In steep landscapes, fitness fell rapidly with deviations from the optimal shape; in shallow landscapes fitness fell gradually. For example, in steep landscapes, a mutation causing the minimal structural deviation from the optimal shape decreased fitness by 30%; in shallow landscapes the minimum decline was 5%. Genotypes with 7 or more structural deviations were non-viable in the steep landscape, whereas genotypes were viable with up to 40 deviations in the shallow landscape. As shown below, this difference in landscape qualitatively affected evolutionary behavior.
We describe our findings for a single target shape,
..(((((....(((((((.((((....)))).))))))).(((.(((((((..((((...(((....)))...))))))))))))))....)))))..
and a single founding genotype,
UUGGUUAUAAUUUCGCUGGGUGGCGCCCCAUAUGGCGAACUGCAUCAAUG
UGACUGUCGAAGGUCGGGACCGAUAUAGACGUUGGGUACCUCUAACCUG.
We repeated our basic simulation with four other target shapes and found qualitatively similar results (not shown). The results address steep landscapes first as these dynamics were the most straightforward.
Steep landscapes obey Kimura-Maruyama equilibrium
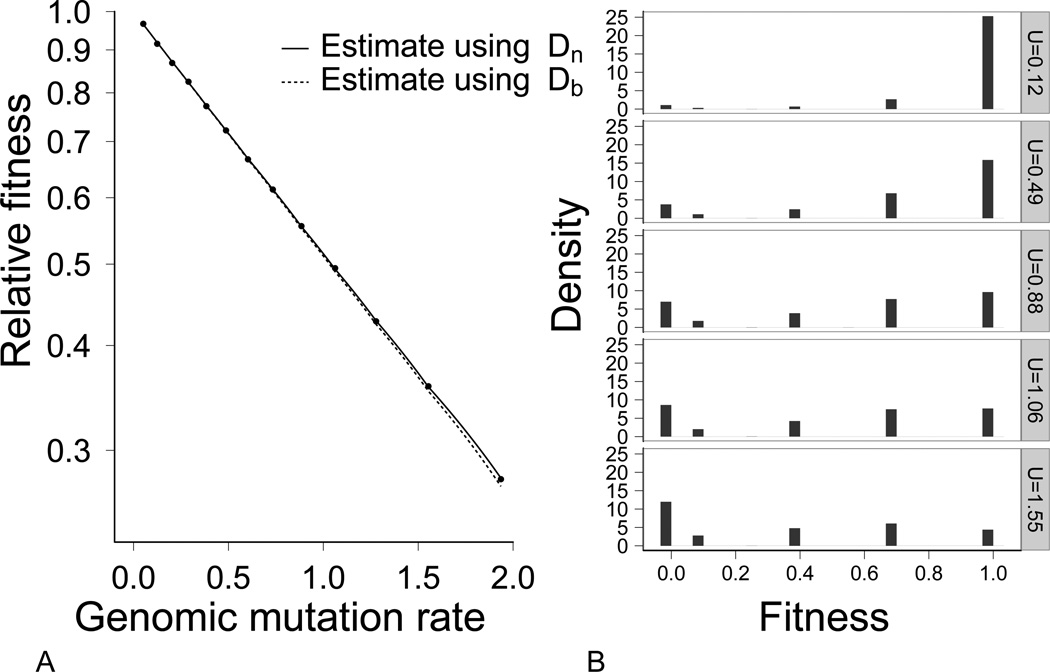
Across a broad range of genomic mutation rates, U, the observed fitness equilibrium in steep landscapes was adequately predicted by both parameterizations of the KM equilibrium, (5) and (6) (Fig. 1A). Thus, the average deleterious mutation fraction across the population (Dn) sufficed to explain the dynamics, and we use it in later calculations of the expected KM equilibrium. With a fecundity of 5, extinction is not expected in these populations until W̅ = 0.2. Fitness dropped this low (and the populations disappeared) only at the highest mutation rates (U > 2.6). Otherwise, populations generally remained at the maximum population size of N = 1000.
Figure 1.
(A) Predicted and observed population mean fitness in steep fitness landscapes across a range of mutation rates. Points correspond to the average of population mean fitness for 25 simulations at a given mutation rate. Expected mean fitness was calculated with the KM equation (1) and parameterized with the observed deleterious mutation rate of either the most-fit genotypes (UDb, dashed line) or the entire population (UDn, solid line). Neither prediction was significantly different from the observed means (for Db: χ2 = 6.734, df = 13, N = 325, p = 0.915; for Dn: χ2 = 5.187, df = 13, N = 325, p = 0.971). Parameters used: γ = 0.15, N = 1000. The Y-axis is on a log scale. (B) Fitness density plots for five different mutation rates. Individual fitnesses fall into discrete categories because of the limited number of fitness effects of deleterious mutations.
The best phenotype persists and evolves robustness in steep landscapes
A property of the deterministic KM equilibrium is that the genotype encoding the best phenotype is retained in the population, although it may be rare. A finite population may lose the best genotype by chance, and an infinite population may even lose it deterministically via an ‘error catastrophe’ (Eigen, 1971). Nonetheless, the best phenotype was invariably retained in the surviving populations with steep landscapes (Fig. 1B). Thus, the ratchet and error catastrophes were absent.
Although the best phenotype was retained, the founding genotype (which encoded the best phenotype) was replaced with one more robust. This evolution of robustness was possible because of the high degree of neutrality in the RNA fitness landscape, such that many different genotypes fold into the same shape and thus have the same number of offspring (van Nimwegen et al., 1999; Wilke and Adami, 2003; Forster et al., 2006). Although two genotypes encoding the same, optimal phenotype have equal average progeny numbers, they may nonetheless differ in their number of grandchildren if they differ in their robustness to mutation, because the progeny of one genotype will be more fit on average.
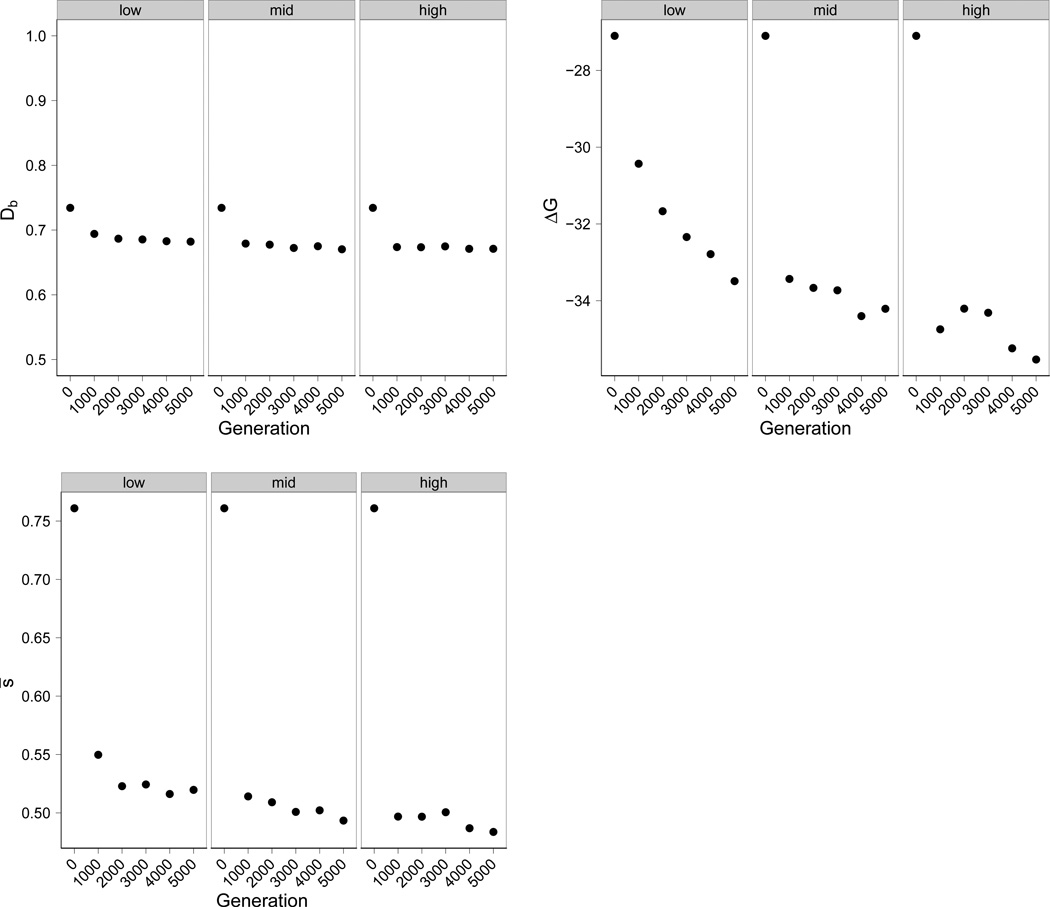
Evolution of robustness of the optimal genotype was evident in three measures: fraction of deleterious mutations (Db), minimum free energy (ΔG), and the harmonic average effect s of deleterious mutations (s̅) (Fig. 2). Intuitively, all three measures are expected to be correlated - more stable folds should be more robust to mutations affecting shape, and the impact on fitness should also be reduced (as in the case of proteins: Bloom et al. (2005)). Indeed, the majority of evolved robustness occurred in the first thousand generations for all three traits, regardless of the mutation rate. There was little subsequent evolution in Db, while ΔG and s̅ each showed continuing declines, especially at the highest mutation rates. The robustness phenotype directly selected is the number of offspring (and subsequent descendants) that retain the best phenotype when mutated.
Figure 2.
Correlated evolution of robustness. Populations at various mutation rates evolved to become more robust by three measures: fraction of deleterious mutations (Db), minimum free energy(ΔG), and the harmonic average effect s̅ of deleterious mutations. The majority of evolution in these measures occurred in the first thousand generations, and subsequent evolution was dependent on the mutation rate. Low, medium, and high mutation rates corresponded to U = 0.12, 0.49, and 1.3, respectively.
The close similarity between KM estimates and observed equilibria is partly because the deleterious mutation rate is estimated from the evolved populations, not the starting population. When the deleterious mutation rate for the best genotype, Db, was calculated using the initial isogenic population, the predicted equilibrium fitness was significantly lower than the observed equilibrium across the various mutation rates (goodness of fit χ2 = 92.37, df = 13, N = 325, p < 10−7). The relative deviation in mean fitness ranged from slight at the lowest mutation rate (0.73% lower than observed) to modest at the highest mutation rate for which populations persisted (30% lower). This error in fitness prediction can be directly attributed to the evolution of robustness, thus providing one reason why the predicted, negative fitness impact of a high mutation rate (based on the initial population) may overestimate its impact in a real setting.
All populations evolved to become more robust, and furthermore, the level of robustness (as the fraction of mutations deleterious) was similar across mutation rates (Fig. S1). We also calculated the average number of segregating beneficial mutations; these mutations generally existed in a small segment of the population (Fig. S2).
Shallow landscapes violate Kimura-Maruyama equilibrium
The same initial genotype and folding algorithms were used for the shallow and steep landscapes, but the fitness effect of a mutation differed. Thus, the genotype-phenotype maps were the same, but the phenotype-fitness maps differed. For the best genotype, a single mutation causing a deviation from the target shape had a minimal fitness effect of s = 0.05, compared to s = 0.3 for the steep landscape. However, the minimal effect of a mutation is a somewhat misleading statistic, at least for the initial genotype used here. The initial genotype had been designed rather than evolved, hence it had been created without consequences for its sensitivity to mutation. For the initial genotype, the harmonic mean (s̅) averaged over all possible point mutations was 0.2. In contrast, the s̅ of a robust genotype (evolved in the steep landscape but evaluated in the shallow landscape) was 0.11. Thus, the initial genotype was presumably also subject to selection for robustness in the shallow landscape, although the impact of that selection is not clear, for reasons developed next.
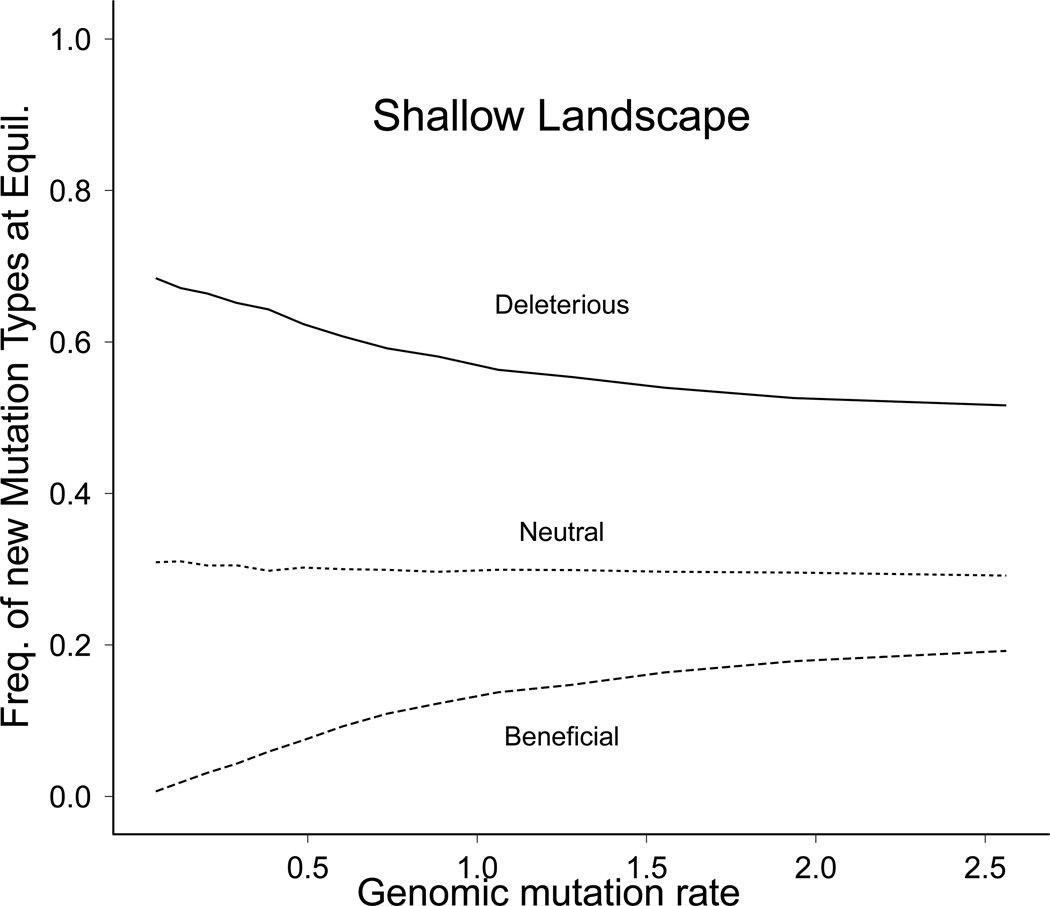
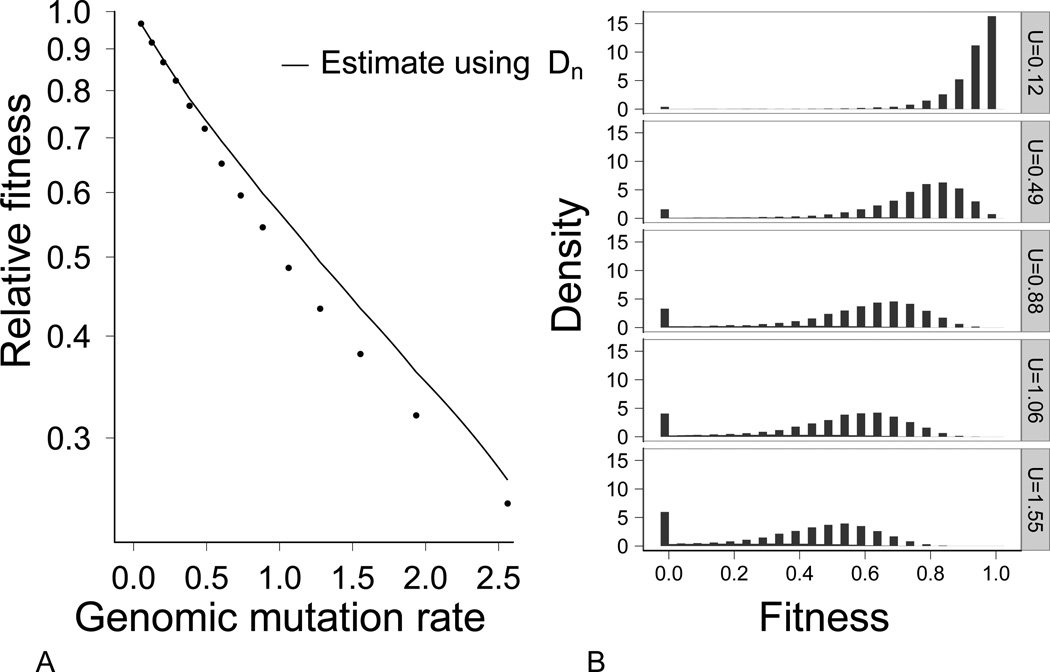
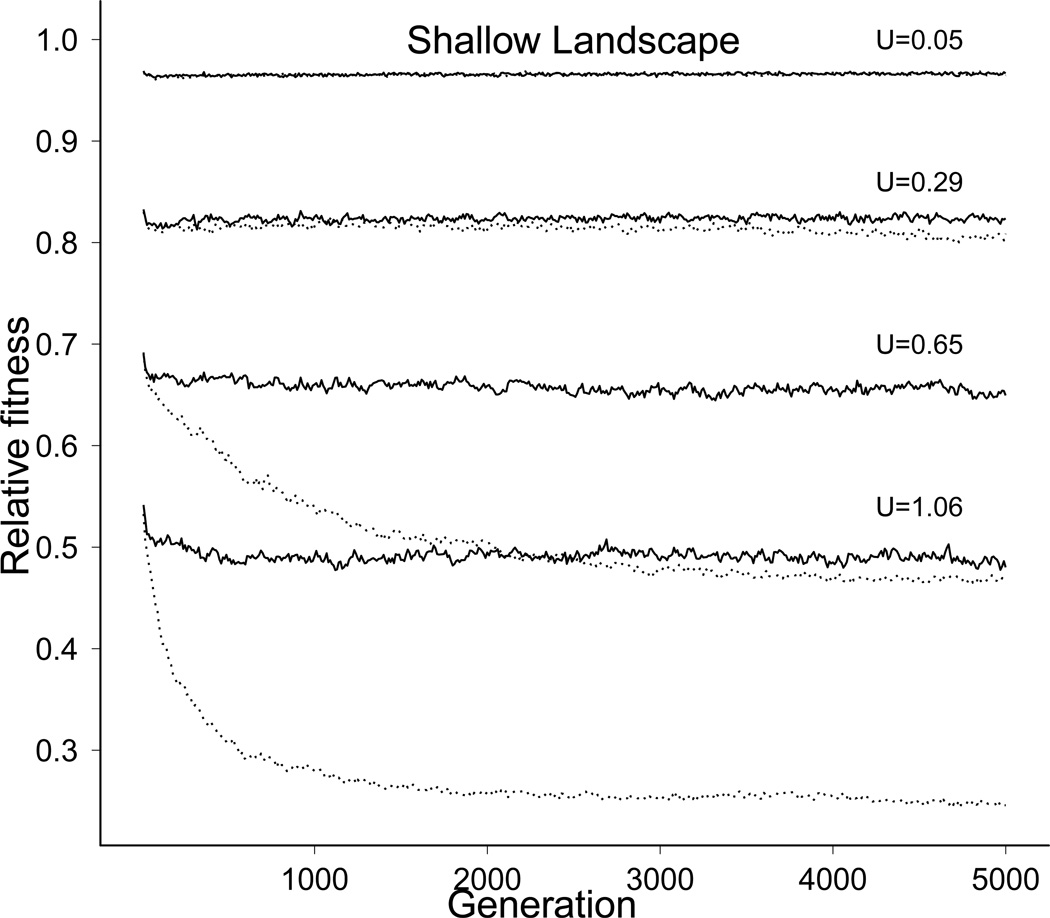
Populations in the shallow landscape behaved differently than those in the steep landscape. The fraction of mutations that were deleterious (Dn) decreased, corresponding to an increase in the fraction of mutations that were beneficial (Fig. 3). Fitness nonetheless equilibrated, and at mutation rates of U = 0.5 and higher, mean fitness started falling below the KM value (Fig. 4A). At genomic mutation rates of U = 0.88 or higher, all genotypes encoding the optimal phenotype were lost (Fig. 4b, explained more fully below).
Figure 3.
Equilibrium prevalence of compensatory (beneficial) mutations and deleterious mutations in shallow landscapes depends on mutation rate. The genomes of all individuals in populations evolved for 5000 generations were analyzed to determine the average fraction of mutations that were deleterious (dashed line), neutral (solid line), or beneficial (dotted line). As mutation rate increased, deleterious mutations became less common and compensatory mutations became more common.
Figure 4.
(A) Mean fitness in populations with shallow fitness landscapes deviates from prediction. Points correspond to the average of population mean fitness for 25 simulations at a given mutation rate. The line corresponds to predicted mean fitness from the KM equation (1), parameterized with UDn because the genotypes encoding the best phenotype were lost from the population at all but the lowest mutation rates, as shown in (B). The observed population mean fitness equilibria are significantly lower than expected from KM (χ2 = 120.12, df = 14, N = 350, p < 10−7). The Y-axis is on a log scale. Parameters used: γ = 0.025, N = 1000. (B) Equilibrium genotype fitness density plots for five different mutation rates. The fitness categories correspond to the fitnesses of individual genotypes. The maximally fit genotypes were lost in the lower two panels.
Fitness equilibration despite loss of the best genotype is potentially puzzling. If loss of the best genotype is ongoing and progressive, which is expected if the process is Muller’s ratchet, fitness is expected to decline continually (Maynard Smith, 1978; Muller, 1964). In searching for the cause of fitness equilibration, we found that compensatory mutations were evolving continually and offsetting the fitness decline. Beneficial mutations - those that increase average offspring number - cannot occur in genotypes encoding the optimal phenotype, but they are possible in most, perhaps all suboptimal genotypes. As long as the optimal phenotype is present, it dominates the genotype structure in the population, such that suboptimal genotypes are continually purged, and beneficial (compensatory) mutations arising in suboptimal genotypes have a small impact on mean fitness. However, once the optimal phenotype is lost, beneficial mutations can evolve in the best of the prevailing genotypes and have a major effect on fitness. Additionally, the evolution of robustness in regards to how much a deleterious mutation affects fitness also becomes important because all individuals have suboptimal fitness. Thus, evolving to be more robust to deleterious mutations increases the chance of progeny surviving.
Following loss of the optimal phenotype, there was ongoing turnover of the best prevailing genotype. The dynamic nature of the best genotype in these populations was observed by comparing the highest-fitness genotype in the population over time (measured every 10th generation for 1000 generations in a single population at each of 6 mutation rates). For a given mutation rate, the number of times the highest fitness increased in the population approximately equalled the number of times the highest fitness decreased; a similar pattern was demonstrated analytically for very small mutation rates (Sella and Hirsh, 2005). The number of maximum-fitness changes was higher at higher mutation rates, but was not obviously different at 1000 generations than at 4000 generations.
The effect of beneficial mutations on these dynamic equilibria was demonstrated in a manner that is feasible only in simulations. During a run, mutations were introduced into a genome as before, but in this case, when each set of mutations was chosen, their combined fitness effect was evaluated in the recipient genome. If the mutations increased fitness, they were disallowed. In one version of this protocol, the total mutation rate was held constant by choosing another set of mutations (potentially at different sites) until a neutral or deleterious combination was found; in another protocol, beneficial mutations were blocked without replacement. In both protocols, fitness declined below - often well below - the equilibrium that had been attained when compensatory evolution was allowed, although the effect was small at low mutation rates (Fig. 5). The rate of fitness decline slowed after 1000 generations, due to a slowdown in the rate of best genotype loss, itself due to the evolution of a lower fraction of deleterious mutations and a larger (relative) effect size of individual deleterious mutations (data not shown).
Figure 5.
Evolution of population fitness through time in shallow fitness landscapes. Population mean fitness across 25 simulations was averaged every ten generations across five different mutation rates. Simulations varied in whether beneficial mutations were allowed (solid lines) or blocked and replaced (dashed lines); mutations were also replaced when they occurred in multiples and their net effect was beneficial. Blocking compensatory mutation in shallow landscapes led to a decline in mean fitness.
Finally, we examined the rate of beneficial mutations. At generation 1000 in 25 replicates evolved with a genomic mutation rate of U = 1.1, we found an average of 367 genotypes that had a fitness at least 20% higher than the mean, which we define as the highly-fit class. Of these 367 genotypes, 33 had unique beneficial mutations arising that generation. Thus, almost 10% of the highly-fit genotypes in the population acquired beneficial mutations in one generation. Multiple beneficial mutations were a general feature at the dynamic equilibrium; mutation rates higher than 0.2 led to at least one individual per generation gaining a mutation that put it in the highly-fit class. At the highest viable mutation rate, U = 2.6, 71 individuals per generation gained a beneficial mutation that put them in the high-fitness class.
Best genotype loss: Muller’s ratchet or error catastrophe?
The optimal genotype can be extinguished through either of two mechanisms: Muller’s ratchet (MR) and an error catastrophe (EC, survival of the flattest) (Muller, 1964;Eigen, 1971; Wilke et al., 2001; Bull et al., 2005). We would like to understand which mechanism, if either, is operating here. The underlying cause in both mechanisms is a high mutation rate that drives the expected frequency of the best genotype low. In an EC, the mutation rate is so high that the deterministic equilibrium of the mutation-free genotype is zero. Thus, if the mutation rate is increased above the EC threshold, the mutation-free genotype will be lost, but the population nonetheless achieves a fitness equilibrium in which selection offsets the deleterious effects of mutation accumulation. In MR, the expected equilibrium frequency of the best genotype is positive, but the expected number of individuals with that genotype is low in the finite population and either never exists (Gessler, 1995) or is lost by chance. As the next-best genotype can be lost by the same process, ad infinitum, there is no fitness equilibrium in the absence of compensatory evolution or reversion.
One useful indicator of whether the ratchet is operating here is to compare the lowest mutation rate at which the best genotype was lost to the lowest expected mutation-rate threshold for operation of MR in a few thousand generations. The expected size of the mutation-free class was given in (7), which may be rearranged and substituted as
| (8) |
If s is variable, use of the harmonic mean (s̅) is recommended (Orr, 2000).
The appropriate threshold n0 is difficult to calculate in this setting (see Rouzine et al., 2008, for calculations for a much simpler model system), so we accept Maynard Smith’s heuristic value of 10 (Maynard Smith, 1978). Using s̅ = 0.11 and Db = 0.67 (based on robust genotypes from the steep landscape and evaluated in the shallow landscape), we arrive at UT = 0.76. This value is close to the observed onset of best genotype loss (≈ 0.88). Given the uncertainty of how to parameterize (8), we consider it a tentatively acceptable fit and, in conjunction with the evidence that loss of the best genotype is continual, cautiously interpret the results as being consistent with a ratchet process.
Reconciling evolution in steep and shallow landscapes
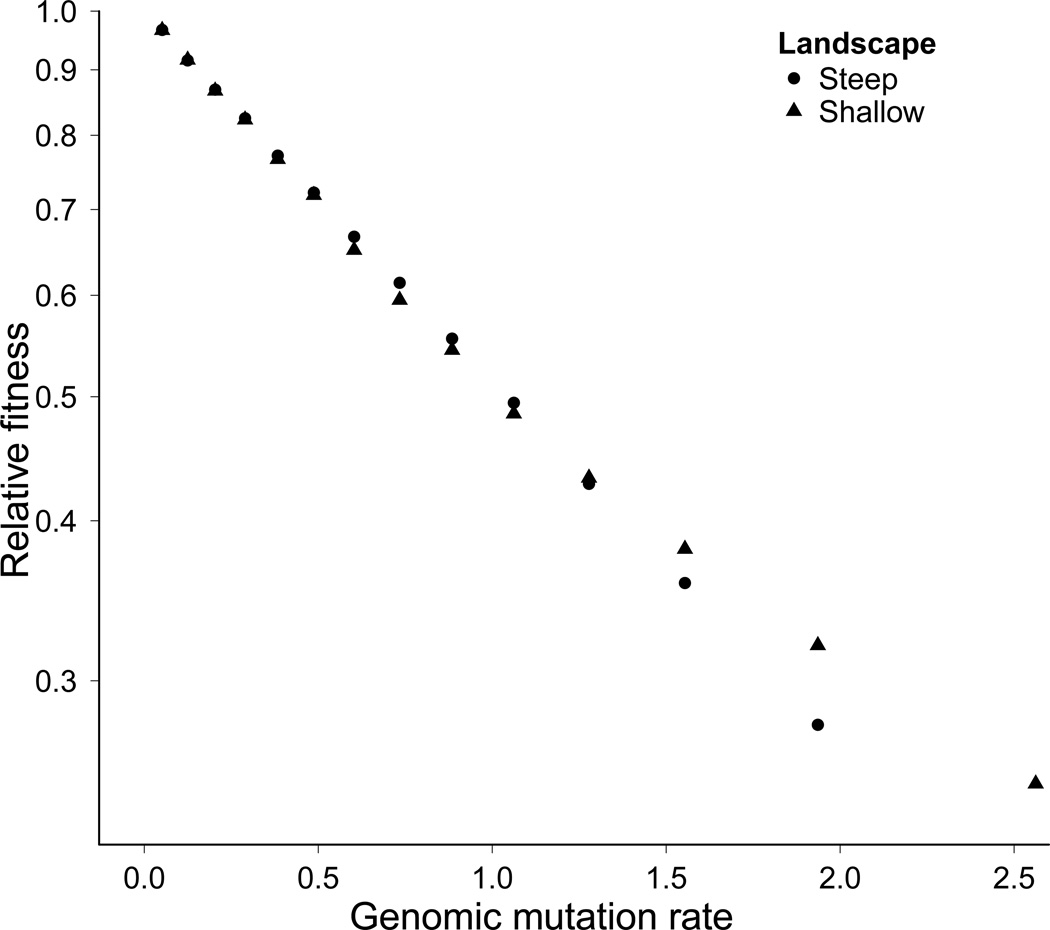
A striking anomaly was evident when comparing fitness equilibria in steep and shallow landscapes for N = 1000. As noted, mean fitness in steep landscapes fit the KM equilibrium, whereas mean fitness in shallow landscapes fell below the KM equilibrium. The anomaly is that, at a given U, equilibrium mean fitness in shallow landscapes actually exceeded fitness in steep landscapes. There are two dimensions to this anomaly, one of which has an easy explanation. For a given U (total mutation rate), the predicted KM equilibria differ between steep and shallow landscapes because different deleterious mutation rates have evolved. The deleterious fraction in shallow landscapes is reduced because a substantial fraction of mutations is now beneficial. Thus at any U, the predicted KM equilibrium is higher for shallow landscapes than for steep ones, so it is not surprising that the observed fitness in shallow landscapes can fall below its predicted KM equilibrium but can be above the equilibrium predicted for the steep landscape.
More notable is the difference of absolute fitnesses between steep and shallow landscapes: fitness equilibrated higher in shallow than steep landscapes at any U, although the effect is noticeable only at the highest rates (Fig. 6). We can offer three potential explanations for this difference, not necessarily independent. First, this difference could arise from some mechanism of the ratchet, because if the population was large enough to avoid loss of the best genotype, equilibrium fitness should be the same in the two landscapes. Recall that equilibrium fitness in the KM model depends only on the deleterious mutation rate, and the deleterious rate should be the same in the shallow and steep landscapes because robustness should be approximately the same if the ratchet does not operate. Our assumption here is that the selective pressure to reduce the fraction of deleterious mutations would be similar in the two fitness landscapes. Thus, operation of the ratchet is the obvious correlate of higher fitness in shallow landscapes and might be a direct or indirect cause.
Figure 6.
Equilibrium mean fitness is higher in shallow vs steep landscapes, most noticeably at high mutation rates; N = 1000. At the highest viable mutation rate, populations evolved under a shallow fitness landscapes survived whereas populations evolved under steep fitness landscapes went extinct.
Second, the occurrence of beneficial mutations itself might increase mean fitness, as genotypes with deleterious mutations could receive compensatory mutations that increase fitness. If beneficial mutations alone (regardless of the ratchet) increase mean fitness, this effect is expected to be stronger in populations occupying shallow landscapes, as genotypes with deleterious mutations persist longer due to weaker purifying selection. Third, as noted above, loss of the best genotype may be a type of error catastrophe - which increases W̅ above that in the KM equilibrium (Bull et al., 2007).
Evolutionary dynamics in smaller populations
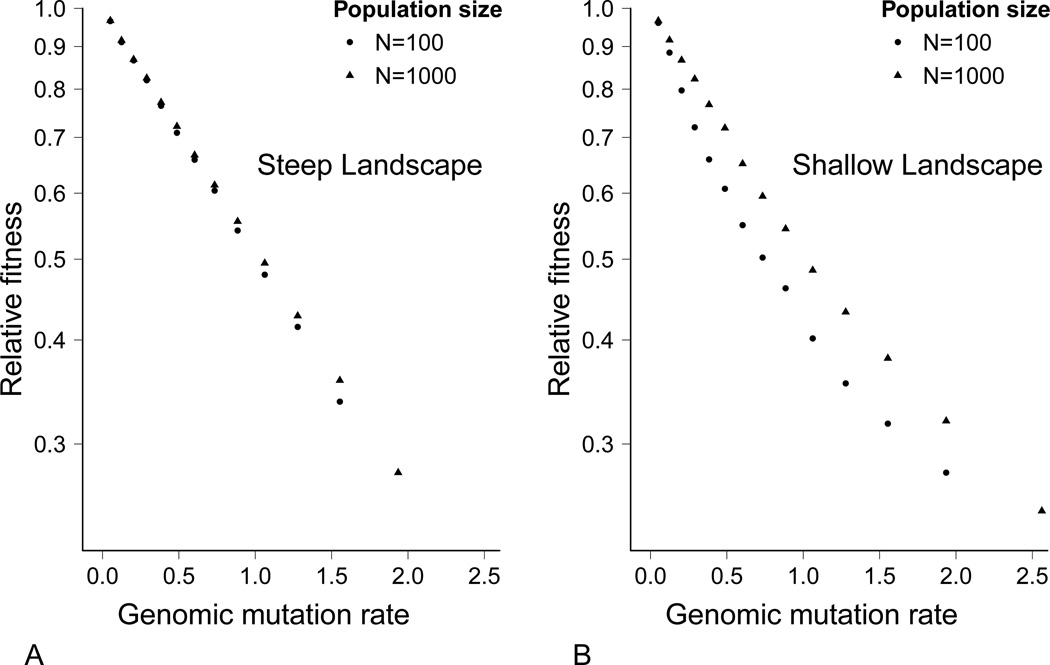
To assess the sensitivity of the foregoing results to population size constraints, simulations were conducted for both fitness landscapes using a smaller population size (N = 100). As with larger populations, the maximum possible population size was generally maintained unless extinction occurred. The equilibrium fitness in the steep landscape was close to that evolved at the larger population size (Fig. 7A). The best phenotype was also maintained across the viable mutation rates. However, the main difference was that these small populations went extinct at a lower mutation rate than did the larger populations. The smaller population size meant the best genotype was less likely to be maintained at the highest mutation rates, leading to their extinction. We have not explored the basis for this difference at which extinction occurs. One possibility might simply be a failure to evolve robustness.
Figure 7.
Comparison of mean fitness in steep and shallow fitness landscapes at different population sizes. (A) Comparison of mean fitness in steep landscape. (B) Comparison of mean fitness in shallow landscape.
For the shallow fitness landscape, the mean fitness was lower in small populations than in large populations (Fig. 7B). Second, the best genotype was lost at all but the lowest mutation rate tested (U = 0.05). As in the steep fitness landscape, populations went extinct at a slightly lower mutation rate than in the large populations.
Which landscape led to a higher genetic load differed between simulations of large and small populations. In contrast to simulations with a larger population size, steep fitness landscapes in general had a higher equilibrium fitness compared to a shallow fitness landscape. One exception was that populations with a shallow fitness landscape were able to persist at a higher mutation rate compared to populations with a steep fitness landscape.
This apparent sensitivity of the mutation load to the size of deleterious mutations and population size has been noted before. For example, Kimura et al. (1963) found in some cases the mutation load in finite populations was dependent on the selection coefficient of deleterious mutations. Specifically, Kimura et al. (1963) showed that populations with a lesser deleterious effect size could in fact have a higher mutation load than a population with a greater deleterious effect size. In a related fashion, we found that which fitness landscape leads to a relatively higher mutation load depends on the population size.
Evolution in populations with intermediate fitness landscape
We also conducted simulations with an intermediate fitness landscape and N = 1000 (fitness decline of 0.06, as opposed to 0.15 for steep landscapes and 0.025 for shallow fitness landscapes). This parameterization led to a mixture of the main features in the steep and shallow landscapes. First, predicted and observed fitness equilibria were in close accordance with each other, as in the steep fitness landscape (Fig. S3A). The best genotype was maintained at most mutation rates but lost at the highest viable mutation rate.
The equilibrium fitness distributions were intermediate. The frequency of the best genotype declined faster than in the steep landscape but not as much as in the shallow landscape (Fig. S3B).
Shallow and steep fitness results apply to more complex genomes
Our previous simulations considered individuals with a single chromosome and fitness landscape. Additional simulations allowed individuals to have genomes of two chromosomes (with no segregation or recombination). Each chromosome was selected for the same phenotype used in earlier simulations, but one chromosome experienced strong selection and the other weak selection. Total genome fitness was the sum of the fitnesses of each chromosome. Across a wide range of genomic mutation rates (population size of 1000), the best phenotype was lost for the chromosome experiencing the shallow landscape but not for the chromosome experiencing the steep landscape. Although it is not straightforward to compare this model with the single-landscape model, and furthermore, the model did not allow interactions between mutations in the different chromosomes, these results at least suggest that a genome with a mix of sites experiencing different sizes of deleterious effects may simultaneously exhibit both types of behavior for its different classes of mutations.
Discussion
We simulated evolution at high mutation rate in asexual populations of size 1000 to examine the interactions of various evolutionary processes. Individuals had a 99-base genome whose phenotype was a secondary structure determined by minimum free energy. Fitness was assigned as offspring number according to the deviation of the genome’s fold from an optimal target shape. The initial population was composed of a genotype with maximal fitness. A genomic mutation rate was imposed, but as the population evolved, so could the proportions of neutral, deleterious, and beneficial mutations. Our primary result is that the strength of selection determined which of two sets of processes dominated evolutionary dynamics.
There are at least six processes to be anticipated in these populations: (1) mutation-selection balance (Haldane, 1927; Kimura and Maruyama, 1966), (2) continual loss of the best genotypes (Muller’s Ratchet or fixation of deleterious mutations, e.g. (Muller, 1964; Haigh, 1978; Charlesworth et al., 1993; Gordo and Charlesworth, 2000; Stephan et al., 1993)), (3) compensatory evolution (Poon and Chao, 2005; Silander et al., 2007; Howe and Denver, 2008; Wilke et al., 2003), (4) clonal interference (Gerrish and Lenski, 1998; de Visser et al., 1999; Miralles et al., 1999), (5) evolution of robustness (Wilke and Adami, 2003), and (6) error catastrophes (van Nimwegen et al., 1999; Wilke, 2001). The simulations allowed us to identify most of these processes and disentangle them, though some difficulties in isolating individual effects remained. When deleterious mutations had large effects (case I), the population was dominated by (1) and (5). With weaker effects (case II), (1)–(4) operated, possibly (5) and (6) as well. Yet mean population fitness was almost indistinguishable between cases I and II, always strongly tied to mutation rate. Despite loss of the best genotypes in case II, fitness equilibrated from the input of compensatory mutations, as anticipated from prior theory (Poon and Otto, 2000) and empirical work (Silander et al., 2007). Furthermore, populations could go extinct if mean fitness dropped low enough, but extinction was observed only at the highest mutation rates. For case I, populations went extinct at U = 2.6 while populations in case II survive. When the population size was 100 populations went extinct at a lower mutation rate (U = 1.93 and U = 2.6 for the steep and shallow landscape, respectively).
The genomic mutation rates used in this study ranged from moderate to high, but potentially in the range experienced by RNA viruses and viroids (Drake et al., 1998; Sanjuan et al., 2004). And although the rates used in our study are high per cell division for organisms with DNA genomes, they are not out of line for some DNA genomes per generation (Lynch et al., 2006). Likewise, the high mutation rates used here would be experienced in bacterial mutator strains and attempts at lethal mutagenesis of viruses - the extinction of viral populations by artificial elevation of mutation rate (Fontanari et al., 2003; Pfeiffer and Kirkegaard, 2003; Grande-Pérez et al., 2005; Gerrish et al., 2007; Springman et al., 2010).
Strong selection relative to mutation rate (case I) led to a dynamic equilibrium between mutation and selection; populations evolved greater robustness by reducing the deleterious mutation rate and reducing the impact of those deleterious mutations that did occur. After an initial period of robustness evolution, population mean fitness was well-predicted by a simple model of mutation-selection balance. Genotypes belonging to the optimal phenotype class persisted in the long term; suboptimal genotypes were purged and replaced with new ones descended from the best genotypes. Compensatory evolution in suboptimal genotypes was of minor importance due to the rapid purging of sub-optimal genotypes, and the retention of the most-fit genotypes precluded the ratchet. Despite retention of the best genotype, populations with a mutation rate of 2.6 mutations per generation or more went extinct because their absolute mean fitness dropped low enough that parents had fewer than one offspring on average; this extinction threshold was as predicted by theory (Bull et al., 2007).
‘Weak’ selection relative to mutation rate (case II) resulted in profoundly different dynamics. The best genotype was lost, followed by the loss of next-best genotypes, and so on. Despite continuing losses, fitness equilibrated dynamically, with continued loss of good genotypes offset by beneficial mutations. While compensatory mutations offset some of the fitness decline, populations with the highest mutation rate used in case II still went extinct.
Robustness evolved in multiple ways in these simulations. Most straightforward was the evolution of genomes that had fewer possible ways to experience deleterious mutations. In addition, genomes became more robust to the effect of a deleterious mutation. This second type of robustness is potentially important when selection is weak, such that suboptimal offspring are maintained for a longer period of time.
There was also some evidence of clonal interference in case II, in that multiple beneficial mutations arose on different genetic backgrounds in a given generation. This interference between beneficial mutations slows down the rate of adaptation in asexual populations Gerrish and Lenski (1998). Population mean fitness equilibrated by generation 1000, however, so any effect of clonal interference would not have been noticeable in our data. Thus, while the necessary condition for clonal interference is present for most simulations (multiple beneficial mutations occurring at the same time on different genotypes), it is unclear clear what, if any effect it had.
The main limitation of our model would seem to be the absence of deleterious mutations with small effects (e.g., s ≤ 0.01). It is widely regarded that selection coefficients below 0.01 are important in evolution, and experimental studies have found that non-lethal mutations often reduce fitness by 1% or less (Sanjuan et al., 2004; Lind et al., 2010). Yet introducing selective coefficients this small into our model leads to unacceptably high fitness of random genotypes, an artifact of the small genome size that computational constraints require at present. In contrast to our study, analytical theory on mutation-selection balance is often developed for small selective effects. Waxman and Peck (2006) examined conditions under which pleiotropy between multiple quantitative traits can lead to the maintenence of an optimal genotype even under high mutation rates. Martin and Gandon (2010) examined the potential efficacy of lethal mutagenesis in an epidemiological framework.
The theory on Muller’s ratchet has also become more sophisticated in recent years. For example, Gordo and Charlesworth (2000) found that Muller’s ratchet can operate in sizable populations, yet it can also stall out if the selection coefficient is sufficiently strong. There have also been several studies that have begun exploring the rate of Muller’s ratchet when mutations have a distribution of selection coefficients (Johnson, 1999; Söderberg and Berg, 2007). While relating results from these models to ours would be useful, and is ultimately needed for a full understanding of the problem, differences in the underlying models make comparisons difficult at present. Indeed, although our populations in shallow landscapes experienced continual loss of the best genotype, we could not unambiguously assign the process to the ratchet versus an error catastrophe. Thus, an obvious next step is to develop methods for identifying when the ratchet per se operates.
Supplementary Material
Acknowledgements
We thank W. Harcombe, R. Heineman, and R. Springman for reading many early versions of these manuscript and giving plenty of helpful advice. We also thank R. Heineman for suggesting the idea of blocking compensatory mutations to understand what effect they have on populations. M. Cowperthwaite and L. A. Meyers provided RNA simulation code that informed an early implementation of our simulations. We thank S. Gandon and both reviewers; one reviewer in particular helped us clarify our presentation and thinking on several points. This research was funded in part from grants NIH GM 57756 to J.J. Bull and NSF EF-0742373 and Cooperative Agreement DBI-0939454 to C.O. Wilke.
References
- Behnel S, Bradshaw R, Citro C, Dalcin L, Seljebotn DS, Smith K. Cython: The best of both worlds. Computing in Science and Engineering. 2011;13:31–39. [Google Scholar]
- Bloom JD, Silberg JJ, Wilke CO, Drummond DA, Adami C, Arnold FH. Thermodynamic prediction of protein neutrality. Proc. Natl. Acad. Sci. USA. 2005;102:606–611. doi: 10.1073/pnas.0406744102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bull J, Sanjuan R, Wilke C. Theory of lethal mutagenesis for viruses. J. Virology. 2007;81:2930–2939. doi: 10.1128/JVI.01624-06. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Bull JJ, Meyers LA, Lachmann M. Quasispecies made simple. PLoS Comput. Biol. 2005;1:450–460. doi: 10.1371/journal.pcbi.0010061. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Charlesworth D, Morgan MT, Charlesworth B. Mutation accumulation in finite populations. J. Herid. 1993;84:321–325. [Google Scholar]
- Cowperthwaite M, Bull JJ, Meyers LA. From bad to good: fitness reversals and the ascent of deleterious mutations. PLoS Comput. Biol. 2006;2:e141. doi: 10.1371/journal.pcbi.0020141. [DOI] [PMC free article] [PubMed] [Google Scholar]
- de Visser JAGM, Zeyl CW, Gerrish PJ, Blanchard JL, Lenski RE. Diminishing returns from mutation supply rate in asexual populations. Science. 1999;283:404–406. doi: 10.1126/science.283.5400.404. [DOI] [PubMed] [Google Scholar]
- Doudna JA. Structural genomics of RNA. Nat. Struct. Biol. 2000;7:954–956. doi: 10.1038/80729. [DOI] [PubMed] [Google Scholar]
- Drake JW, Charlesworth B, Charlesworth D, Crow JF. Rates of spontaneous mutation. Genetics. 1998;148:1667–1686. doi: 10.1093/genetics/148.4.1667. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Drake JW, Holland JJ. Mutation rates among RNA viruses. Proc. Natl. Acad. Sci. USA. 1999;96:13910–13913. doi: 10.1073/pnas.96.24.13910. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eigen M. Selforganization of matter and the evolution of macromolecules. Die Naturwissenschaften. 1971;58:465–523. doi: 10.1007/BF00623322. [DOI] [PubMed] [Google Scholar]
- Fontanari JF, Colato A, Howard RS. Mutation accumulation in growing asexual lineages. Phys. Rev. Lett. 2003;91:218101. doi: 10.1103/PhysRevLett.91.218101. [DOI] [PubMed] [Google Scholar]
- Forster R, Adami C, Wilke C. Selection for mutational robustness in finite populations. J. Theor. Biol. 2006;243:181–190. doi: 10.1016/j.jtbi.2006.06.020. [DOI] [PubMed] [Google Scholar]
- Gerrish PJ, Colato A, Perelson AS, Sniegowski PD. Complete linkage can subvert natural selection. Proc. Natl. Acad. Sci. 2007;104:6266–6271. doi: 10.1073/pnas.0607280104. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gerrish PJ, Lenski RE. The fate of competing beneficial mutations in an asexual population. Genetica. 1998;102/103:127–144. [PubMed] [Google Scholar]
- Gessler DD. The constraints of finite size in asexual populations and the rate of the ratchet. Genet. Res. 1995;66:241–253. doi: 10.1017/s0016672300034686. [DOI] [PubMed] [Google Scholar]
- Gordo I, Charlesworth B. On the speed of Muller’s Ratchet. Genetics. 2000;156:2137–2140. doi: 10.1093/genetics/156.4.2137. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Grande-Pérez A, Lázaro A, Lowenstein P, Domingo E, Manrubia S. Suppression of viral infectivity through lethal defection. Proc. Natl. Acad. Sci. USA. 2005;102:4448–4452. doi: 10.1073/pnas.0408871102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Haigh J. The accumulation of deleterious genes in a population–Muller’s Ratchet. J. Theoretical Biology. 1978;14:251–267. doi: 10.1016/0040-5809(78)90027-8. [DOI] [PubMed] [Google Scholar]
- Haldane JBS. A mathematical theory of natural and artificial selection. Part V: Selection and mutation. Proc. Camp. Phil. Soc. 1927;23:838–844. [Google Scholar]
- Hofacker IL, Fontana W, Stadler PF, Bonhoeffer S, Tacker M, Schuster P. Fast folding and comparison of RNA secondary structures. Monatshefte f. Chemie. 1994;125:167–188. [Google Scholar]
- Howe DR, Denver DK. Muller’s ratchet and compensatory mutation in Caenorhabditis briggsae mitaochondrial genome evolution. BMC Evol. Biol. 2008;8:13. doi: 10.1186/1471-2148-8-62. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Johnson T. The approach to mutation-selection balance in an infinite asexual population, and the evolution of mutation rates. Proc. R. Soc. Lond. B. 1999;266:2389–2397. doi: 10.1098/rspb.1999.0936. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jörg T, Martin OC, Wanger A. Neutral network sizes of biological RNA molecules can be computed and are atypically large. BMC Bioinformatics. 2008;9:464. doi: 10.1186/1471-2105-9-464. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M, Maruyama T. The mutational load with epistatic gene interactions in fitness. Genetics. 1966;54:1337–1351. doi: 10.1093/genetics/54.6.1337. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kimura M, Maruyama T, Crow JF. The mutation load in small populations. Genetics. 1963;48:1303–1312. doi: 10.1093/genetics/48.10.1303. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lind PA, Berg OG, Andersson DI. Mutational robustness of ribosomal protein genes. Science. 2010;330:825–827. doi: 10.1126/science.1194617. [DOI] [PubMed] [Google Scholar]
- Lynch M, Koskella B, Schaack S. Mutation pressure and the evolution of organelle genome architecture. Science. 2006;311:1727–1730. doi: 10.1126/science.1118884. [DOI] [PubMed] [Google Scholar]
- Martin G, Gandon S. Lethal mutagenesis and evolutionary epidemiology. Phil. Trans. R. Soc. B. 2010;365:1953–1963. doi: 10.1098/rstb.2010.0058. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maynard Smith J. The Evolution of Sex. Cambridge: Cambridge University Press; 1978. [Google Scholar]
- Meer MV, Kondrashov AS, Artzy-Randrup Y, Kondrashov FA. Compensatory evolution in mitochondrial tRNAs navigates valleys of low fitness. Nature. 2010;464:279–282. doi: 10.1038/nature08691. [DOI] [PubMed] [Google Scholar]
- Miralles R, Gerrish PJ, Moya A, Elena SF. Clonal interference and the evolution of rna viruses. Science. 1999;285:1745–1747. doi: 10.1126/science.285.5434.1745. [DOI] [PubMed] [Google Scholar]
- Muller HJ. The relation of recombination to mutational advance. Mutat. Res. 1964;106:2–9. doi: 10.1016/0027-5107(64)90047-8. [DOI] [PubMed] [Google Scholar]
- Orr HA. The rate of adaptation in asexuals. Genetics. 2000;155:961–968. doi: 10.1093/genetics/155.2.961. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pfeiffer k, Kirkegaard K. A single mutation in poliovirus RNA-dependent RNA polymerase confers resistance to mutagenic nucleotide analogs via increased fidelity. Proc. Natl. Acad. Sci. USA. 2003;100:7289–7294. doi: 10.1073/pnas.1232294100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Poon A, Otto S. Compensating for ouR load of mutations: freezing the meltdown of small population. Evolution. 2000;54:1467–1479. doi: 10.1111/j.0014-3820.2000.tb00693.x. [DOI] [PubMed] [Google Scholar]
- Poon AF, Chao L. The rate of compensatory mutation in the bacteriophage φ X174. Genetics. 2005;170:1989–1999. doi: 10.1534/genetics.104.039438. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rouzine IM, Brunet E, Wilke CO. The traveling-wave approach to asexual evolution: Muller’s ratchet and speed of adaptation. Theor. Popul. Biol. 2008;73:24–46. doi: 10.1016/j.tpb.2007.10.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanjuan R, Moyas A, Elena SF. The distribution of fitness effects caused by single-nucleotide substitutions in an RNA virus. Proc. Natl. Acad. Sci. USA. 2004;101:8396–8401. doi: 10.1073/pnas.0400146101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sella G, Hirsh AE. The application of statistical physics to evolutionary biology. Proc. Natl. Acad. Sci. USA. 2005;102:9541–9546. doi: 10.1073/pnas.0501865102. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Silander OK, Tenaillon O, Chao L. Understanding the evolutionary fate of finite populations: the dynamics of mutational effects. PLoS Biol. 2007;5:922–931. doi: 10.1371/journal.pbio.0050094. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Söderberg RJ, Berg OG. Mutational interference and the progression of Muller’s ratchet when mutations have a broad range of deleterious effects. Genetics. 2007;177:971–986. doi: 10.1534/genetics.107.073791. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Springman R, Keller T, Molineux I, Bull J. Evolution at a high mutation rate: adaptation obscures the load in phage t7. Genetics. 2010;184:221–232. doi: 10.1534/genetics.109.108803. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Stephan W, Chao L, Smale JG. The advance of Muller’s ratchet in a haploid asexual population, approximate solutions based on diffusion theory. Genet. Res. 1993;61:225–231. doi: 10.1017/s0016672300031384. [DOI] [PubMed] [Google Scholar]
- van Nimwegen E, Crutchfield JP, Huynen M. Neutral evolution of mutational robustness. Proc. Natl. Acad. Sci. USA. 1999;96:9716–9720. doi: 10.1073/pnas.96.17.9716. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Waxman D, Peck JR. The frequency of the perfect genotype in a population subject to pleiotropic mutation. J. Theor. Biol. 2006;69:406–418. doi: 10.1016/j.tpb.2006.01.004. [DOI] [PubMed] [Google Scholar]
- Wilke CO. Selection for fitness versus selection for robustness in RNA secondary structure folding. Evolution. 2001;55:2412–2420. doi: 10.1111/j.0014-3820.2001.tb00756.x. [DOI] [PubMed] [Google Scholar]
- Wilke CO. Quasispecies theory in the context of population genetics. BMC Evol. Biol. 2005;5:44. doi: 10.1186/1471-2148-5-44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilke CO, Adami C. Evolution of mutational robustness. Mutat. Res. 2003;522:3–11. doi: 10.1016/s0027-5107(02)00307-x. [DOI] [PubMed] [Google Scholar]
- Wilke CO, Lenski RE, Adami C. Compensatory mutations cause excess of antagonistic epistasis in RNA secondary structure folding. BMC Evol. Biol. 2003;3:3. doi: 10.1186/1471-2148-3-3. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wilke CO, Wang JL, Ofria C, Lenski RE, Adami C. Evolution of digital organisms at high mutation rate leads to survival of the flattest. Nature. 2001;412:331–333. doi: 10.1038/35085569. [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.