Abstract
How much gene flow is needed to inhibit speciation by the accumulation of Dobzhansky–Muller incompatibilities (DMIs) in a structured population? Here, we derive these limits in a classical migration–selection model with two haploid or diploid loci and unidirectional gene flow from a continent to an island. We discuss the dependence of the maximum gene-flow rate on ecological factors (exogeneous selection), genetic factors (epistasis, recombination), and the evolutionary history. Extensive analytical and numerical results show the following: (1) The maximum rate of gene flow is limited by exogeneous selection. In particular, maintenance of neutral DMIs is impossible with gene flow. (2) There are two distinct mechanisms that drive DMI evolution in parapatry, selection against immigrants in a heterogeneous environment and selection against hybrids due to the incompatibility. (3) Depending on the mechanism, opposite predictions result concerning the genetic architecture that maximizes the rate of gene flow a DMI can sustain. Selection against immigrants favors evolution of tightly linked DMIs of arbitrary strength, whereas selection against hybrids promotes the evolution of strong unlinked DMIs. In diploids, the fitness of the double heterozygotes is the decisive factor to predict the pattern of DMI stability.
Keywords: parapatric speciation, ecological speciation, migration–selection model, Dobzhansky–Muller incompatibility (DMI), epistasis
THE (Bateson–) Dobzhansky–Muller model (DMM) (Bateson 1909; Dobzhansky 1936; Muller 1942) is the standard model to explain the evolution of intrinsic postzygotic isolation. A variety of theoretical studies show the plausibility of this model (reviewed in Coyne and Orr 2004; Gavrilets 2004), and numerous empirical studies report Dobzhansky–Muller incompatibilities (DMIs) across several species of animals and plants (see reviews by Lowry et al. 2008 and Presgraves 2010).
The appeal of the DMM is its generality: Speciation happens as a by-product of divergence without the need of special selection scenarios or complex adaptations to cross fitness valleys (cf. Orr 1995). The sole, but crucial, assumption is sufficient evolutionary time to let the process unfold and the spatial separation of the incipient species during this phase. The plausibility of the DMM as a mechanism for speciation and the widespread belief in the prevalence of allopatric speciation (Mayr 1942; Coyne and Orr 2004) go hand in hand. However, given that even tiny amounts of gene flow (of the order of a single migrant per generation) can have substantial effects on divergence (Slatkin 1987), it is clear that the assumption of strict allopatry is an idealization. This poses the question of the relevance of the DMM in parapatry and thus whether DMIs can originate or be maintained in the presence of gene flow. It has been suggested that the accumulation of DMIs in parapatry is possible (e.g., Gavrilets 1997, 2004; Porter and Johnson 2002; Kondrashov 2003; Agrawal et al. 2011; Nosil and Flaxman 2011). However, usually only the limit of weak migration has been studied. In contrast, we focus on the maximum rates of gene flow that admit the maintenance of a DMI.
A key factor in speciation via the DMM is the mechanism that drives divergence. Although the original DMM is consistent with neutral substitutions that spread solely by genetic drift, all previous results indicate that selection as a driving force is needed in the presence of gene flow (e.g., Gavrilets 1997). Recently, a distinction of two categories was brought forward to describe the selection scenarios that can promote speciation through DMIs in a structured population (Schluter 2009; but see also Turelli et al. 2001; Rundell and Price 2009): Whereas “ecological speciation” refers to the case where divergent selection results in the spread of (potentially incompatible) locally adapted substitutions, “mutation-order speciation” is characterized by fixation of different globally advantageous alleles in populations adapting to similar selection pressures. The latter mechanism is termed “mutation order” because it is assumed to be critically dependent on the order in which substitutions arise (Mani and Clarke 1990).
Whereas speciation due to ecological divergence is supported by considerable empirical evidence, only a few cases of mutation-order speciation have been identified (reviewed in Schluter 2009). Furthermore, simulation studies have strengthened verbal arguments claiming that mutation-order speciation is expected to be less likely than ecological speciation (Unckless and Orr 2009; Nosil and Flaxman 2011). However, there is a lack of analytical work to justify this nomenclature and to quantify the conditions for the evolution of DMIs according to these mechanisms.
In this study, we address these issues in two minimal models for the evolution of a DMI on an island that receives migrants from a continent. We are able to provide an almost complete characterization of the conditions and limits for the origination and maintenance of DMIs in the presence of gene flow. Models, results, and biological interpretations are presented in the main body of the article. Our methods combine classical approaches (Karlin and McGregor 1972a; Lande 1979; Rutschman 1994) with more advanced tools from dynamical systems theory (Hofbauer 1990; Nagylaki et al. 1999). Since our analytical results require elaborate derivations, all details about methods and proofs are collected in the Supporting Information.
Models
To determine the conditions for the origin and maintenance of a DMI, we use classical migration–selection models in continuous time. We assume that a population is divided into two panmictic subpopulations, continent and island, each of infinite size. There is unidirectional gene flow from the continent to the island at rate m. Individuals may be haploid or diploid; both cases are considered in separate sections. Selection acts on two diallelic loci, and ℬ, with alleles a, A and b, B, respectively. Lowercase letters denote the compatible alleles and uppercase letters the incompatible alleles. The fitness schemes are given below. The loci may be linked and recombine at rate r.
We consider the fate of individual substitutions at both loci, but ignore recurrent mutation. A DMI corresponds to a (stable) two-locus polymorphism. It can evolve from a homogeneous ancestral state either by one single-locus substitution in each of the two subpopulations (a so-called derived-derived DMI) or by two subsequent substitutions in the same subpopulation (a derived-ancestral DMI).
For a derived-derived DMI, we assume that the entire population is initially fixed for the “wild-type haplotype” ab. Subsequently, the mutant alleles A and B may invade on the island and the continent, respectively. We assume that on the continent the “continental haplotype” aB is superior to the wild type, whereas on the island the fitness of the “island haplotype” Ab is at least as high as that of the wild type.
We distinguish the following evolutionary scenarios:
Continent–island. Allele B invades first, goes to fixation on the continent, and reaches migration–selection equilibrium on the island. Subsequently, allele A appears on the island.
Island–continent. Allele A invades first on the island. Subsequently, allele B invades and becomes fixed on the continent.
Secondary contact. Both populations are in secondary contact after an allopatric phase. During allopatry, the continent has become fixed for allele B and the island for allele A.
Island–island. Here, aB is the ancestral state. Subsequently, first allele b and then allele A invade on the island.
Continent–continent. Here, Ab is the ancestral state. Allele a and then allele B invade on the continent.
Evolution on the continent is independent of the population composition on the island. We assume that every equilibrium on the continent is monomorphic and any substitution occurs quickly. In all scenarios, the continent is eventually fixed for the continental haplotype aB. We can then treat the continent simply as a source of aB migrants and need only to keep track of the allele frequencies on the island. The different evolutionary scenarios introduced above correspond to different initial conditions for the haplotype frequencies on the island (see Appendix, Initial conditions).
Below, we analyze how the equilibrium structure on the island depends on the model parameters for selection, recombination, and migration. In particular, we are interested in the parameter ranges where the island haplotype Ab can be maintained. Since the alleles a and b will always be present due to immigration, a stable DMI corresponds to an asymptotically stable, fully polymorphic equilibrium on the island. For sufficiently strong migration, the island will always be swamped by the continental haplotype aB (implying loss of A). Therefore, our focus is on the determination of the maximum migration rate mmax that allows for a fully polymorphic equilibrium. If this equilibrium is not globally stable, i.e., if convergence depends on the initial condition, we will investigate under which of the scenarios it can be reached.
The haploid model
Let x1, x2, x3, and x4 denote the frequencies of the four haplotypes ab, aB, Ab, and AB on the island. They satisfy xi ≥ 0 for every i and . We assume that selection acts on individuals during the haploid phase of their life cycle according to the scheme for Malthusian fitness values given in Table 1.
Table 1 . Haplotype fitnesses and frequencies in the haploid model.
| ab: | aB: | Ab: | AB: | |
|---|---|---|---|---|
| Haplotype | wild type | continental | island | recombinant |
| Fitness | w1 = 0 | w2 = β | w3 = α | w4 = α + β − γ |
| Frequency | x1 | x2 | x3 | x4 |
This scheme is entirely general. The fitness of the wild-type haplotype is arbitrarily normalized to 0. The parameters α and β measure a potential selective advantage of the island and continental haplotypes, respectively, on the island (exogeneous selection). They can be positive or negative. However, below we assume that α > 0 because, as will be shown, otherwise a DMI cannot exist. Finally, the epistasis paramter γ measures the strength of the incompatibility among the A and B alleles (endogeneous selection). We assume γ ≥ 0, such that epistasis is negative or absent (γ = 0).
Assuming weak evolutionary forces in continuous time, the haplotype dynamics read
| (1) |
Here, the “dot” denotes the derivative with respect to time, D = x1x4 − x2x3 is the measure of linkage disequilibrium, and
is the mean Malthusian fitness. Alternatively, the dynamics can be written in terms of the allele frequencies and the linkage-disequilibrium coefficient D (see Appendix, Haploid Model).
The diploid model
In the diploid case, selection acts on the 16 different combinations of two-locus haplotypes. Neglecting position effects and assuming no dominance for the A and B alleles in the wild-type (ab) background, we arrive at the fitness scheme with six parameters given in Table 2.
Table 2 . Genotype fitnesses in the diploid model.
| aa | aA | AA | |
|---|---|---|---|
| bb | 0 | α | 2α |
| bB | β | α + β − γ1 | 2α + β − γ3 |
| BB | 2β | α + 2β − γ2 | 2α + 2β − γ4. |
We thus allow for a quadruple of four independent epistasis parameters, Γ = (γ1, γ2, γ3, γ4), for the four different incompatibility genotypes. These genotypes differ in the number of A/B conflicts, one (aAbB), two (AAbB, aABB), or four (AABB), and correspond to the H0, H1, or H2 incompatibilities in Turelli and Orr (2000). As in the haploid case, we assume α, γi ≥ 0. In the most plausible case, epistasis is nondecreasing with the number of conflicts, i.e., γ1 ≤ min [γ2, γ3], max[γ2, γ3] ≤ γ4. Assuming Hardy–Weinberg equilibrium throughout, we can write the dynamics entirely in terms of the haplotype frequencies. These dynamics take the same functional form as in the haploid case (Equation 1), but with the fitness values replaced by the corresponding marginal fitnesses and the diploid mean fitness (File S2, Equations S.101 and S.102).
Results: Haploid Model
We first treat the haploid model for which the exact conditions for the existence of a stable (parapatric) DMI can be derived. These results are based on the analysis of the equilibrium structure of the model, which is described in the Appendix. All proofs and derivations, which require advanced mathematical methods, are given in the supporting information. File S1 contains a complete analysis of the haploid model, which, as a by-product, extends and complements previous studies of haploid two-locus selection (and migration) models. File S2 contains the derivations of the results for the diploid model and File S4 contains a Mathematica notebook with additional supporting material.
We are interested in the maximum rate of gene flow that allows for the evolutionary origin and the maintenance of a DMI in parapatry. In general, this rate depends on the initial conditions that correspond to the different evolutionary scenarios. As it turns out, however, we need to distinguish only two maximum rates, which we denote as and . A globally asymptotically stable internal equilibrium exists if and only if . As a consequence, a stable DMI will evolve from every initial condition (hence, under all evolutionary scenarios). A locally stable internal equilibrium exists if and only if . Local stability is a necessary and sufficient condition for the long-term maintenance of a DMI. If , no DMI can exist under any level of gene flow. In addition to , we consider the equilibrium frequency of the island haplotype at a DMI as a measure of two-locus population differentiation that is achieved for a given set of parameters. With this definition, differentiation is positive if and only if a DMI can be maintained.
Both maximum rates, and , are functions of the selection coefficients α, β, and γ and the recombination rate r. At most one stable internal equilibrium can exist, and extensive numerical calculations did not produce complex attractors such as limit cycles. If a DMI exists for a given set of parameters, the allele frequencies at this equilibrium are thus unique. A (globally) stable DMI for some migration rate implies the existence of a (globally) stable DMI for every positive . Hence, the rates are the unique boundaries of well-defined parameter regimes. Obviously, . If , the evolutionary dynamics are bistable and the DMI will not be reached from every initial condition. Extensive numerical simulations (and a proof for the special case of independent loci) show that a DMI will evolve for such a bistable case if and only if the second substitution enters the population in a deme where the incompatible allele is absent. Clearly, this is the case for secondary contact, but also if the first substitution occurs on the island and the second substitution on the continent or if both substitutions occur on the continent. In contrast, a stable DMI will never be reached for if the first substitution is on the continent and the second on the island or if both substitutions occur on the island. In both these latter scenarios, migrants from the continent carrying the incompatible allele hamper the establishment of the second substitution on the island.
Necessary conditions for stable DMIs
Fully polymorphic equilibria (or complex attractors) cannot exist if all evolutionary trajectories approach the boundary of the allele-frequency space. In File S1, section S.2, we establish necessary conditions for the existence of a DMI by means of Lyapunov functions. In particular, a DMI can exist only if
| (2) |
i.e., the island haplotype Ab must be on a local peak of the fitness landscape, relative to both its single-step mutational neighbors, ab and AB. Most significantly, the condition excludes the evolution of a DMI by a neutral process even in the secondary contact scenario: The substitution of the island allele A must be adaptive, α > 0. We henceforth assume (2) in addition to γ ≥ 0 for all our derivations and results.
This condition does not require that the island haplotype occupies an absolute fitness maximum. The fitness of the continental type aB can be larger; i.e., β > α. If this is the case, however, we can show that a DMI can exist only if
| (3) |
i.e., if continental immigrants are broken up by sufficiently strong recombination. Conditions (2) and (3) constrain the parameter space for a parapatric DMI under any level of gene flow, i.e., even under arbitrarily weak migration. For higher gene-flow rates we find additional conditions, which can be expressed as upper bounds for the maximum gene-flow rate ,
| (4a) |
| (4b) |
| (4c) |
Condition (4a) implies and extends (3). For gene-flow rates above any of these bounds, we obtain global convergence to one of the boundary equilibria. As detailed in the Appendix, Boundary equilibria and global stability, at most three boundary equilibria can exist if m > 0. In addition to the monomorphic equilibrium corresponding to fixation of the continental haplotype (denoted by M2), there are two equilibria with a single-locus polymorphism: An equilibrium Sℬ with locus ℬ polymorphic and locus fixed for allele a exists if the continental haplotype aB is maladaptive on the island and the ancestral type ab resists the immigration pressure (i.e., if m < −β). Similarly, an equilibrium exists (with locus polymorphic and locus ℬ fixed for allele B) whenever the recombinant haplotype AB can resist the immigration pressure (i.e., if m < α − γ).
Limiting cases
Our results for the haploid model are based on a complete analytical characterization of the maximum rates of gene flow admitting a DMI. However, since the analytical expressions for and require multiple case distinctions, the statement of the complete, explicit results is deferred to the Appendix, Boundary equilibria and global stability and Internal equilibria and local stability. Below, we focus on several limiting cases for which the results take a simple form. In particular, we treat the cases of weak migration (small m), complete linkage (r = 0), and independent loci (D = 0). Discussion of these limits already allows us to draw the most important conclusions about DMI stability.
Weak migration:
For m = 0 the haploid two-locus model was already studied by Rutschman (1994); see also Feldman (1971). In this case, the only boundary equilibria are the monomorphic equilibria Mi (where xi = 1), and at least one of them is stable. Rutschman’s results together with those in File S1, section S.5 imply that if an internal equilibrium exists, it is unstable. As a consequence, if m > 0, any stable internal equilibrium must be a perturbation of the monomorphic equilibrium M3 (fixation of the island haplotype) that is pushed into the interior of the state space due to immigration of aB haplotypes. The stability properties of the perturbed equilibrium are the same as for the unperturbed equilibrium (Karlin and McGregor 1972a; Bürger 2009).
We therefore obtain the necessary and sufficient conditions for a stable DMI under weak migration from the stability analysis of M3 if m = 0. Expressed in terms of ,
| (5a) |
and, if ,
| (5b) |
From (5a) we conclude that (2) and (3) are not only necessary, but also sufficient conditions for an asymptotically stable internal equilibrium if migration is sufficiently weak.
A perturbation analysis yields the approximate coordinates of the perturbed internal equilibrium near M3. In particular, the equilibrium frequency of the island haplotype Ab, which we use as our measure of population differentiation, is
| (6) |
The second term describes the loss of Ab due to direct competition with the immigrating continental haplotype aB, whereas the third term results from competition of Ab with the recombination products ab and AB. Equation 6 shows that, for small m, population differentiation increases with the recombination rate r if and only if breaking up the immigrating continental type reduces the competition experienced by the island type. This is the case if either β > α or α−1 + (γ − β)−1 < (α − β)−1. These conditions can be summarized as
| (7) |
Tight linkage:
If the two incompatibility loci are completely linked (r = 0), at most two haplotypes can coexist at an equilibrium (i.e., one of ab, Ab, or AB, in addition to the continental haplotype aB); see File S1, section S.8.1. A fully polymorphic DMI, with haplotypes Ab and aB present, exists and is globally asymptotically stable if
| (8) |
Thus, a bistable regime does not exist for r = 0. The DMI simply leaves the state space through the monomorphic equilibrium M2 as m increases beyond α − β. As a consequence, the population differentiation decreases to zero as m approaches Indeed, we find
| (9) |
Perturbation results guarantee that the same qualitative behavior [i.e., global stability of a DMI and continuous decrease of to zero] holds for recombination rates below a threshold r* > 0.
Independent loci:
If recombination is sufficiently strong relative to selection and migration, we can assume that the loci are in linkage equilibrium. In this case, the evolutionary dynamics reduce from three to two dimensions, and we can determine the exact position and the stability of all internal equilibria (see File S1, section S.8.2). We can exclude cycling behavior and show that at most two internal equilibria can exist, one of which is asymptotically stable whenever it exists. The maximum rate of gene flow admitting a globally stable DMI can be obtained from the formulas for general r in the Appendix, Internal equilibria and local stability, or from Equations S.93 and S.94 in File S1. It simplifies to
| (10) |
where negative values imply that no DMI can exist. For local stability, we find the following condition:
| (11) |
Thus, for sufficiently large γ, i.e., if γ > max[|β|, α/2], we obtain a bistable regime in which evolution of a DMI depends on initial conditions.
An explicit (but lengthy) expression for the level of population differentiation is given in File S1, Equation S.97. An illuminating result is obtained if we study in the limit of strong epistasis, γ → ∞. Here, we find
| (12) |
From (11), we note that in this case. Thus, the amount of population differentiation at the DMI is independent of β for strong epistasis and never falls below 1/2. Compared to tight linkage (Equation 9), this different behavior of results from the fact that, here, the stable internal equilibrium does not leave the state space through one of the boundary equilibria at , but disappears upon merging with an unstable internal equilibrium.
Stability of parapatric DMIs in the haploid model
We can draw several conclusions concerning the conditions and mechanisms for the evolution of parapatric DMIs that summarize our main findings for the haploid model.
First, condition (4b) defines a sharp upper bound on the rate of gene flow that admits a (two-locus) DMI. Because this bound depends only on the exogenous selection coefficients α and β, a DMI is impossible for higher migration rates, irrespective of the choice of γ or r. It is sharp, in the sense that DMIs with an appropriate genetic architecture (in terms of γ and r) can evolve for every rate of gene flow below it. Second, depending on which of the terms on the right-hand side of (4a) is relevant for the bound, the DMIs that remain stable under the highest gene-flow rates may have widely diverging architectures: On the one hand, if , then a tightly linked DMI of arbitrary strength (provided γ > β) will sustain the maximum level of gene flow. On the other hand, if α/4 ≥ α − β, Equation 11 shows that a strong DMI among unlinked loci (r, γ → ∞) can sustain the maximum level of gene flow.
We can understand this result in terms of two different mechanisms that enable the evolution and the maintenance of a parapatric DMI: Whereas the first, the “direct” mechanism is based on selection against maladapted immigrants in a spatially heterogeneous environment, the second, the “indirect” mechanism acts through selection against hybrids and requires epistasis and recombination. The two mechanisms act in different regions of the parameter space, corresponding to different shapes of the fitness landscape on the island (see Figure 1–Figure 3 and the analytical results in the Appendix).
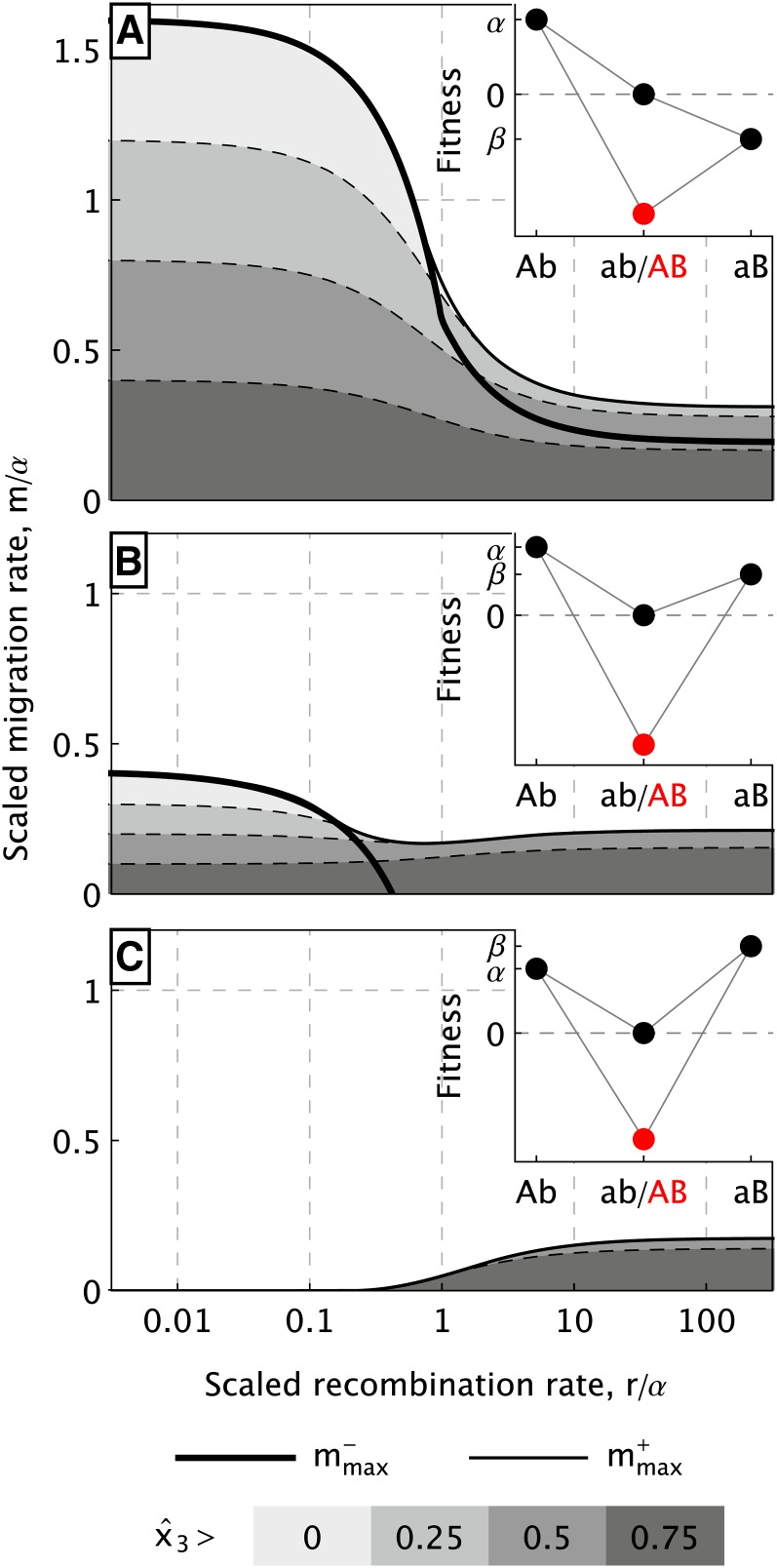
Figure 1 .
Maximum migration rates (black solid lines) and degree of population differentiation (gray areas) as functions of the (scaled) recombination rate r. We identify three regimes. (A) Selection against immigrants for slope-type fitness. Here, β/α = −0.6, γ/α = 2.5. (C) Selection against hybrids in a homogeneous environment. Here, β/α = 1.2, γ/α = 4. (B) Combination of both for intermediate fitness combinations. Here, β/α = 0.6, γ/α = 4. The corresponding type of fitness landscapes is displayed in each respective top right corner.
Figure 3 .
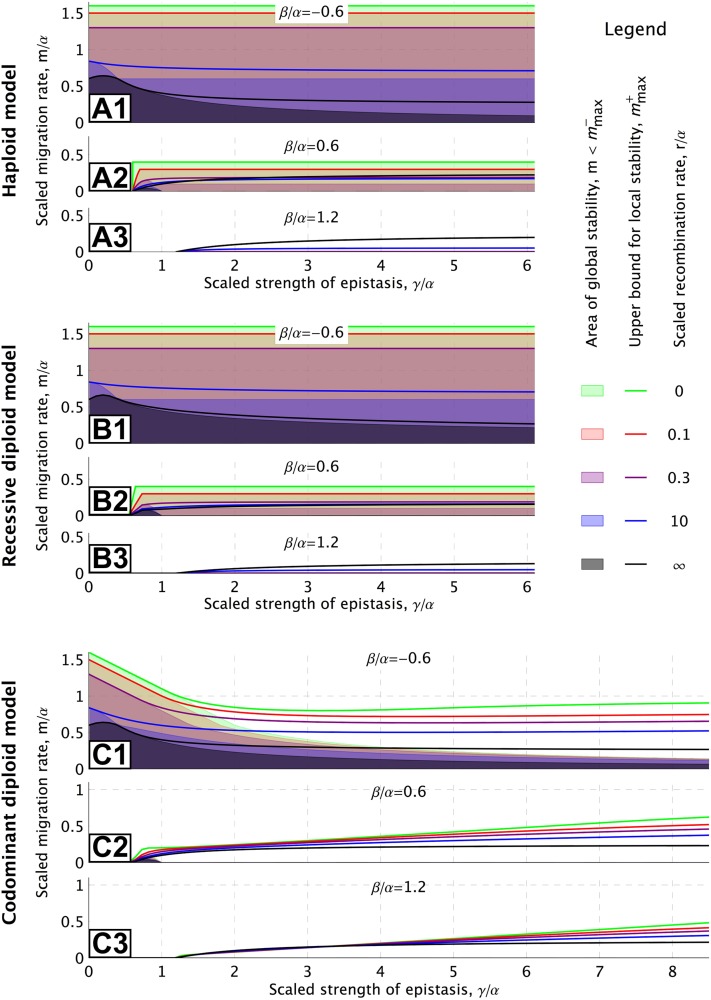
Maximum migration rates as functions of the (scaled) strength of epistasis for the haploid (A1–A3), recessive diploid (B1–B3), and codominant diploid (C1–C3) models and for various recombination rates. Each panel represents a different environmental scenario determined by β. For the haploid model, all curves are determined analytically using the formulas in Appendix, Internal equilibria and local stability. See main text for a detailed discussion of this figure and File S4 for interactive visualization of other parameter values.
Slope-type fitness: Selection against immigrants:
See Figure 1A, Figure 3A1 and area with light shading in Figure 2. A slope-type fitness landscape results under two (nonexclusive) scenarios: (i) local adaptation (β < 0, i.e., the continental haplotype aB is maladaptive on the island; see Figure 1A); and (ii) weak incompatibility (γ < α; hence, aB has lower fitness than the recombinant genotype AB). In this case, a stable DMI can be maintained by selection against immigrants, i.e., if (and only if) the fitness advantage of the island genotype over the invading continental type is sufficiently large to compensate the migration pressure. For sufficiently small m, the island haplotype is nearly fixed at the unique stable equilibrium. Since we assume that the haplotype aB is fixed on the continent, selection against immigrants requires heterogeneous selection across the continent and the island.
Figure 2 .
Parameter ranges corresponding to two different mechanisms for DMI evolution in the haploid model as a function of the heterogeneity of the environment (measured as β/α) and the strength of the incompatibility (measured as γ/α). In the intermediate parameter range (open area), both mechanisms contribute and we see a stepwise transition for various characteristic properties: (1) decrease/increase of population differentiation with increasing recombination rate for weak migration (left/right of dashed line) and (2) decrease/U-shape or increase of with increasing recombination rate (left/right of dotted line).
For slope-type fitness, DMIs are usually, but not always, globally stable (Figure 3A1). For low recombination, global stability extends from m = 0 to the maximum rate Bistability occurs if gene-flow rates are not much lower than and rare island haplotypes are efficiently broken up by recombination, such that a stable boundary equilibrium can be maintained. This is the case, for instance, if both r and γ are large.
From our analytical and numerical results and their graphical representations (see Figures 1A and 3A1 and the interactive visualization in File S4), we conclude the following characteristic properties for the maximum gene-flow rates and the degree of population differentiation:
The maximum migration rate satisfies [this follows from (4b) and (4c) because β < 0 or γ < α]. This maximum is achieved for tightly linked incompatibility loci (r = 0). With increasing r, both and are strictly decreasing (see Figure 1A). This can be understood as follows: As we show in File S1, section S.2.4, D < 0 holds at every internal equilibrium if r < ∞. Thus, recombination increases the frequencies of the ancestral and recombinant types (ab and AB) relative to the continental and island types (aB and Ab). Since at least one of the genotypes ab or AB has a higher fitness than the continental type aB, recombination increases the marginal fitness of at least one of the alleles a or B that enters the island through gene flow. This facilitates the fixation of the respective allele, leading to loss of the DMI.
As might be expected, both maximum rates, and , increase with a steeper slope of the landscape (higher α or lower β; see, e.g., the interactive visualization in File S4). In contrast, Figure 3 shows that the strength of the incompatibility is far less important (and irrelevant if r = 0).
Finally, also the level of differentiation is strictly decreasing if the number of hybrids is increased by increasing r (cf. Figure 1A and Equation 7).
Double-peak fitness with superior continental type: Selection against hybrids:
See Figure 1C, Figure 3A3, and area with dark shading in Figure 2. If β > α, the invading continental type is the fittest genotype on the island (fitness scheme in Figure 1C.) Nevertheless, the island genotype can be maintained in a locally stable DMI if both the ancestral and the recombinant genotypes have relatively low fitness. The condition we need is γ > β > α, thus, a strong incompatibility. In addition, sufficiently strong recombination is required to protect the island genotype Ab by decomposing the invading continental types aB into its constituent alleles (cf. Equation 3). Due to the low fitness of the recombination products ab and AB, both a and B are kept at low frequencies. Thus, recombination creates a drainage through which the invading alleles are discharged.
This second, indirect mechanism for maintaining a stable DMI does not depend on ecological differentiation between the continent and the island; i.e., exogenous selection can be homogenous. Indeed, under several scenarios (substitution on the island first, both on the continent, or secondary contact), evolution of a stable DMI can occur with a homogeneous fitness function across both subpopulations. The resulting DMI is always only locally stable. Also the dependence of and on the model parameters differs distinctly from the one under slope-type fitness (Figure 1C and Figure 3A3):
Since, in haploids, hybrid genotypes are formed only by recombination, selection against hybrids is most efficient for large r. Both and increase with r (cf. Figure 1C).
The efficiency of this mechanism is enhanced by strong epistasis that leads to a deep fitness valley (large α and large γ − β), as evidenced by the dependence of on these parameters (cf. Figure 3A3). From (4b), we infer that a DMI can exist only if . That this upper bound is approached for high r and γ has the following explanation. If all continental migrants recombine with resident island types (when r → ∞), and if all recombinant types AB die (when γ → ∞), only island and wild-type genotypes remain on the island. Then the dynamics of the island types are , which have a stable equilibrium with x2 > 0 if .
Double-peak fitness with superior island type: Combination of both mechanisms:
See Figures 1B, Figure 3A2, and open area in Figure 2. If 0 < β < α < γ, we obtain a double-peak fitness landscape on the island with the island type on the higher peak. In this parameter region, both mechanisms described above interact and contribute to the maximum rate of gene flow in a complex way. There is no simple sharp boundary that separates the parameter regions where either mechanism dominates, but we can illustrate the transition for several characteristic properties.
If recombination is weak relative to the fitness difference of the island and the continental type, r ≪ α − β, the haplotypes compete mostly as entire units and selection against immigrants dominates. The resulting DMI is globally stable for small m, and heterogeneous selection is needed to maintain a parapatric DMI. The maximum rate for a globally stable DMI decreases monotonically with r and is zero if r ≥ α − β (cf. Figure 1B). For higher recombination rates, a locally stable DMI can exist for spatially homogeneous selection; it can evolve from favorable initial conditions.
The dependence of on the recombination rate changes as follows. Whereas is monotone decreasing in r if γ(4β − α) < 3αβ (see Equation S.38 in File S1), otherwise we obtain a U-shaped dependence with a minimum at an intermediate recombination rate; cf. Figure 1B. If , the highest migration rate can be tolerated if the loci are independent because (4b), (4c), and (11) imply if γ → ∞ and r → ∞. increases monotonically with γ, indicating that both mechanisms are more efficient for strong DMIs in this parameter range (cf. Figure 3A2). This can be understood since selection against the B allele (lower fitness of AB) also leads to reduced marginal fitness of the allele (since ab haplotypes are less fit than aB haplotypes if β > 0).
Alternatively, we can ask whether formation of more hybrids (by an elevated r) increases or decreases population differentiation. The answer depends on the level of gene flow. For low m, differentiation decreases with higher r below the threshold implicitly given in Equation 7 and increases monotonically above this threshold (dashed curve in Figure 2; Figure 1B represents a case in which is highest for tight linkage although population differentiation increases with recombination for weak migration). For high gene-flow rates near the maximum values admitting a stable DMI, the dependence of on r can be U-shaped, similar to the dependence of on r.
Results: Diploid Model
Although a comprehensive analytical treatment of the general diploid model seems out of reach, progress can be made for particular cases. For most of our results, we focus on two choices of the epistasis coefficients Γ = (γ1, γ2, γ3, γ4): (1) a recessive model with no fitness costs for double heterozygotes, Γ0 := (0, γ, γ, 2γ); and (2) a codominant model with costs proportional to the number of A/B conflicts, Γ1 := (γ/2, γ, γ, 2γ).
As we will see, these two models represent two main types of DMI structure. Two additional properties make them analytically more tractable than the general case. First, there is no dominance at locus or ℬ if the other locus is monomorphic. In particular, this excludes stable boundary equilibria caused by overdominance: If m = 0, the only equilibria at the boundary are the monomorphic equilibria M1–M4. Second, the condition γ4 = 2γ2 = 2γ3 preserves the symmetry of the haploid model. Thus, the equilibrium structure is symmetric under the transformation α → γ − β and β → γ − α, which corresponds to an exchange of the ancestral haplotype ab and the recombinant type AB.
As in the haploid model, if m > 0, necessary and sufficient conditions for a globally stable DMI can be derived from a stability analysis of the boundary equilibria. For our special models, the same boundary equilibria as in the haploid model exist under the same conditions: The monomorphic equilibrium M2 exists always, and the single-locus polymorphisms or Sℬ exist if m < α − γ or m < −β, respectively (cf. Figure A1 in the Appendix). In general, however, the stability conditions in the haploid and diploid case differ.
Necessary conditions for recessive and codominant DMIs
Necessary conditions for a stable DMI are derived in Sections S.10 and S.12 of File S2. In terms of the maximum rates of gene flow, we find for the epistasis scheme Γ = (γ1, γ, γ, 2γ), which comprises both our special models,
| (13a) |
and, if ,
| (13b) |
There is a striking similarity with the corresponding Equations 5a and 5b for the haploid model. For both models, the conditions α > 0 and γ > β are required for a parapatric DMI, thus excluding neutral DMIs and setting a lower bound for the strength of the incompatibility. For the rest of this section, we therefore assume α > 0 and γ > β.
For the recessive model (γ1 = 0), the conditions (13a) and (13b) coincide with their haploid counterparts. In the codominant model (γ1 = γ/2), selection against double heterozygotes deepens the fitness valley between the island and the continental genotypes. For m = 0, this leads to an increased range of simultaneous stability of the monomorphic equilibria M2 and M3. This is reflected by the conditions (13a) and (13b): whereas the constraints for a locally stable DMI get weaker for larger γ1, the conditions for global stability become more stringent.
For weak migration, the amount of population differentiation, as measured by the equilibrium frequency of the island haplotype, is calculated to
| (14) |
Differentiation increases or decreases with r according to
| (15) |
In the context of the haploid result (Equation 7), we can understand this result as follows: For weak migration, invading alleles appear on the island almost exclusively in heterozygous genotypes containing the island haplotype (i.e., in aBAb, ABAb, or abAb). The dynamics of these three genotypes, together with the homozygous island type AbAb, essentially follow those of a haploid model if the following substitutions are made: βhap → βdip − γ1 and γhap → γdip − γ1.
Finally, for Γ = (γ1, γ, γ, 2γ), we can also derive the following upper bound for (Equation S.111 in File S2):
| (16) |
For , complete analytical results can, in principle, be derived from a local stability analysis of each boundary equilibrium (File S2, section S.13). Since they are quite complex and involve a large number of case distinctions, we discuss only the limiting cases of weak migration, tight linkage (r = 0), and independent loci (D = 0) in more detail.
Recessive DMI model
Tight linkage:
If , there are only two equilibria that can be stable for m > 0. One is the monomorphic equilibrium M2, which is globally stable for m > α − β, but unstable otherwise. The other equilibrium, at which only the haplotypes and are present, gives rise to the DMI. Hence, we recover the result (Equation 8) from the haploid model. Note, however, that this does not imply that the dynamics of the diploid and haploid models are the same.
Independent loci:
In linkage equilibrium, the maximum migration rate is determined from the stability conditions of the single-locus polymorphisms and Sℬ (cf. File S4, section 2.3). We obtain
| (17) |
This expression deviates from the corresponding haploid result (Equation 10). In particular, we obtain a slower decline to zero (∼γ−1/2) as γ → ∞. For local stability, we find as an upper bound in addition to (16). However, we have not been able to derive an exact analytical expression for Numerical results are discussed below.
Codominant DMI model
Tight linkage:
If , local stability analysis of the boundary equilibria yields
| (18) |
As discussed below, this deviates strongly from the haploid and the recessive case. We deduce the following formulas for (cf. File S4, section 2.4). If α > 4β,
| (19) |
and if α ≤ 4β (which implies β > 0),
| (20) |
Independent loci:
Under the assumption of linkage equilibrium, the dynamics of allele frequencies in the codominant model map precisely to those of the corresponding haploid model (cf. File S4). Intuitively, this can be seen as follows: If r → ∞, alleles are combined randomly. To recover the dynamics of the haploid model, we assign to each diploid genotype the average fitness of the corresponding allele combination in the haploid model; e.g., wd(aAbB) = 1/2(wh(ab) + wh(AB) + wh(Ab) + wh(aB)) = α + β − γ/2, which indeed is the fitness in the codominant model. We obtain the same existence and stability results as in the haploid case, namely (10) and (11). All equations reported above are visualized in interactive Mathematica plots in File S4, section 2.4.
Analytical results and conjectures for general epistasis coefficients
In File S4, we analyze how our results for the special epistasis schemes generalize to a diploid model with an arbitrary two-locus incompatibility. Throughout our analysis, we assume that the strength of the incompatibility is nondecreasing with the number of A/B conflicts, i.e., that the epistasis parameters fulfill the condition γ4 ≥ {γ3, γ2} ≥ γ1. Additional (technical) assumptions are needed for some of our formal proofs in File S2. When this is the case, our conjectures are confirmed by perturbation arguments and by numerical simulations. We find the following necessary conditions for a stable parapatric DMI (cf. Equation S.125 in File S2):
| (21) |
The latter condition simplifies to β < γ3 if we exclude overdominance at locus ℬ, which requires γ3 < β < γ4 − γ3. Since overdominance at locus ℬ stabilizes the island genotype, the condition is slightly relaxed in the general case. Without overdominance, we also retain the lower bound on the recombination rate of the codominant model, r > β − α − γ1.
Finally, we find that
| (22) |
provides an upper bound for the maintenance of any (structurally stable) DMI in the diploid model, independent of epistasis parameters or recombination rates. This bound is sharp and is already attained for our two special models: if m < α − β, a recessive DMI (γ1 = 0) exists for any γ > β and complete linkage (r = 0); if m < α, a codominant DMI exists for γ1 → ∞ and r = 0.
An important consequence of (21) and (22) is that a stable neutral DMI (or any DMI with α ≤ 0) is impossible in the diploid continent–island model. A proof of this fact for the general diploid DMI model is given in File S2, section S10. We note that this is not a trivial finding: In particular, our general assumption of nondecreasing γi with the number of conflicts is essential, and counterexamples can be found if γ1 ≫ max[γ3, γ4] (cf. File S4). A special case of potential biological relevance is the scenario of tightly linked loci (r = 0) in the secondary-contact scenario (i.e., in the complete absence of ab and AB haplotypes). In this case, the model reduces to a one-locus two-allele problem and we readily obtain the condition
| (23) |
Thus, a neutral incompatibility can be maintained if γ1 > 0, corresponding to a previous result by Lande (1979). Indeed, the maximum rate of gene flow even increases toward ∞ with growing γ1. As we will see below, this behavior deviates strongly from any other scenario where no haplotype is excluded from the dynamics. Note that the equilibrium is unstable in the full parameter space and thus not a true DMI according to our definition. Indeed, the incompatibility is quickly lost if the ancestral haplotype ab is initially present at a low frequency or if recombination deviates (however slightly) from zero.
Stability of parapatric DMIs in the diploid model
For various parameter combinations, Figure 3B and C display and as functions of the strength of epistasis for the recessive and the codominant model, respectively. Corresponding figures for other choices of epistasis schemes are provided in File S3. As in the haploid model, we find that at most a single stable DMI can exist for given parameters. Locally stable DMIs refer to bistable cases, where a DMI coexists with one (or several) stable boundary equilibria. In these cases, evolution depends on the initial conditions. As in the case of the haploid model, all our numerical results show convergence to the DMI if the second substitution occurs on the continent and for secondary contact. In contrast, a DMI never evolves in a bistable case for the continent–island and island–island scenarios. We find two main types of equilibrium patterns, which are well represented by the recessive or the codominant DMI model.
Recessive incompatibilities:
Comparison of Figure 3B with 3A shows that the maximum gene-flow rates for the recessive diploid model and for the haploid model are very similar. This holds, in particular, for low recombination rates, but even for independent loci the differences are modest. We obtain qualitatively similar results for other choices of the epistasis parameters that do not impose selection against the double heterozygotes, i.e., if γ1 = 0 [see File S3, Figure S4 for Γ = (0, γ, 0, 2γ), Figure S5 for Γ = (0, 0, γ, 2γ), and Figure S6 for Γ = (0, 0, 0, 2γ)].
Codominant incompatibilities:
Comparison of Figure 3C with 3A shows that the maximum rates for the codominant diploid model are very similar to those for the haploid model for high recombination rates [for Γ = (γ/2, γ, γ, 2γ) they are even identical in the limit r → ∞]. However, significant differences emerge if recombination is weak relative to selection, r ≤ min[α, β]. On the one hand, the maximum rate for global stability, , is severely reduced relative to that in the haploid model. Irrespective of the other parameters, we find that as γ1 → ∞. On the other hand, the maximum rate for a locally stable DMI, , can be much larger, in particular for large γ. We thus find large parameter regions with bistable dynamics for the codominant model. Again, models with different choices of the epistasis parameters, but γ1 > 0, show a similar behavior [see Figure S7 in File S3 for the case Γ = (2γ, 2γ, 2γ, 2γ)].
General incompatibilities
For an epistasis scheme that is intermediate between the two special patterns studied above, e.g., Γ = (γ/50, γ/5, γ/5, 2γ), we observe a transition between the recessive and the codominant DMI pattern with increasing γ (in File S3, compare Figure S8 with Figures S2 and S3; see also Figure S9). The maximum gene-flow rates are very similar to those in the recessive DMI model as long as the incompatibility is weak and γ1 ≪ max[α, β]. However, when observed on a larger scale in terms of γ, such that the fitness costs of the double heterozygote are of the order of α and β, the pattern resembles that of the codominant model (File S3, Figure S9).
As in the haploid case, we can understand these results in terms of the fitness landscape and the corresponding mechanisms for the evolution and maintenance of DMIs: heterogeneous ecological selection pressures and selection against hybrids.
For a slope-type fitness landscape, due to either local adaptation (β < 0) or a weak incompatibility (α > max [γ2, γ4 − γ2] and β < min[γ3, γ4 − γ3]), the DMI is maintained by heterogeneous selection. There are no hybrids that are so unfit that they could pose a selection barrier. If gene flow is sufficiently low, we obtain global stability of the DMI even for high recombination (as in the haploid case, always decreases with r but, here, for r → ∞).
The most significant differences between the haploid and the diploid model occur for a double-peak fitness landscape. In diploids, any selection against the double heterozygote F1 hybrids (γ1 > 0) deepens the fitness valley between the peaks and generates a direct, recombination-independent fitness cost for hybrids. In the haploid model, costly hybrids can be produced only by recombination. As a consequence, the difference between both models is strongest for small r. Since the fitness valley protects both local fitness maxima, the evolution of the DMI (which is close to the “island peak”) will always depend on initial conditions. The maximum gene-flow rate depends on the depth of the valley and on its shape. If wAaBa ≫ max[waabb, wAABB] (small γ1), the barrier is most shallow in the center, i.e., at the AaBb hybrids. In this case, selection against hybrids is weakest (and smallest) for low recombination (cf. Figure 4, recessive model). In the opposite case (large γ1) the barrier is most shallow at the recombinant hybrids aabb or AABB of island and continental individuals (cf. Figure 4, codominant model). As a consequence, increases with r.
The individual effects of the epistasis coefficients γ2, γ3, and γ4, are further explored in File S3. Compared to γ1, they are relatively minor provided certain weak conditions are satisfied (File S2). The parameters γ2 (selection against aABB individuals) and γ3 (selection against AABb types) have opposite effects. In particular, reducing γ2 below γ4/2 leads to overdominance at the locus for pB = 1 and thus stabilizes a boundary equilibrium without the island haplotype Ab. In contrast, γ3 < γ4/2 entails overdominance at the ℬ locus for pA = 1 and thus contributes to the stability of a DMI with x3 > 0.
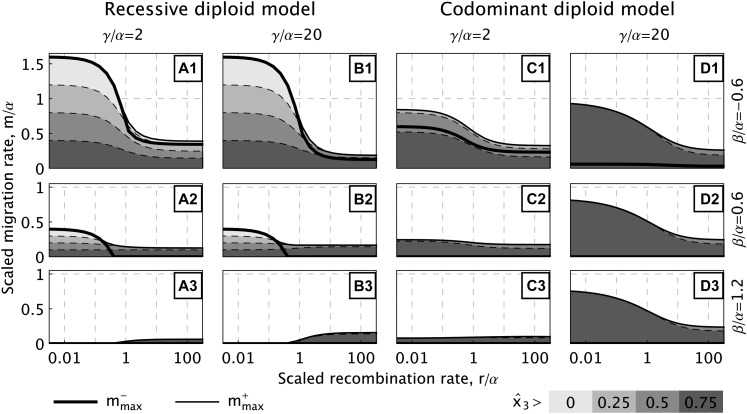
Figure 4 .
Maximum migration rate (solid lines) and population differentiation (shaded areas) in the recessive and codominant diploid models as a function of the recombination rate γ. For each model, two choices for the strength γ of epistasis (weak/strong) and three choices for β, describing different types of selection scenarios (corresponding to local adaptation/heterogeneous/homogeneous environments), are represented. Similar to the haploid model (cf. Figure 1), the results in the recessive model are almost independent of the strength of epistasis (compare A1–A3 and B1–B3), but strongly dependent on the environment (compare rows 1, 2, and 3). In contrast, for the codominant model, and depend only weakly on the environment if epistasis is strong (D1–D3). Generally, the codominant model produces stronger population differentiation than the recessive model (dark shading dominating), although the overall maximum migration rate in scenarios of local adaptation is lower; compare A1 and B1 with C1 and D1.
Discussion
The standard model to explain the evolution of intrinsic postzygotic isolation in allopatry, the Dobzhansky–Muller model, has repeatedly been described as a plausible speciation scenario, also in the presence of gene flow (e.g., Gavrilets 2004; Wu and Ting 2004). However, little is known about the limits up to which the mechanism could work. As phrased by Turelli et al. (2001, p. 341), “we would like to understand how much gene flow is needed to inhibit the accumulation of DMIs.” The origin (and maintenance) of the first incompatibility in a genetically homogeneous ancestral population is the crucial step of this process, since the evolution of any additional DMI can only be easier.
In our study, we address this question for a minimal model with two loci and two alleles. We focus on the particular case of unidirectional gene flow, e.g., from a continent to an island population. For this model, we obtain a complete analytical characterization of the maximum rates of gene flow that permit DMI evolution. The model accounts for exogeneous and endogeneous selection and allows for different temporal–spatial patterns in the origination of the substitutions. We thus can disentangle the relative importance of the external environment, the genetic architecture of the incompatibility, and the evolutionary history for the evolution and maintenance of parapatric DMIs.
Two mechanisms can drive the evolution of a parapatric DMI. In a heterogeneous environment, a DMI can emerge as a by-product of selection against maladapted immigrants. In addition, selection against unfit hybrids can maintain a parapatric DMI even in homogeneous environments. Both mechanisms rely on exogenous selection, but lead to opposite predictions concerning the genetic architecture of the DMI and its dependence on the evolutionary history. Our main results are the following:
The maximum rate of gene flow can never exceed a bound set by exogenous selection pressures. This implies that the adaptive advantage of the single substitutions rather than the strength of the incompatibility is the most important factor in determining whether a DMI can evolve or be maintained in the presence of gene flow. In particular, neutral DMIs cannot exist in parapatry.
In the haploid model, selection against immigrants is most effective in driving the evolution of parapatric DMIs if both incompatibility loci are tightly linked. In contrast, selection against hybrids works best for strong, but loosely linked incompatibilities. The results for the diploid model are very similar to those for the haploid model if the incompatibility is recessive, i.e., if double-heterozygous F1 hybrids are not affected by the incompatibility. In contrast, for codominant incompatibilities, the fitness of double heterozygotes becomes a decisive factor to determine DMI evolution.
In many cases, a DMI will evolve only if the two incompatible substitutions appear in the correct order on the continent and on the island. In particular, if selection acts mainly against hybrids in a homogeneous environment, the outcome of the evolutionary process is dependent on historic contingency.
In the following, we discuss the most important implications that arise from these results and relate them to existing empirical and theoretical work.
The importance of exogenous selection
Our results highlight the importance of exogeneous selection (parameters α and β in the model) and of adaptive evolution during parapatric speciation. At least one of the substitutions involved in a stable parapatric DMI must have a selective advantage on the island relative to the ancestral type (α > 0 for the “island substitution”). This confirms previous claims that neutral postzygotic speciation is impossible in the presence of gene flow (Barton and Bengtsson 1986; Gavrilets 1997; Kondrashov 2003; Lemmon and Kirkpatrick 2006; but see Gavrilets 2004). Although the formal proof of this fact is quite involved for the diploid model (see File S2), there is an intuitive explanation: If both substitutions are neutral, the compatible ancestral haplotype has a marginal advantage over all haplotypes that carry a substitution. Thus, whenever the ancestral type is produced by recombination (or if its initial frequency is positive), it can rise in frequency until the island substitution (the allele that is not present on the continent) is lost. These results also exclude the maintenance of a neutral DMI after secondary contact, even if such a DMI may have originated in a phase of strict allopatry. The only exception is a DMI that is effectively just a single underdominant diploid locus (a single recombinational unit). This may occur, e.g., if both substitutions are joined in an inversion. However, as has previously been shown in a simulation study, even tiny recombination rates preclude the maintenance of a neutral DMI upon secondary contact (Feder and Nosil 2009).
These findings generalize easily to pairwise DMIs in the background of other genetic barriers to gene flow by substituting an effective migration rate (Barton and Bengtsson 1986). Since the maximum rate of gene flow for the maintenance of a neutral DMI is zero, such an incompatibility will be maintained only if isolation is already complete. It thus cannot contribute to the speciation process, even at a late stage. These results are consistent with empirical evidence for signatures of positive selection, which have been observed for most incompatibility genes that have been identified so far (Presgraves et al. 2003; Johnson 2010).
The maximum rates of gene flow for locally or globally stable DMIs increase with a higher selective advantage of the island substitution (higher α) and with higher disadvantage of the incompatible continental substitution (lower β). Strong local adaptation (with α > 0 and β < 0) can enable the accumulation of DMIs under strong gene flow (; e.g., Figure 3, A1 and B1). Since empirical studies have indeed identified cases of very strong divergent selection (e.g., Mullen and Hoekstra 2008), this implies that the evolution of DMIs as a by-product of local adaptation might be possible in nearly sympatric scenarios. However, the level of population differentiation that is maintained by a DMI at high gene-flow rates will become vanishingly low (Figure 1A and Figure 4, A1 and B1).
Stability of a parapatric DMI does not require local adaptation, but is also possible in a homogeneous environment if there is sufficiently strong selection against hybrids (i.e., if γ > β in the haploid model). It is even possible that the “island” substitution is less beneficial on the island than the invading, incompatible “continental” substitution (β > α > 0; e.g., Figure 3, A3–C3). Although the maximum rates of gene flow are lower than for local adaptation ( for haploids, for diploids), the amount of population differentiation that a single DMI can achieve, even close to the maximum migration rate, is still high (Figure 1C and Figure 4, A3–D3). This is in line with classical arguments about hybrid zones by Barton and Hewitt (1989), who claimed that local adaptation might be important to generate variation in the first place, but selection against hybrids is supposed to be more important for maintaining a hybrid zone.
The importance of the genetic architecture of the DMI
Reliable inferences about the genetic architecture of a DMI (its strength γ and its linkage r) must take into account under which mechanism it has evolved. If a DMI is maintained simply as a by-product of local adaptation or direct selection against immigrants in a heterogeneous environment, the strength of the incompatibility (measured by the epistasis parameters) is of minor importance. The maximum admissible migration rates often even decrease with stronger epistasis (e.g., Figure 3, A1–C1). In the selection-against-immigrants scenario, a DMI on the island is most effectively protected from gene flow if tight linkage (low r) of the incompatibility loci maintains the immigrant haplotype aB (e.g., Figure 1A). In contrast, strong recombination will quickly decompose the immigrant type, even if it does not suffer a direct fitness cost. Instead, hybrid haplotypes (ab and AB) are produced. DMIs on the island can withstand the immigration pressure if and only if sufficiently strong selection acts against these hybrids.
In haploid populations, hybrid individuals suffering from an incompatibility are produced only by recombination. This also holds for recessive diploid incompatibilities (γ1 = 0), where double-heterozygous F1 individuals pay no cost. If selection against hybrids is the driving mechanism of DMI evolution, we therefore find that DMI stability against gene flow increases with recombination (cf. Figure 1C). This is different for codominant DMIs, where the incompatibility affects double heterozygotes (H0 incompatibility in the terminology of Turelli and Orr 2000). Here, selection against F1 hybrids (γ1 > 0) can protect the island genotypes from swamping by continental types even if recombination is low or absent. Indeed, the maximum rate of gene flow permitting stable DMIs decreases with recombination if selection against F1 hybrids is strong (cf. Figure 4C3 and D3). Our results conform to related findings by Gavrilets (1997), who noted the importance of F1 fitness for the strength of a barrier to gene flow induced by a DMI in a model of a genetic cline.
The importance of the evolutionary history
The two incompatible substitutions can originate in various temporal–spatial patterns, either on the continent or on the island. They can occur in the presence of gene flow or in a temporary allopatric phase. We find that, with respect to the stability of the DMI, all evolutionary histories can be categorized in two classes. If the second substitution arises on the continent (and the first substitution either on the island or on the continent), or if both alleles originate in an allopatric phase, they are initially protected from incompatibility selection. A DMI will evolve under these conditions whenever the model parameters allow for a stable incompatibility, i.e., independent of initial conditions. In contrast, if the second substitution occurs on the island, a DMI will evolve if and only if the corresponding equilibrium is globally stable (i.e., there is no alternative stable evolutionary endpoint). The intuitive reason is that the second allele faces competition from its incompatible counterpart, which is maintained on the island either due to local selection or due to recurrent gene flow from the continent.
As expected, a favorable evolutionary history is always decisive in a homogeneous environment. The dependence on the history is also increased by high recombination rates and by selection against double heterozygotes in the codominant diploid model. We thus find that historic contingency becomes important in all scenarios in which DMIs primarily evolve due to selection against hybrids. In contrast, DMIs are usually (but not always) globally stable if selection acts directly against immigrants.
The strong dependence on the evolutionary history that we observe is partially a consequence of the migration asymmetry that is inherent to the continent–island model. We can extend our results to include very weak back migration from the island to the continent under the following assumptions. Back migration is much weaker than both selection and migration from the continent, such that the equilibria derived for unidirectional gene flow are only slightly perturbed. Back migration nevertheless is much stronger than recurrent new mutation on the continent, such that the first substitution will reach equilibrium in both demes, independent of its deme of origin. The impact of weak back migration of this type depends on the fitness landscape on the continent. If fixation of the continental haplotype (aB) is the only stable equilibrium on the continent, we retain all predictions from the model with strict unidirectional migration. If the fitness function on the continent is double peaked, with local optima for fixation of either the continental or the island haplotype (aB or Ab), the continental substitution B must occur first, since otherwise both demes fix for the island haplotype. In this case, however, the island substitution A faces competition from the continental B allele and will be able to invade only if the DMI in the unidirectional model is globally stable.
An important consequence of this result is that heterogeneous selection across both demes is a prerequisite for the evolution a parapatric DMI if there is (even minimal) back migration. The same line of arguments also shows that evolution of a codominant DMI may be difficult in the presence of bidirectional gene flow, since strong selection against double heterozygotes will plausibly lead to a double-peak fitness landscape on the continent and on the island. Indeed, most hybrid incompatibility loci that have been identified so far are recessive (cf. Presgraves 2003). This is expected particularly for DMIs that have evolved via gene duplications or selfish elements (Johnson 2010; Presgraves 2010).
Ecological vs. mutation-order speciation
According to Schluter (2009), adaptive postzygotic isolation with gene flow falls into two broad categories. Ecological speciation refers to the case that each substitution of a DMI pair is beneficial in one subpopulation, but deleterious in the other. Speciation is then a by-product of local adaptation. In contrast, the case in which both substitutions are beneficial in both demes is referred to as mutation-order speciation (Mani and Clarke 1990). Characteristic for this second scenario is that speciation depends on the “chance occurrence and fixation of different alleles between populations adapting to similar selection pressures” (Schluter 2009, p. 737).
The present study provides a framework for an adjustment and formal validation of this verbal classification. In our model, local adaptation corresponds to a deleterious effect of the continental substitution on the island (β < 0). “Mutation order” expresses dependence on the evolutionary history, which is the case in all regimes with a locally, but not globally, stable DMI. We find that these types are not exclusive, nor do they cover the entire parameter space where a DMI can evolve: On the one hand, the potential for “pure” mutation-order speciation with (strictly) homogeneous selection across both demes is relatively limited in the continent–island model and becomes impossible if there is back migration. On the other hand, the correct mutation order is often essential in addition to local adaptation to explain the evolution of a DMI, in particular for codominant DMIs in the diploid model. Finally, there is a large parameter range where weak DMIs (with γ < α) evolve under heterogeneous selection, but without the need of local adaptation and independently of the evolutionary history.
From our model, we do not find a clean way to classify the DMIs themselves into categories. Instead, we distinguish two mechanisms that can drive the evolution of parapatric DMIs (cf. Figure 2). This distinction retains some flavor of Schluter’s classification: Selection against immigrants relies on ecological selection due to a heterogeneous environment, whereas selection against hybrids in a homogeneous environment must rely on mutation order. For each mechanism there are parameter regions in which one dominates the other. This has characteristic consequences for predictions concerning the genetic architecture or historic contingency. However, and in contrast to Schluter’s scheme, the two mechanisms are not exclusive and reliable predictions become more complex in the broad transition region.
The limited potential of mutation-order speciation has previously been reported by Nosil and Flaxman (2011), who performed a simulation study in a two-island model. Furthermore, Agrawal et al. (2011) studied the evolution of a DMI in the context of ecological speciation and examined the resulting barriers to neutral gene flow.
Limitations of the model
Our continent–island model of DMI evolution represents a minimal model to investigate under which conditions of the genetics and the environment a single two-locus DMI can evolve. We have shown that in this simple case a comprehensive analytical understanding of these conditions can be achieved. Naturally, several further issues emerge from our study. Maybe the most pressing question is how our results depend on our assumptions about population structure. Since the continent–island model represents an extreme case of asymmetric mutation, it should be complemented by a study of a two-island model with bidirectional migration. As outlined above, we generally expect that DMIs are more difficult to evolve with bidirectional migration, where the second mutation always experiences immediate incompatibility selection. In contrast, the maintenance of a DMI may be possible under even higher migration rates, if part of the gene flow is due to back migration of advantageous types. These intuitive expectations are supported by preliminary results and previous studies (e.g., Karlin and McGregor 1972a; Lande 1979). Further extensions could address DMI evolution in a stepping-stone model or in continuous space, building on the preliminary results by Gavrilets (1997) and Kondrashov (2003), respectively.
As a technical point, we have used continuous-time dynamics, implicitly assuming weak selection. However, numerical checks against a model with discrete generations did not show qualitative changes even for fairly large selection coefficients (results not shown). More significantly, our derivations do not account for genetic drift. Thus, we implicitly assume that drift is much weaker than selection and migration. Following heuristic arguments by Yeaman and Otto (2011) suggests that the stability properties of DMIs should remain unaltered under drift if selection and migration parameters are ≫1/2N. Whereas the regime where drift is much stronger than migration (such that the population is almost always monomorphic) was analyzed by Gavrilets (2000), the case in which all three forces are of similar size has yet to be studied.
Also our assumptions on the genetics of the model are restrictive and call for further study. A valuable (and relatively easy) next step would be to extend the model to nonautosomal incompatibilities, since empirical studies report a growing number of DMIs that involve the sex chromosomes or mitochondria (Presgraves 2003; Chou and Leu 2010). Since we consider only a two-locus DMI, extensions to higher-order incompatibilities would be welcome. We expect, however, that the analysis will be much more complex and results will have to rely on extensive numerical work. Finally, our model considers the origin and maintenance of only a single, first DMI in a previously homogeneous population. Although this is an important question, also with regard to reports of segregating incompatibilities within populations (Cutter 2012), in the context of parapatric speciation the entire dynamics of DMI accumulation up to complete isolation need to be addressed. In the light of a growing number of whole-genome scans for incompatibilities (e.g., Kao et al. 2010), it would be particularly interesting to predict how distribution patterns of DMIs along the genome depend on environmental and genetic conditions.
Our results are informative for an accumulation process in various ways. Primarily, they characterize the conditions for the onset of parapatric speciation via accumulating DMIs. Because the first single DMI will establish population differentiation, this will reduce the effective gene flow between the populations and hence simplify the accumulation of additional incompatibilities. Moreover, if one interprets the maximum migration rate as a maximum rate of effective gene flow, our model can be readily extended to two populations at an advanced stage of the speciation process. In particular, we can also assume that barriers to gene flow have been built by prezygotic mechanisms, such as reinforcement (e.g., Nosil et al. 2003). In this case, our model predicts the maximum residual amount of gene flow that permits DMIs to accumulate and finish the speciation process when other evolutionary forces, such as reinforcement, have become too weak to shut off gene flow (cf. Bank et al. 2012).
Predictions and conclusions
What can we conclude about the possibility of evolution of postzygotic reproductive isolation in the presence of gene flow? We have seen that the substitutions involved in a parapatric DMI must be adaptive. Also, at least some environmental heterogeneity is usually necessary, in particular if there is gene flow from the island back to the continent. In this case, recessive incompatibilities are far easier to evolve than codominant incompatibilities. If selection on the island acts most strongly against maladapted immigrants from the continent, the emergence of recessive DMIs is promoted by tight linkage between loci. Consequently, we expect an advantage for incompatibilities that evolve in regions of low recombination, such as chromosomal rearrangements (Bürger and Akerman 2011; Yeaman and Whitlock 2011). This supports a “genomic islands of speciation” model (Wu and Ting 2004), where DMIs accumulate in clusters on the genome. Incompatibilities are just a by-product of strong diversifying selection in this case, and the evolutionary outcome is largely independent of the chronological order of the substitutions. On the contrary, if selection on the island acts primarily against hybrids, the correct mutation order is decisive. In stark contrast to the “genomic island” picture, incompatibility pairs are rather expected to be loosely linked or unlinked in this case. Also upon secondary contact, populations that have undergone initial divergence under similar selection pressures in allopatry are more likely to maintain incompatibilities that are unlinked.
Although there are still many open questions, the present study provides theoretical groundwork for a characterization of the conditions for the evolution of differentiation via DMIs in parapatry. In particular, our analytical results show that progress on these issues is not necessarily limited to simulation studies. We hope that our methods can serve as a basis for future work on the evolution of reproductive isolation in parapatry and shed light on the ongoing discussion about the plausibility of ecological and mutation-order speciation.
Supplementary Material
Acknowledgments
We thank N. Barton, J. Hofbauer, M. Servedio, and the members of the Doktoratskolleg Populationsgenetik for helpful discussions or comments on the manuscript. C.B. and J.H. are members of the Mathematics and BioSciences Group at the University of Vienna, which is funded by the Vienna Science and Technology Fund through project MA06-01. R.B. is grateful for support by grant P21305-N13 of the Austrian Science Fund.
Appendix
Haploid Model
For the haploid model, we determined the equilibrium structure completely and obtained explicit analytical expressions for the maximum rates of gene flow below which locally or globally stable DMIs can be maintained. Since the proofs are complex and require advanced mathematical arguments, they are given in File S4. File S4 provides a self-contained analytical treatment of the haploid model. For dedicated readers interested in additional results, we also provide a fully annotated Mathematica notebook in File S4. In this Appendix, we give a summary of our results. In particular, we state all formulas for the maximum rates of gene flow that are used in the main body of the article.
For many purposes, it is convenient to write the dynamics in terms of the frequencies p and q of the incompatible alleles (A and B) and the linkage-disequilibrium coefficient D:
| (A1a) |
| (A1b) |
| (A1c) |
We note that D has to satisfy
| (A2) |
Equilibrium structure
Figure A1 sketches the positions in state space of all equilibria that can exist for the haploid model with m ≥ 0. These are the four monomorphic equilibria Mi, where the corresponding haplotype is fixed on the island (xi = 1). Two boundary equilibria with a single polymorphic locus may exist on the edges q = 1 or p = 0. We denote them by and Sℬ (locus , ℬ polymorphic), respectively. There is at most one asymptotically stable internal equilibrium, denoted by IDMI. If it exists we say that a parapatric DMI is maintained. Finally, an unstable internal equilibrium, I0, may exist.
Figure A1 .
State-space diagram, projected onto the plane spanned by the allele frequencies p and q, showing the possible equilibria and initial states of the haploid dynamics. Immigration of continental haplotypes moves the monomorphic equilibrium M3 (which exists for m = 0) into the interior of the state space, thus yielding a stable DMI. Open circles represent instable equilibria, whereas half-filled circles represent equilibria which can be stable or instable. The gray circle represents a potential polymorphic initial state.
In the absence of migration (m = 0), all four monomorphic equilibria Mi exist. In the relevant parameter space (α > 0 and γ > β, see Equation 2), only M2 (the continental haplotype aB is fixed) and M3 (the island haplotype Ab is fixed) can be stable. An unstable internal equilibrium (I0) exists if and only if M2 and M3 are both stable. No further equilibrium can exist in this case. For sufficiently small m > 0, IDMI exists if and only if the island equilibrium M3 is stable for m = 0 [leading to conditions (2) and (3)]. Indeed, IDMI is a perturbation of M3 and enters the state space when m becomes positive. IDMI is globally asymptotically stable if and only if it is the only internal equilibrium. If the unstable internal equilibrium I0 exists, the dynamics are bistable, and IDMI and one of the boundary equilibria (M2, , or Sℬ) are locally stable attractors.
As m increases, there are three different scenarios for the fate of IDMI (File S1, section S.7; note that these patterns in the dynamics do not easily correspond to the mechanisms of DMI evolution that we identify):
If the unstable internal equilibrium I0 exists already at m = 0, we have . Both internal equilibria merge and disappear at , and the previously locally stable boundary equilibrium becomes globally stable.
The unstable equilibrium I0 enters the state space through one of the boundary equilibria at . Both internal equilibria merge and disappear at .
The stable equilibrium IDMI leaves the state space through one of the three boundary equilibria at , which then becomes globally stable for larger m. Thus, an unstable internal equilibrium never exists.
We note that a DMI always exhibits negative linkage disequilibrium unless independent loci are assumed (File S1, section S.2.4). This is not at variance with the usual finding that migration induces positive linkage disequilibrium because in our model the frequencies of the “extreme” gametes (Ab and aB) are x2 and x3.
Boundary equilibria and global stability
At a boundary equilibrium, at least one haplotype frequency xi is zero. For recombination rates r > 0, this is possible only if one of the two loci is monomorphic (we deal with the case r = 0 separately in File S1, section S.8.1). Due to constant immigration of the continental haplotype aB, there are no equilibria with p = 1 or q = 0. Thus, boundary equilibria satisfy p = 0 or q = 1, and hence, D = 0. If m > 0, M2 is the only monomorphic equilibrium. A linear stability analysis reveals that M2 is asymptotically stable if
| (A3) |
The three lower bounds correspond to the invasion criteria for the other three haplotypes. If m < −β, the selective advantage of the wild-type ab over aB is sufficiently large to exceed the growth of the continental type due to migration. Similarly, if m < α − γ, the recombinant-type AB outperforms the continental type near M2. Note that recombination of aB haplotypes with rare ab or AB types does not affect the haplotype frequencies. This is different if rare island haplotypes Ab invade the monomorphic equilibrium M2. Then recombination between aB and Ab reduces the growth rate of Ab in proportion to its frequency. We therefore obtain the criterion m < α − β − r for the invasion of M2 by the island haplotype. We define the following critical migration rates:
| (A4a) |
| (A4b) |
| (A4c) |
The equilibrium has the coordinates and exists if m ≤ α − γ. It is asymptotically stable if
| (A5) |
which requires r > γ − β. Similarly, the equilibrium Sℬ has coordinates , exists if m ≤ −β, and is asymptotically stable if
| (A6) |
which requires r > α. The coordinates and stability conditions of and Sℬ are related by the substitutions α → γ − β and β → γ − α. This substitution exchanges the roles of the wild-type ab and the recombinant haplotype AB in the fitness scheme and expresses an important symmetry of the haploid model. From conditions (A3), (A5), and (A6), we deduce at once that at most one of the boundary equilibria can be stable for given parameters.
From the stability properties of the boundary equilibria, we can derive conditions for a globally stable DMI (and thus for ). In particular, IDMI exists and is globally stable if and only if the boundary of the state space is repelling, i.e., if genotypes that are initially absent can invade every boundary equilibrium. From (A3), (A5), and (A6) we deduce the following values for :
| (A7a) (A7b) (A7c) |
Condition (A7a) delineates the parameter regime with a globally stable DMI () from that where the boundary equilibrium is locally or globally stable. Conditions (A7b) and (A7c) provide analogous delineations for the regions where Sℬ and M2 are stable. In each case, there are two possibilities: If IDMI leaves the state space at , the boundary equilibrium involved in this bifurcation becomes globally stable. If the unstable equilibrium I0 enters the state space at , the corresponding boundary equilibrium becomes locally stable.
Internal equilibria and local stability
The possible internal equilibria are determined in File S1, section S.3. The coordinate p of an internal equilibrium can be expressed as a root of a third-order polynomial. Given p, the coordinate q is the root of a quadratic polynomial. Finally, D is a simple rational function of p and q. Only solutions that fall inside the state space [with p, q ε [0,1] and D has to satisfy (A2)] correspond to equilibria of the model. The explicit solutions are complicated and several case distinctions are necessary to ensure that a triple (p, q, D) is in the admissible range. Therefore, we give explicit formulas for the coordinates of IDMI and I0 only in special cases and rather focus on the conditions for the existence of these equilibria.
As explained above, there are two possibilities how a stable DMI can vanish from the state space as m increases. The equilibrium can leave the state space through one of the boundary equilibria at Alternatively, the internal equilibria IDMI and I0 can merge and disappear at a bifurcation point m = m* that is given by (File S1, section S.4)
| (A8) |
This migration rate corresponds to a bifurcation point of IDMI and I0 if and only if IDMI does not leave the state space if m < m*. Since IDMI can leave the state space only at , the boundaries of the regime with a bifurcation of IDMI and I0 are obtained by equating m* (Equation A8) with (Equation A7). At this boundary, the recombination rate r can take one of the following values:
| (A9) |
| (A10) |
| (A11) |
We further define
| (A12) |
To provide expressions for the upper bound below which IDMI exists, we need to distinguish several cases (cf. Theorem S.5 in File S1). They correspond to the mechanisms maintaining or establishing a DMI that result from the different types of fitness landscapes discussed in the main text.
-
1.Selection scenario 1: 0 < α < β < γ (double-peak landscape with maximum at the continental type). This selection scenario represents the parameter regime in which “selection against hybrids” is driving DMI evolution (area with dark shading in Figure 2). With this fitness landscape, a globally stable internal equilibrium cannot exist; i.e.,
(A13) - If r ≤ β − α, there is no internal equilibrium and the continental equilibrium M2 is globally stable for any m. If r > β − α, IDMI exists if m ≤ m*,
(A14) If , M2 is globally stable.
-
2.Selection scenario 2: 0 < α < β < γ (double-peak landscape with maximum at the island type). This selection scenario represents the intermediate parameter regime (open area in Figure 2) in which both mechanisms interfere. In this case, IDMI exists always for small m. If r < α − β, it is globally stable for m up to
(A15) - Thus, IDMI exists and is stable up to
(A16) If r < r2, the monomorphic equilibrium M2 is globally stable for . If r2 < r < α − β, M2 becomes locally stable at (where I0 enters the state space) and globally stable at (where IDMI and I0 merge). If r ≥ α − β, M2 is already locally stable at m = 0 and becomes the unique globally stable equilibrium at .
-
3.Selection scenario 3: γ − α < 0 < γ − β < α (slope-type landscape with weak DMI γ < α). This selection scenario represents a part of the parameter regime in which “selection against immigrants” drives DMI evolution. In Figure 2, it is represented by the area with light shading for 0 < β/α < 1. With this landscape, IDMI is globally stable for small m, and we have
(A17) -
For the existence of IDMI, we need to distinguish two subcases:
-
i.γ > α/2:
(A18) -
ii.γ < α/2:
(A19)
-
i.
-
4.Selection scenario 4: β < 0 < α < γ − β (slope-type with local adaptation). This selection scenario represents the remaining part of the parameter regime in which selection against immigrants drives DMI evolution. In Figure 2 it is depicted by the area with light shading for β / α < 0. With this landscape, IDMI is globally stable for small m, and we have
(A20) -
For the existence of IDMI, we distinguish two subcases:
-
i.γ + β > 0:
(A21) -
ii.γ + β < 0:
(A22)
-
i.
Initial conditions
The above results show that for sufficiently large values of r, we have in parts of the parameter space. This leads to bistable regimes, where maintenance of a DMI depends on the initial conditions. Depending on the order of substitution events in the evolutionary history of the two populations, in the Models section of the main text we have outlined five scenarios for the evolution of a parapatric DMI. Here, we show how they correspond to three different initial conditions that are illustrated in Figure A1.
For both the continent–island and island–island scenarios, the island allele A enters the island only after the allele frequencies at the locus ℬ have reached equilibrium. Locus ℬ is initially at the polymorphic Sℬ equilibrium, whenever this exists (i.e., if m ≤ −β). Otherwise, the population starts in the vicinity of the monomorphic equilibrium M2. Here, we assume that the ancestral b allele is not completely lost, or reintroduced at very low frequencies, such that the dynamics are not artificially stuck to the q = 1 boundary if this boundary is unstable.
For the island–continent and continent–continent scenarios, A mutants are present on the island while the continent is still fixed for the ab haplotype. A stable single-locus polymorphism with coordinates : results whenever the island allele can invade, which is the case if m < α. Otherwise, the population is initially in the vicinity of the monomorphic equilibrium M1 at which the ancestral haplotype is fixed.
For secondary contact, the island population is, by definition, initially fixed for the island haplotype, i.e., at M3.
For the case of independent loci, we show in File S1 (section S.8.2) that, in a bistable regime, a locally stable DMI will always evolve under the scenarios corresponding to the second or the third initial condition (island–continent, continent–continent, and secondary contact), but never under the scenarios corresponding to the first initial condition (island–island and continent–island). This holds independently of the size of the domain of attraction of the DMI. Extensive numerical calculations show that this finding extends to the general model with linkage.
Footnotes
Communicating editor: L. M. Wahl
Literature Cited
- Agrawal A. F., Feder J. L., Nosil P., 2011. Ecological divergence and the origins of intrinsic postmating isolation with gene flow. Int. J. Ecol. 2011: 1–15 [Google Scholar]
- Bank C., Hermisson J., Kirkpatrick M., 2012. Can reinforcement complete speciation? Evolution 66: 229–239 [DOI] [PubMed] [Google Scholar]
- Barton N., Bengtsson B. O., 1986. The barrier to genetic exchange between hybridising populations. Heredity 57: 357–376 [DOI] [PubMed] [Google Scholar]
- Barton N. H., Hewitt G. M., 1989. Adaptation, speciation and hybrid zones. Nature 341: 497–503 [DOI] [PubMed] [Google Scholar]
- Bateson W., 1909. Heredity and variation in modern lights, pp. 85–101 Darwin and Modern Science, edited by Seward A. C. Cambridge University Press, Cambridge, UK [Google Scholar]
- Bürger R., 2009. Multilocus selection in subdivided populations I. Convergence properties for weak or strong migration. J. Math. Biol. 58: 939–978 [DOI] [PubMed] [Google Scholar]
- Bürger R., Akerman A., 2011. The effects of linkage and gene flow on local adaptation: a two-locus continent-island model. Theor. Popul. Biol. 80: 272–288 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chou J.-Y., Leu J.-Y., 2010. Speciation through cytonuclear incompatibility: insights from yeast and implications for higher eukaryotes. BioEssays 32: 401–411 [DOI] [PubMed] [Google Scholar]
- Coyne J. A., Orr H. A., 2004. Speciation. Sinauer Associates, Sunderland, MA [Google Scholar]
- Cutter A. D., 2012. The polymorphic prelude to Bateson-Dobzhansky-Muller incompatibilities. Trends Ecol. Evol. 27: 209–218 [DOI] [PubMed] [Google Scholar]
- Dobzhansky T., 1936. Studies on hybrid sterility. II. Localization of sterility factors in Drosophila pseudoobscura hybrids. Genetics 21: 113–135 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Feder J. L., Nosil P., 2009. Chromosomal inversions and species differences: When are genes affecting adaptive divergence and reproductive isolation expected to reside within inversions? Evolution 63: 3061–3075 [DOI] [PubMed] [Google Scholar]
- Feldman M. W., 1971. Equilibrium studies of two locus haploid populations with recombination. Theor. Popul. Biol. 2: 299–318 [DOI] [PubMed] [Google Scholar]
- Gavrilets S., 1997. Hybrid zones with Dobzhansky-type epistatic selection. Evolution 51: 1027–1035 [DOI] [PubMed] [Google Scholar]
- Gavrilets S., 2000. Waiting time to parapatric speciation. Proc. Biol. Sci. 267: 2483. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Gavrilets S., 2004. Fitness Landscapes and the Origin of Species. Princeton University Press, Princeton, NJ [Google Scholar]
- Hofbauer J., 1990. An index theorem for dissipative semiflows. Rocky Mountain J. Math. 20: 1017–1031 [Google Scholar]
- Johnson N. A., 2010. Hybrid incompatibility genes: Remnants of a genomic battlefield? Trends Genet. 26: 317–325 [DOI] [PubMed] [Google Scholar]
- Kao K. C., Schwartz K., Sherlock G., 2010. A genome-wide analysis reveals no nuclear Dobzhansky-Muller pairs of determinants of speciation between S. cerevisiae and S. paradoxus, but suggests more complex incompatibilities. PLoS Genet. 6: e1001038. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Karlin S., McGregor J., 1972a. Application of method of small parameters to multi-niche population genetic models. Theor. Popul. Biol. 3: 186–209 [DOI] [PubMed] [Google Scholar]
- Karlin S., McGregor J., 1972b. Polymorphisms for genetic and ecological systems with weak coupling. Theor. Popul. Biol. 3: 210–238 [DOI] [PubMed] [Google Scholar]
- Kondrashov A. S., 2003. Accumulation of Dobzhansky-Muller incompatibilities within a spatially structured population. Evolution 57: 151–153 [DOI] [PubMed] [Google Scholar]
- Lande R., 1979. Effective deme sizes during long-term evolution estimated from rates of chromosomal rearrangement. Evolution 33: 234–251 [DOI] [PubMed] [Google Scholar]
- Lemmon A. R., Kirkpatrick M., 2006. Reinforcement and the genetics of hybrid incompatibilities. Genetics 173: 1145–1155 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lowry D. B., Modliszewski J. L., Wright K. M., Wu C. A., Willis J. H., 2008. The strength and genetic basis of reproductive isolating barriers in flowering plants. Philos. Trans. R. Soc. B 363: 3009–3021 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mani G. S., Clarke B. C., 1990. Mutational order: a major stochastic process in evolution. Proc. R. Soc. Lond. B Biol. Sci. 240: 29–37 [DOI] [PubMed] [Google Scholar]
- Mayr E., 1942. Systematics and the Origin of Species, from the Viewpoint of a Zoologist. Harvard University Press, Cambridge, MA [Google Scholar]
- Mullen L. M., Hoekstra H. E., 2008. Natural selection along an environmental gradient: a classic cline in mouse pigmentation. Evolution 62: 1555–1570 [DOI] [PubMed] [Google Scholar]
- Muller H., 1942. Isolating mechanisms, evolution and temperature. Biol. Symp. 6: 71–125 [Google Scholar]
- Nagylaki T., Hofbauer J., Brunovský P., 1999. Convergence of multilocus systems under weak epistasis or weak selection. J. Math. Biol. 38: 103–133 [DOI] [PubMed] [Google Scholar]
- Nosil P., Flaxman S. M., 2011. Conditions for mutation-order speciation. Proc. Biol. Sci. 278: 399–407 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nosil P., Crespi B. J., Sandoval C. P., 2003. Reproductive isolation driven by the combined effects of ecological adaptation and reinforcement. Proc. Biol. Sci. 270: 1911–1918 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Orr H. A., 1995. The population genetics of speciation: the evolution of hybrid incompatibilities. Genetics 139: 1805–1813 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Porter A. H., Johnson N. A., 2002. Speciation despite gene flow when developmental pathways evolve. Evolution 56: 2103–2111 [DOI] [PubMed] [Google Scholar]
- Presgraves D., 2003. A fine-scale genetic analysis of hybrid incompatibilities in Drosophila. Genetics 163: 955–972 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Presgraves D. C., 2010. The molecular evolutionary basis of species formation. Nat. Rev. Genet. 11: 175–180 [DOI] [PubMed] [Google Scholar]
- Presgraves D. C., Balagopalan L., Abmayr S. M., Orr H. A., 2003. Adaptive evolution drives divergence of a hybrid inviability gene between two species of Drosophila. Nature 423: 715–719 [DOI] [PubMed] [Google Scholar]
- Rundell R. J., Price T. D., 2009. Adaptive radiation, nonadaptive radiation, ecological speciation and nonecological speciation. Trends Ecol. Evol. 24: 394–399 [DOI] [PubMed] [Google Scholar]
- Rutschman D., 1994. Dynamics of the two-locus haploid model. Theor. Popul. Biol. 45: 167–176 [Google Scholar]
- Schluter D., 2009. Evidence for ecological speciation and its alternative. Science 323: 737–741 [DOI] [PubMed] [Google Scholar]
- Slatkin M., 1987. Gene flow and the geographic structure of natural populations. Science 236: 787–792 [DOI] [PubMed] [Google Scholar]
- Turelli M., Orr H. A., 2000. Dominance, epistasis and the genetics of postzygotic isolation. Genetics 154: 1663–1679 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Turelli M., Barton N. H., Coyne J. A., 2001. Theory and speciation. Trends Ecol. Evol. 16: 330–343 [DOI] [PubMed] [Google Scholar]
- Unckless R. L., Orr H. A., 2009. Dobzhansky-Muller incompatibilities and adaptation to a shared environment. Heredity 102: 214–217 [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu C.-I., Ting C.-T., 2004. Genes and speciation. Nat. Rev. Genet. 5: 114–122 [DOI] [PubMed] [Google Scholar]
- Yeaman S., Otto S. P., 2011. Establishment and maintenance of adaptive genetic divergence under migration, selection, and drift. Evolution 65: 2123–2129 [DOI] [PubMed] [Google Scholar]
- Yeaman S., Whitlock M. C., 2011. The genetic architecture of adaptation under migration-selection balance. Evolution 65: 1897–1911 [DOI] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.