Skip to main content
PMC home page
Genetics logoLink to Genetics
. 2012 Jul;191(3):883–894. doi: 10.1534/genetics.112.138578

Megabase-Scale Inversion Polymorphism in the Wild Ancestor of Maize

Zhou Fang *, Tanja Pyhäjärvi †, Allison L Weber ‡,1, R Kelly Dawe §, Jeffrey C Glaubitz **, José de Jesus Sánchez González ††, Claudia Ross-Ibarra †, John Doebley ‡, Peter L Morrell *,2, Jeffrey Ross-Ibarra †,‡‡,2
PMCID: PMC3389981  PMID: 22542971

Abstract

Chromosomal inversions are thought to play a special role in local adaptation, through dramatic suppression of recombination, which favors the maintenance of locally adapted alleles. However, relatively few inversions have been characterized in population genomic data. On the basis of single-nucleotide polymorphism (SNP) genotyping across a large panel of Zea mays, we have identified an ∼50-Mb region on the short arm of chromosome 1 where patterns of polymorphism are highly consistent with a polymorphic paracentric inversion that captures >700 genes. Comparison to other taxa in Zea and Tripsacum suggests that the derived, inverted state is present only in the wild Z. mays subspecies parviglumis and mexicana and is completely absent in domesticated maize. Patterns of polymorphism suggest that the inversion is ancient and geographically widespread in parviglumis. Cytological screens find little evidence for inversion loops, suggesting that inversion heterozygotes may suffer few crossover-induced fitness consequences. The inversion polymorphism shows evidence of adaptive evolution, including a strong altitudinal cline, a statistical association with environmental variables and phenotypic traits, and a skewed haplotype frequency spectrum for inverted alleles.

THE evolutionary role of chromosomal inversions has been studied in a wide array of organisms, from insects (Ayala et al. 2011; Stevison et al. 2011) to birds (Huynh et al. 2011) and plants (Hoffmann and Rieseberg 2008; Lowry and Willis 2010). Examination of inversion polymorphism was fundamental to the early study of selection and adaptive diversity, as well as the basis for understanding the maintenance of neutral polymorphism within populations (Dobzhansky 1950; Hoffmann et al. 2004). Homologous pairing of an inverted and a noninverted chromosome in heterozygotes leads to the formation of an inversion loop, and crossing over in an inversion loop can cause the formation of a dicentric chromosome and an acentric fragment at meiosis I, resulting in terminal deletions of the affected chromosome and gamete death at frequencies that correlate with the size of the inversion (Burnham 1962). Because of the difficulty of homologous pairing and the deleterious effects of homologous crossing over in inversions, inversions are typically observed to disrupt recombination in heterozygous individuals, leading to measurable effects on nucleotide sequence polymorphism, including the generation of extended linkage disequilibrium (LD). Inversion-induced LD has been reported in a variety of organisms, including humans (Bansal et al. 2007), Drosophila subobscura (Munte et al. 2005), and several other species (reviewed in Hoffmann and Rieseberg 2008). Strong differentiation between chromosomal arrangements (as measured by FST) has also been used as evidence of inversions in Drosophila (Andolfatto et al. 1999; Depaulis et al. 1999; Nóbrega et al. 2008).

A variety of circumstances can favor the maintenance or spread of an inversion polymorphism. The inversion may be selected for if the structural rearrangement itself has fitness consequences (Castermans et al. 2007). Natural selection can also favor the spread of an inversion if it contains locally adapted alleles, because inversions can suppress recombination and thus protect adaptive alleles from gene flow (Kirkpatrick and Barton 2006; Machado et al. 2007). Some inversion polymorphisms display strong patterns of geographic structure, consistent with local adaptation to ecological factors such as temperature regimes or water availability (White et al. 2009; Lowry and Willis 2010; Ayala et al. 2011). For example, strong differentiation among ecological zones was observed for an inversion in the mosquito Anopheles funestus (Ayala et al. 2011). In the yellow monkeyflower, Mimulus guttatus (Lowry and Willis 2010), an inversion is involved in local adaptation to Mediterranean habitats through several morphological and phenological traits, while the standard arrangement appears in a perennial ecotype from habitats with high year-round soil moisture. In addition to selection, inversion polymorphisms without strong deleterious effects may also increase in frequency through genetic drift and migration, potentially resulting in fixation in small populations (Bengtsson and Bodmer 1976; Lande 1984).

Here we examine the population-level diversity of a newly discovered 50-Mb inversion found in the wild subspecies of Zea mays (known collectively as teosinte). Inversions in both wild and domesticated Z. mays and related taxa have been reported previously (McClintock 1931; Morgan 1950; Ting 1965, 1967; Kato 1975; Ting 1976), but these were detected cytologically and little is known about their evolution in natural populations. We examine genome-wide patterns of LD in Z. mays, using 941 single-nucleotide polymorphism (SNP) markers genotyped in a diverse sample of 2782 individuals, including representatives of three Z. mays subspecies: domesticated maize (Z. mays ssp. mays), its wild progenitor Z. mays ssp. parviglumis, and the weedy taxon Z. mays ssp. mexicana (hereafter mays, parviglumis, and mexicana, respectively). A region spanning ∼50 Mb on the short arm of chromosome 1 in parviglumis and mexicana demonstrates the highest level of LD in the genome and coincides with a region of high differentiation between mays and parviglumis reported by Hufford et al. (2012). Comparison to other taxa in Zea and Tripsacum suggests that the inverted arrangement is derived. The inverted arrangement is present at population frequencies up to 90% in parviglumis, but completely absent in domesticated maize. We present evidence that the inversion is relatively ancient and has persisted in teosinte populations for sufficient time to permit its widespread occurrence in all 33 natural populations of subspecies parviglumis investigated. Our data further suggest the inversion may be adaptive, as the inverted arrangement shows a strong altitudinal cline and is associated with multiple environmental and phenotypic traits, and the haplotype frequency spectrum of inverted alleles appears inconsistent with neutral evolution.

Materials and Methods

Plant materials and genetic data

Plant materials (Supporting Information, Table S1) included accessions of all four subspecies of Z. mays (1573 ssp. mays, 975 ssp. parviglumis, 161 ssp. mexicana, and 10 ssp. huehuetenangensis), as well as Z. luxurians (17), Z. diploperennis (15), and Z. perennis (9). The panel also included 22 Tripsacum accessions used as outgroups. The 975 parviglumis accessions include 33 populations with at least 10 individuals in each population. The mays samples include 1283 accessions representing ∼250 traditional open-pollinated landraces (including 27 inbred landraces) and 290 modern inbred lines (Table S1).

Genotyping for the genome-wide set of 959 SNPs followed previously described methods (Weber et al. 2007; van Heerwaarden et al. 2010). The SNP discovery panel consisted of 14 mays inbred lines and 16 teosinte partial inbreds (Wright et al. 2005; Weber et al. 2007). We excluded accessions (7 parviglumis, 1 mexicana, and 20 mays) and loci (3 SNPs) with >15% missing data. We also removed SNPs where BLAST searches of context sequence identified multiple locations in the mays reference genome (Release 5a.59) (Schnable et al. 2009). This resulted in a final panel of 941 SNPs (Table S2) from 542 mapped genes. SNP genotypes and their contextual sequences are available at http://www.panzea.org and http://www.rilab.org. A subset of these data has been published elsewhere, including 706 SNPs from 584 parviglumis accessions in Weber et al. (2007); 123 SNPs from 817 parviglumis in Weber et al. (2008); and 468 SNPs from 1127 mays, 100 parviglumis, and 96 mexicana in van Heerwaarden et al. (2011).

The majority of the accessions represent open-pollinated populations that are highly heterozygous, resulting in genotypic data of unknown phase. We computationally phased each of the three subspecies separately using the software fastPHASE (Scheet and Stephens 2006) with 20 random starts and 25 iterations of the expectation-maximization algorithm. For each subspecies, inbred lines (Table S1) were used as training data.

We made use of published Sanger resequencing data from Wright et al. (2005). Wright and coauthors sequenced PCR products from teosinte accessions that had been inbred for two generations. Within the inversion, two individuals with a sequence from one arrangement at one locus and the alternate arrangement at a different locus were deemed heterozygous and removed from the analysis. We limited our analyses to reliably aligned loci on chromosome 1 with n ≥ 10 total sequences and n ≥ 3 of each arrangement. In total, we analyzed 95 loci, including 7 inside the inversion (Table S3; data available at www.panzea.org). We used the top BLAST hit from the Sorghum genome (Paterson et al. 2009) as an outgroup for each locus. Loci were annotated by BLAST comparison to the mays reference genome (Release 5a.59) (Schnable et al. 2009).

Data analysis and divergence time

Summary statistics of the SNP genotyping data and the resequencing data were calculated using the analysis package of the libsequence library (Thornton 2003). Although the absolute values of some summary statistics of the SNP genotyping data may be affected by ascertainment bias (Clark et al. 2005a), the relative values of these statistics are expected to be more robust.

We tested for Hardy–Weinberg equilibrium by treating the inversion as a single biallelic locus. LD (as measured by r2) was calculated for SNPs with a minor allele frequency (MAF) >5%, using the LDheatmap package (Shin et al. 2006) in R (R Development Core Team 2011). To assign individuals to haplotype clusters at the inversion, we used the genetic assignment software STRUCTURE (Pritchard et al. 2000; Falush et al. 2003). We estimated haplotype clusters for values of K ranging from 1 to 5. For each value of K, we used 10 replicate runs of the admixture model, with a burn-in of 100,000 iterations and a run length of 100,000 steps. To compare differentiation inside and outside of the inversion, we divided the sample of parviglumis into the two clusters identified by STRUCTURE and calculated FST (Weir and Cockerham 1984) between these two groups along chromosome 1.

Genetic (Manhattan) distance among inbred parviglumis lines was estimated with the software TASSEL (Bradbury et al. 2007) and calculated separately for SNPs inside and outside of the inversion. We used a Fitch–Margoliash least-squares approach (Fitch and Margoliash 1967) as implemented in the software package PHYLIP (Felsenstein 2005) to estimate a dendrogram for all taxa using the 17 SNPs inside the inversion.

We applied two common tests of neutrality (Hudson et al. 1987; McDonald and Kreitman 1991) to the Sanger resequencing data. For the McDonald–Kreitman (MK) test we used the seven resequenced loci inside the inversion and compared polymorphism at the inverted arrangement to divergence between the inverted arrangement and a Sorghum outgroup. For the Hudson–Kreitman–Aguade (HKA) test, we used 74 loci with ancestral information. HKA tests were performed both for the combined set of sequences and for sequences from each of the chromosomal arrangements separately. Because loci within the inversion are unlikely to be independent, we summed polymorphism and divergence data across loci within the inversion. We used the maximum-likelihood approach of Wright and Charlesworth (2004), running 100,000 Markov chain Monte Carlo (MCMC) iterations, and a starting parviglumis–Sorghum divergence of 60N generations.

We estimated divergence time between the arrangements, using sequences at seven loci from the two observed haplotype groups inside the inversion. We treated samples of the two chromosomal arrangements as distinct populations and estimated divergence time under an isolation-with-migration model as implemented in the software MIMAR (Becquet and Przeworski 2007). We set the inheritance and the mutation rate variation scalars both to 1 and the recombination inheritance and rate variation scalar to (Zri − 1)/(Zi − 1), where Zri is the initial length of locus i and Zi corresponds to the number of base pairs in locus i after filtering out indels and missing data. The mutation rate per generation per base pair was assumed constant across loci and set to 3 × 10−8 (Clark et al. 2005b). The population mutation rate per base pair, divergence time, and the natural logarithm of the population migration parameter were sampled from the uniform distributions U(0, 0.08), U(0, 106), and U(−2, 1), respectively. The exponential growth parameter was set to 6 (other values did not change results considerably). We ran the Markov chain for 5000 burn-in steps followed by 10,000 steps for parameter estimation, repeating our analysis with two independent seeds. Three hundred genealogies were generated per locus for each step of the MCMC. We inferred that convergence was reached when the posterior distributions of both runs were very similar; results reported are the average of both runs.

Association analyses

We used a Bayesian approach (Coop et al. 2010) to test for associations between the inversion and 22 geographical (altitude, latitude, and longitude) and bioclimatic (worldclim.org) variables in the 33 parviglumis populations with ≥10 samples (Table S4). The analysis explicitly accounts for population structure, using a covariance matrix of allele frequencies estimated by 50,000 MCMC steps using all SNPs. We assessed association genome-wide using all SNPs and using a single-marker test, treating the inversion as a single locus. In each case, five separate runs with 50,000 iterations were performed to control for differences among MCMC runs.

To examine whether the inverted arrangement was associated with phenotypic variation, we used phenotype data from Weber et al. (2008). Both phenotype and genotype data were available for 811 individuals. A kinship matrix was estimated from all 941 SNPs, using the options “all” and “additive” in the EMMA R package (Kang et al. 2008). Both genome-wide association and single-marker association (treating the inversion as a single locus) were performed for each of 37 phenotypes. Associations were tested using a mixed linear model as implemented in the software TASSEL (Bradbury et al. 2007). The R package qvalue was used to estimate the false discovery rate (FDR) and identify SNPs that were significant at an FDR of 5% (Storey and Tibshirani 2003).

Cytology

To assess the potential cytological impacts of the inversion, we screened 174 meiocytes from immature tassels of six parviglumis/mays F1 progeny resulting from the cross of two inbred parviglumis each with a single mays inbred line. Meiocytes were collected and staged following Li et al. (2010) and the chromosomes stained with either 1% aceto-orcein or DAPI. Recombination within the inversion was scored as previously described, noting chromosome bridges and acentric fragments at anaphase I (Dawe and Cande 1996).

Results

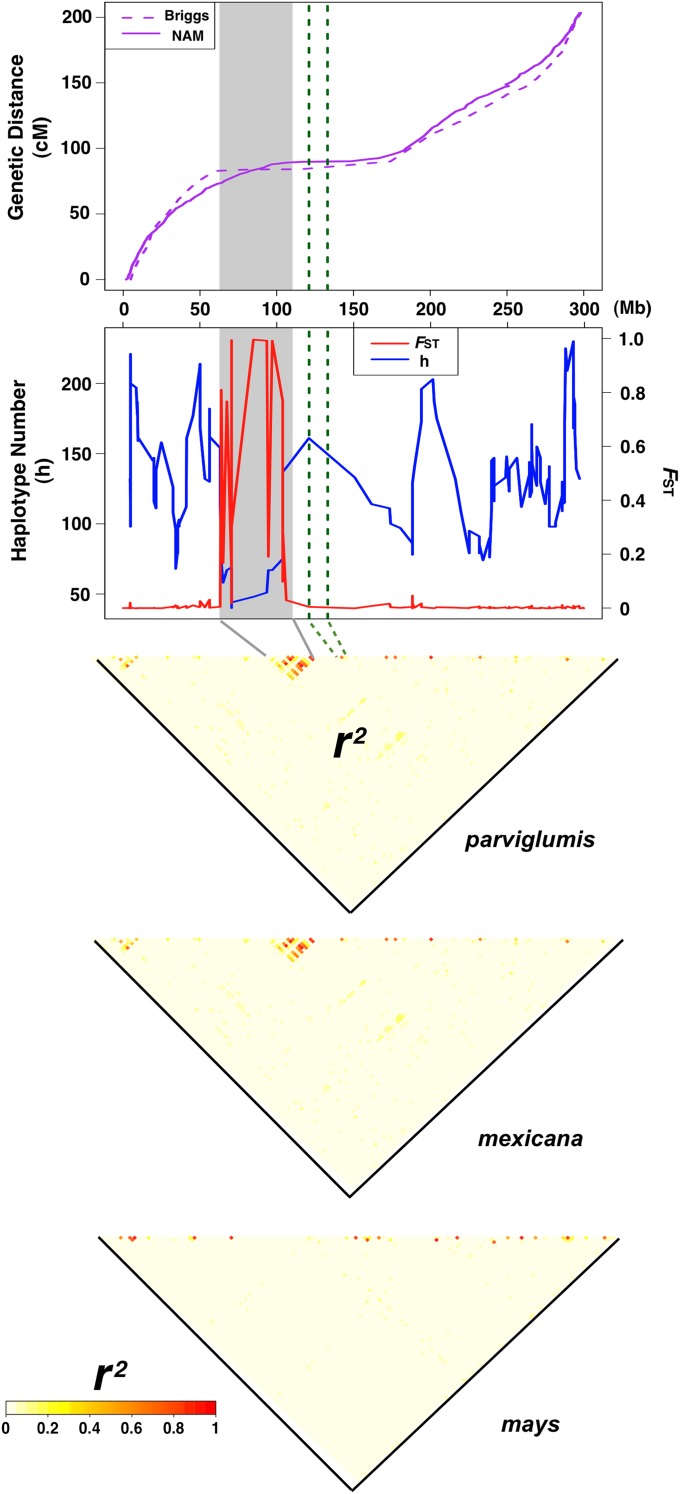
We examined the level of LD in each of the three subspecies of Z. mays with a genome-wide set of 941 SNPs from 2782 samples. Using computationally phased genotypic data, we searched for pairs of markers in high LD (r2 > 0.6) and separated by >1 Mb. Our scan identified two such regions, an ∼50-Mb region on chromosome 1 and an ∼15-Mb span of chromosome 8. Because the region on chromosome 8 is near a likely assembly error in the reference genome (J. Glaubitz, unpublished data), we focused our analysis on chromosome 1. The region of high LD on chromosome 1 in our data corresponds closely to the 65- to 115-Mb region on the physical map of the reference mays genome (B73 RefGen v2, release 5a.59, 2010–2011) recently reported by Hufford et al. (2012) as a putative inversion. Our data reveal high LD (mean r2 = 0.24) among the 17 SNPs from Mb 65.09 to 106.16 (Figure 1), compared to a genome-wide average of 0.004. Gametic disequilibrium, as estimated from unphased SNP genotyping data, also demonstrates this excess of LD (data not shown). Finally, high levels of LD are also evident in genotypic data from a panel of 13 individuals of parviglumis genotyped using the 55,000 SNPs on the MaizeSNP50 Illumina Infinium Assay (Hufford et al. 2012), suggesting that the LD observed is not an artifact of the genotyping platform used.

Figure 1 .

Figure 1 

Open in a new tab

Population genetic evidence for the Inv1n inversion. Top, cumulative genetic distance by physical position along chromosome 1. The dashed curve is based on the teosinte–maize backcross map of Briggs et al. (2007) and the solid curve is from the maize nested association-mapping (NAM) population (Yu et al. 2008). Bottom, haplotype number (blue curve) and FST between the inverted and standard arrangements (red curve). The number of haplotypes present across chromosome 1 was calculated in overlapping 10-SNP windows with 1-SNP increments. The inverted region is marked in gray and the centromere in green dashed lines. Below, LD (r2) is plotted across the chromosome for parviglumis, mexicana, and mays.

The extended region of high LD on chromosome 1 is a putative inversion

Because mays and the teosintes are outcrossing taxa with large effective population sizes, LD in the genome generally declines rapidly with distance (r2 < 0.1 within 1500 bp in domesticated mays) (Remington et al. 2001). The region of high LD is distinct from both the centromere (Wolfgruber et al. 2009) and known heterochromatic knobs (Buckler et al. 1999) and exhibits relatively low recombination (Figure 1). An ∼50-Mb span of high LD is unexpected, and while parviglumis and mexicana show evidence of high LD in this chromosomal region, levels of LD in our large sample of domesticated mays are similar to genome-wide averages (Figure 1). Other wild taxa also do not show an excess of LD on the short arm of chromosome 1, although our power to measure LD in these samples is likely hampered by smaller sample size and SNP ascertainment bias. Finally, a recent genetic map from a BC2S3 population derived from a cross between a mays line and a parviglumis line with the putatively inverted arrangement shows no crossovers inside the ∼50-Mb span in the 881 progeny genotyped, consistent with the putative inversion suppressing recombination in heterozygotes (L. Shannon and J. Doebley, unpublished data). Although final validation will require demonstrating differential marker order in the progeny of self-fertilized individuals homozygous for alternate arrangements (Mano et al. 2012), we view these multiple lines of evidence as a strong case that recombination is suppressed due to an inversion in this region, henceforth identified as Inv1n.

To test for evidence of pairing and recombination within the large Inv1n region, we examined male meiocytes from six F1 plants derived from two crosses between mays and an inbred parviglumis line containing Inv1n. Both hybrids revealed a low frequency of dicentric bridge formation at ∼4% (7/167), but no acentric fragments were observed (Table S5). Although such bridges were rare, an anaphase I bridge in a plant heterozygous for Inv1n was observed (Figure S1). In addition, we observed no obvious reduction in pollen viability or seed set in a total of five F1 plants (data not shown).

Haplotype variation and divergence time

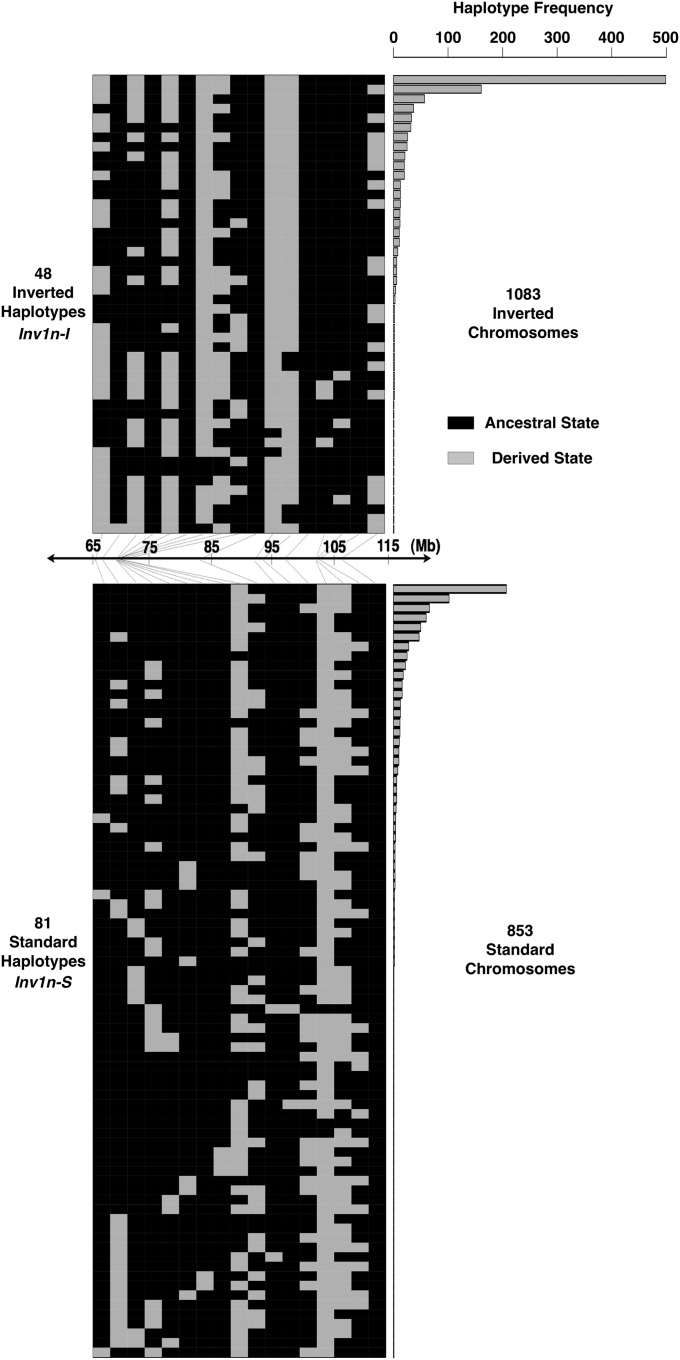
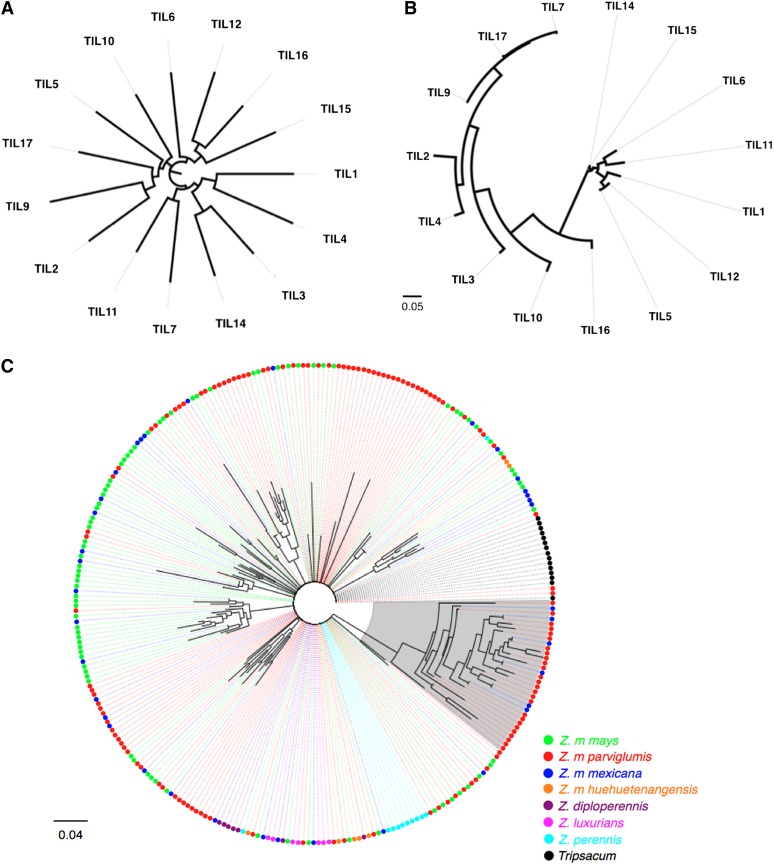
STRUCTURE (Pritchard et al. 2000; Falush et al. 2003) analysis of SNPs on all 1936 parviglumis chromosomes inside Inv1n shows the highest likelihood for K = 2 clusters, a pattern not seen from the full set of genome-wide SNPs (data not shown). These groups are hereafter referred to as Inv1n-I and Inv1n-S for the inverted and standard arrangements, respectively (Figure 2). Recombination among loci within a chromosomal arrangement should be unaffected, and levels of LD within Inv1n-I (mean r2 = 0.11) and Inv1n-S arrangements (mean r2 = 0.07) are indeed low and similar to background levels (Figure S2). Average FST between chromosomes with alternate arrangements is notably higher inside the Inv1n region (0.54) than across the rest of the genome (0.01) (Figure 1). Genetic distance among accessions for SNPs along chromosome 1 outside the Inv1n region shows little evidence of haplotype structure (Figure 3A), while genetic distance for SNPs inside Inv1n divides parviglumis into two clear haplotypic groups representing Inv1n-I and Inv1n-S (Figure 3B). The Inv1n-S cluster includes all taxa of Zea and Tripsacum investigated, and it is parsimonious to assume that the Inv1n-I cluster, present only in parviglumis and mexicana, represents the derived inverted arrangement (Figure 3C). Despite strong differentiation, the two arrangements share polymorphic SNPs (Figure 2), even in homozygous individuals unaffected by haplotype phasing (data not shown). Among the 968 parviglumis samples, 345 (35.6%) are heterozygous at Inv1n, while 369 (38.1%) and 254 (26.3%) are homozygous for the Inv1n-I and Inv1n-S arrangements, respectively. Inv1n-I consists of a smaller number of distinct haplotypes and shows a paucity of rare haplotype variants compared to Inv1n-S (Figure 2).

Figure 2 .

Figure 2 

Open in a new tab

Diagram of haplotype diversity in parviglumis based on the 17 SNPs within Inv1n. Haplotypes are divided into the two clusters identified by STRUCTURE. Each SNP is represented by either the ancestral state (solid) or the derived state (shaded). The frequency of each of the haplotypes from the inverted (top) and standard (bottom) arrangements is shown on the right. The middle bar shows the physical position of each of the 17 SNPs inside Inv1n.

Figure 3 .

Figure 3 

Open in a new tab

(A) Neighbor-joining tree for all SNPs outside Inv1n, using 15 parviglumis inbred lines. (B) Neighbor-joining tree for all SNPs inside Inv1n, using 15 parviglumis inbred lines. (C) Neighbor-joining tree for all unique haplotypes in each taxon, using all SNPs inside Inv1n. The haplotypes in the gray region represent the Inv1n-I arrangement.

Resequencing data from seven loci within Inv1n mirror these results (Table 1). Four loci (PZA00692, PZA00593, PZA03014, and PZA00146) show distinct haplotype clusters consistent with the SNP genotyping data (data not shown), dividing parviglumis into two groups representing Inv1n-I and Inv1n-S. A comparison of the two groups reveals a higher number of fixed differences, fewer shared derived SNPs, and higher average FST (0.53 vs. 0.05) inside the Inv1n region than outside. Average Tajima’s D of the entire sample is higher inside Inv1n (0.58 vs. −0.29), and the lack of rare haplotypes on the Inv1n-I background observed in the SNP data is reflected in the positive Tajima’s D at sequences from these chromosomes (Table 1). All alleles private to Inv1n-I are derived on the basis of the Sorghum outgroup sequence, but 30% of the alleles private to Inv1n-S are ancestral.

Table 1 . Mean (and standard deviation) of summary statistics for 7 resequenced loci inside and 88 loci outside Inv1n.

No. loci n L Ssh Sf Sp h H θπ Taj D Fay and Wu’s H
Inside (Inv1n-I) 7 (6) 14.6 (1.5) 307 (88) 0.3 (0.8) 4.3 (3.1) 2.9 (3.2) 2.3 (1.4) 0.49 (0.41) 0.004 (0.004) 0.37 (1.21) −0.001 (0.003)
Inside (Inv1n-S) 7 (6) 14.6 (1.5) 307 (88) 0.3 (0.8) 4.3 (3.1) 2.9 (2.5) 3.3 (1.7) 0.59 (0.36) 0.004 (0.003) −0.70 (0.56) 0 (0.003)
Outside (Inv1n-I) 88 (68) 13.5 (1.9) 414 (107) 4.7 (4.6) 0.1 (0.9) 4.1 (4.1) 3.9 (1.2) 0.89 (0.21) 0.011 (0.009) −0.22 (0.65) −0.003 (0.017)
Outside (Inv1n-S) 88 (68) 13.5 (1.9) 414 (107) 4.7 (4.6) 0.1 (0.9) 4.7 (3.6) 4.7 (1.8) 0.88 (0.21) 0.010 (0.007) −0.34 (0.62) −0.008 (0.029)
Open in a new tab

The number of loci with an outgroup is listed in parentheses in the “No. loci” column. The numbers in parentheses in other columns are standard deviations: n, number of samples; L, length of the locus; Ssh, number of shared SNPs between Inv1n-I and Inv1n-S; Sf, number of fixed SNPs; Sp, number of private SNPs; h, number of haplotypes; H, haplotype diversity; θπ, pairwise difference per base pair.

We used multiple approaches to estimate the age of Inv1n-I from the resequencing data. Using the MCMC approach of Becquet and Przeworski (2007), which estimates divergence time from patterns of shared polymorphism under an isolation model, divergence was estimated to be ∼296,000 generations, with a 95% confidence interval (C.I.) between 221,000 and 398,000 generations. Assuming a constant rate of substitution of 3 × 10−8 per generation (Clark et al. 2005b), we can also calculate divergence time from net differences in nucleotide diversity (Nei and Li 1979) between Inv1n-I and Inv1n-S, which gives an estimate of 260,000 generations. Finally, estimates of the time to the most recent common ancestor (TMRCA) (Thomson et al. 2000; Hudson 2007) of the complete sample inside Inv1n (308,100 generations, 95% C.I. of 272,800–345,600 generations) and of Inv1n-I alone (133,200 generations, 95% C.I. of 96,500–175,800 generations) are consistent with other methods.

Neutrality tests

On the basis of standard tests of neutrality, there is limited evidence of selection on Inv1n. HKA tests on Inv1n did not detect evidence of balancing selection caused by environmental heterogeneity (P-value = 0.46, divergence to diversity ratio = 2.58). MK (P-value = 0.65) and HKA (P-value = 0.15) tests on resequencing data from the Inv1n-I arrangement failed to reject a neutral model, and Fay and Wu’s H (Fay and Wu 2000) did not differ markedly between the Inv1n-I arrangements or compared to loci outside of Inv1n (Table 1).

Population frequencies and association analyses

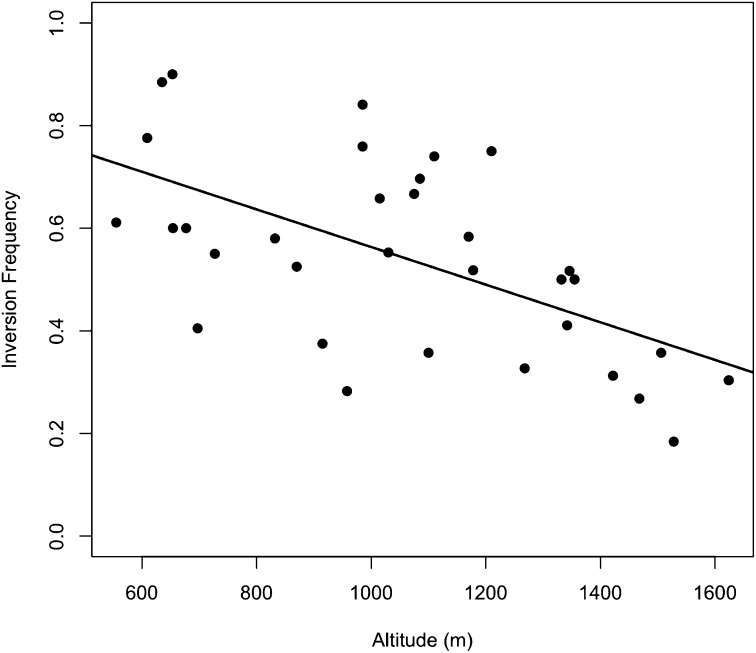
All 33 parviglumis populations sampled were polymorphic for both arrangements at the Inv1n locus, with a mean Inv1n-I frequency of 55%. The frequency of Inv1n-I is negatively correlated with altitude (r2 = 0.34) (Figure 4, Figure S3, and Table S4), ranging from 90% in the Quenchendio population at an altitude of 653 m to 18.4% in Ahuacatitlan at 1528 m. Consistent with this, Inv1n-I occurs at a frequency of only 9.7% in subspecies mexicana, which is found at higher altitudes than subspecies parviglumis (mean altitude of 2091 m vs. 1087 m for our mexicana and parviglumis samples). The most common Inv1n-I haplotype makes up 46% (499/1083) of parviglumis chromosomes with the Inv1n-I variant and does not vary significantly in frequency among populations (χ2 = 2.27, d.f. = 32, P-value = 1).

Figure 4 .

Figure 4 

Open in a new tab

Inv1n-I frequency in parviglumis populations is negatively correlated with altitude. Each point corresponds to a population, with its altitude on the x-axis and Inv1n-I frequency on the y-axis.

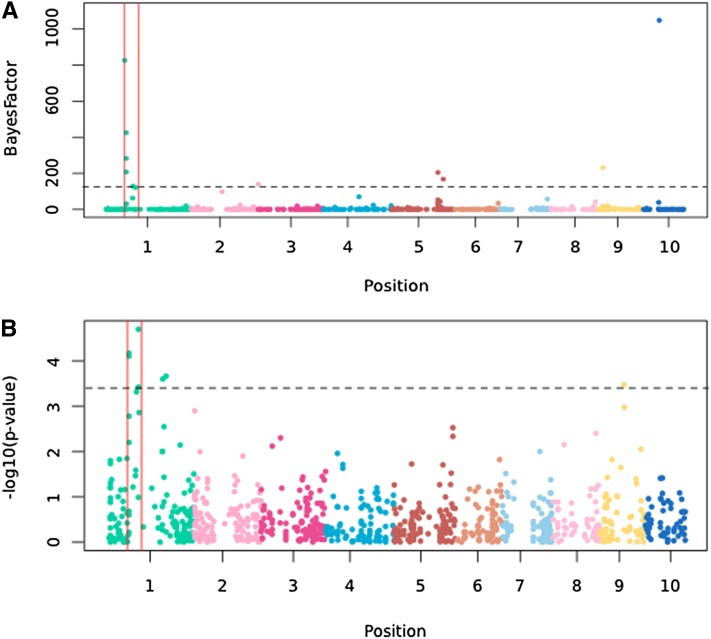
Using a model-based approach (Coop et al. 2010) to control for population structure, we examined the association between Inv1n-I frequency and 22 environmental variables (Table S6). Among environmental variables, altitude was most strongly correlated with Inv1n-I frequency and consistently obtained the highest Bayes factors among runs (mean 136). High Bayes factors were also observed for other bioclimatic variables, including temperature (mean temperature of driest quarter, mean Bayes factor = 49) and precipitation (precipitation of driest month, mean Bayes factor = 48). Genome-wide analysis of all SNPs produced mean Bayes factors for association with altitude ranging from 0.29 to 1048 (Table S6). SNPs in the inversion are 10-fold enriched in the top 5% tail of Bayes factors for altitude and >20-fold enriched in the top 1% tail, strongly suggesting a link between Inv1n and altitude (Figure 5).

Figure 5 .

Figure 5 

Open in a new tab

(A) Bayes factors for correlation between allele frequencies and altitude in 33 natural parviglumis populations. Inv1n is indicated by red vertical lines. The 99th percentile of the distribution of Bayes factors is indicated by a horizontal dashed line. Chromosomes 1–10 are plotted in order and in different colors. (B) Association between all SNPs and culm diameter. SNPs significant at 5% FDR are above the dashed line.

We also used a mixed linear model analysis to test for associations between Inv1n-I and phenotypic data from the same populations (Weber et al. 2008). Inv1n-I appears to be associated with the percentage of male internodes (PSIN) (P-value = 0.0055, r2 = 0.024), percentage of staminate spikelets (STAM) (P-value = 0.0069, r2 = 0.023), culm diameter (CULM) (P-value = 0.0137, r2 = 0.011), and leaf number (LFNM) (P-value = 0.0232, r2 = 0.010) (Table S7), but none of the associations are significant after Bonferroni correction for phenotypes tested and effect sizes for all phenotypes are very small. In addition to testing the inversion as a single locus, we also investigated associations between individual SNPs and phenotypes. For both PSIN and STAM, none of the 17 SNPs in Inv1n were among the 1% of SNPs most strongly associated with the two phenotypes. However, SNPs in Inv1n were enriched in the 1% tail of P-values for both CULM (15× enrichment) and LFNM (3×). None of the SNPs were significantly associated with PSIN or LFNM at a FDR of 5%, while four SNPs outside of the inversion were significantly associated with STAM. Of the seven SNPs significantly associated with CULM at an FDR of 5%, four (PZA00263.14, PZD00077.7, PZA00692.5, and PZA03014.24) are inside Inv1n.

Discussion

Using a genome-wide set of SNPs in a large panel of wild and domesticated Zea, we provide evidence of an ∼50-Mb inversion on the short arm of chromosome 1 of subspecies parviglumis and mexicana. While our cytological data are not directly diagnostic for an inversion, population genetic data preclude alternative explanations. For example, the dramatic reduction in haplotype number in the Inv1n region (Figure 1) could be indicative of a selective sweep (Kim and Nielsen 2004; Nielsen et al. 2005; McVean 2007). However, the largest sweep identified in maize to date is only 1.1 Mb (Tian et al. 2009), and both the age of the inversion and common tests for departures from neutrality do not provide evidence of strong selection. Another alternative explanation would be the presence of strong negative interactions between distantly linked loci, potentially due to synthetic lethality (Boone et al. 2007). Such interactions should not generate extended patterns of elevated LD among intervening SNPs, as crossing over among haplotypes not carrying alleles involved in the negative interaction should not be affected. Both selective sweeps and negative interactions are inconsistent with the presence of only two major haplotypes in the Inv1n region and fail to explain the clinal variation in haplotype frequencies seen at Inv1n-I.

To our knowledge, the only prior evidence for Inv1n is a report of high LD and high FST from a much smaller sample of parviglumis (Hufford et al. 2012), but a number of other large inversions have been previously reported in mays and its wild relatives (Ting 1965, 1967, 1976; Maguire 1966; Kato 1975). These include an ∼50-Mb inversion on the long arm of chromosome 3 in Z. luxurians (Ting 1965) and an ∼35-Mb inversion that covers most of the short arm of chromosome 8 in both mays (McClintock 1960) and mexicana (Ting 1976). While some of these inversions were experimentally induced (McClintock 1931; Morgan 1950), several have also been identified in natural populations of multiple taxa (Kato 1975; Ting 1976).

One of the factors that may limit the geographic spread of large inversions is the potential fitness cost of crossing over. The frequency of chromosome loss is dependent on the inversion size and efficiency of synapsis over the inverted region (Burnham 1962; Maguire and Riess 1994; Lamb et al. 2007). When gene density is low, such as in pericentromeric regions, or there is a lack of continuous homology, chromosomes will often synapse in a nonhomologous manner without recombination (McClintock 1933). In maize, for example, an inversion on the long arm of chromosome 1 similar in size to Inv1n (19 cM) was seen to undergo homologous pairing in only about one-third of cases (Maguire 1966). Since Inv1n is located in a pericentromeric region with low gene density and covers a short genetic distance (2–13 cM), we anticipated that it would rarely pair and recombine with a noninverted chromosome. Our data are consistent with these arguments. We observed repressed recombination around Inv1n and no cytological evidence of crossing over in inversion heterozygotes. SNP data indicate no deviations from expected Hardy–Weinberg genotype frequencies at Inv1n, and we see no obvious evidence of effects on fertility. Given these observations, we suspect that inversion polymorphisms may be relatively common in natural plant populations, especially in regions of the genome with low recombination rates such as pericentromeres. Low recombination has also been offered as an explanation for the lack of underdominance in many pericentromeric inversions in Drosophila (Coyne et al. 1993). As dense genotyping becomes more cost effective, we predict that numerous common inversions will be identified in natural populations of Zea and other organisms.

Origin and age of Inv1n

Our evidence suggests that Inv1n-I is the derived, inverted arrangement. Inv1n-I is not found in Tripsacum or Zea taxa except for parviglumis and mexicana (Figure 3C), and, unlike in Inv1n-S, all SNPs private to Inv1n-I are derived in resequencing data. Both SNP and resequencing data show strong differentiation between the two arrangements (Figure 1 and Table 1). Multiple methods of estimating the age of the Inv1n-I haplotype point to an origin ∼300,000 generations ago. This predates both the split between mexicana and parviglumis and the split between Z. luxurians and Z. mays and is similar to the estimated age of divergence of most species in the genus Zea (Ross-Ibarra et al. 2009). Several considerations suggest that these numbers are plausible. First, the proportion of SNPs shared between parviglumis and mexicana on chromosome 1 does not differ inside or outside of Inv1n (15/17 vs. 134/139, Fisher’s exact test P-value = 0.48), suggesting that the presence of the inversion in both subspecies is likely due to shared ancestral polymorphism rather than recent gene flow. Second, while the estimated age of Inv1n-I is similar to the estimated divergence of species, other species in Zea have narrow distributions (Fukunaga et al. 2005) and presumably small effective population sizes, increasing the potential for loss of variants at low frequency in the ancestral population. Third, Inv1n-I could consist of multiple independent inversions, similar to the inversion polymorphisms identified in the white-throated sparrow (Thomas et al. 2008). In this case, estimates of the age of the inversion would be biased upward, as each inversion would have arisen independently on distinct backgrounds. Such a scenario might also explain the observation of shared polymorphisms between Inv1n-I and Inv1n-S. Our data cannot distinguish the number of independent inversions in the region, however, which would instead require analysis of progeny derived from crosses of multiple individuals homozygous for different haplotypes of Inv1n-I and a more dense set of markers.

While small effective population size may explain the absence of Inv1n-I from other taxa in Zea, its complete absence in our sample of 1573 mays requires additional explanation. Sampling alone is unlikely to play a role, as the vast majority of our mays accessions are landraces, collected from across the Americas, including accessions collected within the range of parviglumis and mexicana. Estimates of the domestication bottleneck and observed levels of diversity in domesticated mays (Tenaillon et al. 2004; Wright et al. 2005) also suggest that drift during domestication is not a compelling explanation, especially given that Inv1n-I occurs at frequencies of up to 90% in the lowland areas where domestication is thought to have occurred (Matsuoka et al. 2002; Piperno et al. 2009; van Heerwaarden et al. 2011). We speculate instead that Inv1n-I may have been selected against in domesticated mays. Our association analysis provides limited evidence in support of this idea, as Inv1n-I is negatively associated with culm width in parviglumis, while domesticated mays has more robust culms than its wild progenitor (Briggs et al. 2007).

Selection on Inv1n

While standard tests of neutrality do not provide evidence for selection, there is reason to believe that Inv1n is not evolving neutrally. First, the Inv1n-I arrangement is widely distributed, segregating in all 33 populations investigated; only two SNPs on chromosome 1 are also polymorphic in all populations. Second, pairwise FST inside Inv1n appears uncorrelated to pairwise FST genome-wide (r2 = 0.04; Figure S4), suggesting that the frequency of Inv1n is not entirely due to isolation by distance. Third, even after correcting for population structure, Inv1n-I frequency is associated with a number of environmental variables (Table S6), including a strong altitudinal cline (Figure 4 and Figure S3). Latitudinal (Anderson et al. 2005; Santos et al. 2005; Umina et al. 2005) and altitudinal clines (Levitan 2001) are commonly observed for inversion polymorphisms and are often thought to be related to temperature adaptation (Levitan 2001; Umina et al. 2005; Balanyá et al. 2006). Fourth, the Inv1n-I arrangement is, to our knowledge, the first inversion in Zea shown to be associated with phenotypic differences (Table S7). These include culm diameter, a trait that differentiates maize from teosinte (Briggs et al. 2007), and tassel morphology (Table S7), which is known to differ between parviglumis and mexicana (Doebley 1983) and between lowland and highland maize (Anderson 1946; Bretting and Goodman 1989). Fifth, the lack of rare variants and the high frequency of the most common Inv1n-I haplotype (Figure 2) suggest that this haplotype may have recently risen to high frequency due to a partial sweep. The observed lack of rare variants is especially striking given the genome-wide pattern of an excess of low-frequency variants (Table 1), an observation reported in multiple studies (Tenaillon et al. 2004; Wright et al. 2005; Moeller et al. 2007; Ross-Ibarra et al. 2009). While the most common haplotype at Inv1n-I does not show signs of extended homozygosity beyond the borders of the inversion (Figure S5) as might be expected if it has been recently swept to higher frequency, the nearest flanking SNPs are 1.1 and 14.6 Mb distant and our power to detect an extended haplotype is low. Sixth, the absence of Inv1n-I from domesticated maize, in spite of recurrent gene flow from both parviglumis and mexicana (Wilkes 1967; Fukunaga et al. 2005; Ross-Ibarra et al. 2009; van Heerwaarden et al. 2011), suggests that the inverted arrangement was selected against at some point during mays domestication or breeding. Finally, we note that, aside from strong divergence between chromosomes of different arrangements, selection may be difficult to detect in diversity data from inversions of an age similar to ours (Guerrero et al. 2012).

Selection may act on inversions because of the fitness consequences of the structural rearrangement itself or of adaptive alleles at loci inside the inversion (Kirkpatrick and Barton 2006). While these scenarios predict somewhat different patterns of diversity (Guerrero et al. 2012), our SNP genotyping data are of insufficient density to distinguish between them. Regardless of the mechanism of selection, the observed altitudinal cline and absence in domesticated mays suggest that Inv1n-I is not ubiquitously adaptive. Even in low-altitude populations where it seems to be favored, a large inversion such as Inv1n may have captured several recessive deleterious alleles, effectively preventing its fixation (Kirkpatrick and Barton 2006).

Supplementary Material

Supporting Information
supp_191_3_883__index.html (2.9KB, html)

Acknowledgments

We thank Kate Hodges for help with cytological scoring; Kevin Volz for help with geographic information systems data and for producing Figure S3; and Graham Coop, Loren Rieseberg, and two anonymous reviewers for helpful comments on earlier versions of the manuscript. This work was carried out using computing resources at the University of Minnesota Supercomputing Institute. We acknowledge funding from the Academy of Finland (to T.P.) and start-up funds from the University of Minnesota Department of Agronomy and Plant Genetics (to P.L.M.) and from the National Science Foundation (NSF) (DBI-0820619 to J.D. and NSF IOS-0922703 to R.K.D. and J.R-I.).

Footnotes

Communicating editor: O. Savolainen

Literature Cited

  1. Anderson A. R., Hoffmann A. A., Mckechnie S. W., Umina P. A., Weeks A. R., 2005.  The latitudinal cline in the In (3R) Payne inversion polymorphism has shifted in the last 20 years in Australian Drosophila melanogaster populations. Mol. Ecol. 14: 851–858 [DOI] [PubMed] [Google Scholar]
  2. Anderson E., 1946.  Maize in Mexico a preliminary survey. Ann. Mo. Bot. Gard. 33: 147–247 [Google Scholar]
  3. Andolfatto P., Wall J. D., Kreitman M., 1999.  Unusual haplotype structure at the proximal breakpoint of In(2L)t in a natural population of Drosophila melanogaster. Genetics 153: 1297–1311 [DOI] [PMC free article] [PubMed] [Google Scholar]
  4. Ayala D., Fontaine M. C., Cohuet A., Fontenille D., Vitalis R., et al. , 2011.  Chromosomal inversions, natural selection and adaptation in the malaria vector Anopheles funestus. Mol. Biol. Evol. 28: 745–758 [DOI] [PMC free article] [PubMed] [Google Scholar]
  5. Balanyá J., Oller J. M., Huey R. B., Gilchrist G. W., Serra L., 2006.  Global genetic change tracks global climate warming in Drosophila subobscura. Science 313: 1773–1775 [DOI] [PubMed] [Google Scholar]
  6. Bansal V., Bashir A., Bafna V., 2007.  Evidence for large inversion polymorphisms in the human genome from HapMap data. Genome Res. 17: 219–230 [DOI] [PMC free article] [PubMed] [Google Scholar]
  7. Becquet C., Przeworski M., 2007.  A new approach to estimate parameters of speciation models with application to apes. Genome Res. 17: 1505–1519 [DOI] [PMC free article] [PubMed] [Google Scholar]
  8. Bengtsson B. O., Bodmer W. F., 1976.  On the increase of chromosome mutations under random mating. Theor. Popul. Biol. 9: 260–281 [DOI] [PubMed] [Google Scholar]
  9. Boone C., Bussey H., Andrews B. J., 2007.  Exploring genetic interactions and networks with yeast. Nat. Rev. Genet. 8: 437–449 [DOI] [PubMed] [Google Scholar]
  10. Bradbury P. J., Zhang Z., Kroon D. E., Casstevens T. M., Ramdoss Y., et al. , 2007.  TASSEL: software for association mapping of complex traits in diverse samples. Bioinformatics 23: 2633–2635 [DOI] [PubMed] [Google Scholar]
  11. Bretting P. K., Goodman M. M., 1989.  Karyotypic variation in Mesoamerican races of maize and its systematic significance. Econ. Bot. 43: 107–124 [Google Scholar]
  12. Briggs W. H., Mcmullen M. D., Gaut B. S., Doebley J., 2007.  Linkage mapping of domestication loci in a large maize teosinte backcross resource. Genetics 177: 1915–1928 [DOI] [PMC free article] [PubMed] [Google Scholar]
  13. Buckler E. S., Phelps-Durr T. L., Buckler C. S. K., Dawe R. K., Doebley J. F., et al. , 1999.  Meiotic drive of chromosomal knobs reshaped the maize genome. Genetics 153: 415–426 [DOI] [PMC free article] [PubMed] [Google Scholar]
  14. Burnham C. R., 1962.  Discussions in Cytogenetics. Burgess Publishing, Minneapolis [Google Scholar]
  15. Castermans D., Vermeesch J. R., Fryns J. P., Steyaert J. G., Van De Ven W. J. M., et al. , 2007.  Identification and characterization of the TRIP8 and REEP3 genes on chromosome 10q21.3 as novel candidate genes for autism. Eur. J. Hum. Genet. 15: 422–431 [DOI] [PubMed] [Google Scholar]
  16. Clark A. G., Hubisz M. J., Bustamante C. D., Williamson S. H., Nielsen R., 2005a.  Ascertainment bias in studies of human genome-wide polymorphism. Genome Res. 15: 1496–1502 [DOI] [PMC free article] [PubMed] [Google Scholar]
  17. Clark R. M., Tavare S., Doebley J., 2005b.  Estimating a nucleotide substitution rate for maize from polymorphism at a major domestication locus. Mol. Biol. Evol. 22: 2304–2312 [DOI] [PubMed] [Google Scholar]
  18. Coop G., Witonsky D., Di Rienzo A., Pritchard J. K., 2010.  Using environmental correlations to identify loci underlying local adaptation. Genetics 185: 1411–1423 [DOI] [PMC free article] [PubMed] [Google Scholar]
  19. Coyne J. A., Meyers W., Crittenden A. P., Sniegowski P., 1993.  The fertility effects of pericentric inversions in Drosophila melanogaster. Genetics 134: 487–496 [DOI] [PMC free article] [PubMed] [Google Scholar]
  20. Dawe R. K., Cande W. Z., 1996.  Induction of centromeric activity in maize by suppressor of meiotic drive 1. Proc. Natl. Acad. Sci. USA 93: 8512–8517 [DOI] [PMC free article] [PubMed] [Google Scholar]
  21. Depaulis F., Brazier L., Veuille M., 1999.  Selective sweep at the Drosophila melanogaster suppressor of hairless locus and its association with the In(2L)t inversion polymorphism. Genetics 152: 1017–1024 [DOI] [PMC free article] [PubMed] [Google Scholar]
  22. Dobzhansky T., 1950.  Genetics of natural populations. XIX. Origin of heterosis through natural selection in populations of Drosophila pseudoobscura. Genetics 35: 288–302 [DOI] [PMC free article] [PubMed] [Google Scholar]
  23. Doebley J. F., 1983.  The maize and teosinte male inflorescence: a numerical taxonomic study. Ann. Mo. Bot. Gard. 70: 32–70 [Google Scholar]
  24. Falush D., Stephens M., Pritchard J. K., 2003.  Inference of population structure using multilocus genotype data: linked loci and correlated allele frequencies. Genetics 164: 1567–1587 [DOI] [PMC free article] [PubMed] [Google Scholar]
  25. Fay J. C., Wu C. I., 2000.  Hitchhiking under positive Darwinian selection. Genetics 155: 1405–1413 [DOI] [PMC free article] [PubMed] [Google Scholar]
  26. Felsenstein J., 2005. PHYLIP (Phylogeny Inference Package), version 3.6 (distributed by the author). Department of Genome Sciences, University of Washington, Seattle
  27. Fitch W. M., Margoliash E., 1967.  Construction of phylogenetic trees. Science 155: 279–284 [DOI] [PubMed] [Google Scholar]
  28. Fukunaga K., Hill J., Vigouroux Y., Matsuoka Y., Sanchez G. J., et al. , 2005.  Genetic diversity and population structure of teosinte. Genetics 169: 2241–2254 [DOI] [PMC free article] [PubMed] [Google Scholar]
  29. Guerrero R. F., Rousset F., Kirkpatrick M., 2012.  Coalescent patterns for chromosomal inversions in divergent populations. Philos. Trans. R. Soc. B 367: 430–438 [DOI] [PMC free article] [PubMed] [Google Scholar]
  30. Hoffmann A. A., Rieseberg L. H., 2008.  Revisiting the impact of inversions in evolution: From population genetic markers to drivers of adaptive shifts and speciation? Annu. Rev. Ecol. Evol. Syst. 39: 21–42 [DOI] [PMC free article] [PubMed] [Google Scholar]
  31. Hoffmann A. A., Sgro C. M., Weeks A. R., 2004.  Chromosomal inversion polymorphisms and adaptation. Trends Ecol. Evol. 19: 482–488 [DOI] [PubMed] [Google Scholar]
  32. Hudson R. R., 2007.  The variance of coalescent time estimates from DNA sequences. J. Mol. Evol. 64: 702–705 [DOI] [PubMed] [Google Scholar]
  33. Hudson R. R., Kreitman M., Aguadé M., 1987.  A test of neutral molecular evolution based on nucleotide data. Genetics 116: 153–159 [DOI] [PMC free article] [PubMed] [Google Scholar]
  34. Hufford M. B., Xun X., van Heerwaarden J., Pyhäjärvi T., Chia J. M., et al. , 2012.  Comparative population genomics of maize domestication and improvement (in press) [Google Scholar]
  35. Huynh L. Y., Maney D. L., Thomas J. W., 2011.  Chromosome-wide linkage disequilibrium caused by an inversion polymorphism in the white-throated sparrow (Zonotrichia albicollis). Heredity 106: 537–546 [DOI] [PMC free article] [PubMed] [Google Scholar]
  36. Kang H. M., Zaitlen N. A., Wade C. M., Kirby A., Heckerman D., et al. , 2008.  Efficient control of population structure in model organism association mapping. Genetics 178: 1709–1723 [DOI] [PMC free article] [PubMed] [Google Scholar]
  37. Kato T. A., 1975.  Cytological studies of maize and teosinte in relation to their origin and evolution. Available at http://www.maizegdb.org/cooperators.php. Accessed June 2012
  38. Kim Y., Nielsen R., 2004.  Linkage disequilibrium as a signature of selective sweeps. Genetics 167: 1513–1524 [DOI] [PMC free article] [PubMed] [Google Scholar]
  39. Kirkpatrick M., Barton N., 2006.  Chromosome inversions, local adaptation and speciation. Genetics 173: 419–434 [DOI] [PMC free article] [PubMed] [Google Scholar]
  40. Lamb J. C., Meyer J. M., Birchler J. A., 2007.  A hemicentric inversion in the maize line knobless Tama flint created two sites of centromeric elements and moved the kinetochore-forming region. Chromosoma 116: 237–247 [DOI] [PubMed] [Google Scholar]
  41. Lande R., 1984.  The expected fixation rate of chromosomal inversions. Evolution 38: 743–752 [DOI] [PubMed] [Google Scholar]
  42. Levitan M., 2001.  Studies of linkage in populations. XIV. Historical changes in frequencies of gene arrangements and arrangement combinations in natural populations of Drosophila robusta. Evolution 55: 2359–2362 [DOI] [PubMed] [Google Scholar]
  43. Li X., Topp C. N., Dawe R. K., 2010.  Maize antibody procedures: immunolocalization and chromatin immunoprecipitation (ChIP), pp. 271–286 in Plant Cytogenetics, Genome Structure and Chromosome Function, edited by H. W. Bass and J. A. Birchler. Springer-Verlag, Berlin/Heidelberg, Germany/New York [Google Scholar]
  44. Lowry D. B., Willis J. H., 2010.  A widespread chromosomal inversion polymorphism contributes to a major life-history transition, local adaptation, and reproductive isolation. PLoS Biol. 8: e1000500 [DOI] [PMC free article] [PubMed] [Google Scholar]
  45. Machado C. A., Haselkorn T. S., Noor M. A. F., 2007.  Evaluation of the genomic extent of effects of fixed inversion differences on intraspecific variation and interspecific gene flow in Drosophila pseudoobscura and D. persimilis. Genetics 175: 1289–1306 [DOI] [PMC free article] [PubMed] [Google Scholar]
  46. Maguire M. P., 1966.  The relationship of crossing over to chromosome synapsis in a short paracentric inversion. Genetics 53: 1071–1077 [DOI] [PMC free article] [PubMed] [Google Scholar]
  47. Maguire M. P., Riess R. W., 1994.  The relationship of homologous synapsis and crossing over in a maize inversion. Genetics 137: 281–288 [DOI] [PMC free article] [PubMed] [Google Scholar]
  48. Mano Y., Omori F., Takeda K., 2012.  Construction of intraspecific linkage maps, detection of a chromosome inversion, and mapping of QTL for constitutive root aerenchyma formation in the teosinte Zea nicaraguensis. Mol. Breed. 29: 137–146 [Google Scholar]
  49. Matsuoka Y., Vigouroux Y., Goodman M. M., Sanchez G., Buckler E. S., et al. , 2002.  A single domestication for maize shown by multilocus microsatellite genotyping. Proc. Natl. Acad. Sci. USA 99: 6080–6084 [DOI] [PMC free article] [PubMed] [Google Scholar]
  50. McClintock B., 1931.  Cytological observations of deficiencies involving known genes, translocations and an inversion in Zea mays. Mo. Agric. Expt. Sta. Bull. 163: 1–30 [Google Scholar]
  51. McClintock B., 1933.  The association of non-homologous parts of chromosomes in the mid-prophase of meiosis in Zea mays. Z. Zellforsch. Mikrosk. Anat. 19: 191–237 [Google Scholar]
  52. McClintock B., 1960.  Chromosome constitutions of Mexican and Guatemalan races of maize. Carnegie Inst. Wash. Yearbook 59: 461–472 [Google Scholar]
  53. McDonald J. H., Kreitman M., 1991.  Adaptive protein evolution at the Adh locus in Drosophila. Nature 351: 652–654 [DOI] [PubMed] [Google Scholar]
  54. McVean G., 2007.  The structure of linkage disequilibrium around a selective sweep. Genetics 175: 1395–1406 [DOI] [PMC free article] [PubMed] [Google Scholar]
  55. Moeller D. A., Tenaillon M. I., Tiffin P., 2007.  Population structure and its effects on patterns of nucleotide polymorphism in teosinte (Zea mays ssp. parviglumis). Genetics 176: 1799–1809 [DOI] [PMC free article] [PubMed] [Google Scholar]
  56. Morgan D. T., 1950.  A cytogenetic study of inversions in Zea mays. Genetics 35: 153–174 [DOI] [PMC free article] [PubMed] [Google Scholar]
  57. Munte A., Rozas J., Aguade M., Segarra C., 2005.  Chromosomal inversion polymorphism leads to extensive genetic structure: a multilocus survey in Drosophila subobscura. Genetics 169: 1573–1581 [DOI] [PMC free article] [PubMed] [Google Scholar]
  58. Nei M., Li W. H., 1979.  Mathematical model for studying genetic variation in terms of restriction endonucleases. Proc. Natl. Acad. Sci. USA 76: 5269–5273 [DOI] [PMC free article] [PubMed] [Google Scholar]
  59. Nielsen R., Williamson S., Kim Y., Hubisz M. J., Clark A. G., et al. , 2005.  Genomic scans for selective sweeps using SNP data. Genome Res. 15: 1566–1575 [DOI] [PMC free article] [PubMed] [Google Scholar]
  60. Nóbrega C., Khadem M., Aguadé M., Segarra C., 2008.  Genetic exchange vs. genetic differentiation in a medium-sized inversion of Drosophila: the A2/AST arrangements of Drosophila subobscura. Mol. Biol. Evol. 25: 1534–1543 [DOI] [PubMed] [Google Scholar]
  61. Paterson A. H., Bowers J. E., Bruggmann R., Dubchak I., Grimwood J., et al. , 2009.  The Sorghum bicolor genome and the diversification of grasses. Nature 457: 551–556 [DOI] [PubMed] [Google Scholar]
  62. Piperno D. R., Ranere A. J., Holst I., Iriarte J., Dickau R., 2009.  Starch grain and phytolith evidence for early ninth millennium BP maize from the Central Balsas River Valley, Mexico. Proc. Natl. Acad. Sci. USA 106: 5019–5024 [DOI] [PMC free article] [PubMed] [Google Scholar]
  63. Pritchard J. K., Stephens M., Donnelly P., 2000.  Inference of population structure using multilocus genotype data. Genetics 155: 945–959 [DOI] [PMC free article] [PubMed] [Google Scholar]
  64. R Development Core Team, 2011.  R: a language and environment for statistical computing, version 2.12.2. R Foundation for Statistical Computing, Vienna. http://www.r-project.org
  65. Remington D. L., Thornsberry J. M., Matsuoka Y., Wilson L. M., Whitt S. R., et al. , 2001.  Structure of linkage disequilibrium and phenotypic associations in the maize genome. Proc. Natl. Acad. Sci. USA 98: 11479–11484 [DOI] [PMC free article] [PubMed] [Google Scholar]
  66. Ross-Ibarra J., Tenaillon M., Gaut B. S., 2009.  Historical divergence and gene flow in the genus Zea. Genetics 181: 1399–1413 [DOI] [PMC free article] [PubMed] [Google Scholar]
  67. Santos M., Céspedes W., Balanyà J., Trotta V., Calboli F. C. F., et al. , 2005.  Temperature-related genetic changes in laboratory populations of Drosophila subobscura: evidence against simple climatic-based explanation for latitudinal clines. Am. Nat. 165: 258–273 [DOI] [PubMed] [Google Scholar]
  68. Scheet P., Stephens M., 2006.  A fast and flexible statistical model for large-scale population genotype data: applications to inferring missing genotypes and haplotypic phase. Am. J. Hum. Genet. 78: 629–644 [DOI] [PMC free article] [PubMed] [Google Scholar]
  69. Schnable P. S., Ware D., Fulton R. S., Stein J. C., Wei F., et al. , 2009.  The B73 maize genome: complexity, diversity, and dynamics. Science 326: 1112–1115 [DOI] [PubMed] [Google Scholar]
  70. Shin J. H., Blay S., Mcneney B., Graham J., 2006.  LDheatmap: an R function for graphical display of pairwise linkage disequilibria between single nucleotide polymorphisms. J. Stat. Softw. 16: 1–10 [Google Scholar]
  71. Stevison L. S., Hoehn K. B., Noor M. A. F., 2011.  Effects of inversions on within-and between-species recombination and divergence. Genome Biol. Evol. 3: 830–841 [DOI] [PMC free article] [PubMed] [Google Scholar]
  72. Storey J. D., Tibshirani R., 2003.  Statistical significance for genomewide studies. Proc. Natl. Acad. Sci. USA 100: 9440–9445 [DOI] [PMC free article] [PubMed] [Google Scholar]
  73. Tenaillon M. I., U’Ren J., Tenaillon O., Gaut B. S., 2004.  Selection vs. demography: a multilocus investigation of the domestication process in maize. Mol. Biol. Evol. 21: 1214–1225 [DOI] [PubMed] [Google Scholar]
  74. Thomas J. W., Cáceres M., Lowman J. J., Morehouse C. B., Short M. E., et al. , 2008.  The chromosomal polymorphism linked to variation in social behavior in the white-throated sparrow (Zonotrichia albicollis) is a complex rearrangement and suppressor of recombination. Genetics 179: 1455–1468 [DOI] [PMC free article] [PubMed] [Google Scholar]
  75. Thomson R., Pritchard J. K., Shen P., Oefner P. J., Feldman M. W., 2000.  Recent common ancestry of human Y chromosomes: evidence from DNA sequence data. Proc. Natl. Acad. Sci. USA 97: 7360–7365 [DOI] [PMC free article] [PubMed] [Google Scholar]
  76. Thornton K., 2003.  Libsequence: a C++ class library for evolutionary genetic analysis. Bioinformatics 19: 2325–2327 [DOI] [PubMed] [Google Scholar]
  77. Tian F., Stevens N. M., Buckler E. S., 2009.  Tracking footprints of maize domestication and evidence for a massive selective sweep on chromosome 10. Proc. Natl. Acad. Sci. USA 106: 9979–9986 [DOI] [PMC free article] [PubMed] [Google Scholar]
  78. Ting Y. C., 1965.  Spontaneous chromosome inversions of Guatemalan teosintes (Zea mexicana). Genetica 36: 229–242 [DOI] [PubMed] [Google Scholar]
  79. Ting Y. C., 1967.  Common inversion in maize and teosinte. Am. Nat. 101: 87–89 [Google Scholar]
  80. Ting Y. C., 1976.  Chromosome polymorphism of teosinte. Genetics 83: 737–742 [DOI] [PMC free article] [PubMed] [Google Scholar]
  81. Umina P. A., Weeks A. R., Kearney M. R., Mckechnie S. W., Hoffmann A. A., 2005.  A rapid shift in a classic clinal pattern in Drosophila reflecting climate change. Science 308: 691–693 [DOI] [PubMed] [Google Scholar]
  82. van Heerwaarden J., Ross-Ibarra J., Doebley J., Glaubitz J. C., Gonzalez Jde J., et al. , 2010.  Fine scale genetic structure in the wild ancestor of maize (Zea mays ssp. parviglumis). Mol. Ecol. 19: 1162–1173 [DOI] [PubMed] [Google Scholar]
  83. van Heerwaarden J., Doebley J., Briggs W. H., Glaubitz J. C., Goodman M. M., et al. , 2011.  Genetic signals of origin, spread, and introgression in a large sample of maize landraces. Proc. Natl. Acad. Sci. USA 108: 1088–1092 [DOI] [PMC free article] [PubMed] [Google Scholar]
  84. Weber A., Clark R. M., Vaughn L., De Jesus Sánchez-Gonzalez J., Yu J., et al. , 2007.  Major regulatory genes in maize contribute to standing variation in teosinte (Zea mays ssp. parviglumis). Genetics 177: 2349–2359 [DOI] [PMC free article] [PubMed] [Google Scholar]
  85. Weber A. L., Briggs W. H., Rucker J., Baltazar B. M., De Jesus Sanchez-Gonzalez J., et al. , 2008.  The genetic architecture of complex traits in teosinte (Zea mays ssp. parviglumis): new evidence from association mapping. Genetics 180: 1221–1232 [DOI] [PMC free article] [PubMed] [Google Scholar]
  86. Weir B. S., Cockerham C. C., 1984.  Estimating F-statistics for the analysis of population structure. Evolution 38: 1358–1370 [DOI] [PubMed] [Google Scholar]
  87. White B. J., Cheng C., Sangare D., Lobo N. F., Collins F. H., et al. , 2009.  The population genomics of trans-specific inversion polymorphisms in Anopheles gambiae. Genetics 183: 275–288 [DOI] [PMC free article] [PubMed] [Google Scholar]
  88. Wilkes H. G., 1967.  Teosinte: the closest relative of maize. Ph.D. Thesis, Bussey Institute, Harvard University, Cambridge, MA [Google Scholar]
  89. Wolfgruber T. K., Sharma A., Schneider K. L., Albert P. S., Koo D. H., et al. , 2009.  Maize centromere structure and evolution: sequence analysis of centromeres 2 and 5 reveals dynamic loci shaped primarily by retrotransposons. PLoS Genet. 5: e1000743. [DOI] [PMC free article] [PubMed] [Google Scholar]
  90. Wright S. I., Charlesworth B., 2004.  The HKA test revisited: a maximum likelihood ratio test of the standard neutral model. Genetics 168: 1071–1076 [DOI] [PMC free article] [PubMed] [Google Scholar]
  91. Wright S. I., Bi I. V., Schroeder S. G., Yamasaki M., Doebley J. F., et al. , 2005.  The effects of artificial selection on the maize genome. Science 308: 1310–1314 [DOI] [PubMed] [Google Scholar]
  92. Yu J., Holland J. B., Mcmullen M. D., Buckler E. S., 2008.  Genetic design and statistical power of nested association mapping in maize. Genetics 178: 539–551 [DOI] [PMC free article] [PubMed] [Google Scholar]

Associated Data

This section collects any data citations, data availability statements, or supplementary materials included in this article.

Supplementary Materials

Supporting Information
supp_191_3_883__index.html (2.9KB, html)
supp_112.138578_138578SI.pdf (2.8MB, pdf)
supp_112.138578_FigureS1.pdf (1.1MB, pdf)
supp_112.138578_FigureS2.pdf (129.4KB, pdf)
supp_112.138578_FigureS3.pdf (1.5MB, pdf)
supp_112.138578_FigureS4.pdf (108.8KB, pdf)
supp_112.138578_FigureS5.pdf (110.4KB, pdf)
supp_112.138578_TableS2.pdf (138.6KB, pdf)
supp_112.138578_TableS3.pdf (70.6KB, pdf)
supp_112.138578_TableS4.pdf (84.3KB, pdf)
supp_112.138578_TableS5.pdf (62.3KB, pdf)
supp_112.138578_TableS6.pdf (70.4KB, pdf)
supp_112.138578_TableS7.pdf (76.4KB, pdf)
supp_112.138578_TableS1.xlsx (234.3KB, xlsx)

Articles from Genetics are provided here courtesy of Oxford University Press

RESOURCES