Molecular dynamics simulations of DNA within a nanopore: arginine-phosphate tethering and a binding/sliding mechanism for translocation

Abstract

Protein nanopores show great potential as low-cost detectors in DNA sequencing devices. To date, research has largely focused on the staphylococcal pore α-hemolysin (αHL). In the present study, we have developed simplified models of the wildtype αHL pore and various mutants, in order to study the translocation dynamics of single-stranded DNA under the influence of an applied electric field. The model nanopores reflect the experimentally measured conductance values in planar lipid bilayers. We show that interactions between rings of cationic amino acids and DNA backbone phosphates result in metastable tethering of nucleic acid molecules within the pore, leading us to propose a “binding and sliding” mechanism for translocation. We also observe folding of DNA into non-linear conformational intermediates during passage through the confined nanopore environment. Despite adopting non-linear conformations, the DNA hexamer always exits the pore in the same orientation as it enters (3′ to 5′) in our simulations. The observations from our simulations help to rationalize experimentally determined trends in residual current and translocation efficiency for αHL and its mutants.

The development of single-molecule sensors from engineered protein pores is an important area in bionanotechnology (1, 2). To date, work in this area has largely focused on the bacterial pore-forming toxin α-hemolysin (αHL) from S. aureus, although recently a few other bacterial membrane proteins have been investigated as potential alternatives to αHL (3–6). The αHL pore is a homo-oligomeric heptamer, with a transmembrane (TM) 14-stranded β-barrel domain connected to a large water-filled extramembraneous cap. Analyte molecules are detected when they modulate the ionic current passing through the pore in an applied potential. The extent of current block can be used to identify the analyte molecule, whereas the frequency of blocking events enables determination of the analyte concentration. One of the major advantages of this technique is that single molecules can be detected (7).

The potential of protein nanopores for low-cost single molecule DNA sequencing has been explored both experimentally and theoretically (8–10). Issues with the ability to distinguish related DNAs (11, 12) and the frequency of occurrence of translocation events (13) have so far prevented the incorporation of this technology into a DNA-sequencing device. It is known that mutations in the lumen of the TM domain of αHL can have a profound effect on the translocation of DNA (14) suggesting that the interaction between the lumen-lining residues of αHL and the DNA molecule play a key role in the process of translocation. Consequently there have been attempts to modify the engineered protein by augmenting the wild-type (WT) pore via site directed mutations. However, this has been carried out in the absence of detailed lack of knowledge of DNA-αHL interactions at the molecular level.

Molecular dynamics (MD) simulations provide a route to studying the dynamics of biological molecules in environments that mimic experimental conditions (15–17) and have been successfully employed to study the translocation of DNA molecules through αHL (18–20), as well as in the design of other pore-based systems (21). However, the possibility of high throughput simulations of such systems is hindered by the complexity and large size of the protein pore. In the present study, we have developed a simplified model of the αHL pore. Our model is based on part of the TM barrel region of αHL and includes the lumen-facing sidechains, described in atomistic detail, surrounded by a membrane-mimetic slab. We demonstrate that in the presence of an applied electric field, the model reflects the experimentally determined current-voltage relationships of the full-length protein. Furthermore, the simulations enable us to predict the conformations adopted by the DNA within the confined geometry of the nanopore. We show that key lysine residues (in the wild-type protein) or arginine residues (in designed mutants) within the pore lumen lead to electrostatic interactions that tether the DNA backbone during translocation, and in some cases nucleate partial folding of the DNA. The induction of partially folded single-stranded (ss) nucleic acid conformations helps to rationalize the observed differences in current and DNA translocation efficiency between the experimentally characterized mutants, and the wild-type αHL pore.

Methods

Constriction sites in αHL play a key role in determining the translocation characteristics of analytes (13). The narrowest constriction is located at the mouth of the TM barrel close to the vestibule (i.e. cis side), and consists of charged rings of Glu111 and Lys147 residues. In light of this observation, we constructed a simplified model of the lumen of the α-hemolysin pore by deleting all regions of the protein except a small section of the transmembrane β-barrel, and retaining only the sidechains of the inner, barrel lumen residues (Fig. 1A). The removal of the membrane-facing sidechains reduces the complexity of the model, giving a minimal model that retains the conformational landscape of the pore-lining at the constriction. This minimal model is simple enough to enable a high-throughput simulation approach. The resulting nanopore was placed in the center of a uniform slab of methane particles, whose width roughly corresponds to that of the hydrophobic acyl tail region of a typical biological membrane. Three central concentric methane rings were used to taper the slab width to that of the nanopore, resulting in the final slab-nanopore system shown in Fig. 1B. Snapshots of a full αHL -DNA system compared to the equivalent model pore system are shown in Fig. S1.

Figure 1.

Summary of model pore system setup. (A) X-ray structure of the full αHL protein pdb code = 7AHL and (B) the model pore embedded in a methane slab. The protein barrel region that was incorporated into the model pore is colored yellow in A and B. Cut-away view of the molecular surface of the model pore embedded within a methane slab (C). The charged residues E111 and K147 (red and blue respectively) at the cis (near vestibule) mouth of the barrel are included in the model, whereas the trans mouth (opposite end from vestibule) is truncated at residue N123 (green).

The system was solvated with water and 1M NaCl, corresponding roughly to the experimental salt concentration. Ions were added by replacing random water molecules using the genion script within GROMACS. There were ~8–10 ions within the pore at the start of the simulations. Additional systems were created by introducing point mutations within the pore, based on those reported in the literature (13). Simulations were performed in which a 6-mer ssDNA (polyG) molecule was placed above the mouth of the pore (i.e. cis side) of the protein. The DNA was partially pre-threaded into the pore at the start of the simulations, ie the terminal nucleotide was positioned into the mouth of the pore just beyond the K147 ring of charges. As these residues are thought to provide an energetic barrier to DNA translocation, we pre-threaded the DNA to facilitate translocation on the timescale of the simulations. The ssDNA hexamer was constructed using the Builder module of Quanta (Accelrys Inc) and was in an essentially linear conformation at the start of the simulations. The full systems were composed of one ssDNA molecule, the nanopore (~200 residues), ~1,000 methane slab particles, ~4,500 water molecules and ~100 Na⁺ and Cl⁻ ions, in a box of approximate dimensions of 5 × 5 × 8 nm³. Successive energy minimizations were performed during each stage of setup, to relax contacts between protein, slab, DNA and solvent. The systems were subjected to an equilibration procedure in which positional restraints were applied to the nanopore, methane slab and DNA while the water and ions were allowed to relax during short MD simulations. These restraints were gradually removed, until only the nanopore backbone and methane slab particles were weakly restrained, prior to production runs. Each simulation was of minimum duration 20 ns (but often extended in order to observe complete translocation events), and was performed at least three times to ensure reproducibility. A uniform electric field equivalent to a potential across the slab of ~600 mV was applied. Atomistic simulations used an extended united atom version of the GROMOS96 forcefield (22, 23). The simulations were performed at 300 K with a pressure of 1 bar, using the Berendsen thermostat and barostat (24). Non-bonded interactions were truncated at 1.2 nm. Electrostatics were treated using particle mesh Ewald (25).

Testing of Simulated Electrolyte Properties

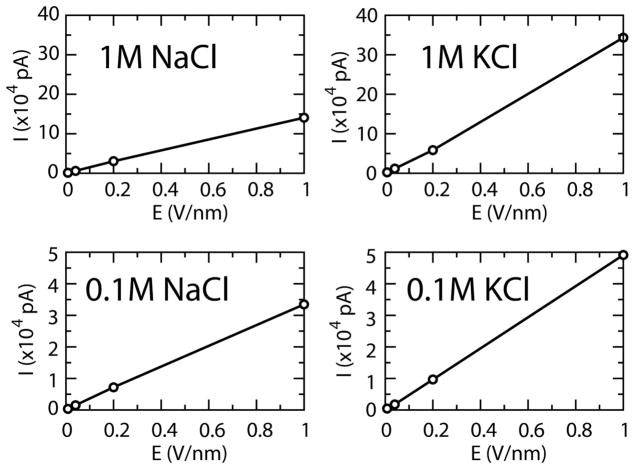
For all current estimates, the instantaneous current was calculated as in (18). A set of simulations of various electrolyte compositions were carried out to explore the ion parameters accuracy. Boxes of equal length (5 nm) were filled with NaCl or KCl solutions, at a salt concentration of 0.1 M or 1 M, and simulated in the presence of a uniform electric field along an arbitrary axis. Values for the electric field strengths of 8, 40, 200, and 1000 mV/nm were used. An initial simulation of a 0.1 M NaCl solution under the influence of a 1000 mV/nm electric field was performed for 100 ns to establish the effect of simulation timescales on the measurements of electrolyte transport properties, revealing that sampling of over ~4 ns yielded no significant change in the observed current estimate (or associated error) (Fig S1b). Therefore, all further electrolyte test simulations were performed for 10 ns, with 2 ns used for equilibration and the subsequent 8 ns used for analysis. As expected, the total ionic (Na⁺/K⁺+Cl⁻) currents were found to be linearly proportional to the applied electric field, for both KCl and NaCl solutions (Fig. 2).

Figure 2.

Relationship between simulated mean current and applied electric field for various electrolyte solutions.

Bulk conductivities were extrapolated from the curves, revealing reasonable agreement with experimental measurements (26) (Table 1) Anion/cation current ratios were also calculated from these simulations. At significant voltages (i.e. >8 mV/nm), the simulated current ratios were independent of the electric field strength (the dependence at low voltage is likely due to under-sampling). Values of ~1.6–1.7 in these simulations were observed for NaCl (Table 2), compared to an experimental estimate of 1.52 (according to Coury, 1999 as cited in (18)). Ratios of ~0.8–1 were obtained for KCl (Table 3), compared to 1.04 experimentally. Thus, the correct relative ranking of anion and cation magnitudes was obtained only for NaCl, and so all subsequent hemolysin model-pore simulations were performed in the presence of NaCl solution.

Table 1.

Conductivity measurements for each electrolyte solution.

Electrolyte	Simulated Conductivity (S/m)	Experimental Conductivity (S/m)
1M NaCl	5.59	8.16 (26)
0.1M NaCl	1.33	1.381
1M KCl	13.85	11 (18)
0.1M KCl	1.97	1.291

¹From commercial conductivity standards

Table 2.

Anion/cation current ratios for 1M KCl electrolyte solutions at varying field strength.

E (mV/nm):	8	40	200	1000
I[Cl−] (nA)	1.1	5.8	27.4	153.9
I[K+] (nA)	1.2	5.9	31.1	189.6
I[Cl−]/I[K+]	0.9	1.0	0.9	0.8

Table 3.

Anion/cation current ratios for 1M NaCl electrolyte solutions at varying field strength.

E (mV/nm):	8	40	200	1000
I[Cl−] (nA)	0.8	3.9	19.3	86.5
I[K+] (nA)	0.7	2.3	11.1	54.1
I[Cl−]/I[K+]	1.2	1.7	1.7	1.6

Experimental IV curve measurements

Purified WT αHL monomers were made in a cell-free Escherichia coli in vitro transcription translation system (Promega) followed by oligomerisation on rabbit red blood cell membranes. The HL heptamers were purified by SDS-PAGE as described previously. (27, 28) Electrical measurements were acquired from single alpha-hemolysin channels inserted in 1,2-diphytanoyl-glycero-3-phosphocholine lipid (Avanti Polar Lipids) bilayers as described previously (28). Single-channel currents were measured on Axopatch 200B amplifiers (Molecular Devices) equipped with 1440A digitizers, and were analysed using pClamp 10 software (Molecular Devices). Current-voltage curves were generated by measuring the mean open-pore current during 2-second constant-voltage sections, as the applied voltage was stepped in 20 mV increments from +200 mV to −200 mV with an automated routine.

Results

We first sought to test how well the model nanopores could reproduce trends in experimentally measured ionic currents for the full-length αHL pore and a series of mutants in the absence of DNA (13). To evaluate the ‘wildtype’ model nanopore, we calculated the current from a series of simulations under different applied voltages to construct a simulated IV curve. The current was calculated using the method described in (18). Comparison of the simulated IV curve with our experimentally measured values revealed that the simulations were able to reproduce not only the trends but also the magnitude of the experimentally measured currents, giving us confidence in the model nanopore (Fig. 3).

Figure 3.

Simulated (black) and experimental (blue) IV curves. The experimental IV curve has been extrapolated from 200 to 600 mV by non-linear regression.

To obtain (i) the best resolution in calculating the current from simulations (enough ions moving through the pore to be confident of accurate values) and (ii) translocation of DNA on an accessible simulation timescale we performed all subsequent simulations at an applied transmembrane voltage of 600 mV; we note that the same bias has previously been used in simulations of ion translocation through aH (18). Encouragingly, our simulations of open-pore mutant nanopores also yielded good agreement with the experimental values reported by Maglia et al (13). Having established validity of the model nanopores in open pores simulations, we next sought to measure the ion flow in the presence of DNA. The residual currents measured during cis-to-trans DNA translocation events under an applied voltage, performed by Maglia et al (13), are compared to the observed ion flux through the αHL pore during 20 ns simulations in the presence of a translocating ssDNA 6mer (Table 4). The experimental current trends were well preserved within the statistical error of our data (estimated by performing at least three repeat simulations per mutant). Five mutants known to exhibit low residual currents in the presence of DNA (T115R, T117R, G119R, N121R, and N123R) were observed to slow the rate of ion flux through the nanopore to ~1 ion ns⁻¹. This rate progressively increased for the M113R, WT, E111N, and M113D pores, with respective flux rates of ~ 2, 4, 6, and 7 ions ns⁻¹. Thus, the relative conduction magnitudes were also well reproduced compared to the low-current mutants, with the exception of the M113D mutant. However, this mutant did not measurably bind DNA experimentally (13) ; i.e. the published value was for the open-pore current. Our observed M113D open core current was approximately an order of magnitude larger than the low-current mutants. Indeed, DNA translocation was not observed in the M113D mutant simulations, yielding an ion flux comparable to the control simulation in the absence of DNA. Moreover, manually placing DNA inside the M113D nanopore mouth resulted in rapid ejection from the cis side within ~5 ns. The presence of the additional ring of negative charge evidently presents too high a barrier for DNA entry.

Table 4.

Summary of ion flow and DNA translocation behavior.

System	Simulated open pore current(pA) 1	Extrapolated open pore current at600 mV (pA) 2	Simulated residual ion count 3	Extrapolated partial current(pA) (13)4	DNA translocation in 20 ns5
M113D	489±9	567	n/a	n/a	None
E111N	824±53	694	114±12	76.34	Full
WT	680±53	634	80±16	69.74	Partial
M113R	580±38	709	17±2	28.36	Partial
T117R	519±13	572	24±14	17.16	Partial
N123R	427±32	390	23±6	11.7	Partial
G119R	460±22	562	15±9	11.24	Full
N121R	439±8	486	14±20	14.58	Partial
T115R	521±14	618	7±6	12.36	Partial

¹Simulated currents in the absence of DNA, calculated as in (18).

²Extrapolated from experimental IV curves of the open pore at +120 mV in (13).

³Ion flux in the presence of DNA (i.e. residual), once two DNA bases had crossed the K147 constriction.

⁴Calculated from experimental percentage block in (13) applied to the extrapolated currents from the IV curve.

⁵Observed translocation behavior included “none” (no entry into the pore), “partial” (DNA strand does not completely translocate through the pore in 20 ns) or “full” (the strand both enters the pore and exits on the trans side).

Having established the accuracy of the model nanopores in reproducing the full-length αHL DNA-induced residual conductance measured experimentally, we next analyzed the behavior of DNA within the pore. This is of particular interest in the context of specific interactions between the DNA molecule and the inner pore surface, which are likely to be important in determining translocation efficiency and ion flux modulation, and are thus of direct interest for biosensor design. In all simulations, the charged ring of K147 residues on the inner pore surface led to meta-stable retention of the DNA molecule at the cis constriction site. This resulted from electrostatic “tethering” of the DNA strand, particularly via the acidic phosphate groups, to the ε-amino groups of the lysine sidechains. In the case of the WT pore, such tethering led to a step-wise process of translocation (Fig. 4), with a phosphate group being typically bound at the K147 ring constriction for ~1 ns, before the interaction was stochastically broken, enabling further translocation and subsequent binding of a downstream phosphate group (Fig. S2). Such step-wise, progressive “binding and sliding” within the nanopore is reminiscent of the proposed mechanisms of analyte transport in some membrane protein channels (29, 30). A similar step-wise mechanism has been observed in simulations of RNA translocation through carbon nanotubes (31). Once the entire DNA molecule (and hence all backbone phosphate groups) had traversed the K147 ring, its interactions with the inner pore surface, partly as a result of the adoption of partially folded, nonlinear conformational states, presented kinetic barriers which slowed its translocation speed within the confined environment of the nanopore. These conformational states, stable on the timescale of up to several nanoseconds, could be characterized by the DNA end-to-end distance (Fig. 5). The initial, extended state (~2.4 nm in length) was observed to gradually adopt partial horseshoe-type hairpin or helical structures (~1.9 nm) within the pore, following tethering of the final few phosphate groups of the DNA molecule by the K147 ring (Fig. S3).

Figure 4.

Snapshots showing the location of the K147 and E111 residues in the model wildtype pore and their interaction with the translocating DNA. (A) Location of the ring of K147 (green) and E111 (blue) residues. The backbone of the pore is colored yellow. (B) Interaction of three K147 sidechains with two DNA phosphates. The phosphorus atoms of the DNA backbone are shown in red space-filling format; the bases and sugars are colored pink. (C) The interaction of an E111 sidechain with a base amine group. (D) The interaction of an E111 sidechain with a sugar hydroxyl group.

Figure 5.

Summary of the DNA conformations observed in the simulations of WT and mutants, and the corresponding DNA end-to-end distance. For each conformation, the DNA is grey and green, the pore backbone is shown in orange. For irregular conformations induced by arginine rings within the pore, the arginine residues are shown in blue (“2- induced”).

The translocation efficiency of the WT pore was also hampered by weak interactions between carboxylate groups of the E111 ring and the amine and hydroxyl groups of the nucleotide bases and 5′-prime terminus, respectively (Fig. 4). As a result, these simulations had to be extended for up to 50 ns in order to observe complete DNA exit on the trans side.

The E111N mutant exhibited a similar step-wise, phosphate-binding/DNA sliding mechanism (Fig. S2), but in the absence of interactions from E111, an increased translocation rate resulted. The absence of this “carboxylate ring” reduced the electrostatic barrier for passage of the anionic DNA molecule, easing the phosphate pathway, as well as eliminating the additional hydrogen-bonding interactions with bases, in comparison with the WT pore. As a result, the DNA molecule retained an approximately linear conformation during translocation (Fig. S3), prior to pore exit on the trans side. This observed lack of folded/collapsed ssDNA conformations within the E111N mutant provides a molecular explanation for the increased ionic conductance in this mutant compared to the WT pore, observed both here and experimentally (Table 4).

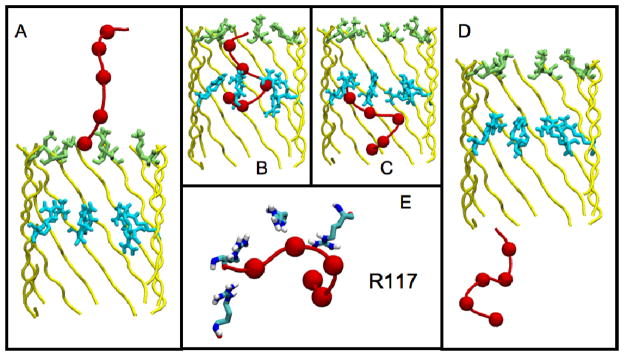
In comparison with the WT protein, for the low-current arginine mutants, the presence of additional positive charge deep within the pore resulted in frequent DNA folding/deformation events, which slowed translocation even beyond the K147 ring. In essence, the presence of additional cationic amino acid sidechains provided a second anchoring point for DNA phosphate binding (Fig. 6). This is consistent with experimental measurements of the full-length aHL, which suggest such mutations lead to a longer mean translocation time per strand than observed with the WT pore (13). The anchoring effect of guanidinium groups contributed by the ring of arginine residues at various points along the pore led to the frequent formation of non-linear ssDNA conformations during translocation. We note that the DNA always exits the pore in the same orientation as it enters (3′ to 5′) and the terminal nucleotide always exits first i.e. there is no ‘overtaking’ of the bases as they exit the pore. Similarly to the DNA behavior within the WT nanopore, these conformational states were stable on the nanosecond timescale, but were more drastically non-linear in structure, characterized by a DNA end-to-end distance < 1.9 nm (Fig. 5). In the case of the M113R, T115R, and T117R mutants in particular, the close proximity of the arginine rings to the K147 ring at the pore mouth (~0.4, ~0.8 and ~1.4 nm, respectively, for mean C_α-C_α distance along the pore axis) enabled simultaneous tethering of phosphates separated by only one or two nucleotides (Fig. 6). The “sliding” of DNA along the pore axis, between sequential phosphate-binding sites on the closely apposed cationic rings, induced irregularly twisted DNA structures whose bases often became unstacked during passage between lysine and arginine anchoring sites. In the case of the G119R, N121R, and N123R mutants, DNA translocation was also subject to anchoring via phosphate-arginine interactions, but the greater distance along the nanopore axis from the K147 ring resulted in less drastic induction of DNA deformation, so that most commonly, folded hairpin-like structures were observed within the barrel lumen.

Figure 6.

Summary of the interactions of the DNA as it translocates through the T117R mutant. In A–D, the pore backbone is colored yellow, with the K147 (green) and R117 (cyan) residues highlighted; the DNA backbone and its component phosphate groups are shown in red. (A) Electrostatic interactions between the ring of K147 residues and phosphate groups of the DNA molecule as it enters the pore. (B) Interactions between the DNA molecule and the K147 and R117 sidechains induce non-linear DNA conformations, and tethering around the R117 ring. (C) Once electrostatic interactions with the K147 rings are broken, the DNA molecule remains tethered to the R117 ring, slowing the translocation rate. (D) Following translocation past the R117 ring, exit of DNA from the trans mouth of the nanopore trans mouth could be observed (after ~ 40 ns). (E) A close-up of the DNA-R117 tether, showing simultaneous interaction of four R117 residues with three DNA phosphate groups.

Whilst additional sampling is required for a complete characterization of these induced DNA conformations and their relative probabilities of formation, similar translocation dynamics were observed for preliminary simulations in the presence of 12mer ssDNA molecules based on the x-ray structure from (32) with sequence ACCGACGTCGGT. The existence of such folded structures within the barrel lumen helps to explain the reduced conductance and altered translocation efficiency of ss nucleic acid molecules in the context of each arginine mutant. Indeed, experiments with such mutants in which a DNA molecule is tethered to αHL resulted in a comparatively higher ionic current compared to when the DNA is free in solution, suggesting that tethering may help convert the meta-stable, translocating folded states into linear structures (6). Simulations are underway to test this hypothesis.

Discussion

The simplified pores we have created reproduce the general trends of ion flow and DNA translocation measured experimentally for the αHL protein and various mutants. Furthermore, the results presented here suggest that the vestibule of the αHL pore plays only a minor role in the interplay between DNA translocation and ion flow, following DNA “capture” and even less once the DNA has threaded into the barrel region. Thus, we have shown that it is possible to mimic the important features of the full αHL–DNA experimental setup with a simplified in silico system. We note that a similar approach has also been used to study MspA, another protein pore of interest in DNA sequencing (33).

We have demonstrated that the process of DNA translocation in the presence of an applied voltage is strongly influenced by the number and position of rings of cationic amino acids on the inner pore surface. The sidechains of these residues had an electrostatic “tethering” effect on the acidic phosphate groups along the backbone of the DNA molecule, leading to its metastable retention. In particular, this resulted in an approximate step-wise translocation mechanism which we refer to as “binding and sliding”, drawing parallels to the analyte transport process in membrane proteins, including those specific for sugars (29) or nucleosides (30). Concomitant with this process was the appearance of nonlinear DNA conformations, which were observed to affect both translocation efficiency and ion flux. The mutation of inner pore-lining residues to arginine resulted in the propagation of the tethering effect, and resulted in the induction of hairpins and other non-linear structures within the single-stranded DNA molecule. Ultimately, this served to slow the rate of DNA translocation, as well as leading to a reduced measurable current, as observed experimentally. Despite the DNA adopting non-linear conformations, it exits the pore in the same orientation as it enters with the terminal nucleotide exiting first in all our simulations. Thus, our model helps to rationalize the interplay between pore mutations and DNA detection at the molecular level, and in particular, the influence of secondary structure formation on current flow and translocation efficiency, two key properties in the context of biosensor design.

Our study of multiple αHL mutants has highlighted the importance of arginine-phosphate interactions in determining the trajectory and conformation of single-stranded DNA within the confined nanopore environment. Electrostatic interactions between arginine sidechains and phosphate groups are extremely strong and have even been described as “covalent-like” (34), hence explaining their widespread occurrence in biological interactions, from highly specific protein-protein recognition within a variety of signaling cascades, to the stabilization (35) or modulation (36) of protein-lipid complexes. Furthermore the interaction of arginine residues with nucleic acid phosphate groups has been identified as a key feature in the DNA readout mechanism of e.g. transcription factors (37), and has been proposed as a specific RNA recognition mechanism, in which a guanidinum group binds between two phosphate groups to form a so-called “arginine fork” (38). Thus, it is unsurprising that the presence of rings of arginines within the mutants has such a large influence on the translocation behavior of DNA within the hemolysin channel.

It is perhaps useful to reflect upon the limitations of the current study; in particular we have only reported simulations of short DNA strands; hexamers, while DNA sequencing usually uses longer strands. Encouragingly, the simplicity of our minimal model yields a reduced system size compared to the full αHL protein, and thus in future studies it will be possible to extend the study to longer strands of DNA. Until now, it has been difficult to predict the likely effect of introducing novel pore mutations. Our model has been shown to be successful in reflecting trends in experimental data for such mutants, as well as rationalizing this data in the context of the interaction of the DNA molecule with the inner pore surface, and its induced conformation. It should thus also be suitable as a high-throughput computational approach for predicting the effects of novel mutations in αHL (or related nanopores), potentially providing a more rational route to the design of nanopore-based biosensors.

Abbreviations

S. aureus

Staphylococcus aureus

α HL

α-hemolysin

WT

Wildtype

MD

Molecular Dynamics

TM

Transmembrane

ss

Single-stranded