Non-Euclidean geometry of twisted filament bundle packing

Abstract

Densely packed and twisted assemblies of filaments are crucial structural motifs in macroscopic materials (cables, ropes, and textiles) as well as synthetic and biological nanomaterials (fibrous proteins). We study the unique and nontrivial packing geometry of this universal material design from two perspectives. First, we show that the problem of twisted bundle packing can be mapped exactly onto the problem of disc packing on a curved surface, the geometry of which has a positive, spherical curvature close to the center of rotation and approaches the intrinsically flat geometry of a cylinder far from the bundle center. From this mapping, we find the packing of any twisted bundle is geometrically frustrated, as it makes the sixfold geometry of filament close packing impossible at the core of the fiber. This geometrical equivalence leads to a spectrum of close-packed fiber geometries, whose low symmetry (five-, four-, three-, and twofold) reflect non-Euclidean packing constraints at the bundle core. Second, we explore the ground-state structure of twisted filament assemblies formed under the influence of adhesive interactions by a computational model. Here, we find that the underlying non-Euclidean geometry of twisted fiber packing disrupts the regular lattice packing of filaments above a critical radius, proportional to the helical pitch. Above this critical radius, the ground-state packing includes the presence of between one and six excess fivefold disclinations in the cross-sectional order.

Packing problems arise naturally in a multitude of contexts, from models of crystalline and amorphous solids to structure formation in tissues of living organisms. Though often easy to state, packing problems are notoriously difficult to solve. The cannonball stacking of spheres, for example, conjectured by Kepler to be the densest packing in three-dimensional space (1), was only proven so in 1999, and even then with the aid of a computer algorithm (2). In some cases, like the densest packing of spheres, the face-centered cubic lattice—or its two-dimensional analogue, the densest packing of discs, the hexagonal lattice—the optimal structure is a regular, periodic partition of space. In many problems, however, perfect lattice packings are prohibited, and optimal structures necessarily lack the translational and rotational symmetry of periodic order. A well-known example is the problem of finding the densest packing of N discs on a sphere of a given radius, known alternately as the Tammes or the generalized-Thomson problem (3). In this problem, spherical topology requires a variation in the local packing symmetry: All states possess at minimum 12 discs whose nearest-neighbor geometry is fivefold coordinated (4). Beyond its relevance to structural studies of such diverse materials as spherical viral capsids (5) and colloid-stabilized emulsions (6, 7), the problems involving point or disc packing on spheres serve as an important example of systems where topological defects—fivefold disclinations in an otherwise sixfold packing—are necessary components of optimal, or ground-state, structure (8, 9).

In this article, we demonstrate that the geometry of an important class of materials, twisted filament bundles and ropes, belongs to this unusual class of geometrically frustrated packing. Indeed, the packing of twisted bundles shares an intimate and unexplored connection with the Thomson problem. Helically twisted assemblies of multiple filaments or strands are not only key structural elements in macroscopic materials—cables, ropes, yarns, and textile fibers—but they also constitute an important class of macromolecular assemblies in biological materials at the nanoscopic scale. Fibers of extracellular proteins like collagen (10) and fibrin (11) are well-known to organize into twisted assemblies, and the helical twist of multifiber cables has been implicated in the assembly thermodynamics of sickle-hemoglobin macrofibers (12). Whereas the helical twist of human-made ropes is built in to optimize mechanical properties—such as bending compliance (13) and tensile strength (14)—the twist of self-assembled ropes of biomacromolecules derives from torques generated by interactions between helical (i.e., chiral) molecules (15, 16).

The complexity of cross-sectional packing in this archetypal material geometry has long been a subject of study, particularly from the viewpoint of the mechanical properties of manufactured textiles (14, 17) and wire ropes (13). The problem is best visualized from the perspective of the planar cross-section of a twisted bundle, as shown in Fig. 1A, which shows the cross-section of filaments away from the helical center of rotation to be distorted and stretched azimuthally. This distortion arises from the tilting of filaments into the horizontal plane, and is responsible for the nontrivial constraints on number, position, and arrangement of filaments placed a given radius from the bundle center (18, 19).

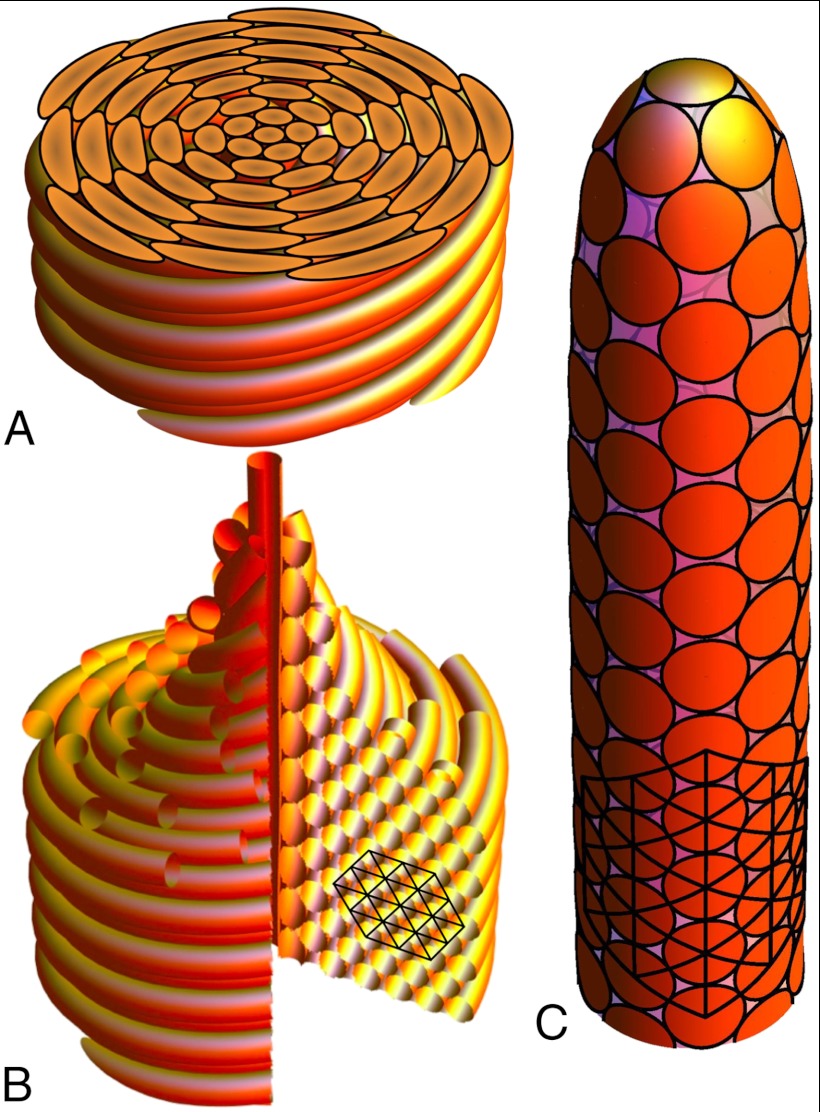
Fig. 1.

Three views of a twisted bundle packing. In A, the horizontal cross-section of a twisted bundle, where circular filament sections become distorted, “stretched” along the azimuthal direction, depending on the tilt and curvature of the filament backbones. In B, a vertical slice through the bundle reveals hexagonally close packing far from the core. In C, the dual representation of the twisted bundle packing as a disc packing covering a bundle-equivalent dome.

Below we show that the distortion of the cross-sectional shape of filaments in a planar section of a twisted bundle is identical to the shape distortion arising from the projection of a packed array of discs on a non-Euclidean surface onto the plane. That is, the problem of packing twisted bundles can be mapped one-to-one onto the problem of packing discs on a 2D surface with the topology of a hemispherically capped cylinder, a surface we refer to as the bundle-equivalent dome (see Fig. 1C). From this unique and surprising perspective, we demonstrate a number of previously hidden properties of packing in twisted bundles, leading to a rich spectrum of optimal structures even in the simplest models of filamentous materials. First, the effectively spherical geometry corresponding to the bundle center obstructs regular, periodic packing: Like the disc packings of a dome, the core packing of large twisted bundles possess a deficit of precisely six neighbors, relative to a sixfold dense packing of tubes (i.e., the equivalent of six excess fivefold coordinated sites in an otherwise sixfold Delaunay triangulation). Second, we find that geometry of filament packing becomes Euclidean far from the bundle center and topologically equivalent to disc packings on a cylinder whose circumference is equal to the helical pitch of rotation, P. Third, we classify all asymptotically close-packed twisted bundles and show that these correspond to the countably infinite number of ways to wrap a hexagonal lattice around a cylinder. Among these asymptotically close-packed structures, we construct lower bounds for the densest packing of bundle cores and show that the densest among these have a lower than sixfold symmetry, a requirement for compatibility of the local bond geometry with the “hidden” spherical geometry of the core. Finally, we show by numerical computation that the purely geometrical considerations of twisted bundle packing have universal consequences for energy-minimizing configurations of adhesive filaments: Ground-state structures possess an excess number of fivefold disclinations that is sensitive only to the ratio of helical pitch to bundle diameter.

Metric Geometry of Twisted Bundle Packing

The hidden non-Euclidean geometry of packing in twisted bundles follows from elementary considerations of interfilament distance. We consider filament bundles, twisted around the 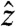axis at a uniform rate of helical rotation, Ω = 2π/P. Given the position, x = (x,y), of a filament center in the z = 0 plane, the centerline of the filament is described by the helical curve,

[1]

where x = 0 is the rotation axis. Hence, the center of each filament or strand follows a helical curve of radius, ρ = |x|, and pitch, P. The center-to-center separation between two filaments that sit at x₁ and x₂, respectively, in the reference plane, is a function Δ(z) of the vertical separation z between points of comparison,

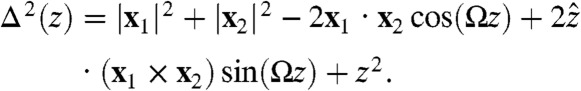[2]

In problems of fiber packing, the relevant distance between a pair of given filaments is the distance of closest approach, or

[3]

As shown in Fig. 2A, the closest separation between two filaments takes place along a vector Δ_∗ = r₂(z_∗) - r₁(0), where z_∗ is the vertical offset at this separation. Clearly, Δ_∗ is perpendicular to both filaments at the end points of centerline contact. Additionally, notice that any two helical curves are always nearer than their separation in the reference plane because Δ_∗ ≤ Δ(0).

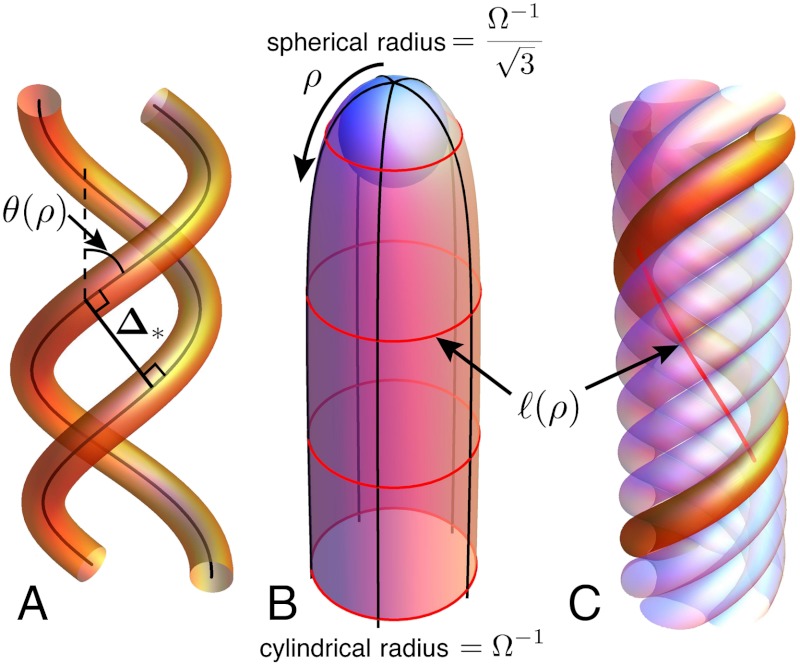
Fig. 2.

The distance of closest approach between two helical filaments is shown schematically in A. (B) The bundle-equivalent dome, where ρ denotes the arc distance from the pole. Red contours, lines of latitude on this surface, correspond to the red trajectories in C in bundles, along which a filament returns to itself.

In purely geometric formulations of filament packing, excluded volume considerations require that Δ_∗≥d, where d is the filament diameter (18). Enforcing this constraint requires the solution to the transcendental equation, dΔ²/dz|_z∗ = 0, for the value of vertical offset z_∗ at the point of closest approach between a given filament pair. Here, we take advantage of the fact that the vector separating closest contact between a pair of helical curves, Δ_∗, intersects the helical curves intermediate to the filament pair, perpendicular to their orientation. Hence, the distance of closest approach between a pair of helical filaments may be subdivided into the distances of closest approach between a series of more closely spaced filaments. Given this integral property, we consider the separation between filaments that are spaced at an infinitesimal separation in the planar section. Adopting polar coordinates, x = ρ cos ϕ and y = ρ sin ϕ, and considering a filament pair whose reference plane positions are given by (ρ,ϕ) and (ρ + δρ,ϕ + δϕ), to lowest order in separation we have

[4]

and

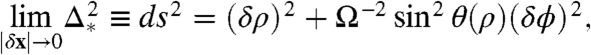[5]

where

[6]

corresponds to the local tilt angle of a filament in the bundle at ρ with respect to 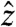(see Fig. 2A). Hence, Eq. 5 shows that twisted filament bundles are imbued with a Riemannian metric that maps separations between infinitesimally spaced filaments in a planar section to the true distance of closest approach in 3D.

One can better understand the unusual metric properties of bundle packing by constructing the surface that carries the metric in Eq. 5 and embedding it in 3D. This dome, or silo-like surface, is shown in Fig. 2B. Integrating ds around azimuthal loops, the perimeter, ℓ(ρ), of this axially symmetric surface has the following dependence on arc distance from the “pole” at ρ = 0,

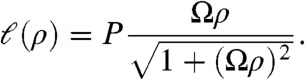[7]

These 3D curves corresponding to the lines of perimeter are shown in Fig. 2C to be curves of constant ρ that pass perpendicular to filament tilt and connect a filament to itself at a different height. Near the ρ = 0 pole (bundle center), not unlike the surface of a sphere, the perimeter increases more slowly than the Euclidean plane. Indeed, from the metric in Eq. 5 we can show the Gaussian curvature of the surface (20) is everywhere positive and largest at the pole,

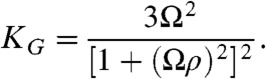[8]

Far from the pole, the perimeter approaches a finite value, ℓ(ρ → ∞) = P, and the surface becomes asymptotically flat (K_G → 0) and cylindrical. To be clear, the bundle-equivalent dome cannot be embedded “within” the twisted bundle, with the surface normal to the helical curves, although it is embeddable in R³ independently and it shares essential metric properties with twisted bundles. Although we have deduced the geometry of this bundle-equivalent dome by considering infinitesimally spaced filaments, it is important to emphasize that the distance relationships encoded in this surface geometry are identical to interfilament distances in 3D bundles at finite separation. In other words, the geodesic distances measured between two points (ρ₁,ϕ₁) and (ρ₂,ϕ₂) on the bundle-equivalent dome are equal to the distance of closest approach between filaments at those positions in the bundle.

An indirect connection between twisted bundle geometry and the geometry of positively curved surfaces is implied by results of nonlinear elasticity theory of twisted columnar arrays: Stresses in the cross-section of twisted bundles are formally equivalent to the stresses in a crystalline membrane on a sphere (21–23). The present analysis extends this connection beyond the limit of infinitesimal filaments and beyond the limit of small twist, establishing the equivalence between discrete packings of finite diameter discs and filaments. A more abstract connection between these problems is implied by Kléman, who demonstrated that certain twisted filament packings are commensurate with the geometry of S³ (24, 25). In light of the present analysis, we find a direct connection between these filament and disc packings that exists between two structures that are (independently) embeddable in 3D Euclidean space, the twisted bundle and disc-packed dome.* Any nonoverlapping configuration of discs on this bundle-equivalent dome corresponds one-to-one with a spacing-filling twisted bundle of filaments with circular cross-section. An example of a 3D bundle and its dual representation as a disc packing is shown in Fig. 1. Specifically, this correspondence means that the horizontal section of the twisted bundle (shown in Fig. 1A) may also be generated by a projection of the disc packing in Fig. 1C that preserves distances along the radial direction (i.e., azimuthal-equidistant projection).

The mapping of the geometry of twisted bundles onto the 2D surface carrying the same metric properties offers a privileged perspective on both the local and global constraints of bundle packing. Firstly, the positive Gaussian curvature of the bundle-equivalent surface implies that it is impossible to evenly space filaments with a sixfold symmetric hexagonal packing because the “kissing number” of discs on this surface is less than six (fewer than six nonoverlapping discs can contact a central disc) (25, 27). Curvature is concentrated near the pole (ρ = 0) and, in densely packed states, its effect is to promote filaments with five (or less) rather than six nearest neighbors near the center of a twisted bundle. For example, consider the central, fivefold coordinated filament in Fig. 1. As the surface geometry becomes Euclidean asymptotically far from the pole, 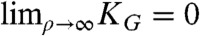, a dense bundle will become hexagonally close packed far from the rotation axis.

Going one step further, we may characterize the distribution of defects in the lattice packing, disclinations, that characterize deviations from sixfold coordination of nearest-neighbor geometry. The topological disclination charge is computed from the numbers of n-fold vertices in the nearest-neighbor bond network, V_n,

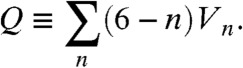[9]

For an infinite bundle, corresponding to a bundle-equivalent dome of infinite height, the Gauss–Bonnet theorem relates the surface curvature to a total topological charge of the packing, Q = 6χ, where χ = (2π)^-1∫dAK_G = 1 is the Euler characteristic of the surface. Thus, we find the topological charge of any sufficiently large twisted bundle packing is exactly six. For example, assuming neighbors have only five-, six-, and sevenfold coordination, Q = V₅ - V₇. We see that any twisted bundle, provided its radius is sufficiently large, must possess at minimum six fivefold disclinations in the packing, consistent with a Delaunay triangulation of the dual surface packing of discs in Fig. 1. Although these topological constraints apply to any twisted bundle packings, we show in the next sections that they have significant consequences for bundles that are geometrically or thermodynamically optimal.

Asymptotically Close-Packed Filament Bundles

The geometric equivalence between twisted fiber packing and packing on the bundle-equivalent dome shown in Fig. 1 offers a unique insight into the structure of maximally dense bundles. In particular, we note that the geometry of filament packing becomes Euclidean, with the periodic topology equivalent to a cylinder of radius, Ω^-1, far from the bundle center where Ωρ≫1. Importantly, this geometry implies that the maximum density of any sufficiently large-radius bundle is achieved by hexagonal close packing of nearly toroidal filaments in the Ωρ≫1 regions (see Fig. 1B).

We may classify all such asymptotically close-packed bundles in terms of the wrapping of a commensurate 2D hexagonal lattice around the bundle-equivalent dome at Ωρ → ∞. Like the well-known geometry of carbon nanotubes (28), given the lattice vectors in the 2D plane, a₁ = d(1,0) and 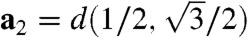, we define the vector P(n,m) = na₁ + ma₂ to describe the wrapping direction of the hexagonal lattice around the circumference of the cylinder. Because 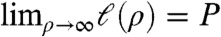, we find that each integer pair, (n,m), corresponds to an asymptotically close-packed bundle of helical pitch,

[10]

Given this countably infinite set of known commensurate close-packing geometries at large radius, it remains to determine filament packing geometry at the core, where the local geometric constraints disrupt sixfold hexagonal packing, necessarily lowering the volume fraction below the close-packing limit of discs in a plane, .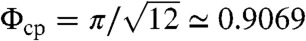

To study the geometric limits of packing in the cores of asymptotically close-packed bundles, we employ a deterministic packing algorithm that sequentially adds filaments to an existing outer “collar” of filaments until the interior of the bundle is fully packed (see SI Text for details). Other than the distinction that the present algorithm grows a packing cluster in the opposite direction—that is, from the outside to the inner core–it is identical to an algorithm used to generate disc packings on spherically and hyperbolically 2D curved surfaces (29). We initiate the algorithm by placing a row of n discs along a₁ and a row of m discs along a₂, wrapped at the appropriate orientation around the dome at a large finite arc distance from the pole (ρ ≃ 5P). Assuming that the packing maintains this regular geometry at larger radii, we sequentially add filaments to the inner region via an algorithm that searches for the pocket of two-filament contact furthest from the pole and occupies it with an additional filament, which proceeds until no further filaments can be added. The algorithm makes small adjustments to the arc distance of initial collar until the volume fraction at the core is maximum. We measure core volume fraction by mapping the disc packing onto the planar cross-section of a twisted bundle (by an azimuthal-equidistant projection) and computing the fraction of area, Φ, occupied by the distorted filament sections within a circle of radius ρ_c ≡ 3P.^†

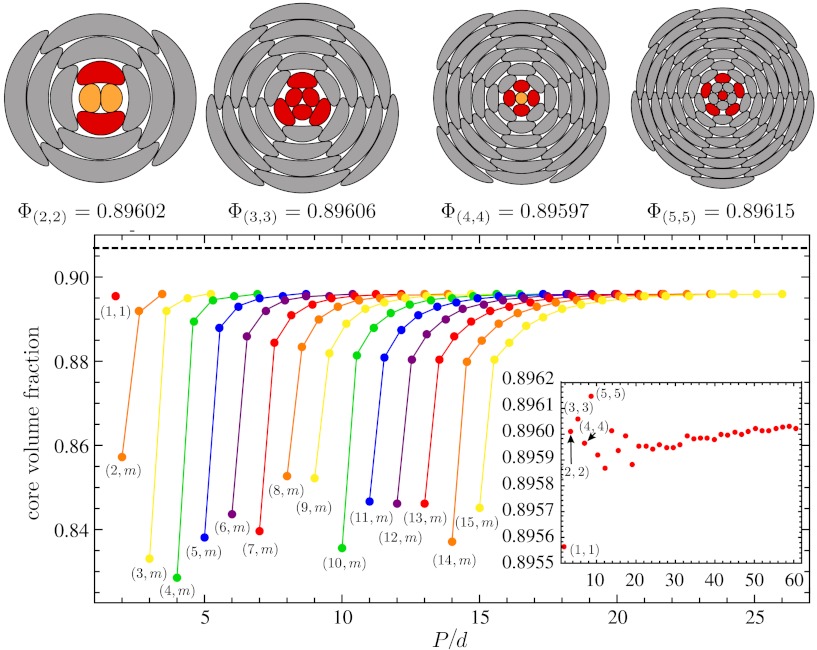
Fig. 3 shows core packing fractions of asymptotically dense bundles for m ≤ n ≤ 15. Because of the impossibility of continuing perfect hexagonal geometry into the core of twisted bundles, volume fractions are in the range 0.82 < Φ < 0.9, at least 1% less dense than the close-packing limit of straight cylinders. One trend is immediately apparent, for a given family of packings at fixed n, the maximal density core structures universally are given by the (n,n) symmetry, so-called “armchair” packings in the nanotube nomenclature. Conversely, the (n,0), or “zig-zag,” give the lowest density for a given n, and the packing fraction of (n,m) bundles for a given n is a monotonically increasing function of m. The distinction between (n,0) and (n,n) packing can easily be understood to derive from the fact that the decreasing perimeter available as the core is approached effectively compresses the hexagonally close-packed geometry along the vector P. For (n,0) bundles, this direction is along a nearest-neighbor bond (say along a₁). Because nearest-neighbor directions are incompressible, (n,0) bundles cannot maintain the close-packed lattice topology for finite ρ. For (n,n) bundles, the azimuthal contraction takes place along the next-nearest-neighbor direction, a compressible axis of the packing that allows the regular topology of the ρ → ∞ packing to be maintained to the core.

Fig. 3.

The cross-sections of core packings for asymptotically close-packed bundles with (n,n) symmetry with n < 6 are shown at the top. Filaments shown are within P from the rotation center. Red and orange filaments, respectively, label filaments with five- and fourfold coordination in the nearest-neighbor packing. The plot shows the core volume fraction of asymptotically dense bundles, (n,m) for m ≤ n ≤ 15 (joined points share the same n value). The dashed line shows the packing fraction of hexagonally close-packed cylinders. Inset shows the volume fractions of (n,n) packings for n ≤ 35, points n ≤ 5 labeled.

The inset of Fig. 3 shows the packing fractions obtained for the (n,n) structures for n ≤ 35. The densest packings found tend be concentrated at low P, for n < 6. The large-n results suggest a convergence to a limiting packing fraction of Φ ≃ 0.8960, not unlike the large-n convergence of area fraction observed in numerical studies of disc packing on spheres (30). The maximal core density is found for a (5,5) packing, for which Φ_(5,5) = 0.89615. The relatively high packing fractions of the n < 6 armchair packings are consistent with the local constraints of packing at the core which prohibit a filament kissing number ≥6, an unavoidable conflict with the hexagonal symmetry of asymptotically close-packed regions. As shown in Fig. 3, core packings possess a nonzero number of five- and fourfold coordinated sites in the nearest-neighbor geometry, denoted as V₅ and V₄, respectively. In the absence of other defects, topology requires V₅ + 2V₄ = 6. For n < 6, the C_n symmetry of (n,n) packings are commensurate with the less than sixfold symmetry of dense packing at the core. Note, in particular, the (5,5) packing whose fivefold symmetry is consistent with the coordination geometry of the central filament. This structure is uniquely compatible with the packing constraints at the core and the asymptotically close-packed regions. For this helical pitch, 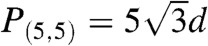, the kissing number of the central filament in the (5,5) structure is very nearly equal to five.^‡ Because of the near coincidence of perfect packing in the core and far from the center, we conjecture the (5,5) packing to be the densest possible packing of any helically twisted filament bundle.

Self-Assembled Ground States of Twisted Bundles

The frustration of twisted bundle packings has a profound influence on not only the structure of geometrically optimal bundles of unlimited size, but also on the minimal-energy structures that form under the influence of mutual attractive forces between filaments in finite-diameter twisted bundles. We explore the cross-sectional packing of self-assembled twisted bundles using a computational approach (see SI Text for full details). Whereas bundles are fully 3D structures, we assume that all cross-sectional slices of a bundle are identical up to a rotation around the center of the bundle, allowing us to fully describe the structure by specifying filament positions in a given 2D plane. We model filament interactions via a Lennard–Jones interaction between elements of arc length on opposing filaments. Integration of these interactions along the arc length of a neighbor filament yields an effective interaction per unit length that depends only on the distance of closest approach between a filament pair (22),

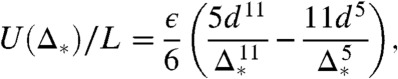[11]

where ϵ is energy per unit length of the attractive well, and d is the preferred interfilament separation. To calculate Δ_∗ between filaments a and b in a computationally efficient manner, a numerical approximation for vertical separation between filament contact, z_∗, is used in Eq. 2,

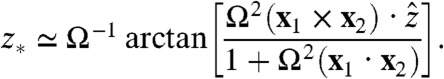[12]

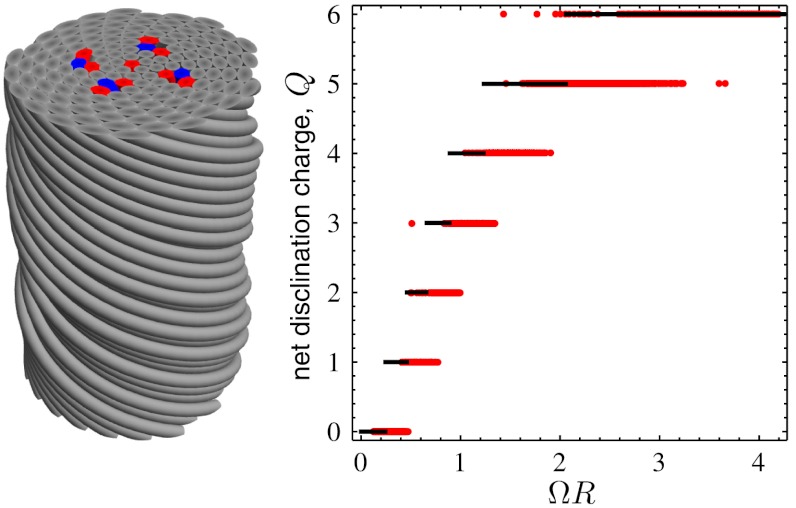
This approximation interpolates between the solution for z_∗ in both limits of large and small Ω²ρ₁ρ₂, and is accurate to within a few percent of total bundle energy for all configurations. Starting with random initial configurations of in-plane filament coordinates, the total energy is minimized by steepest descent. To account for the plethora of local energy minima for large bundles, minimizations were randomly initiated 200–2,000 times depending on the number of filaments. For each value of Ω and filament number, N, only the lowest energy structures were analyzed. To determine the nearest-neighbor packing of bundles, filament coordinates undergo an isothermal coordinate (conformal) mapping to the 2D plane, after which the standard Delaunay triangulation is performed. The resulting structures are characterized according to their radius, R, defined as the mean radius of boundary filaments. An example structure of N = 142 filaments at a rate of twist Ω = 0.27d^-1, is shown in Fig. 4, with five- and sevenfold disclinations highlighted in the cross-section. We begin by analyzing the total topological charge of disclinations, Q, in minimal-energy bundles in the range N = 16–193 as a function of increasing twist shown in Fig. 4. For finite radius bundles, we find that Q is determined by the parameter ΩR alone. For small, weakly twisted bundles, ΩR ≈ 0, the packing is hexagonal and defect-free. Above a threshold value of ΩR, excess fivefold disclinations appear in the packing, increasing in a stepwise fashion to a maximal number of Q = 6 for large ΩR. We note that for small (ΩR), these transitions are well described by the continuum theory of refs. 21 and 22, which predicts, for example, a threshold twist for a single fivefold disclination at 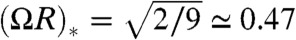, which compares well to a mean critical threshold observed in the current simulations of (ΩR)_∗ ≃ 0.44. However, the continuum theory does not accurately describe the (ΩR)≫1 regime, notably failing to capture the maximum topological charge of twisted bundles, Q = 6.

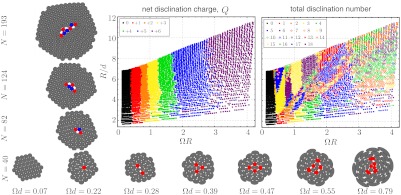
Fig. 4.

On the left, a minimal-energy twisted bundle with 142 filaments and Ω = 0.27d^-1. Five- and sevenfold coordinated filaments are shown as red and blue, respectively, and sixfold filaments are shown gray. On the right, the net topological charge of minimal-energy bundle assemblies is plotted as a function of twist, with results from simulated packings shown in red. The solid black lines show the integer values of Q closest to 6χ(R).

The stepwise increase of defect charge in minimal-energy bundles derives from the geometric correspondence between bundle packing and disc packing on domes. To see this connection, we consider the integrated Gaussian curvature over the finite domain, M, of the packing that covers a portion of the bundle-equivalent dome, χ(M) = (2π)^-1∫_MdAK_G. We generalize the notion of the Euler characteristic to triangulations with an open boundary, where the boundary of the triangulation derives from the filaments at the outer periphery of the bundle. Given the set of internal angles θ_b at the vertices, b, that sit at the boundary of the triangulation, we may show

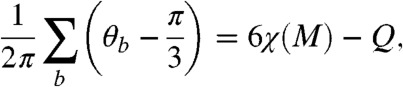[13]

where we take the geodesic curvature of the boundary edges to be zero. The sum on the left-hand side above is nonzero, when internal angles of the bond triangulation at the boundary deviate from the geometry of equilateral triangles on flat surfaces. Assuming distortions from equilateral bond geometry are energetically costly, it is reasonable to expect that the internal packing topology adjusts to minimize this internal angle deviation, or that defect charge is determined by min _Q|6χ(M) - Q|. Approximating the M as an axisymmetric domain of arc-radius ρ = R, we calculate the Euler characteristic of the bundle-equivalent dome as a function of size,

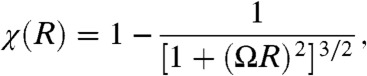[14]

which is consistent with the requirement that Q = 6 for infinite-radius bundles. The optimal values of defect charge predicted by this purely geometric argument are depicted as solid, black lines in Fig. 4, showing very reasonable agreement with the results of energy-minimal bundles. In Fig. 5, Left, we plot a phase diagram to show the net topological charge of minimal-energy structures in terms of both reduced twist ΩR, and bundle size relative to filament diameter, R/d. This view more clearly demonstrates that Q is predominantly determined by ΩR and largely independent of the microscopic filament size d, further emphasizing the fact that geometrical constraints on twisted bundle packing severely restrict the value of net disclination charge in minimal-energy states.

Fig. 5.

Cross-sections of simulated bundle ground states for fixed filament number and increasing twist (Bottom) shown increasing topological charge, excess fivefold defects. For increasing filament number (bundle size) and fixed twist (Left), Q remains fixed while total disclination number grows (excess 5–7 pairs). The phase diagrams show the net topological charge and total disclination number of simulated packings plotted in terms of reduced twist, ΩR, and bundle size R/d.

For comparison, we also show a phase diagram indicating the total disclination number (i.e., 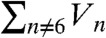) in minimal-energy bundles in Fig. 5, Right. This phase diagram emphasizes clearly that, although the net charge of defects is determined by ΩR, the generalized Euler character alone is not sufficient to discriminate among the many ways of achieving a given value of Q.

Whereas the boundaries between the regions of constant Q in Fig. 5 are largely vertical, the total disclination number of minimal-energy bundles exhibits many more domains divided by phase boundaries showing a much more complex dependence on twist and bundle size. Although we find even more complex packings (with four- and eightfold defects) among minimal-energy bundles, in large part, the trend of increasing R/d at fixed ΩR is characterized by the vertical sequence of Q = 1 cross-sections shown in Fig. 5. As bundle size increases, fivefold disclinations become progressively extended by neutral chains of 5–7 disclination pairs. These grain boundary scars have been predicted (31) and observed (6, 7) to appear in crystalline order on curved surfaces as a means of screening the large stresses in the neighborhood of geometrically favored disclinations. Consistent with our present findings for this analogous, geometrically frustrated system, the length of these scars (and hence the total disclination number) is found to be an increasing function of R/d.