Detecting symmetry and faces: Separating the tasks and identifying their interactions

Abstract

Face and symmetry processing have common characteristics, and several lines of evidence suggest they interact. To characterize their relationship and possible interactions, in the present study we created a novel library of images in which symmetry and face-likeness were manipulated independently. Participants identified the target that was most symmetric among distractors of equal face-likeness (Experiment 1) and identified the target that was most face-like among distractors of equal symmetry (Experiment 2). In Experiment 1, we found that symmetry judgments improved when the stimuli were more face-like. In Experiment 2, we found a more complex interaction: Image symmetry had no effect on detecting frontally viewed faces, but worsened performance for nonfrontally viewed faces. There was no difference in performance for upright versus inverted images, suggesting that these interactions occurred on the parts-based level. In sum, when symmetry and face-likeness are independently manipulated, we find that each influences the perception of the other, but the nature of the interactions differs.

Face processing and symmetry perception are critical for navigating in the social environment. All human faces are objects that have similar, quasisymmetrical, spatial configurations—specifically, two eyes, a nose, and a mouth aligned in a fixed arrangement. This stereotypy facilitates the holistic processing of faces (Fantz, 1961). Marked deviation from symmetry is inconsistent with a face-like arrangement, and subtle deviations, while consistent with being face-like, carry ethological significance, such as head orientation or facial expression.

Along with these informal observations, experiments demonstrate common features of face and symmetry processing. Face processing relies on the comparisons of features and their locations, rather than on mere detection of discrete features; the same is true of symmetry processing (Rainville & Kingdom, 2000; Victor & Conte, 2005; Wagemans, 1995). Face recognition is best in a vertical configuration (Jacques & Rossion, 2007), and symmetry perception is also superior for vertically oriented images (Corballis & Roldan, 1975; Pashler, 1990).

Given these commonalities, it is not surprising that face processing and symmetry perception interact. Recent fMRI studies suggest specialization for processing symmetry in faces. Chen, Cao, and Tyler (2007) found that right occipital face area (OFA) and intraoccipital sulci (IOS) were more responsive to changes in symmetry in faces than to changes in symmetry in scrambled objects or in scrambled faces. Caldara and Seghier (2009) demonstrated greater activation in the fusiform face area (FFA) to symmetrical than to asymmetrical face-like objects. Conversely, perceptual studies have also shown that face identification is superior when facial features are symmetric (Little & Jones, 2006; Rhodes, Peters, Lee, Morrone, & Burr, 2005; Troje & Bulthoff, 1997).

Although there is ample evidence that symmetry and face processing interact, the nature of these interactions is unclear, owing to a basic confound: Faces, typically, are symmetric. To unravel these interactions, we developed and used a novel stimulus set in which symmetry and face-likeness were independently varied.

The first experiment was motivated by the observation that there is a specialized processing of face-like objects for symmetry (Caldara & Seghier, 2009; Chen et al., 2007; Sirovich & Meytlis, 2009). We sought to characterize the computation—specifically, whether it is sensitive to symmetry per se, or simply to relative positions of features. Our specific motivation was that in previous studies of symmetry processing in face-like objects, symmetry judgments were driven by positions between facial features (Chen et al. 2007; Little & Jones, 2006; Rhodes et al., 2005). However, judgments of relative positions of facial features are highly accurate, even when these judgments are not part of a symmetry task (Haig, 1984). Thus, it is unclear whether the above observations indicate enhanced processing of symmetry per se, or rather reflect enhanced processing of relative position. To distinguish these alternatives, we needed to focus on symmetry judgments that were not driven by positions of features. To do this, we used symmetry judgments driven only by correlations among pixel values (Rainville & Kingdom, 2002). We found that for such correlation-driven symmetry judgments, performance for face-like objects remains superior to performance for non-face-like ones, thus implying that the specialized processing is truly a matter of symmetry extraction at an abstract level and goes beyond positional judgments.

In the second experiment, we addressed the question of whether judgments of face-likeness (i.e., identifying an object as a face) are enhanced for symmetric objects versus asymmetric ones. That is, does identification of an object as a face make use of symmetry? Some evidence suggests that this is the case. For example, in a prior study, Cassia, Kuefner, Westerlund, and Nelson (2006) showed that vertical displacement of facial features—that is, making them less symmetric—impaired the determination of whether the face was upright. However, this form of face manipulation introduces a possible confound: Altering symmetry by moving features affects face-likeness. Our stimulus set allowed for a change in the level of symmetry without affecting face-likeness. Experiments based on these stimuli revealed that there is an interaction between face detection and symmetry, but it is modulated by viewpoint: When viewpoint and symmetry are in conflict, face detection is impaired.

In both experiments we used stimulus inversion (Valentine, 1988; Yin, 1969) to distinguish between parts-based and holistic mechanisms shared by symmetry processing and face detection. Our findings indicate that the aforementioned interactions between face detection and symmetry processing were primarily at the parts-based level.

Method

Creation of the image library

As a preliminary to the experiments, we created a library of images in which face-likeness and symmetry varied independently. To create these images, we manipulated photographic images of 394 faces by a series of steps consisting of thresholds, randomization, and contrast flips. This allowed us to dissociate symmetry and face-likeness. (Note that although the image library included both frontal and nonfrontally viewed faces, viewpoint was not used to dissociate symmetry and face-likeness).

The procedure we used to do this is diagrammed in Fig. 1 and is detailed in the Appendix. The net result of these transformations was 11,426 binary (black and white) images, each on a relatively coarse grid (18 × 24 checks). We chose this grid size to be fine enough so that form was readily visible, but coarse enough so that the individual checks were also visible.

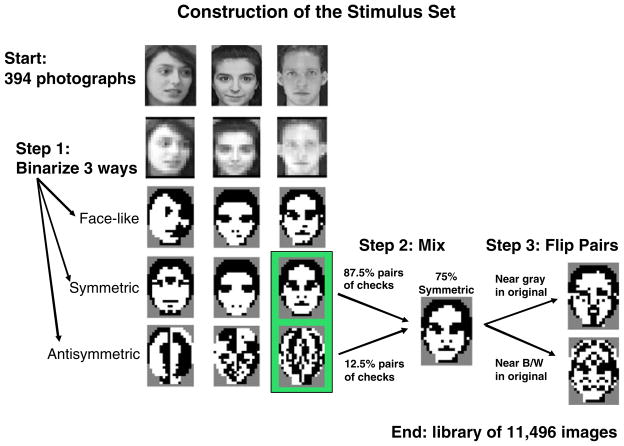
Fig. 1.

Schematic of steps in the generation of the stimulus library from the original 394 gray-level photographs. The first step of the process consists of binarization; this is illustrated for three photographs (top left of the figure). Each face is binarized in one of three ways, leading to a maximally face-like image, a maximally symmetric image, or a maximally antisymmetric image (bottom three rows on left). Next, an image is formed by mixing two of these binarized images so that a specific level of symmetry is achieved. At the third step of processing, bilaterally symmetric pairs of checks are flipped in contrast (lower right). This preserves the level of symmetry but can markedly alter face-likeness. If the flipped checks corresponded to original-image pixels that were close to gray (upper arrow), then flipping their contrast results in a face-like image; if the flipped checks corresponded to original-image pixels that were near black or white (lower arrow), then flipping their contrast results in a non-face-like image. See the Appendix for further details of the algorithm and Fig. 2 for more examples from the stimulus library

Characterization of the image library

In the two main experiments that follow, symmetry and face-likeness were the independent variables. Examples of the stimuli from the image library are illustrated in Fig. 2. To assign values of each of these quantities to each image in the library, we proceeded as follows.

Fig. 2.

Examples drawn from the library of 11,426 images. Below each image are its values of C (symmetry strength, range: 0 to 1) and F (face-likeness, range: 1 to 4)

Quantification of symmetry

We quantified symmetry by the parameter C, defined as (fraction of pairs of checks that match in luminance) − (fraction of pairs of checks that mismatch). For C = 1, the stimulus is perfectly symmetric (all check pairs match across the vertical midline); for C = 0, it is random (half match, half mismatch), and for C = −1, it is antisymmetric (all check pairs mismatch). See also Victor and Conte (2005). For all stimuli used in these experiments, C was between 0 and 1.

Quantification of face-likeness

Since face-likeness is subjective, we used a rating procedure to determine its value. Our multiracial rating panel consisted of five males and five females ranging in age from 22 to 48. Five of the raters subsequently participated in Experiment 1, and two of these five participated in Experiment 2. Each rater scored half (5,713) of the 11,426 blocked and binarized images over three testing sessions. Images scored by each rater were selected by a randomized design that equated, as much as possible, the number of images derived from each of the 29 image processing pathways (see the Appendix) and the number of images jointly scored by subsets of the raters. Images were presented under free-view conditions at a distance of 57 cm, corresponding to an image size of 8.25 × 10 deg. of visual angle. Raters used a mouse to record ratings on a four-point scale, where “1” was the least face-like and “4” was the most face-like. A consensus rating, F, was derived from the individual ratings by taking the first principal component of the array consisting of each individual’s rating of each image, after allowing for an arbitrary offset (across all images) for each rater. Since, by design, each observer rated only half of the images, we used a missing-data principal components analysis (Shum, Ikeuchi, & Reddy, 1995) procedure. The procedure does not attempt to “fill in” the missing data; it merely assigns zero weight to the observations that are missing. The Shum et al. procedure was readily adapted to include an arbitrary offset for each rater, since it is an iterative method that entails a linear regression at each step. The use of principal component analysis also builds in an arbitrary multiplicative scale factor for each rater; the offset and multiplicative scale factor take into account an individual’s preferences for using only a portion of the rating scale.

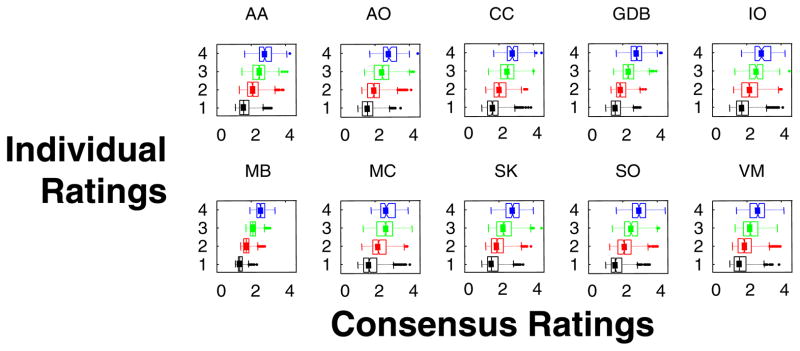
The individual ratings were consistent, and the consensus was captured by their first principal component, which contained 40% of the variance. The remaining variance was scattered throughout the other components, with only 16% of the variance in the second principal component. A second measure of this consistency is shown in Fig. 3, which indicates that each rater’s scores, individually, were highly correlated with the consensus rating. Correlation coefficients between individual raters’ scores and the consensus ranged from .41 to .86. (For comparison, test–retest correlations for two raters were .79 [M.C.] and 0.77 [A.A.]). To give the reader a more intuitive idea of what these consistency measures mean, there was virtually no confounding of the two ends of the continuum: This accounted for only 3.8% of the pairs of ratings. On the other hand, 43.6% of rating pairs agreed exactly, and 37.3% of the rating pairs differed by one step on the rating scale. There was no detectable dependence on gender or race.

Fig. 3.

Correspondence of individual face ratings with the consensus ratings. For each of 10 raters (5 M, 5 F), boxplots indicate the distribution of consensus ratings for the images that the rater scored at each level of face-likeness, from 1 (least face-like) to 4 (most face-like). Consensus ratings for each image were determined by missing-data principal components analysis (see the Method section)

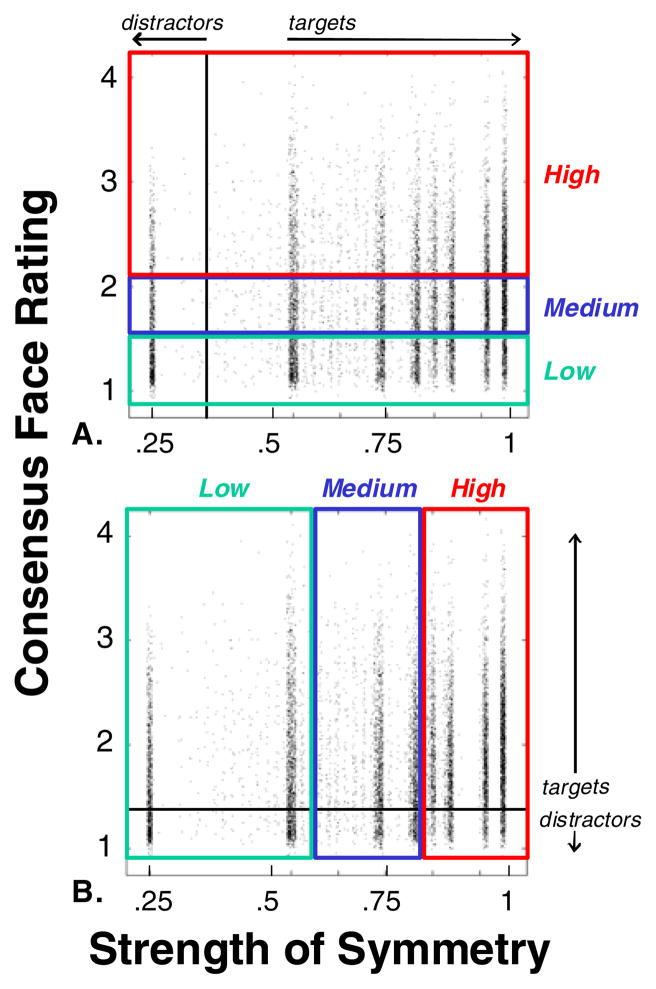
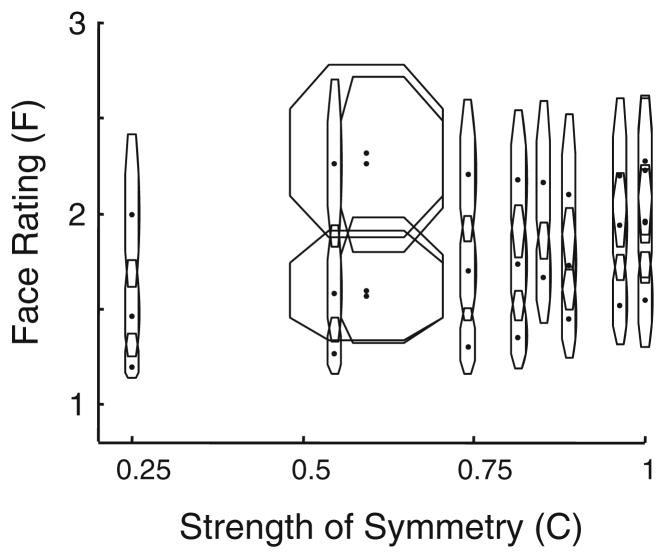
Distribution of consensus face ratings and symmetry

Figure 4 shows the joint distribution of consensus face ratings and the symmetry strength, C. The range of symmetry values covered a range from low symmetry (C = 0.25, meaning that 62.5% of checks match across the midline, and 37.5% of checks mismatch) to completely symmetric (C = 1, all checks match across the midline).

Fig. 4.

Distribution of the consensus ratings and symmetry strength for all images in the library. Each dot represents one image; dot positions are slightly jittered to avoid overlap. They are identical in each panel, but the panels are subdivided in different ways to illustrate the experimental design. In Panel a, the horizontal colored stripes correspond to the low, medium, and high face-like bands used in Experiment 1. In Panel b, the vertical colored stripes correspond to the low, medium, and high symmetry bands used in Experiment 2. Typical stimulus examples illustrating the range of the library are shown in Fig. 2. The vertical bands of high density correspond to symmetry values that result from specific choices made in the image synthesis process (see the Appendix). For all symmetry values, the gamut of face-like ratings in the library is similar

Construction of stimuli

We then drew samples from this image library to create stimuli for the two experiments. In Experiment 1, we asked whether making symmetry judgments is influenced by face-likeness. To address this, we divided the image library into three subsets of similar face-likeness, each containing approximately one-third of the images—the three horizontal colored bands of Fig. 4a. Each stimulus in Experiment 1 consisted of four images drawn from a single band of face-likeness: one unique target with higher symmetry drawn from one of four ranges (C = 0.6 to 0.7; C = 0.7 to 0.8; C = 0.8 to 0.9; C = 0.9 to 1.0), and three distractors with low symmetry (range, C = 0.25 to 0.35). Thus, within each trial, target and distractors differed systematically by the amount of symmetry, but had similar levels of face-likeness, since they were drawn from the same band. The difference in symmetry (the cue strength) and the overall level of face-likeness (irrelevant to the target) were independently varied from trial to trial.

In Experiment 2, we asked the converse question—whether detection of faces is influenced by symmetry. Correspondingly, we divided the image library into three subsets according to the symmetry parameter C, each containing approximately one-third of the images—the vertical colored bands of Fig. 4b. Each stimulus in Experiment 2 consisted of four images drawn from a single band: one unique target with a higher face-like rating drawn from one of four ranges (1.4 to 1.675, 1.675 to 1.97, 1.97 to 2.36, and 2.36 to 4.5), and three distractors with a low face-like rating (range, 0 to 1.4). Thus, within each trial, target and distractors differed systematically in face-likeness, but had similar levels of symmetry. The difference in face-likeness (the cue strength) and the overall level of symmetry (irrelevant to the target) were independently varied from trial to trial.

In both experiments, the widths of the bands were chosen to be comparable to the precision with which observers were able to make judgments—either of symmetry (Victor & Conte, 2005) or of face-likeness (in the preliminary rating experiment).

Participants

Experiment 1 was conducted in six participants (three male, three female), ages 22 to 48 years (average age: 30). Participants included both practiced and novice psychophysical observers. Five of the six were raters of the image library. Practiced participants (four of the six) had participated in a previous related task involving targets in the same positions relative to fixation. Other than author M.C. and A.A., the remaining participants were naive to the purpose of the experiment. All had visual acuities (corrected if necessary) of 20/20 or better. Experiment 2 was also conducted in six normal participants (six female), ages 21 to 48 (average age: 25). Three of the participants (M.C., C.C., and G.D.B.) were raters of the image library and also participated in Experiment 1. The remaining participants were unpracticed, and—excluding authors M.C. and R.J.—were naive to the purpose of the experiment.

Apparatus and stimulus presentation

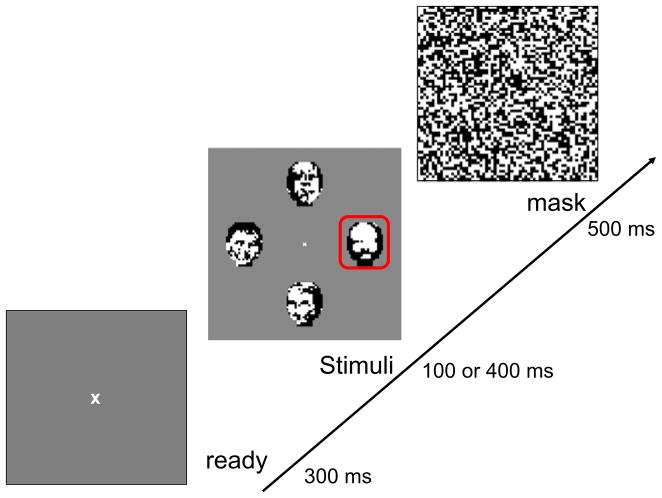
Visual stimuli were produced on a Sony Multiscan 17seII (17-in. diagonal) monitor, with signals driven by a PC-controlled Cambridge Research VSG2/5 graphics processor programmed in Delphi II to display bitmaps precomputed in MATLAB. The resulting 768 × 1,024 pixel display had a mean luminance of 47 cd/m², a refresh rate of 100 Hz, and subtended 11 × 15 deg at the viewing distance of 102.6 cm. The monitor was linearized by lookup table adjustments provided by the VSG software. Stimuli used in both experiments consisted of four vignetted arrays of 18 × 24 checks on a mean gray background. Each check occupied 4 arcmin of visual angle, and stimulus contrast was 1.0. The arrays were positioned along the cardinal axes, with centers 200 arcmin from fixation. A full-field random checkerboard mask was presented for 500 ms following each presentation of the stimulus frame. Figure 5 diagrams the layout of the arrays and time course of the trials.

Fig. 5.

The time course of the four-AFC trials. The outline box, indicating the target in this sample trial, does not appear during stimulus presentation

Procedure

Experiments (see Fig. 5) were organized as blocks of four-alternative forced choice trials. Target location (top, bottom, left or right) was randomized and counterbalanced within each block of trials. Prior to data collection, all participants practiced the task until performance became stable. Trials were self-paced, with sessions lasting 1 to 1.5 hr with breaks when necessary. In each experiment, participants completed a total of 2,880 trials in two testing sessions on separate days. Blocked conditions were counterbalanced across days and across participants. This procedure was different than that used for acquiring the face ratings because the purpose of the face ratings simply was to obtain considered judgments about face-likeness to serve as an independent variable, whereas the four-alternative forced choice trial design enabled us to test the effects of this variable on early visual processing.

In Experiment 1, the participants’ task was to identify the image that was the most symmetric and to respond as quickly and accurately as possible via a button press on a response box with four buttons positioned corresponding to the four images. They were also instructed to maintain central fixation rather than to attempt to scan the individual arrays. Responses and reaction times (RTs), measured with respect to the onset of the stimulus frame, were collected via the Delphi II display software. Trials in which the participant responded before the onset of the stimulus or after 3,000 ms were discarded and repeated at the end of each stimulus block. For both experiments, our psychophysical performance measures were fraction correct and RT.

Two variations on this basic design were used: viewing time (100 ms vs. 400 ms) and image inversion. In the trials in which the images were inverted, they were kept in the same relative locations as in the upright trials, and the same images were used for both conditions. Different images from the library were used for the 100-ms and the 400-ms conditions. These four kinds of trials (100 ms upright, 100 ms inverted, 400 ms upright, 400 ms inverted) were presented in separate blocks, on both days of testing, and in counterbalanced order across observers.

In Experiment 2, the procedure was identical to that in Experiment 1, except that the participant’s task was to select the image that was most face-like. Note that although the procedure was the same, the stimuli were different: The target was more face-like than the others, but all were similar in symmetry, as was described previously.

Results

We conducted two experiments of parallel design: Experiment 1, to determine whether symmetry detection is influenced by face-likeness, and Experiment 2, to determine whether detection of faces is influenced by symmetry. We begin by describing how performance depended on the experiment-specific parameters and their interactions; this will be followed by post hoc analyses.

Our main finding in Experiment 1 was that symmetry detection was enhanced for face-like objects. Our overall finding in Experiment 2 was that face detection was reduced for highly symmetric objects, and a post hoc analysis of the interaction with viewpoint suggested that the basis of this impairment was a cue conflict. In both experiments, the interaction between symmetry detection and face-likeness was similar for upright and inverted faces.

Experiment 1: Is symmetry detection influenced by face-likeness?

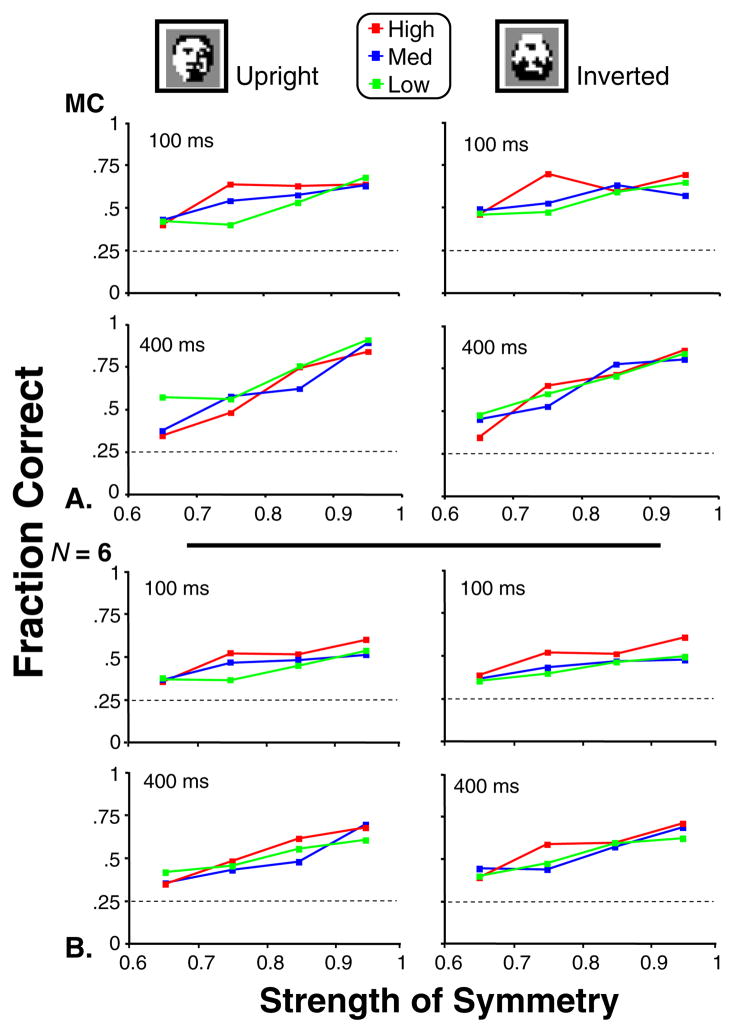
Figure 6 shows the fraction of correct responses obtained in Experiment 1, for a single participant (M.C., Panel A), and the group average (N = 6, Panel B).

Fig. 6.

Performance in Experiment 1 for the low, medium, and high bands of face-likeness. Fraction correct is plotted as a function of symmetry strength for participant M.C. (Panel a) and is averaged across the six particpants (Panel b). Dotted lines represent chance performance level. Standard errors are approximately 0.06 (one participant) and 0.025 (N = 6), via binomial statistics. The abscissa labels correspond to ranges of values for symmetry: 0.6 to 0.7, 0.7 to 0.8, 0.8 to 0.9, and 0.9 to 1.0

With a 100-ms stimulus duration time, the mean fraction correct (across all participants) ranged from 0.38 to 0.60 over the symmetry range tested. These findings are comparable to the previously reported range of fraction-correct performance using symmetric and near-symmetric check arrays (Victor & Conte, 2005). On average, performance improved by 0.08 with longer stimulus duration (400 vs. 100 ms). Averaged RTs (measured from the end of the stimulus) increased slightly with stimulus duration (885 ms at 400 ms vs. 736 ms at 100 ms), but there were no differences in RT for upright versus inverted images.

A full-factorial ANOVA (SPSS Version 11), with fraction correct as the dependent variable, was performed with the following variables as factors: participant, time (100 ms vs. 400 ms), symmetry, face rating, and orientation (upright vs. inverted). ANOVA results are summarized in Table 1.

Table 1.

Results of the full-factorial ANOVA of Experiment 1. Column 1: all main effects; all pairwise and three-way interactions that were significant in Experiment 1 or 2; and the lack of an interaction between face rating, symmetry, and orientation (for 17,280 observations). Columns 2–4: Analysis of viewpoint. Column 2 shows the results of the full-factorial ANOVA adding viewpoint as a factor. Columns 3 and 4: ANOVA of the subsets of the data consisting of the frontally viewed images (5,988 observations, Column 3) and the nonfrontally viewed images (11,292 observations, Column 4)

Experiment 1-Which is most symmetric?
	Five Factors		Six Factors		Five Factors
					Frontal View		Nonfrontal View
	F	P	F	P	F	P	F	P
Main Effects
Participant	48.55	< .001	43.26	< .001	17.64	< .001	29.94	< .001
Time	105.09	< .001	91.11	< .001	33.33	< .001	68.66	< .001
Symmetry	159.59	< .001	134.35	< .001	42.08	< .001	117.94	< .001
Face Rating	21.18	< .001	22.30	< .001	16.98	< .001	9.30	< .001
Orientation	5.94	< .05	4.13	< .05	0.43	NS	6.59	< .05
Viewpoint			2.68	NS
Significant Two-way Interactions
Participant x Time	2.90	< .05	2.46	< .05	1.33	NS	2.87	< .05
Participant x Symmetry	2.77	< .001	2.76	< .001	1.48	NS	1.97	< .05
Time x Symmetry	12.05	< .001	9.89	< .001	3.61	< .05	8.29	< .001
Participant x Face Rating	2.28	< .05	2.19	< .05	1.72	NS	2.01	< .05
Face Rating x Symmetry	5.00	< .001	4.64	< .001	3.01	< .05	5.38	< .001
Face Rating x Time	2.03	NS	1.80	NS	6.06	< .05	6.94	< .05
Significant Three-way Interactions
Participant x Time x Face Rating	2.71	< .05	2.66	< .05	1.81	NS	1.90	< .05
Face Rating x Time x Symmetry	3.25	< .05	2.40	< .05	1.70	NS	5.06	< .001
Face Rating x Symmetry x Orientation	1.51	NS	1.42	NS	1.11	NS	1.15	NS

The ANOVA revealed significant main effects for all factors (p < .001 for all but orientation; p < .05 for orientation). Two kinds of pairwise interactions were significant. One kind of interaction was between the subject factor and a stimulus parameter; these interactions indicated intersubject variability in the main effects of time (p < .05), symmetry (p < .001), and face rating (p < .05). The other kind of interaction was between two stimulus parameters. The first (time x symmetry, p < .001) indicated that the effect of increased presentation time on performance was larger for high-symmetry targets than for low-symmetry targets. The second interaction was between symmetry and face rating (p < .001). This interaction indicated that symmetry detection was enhanced for stimuli that were rated more face-like (see also Fig. 6). The significance of these interactions and their signs were confirmed by a logistic regression analysis (SPSS Version 11).

If the mechanism for symmetry detection in face-like objects was dependent on holistic face processing, then we might expect that the interaction would depend on whether images were upright or inverted—that is, on orientation (Yin, 1969). However, there was no detectable three-way interaction between symmetry, face rating, and orientation. That is, the enhancement of symmetry detection for face-like images was the same for upright face-like images as for inverted ones.

Post hoc analyses

We conducted several auxiliary analyses to identify other potential influences on performance. An analysis of the error patterns for each participant showed that incorrect responses were not biased to a particular array location, or to the most face-like distractor. Practiced and novice participants performed equally well. Exposure to specific images also played no identifiable role: For the participants who also served as raters, there was no difference in performance for novel images versus previously rated images.

As was mentioned in the Method section, the stimulus library included images derived from faces photographed in frontal and nonfrontal views. However, viewpoint did not influence our results. To show this, we partitioned the stimulus set into two categories: frontal view or nonfrontal view. We determined these categories from the original photographs (140 frontal; 254 nonfrontal) and subsequently divided each trial into categories according to whether the target image was derived from a frontal view or nonfrontal view photograph. This additional factor (viewpoint: frontal vs. nonfrontal) was added to the full factorial ANOVA described previously. Significant interactions are summarized in Table 1, columns 2–4. There was no main effect of this factor; all interactions described above remained significant (at similar p values), and an effect of orientation (i.e., an inversion effect) did not emerge. Moreover, the positive interaction of face rating and symmetry was present (p < .05) when the analysis was restricted to the frontal or nonfrontal subsets.

In sum, the results of Experiment 1 show that symmetry judgments were modestly enhanced by face-likeness, but this enhancement was similar for upright and inverted faces.

Experiment 2: Is detection of faces influenced by symmetry?

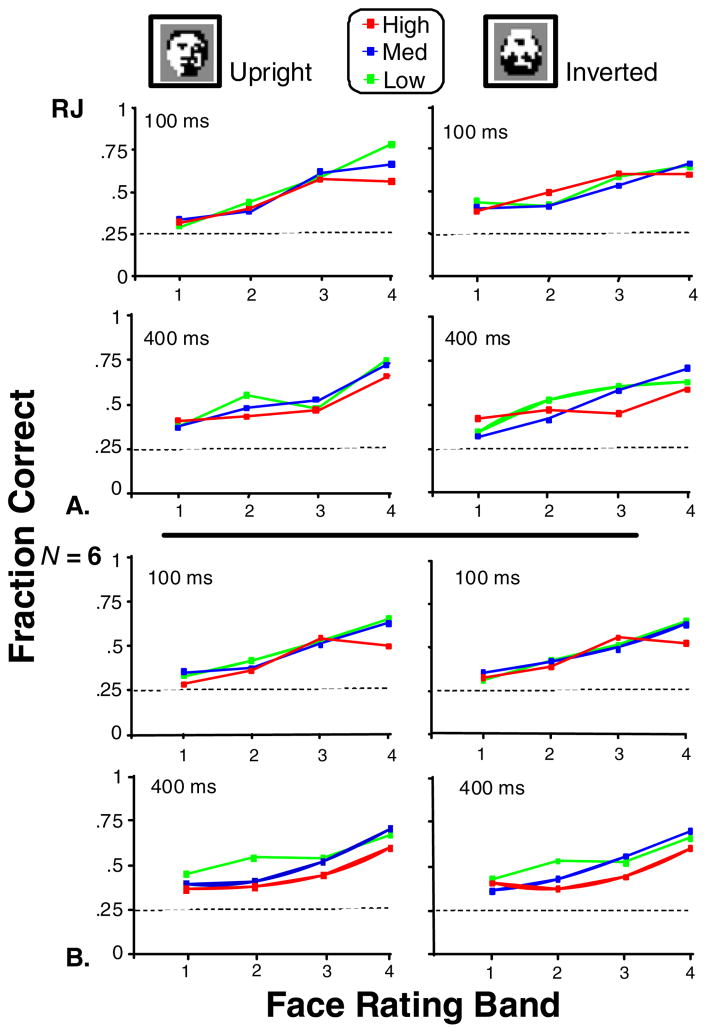
Figure 7 shows the fraction of correct responses obtained in Experiment 2, for a single observer (R.J., Panel A), and the group average (N = 6, Panel B). With a 100-ms stimulus duration time, the mean fraction correct (across all participants) ranged from 0.33 to 0.61 over the face-likeness range tested. On average, performance improved by 0.03 with longer stimulus duration (400 vs. 100 ms). Averaged RTs (not shown) increased with stimulus duration (632 ms at 400 ms vs. 528 ms at 100 ms).

Fig. 7.

Performance in Experiment 2 for the low, medium, and high symmetry bands. Fraction correct is plotted as a function of face ratings for participant R.J. (Panel A) and is averaged across the six participants (Panel B). The abscissa labels correspond to ranges of values for face ratings: Band 1 is 1.4 to 1.675; Band 2 is 1.675 to 1.97; Band 3 is 1.97 to 2.36; and Band 4 is 2.36 to 4.5. Other details are the same as in Fig. 6

As in Experiment 1, a full-factorial ANOVA with fraction correct as the dependent variable was performed with the following variables as factors: participant, time (stimulus duration), symmetry, face rating, and orientation (upright vs. inverted). Results are summarized in Table 2. The ANOVA revealed significant main effects (p < .001) for all factors other than orientation, which was not significant (p > .05). Confirming that the participants were, in fact, responding on the basis of face-likeness, the largest main effect was seen for face rating. Two pairwise interactions were significant. The first interaction was between face rating and symmetry (p < .001). This interaction indicated that symmetry hindered the detection of the highly face-like targets (see also Fig. 7). The second interaction was between face rating and time, (p < .001). This interaction indicated that the effect of increased presentation time on performance was larger for more-face-like targets than for less-face-like ones. The significance of these interactions and their signs were confirmed by a logistic regression analysis.

Table 2.

Results of the full-factorial ANOVA of Experiment 2. Details are the same as in Table 1 except that the number of observations for the frontally viewed images is 6,072, and for the nonfrontally viewed images it is 11,208

Experiment 2- Which is most Face-like?
	Five Factors		Six Factors		Five Factors
					Frontal View		Nonfrontal View
	F	P	F	P	F	P	F	P
Main Effects
Participant	9.51	< .001	6.58	< .001	1.24	NS	9.49	< .001
Time	15.54	< .001	17.94	< .001	10.75	< .001	7.08	< .05
Symmetry	24.80	< .001	12.92	< .001	0.24	NS	46.95	< .001
Face Rating	225.95	< .001	202.24	< .001	69.32	< .001	162.00	< .001
Orientation	0.21	NS	0.53	NS	1.61	NS	0.28	NS
Viewpoint			3.58	NS
Significant Two-way Interactions
Participant x Time	1.30	NS	1.27	NS	0.69	NS	1.73	NS
Participant x Symmetry	1.14	NS	0.97	NS	1.17	NS	1.47	NS
Time x Symmetry	2.87	NS	2.25	NS	0.81	NS	4.47	< .05
Subject x Face Rating	1.09	NS	1.12	NS	1.15	NS	0.84	NS
Face Rating x Symmetry	4.20	< .001	2.35	< .05	1.71	NS	7.74	< .001
Face Rating x Time	7.49	< .001	2.49	NS	1.17	NS	17.02	< .001
Significant Three-way Interactions
Participant x Time x Face Rating	0.95	NS	1.01	NS	0.78	NS	0.88	NS
Face Rating x Time x Symmetry	5.33	< .001	6.53	< .001	6.57	< .001	2.05	NS
Face Rating x Symmetry x Orientation	0.42	NS	0.43	NS	0.49	NS	0.70	NS

As in Experiment 1, the three-way interaction between symmetry, face rating, and orientation was not significant. That is, the interference of symmetry with the detection of face-like images was the same for upright, as it was for inverted, images.

Post hoc analyses

As in Experiment 1, we conducted several post hoc analyses to identify other potential influences on performance. There was no bias to respond to one array location; there was no difference between novice and experienced participants, and, among raters, there was no difference between performance on previously rated and previously unseen images. There was also no difference in performance between participants who had rated the images versus participants who had not.

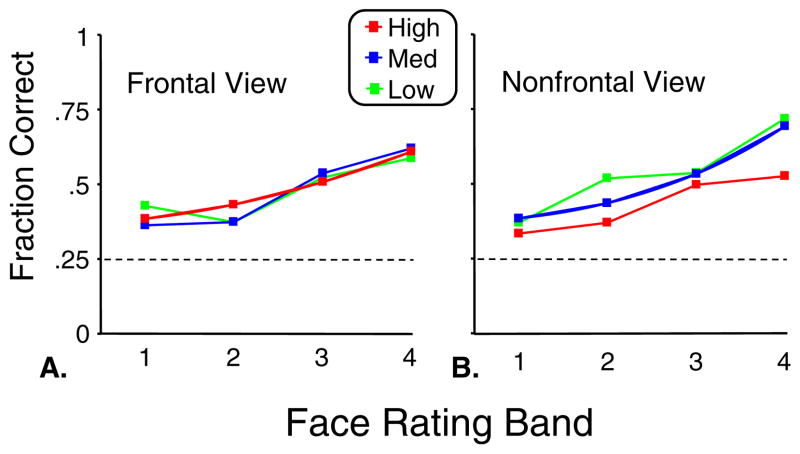
We used the same procedure as in Experiment 1 to determine whether viewpoint influenced the results. When viewpoint was included in the ANOVA, it did not produce a significant main effect (column 2 of Table 2). However, the negative interaction between face rating and symmetry was lost when viewpoint was included as a factor (columns 3 and 4 of Table 2). The reason for this loss is seen from the separate analysis of the frontal and nonfrontal subsets. For frontal views, there was no interaction of face rating and symmetry, but for nonfrontal views, a strong negative interaction was present (p < .001). This is further illustrated in Fig. 8, which separately shows performance for the frontal and nonfrontal subsets. For the frontal subset, there was no effect of symmetry on face detection (Fig. 8a). But for the nonfrontal subset, performance was worse for the more symmetric images (Fig. 8b).

Fig. 8.

Performance in Experiment 2 for frontal view (Panel a) and nonfrontal view (Panel b) targets. Data are averaged across viewing duration (100 and 400 ms) and the six participants. Symmetry has no effect for the frontal targets and hinders performance for the nonfrontal targets. Dotted lines represent chance performance level. Values for face ratings are the same as in Figure 7

In sum, the results of Experiment 2 show that when targets and distractors were symmetric, discrimination of face-like and non-face-like images was reduced. Although the nature of the interaction differed from that of Experiment 1, the results of Experiment 2 also demonstrated no dependence of the interaction on image orientation (upright vs. inverted).

Discussion

To probe the relationship between symmetry perception and face processing, we carried out two parallel experiments. In the first, we examined how face-likeness influences judgments of symmetry; in the second, how symmetry influences judgments of face-likeness.

In the two experiments, there was a qualitative difference in how the mechanisms for symmetry processing interacted with the mechanisms for face perception. In Experiment 1, the interaction was positive: Accuracy for detecting greater degrees of symmetry improved when the stimuli (the targets and the distractors) became more face-like. But in Experiment 2, the interaction was negative: Accuracy for detecting greater degrees of face-likeness worsened when the stimuli became more symmetric.

The negative interaction in Experiment 2 at first appears quite puzzling: Why should face detection be impaired when stimuli are symmetric? One clue is that this interaction is present only for images in non-frontal view. This suggests that a cue conflict is occurring: Faces in non-frontal view shouldn’t be symmetric. Put another way, the images that are difficult to recognize as faces are those for which their high symmetry suggests a frontal view, but their feature positions indicate a nonfrontal view. Thus, it appears that symmetry analysis is used for identification of faces, but it is not simply that symmetrical objects are more likely to be seen as faces; rather, symmetry and viewpoint must be consistent.

A significant aspect of our results is that we found no difference in performance for upright versus inverted stimuli for both experiments. This “inversion effect” (Yin, 1969) is important because it is a marker that holistic processing strategies are engaged (Farah, Wilson, Drain, & Tanaka, 1998; Gauthier & Tarr, 2002; Tanaka & Farah, 1993). In prior studies, which looked at face perception and symmetry processing, Rhodes and colleagues found an inversion effect (Rhodes, Peters, & Ewing, 2007; Rhodes et al., 2005), but Little and Jones (2006) did not. This discrepancy in the findings is likely because of differences in procedures and stimuli. Namely, observers in the Little and Jones study had unlimited viewing of the stimuli, whereas in the studies by Rhodes and colleagues, the SOA was limited to 1,000 ms (Rhodes et al., 2007) or 200 ms (Rhodes et al., 2005). Furthermore, Rhodes et al. (2007, 2005) and Little and Jones (2006) used photographic images rather than discretized ones such as those we created, and they used different means to vary symmetry. We varied symmetry by inverting the contrast of individual checks; in studies based on photographic images, symmetry was varied by moving entire facial features by small amounts. The significance of this technical difference is that symmetry judgment in the present study required a comparison of luminance patterns, comparable to most psychophysical studies of symmetry (e.g., Rainville & Kingdom, 2000; Tyler, 2002). In contrast, when symmetry is altered by moving entire features (as it was in the aforementioned studies), symmetry judgments become positional judgments—allowing other face-specific processing mechanisms to be engaged (Haig, 1984).

In prior experiments that examined both symmetry and face processing, there was a significant enhancement for symmetry detection in face-like objects versus non-face-like ones (Cassia et al., 2006). Behavioral, physiological, and imaging studies have shown that humans have expertise in processing face-like objects versus other classes of objects (Cassia et al., 2006; Gauthier & Tarr, 2002; Kanwisher, McDermott, & Chun, 1997); therefore, the mere fact that an object is face-like may improve performance in symmetry detection. However, in Experiment 1, the effect of face-likeness was at the parts-based level. This result highlights the importance of using stimuli that allow face-likeness and symmetry to be varied independently.

In conclusion, we created an image library in which symmetry and face-likeness are independently manipulated, and in which symmetry per se is dissociated from positional judgments. Parallel experiments based on this stimulus library show that symmetry and face-likeness do interact, but the interaction is complex: Face-likeness enhances symmetry perception, and symmetry acts to impede perception of face-likeness if it is inconsistent with viewpoint. Moreover, the absence of an inversion effect points to an interaction at the parts-based level. These results are consistent with the presence of distinct but overlapping cortical modules for perceiving faces and detecting symmetry.

Appendix

In this Appendix, we detail the creation of the image library, schematized in Fig. 1 of the main article. As detailed below, the library was created by applying each of a family of transformations to a set of photographic images of faces. Doing this consisted of a three-step procedure: (a) binarization, (b) adjustment of symmetry, and (c) alterations that did not change symmetry.

The starting images consisted of the Olivetti (now the AT&T) library of 394 black and white photographs of 40 male and female faces. Each face was available in nine or 10 frontal and nonfrontal views; in total, the library contained 140 frontal and 254 nonfrontal images. Three examples of these starting images are shown at the top of the three columns in Fig. 1. The library is publicly available at: www.cl.cam.ac.uk/research/dtg/attarchive/facedatabase.html

To binarize each photographic image, it was first blocked into an 18 × 24 grid of checks (second row of Fig. 1). That is, each check of the grid was filled with the average luminance of the original photograph within that check. After all images were blocked, they were hand-traced to determine the checks that were at least 50% within the face. The checks that met this criterion in more than half of the images were retained as a common “aperture” for all of the faces. This aperture contained 322 of the 432 original checks; all but two checks were in symmetric pairs. Regions outside of the common aperture were replaced by gray (luminance halfway between black and white).

Checks within the common aperture were binarized into black and white by three separate methods (third, fourth, and fifth rows of Fig. 1). Our goal at this stage was to create images that resembled the original but had varying degrees of symmetry. In the first binarization method (third row of Fig. 1), a check was colored either black or white, depending on whether its luminance was above or below the median gray level of its image. The resulting binary image matched the original image closely, but its symmetry was not controlled. The other two binarization methods controlled symmetry. In the second method (fourth row of Fig. 1), we considered the checks in pairs, yoking together each pair of checks whose positions were bilaterally symmetric. The average luminance of each pair was calculated. Yoked pairs whose mean luminance was above the median were colored white, and yoked pairs whose mean luminance was below the median were colored black. This resulted in binary images that were perfectly symmetric, and, within this constraint, matched the original image as much as possible. In the third method (fifth row of Fig. 1), we compared the luminance of the two checks within each yoked pair. We colored the lighter check white, and the darker check black. Note that in the second method, all checks matched across the midline (C = 1), whereas in the third method, all checks mismatched (C = −1), but both retained the structure of the face.

The second step (labeled “Mix” in Fig. 1) used these images to create face-like images of specific degrees of symmetry. To do this, we created an image by drawing check pairs from two of the three binarized images just constructed. In the example shown, 87.5% of the check pairs of the symmetric image were mixed with 12.5% of the antisymmetric image, resulting in an image that was 75% symmetric (C = 0.75). Choosing other proportions of check pairs from images derived from the three binarization methods allowed us to achieve any level of symmetry; we did this to create images with symmetry levels ranging from C = 0.25 (62.5% of the pairs matched) to C = 1 (all of the pairs matched). Although in principle this approach can yield images that are primarily antisymmetric (by using a mixture that is dominated by the antisymmetric image), we did not do this; all images created at this step had a symmetry value C in the range 0 to 1.

In the third and final step (bottom right of Fig. 1), we manipulated the images so that face-likeness was altered, but symmetry was maintained. To do this, we again chose yoked pairs of checks in bilaterally corresponding positions and flipped the contrast of both checks. Since checks were flipped in pairs, this did not influence the level of symmetry, but it did result in distortion of the image. To control this distortion, these pairs were selected one of two ways. The first way was to choose pairs that were close to gray in the original photograph. Flipping the contrast of these checks introduced minimal additional distortion, since black and white were approximately equidistant from their original luminances. The second way was to choose pairs that were close to black or white in the original photograph. Flipping the contrast of these resulted in maximal distortion, since the flips would change checks that nearly matched the original, to checks that mismatched substantially.

In all, we used 29 mixtures of the three binarization methods and the two pair-flip methods, detailed in Table 3. These 29 “processing pathways” were selected from more than 70 candidates, following informal screening by two of the authors (M.C., J.V.) to ensure that the gamuts of symmetries and face-likenesses were covered. Each of these 29 processing pathways was applied to each of the 394 original photographs, yielding a stimulus set consisting of 11,426 ( = 394*29) images.

Table 3.

Details of generation of face image library. Each row of the table describes a single processing pathway, consisting of a mixture of binarization methods, followed by a mixture of pair flips. For further details, see Fig. 1 and the Appendix

Processing Pathways for Stimulus Creation
Processing Pathway	Fraction of Checks Subject of Each Binarization Method			Fraction of Checks Subject to Pair Flips		C
	Method 1: Independent	Method 2: Symmetric	Method 3: Antisymmetric	Low-Distortion Pair Flips	High-Distortion Pair Flips
1	0.500	0.500	0.000	0.0	0.0	depends on face
2	0.300	0.700	0.000	0.0	0.0	depends on face
3	0.100	0.900	0.000	0.0	0.0	depends on face
4	0.000	1.000	0.000	0.0	0.0	depends on face
5	0.500	0.500	0.000	0.2	0.0	depends on face
6	0.300	0.700	0.000	0.2	0.0	depends on face
7	0.100	0.900	0.000	0.2	0.0	depends on face
8	0.000	1.000	0.000	0.2	0.0	depends on face
9	0.000	0.500	0.500	0.0	0.0	0.25
10	0.000	0.700	0.300	0.0	0.0	0.55
11	0.000	0.825	0.175	0.0	0.0	0.75
12	0.000	0.875	0.125	0.0	0.0	0.80
13	0.000	0.925	0.075	0.0	0.0	0.90
14	0.000	0.975	0.025	0.0	0.0	0.95
15	0.000	1.000	0.000	0.0	0.0	1.00
16	0.000	0.500	0.500	0.2	0.0	0.25
17	0.000	0.700	0.300	0.2	0.0	0.55
18	0.000	0.825	0.175	0.2	0.0	0.75
19	0.000	0.875	0.125	0.2	0.0	0.80
20	0.000	0.925	0.075	0.2	0.0	0.90
21	0.000	0.975	0.025	0.2	0.0	0.95
22	0.000	1.000	0.000	0.2	0.0	1.00
23	0.000	0.500	0.500	0.0	0.2	0.25
24	0.000	0.700	0.300	0.0	0.2	0.55
25	0.000	0.825	0.175	0.0	0.2	0.75
26	0.000	0.875	0.125	0.0	0.2	0.80
27	0.000	0.925	0.075	0.0	0.2	0.90
28	0.000	0.975	0.025	0.0	0.2	0.95
29	0.000	1.000	0.000	0.0	0.2	1.00

Figure 9 shows the joint distribution of the symmetry index C and the face rating F (see the Method section for how face-likeness was quantified). Each octagon shows the range of values of C and face ratings for one of the aforementioned processing pathways. Two points are worth emphasizing. First, the library as a whole covers a range of face ratings and symmetries and allows for selection of stimuli in which these attributes vary independently. Second, the level of symmetry and face-likeness is primarily determined by our manipulations, not by the characteristics of the original photographs. Figure 9 shows this because each original image—including faces that were frontally viewed and those that were not—contributed a point in all 29 octagons.

Fig. 9.

The distribution of symmetry index and face-likeness across the image library, grouped by the processing streams shown in Table 3. Each octagon indicates the distribution of symmetry level and face-likeness of all 394 images that were processed according to one processing stream. The extent of each octagon indicates the interquartile range of the symmetry index (C) and the face rating (F). The points indicate the median values represented by each octagon. A minimum nonzero width (0.02) was used to ensure visibility of overlapping octagons. Note that in either dimension (symmetry and face rating), the scatter of the octagons is far larger than the extent of any single octagon. That is, the effect of our manipulations on symmetry and face ratings was much larger than the variability present in the original images

Finally, we mention why it is possible to create images that have a high degree of face-likeness and a low degree of symmetry, even in frontal view. Two factors contribute to this. First, some aspects of the face, such as hairline, can be highly asymmetric, even in frontal view, and still convey a very face-like appearance. Second, some paired parts of the photographic image differ sufficiently in the original grayscale so that when it is binarized at the median, one is mapped to black, and one is mapped to white. The checks from the antisymmetric component (bottom row on the left of Fig. 1) capture these idiosyncrasies, and mixing them into the final image leads to face-like images that are frontally viewed but nevertheless asymmetric. Conversely, these same considerations allow for the construction of images that are nonfrontally viewed, but nevertheless have a high degree of symmetry.