A patient-driven adaptive prediction technique to improve personalized risk estimation for clinical decision support

Abstract

Objective

Competing tools are available online to assess the risk of developing certain conditions of interest, such as cardiovascular disease. While predictive models have been developed and validated on data from cohort studies, little attention has been paid to ensure the reliability of such predictions for individuals, which is critical for care decisions. The goal was to develop a patient-driven adaptive prediction technique to improve personalized risk estimation for clinical decision support.

Material and methods

A data-driven approach was proposed that utilizes individualized confidence intervals (CIs) to select the most ‘appropriate’ model from a pool of candidates to assess the individual patient's clinical condition. The method does not require access to the training dataset. This approach was compared with other strategies: the BEST model (the ideal model, which can only be achieved by access to data or knowledge of which population is most similar to the individual), CROSS model, and RANDOM model selection.

Results

When evaluated on clinical datasets, the approach significantly outperformed the CROSS model selection strategy in terms of discrimination (p<1e–14) and calibration (p<0.006). The method outperformed the RANDOM model selection strategy in terms of discrimination (p<1e–12), but the improvement did not achieve significance for calibration (p=0.1375).

Limitations

The CI may not always offer enough information to rank the reliability of predictions, and this evaluation was done using aggregation. If a particular individual is very different from those represented in a training set of existing models, the CI may be somewhat misleading.

Conclusion

This approach has the potential to offer more reliable predictions than those offered by other heuristics for disease risk estimation of individual patients.

Complexity in decisions involving multiple factors and variability in interpretation of data motivate the development of computerized techniques to assist humans in decision-making.^1–3 Predictive models are used in medical practice, for example, for automating the discovery of drug treatment patterns in an electronic health record,⁴ improving patient safety via automated laboratory-based adverse event grading,⁵ prioritizing the national liver transplant ‘queue’ given the severity of disease,⁶ predicting the outcome of renal transplantation,⁷ guiding the treatment of hypercholesterolemia,⁸ making prognoses for patients undergoing certain procedures,^{9 10} and estimating the success of assisted reproduction techniques.¹¹ Numerous risk assessment tools for medical decision support are available on the web^12–14 and are increasingly available for smart phones.^15–17

While many predictive models have been developed and validated on data from cohort studies, little attention has been paid to ensure the reliability of a prediction for an individual, which is critical for point-of-care decisions. Because the goal of predictive models is to estimate outcomes in new patients (who may or may not be similar to the patients used to develop the model), a critical challenge in prognostic research is to determine what evidence beyond validation is needed before practitioners can confidently apply a model to their patients.¹⁸ This is important to determine a patient's individual risk.^19–21 As each model is constructed using different features, parameters, and samples, specific models may work best for certain subgroups of individuals. For example, many calculators and charts use the Framingham model to estimate cardiovascular disease (CVD) risk.^{8 22–24} These models work well, but may underestimate the CVD risk in patients with diabetes.²⁵ Table 1 illustrates a case in which a patient can get significantly different CVD risk scores from different online risk estimation calculators. This type of inconsistency provides another motivation for selecting an appropriate model.²⁹

Table 1.

The same patient can get different risk scores from different online tools

Patient: Bob
Age, years	38
Smoker	Yes
Total cholesterol	235 mg/dl
HDL cholesterol	39 mg/dl
Treatment for HBP	Yes
…	…
Systolic blood pressure	145 mm Hg
Family history of early heart disease	Yes
Bob's cardiovascular disease risk
NHLBI risk assessment web tool26	16%
American Heart Association online27	25%
Cleveland Clinic28	20%

HBP, high blood pressure; HDL, high-density lipoprotein; NHLBI, National Heart, Lung, and Blood Institute.

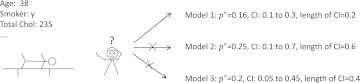
In order to obtain a patient-specific recommendation at the point of care, it is necessary that physicians interpret the information in the context of that patient. These scenarios are related to personalized medicine, which emphasizes the customization of healthcare.^{30 31} In this research, we address the problem of selecting the most appropriate model for assessing the risk for a particular patient. We developed an algorithm for online model selection based on the CI of predictions so that clinicians can choose the model at the point of care for their patients, as illustrated in figure 1.

Figure 1.

A clinician has to decide at the point of care which model to use, given the characteristic of the patient. Note that p* is the probability estimate for this particular patient. CI is the confidence interval for this estimate, or prediction. The clinician chooses the model that produces the prediction with the narrowest CI.

Our approach is purely data driven because it adapts to any ‘appropriate’ model that is available for assessing the risk of a patient without the need for external knowledge. The ‘appropriateness’ refers to the ability of the model to generate a narrow CI for the individualized prediction. The article is organized as follows: the following paragraphs present related work, the Methods section introduces the details of the proposed method, the Results section presents results on simulated and clinically related datasets, and the Discussion section discusses advantages and limitations.

A possible approach to determining the best model for a patient is to compare the patient with individuals in the study population used to build the model. However, it is non-trivial to gather datasets from every published study. The barriers are partly related to the laws and regulations on privacy and confidentiality.³² Therefore, we aimed at developing a new method to determine the most reliable predictive model for an individual from a candidate pool of models without requiring the availability of training datasets. Note that our motivation for selecting the appropriate model in a distributed environment is somewhat different from the one that motivates adaptive model selection. Adaptive model selection operates in a centralized environment and searches for an optimal subset of patterns from the entire training set to minimize certain loss functions.³³

The idea of data-driven model selection for medical decision support is related to dynamic switching and mixture models,³⁴ which emphasize capturing the structural changes over time to adapt a predictive model. Fox et al³⁵ proposed a method for learning and switching between an unknown number of dynamic modes with possibly varying state dimensions. Huang et al³⁶ presented a segmentation approach that divided deterministic dynamics in a higher-dimensional space into segments of patterns. Siddiqui and Medioni³⁷ developed an efficient and robust method of tracking human forearms by leveraging a state transition diagram, which adaptively selected the appropriate model for the current observation. Other methods were used in the context of wireless sensor networks in which the goal was to provide an effective way to reduce the communication effort while guaranteeing that user-specified accuracy requirements were met. For example, Le Borgne et al³⁸ suggested a lightweight, online algorithm that allowed sensor nodes to determine autonomously a statistically good performing model among a set of candidate models.

However, most of the aforementioned methods describing real-world physical systems are not directly applicable to medical decision support because they rely on physical laws that are not applicable to medical decision-making. We propose a novel data-driven method to estimate the probability of the binary outcome for each new patient. In particular, based on patient characteristics, our method chooses the model that is most appropriate (ie, the one with the narrowest CI) from a set of candidate models and uses its predicted probability.

Methods

A patient-driven adaptive prediction technique

We consider a binary classification task. Let $Y_K\in \left\{0,1\right\}$ and X_K = < x₁,…,x_i…,x_n >, respectively be the true class label (ie, the outcome of interest) and the vector of feature values (ie, the vector representing values for age, gender, blood pressure, etc) of the kth individual. Then, X_j and Y_j ($j\in (1,\dots ,m)$ correspond to the jth subpopulation of individuals from the training population (X_j ⊆ X, Y_j ⊆ Y), where X and Y denote the corpus of features and class labels in the entire population, respectively. Note that m denotes the number of models, which are trained from individual pairs of feature vectors X_j and label vectors Y_j. In particular, we can build a classifier $f_j:{\mathbf{X}}_{\mathbf{J}}\to {\mathbf{Y}}_{\mathbf{J}}$ by minimizing some loss function, for example, the hinge loss for a support vector machine^{39 40} or the Hamming distance for a model based on conditional random fields.^{41 42}

To simplify the analysis, we assume that all candidate models are constructed by minimizing the log loss function commonly used in logistic regression, as this is a model widely used and published in biomedical research,^{21 43–45} but that they use different training populations. Under this scenario, imagine a test pattern X* (ie, feature values of a new patient) that corresponds to the clinical findings and demographic information of a patient for whom we want to assess the risk of developing CVD. Given a finite number of models f₁,…,f_i,…,f_m built on different training data in previous studies, the question is which model would be most appropriate for a novel pattern X* encountered at the point of care.

Intuitively, we can think of finding out which model used a training set population that best matches X*, and choose that model built to predict the outcome of X*. In reality, however, this is often impossible because the training data are often unavailable. In addition, the computational burden of case-wise comparisons is huge, and thus may not be applicable at the point of care. Therefore, a practical solution to the problem should avoid the need for accessing the training data. Our approach, a patient-driven adaptive prediction technique (ADAPT), only needs the model coefficients (ie, the weights of a logistic regression model), and the covariance matrix of these coefficients to assess the reliability of their predictions. In particular, we pick the model f* that generates the narrowest CI for the prediction of a test pattern X*

$$\mathit{f}*(\mathit{X}*)={\text{argmin}}_{\left|\mathit{C}{\mathit{I}}_{\mathit{j}}\text{(}\mathit{X}*)\right|}{\mathit{f}}_{\mathit{j}}\text{(}\mathit{X}*),\forall j\in (1,\dots ,\mathit{m})$$ (1)

where CI_j (X*) is the CI of the jth model predicting the test pattern X*, and m is the number of available models to choose from. The CI of individual predictions are calculated using the covariance matrix of the coefficients⁴⁶ and the feature values for the individual. In well-specified models, the non-diagonal elements of this matrix should be close to zero. For a well-specified model, the CI is wider if a test pattern is closer to the decision boundary; it is narrower if a test pattern (ie, feature values of a new patient) is further away from the decision boundary. Another factor determining the width of the CI is associated with the ‘local density’ in the region where the test pattern would lie if it were part of the training set. That is, in areas with high density, the prediction is more stable, and thus it has a smaller CI. Away from high-density areas, the predictions become less stable, as there is weaker evidence to support the predictions.

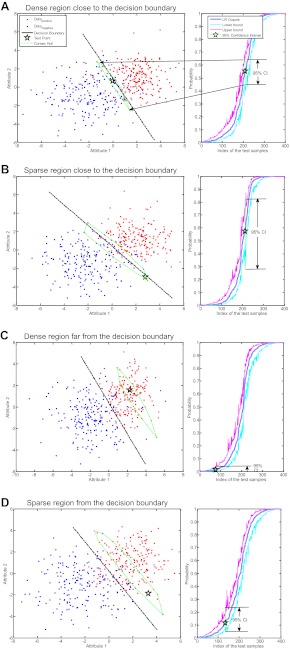
Both situations are illustrated in figure 2, where simulated data are used to build a logistic regression model. Different test patterns were arbitrarily selected to illustrate the effects of a point (1) being in a dense region (ie, several individuals with similar characteristics) versus a sparse region (ie, few individuals with similar characteristics), and (2) being close the zone of highest uncertainty, the decision boundary. We illustrate the four possible combinations, ie, a point close to the decision boundary in a dense region, close to the decision boundary in a sparse region, far from the decision boundary in a dense region, and far from the decision boundary in a sparse region. The widths of their CI are summarized in table 2. The values in the first column are smaller than those in the second column. This illustrates our first point that the CI get narrower when the test pattern is further away from the decision boundary. On the other hand, the values in the first row are smaller than those in the second row, which illustrates our second point that narrow CI are associated with dense regions. The narrowest CI (ie, 0.02) among these four arbitrarily selected illustration points corresponds to the prediction of the pattern lying in a dense region far from the decision boundary. For details, please refer to our discussion about mathematical implications of individualized CI in supplementary appendix A (available online only).

Figure 2.

Applying a logistic regression (LR) model to four test patterns (stars) in two dimensions. The dots correspond to positive and negative samples drawn from two Gaussian distributions N ((2,1), (2,0;0,2)) and N ((−2,−1), (4,0;0,3)), respectively. Each graph illustrates a test pattern, a 95% CI in the output space, and its neighborhood convex hull (ie, points that receive similar estimates by the model).

Table 2.

Width of CI of predictions of test patterns in figure 1A–D

Local density	Distance to decision boundary
	Near	Far
High	0.19	0.02
Low	0.58	0.17

Data description

We used both simulated data and a clinical dataset to demonstrate the algorithm. The simulated data were simple and designed to make it easy to understand how the algorithm works through visualization and perfect knowledge of the gold standard. The clinical data were used to illustrate the algorithm in a more realistic scenario.

Simulated data

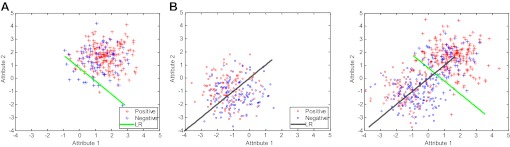
To verify the efficacy of the proposed method, we simulated two datasets (X_A, X_B) by sampling from two-dimensional Gaussian distributions, $\mathit{N}\left((1.5,1.5),\left[\begin{array}{c}1,0\\ 0,1\end{array}\right]\right)$ and, $\mathit{N}\left((-1,-1),\left[\begin{array}{c}1,0\\ 0,1\end{array}\right]\right)$, respectively. Next, we assigned class labels of these simulated data using the logistic regression model, ie, drawing random samples from the binomial distribution using probability $\mathit{p-}={\text{logit}}^{-1}\left({\omega }_0+{\displaystyle {\sum }_{i=1}^2{\omega }_i}{x}_i^l\right)$, where $x_i^l$ is the ith feature of the ith sample in one of the simulated datasets and $W={\left[{\omega }_0,{\omega }_1,{\omega }_2\right]}^{\prime }$ is the weight (ie, intercept and coefficients) parameter. In particular, we used weight vectors that are nearly orthogonal to each other (${\mathit{W}}_{\text{A}}={[-0.3,0.5,0.5]}^{\prime }$), ${\mathit{W}}_{\text{B}}={[0,-0.5,0.5]}^{\prime }$ so that class labels generated by one model would generalize poorly to the other. For both datasets, we drew 300 samples, of which 80% were used for training, and the remaining 20% were used for testing. Figure 3 illustrates an instance of both datasets, and decision boundaries of logistic regression models learned from them. One can see that the decision boundaries are close to orthogonal, which matches our simulation.

Figure 3.

Simulated datasets for model evaluation. The first and second subfigures show datasets XA, XB, and decision boundaries logistic regression (LR)(A), LR(B) learned from each dataset. We show both datasets combined, and their nearly orthogonal decision boundaries in the last figure.

We repeated the sampling process 50 times to evaluate the overall performance of our proposed method for picking the right prediction model. We compared it with two other model selection techniques. Table 3 lists different strategies for model selection. Note that BEST, which includes A2A and B2B, was meant to have the best performance (ie, expected to have the best results because data from a test set from population X are used in a model built from a training set from population X), CROSS, which includes B2A and A2B that were meant to be baselines of the CROSS model selection strategy (ie, expected to have the worst performance, because models trained on a training set from population X are tested on a sample from population Y), and RANDOM, which refers to a RANDOM model selection strategy, was meant to represent what online users might be doing (ie, they use any calculator they can find online), which is expected to have an intermediary performance between the best and worst model selection strategies. We acknowledge that the simulation data cannot serve as a ‘perfect benchmark’. The goal was to illustrate the efficacy of ADAPT in a simple and intuitive two-dimensional case. An evaluation in a more realistic dataset is certainly warranted, so we also compared those four strategies using clinical data.

Table 3.

Different strategies (BEST, CROSS, RANDOM, and ADAPT) to choose a model to predict simulated test cases

Strategies	Details
BEST
A2A	Trained on A (80%), evaluated on A (20%).
B2B	Trained on B (80%), evaluated on B (20%).
CROSS
A2B	Trained on A (80%), evaluated on B (20%).
B2A	Trained on B (80%), evaluated on A (20%).
RANDOM	Randomly selected model learned from either training set of A or B to evaluate the test cases.
ADAPT	Use our proposed method to choose a model for each of the test cases.

Clinical data

We applied our method to two clinical datasets for illustration purposes. The myocardial infarction (MI) data contain information about patients with and without MI. These patients were seen at emergency departments at two medical centers in the UK,⁴⁷ where 500 patients with chest pain were observed in Sheffield, England, and 1253 patients with the same symptoms were observed in Edinburgh, Scotland. The total number of patients is 1753, and the feature size is 48. The target is a binary variable indicating whether a patient had an MI or not.

We preprocessed those data by replacing every categorical feature by a number of binary ones to preserve the categorical information. To construct learning models, we randomly split both datasets into (80%/20%) training and test sets. Note that the proportion of the positive outcomes of training and test sets were approximately the same. We compared our proposed method, ADAPT, with other strategies, as indicated in table 4. Similar to the simulation study, E2E and S2S were meant to represent the best performing strategies, S2E and E2S represent baselines of CROSS model selection (ie, the worst performing strategy), and RANDOM refers to the RANDOM model selection strategy, similar to what we did for the simulated data.

Table 4.

Different strategies (BEST, CROSS, RANDOM, and ADAPT) to choose the model to predict test cases

Strategies	Details
BEST
E2E	Trained on Edinburgh data (80%), evaluated on Edinburgh data (20%).
S2S	Trained on Sheffield data (80%), evaluated on Sheffield data (20%).
CROSS
E2S	Trained on Edinburgh data (80%), evaluated on Sheffield data (20%).
S2E	Trained on Sheffield data (80%), evaluated on Edinburgh data (20%).
RANDOM	Pick a random model learned from either training set to evaluate a given test set.
ADAPT	Use our proposed method to choose model.

We repeated the random split 50 times, and evaluated discrimination and calibration, as explained next.

Evaluation methods

We used two measures, the area under the receiver operating characteristic curve (AUC)⁴⁸ and the Hosmer–Lemeshow goodness-of-fit test (HL test),⁴⁹ to evaluate the performance of predictive models in terms of discrimination and calibration, respectively. In particular, we used a one-tailed paired t test to compare the performance of the models through cross-validation.

Area under the receiver operating characteristic curve

The AUC measures the predictive model's ability to discriminate positive and negative cases: an AUC of 0.5 corresponds to a random assignment into one of the two categories, and an AUC of 1.0 corresponds to a perfect assignment. Predictive models used in medical decision-making vary widely between these two extremes, but most published models have AUC exceeding 0.7, and just a few have AUC over 0.9.

HL test

The HL test measures how well the model fits the data. As there is no gold standard for the probability estimate for one individual, cases are pooled into groups and the sum of probabilities in the groups is compared with the sum of positive cases in these groups using a χ² test. When the p value for the test is below 0.05, we reject the hypothesis that the model fits the data well. Note that we adopted the C version of the HL test for which equal-sized subgroups (ie, deciles in our case) are sorted by probability estimates.

Results

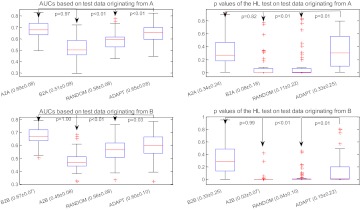
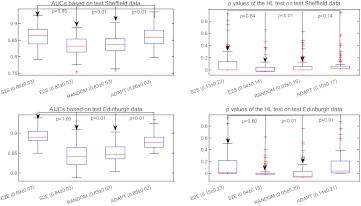
Figure 4 shows the AUC and p values of the HL test obtained by applying different model selection strategies to the simulated data (described in the Simulated data section). The strategies of comparison include the BEST strategy (ie, A2A and B2B), the CROSS strategy (ie, B2A and A2B), the RANDOM strategy, and the ADAPT strategy. There are four plots in this figure. The first two plots (ie, subfigures on the first row) correspond, respectively, to AUC and to the p values of the HL test, after applying all four strategies to the test set originating from A. The last two plots (ie, subfigures on the second row) show the results of applying the model on the test set originating from B. Our method labeled ADAPT significantly outperforms the CROSS and RANDOM model selection strategies for both indices, as indicated by the p values in the figure. As expected, the CROSS strategy (ie, B2A and A2B) performed poorly.

Figure 4.

Comparison of different strategies including BEST (A2A and B2B), CROSS (A2B and B2A), RANDOM, and ADAPT in discrimination (area under the receiver operating characteristic curve; AUC) and calibration (p value for Hosmer–Lemeshow (HL) decile-based test) using simulated data. Note that x±y in the labels of the x-axis indicates that the mean equals x, and the standard deviation equals y.

In figure 5, we illustrate the results of applying different model selection strategies to the clinical data (described in the Clinical data section). The strategies compared include BEST (ie, E2E and S2S), CROSS (ie, E2S and S2E), RANDOM, and ADAPT.

Figure 5.

Comparison of effectiveness of different strategies (ie, BEST, CROSS, RANDOM, and ADAPT) in discrimination (area under the receiver operating characteristic curve; AUC) and calibration (p value for Hosmer–Lemeshow (HL) decile-based test) for the clinical data. Note that x±y in the labels of the x-axis indicates that the mean equals x, and the SD equals y.

In the first experiment with the Sheffield data, ADAPT has higher discrimination than the CROSS strategy E2S (p<1e–14) and the RANDOM strategy (p<1e–12) based on a one-tailed paired t test. Our method also demonstrates better calibration performance than the CROSS strategy E2S (p=0.006), but it is not significantly better than the RANDOM strategy (p=0.14). Our approach demonstrated very comparable discrimination (p=0.85) and calibration (p=0.84) with the BEST strategy S2S, the ideal situation of using the same population to evaluate a test case.

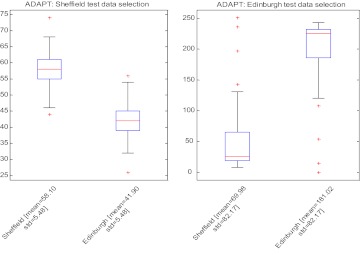
The second experiment with the Edinburgh data involves more testing samples compared with the Sheffield experiment. The AUC of our proposed method was significantly higher than both the CROSS strategy S2E (p<1e–43) and the RANDOM strategy (p<1e–33), and it was comparable to that of the BEST strategy E2E (p=1.0). The calibration of our method was better than those of two other strategies (S2E p=0.0017, RANDOM p=0.0072), and it was comparable to the BEST strategy E2E (p=0.60), the ideal scenario for testing. Figure 6 shows the distributions of models picked by ADAPT. As expected, most Sheffield test cases selected the model based on the Sheffield training data, and the equivalent result was true for the Edinburgh test cases.

Figure 6.

Distribution of model selected using ADAPT. AUC, area under the receiver operating characteristic curve; HL, Hosmer–Lemeshow test.

Discussion

We investigated challenges in selecting models to predict risks for individual patients. While many previous studies have shown good predictive accuracy for cohort studies, they did not always make clear which model would be most appropriate for an individual. Due to the real-world concerns related to privacy and confidentiality,⁵⁰ it is often difficult to access the raw data that were used to construct these predictive models. We developed ADAPT to consider the model-specific information that may be published without the accompanying training datasets. Many articles describe the coefficients and their p values, but the publication of variance of coefficients or their CI is less frequent. Even rarer is the publication of the full covariance matrices, although preprocessing to eliminate variables with high correlation makes the non-diagonal elements relatively unimportant. The matrix diagonal (ie, the variance of the parameters) contains the information that is critical for our method. We believe authors would be willing to disclose these matrix diagonals, as they do not increase the risk of subject re-identification significantly. In addition, if online calculators included the CI for a prediction (which is currently not the case), it would be trivial to ‘manually’ select the model associated with the narrowest CI for a particular prediction. Our approach automates this process and exhibits adequate discrimination and calibration, as measured by the AUC and the HL test in the prediction of risks for an individual patient. It adaptively picks the model that is most appropriate for the individual at hand given the available information.

Another advantage of ADAPT is that the approach can assess models trained differently. In practice, even for the same risk prediction task, different institutions might build their models with different features, for example, the three CVD risk models^26–28 shown in table 1 used seven, 17, and eight feature variables, respectively. The model from the American Heart Association²⁷ consists of a superset of features included in the other models (ie, National Heart, Lung, and Blood Institute²⁶ and Cleveland Clinic).²⁸ Such differences, however, would not be an obstacle for ADAPT, as our model always evaluates ‘appropriateness’ in output space, which is one-dimensional. As long as a comprehensive set of patient feature values is available (ie, 17 in the case of CVD), we can calculate individualized CI for each of the models listed above without determining how many features were used to train the model at each hospital/institution. Evidently, if just certain feature values are available for a given patient, only certain models will generate a prediction. The model resulting in the narrowest individualized CI for the prediction would be the one selected, such as the one conducted in our study (see supplementary appendix B, available online only). Regarding evaluation matrices, although we believe AUC and HL tests are general evaluation standards that are used by many, we noticed that models could be evaluated using other evaluation indices, which we would like to explore in our future work.

Despite results showing performance advantages of ADAPT over other strategies in terms of discrimination and calibration using simulated data, our simulation study has important limitations. Orthogonal training patterns are not common in real-world data: we used this two-dimensional simulated data mainly for illustration purposes. Although our preliminary results from the application of ADAPT to the MI data confirm the performance advantage of ADAPT over CROSS model adaption and RANDOM model selection strategies, these datasets were relatively small. In the future, we plan to use larger datasets that are increasingly being collected at healthcare institutions for predictive model building and validation. Additional concerns relate to the fact that CI may not always offer enough information to rank the reliability of predictions, and our evaluation was done on the aggregate. If a particular individual is very different from those represented in the training set of existing models, the CI may be somewhat misleading. Indeed, the problem of assessing the best result for the particular individual at hand is still an open question, as the individual gold standard for the prediction is not available (ie, the observation is binary—the patients develop or do not develop CVD, but the true gold standard for an individual prediction is the true probability for the patient to develop the condition, which is not known). In the future, we would like to work towards the development of better proxies for the gold standard than the ones currently available, investigate data-driven model selection for models constructed using larger datasets across multiple sites, and extend our framework to include kernel methods.

In summary, this article describes a new method for selecting one among several competing models for a given individual, and our results show that there are positive effects on discriminatory performance. All experiments described in this article were conducted in a laboratory environment. The evaluation of the method as a part of a clinical decision support system is certainly warranted to verify its performance in a clinical environment.