SURFACE-BASED TBM BOOSTS POWER TO DETECT DISEASE EFFECTS ON THE BRAIN: AN N=804 ADNI STUDY

Abstract

Computational anatomy methods are now widely used in clinical neuroimaging to map the profile of disease effects on the brain and its clinical correlates. In Alzheimer’s disease (AD), many research groups have modeled localized changes in hippocampal and lateral ventricular surfaces, to provide candidate biomarkers of disease progression for drug trials. We combined the power of parametric surface modeling and tensor-based morphometry to study hippocampal differences associated with AD and mild cognitive impairment (MCI) in 490 subjects (97 AD, 245 MCI, 148 controls) and ventricular differences in 804 subjects scanned as part of the Alzheimer’s Disease Neuroimaging Initiative (ADNI; 184 AD, 391 MCI, 229 controls). We aimed to show that a new multivariate surface statistic based on multivariate tensor-based morphometry (mTBM) and radial distance provides a more powerful way to detect localized anatomical differences than conventional surface-based analysis. In our experiments, we studied correlations between hippocampal atrophy and ventricular enlargement and clinical measures and cerebrospinal fluid biomarkers. The new multivariate statistics gave better effect sizes for detecting morphometric differences, relative to other statistics including radial distance, analysis of the surface tensor and the Jacobian determinant. In empirical tests using false discovery rate curves, smaller sample sizes were needed to detect associations with diagnosis. The analysis pipeline is generic and automated. It may be applied to analyze other brain subcortical structures including the caudate nucleus and putamen. This publically available software may boost power for morphometric studies of subcortical structures in the brain.

1. Introduction

Alzheimer’s disease (AD) presents a severe and growing public health crisis. The disease doubles in frequency every 5 years after age 60, afflicting 1% of those aged 60 to 64, and 30–40% of those over 85. A number of promising treatments of AD are being investigated (Forette et al., 2002). As new treatments are developed, imaging techniques are being proposed to track, in detail, whether the disease is modified by interventions (Jack et al., 2003; Fox et al., 2005; Reiman, 2007; Thompson et al., 2007; Frisoni et al., 2010). MRI-based measures of atrophy in several structures, including the whole brain (Fox et al., 1999), entorhinal cortex (Cardenas et al., 2009), hippocampus (Jack et al., 2003; Thompson et al., 2004a; Morra et al., 2009a; Qiu et al., 2009; Apostolova et al., 2010; den Heijer et al., 2010; Wolz et al., 2010), caudate volumes (Madsen et al., 2010), and temporal lobe volumes (Hua et al., 2010), as well as ventricular enlargement (Jack et al., 2003; Thompson et al., 2004a; Chou et al., 2010), correlate closely with differences in cognitive performance, supporting their validity as markers of disease. Of all the MRI markers of AD, hippocampal atrophy assessed on high-resolution T1-weighted MRI is perhaps the best established and validated. In addition, ventricular enlargement is a highly reproducible measure of disease progression, owing to the high contrast between the cerebrospinal fluid (CSF) and the surrounding brain tissue on T1-weighted images. As a result, a key research goal is to develop valid and efficient morphometric measures that correlate with cognitive assessments and biological markers of the disease by automatically analyzing structural MR images of brain substructures.

Many studies of subcortical structures in AD have used volume as the outcome measure (Jack et al., 2003; Jack et al., 2004; Ridha et al., 2008; Holland et al., 2009; den Heijer et al., 2010; Dewey et al., 2010; Wolz et al., 2010), but some recent studies (Thompson et al., 2004a; Styner et al., 2005; Apostolova et al., 2008; Ferrarini et al., 2008b; Qiu et al., 2008; Chou et al., 2009; Morra et al., 2009b; Qiu et al., 2009; Apostolova et al., 2010; Chou et al., 2010; Madsen et al., 2010; Qiu et al., 2010) have demonstrated that surface-based analysis may offer some advantages over volume measures. Surface-based methods have been applied to study hippocampal subfield atrophy; they can also produce detailed maps of point-wise correlations between atrophy and cognitive assessments or biological markers of disease. They provide promising measures of disease burden for clinical trials.

In surface-based brain imaging analysis, a common approach to register brain surfaces across subjects is to compute an intermediate mapping to a canonical space, such as a sphere (Dale et al., 1999; Fischl et al., 1999; Chung et al., 2005; Styner et al., 2005; Tosun and Prince, 2005; Wang et al., 2005b; Carmichael et al., 2007b; Gutman et al., 2008; Tosun and Prince, 2008; Yeo et al., 2008). However, because of the complex branching topology of some subcortical structures, it generally requires substantial distortions to map these structures to a sphere (Wang et al., 2010d). In Qiu and Miller (2008) and Qiu et al. (2008; 2009; 2010), the large deformation diffeomorphic metric mapping (LDDMM) method was used to generate models of substructure shapes based on template shapes that were mapped onto segmented subcortical volumes. The resulting deformation maps encoded the local shape variation of each subject relative to the template. Another common practice is to register subcortical surfaces with parametric meshes that are either imposed on manually traced boundaries (Thompson et al., 2004a) or automatically segmented (Chou et al., 2009; Morra et al., 2009b). Recently, we introduced a parametric surface modeling approach using concepts from exterior calculus that provided a rigorous framework to study subcortical surfaces (Wang et al., 2010d). Our method has been successfully applied to study HIV/AIDS (Wang et al., 2010d) and AD (Wang et al., 2010b; Wang et al., 2010c).

One important question for substructural surface analysis is which surface-based statistics carry the most useful morphometric information to detect disease effects. Shape statistics, such as radial distance (distances from the medial core to each surface point) (Styner et al., 2004; Thompson et al., 2004a; Carmichael et al., 2006; Carmichael et al., 2007b, a; Carmichael et al., 2007c; Thompson et al., 2007; Apostolova et al., 2008; Chou et al., 2008; Chou et al., 2009; Morra et al., 2009b; Apostolova et al., 2010; Chou et al., 2010; Morra et al., 2010), spherical harmonic coefficients (Styner et al., 2005; Gutman et al., 2009), local area differences (related to the determinant of Jacobian matrix) (Woods, 2003; Ferrarini et al., 2006; Ferrarini et al., 2007; Ferrarini et al., 2008a; Ferrarini et al., 2008b; Qiu et al., 2010), and Gaussian random fields of vectors (Bansal et al., 2007) have been applied in substructure shape analyses. Surface tensor-based morphometry (TBM) (Davatzikos et al., 1996; Thompson et al., 2000; Woods, 2003; Chung et al., 2008) is an intrinsic surface statistic that examines spatial derivatives of the deformation maps that register brains to common template and construct morphological tensor maps. In our recent studies (Wang et al., 2008; Wang et al., 2009; Wang et al., 2010d), surface multivariate TBM (mTBM) was shown to be more sensitive for detecting group differences than other standard statistics.

A local volume change, in a structure such as the ventricles, may be decomposed in terms of the surface area and radial expansion of the object. All smooth deformations may be divided into two components; one that is within the surfaces (described by Log-Euclidean metrics on the surface metric tensor) and another along the surface normal direction. In computational anatomy research, existing surface-based methods have been developed to capture all possible smooth transformations of the local surface geometry (Chung et al., 2003; Thompson et al., 2004a; Chung et al., 2008). As reported in this paper and in our prior work (Leporé et al., 2008; Wang et al., 2010d), statistical power was significantly improved after we considered components of deformations in multiple directions. Intuitively, radial distance and mTBM are complementary, as radial distance describes deformations roughly along the surface normal direction, while mTBM can detect deformations within surfaces, including differences in the surface metric tensor induced by the particular surface parameterization. So we propose that a combination of radial distance and mTBM will offer a more complete set of surface statistics for subcortical morphometry study and hypothesize that mTBM may boost statistical power to detect disease effects in subcortical structure research.

In this paper, we combine parametric surface modeling and tensor-based morphometry to study hippocampal differences associated with AD and mild cognitive impairment (MCI) in 490 subjects (97 AD, 245 MCI, 148 controls) and ventricular differences in 804 subjects scanned as part of the Alzheimer’s Disease Neuroimaging Initiative (ADNI; 184 AD, 391 MCI, 229 controls). In the first study, our proposed multivariate statistics are used to detect areas of statistical significant deformation associated with clinical measures. For comparison, we also compare the new statistics with other popular subcortical surface statistics including mTBM (Wang et al., 2010d), radial distance (Pizer et al., 1999; Thompson et al., 2004a) and TBM (Davatzikos et al., 1996; Woods, 2003; Chung et al., 2008).

Cerebrospinal fluid (CSF)-derived biomarkers of AD pathology, including levels of tau protein (Tau), 181-phosphorylated tau protein (pTau181p), beta amyloid (Aβ_1-42), Tau/Aβ_1-42 and pTau_181p/Aβ_1-42 ratio values, are accepted measures of known aspects of AD pathology, although they are highly invasive, requiring a lumbar puncture to obtain a sample of CSF. There is increasing evidence that neuroimaging may provide accurate, reproducible measures of brain atrophy that correlate, to some extent, with more invasive measures of the underlying pathology (Whitwell et al., 2008; Chou et al., 2009; Henneman et al., 2009; Chou et al., 2010; Vemuri et al., 2010). By assessing correlations between CSF biomarkers and brain measures from structural MRI, we are able to further validate the utility of MRI measurements as non-invasive measures of pathology in AD, even in the pre-clinical stages. In a second experiment, we set out to test whether our new statistics can help detect these correlations. In addition, we checked the statistical power of the new statistics by gradually reducing sample sizes required to detect various associations.

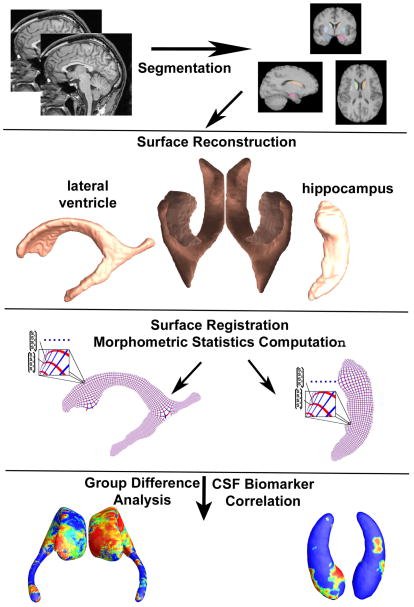
Fig. 1 gives an overview of our multivariate subcortical structure morphometry system. We used the segmented images from our prior work on the hippocampus (Morra et al., 2009b) and lateral ventricles (Chou et al., 2010). We then built subcortical structure surface models using a level-set based topology preserving method (Han et al., 2003). We computed surface registrations using the canonical conformal holomorphic one-form method (Wang et al., 2009; Wang et al., 2010d). A multivariate morphometry feature vector was then computed at each surface point and used to compute statistical maps of group differences and correlations with CSF biomarkers and clinical assessments.

Fig. 1.

A flow chart of the steps in our multivariate statistical analysis of brain morphometry. In our system, the subcortical structures are segmented as in prior work (Morra et al., 2009b; Chou et al., 2010). We then reconstruct the surfaces and compute conformal coordinates for registration. The computed statistics are used for group difference analysis and analysis of correlation with CSF biomarkers.

2. Subjects and Methods

2.1 Subjects

The Alzheimer’s Disease Neuroimaging Initiative (ADNI; (Mueller et al., 2005a; Mueller et al., 2005b; Jack et al., 2008; Miller, 2009), loni.ucla.edu/ADNI) is a large multi-center longitudinal MRI and FDG-PET (fluorodeoxyglucose position emission tomorgraphy) study of 800 adults, ages 55 to 90, including 200 elderly controls, 400 MCI subjects, and 200 AD patients. The primary goal of ADNI has been to test whether serial MRI, PET, other biological markers, and clinical and neuropsychological assessments acquired in a multi site manner mirroring enrollment methods used in clinical trials, can replicate results from smaller single site studies measuring the progression of MCI and early AD.

In this study, we used the 804 available baseline MRI scans, including 184 AD patients (age: 76.1 ± 7.6 years), 391 amnestic MCI subjects (75.0 ± 7.3 years), and 229 healthy elderly controls (76.0 ± 5.0 years). All subjects underwent thorough clinical and cognitive assessment, including the Mini-Mental State Examination (MMSE) score (Folstein et al., 1975), Clinical Dementia Rating (CDR) (Berg, 1988) and Delayed Logical Memory Test (Wechsler, 1987), at the time of scan acquisition.

Several measures were obtained from the CSF, including levels of beta amyloid 1–42 (Aβ_1-42), tau protein (Tau), phosphorylated-tau protein 181 (pTau_181p), the tau to Aβ_1-42 ratio (Tau/Aβ_1-42), and p-tau to Aβ_1-42 ratio (pTau_181p/Aβ_1-42). CSF is in direct contact with the brain and thus may reflect brain-associated biochemical events better than any other biological fluid. CSF Aβ_1-42, Tau and pTau_181p have been linked to AD-associated neuropathological changes, and they are the most widely studied biomarkers for AD. CSF Aβ_1-42 levels are consistently lower in AD (Motter et al., 1995), and can distinguish patients with mild AD from healthy controls with reasonable accuracy (Blennow and Hampel, 2003).

2.2 Image acquisition and preprocessing

We analyzed baseline T1-weighted MRI scans from the ADNI dataset (http://www.loni.ucla.edu/ADNI). All T1-weighted images were automatically skull-stripped using the Brain Suite Extraction software (Shattuck and Leahy, 2002), and subsequently manually edited to correct for any imperfections in the automatic segmentation. These images were then spatially normalized to the ICBM space with a 9-parameter (3 translations, 3 rotations and 3-scales) linear transformation using Minctracc algorithm (Collins et al., 1994) for the correction of head tilt and alignment. To equalize image intensities across subjects, registered scans were also histogram-matched. We extracted surface models of the hippocampus using our adaptive boosting method (N=490; Morra et al. (2009b)). We also created surface mesh models of the lateral ventricles using our multi-atlas fluid image alignment (MAFIA) method that combines multiple fluid registrations to boost accuracy (N=804; Chou et al. (2010)).

Once we obtained the binary segmentation, we used a topology-preserving level-set method (Han et al., 2003) to build genus-zero surface models. Based on that, the marching cubes algorithm (Lorensen and Cline, 1987) was applied to obtain triangular surface meshes. To increase the signal-to-noise ratio, we applied a surface-based smoothing method to all surface meshes. Our surface-based smoothing method consisted of two steps, mesh simplification using “progressive meshes” (Hoppe, 1996) and mesh refinement by Catmull-Clark subdivision surfaces (Catmull and Clark, 1998). By applying a few iterations of mesh simplification and subdivision operations consistently to all surfaces, we obtained relatively smooth but accurate surfaces that are suitable for computing derivative maps. The derivative map used in surface-based TBM is based on a discrete approximation and is somewhat affected by the smoothness of surface. As such, these surface fairing or surface-based smoothing steps are helpful, to improve the stability of the estimation.

2.3 Hippocampal and Lateral Ventricular Surface Registration

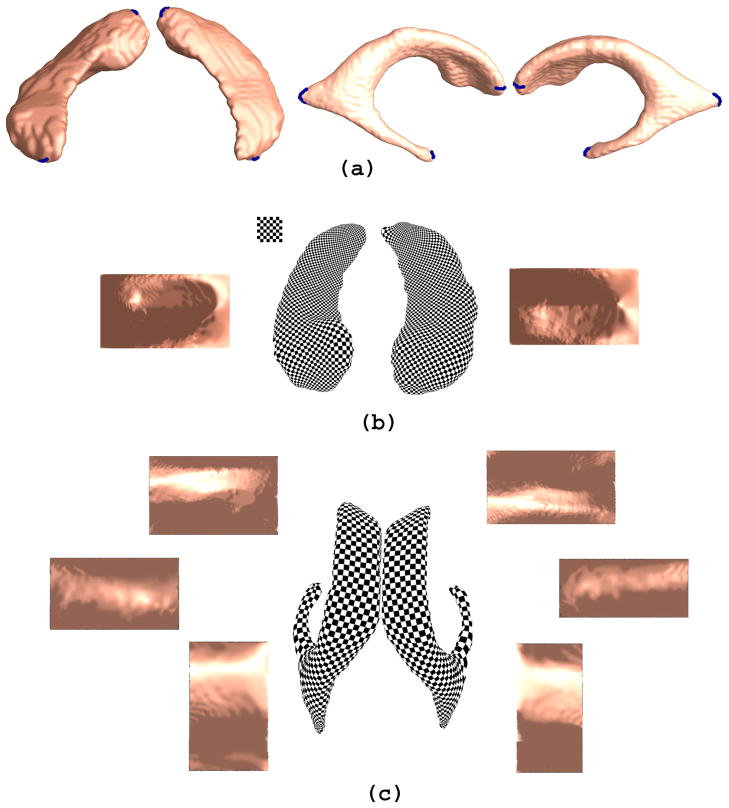
A key barrier for subcortical structure surface parameterization is the complex topology, e.g. “multiple-arm” structure of the lateral ventricles. Using a method based on holomorphic differentials, we induced conformal grids on these surfaces (Wang et al., 2007; Wang et al., 2009; Wang et al., 2010d). The computation is intrinsic and efficient. Specifically, we left two holes at the front and back of the hippocampus, representing its anterior junction with the amygdala and its posterior limit as it turns into the white matter of the fornix (as shown in Fig. 2(a)). The hippocampus was then represented as a genus zero surface with two open boundaries, i.e., a cylinder, and was conformally mapped to a rectangle (Fig. 2(b)). To model the lateral ventricular surface, we automatically located and introduced three cuts, based on the topology of the lateral ventricles, in which several horns are joined together at the ventricular “atrium” or “trigone” (as shown in Fig. 2(a)). With the holomorphic flow segmentation method (Wang et al., 2007), each lateral ventricular surface was automatically partitioned into 3 pieces (Fig. 2(c)). These three pieces are roughly three horns of the lateral ventricle: anterior horn, posterior horn and inferior horn. The surface segmentation was done by tracing curves that go through the zero point and have equal parameter coordinates (Wang et al., 2007). Although surface geometry is widely variable across subjects, these zero point locations are stable and intrinsically determined by the surface conformal structures. The resulting surface partitions are very robust and stable. We registered the hippocampal and lateral ventricular surfaces across subjects using constrained harmonic maps (Wang et al., 2009; Wang et al., 2010d). The constrained harmonic map can be computed as follows.

Fig. 2.

Holomorphic one-forms are used to induce a conformal parameterization on hippocampal and lateral ventricular surfaces. The checkerboard image on the parameter domain is shown on the top left corner of (b). The shading effect on the parameter space is generated by rendering the original 3D surface with the surface normal directions on each point. In (a), boundaries generated in the topology optimization step are labeled in blue color. In (b), each side of the hippocampal surface is conformally mapped to a rectangle in the parameter domain. In (a), based on its conformal parameterization, each side of the lateral ventricular surfaces is automatically divided into three pieces. There are three horns of the lateral ventricle per hemisphere: the anterior horn, posterior horn and inferior horn. After the separation, each horn is conformally mapped to a rectangle in the parameter domain. The parameterization results are used for surface registration and morphometric analysis.

Given two surfaces and S₁ and S₂, whose conformal parameterizations are τ₁: S₁ → ℜ² and τ₂: S₂ → ℜ², we want to compute a map φ: S₁ → S₂. Instead of directly computing φ, we can easily find a harmonic map between the parameter domains. We look for a harmonic map, τ: ℜ² → ℜ², such that

$$\tau \circ {\tau }_1(S_1)={\tau }_2(S_2),\tau \circ {\tau }_1(\partial S_1)={\tau }_2(\partial S_2),\mathrm{\Delta }\tau =0.$$

Then the map φ may be obtained by $\phi ={\tau }_1\circ \tau \circ {\tau }_2^{-1}$. Since τ is a harmonic map, and τ₁ and τ₂ are conformal maps, the resulting φ is a harmonic map. For landmark curves need to be matched, such as the boundaries of each component of the ventricle or hippocampus, we guarantee the matching of both ends of the curves. We also match the rest of the curves in 3D based on unit speed parameterizations of both curves.

2.4 Multivariate Surface Morphometry Statistics

Suppose ø: S₁→S₂ is a map from S₁ to S₂, the derivative map of ø is the linear map between the tangent spaces, dø: TM(p)→TM(ø(p)). In practice, smooth surfaces are usually approximated by triangle meshes. The derivative map dø is approximated by the linear map from one face [v₁, v₂, v₃] to another one [w₁, w₂, w₃]. Let J be the discrete derivative map from a face on anatomical surface to a face on the parameter domain. Using v_i, w_i, i=1, 2, 3, to represent the 3D position of points v_i, w_i, i=1, 2, 3, the derivative map can be computed by

$$J=[w_3-w_1,w_2-w_1]{[v_3-v_1,v_2-v_1]}^{-1}.$$

We define the deformation tensor as S=(J^TJ)^1/2 (Wang et al., 2008; Wang et al., 2010d). Our surface multivariate tensor-based morphometry (mTBM) statistics considered a new family of metrics, the “Log-Euclidean metrics” (Arsigny et al., 2006) of S so that the transformed values form a vector space, and statistical parameters can be computed easily using the standard formulae for Euclidean spaces (Leporé et al., 2008; Wang et al., 2010d). Our parametric surfaces provide a natural framework to compute mTBM. Our prior results (Wang et al., 2009; Wang et al., 2010d) showed that applying mTBM together with holomorphic differentials and surface fluid registration led to improved signal detection power relative to more standard Jacobian matrix statistics (Wang et al., 2010c; Wang et al., 2010d).

Subcortical structure surfaces usually do not have strong curvature contrasts, but most of them partially have a tube-like shape. The atrophy and enlargement of subcortical structures directly affect the distance from each surface point to its medial core (analogous to the center line in a tube). This distance - the radial distance - describes morphometric changes mainly along the surface normal direction. Many subcortical studies have used this statistic (Pizer et al., 1999; Bansal et al., 2000; Gerig et al., 2001; Thompson et al., 2004a; Apostolova et al., 2007; Morra et al., 2009b; Yushkevich, 2009; Chou et al., 2010). On the other hand, the mTBM captures deformations such as rotation, dilation, and shear with surfaces that perpendicular to the surface normal direction. So these two statistics are complementary to each other. To improve morphometric analysis, it is crucial to capture subtle differences along all possible directions. So we propose a new multivariate statistic consisting of both statistics: the surface metric tensor (Leporé et al., 2008; Wang et al., 2010d) and radial distance (Pizer et al., 1999; Thompson et al., 2004a). Considering a subcortical surface with a conformal parameterization, we defined the radial distance as the distance from each parametric surface point to the center of 3D positions of the iso-u curves in the parameter domain; e.g., in Fig. 1, the red curves are the selected iso-u curves on ventricular surface and hippocampal surface. With a conformal surface parameterization, the computation of radial distance is robust and efficient.

When we say that mTBM can assess regional differences in rotation, dilation and shearing, we are referring to computed the deformations within the surfaces, that relate the geometry of each individual to the mean shape. We do not mean that mTBM is sensitive to the global affine transforms that reflect the overall scale of the brain, as these discounted by the preprocessing. In the global normalization step, a 9-parameter transform is applied to match the overall size of the brain to a standard brain template. This discounts major inter-subject variations in brain scale, which, like head size and height, are removed to make it easier to detect more regional effects of disease on anatomy. After this normalization is applied, our surface-based analysis will still detect any scaling, shearing or rotation of the structure that remains after the global normalization has been applied. If a disease were to cause the ventricles to be increased in size relative to the overall scale of the brain, mTBM would still pick up this effect, as it would remain after the global anatomical normalization. If a structure was sheared in a way that was still evident after global normalization, then it would still be picked up by the mTBM analysis. In terms of rotation, the types of rotation picked up by mTBM are local rotations of the surface, such as torquing effects, that remain after the overall global normalization of the brain.

2.5 Statistical Maps and Analysis

A “Log-Euclidean metric” (Arsigny et al., 2006) on the set of deformation tensors, S, is computed as the matrix logarithm, log(S). Since the deformation tensor, S, is a positive definite matrix, the first 3 of the 4 vector elements, analyzed in mTBM, are the logarithm of the deformation matrix, S. We define the new multivariate surface morphometry statistic as a 4 × 1 feature vector consisting of the logged deformation tensor (3 × 1) and the radial distance (a scalar). Of course, it would be possible to consider the surface tensor only and restrict the test to assess the surface metric only, if needed. We applied the Hotelling’s T² test (Hotelling, 1931) on sets of values in deformation feature space to study the statistical group difference (Leporé et al., 2008; Wang et al., 2010d). Given two groups of 4-dimentional vectors U_i, i=1,…,p, V_j, j=1,…,q, we use the Mahalanobis distance M to measure the difference between the mean vectors of two different groups of subjects,

$$M=(\overline{U}-\overline{V}){\mathrm{\sum }}^{-1}(\overline{U}-\overline{V})$$

where Ū and V̄ are the means of the two groups and Σ is the combined covariance matrix of the two groups. We ran a permutation test with 10000 random assignments of subjects to groups to estimate the statistical significance of the areas with group differences in surface morphometry. The covariate (group membership) was permuted 10000 times. The probability was estimated as the ratio of the Mahalanobis distance for a random assignment larger than the group Mahalanobis distance with the true group membership. The probability was later color coded on each surface point as the statistical p-map of group difference.

We applied multiple linear regression (Casella and Berger, 1990) to study statistical shape correlation with CSF biomarkers. The CSF biomarkers were used as the predictor and the feature vectors as the outcome variable. We estimated the p value of the F statistic to build the p-map for these correlations.

All group difference p-maps and correlation p-maps were corrected for multiple comparisons using the widely-used false discovery rate method (FDR) (Benjamini and Hochberg, 1995). The FDR method decides whether a threshold can be assigned to the statistical map (of correlations) that keeps the expected false discovery rate below 5% (i.e., no more than 5% of the voxels are false positive findings). This threshold, the critical p value, is based on the expected proportion of voxels with statistics exceeding any given threshold under the null hypothesis (Benjamini and Hochberg, 1995). It is the highest threshold p value that controls the FDR at the given threshold, e.g., 5%.

To rank which clinical measures or CSF biomarkers were most strongly associated with hippocampal and ventricular morphology, we created cumulative distribution function (CDF) plots of the resulting uncorrected p-values (as in a conventional false discovery rate analysis). The critical p value, which is the highest non-zero point at which the CDF plot intersects the y = 20x line, represents the highest statistical threshold (if there is one) that can be applied to the data, for which at most 5% false positives are expected in the map. Use of the y = 20x line is related to the fact that significance is declared when the volume of suprathreshold statistics is more than 20 times that expected under the null hypothesis. If there is no such intersection point (other than the origin), there is no evidence to reject the null hypothesis. Our empirical CDFs of p-values are the flip of the more common FDR PP plot; steeper CDFs show stronger effect sizes. We have used this procedure to study statistical maps in several prior papers (Hua et al., 2008; Morra et al., 2009a; Chou et al., 2010).

3. RESULTS

3.1 Linking Hippocampal and Lateral Ventricular Morphometry and Clinical Characteristics

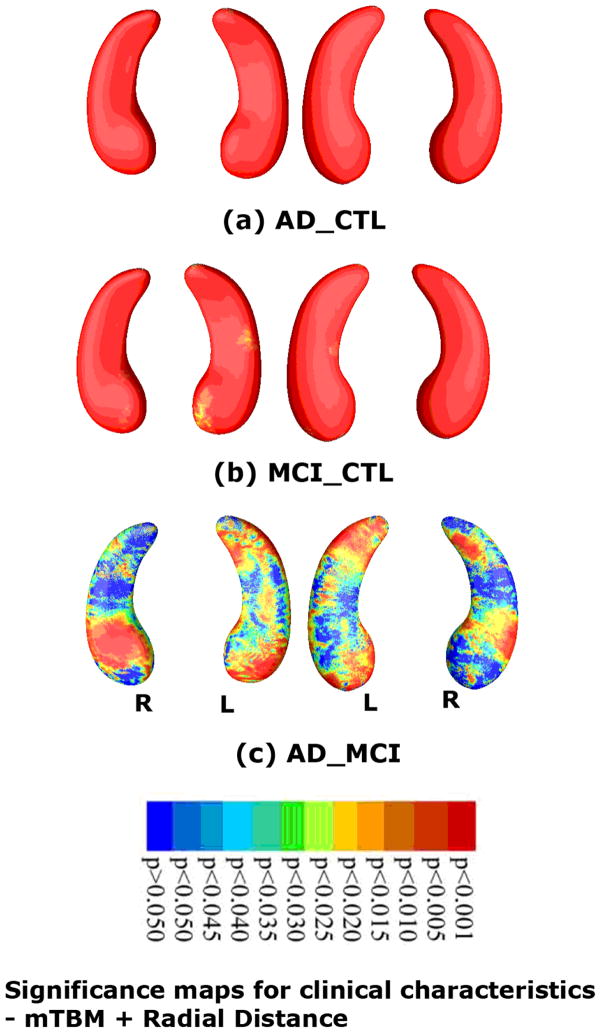
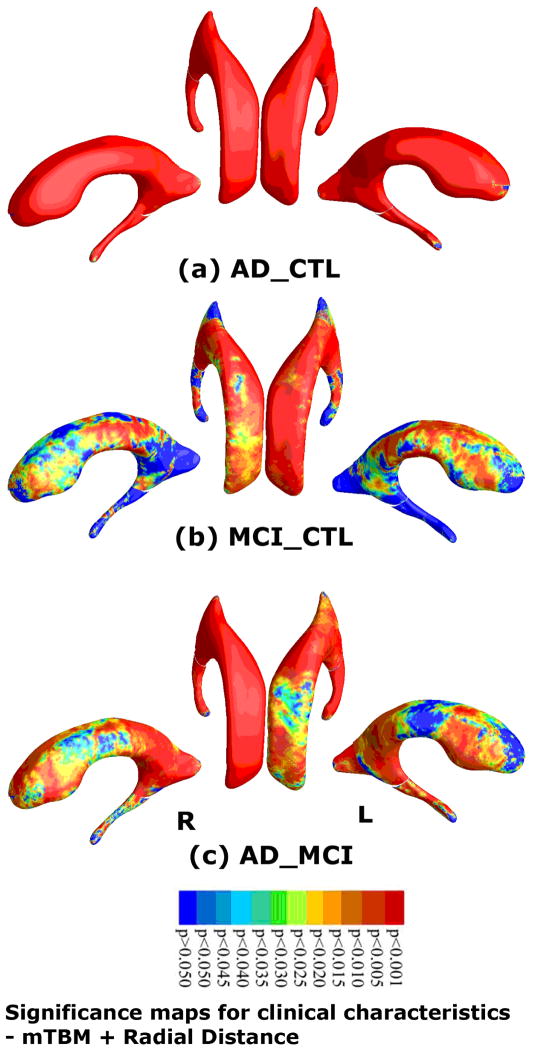
At each surface point, was associations were assessed between multivariate statistics and clinical measures at baseline. Our method picked up strong group differences in both hippocampal atrophy and ventricular enlargement between diagnostic groups. Fig. 3 shows statistical maps of hippocampal atrophy in AD vs controls (with critical p value: 0.0494), MCI vs controls (critical p value: 0.0489), and AD vs MCI (critical p value: 0.0175). Fig. 4 shows a statistical map of ventricular enlargement in AD vs controls (critical p value: 0.0494), MCI vs controls (critical p value: 0.0319), and AD vs MCI (critical p value: 0.0486).

Fig. 3.

Statistical p-map results with the new multivariate statistics (mTBM (Wang et al., 2010d) and radial distance (Thompson et al., 2004a)) on hippocampal surfaces show group differences among three different groups, of AD subjects (N=97), MCI subjects (N=245) and control subjects (N=148). Non-blue colors show vertices with statistical differences, at the nominal 0.05 level, uncorrected. Critical p values for these maps are shown in Table 1. The critical p-value is the highest threshold that can be applied to the statistical map while keeping the false discovery rate below 5%.

Fig. 4.

Statistical p-map results based on the new multivariate statistic (mTBM (Wang et al., 2010d) and radial distance (Thompson et al., 2004a)) on ventricular surfaces show differences among three different groups, of AD subjects (N=184), MCI subjects (N=391) and control subjects (N=229). Non-blue colors show vertices with statistical differences, at the nominal 0.05 level, uncorrected. Critical p values for these maps are shown in Table 2.

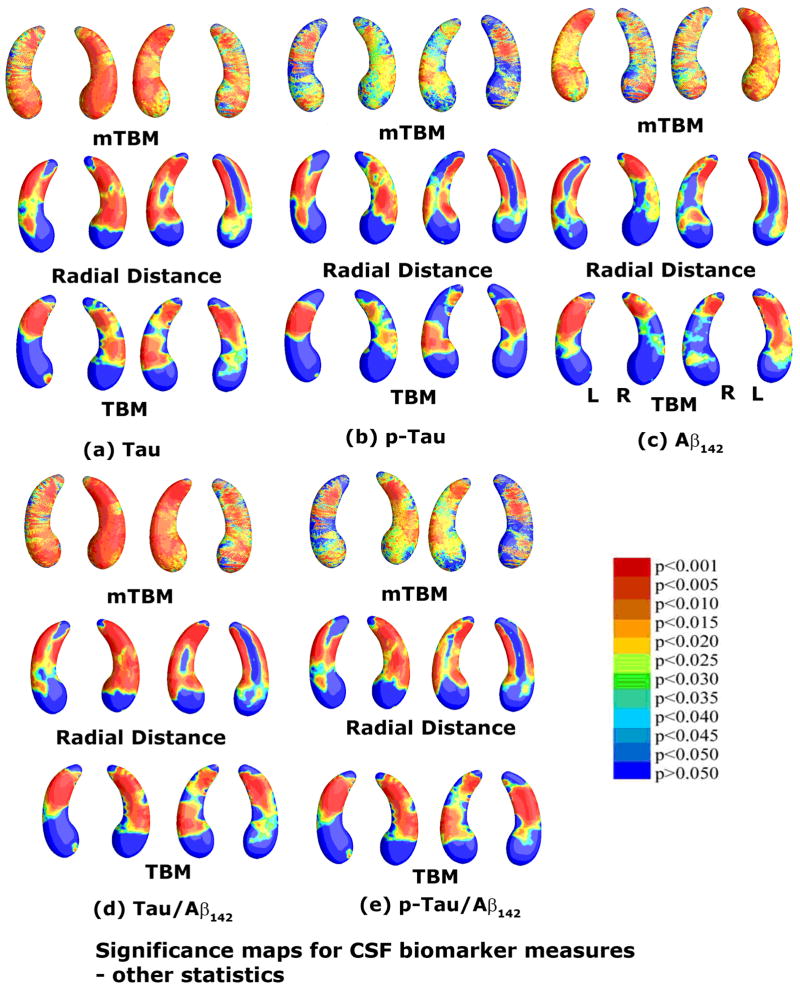
3.2 Correlation Analysis of Hippocampal and Lateral Ventricular Morphometry with Cerebrospinal Fluid (CSF) Biomarkers

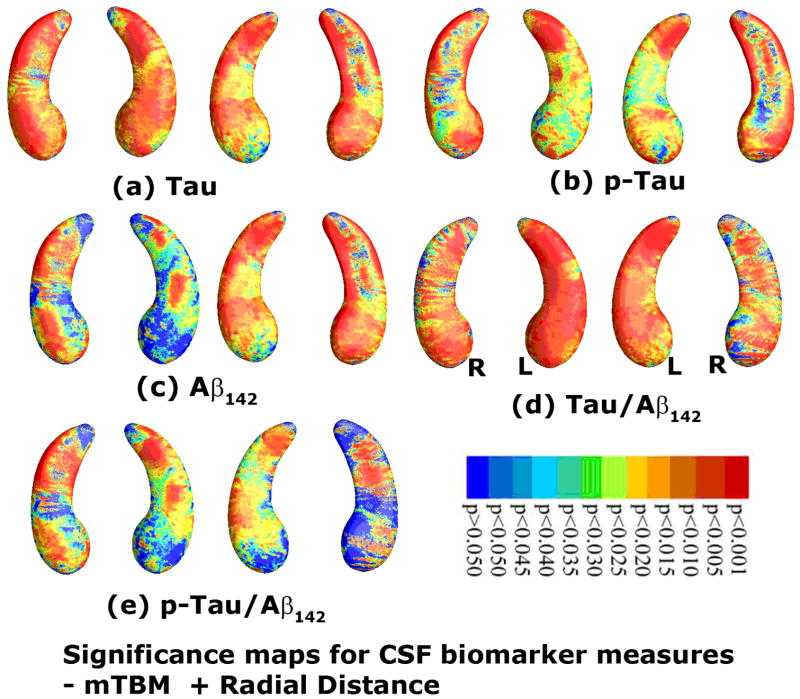
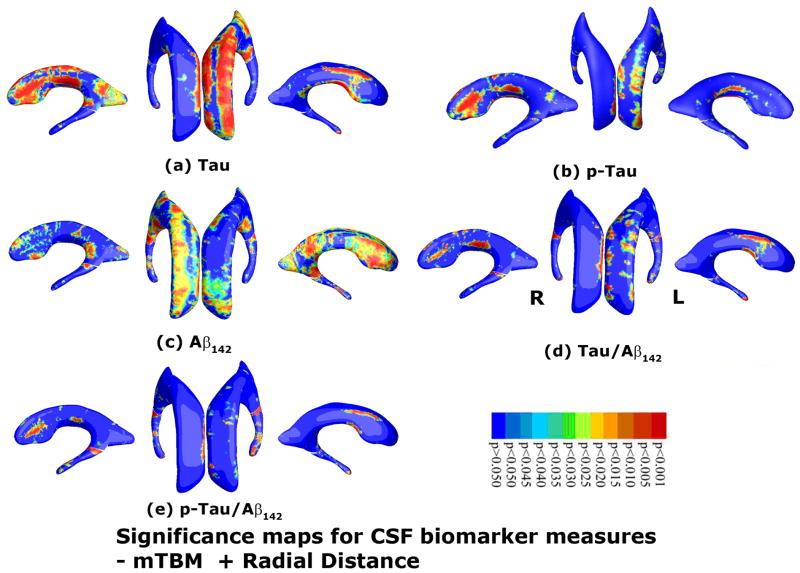
As an illustration, we studied whether the new morphometry features were correlated with cerebrospinal fluid (CSF) biomarker levels and ranked the order of how strong these associations were. Figs. 5(a)–(e) show correlation maps relating hippocampal morphometry to CSF levels of Tau, pTau_181p, Aβ_1-42, Tau/Aβ_1-42, and pTau_181p/Aβ_1-42. Correlations were significant between hippocampal atrophy and all five CSF biomarkers in the pooled data (entire sample of all AD, MCI and normal subjects). The critical p values were 0.0446 (Tau), 0.0218, (pTau_181p), 0.0444 (Aβ_1-42), 0.0455 (Tau/Aβ_1-42), and 0.0336 (pTau_181p/Aβ_1-42), respectively. Figs. 6(a)-(e) show correlation maps relating ventricular morphometry to CSF levels of Tau, pTau_181p, Aβ_1-42, Tau/Aβ_1-42, and pTau_181p/Aβ_1-42. We found some areas of correlation between ventricular enlargement and all five CSF biomarkers in the pooled data (entire sample of all AD, MCI and normal subjects). However, the result with pTau_181p did not pass the FDR test. The critical p values were 0.0052 (Tau), n.s. (pTau_181p), 0.0005 (Aβ_1-42), 0.0008 (Tau/Aβ_1-42), and 0.0008 (pTau_181p/Aβ_1-42), respectively.

Fig. 5.

Correlations between local hippocampal atrophy and CSF biomarker levels, detected with the proposed multivariate statistics. The studied CSF biomarkers include Tau (a, N=271), pTau_181p (b, N=270), Aβ₁₄₂ (c, N=271), and ratios of Tau/Aβ₁₄₂ (d, N=271) and pTau/Aβ₁₄₂ (d, N=270). Non-blue colors show vertices with statistical differences, at the 0.05 level, uncorrected. Critical p values for these maps are shown in Table 1.

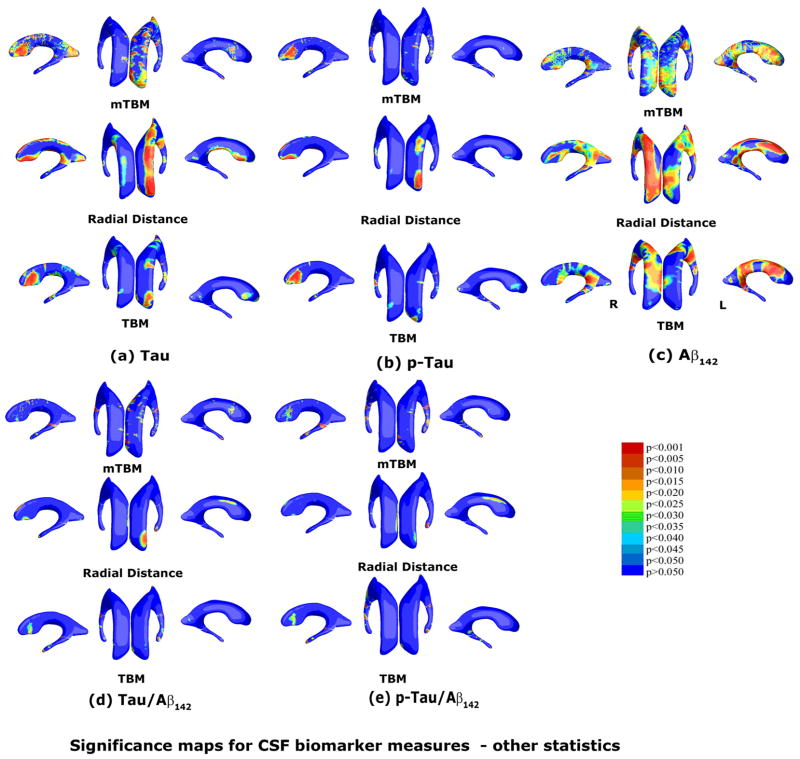
Fig. 6.

Correlation between local hippocampal atrophy and CSF biomarker levels with the proposed multivariate statistics. The studied CSF biomarkers include Tau (a, N=397), pTau_181p (b, N=395), Aβ₁₄₂ (c, N=397), and ratios of Tau/Aβ₁₄₂ (d, N=397) and pTau/Aβ₁₄₂ (e, N=394). Non-blue colors show vertices with statistical differences, at the 0.05 level, uncorrected. Critical p values for these maps are shown in Table 2.

3.3 Comparison with other Morphometric Statistics

To explore whether there is a gain in power to detect disease-related effects with the new multivariate statistics, we studied three other statistics: (1) the surface metric tensor (Wang et al., 2009; Wang et al., 2010d), (2) radial distance (Pizer et al., 1999; Thompson et al., 2004a) and (3) TBM – the determinant of Jacobian matrix (Davatzikos, 1996; Chung et al., 2008). Given our holomophic 1-form based surface registration results, these statistics were computed at each surface point across the population. For statistics (1) we used the Hotelling’s T² test to compute group mean differences, and multiple linear regression for correlations with CSF biomarkers. In cases (2) and (3), we applied Student’s t test to compute the group mean difference and the Person correlation coefficient for correlation experiments.

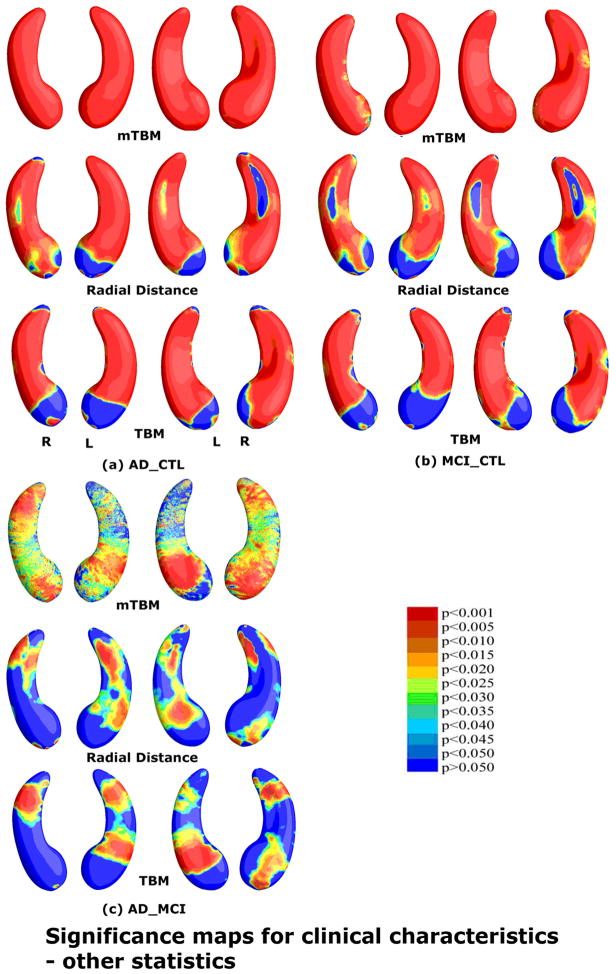
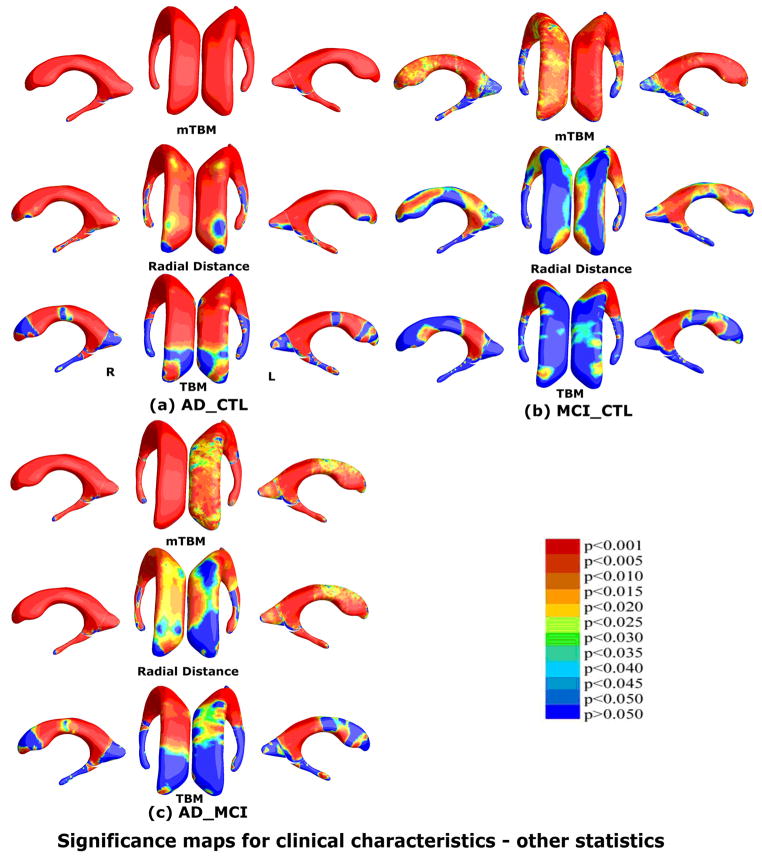
A thorough comparison was made between our proposed multivariate statistic and three other statistics for both the hippocampus and lateral ventricles. Fig. 7 and Fig. 9 show group difference statistical maps for the hippocampus and lateral ventricles, respectively. Fig. 8 and Fig. 10 show the correlation maps for the hippocampus and lateral ventricles, respectively. For each statistic, we also computed the FDR corrected overall significance values (Table 1 for hippocampus and Table 2 for lateral ventricle). Overall, the new statistics detected larger areas of statistically significance and achieved the highest critical p values in most of experiments (note that higher critical p values indicate stronger effects). This shows the additional statistical power offered by our newly introduced multivariate surface statistic.

Fig. 7.

Comparison of three other statistics for detecting group differences in the same hippocampal surface dataset as the one in Fig. 3. The three statistics are mTBM (Wang et al., 2010d), radial distance (Thompson et al., 2004a) and TBM (Chung et al., 2008). Non-blue colors show vertices with statistical differences, at the 0.05 level, uncorrected. Critical p values for these maps are shown in Table 1. The statistical results show that new multivariate statistic outperformed the other three statistics except for the AD-MCI comparison where mTBM was the best.

Fig. 9.

Comparison of three other statistics for group difference study on the same ventricular surface dataset as Fig. 5. The three statistics are mTBM (Wang et al., 2010d), radial distance (Thompson et al., 2004a) and TBM (Chung et al., 2008). Non-blue colors show vertices with statistical differences, at the 0.05 level, uncorrected. Critical p values for these maps are shown in Table 2. The new multivariate statistics outperformed these three statistics except for the MCI-CTL group comparison where mTBM was the best.

Fig. 8.

Comparison of three other statistics for assessing CSF biomarker correlations in the same hippocampal surface dataset as Fig. 5. The three statistics are mTBM (Wang et al., 2010d), radial distance (Thompson et al., 2004a) and TBM (Chung et al., 2008). Non-blue colors show vertices with statistical differences, at the 0.05 level, uncorrected. Critical p values for these maps are shown in Table 1. The new multivariate statistics outperformed the other three statistics in all five tests.

Fig. 10.

Comparison of three other statistics for assesssing CSF biomarker correlations on the same ventricular surface dataset as Fig. 7. The three statistics are mTBM (Wang et al., 2010d), radial distance (Thompson et al., 2004a) and TBM (Chung et al., 2008). Non-blue colors show vertices with statistical differences, at the 0.05 level, uncorrected. Critical p values for these maps are shown in Table 2. Compared to our prior work (Chou et al., 2010), the new multivariate statistics improved Tau related biomarker correlations. For Aβ₁₄₂, the radial distance had the best statistical power, consistent with our prior work (Chou et al., 2010) (Note in Chou et al. (2010), the statistical results were adjusted for age, sex, and educational level. However, the adjustment did not change the rank order of the results).

Table 1.

The critical p values for correlations between CSF biomarkers and hippocampal atrophy (N=490)

	mTBM + Radial Distance	mTBM	Radial Distance	TBM
AD-CTL	0.0492	0.0487	0.0438	0.0385
AD-MCI	0.0252	0.0332	0.0183	0.0054
MCI-CTL	0.0496	0.0480	0.0418	0.0379
Tau	0.0446	0.0435	0.0268	0.0170
pTAU181p	0.0218	0.0061	0.0164	0.0092
Aβ1-42	0.0444	0.0402	0.0226	0.0152
Tau/Aβ1-42	0.0455	0.0433	0.0287	0.0228
pTau181p/Aβ1-42	0.0336	0.0278	0.0238	0.0174

Table 2.

The critical p values for detection of associations with lateral ventricular surface morphometry (N=804)

	mTBM + Radial Distance	mTBM	Radial Distance	TBM
AD-CTL	0.0494	0.0487	0.0449	0.0229
AD-MCI	0.0486	0.0475	0.0403	0.0168
MCI-CTL	0.0319	0.0329	0.0157	0.0076
Tau	0.0052	0.0001	0.0010	not defined
pTAU181p	not defined	not defined	not defined	not defined
Aβ1-42	0.0005	3.70E-05	0.0039	0.0002
Tau/Aβ1-42	0.0008	0.0004	not defined	0.0003
pTau181p/Aβ1-42	0.0008	0.0004	not defined	0.0004

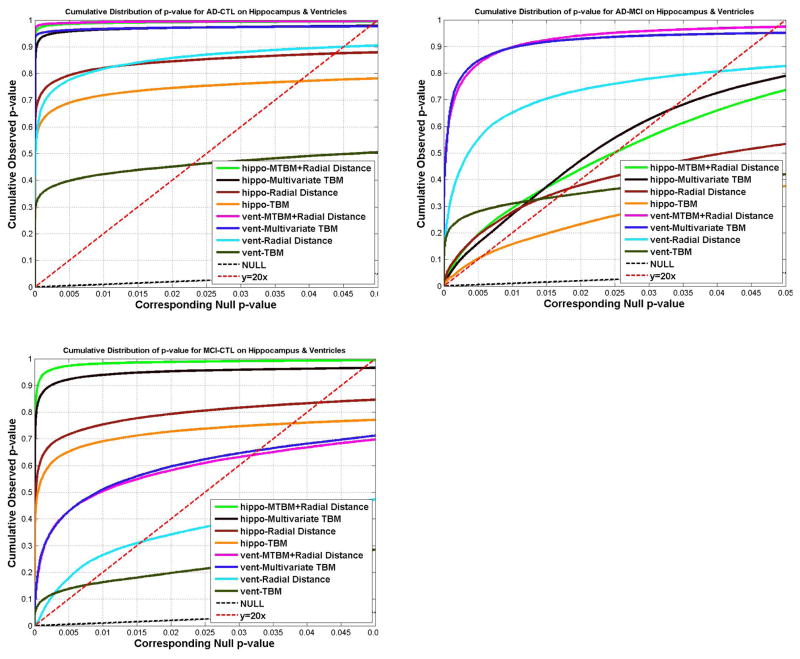
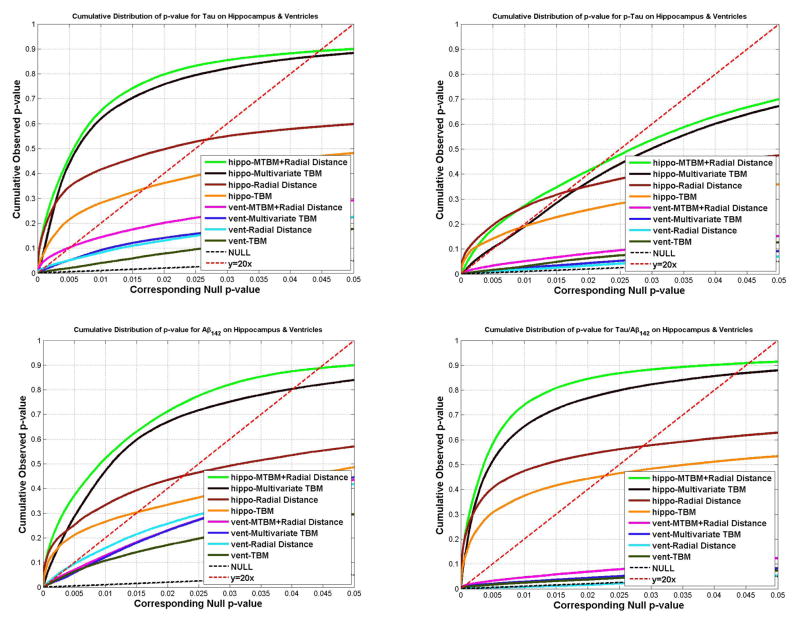
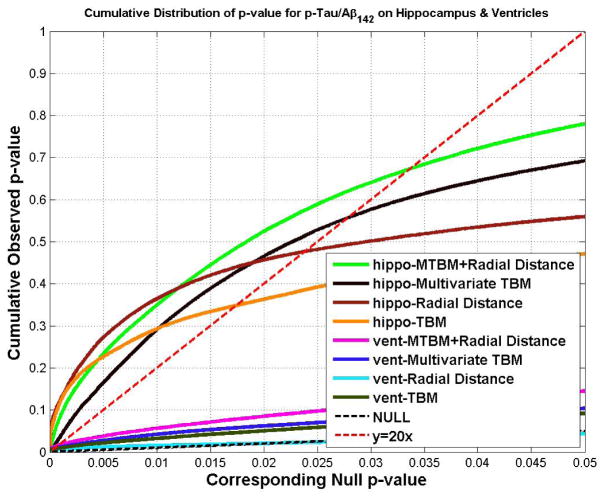
Figs. 11 and 12 show the cumulative distribution functions (CDF) of the p-values observed for correlations with various clinical measures, and correlations with CSF biomarkers. For each study, the CDFs of four statistics on hippocampus and lateral ventricle are shown together. The CDFs are plotted along with the line y=20x. The x value at which the CDF plot intersects the y=20x line represents the highest statistical threshold that can be applied to the data, for which at most 5% false positives are expected in the map. For all 16 experiments (8 experiments each for hippocampus and lateral ventricle), the CDF curve of the new statistic (based on mTBM and radial distance), has the furthest deviation from the curve of y=20x, except for the correlation with Aβ_1-42 for the lateral ventricles, and the group difference between AD and MCI for the hippocampus, where radial distance achieved the best results for Aβ_1-42 and the lateral ventricle and mTBM was the best for detecting hippocampal differences between AD and MCI.

Fig. 11.

The cumulative distributions of p-values for difference detected between three diagnostic groups (AD, MCI, CTL) versus the corresponding cumulative that would be expected from a null distribution for multivariate statistics (hippocampus: green; ventricle: pink) and results of three other statistics. The color-coded p-maps are shown in Fig. 3 and 5, and their critical p-values are show in Table 1 and 2. In the CDF, the critical p values are the intersection point of the curve and the y=20x line. In a total of 6 comparisons, the new multivariate statistics achieved the highest critical p values in 4 experiments.

Fig. 12.

The cumulative distribution of p-values for correlations detected between hippocampal atrophy/ventricular enlargement and CSF biomarker levels. Also shown are the CDF that would be expected from a null distribution of multivariate statistics (hippocampus: green; ventricle: pink) and results for three other statistics. The colored p-maps are shown in Fig. 4. and 6., and their critical p values are in Table 1 and 2. In the CDF, the critical p-values are the intersection point between the curve and y=20x line. For hippocampal atrophy, the new multivariate statistics detected correlations and outperformed all other statistics. For ventricular enlargement, no statistics showed significant correlations with pTau_181p. In the other four comparisons, the new multivariate statistics achieved the highest critical p values in three experiments. For correlations with Aβ₁₄₂, the radial distance achieved the highest critical p-value.

For the hippocampus, our new combined statistic detected strongest correlations for all CSF biomarkers and outperformed all other statistics (Fig. 12 and Table 1). The new combined statistic was also the “winner” for detecting group differences between AD and controls, and between MCI and controls (Fig. 11 and Table 1). For detecting group differences between AD and MCI, mTBM showed the strongest signal detection power and the new combined statistic was the second. For this particular experiment, there was a sharp difference between mTBM and radial distance while the differences for other cases are not as strong. We hypothesized that the regions where radial distance did not have much detection power overlapped with the regions where mTBM had a strong detection power. As a result, the combined statistic gave results that were dominated by the radial distance statistic. A visual comparison of their statistical p-maps in Fig. 3 and Fig. 7 gave evidence to support this hypothesis. This also supports our intuition that mTBM and radial distance are two features that are complementary. Their combination may greatly improve the statistical power in subcortical morphometric analyses.

For the lateral ventricles, the new combined statistic showed the strongest detection power for group differences between AD and controls, and between MCI and controls (Fig. 11 and Table 2). The performance of the new combined statistic and mTBM were comparable for the MCI versus control group difference. In correlation analyses, the combined statistics achieved the highest FDR corrected overall significant values for Tau, Tau/Aβ_1-42, pTau_181p/Aβ_1-42 (Fig. 12 and Table 2). None of these four statistics detected any correlation for pTau_181p. For correlation with Aβ_1-42, the radial distance metric showed the strongest detection power. This is consistent with our prior research (Chou et al., 2009; Chou et al., 2010). Overall, the new multivariate statistics performed very well in detecting group differences and offered some marginal benefits for CSF biomarker correlations with ventricular enlargement.

3.4 Empirical Estimation of the Minimal Sample Sizes Necessary to Detect Disease Effects

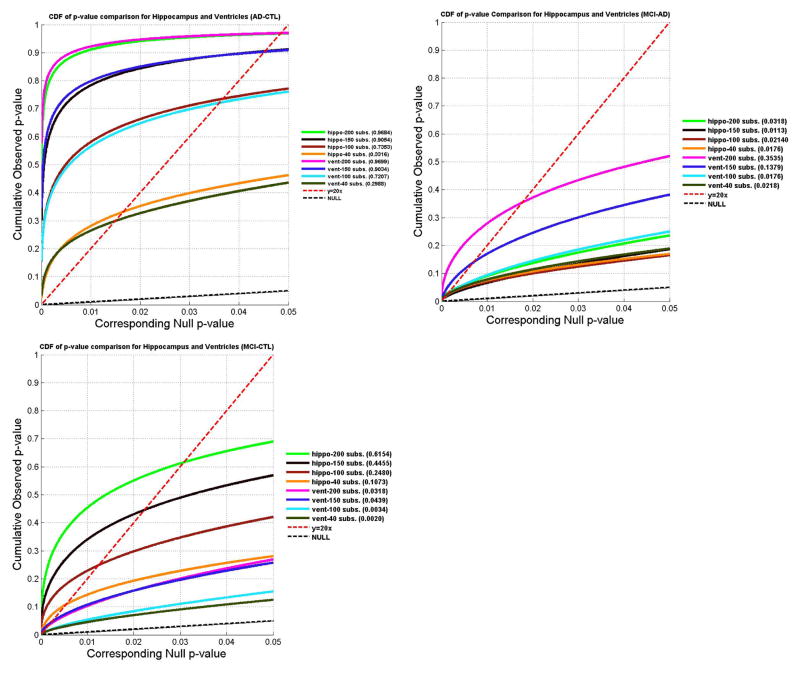
We hypothesized that our proposed multivariate morphometry feature may boost power by reducing sample size estimates required to observe effects, in both morphometry studies and potentially also in clinical trials (Hua et al., 2010; Kohannim et al., 2010). Similarly to our prior work (Morra et al., 2009a), we used an empirical estimate of the minimal sample sizes necessary to detect the well-known associations between substructural morphometry and clinical diagnosis. In general, the significance of disease effects tends to decrease, as the sample size is reduced. Such experiments can be used to argue that the proposed multivariate statistics even work with small N.

We randomly selected N subjects from the original dataset. The number of subjects from each clinical diagnostic group was chosen to preserve the ratios between control, MCI and AD sample sizes. Due to this, the smaller samples were not always subsets of the larger ones. We calculated group differences or correlations based on the selected new samples. FDR was applied to determine if detected effects were significant. To eliminate random effects, e.g. if an outlier was chosen, we repeated the process 100 times. We calculated CDFs for each obtained p-map and the average of all calculated CDFs was reported as the final CDF. As an illustrative experiment, we examined morphometric group difference among three clinical groups (AD, MCI and control).

As shown in Fig. 13, reducing the sample size, N, generally decreases the detected effect size, as is reflected in lower FDR critical p-values. Fig. 13 also shows estimates of how many subjects are necessary to detect a specific effect reliably (i.e., reject the null hypothesis, if FDR is used to control for multiple comparisons). In our experiments, we showed the proposed multivariate statistics pick up AD-CTL group differences when N=40 for both hippocampus and ventricles; for AD-MCI group differences, the test still works when N=40; for MCI-CTL group differences, the lower bound is around N=100 for both hippocampus and ventricles. The minimal effective sample sizes for hippocampus were much lower than those reported in our earlier work (Morra et al., 2009a) where radial distance was used as the statistic.

Fig. 13.

Effects of varying the sample size: CDFs of p-values measuring the effect sizes for diagnostic group differences (among AD, MCI and CTL) for both hippocampal atrophy and ventricular enlargement. The numbers in red colors are the critical p-values for each experiment. In each round of experiments, we randomly choose N subjects from the original dataset while keeping the same ratio of subject numbers across groups. To reduce arbitrary sampling effects, we repeat the process 100 times and average the obtained CDFs. In general, as N decreases, the power to detect a given effect is less. A sensitive statistic is able to pick up correlations even with a relatively small N. In our experiments, we show that the proposed multivariate statistic picks up an AD-CTL group difference when N=40 for both the hippocampus and ventricles; to detect the AD-MCI group difference, it still works when N=40; for the MCI-CTL group difference, the lower bound is around N=100 for both hippocampus and ventricles. The minimal effective sample sizes for the hippocampus are comparable to, or lower than, those reported in our prior work (Morra et al., 2009a) in the same dataset when radial distance was used as the statistic.

4. DISCUSSION

There are three major contributions in the current study. First, we described and validated a new surface multivariate statistical analysis that encodes more complete information on subcortical structure morphometry. While radial distance and mTBM achieved reasonable success in prior brain subcortical morphometry studies (Thompson et al., 2004a; Apostolova et al., 2008; Morra et al., 2009b; Chou et al., 2010; Madsen et al., 2010; Wang et al., 2010d), we showed that these two statistics are in fact complementary since radial distance mainly measures the atrophy or dilation approximately along the surface normal direction and mTBM measures deformations within surfaces. We proposed a new multivariate surface statistic based on both statistics, and showed that it can further improve statistical power in a subcortical morphometric analysis. Second, we built an automatic holomorphic one-form based software pipeline (Wang et al., 2007; Wang et al., 2010d) to analyze structural differences in the hippocampus and lateral ventricles. With holomorphic one-forms, we were able to compute conformal parameterizations of subcortical structures and match surfaces by constrained harmonic maps (Wang et al., 2007; Wang et al., 2010d). The method has a solid theoretical foundation and provides a rigorous framework to represent, split, parameterize, match, and measure surfaces. Our system can analyze the complex (branching) topology of subcortical surfaces. Third, in one of the largest MRI studies to date, we applied our new system to the ADNI dataset. Our experimental tests included the segmented hippocampus (N=490) and lateral ventricle (N=804) datasets from two of our prior ADNI studies (Morra et al., 2009b; Chou et al., 2010). We performed a thorough analysis to compare our new statistics with several other popular statistics for computing associations between subcortical morphometry, clinical measures, and CSF biomarkers. Our experimental results demonstrated that the new statistics may offer improved statistical power compared to other traditional statistics.

With the proposed multivariate statistics, we studied differences between three diagnostic groups: AD, MCI and controls. As expected, we found very strong morphometric differences between AD and control groups (overall critical p-values: 0.0492 for the hippocampus and 0.0494 for the lateral ventricle) and strong morphometric differences between MCI and control groups (AD versus MCI, critical p-values: 0.0252 for the hippocampus and 0.0486 for the lateral ventricles; MCI versus controls, critical p-values: 0.0496 for the hippocampus and 0.0319 for the lateral ventricles). We compared the statistical power (determined by FDR corrected overall significant values) with three other morphometric statistics, (1) mTBM (Wang et al., 2009; Wang et al., 2010d), (2) radial distance (Pizer et al., 1999; Thompson et al., 2004a) and (3) TBM – based on the determinant of the Jacobian matrix (Davatzikos, 1996; Chung et al., 2008). Except for the group difference between AD and MCI groups in the hippocampus (where mTBM achieved the highest critical p-value), the new statistic demonstrated the strongest or comparable statistical power for all other five comparisons (details are in Table 1 and 2). Even for the AD-MCI group difference in the hippocampus, it is clear that the multivariate statistics may offer greater statistical power than the traditional morphometric statistics such as TBM and radial distance.

We studied whether our shape measures correlate well with accepted measures of pathology in the CSF. In the pooled ADNI sample (combining patients with AD, MCI, and controls), we correlated both hippocampus and lateral ventricle shape morphometry with measures of CSF-derived biomarkers of AD pathology, including levels of Tau, pTau_181p, Aβ_1-42, Tau/Aβ_1-42 and pTau_181p/Aβ_1-42 ratio values. We also compared the statistical power for the three other statistics. The results were mixed. We found (1) hippocampal atrophy correlates with all CSF biomarkers (critical p-value, Tau: 0.0446; pTau_181p: 0.0218; Aβ_1-42: 0.0444; Tau/Aβ_1-42: 0.0455; pTau_181p/Aβ_1-42: 0.0336), (2) for hippocampal atrophy, the new statistic achieved the highest statistical power in all five tests compared with the 3 other statistics; (3) for lateral ventricular enlargement, the new statistic achieved the highest statistical power in three of five tests (critical p-value, Tau: 0.0052; Tau/Aβ_1-42: 0.0008; pTau_181p/Aβ_1-42: 0.0008). None of the four statistics detected a strong correlation with pTau_181p. For Aβ_1-42, the radial distance achieved the highest critical p-value of 0.039. The results agree with our prior work (Chou et al., 2010) where radial distance was applied to study ventricular enlargement. The proposed multivariate statistics offered some marginal improvements over the barely detectable CSF biomarker correlations for the lateral ventricles. The detailed FDR corrected critical p-value comparisons are in Table 1 and 2.

The detected correlations between brain morphometry and CSF biomarkers are of interest. Among the major neuropathological hallmarks of AD are the extracellular deposition of beta amyloid protein - Aβ- and intracellular accumulation of tau protein. The CSF biomarkers represent the most direct means to assess the level of pathology in the CSF, although they are extremely invasive. For example, not everyone is willing to have a lumbar puncture (spinal tap), due to the risk of serious injury to the spinal cord, or infection, if there are any problems in performing the procedure. As such, the CSF markers have a privileged position in empirical research on AD, as they are direct measures of the contributing pathology, but they are highly invasive. By contrast, MRI scanning is only mildly uncomfortable and is relatively risk-free and non-invasive. The notion that MRI markers, to some extent, track those obtained via CSF measures is useful for subjects who can tolerate an MRI but not a spinal tap. In addition, it offers further validation of brain morphometry as a measure of disease burden if it tracks, to some extent, CSF measures of the pathology. Finally, it is of interest to determine which biomarkers are most tightly correlated with current and later MRI measures. Our studies correlating CSF biomarkers and structural MRI measurements may further make a case for using MRI measurements as surrogates of disease progression in AD, even in pre-clinical stages (for related work, please see (Whitwell et al., 2008; Chou et al., 2009; Henneman et al., 2009; Chou et al., 2010; Vemuri et al., 2010)).

In addition, we explored how many subjects were necessary to detect a statistically significant linkage between diagnosis and morphology. To investigate this, we randomly chose certain number of subjects from our initial sample while preserving the ratios of the sample sizes for the three groups, yielding groups of size N=200, N=150, N=100 and N=40. To reduce effects of sampling, this process was repeated for 100 times. The mean of the aggregate cumulative distribution function was plotted in Fig. 13. Experimental results showed that with reduced sample sizes, the new statistic still achieved good discrimination power for detecting group differences. The results are comparable or better than those reported in our prior work (Morra et al., 2009a).

By contrast with our earlier work that split the surface meshes at extreme points along the x and y directions in the image space, we instead use an intrinsic method that makes the landmark placement on the surfaces more reliable. For instance, the superior and inferior horns of the ventricles are visible in coronal sections until they merge at the atrium. If this junction were defined by the first coronal section in which the atrium appears, it would depend on the angulation of the brain, which may depend on the accuracy of the global normalization of the brain. To avoid this source of unreliability, we instead use a completely intrinsic topology optimization step to improve the surface parameterization results (Wang et al., 2007; Wang et al., 2010d). This is similar to work in the graphics literature, e.g. Jin et al. (2004). With the added boundaries at the surface junctions, the surfaces become multiply connected domains. The placement of these boundaries relative to the object is only dependent on the intrinsic geometry of the surfaces, and not how it is aligned into a 3D space. It also does not depend upon landmark placement by a human rater. There is some hand digitization error (noise) in the ventricular landmarking, which affects the overall surface geometry, but this is greatly reduced by the multi-atlas segmentation method we use for ventricular segmentation (Chou et al., 2009). Using holomorphic 1-form and Hodge theory, it is straightforward to compute uniform conformal parametric meshes once the landmark boundaries are established. This partitions the surface into a set of parametric patches. In (Wang et al., 2010d), we found that for ventricular surface analysis our method is better than using a spherical conformal grid, which can produce large distortions of the grid at the poles of the sphere. From our experience, the rest of the parametric grid is not highly sensitive to the selected landmark locations. This is probably because the computation of the holomorphic 1-form grid is equivalent to solving a linear system, so the solution is very stable with respect to small perturbations in the boundary conditions.

Topology of Surface Models

For the hippocampus, one can choose to represent it as a spherically parameterized mesh or using a cylindrical topology with one or two open ends (or in some papers, M-reps or cm-rep are used, which induce a surface surrounding a medial curve, but use the medial curve and radial spokes as coordinates). In our work, we tended to use a cylindrical parameterization for the hippocampus (see, e.g., (Thompson et al., 2004a)), because the white matter fiber tract coming out of the back of the hippocampus (the fornix) is really just a continuation of it, so it makes sense to leave the back open like a cylinder as it is not anatomically closed off. If we closed it off, we would be adding some shape information that is not really present in the anatomy. Another advantage of choosing a cylinder rather than a sphere is that spherical meshes can lead to grid cells that are bunched up or distorted near the poles. This can cause some trouble with discretizing PDEs on the surface, and if the surfaces are flattened, there can be an enormous range in the Jacobian values. These grid uniformity issues can be addressed in other ways, such as using covariant PDEs to make solutions invariant to the surface parameterization ((Thompson et al., 2004b)), or using an “origami box” or subdivided Platonic solid topology for the spherical mesh (Thompson et al., 2004b)).

Generally speaking, the parameterization of topologically complicated, branching surfaces is difficult. There are usually highly distorted areas at surface branch points or pointed regions of structures. With the topology optimization we introduced for surface partitioning using holomorphic 1-forms (Wang et al., (2007; 2010d)), we were able to compute stable and detailed parameterizations for branching and merging surface regions while introducing uniform parameterizations.

In our prior work (Wang et al., 2010d), we compared mTBM to four other tensor-based statistics derived from the Jacobian matrix. The other statistics were: (1) the pair of eigenvalues of the Jacobian matrix, treated as a 2-D vector; (2) the determinant of Jacobian matrix; (3) the largest eigenvalue of Jacobian matrix; and (4) the smallest eigenvalue of Jacobian matrix. Our experimental results showed that the areas of surface abnormalities detected by different tensor-based surface statistics were relatively consistent. The experiments also strongly suggested that the multivariate TBM method has greater detection power in terms of effect size, probably because it captures more directional and rotational information when measuring geometric differences. Here we also computed the other three tensor-based statistics and found their detected abnormalities are consistent with, but usually less powerful than, TBM and their detection sensitivities are in line with our prior work (Wang et al., 2010d).

Relationship of Morphometry to Biological Processes

Atrophy of brain structures is associated with cognitive impairment in normal aging and AD (Frisoni et al., 2010), and typically results from a combination of neuronal atrophy, cell loss, and impairments in myelin turnover and maintenance, and corresponding reductions in white matter volume. These cellular processes combine at the macroscopic level to induce observable differences on brain MRI. Several of processes (such as cellular atrophy) occur with normal aging, and others (including neuronal loss) are further promoted by amyloid plaque and neurofibrillary tangle deposition. Although surface expansion and contraction are less traditional measures of morphometry, it is likely that they simply reflect the same processes that cause progressive brain tissue loss. Our work, as well as some approaches developed by other groups (e.g. Ferrarini et al. (2008b); Qiu et al. (2008); Yushkevich (2009)), measures the extent and severity of hippocampal and ventricular shape deformations as a proxy for hippocampal atrophy and ventricular enlargement. The detected expansion or compression of the surface areas are associated with macrostructural and microstructural loss in different brain regions and their association with cognition and CSF biomarkers makes them useful indices of the neurodegenerative process.”

Detection of Changes Parallel to the Tangent Plane to the Surface

mTBM differs from radial distance mapping approaches (such as Thompson et al., 2004a), in that it also attempts to detect changes in the local surface parameterization, or surface metric tensor, as well as relative displacements or translations of the entire surfaces. Surface deformations that occur within the surface tangent plane could just simply reflect reparameterizations of the surface, i.e., changes in the coordinate system, while the object shape remains the same. It could be argued that these might be irrelevant from the standpoint of understanding anatomy. However, it is really not true that these lack anatomical information. In a great deal of our work on cortical surface matching, e.g., Thompson et al. (2004b), we focused on computing flows in surface parameter spaces that better match cortical sulci, or other anatomical features that are consistently found and lie in the surface. Other more automated methods have attempted to match curvature profiles and/or intrinsic geometric features that lie within the surfaces (Fischl et al., 1999; Wang et al., 2005a). In these instances, a higher order correspondence is estimated and enforced, to encode information on the distribution of features lying within a surface. In that setting, when there is a deliberate effort to enforce higher order surface correspondences in the mappings that match anatomy across subjects, it is fair and relevant to assess the changes in the surface metric. Such changes will be sensitive to empirical data on features that match in the parameter space across subjects. In other cases, however, where no features are deliberately matched within the surfaces, the surface metric may simply reflect more global information about the structure, such as its overall size, surface area or aspect ratio. These features would be reflected in the surface metric tensor that is analyzed in mTBM.

Comparing Feature Vectors across Subjects

To see how group statistics are performed, we note that, strictly speaking, the deformation tensor lies on the tangent bundle of the source surface. A processing sequence could be set up whereby the surface metric tensors are then convected through a secondary flow onto a common surface, for comparisons. In other words, a ‘pull-back’ mapping could be applied to all the metric tensors to transport them into a common reference frame, such as the parameter space of a mean surface, or of a typical subject. This would be analogous to the operation in nonlinear registration of diffusion tensors where the local rotational component of the deformation maps is computed and is applied to rotate the diffusion tensors (Chiang et al., 2008). Rather than adopt such a system, we treated each surface metric tensor as a 2D matrix and used the correspondence field across subjects to form a set of these matrices for comparisons. As such, the measures of rotation in each metric tensor are relative to the surface coordinates of that subject.

Strictly speaking, the analysis of the surface metric may also pick up differences occurring in the normal direction as well, especially if these differences vary across the surface. For example, the biological meaning of a statistical difference in a tensor eigenvalue would be that the structure is abnormally dilated (on contracted) along the grid lines on the surface mesh. This may reflect a radial expansion, or an anterior-posterior stretching, or both.

We admit that in general, a difference in the tensors may initially be more difficult to interpret than a difference in a structure’s volume or surface area. Even so, if mTBM detects a group difference, the result could be followed up with an analysis of the individual eigenvalues or rotations in the tensor to home in on a more specific biological interpretation of the differences. In our results, the p-value map retrieved by the radial distance and TBM may be of more interest than the overall statistic of differences in both aspects at once, as they highlight local areas of significance, thus suggesting a precise and local effect of the disease on anatomy.

In our work, we applied a nonparametric, multivariate permutation testing on Hotelling’s T² statistics. However, standard multivariate random field theory may be also applicable to analyze the new multivariate statistics. For instance, in (Worsley et al., 2004; Taylor and Worsley, 2008), results based on random field theory for Roy’s maximum root was proposed. The inference for Roy’s maximum root is based on the Roy’s union-intersection principle (Roy, 1953). Recently, Chung et al. (2010) used this statistic to quantify abnormal local shape variations of the amygdala in 22 high-functioning autistic subjects.

The current work focuses on describing structural differences at the group level, and assessing correlations between anatomy and major CSF biomarkers. The findings further establish structural MRI measures as less invasive surrogate markers of AD. Future work will focus on using the proposed feature vectors along with statistical classifiers such as sparse multinomial logistic regression (SMLR) (Krishnapuram et al., 2005) or support vector machines for diagnostic classification (Kohannim et al., 2010). More recently, morphometric maps have also been used to classify individual subjects into diagnostic groups. In one study (Sun et al., 2009), maps of cortical gray matter density achieved 86.1% accuracy in discriminating psychotic patients from control subjects, in leave-one-out tests. In related work, Ferrarini et al. (2008b) proposed the notion of biomarker nodes, i.e., regions on surface meshes that contribute most to diagnostic classification; they tested their approach on ventricular surface models from patients with Alzheimer’s disease and controls. Our ongoing work is focusing on using conformal parameterization, mTBM and a multinomial logistic regression classifier to identify surface biomarkers for the diagnostic classification problem (Wang et al., 2010a).

The proposed multivariate statistic for analyzing subcortical surfaces is quite general. There are several methods that match surfaces of subcortical structures using parametric surfaces, such as contour parameterization (Thompson et al., 2004a; Morra et al., 2009a; Chou et al., 2010), SPHARM (spherical harmonic) methods (Styner et al., 2005), large deformation diffeomorphism metric matching (LDDMM) (Qiu et al., 2008; Qiu et al., 2009; Qiu et al., 2010), and the holomorphic one-form method (Wang et al., 2010d). Once the surface mapping is established, the Jacobian matrix and radial distance can always be computed and the multivariate statistics can then be directly applied. Compared with the conventional Jacobian determinant (Qiu and Miller, 2008; Qiu et al., 2008; Qiu et al., 2009; Qiu et al., 2010), the logarithmic transforms are applied to convert the tensors into vectors that are more tractable for use with Euclidean operations. Together with the radial distance, the statistics can be compared by using the Hotelling’s T² test at each surface point. Potentially, the new statistics can be used with any other subcortical surface registration methods.

There are two main caveats when applying the new statistics to study subcortical structure morphometry. First, just because the new statistics have greater effect sizes, it does not mean that they are true, as we do not have ground truth information on the true extent of hippocampal atrophy and ventricular expansion in AD. However, prior work (Pizer et al., 1999; Gerig et al., 2001; Thompson et al., 2004a; Styner et al., 2005; Yushkevich, 2009; Wang et al., 2010d) has reported reasonable success with mTBM or radial distance in subcortical structure analyses. It is logical to say that the analysis results should arise from true systematic differences in brain structure that lead to distortions in surface morphology. On the other hand, the multivariate statistics usually require a large number of subjects to estimate accurately. For this reason, in the current ADNI dataset (N=804), we were able to show the power advantage of the multivariate statistics to reveal correlations between subcortical structure morphometry and clinical characteristics or CSF biomarker measures. Second, if a difference in the 4×1 feature vector is detected, then it is incumbent upon the user to see if it can be traced back to a component effect that is simpler and has a more direct interpretation. For instance, it could be that the difference detected is interpretable in terms of a change in the radial distance only, or an expansion of the surface, or both. As the statistics can also be computed for the radial distance and surface metric as subcases, a statistical test that finds an association can then be followed up using post hoc tests to better characterize the sources of the morphometric difference, if that is possible, in simpler terms. In future, we will apply our multivariate statistical framework to other subcortical structures, such as the caudate nucleus and putamen. We have recently applied subcortical surface analyses to study the effects of obesity on hippocampal morphometry and genetic influences on caudate structure, among other effects. The early prediction of imminent AD based on subcortical structure measures is an important and challenging problem. The proposed multivariate measures may help in detection of degenerative effects, and may also benefit imaging genetics research (Ho et al., 2010). With multivariate features, it is natural to apply machine learning methods to perform computer-assisted diagnosis and predict future clinical decline (Sun et al., 2009; Kohannim et al., 2010; Wang et al., 2010a). Hippocampal atrophy and ventricular enlargement are established manifestations of AD pathology, and our work may offer a foundation for inferences regarding disease progression.

Research Highlights.

• Novel multivariate statistics consisting of multivariate TBM and radial distance

• A conformal geometry based hippocampal and ventricular surface registration system

• Hippocampal and ventricular group difference and CSF biomarker correlation on ADNI

• Comparison with three other statistics and empirical study with reduced sample size

• A fully automatic brain subcortical morphometry system in the public domain