BROMOC-D: Brownian Dynamics/Monte-Carlo Program Suite to Study Ion and DNA Permeation in Nanopores

Abstract

A theoretical framework is presented to model ion and DNA translocation across a nanopore confinement under an applied electric field. A combined Grand Canonical Monte Carlo Brownian Dynamics (GCMC/BD) algorithm offers a general approach to study ion permeation through wide molecular pores with a direct account of ion–ion and ion–DNA correlations. This work extends previously developed theory by incorporating the recently developed coarse-grain polymer model of DNA by de Pablo and colleagues [Knotts, T. A.; Rathore, N.; Schwartz, D. C.; de Pablo, J. J. J. Chem. Phys. 2007, 126] with explicit ions for simulations of polymer dynamics. Atomistic MD simulations were used to guide model developments. The power of the developed scheme is illustrated with studies of single-stranded DNA (ss-DNA) oligomer translocation in two model cases: a cylindrical pore with a varying radius and a well-studied experimental system, the staphylococcal α-hemolysin channel. The developed model shows good agreement with experimental data for model studies of two homopolymers: ss-poly(dA)_n and ss-poly(dC)_n. The developed protocol allows for direct evaluation of different factors (charge distribution and pore shape and size) controlling DNA translocation in a variety of nanopores.

1. Introduction

Voltage-driven transport of biopolymers across cell membranes via wide pores is of a central importance to the normal cell function² and bacterial pathogenicity.^3,4 The pragmatic value of these transport systems is most strikingly illustrated by their applications in a wide variety of modern nanotechnology applications spanning from analyte detection⁵⁻⁷ and sample preparations with high degrees of purification⁸ to the use of these proteins for rapid DNA sequencing.⁹ An idea to use bacterial toxins as polymer counting and later as DNA sequencing devices was first formulated in the mid-1990s and then implemented with the α-hemolysin (αHL) channel by Kasianowic and colleagues.¹⁰ In the following years, a constantly growing number of papers addressing various aspects of DNA and ion dynamics in biological nanopores were published.^9,11−13 In the typical experimental setup, a pore-forming protein is reconstituted into a lipid bilayer membrane that separates two chambers with symmetric or asymmetric ionic solutions. When a voltage is applied, the electric field drives ions through the pore and the ion current can be measured. Subsequently, DNA molecules are added to the solution bathing one side of the membrane. Since DNA molecules are charged, they will be driven by the electric potential through the pore, and their blocking effect on the open-channel current is evaluated. While threading, the DNA molecule blocks the current of ions, and blockade events can be detected as a transient decrease in the ionic current that can be mapped to the sequence of nucleotides threaded through the pore. Thus, by monitoring the ion current, one can indirectly measure properties of the translocation process.

Although these advances in experimental studies suggest that such a system could be developed into an ultrafast method of DNA sequencing, it is necessary first to elucidate the physical mechanism underlying polymer translocation through biological pores. An obvious problem is that single-stranded DNA (ss-DNA) is a large and floppy polymer that seems to be still fully or partially hydrated, and maintaining sufficient ionic atmosphere while in the pore and thus sensing has to rely on relatively weak forces between the wall of a nanopore and transported polymer, modification of DNA conformational dynamics by the nanopore confinement, and differences in nucleotide–ion interactions.^14,15 Furthermore, DNA escape dynamics may not necessarily fit into exponential kinetics showing a nontrivial dependence on the voltage and temperature.¹⁶ Because of the complexity of the translocation kinetics, very noisy recordings pose a natural challenge to achieving a good contrast in the signal from different nucleotides to the level required for accurate sequencing.^17,18 There is also a growing consensus that specific DNA–protein interactions could and should be exploited for amplification of the signal. However, targeted modification of a biological pore requires detailed information about the dynamics of a floppy ss-DNA molecule in confinement and its effect on ion currents.^19,20

Arguably, the best approach to this problem is to use modern atomistic simulations with explicit account for ions, DNA, and a protein dynamics.¹⁵ While it is feasible to simulate a full assembly for hundreds of nanoseconds, direct evaluation of ion currents may represent a significant challenge that requires simulations with grand canonical ensembles, absorbing boundaries or dual-volume systems that manage accumulation of ions on one side of the membrane. The size of the system makes it prohibitive for brute-force microsecond simulations that may be required for studies of relevant conformational dynamics of flexible DNA chains and makes every application of atomistic simulations to nanopores a tour-de-force exercise in computational power.

To reduce the dimensionality of the problem, several theoretical approaches have been used to study a charged polymer translocation across membranes.²¹⁻²³ Some of them focus on the DNA translocation dynamics alone and use implicit treatment for ion–ion and ion–DNA interactions, often representing the pore by cylindrical or conical confinement with uniform charge distribution. While this is an attractive route for studies of solid-state nanopores, it is limited in a realistic description of protein nanopores. Recent attempts were based on the applications of Langevin dynamics to DNA translocation in the pore represented by nonuniform 1D potential.²⁴ An alternative approach may be found in a reduced representation of the modeled protein and solvent by solving the Poisson–Boltzmann equation for the electric field created by the pore and surrounding media, while still modeling DNA and ion translocation dynamics explicitly. For wide pores, such as nanopores, approaches based on a Grand-Canonical Monte Carlo combined with Brownian Dynamics offered an excellent platform for studies of open-channel currents in α-hemolysin.²⁵⁻²⁷ Even with DNA blocking ionic currents, α-hemolysin retains relatively high levels of conductance, indicating a continuous water-filled pathway that has been also confirmed computationally with extensive MD simulations.²⁸ Accordingly, in this paper, we present a theoretical strategy based on GCMC/BD that includes development of the parameters for ion–DNA interactions compatible with the established coarse-grained model for DNA published by de Pablo and colleagues¹ and its application to polymer dynamics and ion current simulations in cylindrical and arbitrarily shaped pores with nonuniform charge distribution (α-hemolysin).

2. Methods and Computational Models

In this section, we introduce basic approximations, simulation algorithms, and details of the force-field implementation and analysis for studies of DNA translocation with the previously developed GCMC/BD method.²⁹ The Fortran-90 code for GCMC/BD simulations of DNA in nanopores is based on an earlier version of the GCMC/BD program.^25,29,30 All of the developed programs (BROMOC and analysis suite) and documentation are freely available to the academic community by request.

2.1. GCMC/BD Algorithm

Brownian Dynamics (BD) represents an attractive computational approach for simulating the permeation process through wide channels over long time scales at a cost of treating solvent and membrane degrees of freedom implicitly, while describing ion dynamics explicitly. The approach consists of generating the trajectory of the ions as a function of time by numerically integrating the stochastic equation of motions using some effective potential function to calculate the microscopic forces acting on mobile particles in the system. From a microscopic point of view, this effective potential is a many-body potential of mean force (PMF or W(r₁,r₂,...)), which rigorously introduces a reversible thermodynamic work function (free energy) to assemble a particular configuration of the particles in the system while averaging over the remaining degrees of freedom as an effective mean field. In the case of wide aqueous pores, a continuum electrostatic description in which the solvent is represented by a featureless dielectric medium is often a useful and accurate approximation. Thus, the equation of motion governing dynamics of the system is a specific form of the general Langevin equation:³¹

1

where W(r₁,r₂,...) is a many-body PMF that describes interactions between ions, DNA sites and ion–DNA, the effect of applied membrane voltage, and the reaction field and static field emerging from a protein charges. D_i is a position-dependent diffusion coefficient which was kept to corresponding bulk diffusion values for both ions and nucleotides in the current study, and ξ_i(τ) is a term introducing a Gaussian random noise to the system dynamics. In the GCMC/BD scheme, BD moves are coupled with the Grand Canonical Monte Carlo (GCMC) run, allowing the simulation of a fluctuating number of particles. Briefly, it consists of constructing a random walk (discrete time Markov chain) of the configuration of the system during which particle creation and destruction can occur, allowing for a constant chemical potential of the simulated system.²⁹ The GCMC algorithm can be used to simulate equilibrium as well as nonequilibrium conditions of ion diffusion and permeation under an applied electric field. The GCMC/BD algorithm has been incorporated into the new code where the BD trajectory of ions is generated.

2.2. Mesoscale DNA Model

A mesoscale model development for DNA has been described in the literature.^1,32 This DNA coarse-grain model reduces the complexity of a nucleotide to only three interaction sites, one for the phosphate, sugar, and base. There are four different base sites, one for each type of base in DNA. The backbone phosphate and sugar sites are placed at the center of mass of the respective moiety. For purine bases (adenine and guanine), the site is placed at the N1 position. For pyrimidine bases (cytosine and thymine), the site is placed at the N3 position. The coordinates for each of the sites just described were determined from the standard coordinates for the B isoform. The parameters for this DNA force field can be divided into bonded and nonbonded interactions, including an optional implicit representation of ions through Debye–Hückel Coulombic screening of the interactions between phosphates. The bonded interactions can be divided further into (i) covalent bonding interactions (two-body contribution; U_bond), (ii) bond angle interactions (three-body contribution; U_angle), and (iii) dihedral angle interactions (four-body contribution; U_dihedral). The equilibrium distances and angles in these terms are set equal to the values obtained from the atomic coordinates of the standard model of the B form of double-stranded DNA (ds-DNA). The (pairwise) nonbonded interactions can be divided into (a) intrastrand base-stacking interactions (U_stack), (b) hydrogen bonding interactions (U_bp), (c) excluded volume interactions (U_ex), (d) coulomb interactions (U_ij), and (e) solvent-induced contributions (U_solvent). The potential energy of the polymer (U_DNA) in this case is expressed as

2

The base-stacking contribution accounts for the strong hydrophobic attraction between adjacent nucleotides and provides additional bending rigidity to the DNA molecule. Hydrogen bonding, along with base-stacking interactions, provides structural stability in DNA duplexes, while it may not be overly important for simulations of the fully stretched ss-DNA molecules. Nevertheless, the model allows for multiple inter- and intrastrand interactions, thus extending the range of applicability to both ds-DNA and ss-DNA.³³⁻³⁷ The next term accounting for excluded volume interactions are purely repulsive. Finally, the solvent-induced contribution is a novel ad hoc contribution introduced in the force field meant to represent (implicitly) many-body effects associated with the arrangement of water during the reversible denaturation of DNA. The interested reader is advised to refer to the original work of de Pablo and colleagues.^1,32 The DNA mesoscale model has been combined with the GCMC/BD algorithm described. The set of parameters for the coarse-grain model of the DNA force field is exactly the same as in ref (32). Bond constants, the bending constant, and the torsional constant were originally parametrized as a function of an ε parameter which we called the force field parameter. The “force field” parameter is used to control the depth of the well for potential in intrastrand base-stacking interactions, excluded volume interactions, and strength energy for the hydrogen bonding potential and can be modified. Forces for bonded interactions are derived by chain rule differentiation of the potential for bonds and angles and by using first principles of mechanics for dihedral forces. These dihedral force expressions require significantly fewer numerical operations and are equivalent to those more commonly used and obtained by mathematical differentiation.³⁸

2.3. Modeling of ss-DNA Dynamics in the α-Hemolysin Channel

The structure for α-HL was taken from Protein Data Bank (Protein Data Bank entry: 7ahl). In all GCMC/BD simulations, the protein was treated as a rigid structure with a dielectric constant of 2 surrounded by a high dielectric solvent (ε_m = 80) and embedded in a 32-Å-thick membrane (ε_m = 2). The choice of dielectric constant for the aqueous region was motivated by the large size of the pore, which can be safely assumed to be well-represented by a bulk continuum value and has been shown to provide an accurate approximation in the case of wide protein pores. The channel was positioned along the z axis with the center of the membrane at Z = 34.1 Å. The salt concentrations of interest were maintained by two 3.5 Å buffers positioned from −90.75 to −87.75 Å and from 87.75 to 90.75 Å along the z axis. A snapshot of the simulation system is shown in Figure 1. We have considered two different homopolymeric strands (ss-poly(dA)_x and ss-poly(dC)_x, where x is the number of nucleotides) simulated at different voltages and electrolyte concentrations. A uniform diffusion coefficient of 0.001 Ų/ps was assigned to all nucleotides. The explicit inclusion of the position-dependent diffusion may be important for obtaining 1:1 correspondence to the experimental data.^39,40 It should be noted, however, that passive diffusion of the strand is a secondary factor in translocation under an applied force (see below) and in refs (41) and (42).

Figure 1.

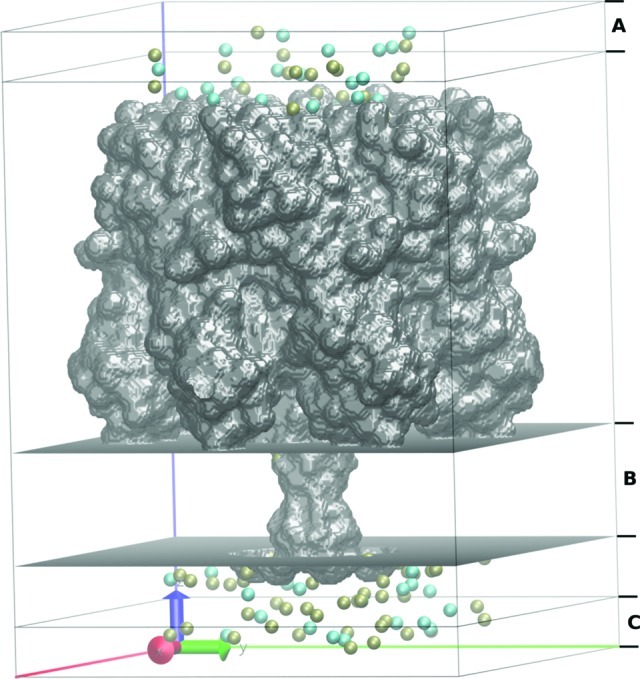
Molecular graphics view of the orthorhombic simulation box in GCMC/BD of the α-hemolysin pore bathed in a 0.3 M KCl solution. K⁺ (tan) and Cl^– (cyan) ions are located in the pore and in the buffer regions (A and C regions). Transmembrane zone is shown as region B.

A model for coarse-grained DNA has been previously developed for an implicit solvent model based on a canonical Debye–Hückel approximation.(1) However, the main goal of recent development is to enable studies of DNA and ion dynamics. Therefore, we introduce potential terms that describe interactions of DNA sites and mobile ions modeled explicitly. The multiparticle Potential of Mean Force (PMF) that has been used to control the system dynamics is expressed as

3

where W(r₁,r₂,...) is a many-body PMF that describes interactions between mobile particles and depends on all particle coordinates. U_DNA is the internal DNA potential described in eq 2. U_ij is a pairwise particle interaction potential for DNA sites–ions and ions–ions separated by distance r_ij. U_core is a repulsive core potential that prevents overlap between mobile particles and a protein or bilayer continuum, and it is a function of r_i, the Cartesian coordinate of particle i (ion or DNA site). W_sf is a static field potential for all charged particles that combines the effect of the protein static charges and the applied external electric potential. W_rf is a reaction field arising from the electrostatic polarization of the various dielectric boundaries and the implicit salt in the outer region.

More specifically, the direct pairwise particle interaction potential (U_ij) is described in eq 4:

4

where ε_ij and σ_ij are the parameters of the Lennard-Jones 6–12 potential, q is the charge of the mobile particle i and j, ε is the vacuum permittivity, ε_bulk is the dielectric constant of the media (80 for water), and W_sr is the short-range potential.

Equation 4 is composed of (a) a primitive model potential term that has been extensively used in statistical mechanical studies of ionic solutions and (b) water-mediated short-range ion–ion and ion–DNA interactions with a form of damped oscillations to take into account the water-mediated interactions. The term a is composed by Lennard-Jones (LJ) and Coulombic interaction potential terms. LJ parameters were adjusted so as to reproduce pairwise Radial Distribution Functions (RDF) from atomistic simulations.

The short-range (SR) water-mediated potential (W_sr) has the following functional form introduced by Im and Roux for ion–ion short-range (SR) potential:³⁰

5

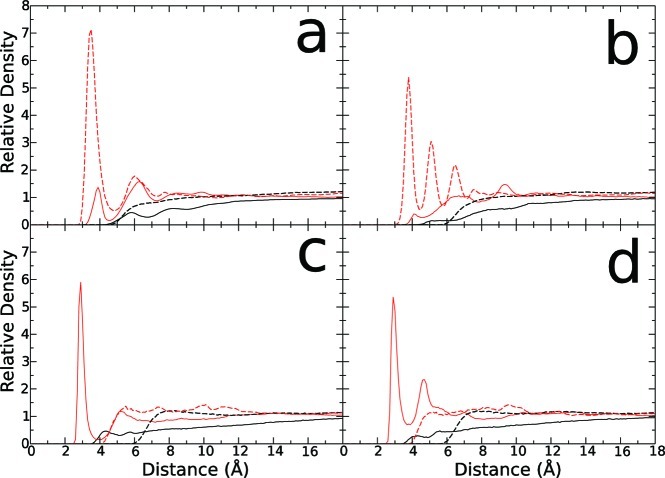
All of the coefficients were empirically adjusted until reasonable agreement was achieved between ion–nucleotide RDFs obtained from explicit all-atom MD simulations (Figure 2) of ss-DNA and from GCMC simulations. The developed parameters for LJ and SR potentials are collected in Table 1. In Figure 2, RDFs computed from all-atom MD simulations are shown.

Figure 2.

Atomistic molecular dynamics radial distribution function of DNA sites–ions (solid line) in comparison to RDFs from BROMOC simulations (dotted line). In black, Cl^– anion. In red, K⁺ cation. (a) Phosphate, (b) sugar, (c) adenine, (d) cytosine.

Table 1. Parameters for Nonelectrostatic Part of the Effective Ion–Ion/DNA Site Interaction Potential.

site/ion	ion	σ (Å)	ε (kcal/mol)	c0	c1	c2	c3	c4
K+	K+	3.14	0.087	–0.600	4.40	0.90	0.80	0.25
Cl–	K+	3.59	0.114	–3.700	2.90	0.90	0.80	0.00
Cl–	Cl–	4.04	0.150	–0.500	4.90	0.90	0.80	0.25
P	K+	3.25	0.125	–1.150	3.50	1.50	0.75	0.00
S	K+	3.65	0.075	–0.750	3.75	2.90	1.50	0.10
A	K+	4.65	0.200	–0.050	4.95	1.50	0.70	0.05
C	K+	4.42	0.200	–0.025	4.65	1.50	0.70	0.05
P	Cl–	5.45	0.100	–0.025	5.75	0.75	0.75	0.05
S	Cl–	6.85	0.100	–0.025	6.35	3.00	0.50	0.05
A	Cl–	6.69	0.200
C	Cl–	6.49	0.200

The static-field electrostatic potential (W_sf) was evaluated by solving the Poisson–Boltzmann equation with a focusing method on a coarse grid first (a grid spacing of 1.5 Å) followed by a second calculation on a finer grid (201 Å × 201 Å × 281 Å points with a grid spacing of 0.5 Å). The trans-membrane potential contribution was calculated with a modified version of the PB equation.⁴³W_rf was calculated on a same grid size with a grid spacing of 0.5 Å.^26,44 The GCMC/BD simulation trajectories were generated with a time step of 20 fs. Each production run has been preceded by the equilibration run with 1 000 000 MC steps combined with 100 GCMC iterations to obtain well-equilibrated placement of the counterions. In the translocation studies, a DNA molecule has been placed such that its center of mass coincides with the geometric center of the nanopore. The main goal was to study the effect of the DNA on the ion dynamics in the pore. The problem in the DNA capturing rate, although important, is not in focus or even reachable for current study. All of the GCMC/BD simulations were ranging from 1 to 5 μs.

2.4. All-Atom MD Simulations

To obtain equilibrium ion-density distribution in the pore, self-diffusion coefficients for nucleotides, position-dependent dielectric constants, as well as initial guesses on LJ parameters between ions and DNA sites, a series of MD simulations have been performed. Equilibrium all-atom MD simulations for α-HL/membrane systems were run for 25 ns with the NpT ensemble using the NAMD 2.7b1 program⁴⁵ package using a previously developed protocol from Comer et al.⁴⁶ The total number of atoms for MD simulations is ∼270 000. Briefly, the all-atom system contains α-HL toxin embedded into a POPC (1-palmitoyl-2-oleoyl-sn-glycero-3-phosphocholine) bilayer patch, ss-poly(dA)₄₀ or ss-poly(dC)₄₀ solvated by 1000 mM of KCl aqueous solution with 3′ entry to the pore. Average self-diffusion coefficients for nucleotides were computed for free ss-poly(dA/C)₄₀ in 1000 mM KCl from the mean-square displacement of the nucleotides' center of mass. The average self-diffusion coefficient was found to be ∼0.001 Ų/ps and is in accord with previous studies.⁴⁷ This value of the transport coefficient was used for BD simulations. The MD setup corresponds to one previously used by the Aksimentiev group and is known to faithfully reproduce experimental data on current blockade.⁴⁶

The position-dependent dielectric constants were evaluated using average fluctuations in a dipole moment of the volume slice (5 Å) along the z axis of the system using the following equation:

6

where ⟨V⟩ is the average volume occupied by solvent molecules in the slice estimated by a grid-search algorithm. A similar approach was used in several MD studies of membrane proteins.⁴⁸ A high-frequency correction ε_∞ has been set to a constant value of 2.0. The position-dependent profiles of the dielectric constants from equilibrium MD simulations (no applied voltage) suggest that the effective dielectric constant for water captured in the stem region (almost entire trans-membrane region of α-HL channel; Figure 1, region B) in the presence of DNA is ∼40.

Determination of the DNA–Ion and Ion–Ion Parameters

As stated above, LJ-parameters describing interactions between nucleotide sites (base, sugar, phosphate) and ions (K⁺, Cl^–) as well as ions–ions were obtained from a series of separate simulations of ss-poly(dX)₁₄ in 1 M KCl (X = A, C, G, and T). Using charmm-gui.org, single-stranded B-DNA was built and solvated in a truncated octahedron box with 21 177 TIP3 waters, 141 Cl^– anions, and 154 K⁺ cations. All simulations were performed using NAMD 2.8 with the standard CHARMM27 force field, an integration time step of 2 fs, a cutoff of 12 Å, periodic boundary conditions, and particle-mesh Ewald (PME). The initial system was minimized performing 5000 steps followed by 300 000 steps of equilibration in the NpT ensemble at 1 atm and 300 K using a Langevin Piston and Lowe-Andersen thermostat. The DNA backbone was restrained using the minimized structure during the rest of the simulations to prevent self-interactions and to maximize DNA–ion interactions. After the short equilibration of 0.5 ns, a production run of 25.6 ns simulations in the NVT ensemble was performed for ss-poly(dA)₁₄, ss-poly(dC)₁₄, ss-poly(dG)₁₄, and ss-poly(dT)₁₄ using the last configuration from equilibration. For RDF computation, atomistic DNA coordinates were converted to coarse grained DNA site coordinates according to the de Pablo et al. coarse-grain model definition.¹ The resulting ion-site RDF functions were used for fitting of the ion–DNA short-range parameters using the protocol described by Im and Roux.³⁰

2.5. Translocation Rates

DNA displacements (d) along the channel axis (z axis) were computed as the dot product of the Geometric Center of Phosphates (GCP) coordinates and a vector along the z axis (eq 7).

7

Translocation rates were computed at time t_r, that is, when the root-mean-square displacement of GCP (σ, eq 8) for n independent simulations becomes equal to L.

8

The root-mean-square displacement of GCP can be expressed as a function of the average GCP displacement (eq 9) plus a diffusive displacement component f (eq 10).

9

10

The average GCP displacement is the voltage-driven displacement. For no external potential bias, the voltage-driven displacement tends to zero and the root-mean-square displacement tends to the diffusive displacement. Voltage-driven translocation rates (k_t) were computed using eq 11, and translocation rates that include diffusive displacement (k_d) were computed using eq 12.

11

12

2.6. Root Mean Square Displacements

To assess conformational dynamics of the confined polymer, three different Root Mean Square Displacements (RMSD) were computed for beads representing every nucleotide (phosphate sites) from ss-DNA translocation through the pore simulations:

The absolute bead RMSD to characterize monomer dynamics:

13

The bead RMSD relative to geometric center (GC) to assess chain extension:

14

The RMSD of the chain geometric center (GC) to evaluate total displacement of an entire chain:

15

where r is the position vector of the bead i or geometric center (GC), M is the number of chains (for ss-DNA M is equal to 1), and N is the number of beads per chain. RMSDs were computed without previous alignment. zRMSD are RMSDs computed using only the z coordinate.

3. Results

Here, we present some computational illustrations of the developed framework for simulating DNA dynamics in nanopores. All GCMC/BD simulations were run on a single-core Xeon 2.4 GHz processor. The run-time for 1 μs of a GCMC/BD simulation for ss-poly(dA/C)₂₅ blocking α-hemolysin ranges from 1 day in 300 mM KCl to 12 days in 1 M KCl. MD simulations, on the other hand, took up to 3 months to run on 128/256 cores on a supercomputer cluster to reach up to 100 ns of sampling.

3.1. Melting Simulations of the ds-DNA: Debye–Hückel Approximation vs Explicit Ions

A gold standard for evaluations of DNA force-field simulations with implicit and explicit ions is its ability to reproduce melting thermodynamics for ds-DNA (strands separation). For melting simulations, we consider an aqueous 0.069 M monovalent salt (KCl) solution at a temperature of 317 K (experimental T_m for the studied strand is 317.4 K³²). The ds-DNA sequence used for simulations is 5′-AGTAGTAATCACACC-3′. Each base pair in the DNA coarse-grain force field, characterized by the separation r_ij between intra- or interstrand sites i and j, is described by characteristic energies ε_ij ∈ [ε_AT, ε_CG] and characteristic lengths σ_ij ∈ [σ_AT, σ_CG], where ε_ij = ε_ji; σ_ij = σ_ji; and A, T, C, and G correspond to adenine, guanine, cytosine, and thymine bases, respectively. A complementary base pair is considered to be hydrogen-bonded when the separation between bases is r_ij < σ_ij + 2.0 Å. The ratio between the unpaired bases and the total bases (f) is used to evaluate the melting process. A time step for melting simulations was set to 10 fs. This value is lower than the maximum time step allowing stable integration of system’s dynamics (previous studies used time-steps up to 30 fs).^1,32

By means of the developed code, f values are computed each N simulation steps. From these consecutive measurements of fluctuating quantity f, one can obtain the time average of denatured bases fraction (⟨f⟩) in a simulation. In our simulations, we’ve used the blocking method⁴⁹ enabling evaluation of the statistical convergence for trajectories. Following the de Pablo protocol, we have included the solvent-induced contribution inside the DNA coarse-grain force field as well as an effective dielectric constant, which takes into account a dependence on the temperature and KCl concentration. The Debye–Hückel implicit ion concentration used was 0.069 M. An account for these terms only slightly reduces ⟨f⟩ value compared to similar simulations using the original force field described in ref (1). Selecting an optimal value for the diffusivity of coarse-grained DNA sites is not a trivial issue. A self-diffusion coefficient for adenine was estimated from equilibrium MD simulations to be 6.8 × 10^–4 Ų/ps for periodic systems. Experimental data provides transport coefficients between 1.3 and 1.8 × 10^–3 Ų/ps in the absence of an electric potential bias. To evaluate the effect of the diffusion constant on the melting temperature, we run several BD simulations with different transport coefficients. It was found that obtaining a statistically converged estimate for a melting temperature from multiple runs using elevated diffusion constants becomes extremely difficult. An increase in DNA diffusivity generates a modest but notable increase in <f > as expected (data is not shown). Several simulated systems did not show a significant fraction of ss-DNA at all. This indicates that one would need a large number of simulations to achieve a complete statistical convergence for melting simulations, and that standard deviation of the average value can be significant. Similar conclusions have been reached recently by de Pablo and colleagues.³²

To evaluate the explicit account of ion–nucleotide interactions, we repeated GCMC/BD melting simulations for the same salt concentration. K⁺ and Cl^– excess chemical potentials for a 0.069 M KCl salt solution were obtained from previous results for the excess chemical potential of monovalent salts²⁹ using polynomial interpolation. For melting simulations with explicit ions, we have used a spherical system with a radius of 50 Å and a buffer region range from 40 to 50 Å. A total of 40 independent simulations were run to estimate ⟨f⟩, and the diffusion constant for DNA sites was set to 1.0 × 10^–3 Ų/ps. According to these results, the maximum fraction (⟨f⟩ ) of denatured GC (guanine–cytosine) base pairs is 0.62, and the distribution function is approximately normal, in good accordance with the experimentally reported value of 0.6.^1,32 As expected, ⟨f⟩ increases when the attractive component of the Lennard-Jones potential for DNA–-ion interactions is increased.

3.2. DNA Translocation through Cylindrical Channels

A cylindrical pore provides arguably a simplest model for a biological or synthetic nanochannel. An advantage of such a toy model is obvious; a transmembrane potential has an analytical solution in the limit of Debye–Hückel approximation. An additional term accounting for repulsive interactions can easily be included into the potential function. In our simulations, a repulsive potential is smoothed with a polynomial radial function, and therefore discontinuities are avoided in calculations of repulsive forces. Despite its simplicity, this model may provide a great platform for studies of DNA translocation time-dependence on ionic strength, temperature, or dielectric constant of the solution. To estimate DNA translocation time, we calculated the fraction of DNA sites inside of the channel each N time steps. Thus, one can extrapolate the total DNA translocation time from a fraction of DNA sites inside the channel. For simulations, we consider an aqueous 1 mol of an implicit monovalent salt solution at a temperature of 275.15 K with a membrane thickness of 50 Å, and the cylindrical pore radius is 9 Å, which approximates a constriction zone radius of α-hemolysin. A repulsive potential that prevents core–core overlap between DNA sites, the channel, and membrane was set to 200 kcal/mol, and a switch region of 1.0 Å was set. Initially, a ss-poly(dA)₁₂ was positioned at the entrance of a cylindrical channel on the side where electrostatic potential is favoring entrance to the pore confinement.

Generic cylindrical confinement without heterogeneous wall-charge distribution led to a Gaussian-like distribution of the translocation times. Table 2 collects results for ss-poly(dA)₁₂ translocation across the cylindrical channel with a 3′ entrance with two biasing potentials of V_mp = 300 and 900 mV. Although all ss-DNAs were positioned near an entrance to the cylindrical channel, a capture of the monomer that will lead to a complete translocation occurs only in a few cases for a constant simulation time, while partial DNA translocations through a cylindrical channel occur in all of them. This is in agreement with a rather broad distribution of translocation times observed experimentally.¹² The significant entrance barrier is linked to the presence of an entropic barrier so that total translocation can only happen for a handful of relatively “low” probability captured states of flexible ss-DNA.²³

Table 2. Dependence of the Capture t_capture and Translocation t_D Times for 3′ss-poly(dA)₁₂ Translocation Across Cylindrical Channel on the Diffusion Constant and Force-Field Parameter ε.

D(Å2/ps)	ε (kcal/mol)	Vmp (mV)	tcapture (ns)	tD (ns)
1.0 × 10–2	0.01839	0.9	1.5	83.2
0.5 × 10–2	0.01839	0.9	19.3	171.1
1.0 × 10–2	0.1839	0.9	1.0	80.2
0.5 × 10–2	0.1839	0.9	1.1	193.1
1.0 × 10–3	0.1839	0.9	1.4	1264.3
1.0 × 10–2	1.839	0.9	33.7	114.7
0.5 × 10–2	1.839	0.9	41.3	221.8
1.0 × 10–2	0.1839	0.3	35.5	303.2
0.5 × 10–2	0.1839	0.3	222.1	610.2

Several DNA configurations blocking a model channel have a hairpin-like structure of the freely hanging tail that prevents DNA crossing. To explore the contribution of different factors affecting this process, several values for DNA diffusivity, force field parameter controlling intramolecular rigidity, and transmembrane potential have been used. The summary of key findings is shown in Table 2. As expected, complete translocation time increases when DNA diffusivity is decreased. The force-field parameter (ε) that controls the DNA flexibility has little impact on the translocation dynamics. Finally, a major factor for the cylindrical channel determining speed of translocation is an applied potential bias, while a self-diffusion of individual nucleotides has only a secondary role to play (Table 2). These findings are in agreement with the previous atomistic simulations^42,50 as well as with experimental data that suggest that DNA diffusion in the nanopore is hindered and the major driving force for translocation is the electrophoretic drift.⁵¹

3.3. Equilibrium Ion Distributions

Figure 3 shows the equilibrium distribution of K⁺ and Cl^– along the pore axis. The ss-DNA molecule spans (on average) from −75 Å (extracellular cap) to 65 Å (intracellular milieu), which gives an average base to base distance of approximately 4.8 Å for ss-poly(dA)₄₀ (average from 10 separate simulations) and 4.9 Å ss-poly(dC)₄₀. Similar measurements for the base-to-base distance (C1′ to C1′ distance) from equilibrium MD are 4.6 and 5.2 Å for ss-poly(dA)₄₀ and ss-poly(dC)₄₀, respectively. These distances are in some contrast with reports on the observed fully stretched DNA conformations observed during steered MD simulations.⁵² However, the equilibrium MD and GCMC/BD simulations were run in the absence of strong biasing forces (up to 1.2 V) used in previous MD studies. The distributions for both ions inside the channel drastically differ from that reported for a nonblocked pore.^25,50

Figure 3.

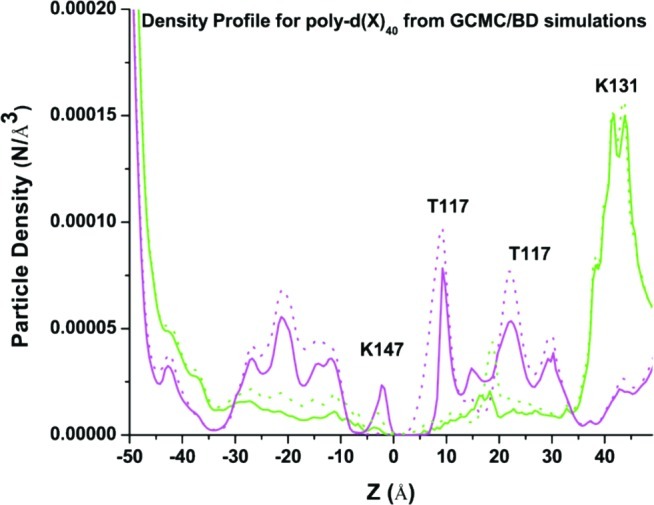
Ion density along the pore stem from GCMC-BD simulations with coarse-grained models of 5′-poly d(A)₄₀-3′ (shown in solid lines) and 5′-poly d(C)₄₀-3′ (shown in dotted lines) for K⁺ and Cl^– show in magenta and green, respectively.

The presence of a DNA molecule in the wide extra-cellular cap (from 40 to 0 Å) leads to an increase in the number of K⁺ ions and an apparent depletion of anion concentration. The Cl^– concentration in the stem region (from −2 to −51 Å) is approaching 0.0, with one notable exception around Z = 17 Å. The position of this peak correlates with the positions of several threonine residues (centered approximately at T₁₁₅). Interestingly, there is no well-defined peak in the anion concentration profile around a crucial residue for DNA capture and translocation (K₁₄₇),¹⁹ located in the constriction zone around Z = 0.0 Å. This may indicate that salt-bridging between phosphates and lysine side-chains are predominant, preventing interactions with small mobile ions. The density profile for K⁺ shows an increase in the number of ions for both cap and stem regions of the pore. This may indicate that ion-selectivity of the channel is reprogrammed by DNA and now its highly selective cation channel. MD simulations show the same trend with the anion-depleted area spanning for over 20–30 Å in the stem region, in agreement with previously published reports.²⁸

Both simulation approaches show an apparent periodicity in positions of peaks in the density profile for K⁺ that is expected because of spacing phosphate charges in DNA. It is worth mentioning that the initial MD setup was produced with a Monte Carlo placement of counterions, and a number of Cl^– ions were introduced in a stem region and the channel. It was found that it is hard to get a converged density profile in nanosecond simulations, and anion density in the stem region was continuously decreasing as a function of simulation time. A similar trend was observed in simulations with coarse-grained models with a time-scale required to reach converged profiles in hundreds of nanoseconds. The density profiles for both studied polynucleotides display notable differences. For example, the cation density profile for ss-poly(dC)₂₅ displays slightly greater ion densities than that for ss-poly(dA)₂₅ in the pore region with a well-defined peak around Z = −21 to −24 Å that correlates with positions of N121 and N139 both proposed to be playing an important role in the nucleotide contrast measurements.²⁰

3.4. Translocation of ss-DNA Oligomers through Model Biological Pore α-Hemolysin

An ultimate goal of nanopore-based sequencing is the enabling of high-sensitivity discrimination for signals produced by purine and pyrimidine bases. This discrimination in blockade levels may be enhanced by the mutations in the biological pore or chemical modifications of the translocated strand.^9,19 The molecular design of pores would require an in-depth understanding of DNA–pore interactions as well as of DNA dynamics in the confinement. To test whenever the coarse-grained description of DNA could capture differences in translocation dynamics, we considered two different homopolymers. Experimental data on DNA dynamics in nanopores have shown that the distribution of translocation events is complex and cannot be described by a standard exponential distribution.^16,19 From the histogram of translocation duration, one can obtain the most probable translocation time. However, these long-living states of DNA in a channel are outside the scope of this paper and beyond time-scales accessible by atomistic simulations.

To simplify our comparisons, we have used the same initial conditions, homopolynucleotides with the same number of nucleotides. In all of our studies with model cylindrical pores, ss-poly(dC)_n strands translocate across model cylindrical pores considerably faster than ss-poly(dA)_n. In the absence of the stabilizing interactions between nanopore and ss-DNA, the size difference may explain this result. A bulkier adenine base in a cylindrical pore is expected to have greater hydrodynamic friction and therefore would slow down more than C.^23,53 The experimental data, however, show a much more complex dependence of the translocation times on the chemistry of the base. An extension of the GCMC/BD algorithm with its realistic description of the heterogeneous charge distribution in the channel, dual buffers, and explicit account for ion dynamics to studies of real protein systems held great promise. To test its performance and compare it to all-atom simulations, we have focused on studies of two homopolymers with different bases, namely, poly(dA)_n and poly(dC)_n.

3.5. A/C Contrast in Simulations with Tethered Polymer

Coarse-grained simulations are able to predict blocked currents that clearly show discrimination between A and C. To enable an efficient comparison to experimental data often reported for biotin/streptavidin tethered DNA, we constrain one of the ends of the DNA (5′), thus modeling the ion current blockade for the 3′ entry of ss-DNA. On the basis of the results of all-atom simulations, we set the dielectric constant in the stem region of the protein to ε = 40 in the presence of ss-DNA. For these proofs-of-principle simulations, we used uniform bulk constants for ions and nucleotides in this work without scaling diffusion coefficients of ions and nucleotides inside the nanopore confinement. Under these conditions, the open pore current for 1 M KCl and V_mp = 120 mV is ∼186 ± 2 pA (55 pA for the K⁺ component and 131 pA for Cl^–), while blocked currents are 7 ± 3 pA (5 pA for the K⁺ component and 2 pA for Cl^–) and ∼13 ± 2 pA (11 pA for the K⁺ component and 2 pA for Cl^–) for the poly d(A)₄₀ and poly d(C)₄₀ blockades, respectively. An open pore is weakly anion selective, but the presence of ss-DNA renders it highly cation selective instead. This finding is in accord with results of atomistic simulations reported earlier.²⁸ In both cases, an averaged blocked current is between 3 and 8% of that for an open pore depending on the nucleotide, showing a somewhat deeper blockade than experimentally measured currents (12–15% in the experimental recordings).

The apparent difference may be related to the simplified treatment of nucleotide–ion interactions in the stem region. As a result, a more rigorous approach is required to fit interacting potentials between ions and nucleotides to include multibody effects. The use of implicit solvent may also lead to an increase in permeation barriers affecting blocked currents. Atomistic simulations also provide only indirect comparisons to experimental data as well, owed to imperfect force fields, insufficient sampling, and the much higher voltages usually used.¹⁵ It is important to point out the fact that blocked currents display an apparent dependence on the starting conformation of the captured polymer. Figure 4 shows the distribution of probabilities for residual currents for poly d(A)₄₀ and poly d(C)₄₀ blockades obtained from 20 independent simulations of 1 μs each. It is evident that ion currents are modulated by the conformational dynamics of the captured DNA. The noisy currents are well documented in a number of ss-DNA translocation studies across the nanopore.^9,54 In all-atom MD simulations, it may be challenging to run multiple replicas of the system required to obtain a convergent estimate for the blocked currents, whereas the method presented in this paper allows for multiple runs of several microseconds.

Figure 4.

Distribution of residual currents determined from 20 separate simulations with ss-d(A)₄₀ and ss-d(C)₄₀ blocking the pore. C = 1 M of KCl and V_mp = 120 mV.

It was suggested that a comparison of the relative properties or a contrast in this case could be more meaningful. A common measure for the contrast is the difference between residual currents ΔI_RES^{poly(dA)–poly(dC)}, e.g., blocked current divided by an open-pore current. Ashkenasy et al. reported that ΔI_RES for 3′ entry and immobilized DNA is ∼−10%, while Purnell et al. have reported ΔI_RES^{poly(dA)–poly(dC)} to be around −2.9%.⁵⁴ Theoretical estimates show ΔI_RES to be around −3%, in good accord with published data from Purnell et al.⁵⁴ and previous simulations with all-atom force fields. It has been shown before that an amount of the blockade in hemolysin does display strong voltage dependence, which seems to be supported by the current simulations. Therefore, the model presented here allows for reasonable resolution between A and C. The model also allows for discrimination between purine and pyrimidine bases in terms of their translocation rates (Table 4) as seen in experiments.⁹ In spite of all approximations used, the results show that the coarse-grained DNA model combined with explicit ions may offer a powerful instrument to study DNA dynamics in the nanopore.

Table 4. Orientation-Dependent Dynamics of poly-(dX)₄₀ from 1 μs of Simulation in 1 M of KCl and V_mp = 120 mV^a.

	en- trance	velocity (Å/μs)	zRMSDa (Å)	zRMSDc (Å)	zRMSDr (Å)
poly d(A)40	3′	1.6	5.1 ± 1.5	2.8 ± 1.5	4.1 ± 0.9
	5′	2.7	7.0 ± 1.9	2.7 ± 1.6	6.3 ± 1.8
poly d(C)40	3′	1.1	3.7 ± 0.8	1.6 ± 1.4	3.4 ± 0.8
	5′	1.7	5.3 ± 1.1	1.8 ± 1.3	5.0 ± 1.2

^azRMSDa = absolute root mean square displacement of all phosphates. zRMSDc = root mean square displacement of geometric center of phosphates. zRMSDr = root mean square displacement of all phosphates relative to the geometric center. The standard errors were estimated from 20 separate simulations.

3.6. Microsecond-Range Dynamics of ss-DNA in α-Hemolysin

Finally, with a microsecond simulation range, it is possible to access slow dynamics of the confined ss-DNA. Table 4 shows a collection of different zRMSDs (computed using z axis only) allowing a simple description of different modes of the confined DNA molecule. Of particular interest is zRMSDr, which characterizes displacement alongside the z axis of the DNA phosphates with respect to the DNA geometric center (equivalent to zRMSDa removing DNA translation). Traditionally, in polymer theory, this function is used to characterize the extension/compaction movements of a polymer in solution. Calculations show that captured DNA undergoes reptation-like dynamics, where the end to end distance for the capture portion of the DNA molecule fluctuates between 57 and 80 Å in just 1 microsecond of simulation. The amplitude of this movement is comparable to the vertical translocation itself. These slow modes may explain an excess noise in the electrophysiological recordings of the DNA blockade of ion currents,¹⁷ and the strategy targeting suppression of these modes may help to improve the base contrast. They are shown to be DNA-orientation-dependent and likely are related to intrinsic conformational dynamics of DNA.

3.7. Voltage and Concentration Dependence of the ss-DNA Translocation Across α-Hemolysin

BROMOC simulations were performed to examine the effect of salt concentration as well as voltage bias on the translocation rate. It is important to mention that these simulations are reported for already-captured DNA. Therefore, these are not accounting for a capture probability and its dependence on applied voltage that is known to show a considerable dependence on the capture voltage.^55,56 To assess the effect of salt concentration on the translocation rate of single stranded DNA, three different salt (KCl) concentrations have been used: 0.15, 0.3, and 1.0 M KCl. The translocation is faster when the ion concentration is decreased, which might be ascribed to an ion shielding effect. When the number of ions that interact with ss-DNA is low, the ion shield around ss-DNA is absent or less likely to be complete. Therefore, the effective volume of the ss-DNA molecule is smaller, and the net charge is more negative, thus speeding up the translocation process. To assess the effect of external applied voltages on the ss-DNA translocation rate, we applied five different voltages (50, 120, 200, and 300 mV) generally accessible to experiments. Translocation rates display only a modest increase as a function of applied voltage. This finding is consistent with available experimental data⁴¹ (Table 3).

Table 3. Translocation Rate of poly-(dA)₄₀ with 3′-End Entrance As a Function of Salt (KCl) Concentration and External Electric Potential^a.

	50 mV	120 mV	200 mV	300 mV
0.15 M		2.8 ± 0.04
0.3 M	1.2 ± 0.04	1.8 ± 0.03	1.9 ± 0.03	2.1 ± 0.03
1.0 M		1.6 ± 0.03

^aUnit for velocity is Å/μs. The standard errors were estimated from 10 separate simulations

3.8. Effect of DNA Orientation on Translocation Rate

Table 4 summarizes findings on the orientational discrimination of the DNA transport across wt-αHL. The translocation rates were estimated as described in section 2.5. PolyA entering the pore at the 5′ end displays faster translocation rates when compared to the 3′ entrance. This is in good agreement with experimental findings, where it was reported that ss-DNA translocates up to 1.7 times faster depending on its orientation.²⁸ It has been suggested that orientational discrimination is defined by the fine differences in interactions between captured DNA and the αHL pore. While protein–DNA contacts play an important role in the translocation of DNA, the results in Table 4 suggest that intrinsic dynamics of ss-DNA itself may be an important factor to consider. The captured strand undergoes reptation-like dynamics that can be facilitated or inhibited by the confinement. Table 4 summarizes key characteristic functions of the polymer dynamics in the nanopore. It is evident that 5′ entry results in a considerable increase in most of the computed MSDs characterizing the displacement of the strand along the pore.

4. Discussions

The combination of the well-established coarse-grained model with the developed GCMC-BD algorithm led to results that are in reasonable agreement with experimental data on the polymer translocation across a nanopore with nonuniform charge distribution. An advantage of the developed scheme is that it allows 3D sampling of the polymer dynamics inside the pore on a microsecond time scale. Furthermore, the developed scheme allows for investigation of the microscopic factors controlling DNA dynamics in the pore. To explore voltage-dependent dynamics, we focus on a truncated hemolysin system similar to that reported earlier, as well as a model state with a cylindrical pore.

4.1. Voltage Effects on DNA Translocation Rates in Model Cylindrical Pore

For a matter of comparison with a biological pore, voltage-driven translocation rates (k_t) and translocation rates with diffusive displacement (k_d) were computed as described in the Methods and Computational Models section for the single stranded adenine dodecamer (poly(dA)₁₂) in a cylindrical pore. The oligomer geometric center was positioned at the middle of the cylindrical pore. The pore was 50-Å-long with 9 Å radii, and an internal repulsive wall of 1 Å with a repulsion constant of 200 kcal/mol. The temperature used was 300 K; a dielectric constant of 80 and a diffusivity for DNA of 0.001 Ų/ps were also used. We used an implicit ionic solution with an ionic strength of 0.3 M. There are only repulsive forces operating between this phantom membrane and the DNA. During all translocation simulations, different external voltages were applied: 0, 150, 250, 500, and 1000 mV. Translocation simulations for each voltage were repeated 30 times using different random seed numbers. The rates (k_t and k_d) were computed at L = 12 Å (see section 2.5) and are plotted in Figure 5. As can be seen, the voltage-driven translocation rates component is important in the studied potential bias range. Both rates display a linear dependence on the applied potential with similar slopes. At 0 mV, k_t intercepts at ∼0 Å/μs, while k_d is positively displaced due to the small but statistically significant diffusive displacement component (f). The decomposition of the translocation rates clearly shows that applied force (voltage) is the main driver of translocation, while the diffusional component is only a secondary factor. Comparing these translocation rates with those in the more realistic pore, α-hemolysin, we observe that rates are considerably higher in the first. This can be explained due to the electrostatic interaction between DNA and hemolysin that is a crucial fact and acts as a “friction” retarding DNA translocation. This “friction” can be the reason for the nonlinear translocation velocity/applied voltage dependence.

Figure 5.

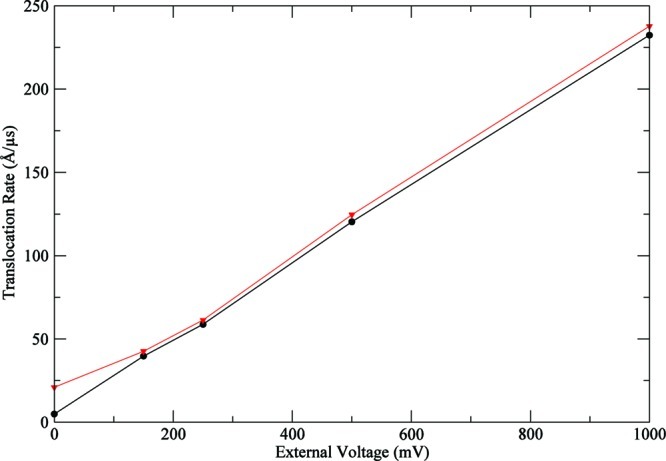
Translocation rates dependence on the external voltage for A-dodecamer in a 9 Å (width) × 50 Å (length) cylindrical pore. In black, voltage-driven translocation rates (k_t). In red, translocation rates with diffusive displacement (k_d).

4.2. DNA Translocation in a Nanopore with a Nonuniform Charge Distribution

To study the voltage-dependence of polymer translocation in a nanopore with nonuniform charge distribution, we chose a truncated form of the α-hemolysin protein shown in Figure 6A. The stem region was proposed to be a computationally amenable alternative to the full channel. It contains residues forming a proposed constriction zone and thus can provide a reasonable description of the actual pore, considerably reducing computational burden. Reduction in the DNA translocation time in artificial and biological nanopores is one of the key factors in the development of potentially useful sequencing devices.⁵⁷ First, we simulated ss-DNA transport across the truncated pore with all charges on. Figure 7 shows time-dependence of the displacement of the 5′-ss-poly(dA)₂₅-3′ as a function of the applied voltage. The results collected in Figure 7 show no clear dependence of the displacement on the applied voltage in part due to limited simulation times. Nonexponential escape dynamics has also been reported experimentally, where an anomalously long residence time of the polymer in nanopores was measured.¹⁶

Figure 6.

The sagittal dissection of the model pore in surface representation. The implicit membrane zone is indicated by a solid black line. The pore orientation in the membrane is marked by the two lysine residues (K147 cis side and K131 trans side). K⁺ and Cl^– ions are shown as magenta and green spheres, respectively. The initial positioning of the ss-d(A)₄₀ portion confined in the pore region is shown as ball and sticks.

Figure 7.

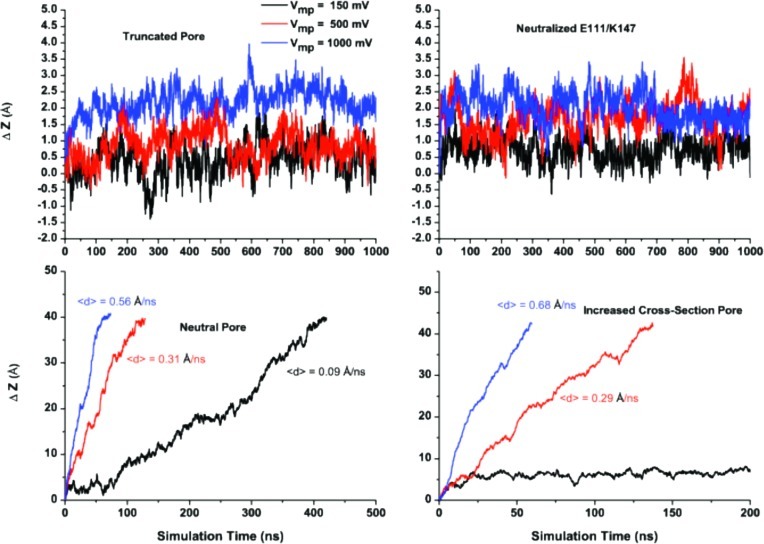
Effect of the pore confinement on the voltage-dependence of translocation. Top: Time series for the polymer displacement as a function of applied voltage along the z axis of the truncated pore fully charged and with the neutralized first constriction zone, e.g., E111/K147 are shown on the left and right panels, respectively. Bottom left: Voltage-dependence of the DNA displacement in the neutralized pore. Velocity was determined from a linear fit of the time series for displacement. Bottom right panel: Same with an increased pore cross-section. The stern radius assigned to every atom has been scaled down by 50%, while all of the partial charges were kept on the amino acids forming the pore.

To elucidate the role of geometry in the translocation dynamics of DNA inside the pore, we neutralized pore-forming residues, e.g., retaining the same accessible volume but removing the protein static field or increasing accessible volume across the pore. A salt concentration of 1 M of KCl was maintained in all of the simulations. Thus, it is expected that most of the pore charges will be effectively screened by the mobile counterions. The complete neutralization of the beta-barrel led to almost linear dependence of the translocation velocity on the applied voltage. This may suggest that pore-specific interactions with DNA play an important role in determination of translocation rates, while the confinement presented by the pore is insufficient to explain anomalous escape dynamics of the biopolymer. At the same time, a 2-fold increase in the solvent-accessible area allows for almost complete elimination of the electrostatic hindering and, again, recovers linear dependence of DNA translocation rates on the applied voltage seen in the model cylindrical pore. Interestingly, this pore clearly shows that there is a minimal voltage requirement for fast translocation of ss-DNA. The use of a membrane potential of 150 mV or lower is insufficient to enable complete translocation in 1 μs of simulation. At the same time, higher voltages produced essentially linear dependence of the displacement on simulation time.

Next, we examined the effect of the charges in the first constriction zone proposed to play a significant role in ss-DNA transport across α-hemolysin.^19,55 The removal of the charges at the first constriction zone alone is insufficient to provide linear dependence on the applied voltage. This finding is in good agreement with the range of mutations that were aiming at a decrease of the threshold barrier by replacing charged residues at or near the first constriction zone.⁵⁵ Nevertheless, the pore with a neutral pair of residues (K147–E111) show greater displacements at higher voltages. Experimentally, removal of E111 (E111N) led to a 2-fold increase in the most probable translocation time.⁵⁵

5. Conclusion

A comprehensive theoretical scheme developed in this work extends the existing GCMC/BD algorithm for the simulation of ion to DNA dynamics in model and biological pores. It was found that the molecular introduction of the DNA molecule modifies ion distribution along the pore axis, converting it into a cation selective channel. Atomistic simulations supported these results. It was also shown that ss-DNA affects ion distribution in the stem region in a sequence-dependent mode both in atomistic and coarse-grained simulations. The results obtained using CG-GCMC/BD simulations appear to be consistent with the available experimental data. This indicates that both atomistic and coarse-grained approaches are able to capture the essential electrostatic interactions among ions, solvent, and protein. The proposed approach is capable of reproducing some of the key features for DNA translocation in nanopores, e.g., an asymmetric 5′ vs 3′ entrance and purine vs pyrimidine discriminative translocation. In a series of computational tests, it was shown that the developed protocol allowing for simulations reaching up to tens of microseconds is readily available at a relatively low computational cost, thus providing a platform for the rational design of a pore with programmed properties. This simulation time can even be increased by the parallelization of BROMOC code. Several theoretical papers reporting an extension of coarse-grained DNA models to explicit ion simulations have been published providing the scientific community with at least three different force fields to be tested and thus offering an inexpensive computational tool that may enhance our understanding of polymer dynamics in nanopores. BROMOC-D will provide better accuracy results by improving pairwise interaction potentials and diffusivity models. The short-term future goal is to adopt a robust methodological approach to develop nucleotide–ion parameters for the coarse-grained implementation of DNA. This can be done utilizing a recently developed scheme based on reversed Monte Carlo from Lubartsev et al.,⁵⁸ allowing better effective potentials, which include a more realistic description of solvent-mediated effects based on matching distribution functions.

Supporting Information Available

Movie S1: Ions and ss-DNA dynamics in the confinement of alpha-hemolysin from 1 μs simulation in 1 M of KCl. This information is available free of charge via the Internet at http://pubs.acs.org/

The authors declare no competing financial interest.

Author Contributions

^† Denotes equal contribution

Funding Statement

National Institutes of Health, United States