Rapid hybridization of nucleic acids using isotachophoresis

Abstract

We use isotachophoresis (ITP) to control and increase the rate of nucleic acid hybridization reactions in free solution. We present a new physical model, validation experiments, and demonstrations of this assay. We studied the coupled physicochemical processes of preconcentration, mixing, and chemical reaction kinetics under ITP. Our experimentally validated model enables a closed form solution for ITP-aided reaction kinetics, and reveals a new characteristic time scale which correctly predicts order 10,000-fold speed-up of chemical reaction rate for order 100 pM reactants, and greater enhancement at lower concentrations. At 500 pM concentration, we measured a reaction time which is 14,000-fold lower than that predicted for standard second-order hybridization. The model and method are generally applicable to acceleration of reactions involving nucleic acids, and may be applicable to a wide range of reactions involving ionic reactants.

Nucleic acid hybridization is ubiquitous in molecular biology, biotechnology, and biophysics, and has been instrumental in the development of numerous important techniques including genetic profiling (1, 2), pathogen identification (3, 4) sequencing reactions (5), and single-nucleotide polymorphism typing (6). In nucleic acid hybridization, two single-stranded nucleic acid molecules with complementary sequences bind and form more stable double-stranded molecules. Diffusion, transport, and reaction rates limit hybridization of nucleic acids at low concentrations (7). While diffusion and transport limitations can be effectively overcome using mixing and flow control methods (8–10), reaction rates still limit assay times and sensitivity (7, 11).

Nucleic acid amplification techniques (e.g., polymerase chain reaction, PCR) are often used as an initial step to improve sensitivity and accelerate hybridization. However, amplifications such as PCR can suffer from as much as 10,000-fold amplification bias (1, 4), require significant sample preparation (12), can be difficult to reproduce quantitatively across laboratories (13), and require a well-controlled environment (12). Amplification-free hybridization avoids amplification-associated sequence bias and may be particularly important for applications beyond the conventional laboratory settings.

Temperature, monovalent salt concentration, and divalent cation concentration (in particular, magnesium ion) are most commonly used to control the rate of hybridization. The hybridization of short oligonucleotides in the presence of 50 mM MgCl₂ has been reported as fivefold faster than at 1 mM MgCl₂ (14). Similarly, higher salt concentration and higher temperatures can accelerate reactions (14–16). However, these approaches reduce the energy of binding events and strongly affect specificity. Adjustment of these hybridization parameters is therefore often a trade-off between acceleration and specificity (12, 17). Other methods such as volume exclusion by inert polymers (e.g., dextran sulfate) (18, 19), and the phenol emulsions reassociation technique (PERT) (20, 21) achieve 10- to 100-fold hybridization accelerations, but are complex to automate or control. Dave and Liu (22) recently used organic solvents for 70-fold hybridization acceleration, with negligible loss of specificity.

Isotachophoresis (ITP) is an electrophoresis technique that uses two buffers consisting of a high mobility leading electrolyte (LE) and a low-mobility trailing electrolyte (TE). In peak-mode ITP (23) sample species with mobilities bracketed by those of the LE and TE focus into an order 10 μm scale TE-to-LE interface. This focusing can preconcentrate, mix reactants, and expedite reactions with negligible change of the hybridization energy associated with binding events. ITP makes use of standard, aqueous buffer ions and simple microfluidic channels or capillaries.

We present an analytical model, experimental validation, and demonstration of on-chip ITP-driven acceleration of nucleic acid hybridization, enabling more than 10,000-fold increase in hybridization rates for dilute samples. Preconcentration with ITP has been applied to antibody-antigen reactions or nucleic acid hybridization reactions for increasing reaction rate or better sensitivity. Kawabata and co-workers showed an on-chip immunoassay method employing ITP for the enhanced sensitivity of immune reaction (24). Persat et al. (25) and Bercovici et al. (26) each presented the simultaneous extraction and detection of nucleic acids by combining ITP and the hybridization of molecular beacons and target nucleic acids. Persat et al. (25) applied it to sequence specific detection and quantification of miRNA in human liver from pre-purified total RNA. Bercovici et al. (26) applied it to rapid detection and identification of bacterial urinary tract infection. Despite these recent successful applications and strong interests in ITP-based hybridization kinetics, we know of no study to date that has presented analysis of the coupled ITP and reaction process. We here offer a study aimed at understanding the coupling of ITP with hybridization kinetics, and present a model that captures the relevant dynamics. We find the kinetics of ITP has an inverse square root dependence on concentration of excess reactant, which is in contrast to the inverse dependence for the standard second order hybridization. This result predicts significant acceleration of hybridization rate for low-reactant concentrations, the most challenging regime. We also present a detailed experimental study and use this to validate our model.

Results

Standard Second-Order Hybridization Reaction Kinetics.

We analyze kinetics of homogenous nucleic acid hybridization (e.g., in aqueous buffer) where two single-stranded DNA species A and B form double-stranded DNA, AB. Following Tsourkas’ notation (27), the second order hybridization reaction can be expressed as

[1]

Here c_A and c_B are the concentrations of the reactants A and B, and c_AB is the concentration of the product AB. k_on and k_off are respectively the reaction on- and off-rate constants, determined in part by the sequence and length of the nucleotides. Denoting the total concentrations of species A and B as A₀ and B₀, respectively, species conservations are given by:

[2]

Before introducing the effects of ITP, we first review characteristics of the well-known model for standard second-order hybridization kinetics. An interesting limit for our studies is the case of excess concentration of one species A, such that A₀≫B₀, and the case of a sufficiently low equilibrium constant, K = k_off/k_on ≪ A₀. In this regime, the fraction of reactants hybridized, f_std = c_AB/B₀, can be expressed (28) as:

[3]

The subscript “std” indicates a property associated with this “standard” second-order hybridization (without ITP). Accordingly, f_std is initially zero and approaches unity as reaction progresses. From. Eq. 3 the total amount of hybridization product at steady state is given by the total concentration of the low-abundance species, B₀. The characteristic hybridization time scale for 50% completion of reaction, τ_std, is given by

[4]

τ_std is thus inversely proportional to the total concentration of the excess species, resulting in longer hybridization time as the excess species concentration is reduced. This limit serves as an important comparison to the ITP-based reaction described below.

ITP-Aided Hybridization Kinetics Model.

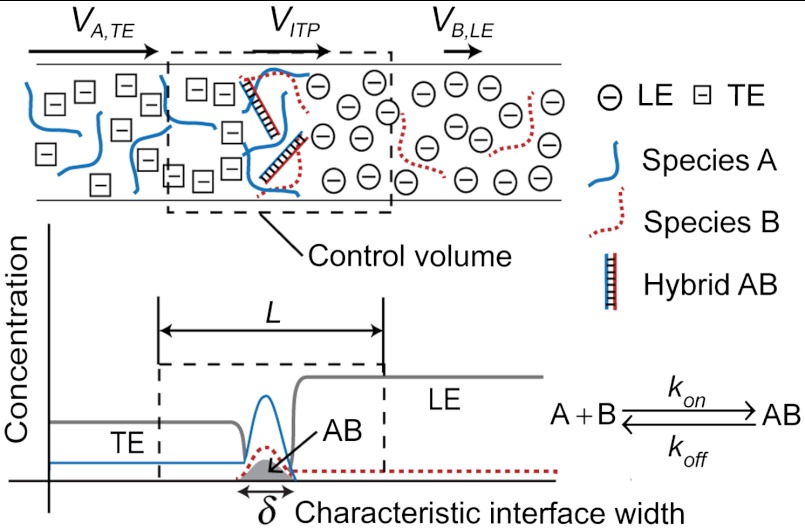
We present both numerical and analytical models that capture the coupled dynamics of ITP focusing and reaction kinetics. ITP drives simultaneous and continuous mixing and focusing of reactants into a common electromigrating reaction zone. In this reaction zone, highly concentrated reactants rapidly produce hybridization product. The process is described qualitatively in Fig. 1. To simplify the analysis, we consider a case in which the species A and B are initially mixed with TE and LE, respectively. TE and LE are chosen such that their electrophoretic mobilities bracket those of A, B, and AB. This is possible as DNA mobility in an aqueous buffer is only weakly dependent on its size, and varies approximately in the range (3.2–3.8) × 10^-8 m² V^-1 s^-1 (29). Species A and B mix and react only at the ITP interface. The characteristic ITP interface width δ is determined by a balance between electromigration and diffusion. For constant current, ITP theory predicts constant δ; however, in practice, several factors may cause its increase in time (30, 31).

Fig. 1.

Schematic depicting acceleration of nucleic acid hybridization reactions using ITP. Two single-stranded DNA species A and B are focused at a narrow (order 10 μm) interface between the TE and LE in a microchannel. TE and LE are chosen such that their mobility bound all of the nucleic acid mobility. In this model system, species A is mixed with TE, and species B is mixed with LE, thus reaction occurs only at the interface where both species focus. The high concentrations of reactants at the interface lead to a corresponding increase in hybridization reaction rate. The arrow lengths at the top respectively denote the relative speed of species A in TE, of the ITP interface, and of species B in LE (LE and TE ions migrate at velocities equal to that of ITP interface). We consider a control volume moving with the interface at a velocity V_ITP. The control volume extends over a length L, which is significantly larger than the characteristic interface width, δ, as shown.

For the numerical model, we regard the ITP interface width as a time-varying quantity δ(t) and assume colocated Gaussian concentration profiles for all focused species. As described by Garcia-Schwarz et al. (31), this assumption is reasonable when the mobilities of focused species are significantly greater and less than the those of TE and LE, respectively, and when concentration of focused species is significantly lower than those of both TE and LE, as we consider here. The species concentrations c_i are assumed unsteady and one-dimensional, so the conservation equations in the frame of reference of the moving ITP zone are

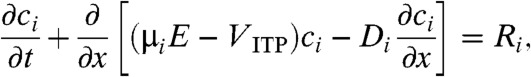[5]

where μ_i and D_i are respectively species electrophoretic mobility and diffusivity; E is the local electric field; and i represents species A, B, or AB. R_i is the reaction source term equal to -k_onc_Ac_B + k_offc_AB for i = A and B, and equal to k_onc_Ac_B - k_offc_AB for i = AB. The electrophoretic mobility is defined as μ = u/E where u is species drift velocity, thus V_ITP can be expressed as μ_LE ∗ E_LE, where E_LE is the electric field in the LE zone. We integrate these equations over the control volume of Fig. 1, and so express the problem in terms of a volume-averaged concentration 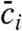defined as

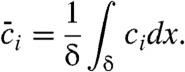[6]

We approximate the volume averaging over the control volume as an integration over the ITP interface width δ because the concentration of DNA species in the ITP zone is often 10³ to 10⁴ times higher than that in the TE and LE zones. Our volume averaging yields:

[7]

with η_TE and η_LE given by

[8]

Here, subscripts “TE”, “LE”, and “CI” denote respectively properties related to the trailing, leading ions (the anions of the TE and LE), and the (cationic) counter ion. The superscript “well” denotes a property at the upstream reservoir containing TE at its initial concentration. A₀ and B₀ are the respective reservoir concentrations of species A and B in the TE and LE wells. See SI Materials and Methods for the details of this derivation. The first term on the righthand side of the Eqs. 7i–ii represents the influx into the control volume due to electromigration (evaluated at the influx control surfaces shown in Fig. 1, each of which is significantly away from the ITP zone). The second term on the righthand side of these two equations represents the effect of varying ITP interface width on the volume-averaged species concentration. The ITP interface width, δ, can be measured as a function of time from an ITP experiment focusing a fluorescent species. See Khurana et al. (23) for general formulation of the analyte accumulation rate parameters V_ITP, c_LE, and ion mobilities. We numerically solve this set of non-linear ordinary differential equations (ODEs) for the volume averaged species concentrations to describe nucleic acid hybridization kinetics under ITP focusing.

For an analytical solution, we assume constant interface width δ(t) = δ_o, one species at excess concentration at the ITP interface, and sufficiently low equilibrium constant, K. For ITP, the latter two can be expressed as:

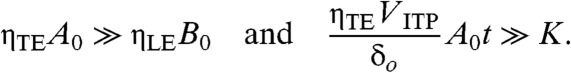[9]

In this limiting regime analogous to what we explored for the standard second-order kinetics, we obtain the exact (the first equality) and approximate (the second equality) analytical solutions to Eq. 7:

[10]

where and erfi is the so-called imaginary error function, erfi(x) = -ierf(ix), which yields real values. We obtain the approximate analytical solution by expanding erfi in a Taylor series and keeping only the leading-order term. We will present both numerical and exact analytical model solutions in the following section.

Hybridization Acceleration by ITP.

We investigate the approximate analytical model (second equality of Eq. 10) in comparison with the standard case, Eq. 3, to gain physical insights on hybridization kinetics under ITP conditions. There are two key differences. First, the ITP case contains a time-dependent prefactor B_0,ITP, unlike the constant B₀ in standard hybridization. B_0,ITP is a linear function of time, and represents an ever-increasing limit for the possible product concentration at the ITP interface. Normalizing 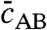by B_0,ITP, we derive the fraction of reactants hybridized within the ITP interface,

[11]

We now point out the second difference versus the standard case: the second-order time term, t², in the exponent. This dependence reflects the simultaneous effects of the second-order reaction and ITP-aided increase in total concentration of the excess species A, which is proportional with time. The time scale for half of the low-abundance species to be hybridized at the ITP interface is given by

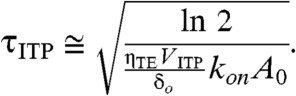[12]

We see the standard case’s time scale was inversely proportional to total concentration, while the ITP-driven reaction time scale has an inverse square-root proportionality on reservoir concentration. We can define a figure of merit for the hybridization “acceleration” as the ratio of the standard hybridization time scale to the ITP-driven hybridization time scale as follows:

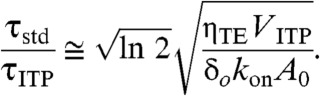[13]

This result demonstrates the dramatic speed-up in reaction rate offered by ITP, particularly in the most challenging regime of low k_on and A₀ values. Fig. 2 shows a plot of τ_std/τ_ITP for the variation of reactant concentrations, and relevant kinetic on-rate constants. For example, at 100 pM, the approximate analytical model predicts τ_std/τ_ITP of 10,000. The prefactor implies that the acceleration is dependent on the value of fraction of hybridization. If we compare the standard and ITP characteristic time scales to reach higher value of fraction hybridized, the figure of merit will have higher value of prefactor. Note the results of Fig. 2 are independent of the absolute value of B₀ so long as B₀ is much lower than A₀, as per our assumptions. See SI Materials and Methods for similar scaling analyses in terms of current density, j. We also present in Fig. S1 a comparison of the fraction of species hybridized for the ITP versus standard hybridization kinetics.

Fig. 2.

Analytical model results showing the ratio of standard hybridization half-time to ITP hybridization half-time for a relevant range of initial reactant concentrations and on-rate constants. The acceleration factor (time scale ratio) increases with both decreasing initial concentration and decreasing on-rate constants. For example, for a typical k_on of order 10³ M^-1 s^-1, and A₀ of 100 pM, we see over 10,000-fold increase in hybridization rate. For these calculations, we used typical parameter values of η_TE = 50, V_ITP = 100 μm/s, and δ_o = 50 μm.

Experimental Validation of ITP Hybridization Kinetics Model.

We experimentally validated the numerical and analytical hybridization models for ITP. We used hybridization of DNA molecular beacons (MBs) (32, 33) and synthetic DNA oligonucleotides (targets) to quantify hybridization rate [the probe sequence we used is a 27 base universal probe sequence for bacteria (34)]. We used targets as excess species, A, and MBs as low-abundance species, B. The model predictions are plotted with no fitting parameters. We substituted the experimentally measured parameter values, and obtained the numerical solution for our experimental conditions using fourth-order Runge-Kutta integration (35). δ(t) in the numerical model is approximated as a linear function whose slope and intercept are extracted from measurements of ITP zone width versus time. Details associated with experiments to quantify parameters including kinetic on-rate constants (k_on), ITP velocity (V_ITP), and ITP interface width (δ) are presented in Figs. S2–S4.

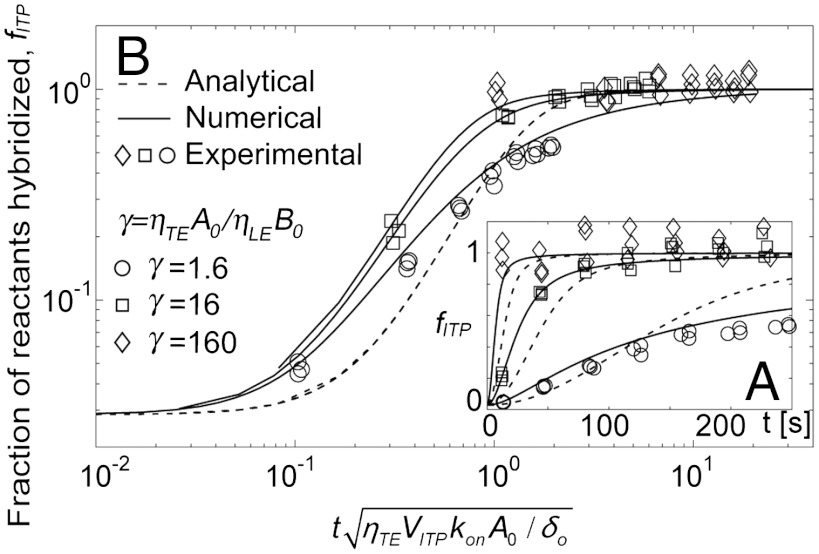
In Fig. 3A, we present the fraction of reactants hybridized, f_ITP, versus time for the exact analytical solutions (first equality of Eq. 10, dashed lines), numerical solutions (Eq. 7, solid lines), and experimental data (symbols). We show three replicates for each of three experimental conditions: γ = η_TEA₀/η_LEB₀ = 1.6, 16, and 160. We see good agreement between the experimental data and the numerical model for two orders of magnitude range of excess reactant concentration. The numerical model is applicable to a wide range of hybridization reactions without restrictions on the initial species concentrations. The analytical model captured overall trends and the time scale of the kinetics serving as a reasonably close approximation to ITP reaction kinetics. However, the analytical model shows deviations from the data, which we attribute to its two key assumptions: constant interface width and one excess species (γ≫1). The former resulted in underprediction of reactant concentrations at short times and overprediction at large times due to time-averaging the increasing interface width. The γ = 1.6 case shows additional error for times greater than about 100 s as this case falls outside the excess species assumption. We compare error resulted from each assumption in Fig. S5.

Fig. 3.

Comparison of analytical and numerical predictions using the ITP-based hybridization kinetics model with experimental data. Shown are the fraction of reactants hybridized, f_ITP, obtained from measured total fluorescence intensity of hybrid and MBs, as per Eq. 14. Solid lines present numerical solutions based on the coupled ordinary differential equations [Eq. 7] with a time-varying width approximated as a first order polynomial. Dashed lines present the analytical model based on the second equality of Eq. 10. (A) We show the experimental data versus time at target concentrations of 1, 10, and 100 nM, and a fixed molecular beacons concentration of 10 nM. (B) We show the same data plotted in log-log scale with the time axis normalized by the characteristic time scale predicted by the analytical model [Eq. 12]. No fitting parameters were used in the predictions: k_on,V_ITP, δ(t), δ_o are measured from experiments. All parameter values used for the model predictions are presented in SI Materials and Methods.

Fig. 3B shows the collapse of data trends provided by the scaling derived from our approximate analytical model. We plotted the same data as that of Fig. 3A on a time axis normalized by the characteristic time scale suggested Eq. 12. We observe good collapse of the experimental data into a band grouped around the model curves. This strongly corroborates the predicted 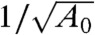dependence of the characteristic time scale associated with ITP hybridizations. As predicted, the analytical solutions are all represented by a single curve (dashed line), but slightly shifted from the experimental data band, which we attribute to implementation of the timeaveraged interface width. We discuss the repeatability and robustness of ITP-hybridization in SI Materials and Methods.

Demonstrations of Hybridization Acceleration Using ITP.

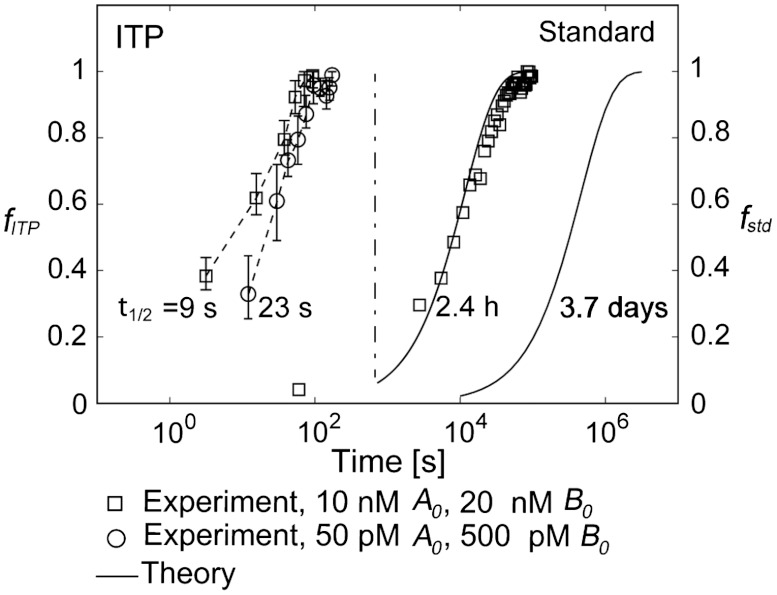
In Fig. 4, we present a demonstration of the reaction acceleration offered by ITP for DNA hybridization. Plotted are the fractions of reactants hybridized versus time for 10 nM MB and 20 nM target concentration (squares), and for 50 pM MB and 500 pM target concentration (circles). For the former case, we directly compare half times extracted from the experimental data of both standard and ITP hybridization. For the latter case, we present experimental measurements for the ITP hybridization, and compare these to a prediction of the standard case since the associated hybridization experiments take over 10 days to reach steady state. We attempted these but found it difficult to extract meaningful data due to longterm effects such as fluorophore photobleaching and variations in environmental conditions (e.g., room temperature). We measured a half time of reaction of 2.4 h for the standard second order reaction at 10 nM MB and 20 nM target concentrations. By comparison, the ITP hybridization half time for the same reaction was 9 s. This constitutes a 960-fold acceleration, and gives a direct demonstration of DNA hybridization speed-up using ITP. The 50 pM MB and 500 pM target hybridization prediction for the second-order experiment was 3.7 days to complete 50% of the reaction. ITP experiments with the same loading concentrations yielded a reaction half time of 23 s; a 14,000-fold lower time scale. The results shown in Fig. 4 experimentally confirm the predicted reaction acceleration, and again validate the characteristic time scale derived from the analytical model.

Fig. 4.

Experimental demonstration of the 960-fold and 14,000-fold hybridization acceleration for reactions with order 10 nM and 100 pM DNA oligonucleotides, respectively. The fraction of reactants hybridized is presented against time for both standard hybridization (right two curves) and ITP-based hybridization (left two curves). Each data point shown for ITP-based hybridization is the average of four realizations with range bars representing the full absolute range of measured values. Solid lines denote theory predictions based on Eq. 3 using experimentally measured k_on of 4750 M^-1 s^-1. For the case of 10 nM molecular beacons and 20 nM target concentration (squares), the half-times for standard and ITP-based hybridization were 2.4 h and 9 s, respectively, constituting a 960-fold hybridization speed up. For the case of 50 pM beacons and 500 pM target concentration (circles), we compare experimental data of ITP hybridization with the theory-prediction for the standard hybridization since standard hybridization experiment required more than 10 days to reach steady state. The expected half time of 3.7 days of the second order standard hybridization was significantly reduced to an experimentally measured 23 s using ITP, indicating a 14,000-fold hybridization speed up.

Discussion

We presented a reduced-order numerical model, a closed-form analytical solution, validation experiments, and demonstrations of a novel assay for accelerated reaction kinetics under ITP. Our assay is based on cofocusing and mixing of nucleic acids at a narrow, order 10 μm ITP interface. The focusing of species results in locally high concentrations, and thereby accelerates their binding.

We used volume-averaging of the relevant conservation equations to obtain a simplified numerical model consisting of ordinary differential equations describing the dynamics of two-species hybridization in an ITP interface. Under the simplifying assumptions of a constant ITP interface width and one abundant species, we obtained a closed-form analytical solution. This solution reveals a new characteristic time scale inversely proportional to the square-root of initial concentration (versus the inversely proportional relation in the standard case). The model provides good qualitative prediction across a wide range of conditions. The main source of inaccuracy of the analytical model is its simplifying assumption of constant ITP interface width. ITP interface width determines volume-averaged concentrations and therefore hybridization rate. ITP width can vary as ITP interface migrates through the channel due to changes in the dispersion dynamics (31).

ITP-based hybridization is most beneficial at low concentration. For example, at 1 μM hybridization is accelerated order 100-fold, but 10,000-fold and higher at < 100 pM. We compared the ITP-hybridization and standard reaction cases to demonstrate the dramatic increase of reaction time offered by ITP. At 500 pM target concentration, the measured time scale of the ITP hybridization reaction was 14,000-fold lower than that predicted for the standard second order reaction. Two limitations to the process are that the total amount of reacted species is limited by the volume of the microfluidic channel, and that the process as demonstrated here is applicable only to ionic reactants.

We focused on DNA hybridization and used molecular beacons as the low-abundance reacting species to monitor reaction rates. However, ITP is applicable to a wide range of chemical and biological species, and the model and method presented here likely can be applied to achieve rapid reactions of other charged species, from small molecules to macromolecules. A large number of chemical and biological assays rely on detecting the binding of a molecular probe and specific target molecule, and are often limited by reaction rates. ITP-based hybridization has the potential to improve both the detection time and the limit of detection of such sensors. This could be particularly beneficial to chemical and biological sensors intended for use at the point-of-need, including point-of-care diagnostics, forensics, and environmental monitoring.

Materials and Methods

DNA and Buffers.

We quantified hybridization kinetics using DNA molecular beacons (MBs) (32, 33) and synthetic DNA oligonucleotides (targets). MBs yield 10- to 100-fold fluorescence intensity enhancement as they bind to target sequences (14, 32). The 27-mer MB probe sequence was perfectly complementary to our target sequence, and flanked by six bases complementary to each other. We labeled the 5′ terminus with Cy5, and the 3′ terminus with Black Hole Quencher 2 (BHQ2): 5′-/Cy5/CCG AGC [CAT CGT TTA CGG CGT GGA CTA CCA GGG] GCT CGG/BHQ2/-3′ (probe sequence in brackets). The target sequence was 5′-TAG ATA [CCC TGG TAG TCC ACG CCG TAA ACG ATG] TCG ACT-3′. The DNA species were purchased from Integrated DNA Technologies (IDT), and 100 μM MBs and 1 mM target oligonucleotides stock solutions were stored at -20 °C.

For the ITP hybridization model validation experiments (Fig. 3), we mixed 10 nM MB in the leading electrolyte (LE) buffer composed of 250 mM HCl, 500 mM Bistris, 2 mM MgCl₂, and 0.1% polyvinylpyrrolidone (PVP). We used PVP for suppression of elctroosmotic flow (EOF) (36) and equal concentrations (in all experiments) of Mg²⁺ to promote kinetic rates of hybridization (14). We used 1, 10, and 100 nM target DNA concentrations in the trailing electrolyte (TE) buffer composed of 100 mM Tricine, 100 mM Bistris.

For demonstration of rapid ITP hybridization (Fig. 4), we used the same LE buffer as in the validation experiments, except we used 1% PVP for enhanced EOF suppression. Here, our TE buffer was 20 mM Tricine, 40 mM Bistris, and 1% PVP. The lower, 20 mM TE buffer concentration results in higher electric fields (23), thus providing higher accumulation rates at the expense of lower buffering capacity. For the demonstration of 960-fold acceleration, we performed both ITP and standard hybridization experiments using 10 nM MBs and 20 nM targets. To show 14,000-fold speed-up, we performed ITP experiments using 50 pM MBs with 500 pM target DNA, and compared the data with theory based predictions.

Tricine, Bistris, and MgCl₂ were obtained from Sigma-Aldrich. PVP (MW 1.3 MDa) was purchased from ACROS Organics (Thermo Fisher Scientific). All solutions were prepared in UltraPure DNase/RNase free deionized (DI) water (GIBCO Invitrogen). 1 M concentration buffer stock solutions were kept at room temperature.

Experimental Validation of ITP Hybridization Model.

For our validation experiments, we used 40 mm long, 21 μm inner diameter capillaries (TPS020375, Polymicro Technologies) glued on a glass cover slide as microchannels, and the preparation procedure is provided in Measurements of ITP parameters (SI Materials and Methods) were performed under a 1.3 μA constant current from a high voltage source meter (2410, Keithley Instruments) between the two wells. From each ITP hybridization experiment, we recorded the fluorescence intensity versus time at seven fixed stations located 4 mm apart. As a negative control, we first performed ITP experiments with MBs in LE, but no targets in TE to record the background fluorescence of MBs. We then used the same ITP processes with both MBs in LE and targets in TE to collect hybridization signal.

Demonstrations of Hybridization Acceleration Using ITP.

For the standard hybridization data of Fig. 4, we injected premixed MBs and targets in LE buffer from an aluminum foil covered 1 mL syringe to the microchannel at 1 μl/h flow rate using a syringe pump (KDS210 KD Scientific Inc.). We initiated acquisition of fluorescence intensity data in less than 5 min from the time of MB and target mixing, and continued recording until the steady state. For the ITP hybridization, we followed the same protocol of model validation experiments, but here used 2200 V constant voltage. To this end, we used two source meters sharing a common ground and applied -1100 V and +1100 V from each device. We used six observation points located at distances of 4, 12, 20, 24, 28, and 32 mm from the TE well for 10 nM MBs and 20 nM target hybridization. We used 10 observation points at distances of 8, 16, 20, 24, 28, 32, 36, 40, 42, and 44 mm (total channel length was 50 mm for this case) for hybridization of 50 pM MBs with 500 pM target.

ITP Hybridization Data Analysis.

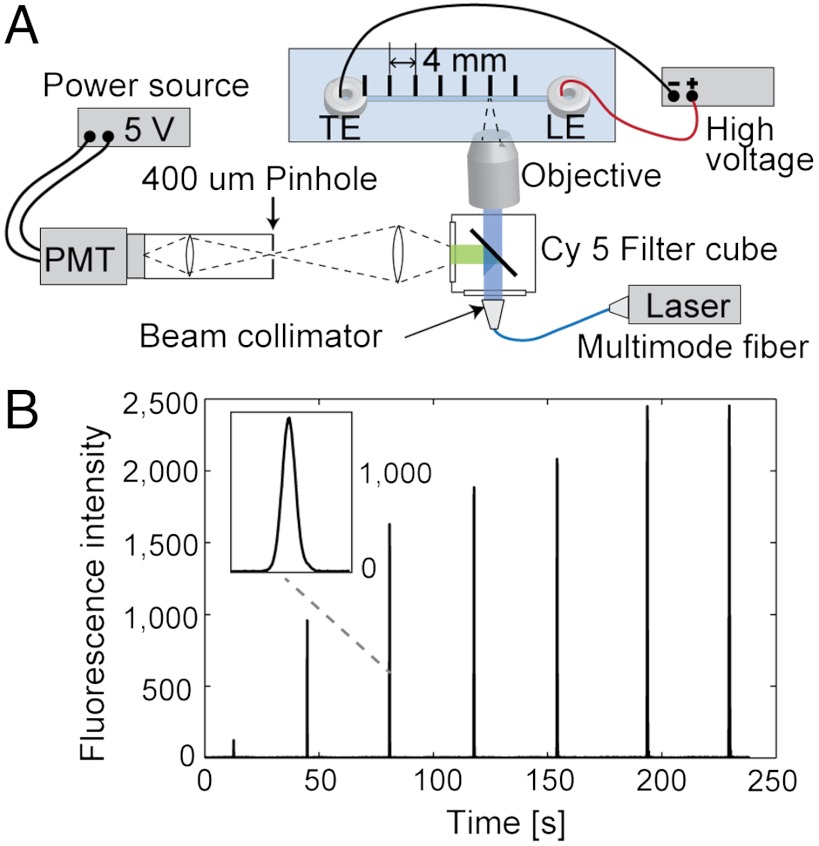
From the raw fluorescence intensity data shown as peaks in Fig. 5B, we first extracted total fluorescence intensity at each station by integrating the signal above the baseline determined from the auto-leveling baseline correction method (37). We then fit each peak with a Gaussian distribution to determine standard deviation, σ, and integrated the underlying signal over a ± 3σ time range (see Fig. S4). The total fluorescence intensity of hybrids (I_AB) and ensemble averaged total fluorescence of MBs (I_B) were then converted into fraction of reactants hybridized using the relation,

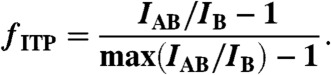[14]

Derivation of Eq. 14 is given in SI Materials and Methods.

Fig. 5.

Schematic of the ITP-based DNA hybridization experimental setup and example raw data. (A) We used a custom point-wise confocal setup built around an IX70 inverted epifluorescent microscope (Olympus). The 1 mW intensity of light from a 642 nm laser diode (Stradus-642, Vortran Laser Technologies) was transmitted through a multimode optical fiber (M31L05, Thorlabs,) to the microscope’s illumination port. The fiber coupler (FiberPort PAF-X-7-A) was used on the laser end, and a beam collimator and expander (F230FC-A) were used on the microscope end, all from Thorlabs. The microscope was equipped with a Cy5 filter-cube (Cy5-4040A, Semrock) and a water immersion objective (LUMPlanFL 60×, NA = 0.9, Olympus). The confocal setup consisted of a 1 inch biconvex lens with a focal length of 50 mm (LB1471-A, Thorlabs) and a 400 μm pinhole. Light was directed into the photomultiplier tube (PMT) module (H6780-20, Hamamatsu Photonics) operated at a sampling rate of 66.7 Hz. The PMT signal was digitized using a data acquisition unit (C8908, Hamamatsu Photonics). We used in-house MATLAB codes (R2007b, Mathworks) to control and record the data from the PMT. (B) Typical raw signal obtained from ITP hybridization experiments. At each location, we recorded a Gaussian-like profile as the ITP interface passed through the detector’s measurement volume, then moved the microscope stage to the next location. Inset shows a close-up view of raw signal data.