High-cost, high-capacity backbone for global brain communication

Abstract

Network studies of human brain structural connectivity have identified a specific set of brain regions that are both highly connected and highly central. Recent analyses have shown that these putative hub regions are mutually and densely interconnected, forming a “rich club” within the human brain. Here we show that the set of pathways linking rich club regions forms a central high-cost, high-capacity backbone for global brain communication. Diffusion tensor imaging (DTI) data of two sets of 40 healthy subjects were used to map structural brain networks. The contributions to network cost and communication capacity of global cortico-cortical connections were assessed through measures of their topology and spatial embedding. Rich club connections were found to be more costly than predicted by their density alone and accounted for 40% of the total communication cost. Furthermore, 69% of all minimally short paths between node pairs were found to travel through the rich club and a large proportion of these communication paths consisted of ordered sequences of edges (“path motifs”) that first fed into, then traversed, and finally exited the rich club, while passing through nodes of increasing and then decreasing degree. The prevalence of short paths that follow such ordered degree sequences suggests that neural communication might take advantage of strategies for dynamic routing of information between brain regions, with an important role for a highly central rich club. Taken together, our results show that rich club connections make an important contribution to interregional signal traffic, forming a central high-cost, high-capacity backbone for global brain communication.

Integrative brain function depends on neuronal signaling within a complex network of connections linking brain regions (network nodes), the human connectome (1–3). A large proportion of cortico-cortical axonal connections link neurons locally through means of intracortical (gray matter) and short-range white matter axons (4, 5). In contrast, only a small fraction of axonal connections are involved in global communication between distant parts of the network. This long-distance cortico-cortical connectivity, accessible on the macroscopic scale to noninvasive diffusion imaging and tractography, is the primary focus of our study. Not all brain regions contribute equally to the global structure of the network. So-called “brain hubs” display an above-average level of connectivity and are more centrally embedded (6–11). In addition to being individually highly connected (“rich”), brain hubs exhibit a strong tendency to link to each other, forming a structural core (6) or “rich club” (7). A rich club is defined as a subset of nodes maintaining a large number of connections across the network (i.e., high degree) while at the same time forming mutual connections with a density significantly greater than expected on the basis of their degree alone (12, 13). The brain’s cortical rich club was recently shown to consist of a selective set of frontoparietal hubs, including portions of bilateral precuneus and superior frontal cortex, together with regions overlapping the anterior and posterior cingulate cortex and the insula (7). Individually, these brain hubs engage in a wide range of behavioral and cognitive tasks and have been implicated in efficient integration of information between remote parts of the brain (14–16). Their aggregation into a connected rich club suggests the hypothesis that rich club regions do not act as separate entities but instead operate as a single coherent collective, a focal and centrally embedded network, with rich club connections forming a connectivity backbone linking diverse sets of regions across the brain.

In this report we investigate aspects of network cost and communication capacity for rich club connections based on in vivo diffusion magnetic resonance imaging (MRI) measurements, in relation to their topology and spatial embedding in the human brain network. Large-scale rich club connections are shown to be relatively high cost, with a tendency to link regions across long physical distances. At the same time, rich club connections participate in a large number of short communication paths, thus carrying a high proportion of the brain’s signal traffic. Closer examination of the structure of these paths across the brain reveals a sequential organization suggestive of some efficient strategies for dynamic routing of interregional signals, with a central role for rich club connections.

Results

Rich Club Organization.

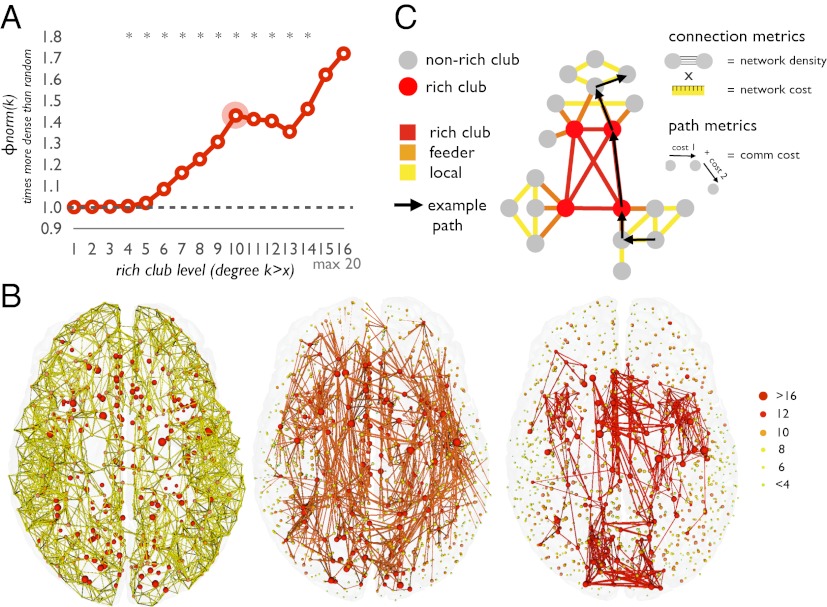
Diffusion tensor imaging (DTI) data of 40 healthy subjects were used to map the large-scale connectivity structure of the brain network, parcellating the cortical sheet into 1,170 distinct evenly sized parcels and determining a group-averaged level of connectivity as the number of reconstructed streamlines between all parcels. A second set of 40 healthy subjects was used to replicate the findings of the principal dataset. Confirming an earlier report (7), the human connectome, mapped here in an independently acquired dataset, was again found to exhibit rich club organization, indicated by a significant tendency for highly connected hub nodes to show an above-random level of interconnectivity, with up to 40% more connectivity than expected by chance (P < 0.05, Bonferroni corrected, Fig. 1A). Confirming previous findings, the rich club comprised a set of spatially widely distributed brain regions (7, 17), including portions of the precuneus, anterior and posterior cingulate cortex, superior frontal cortex, superior parietal cortex and the insula, all in both hemispheres (Fig. 1B). All results reported here refer to the rich club with a degree k >10 (Fig. 1A, other levels give similar results), comprising a total of 16% of the nodes and 12% of the (binary) edges of the network.

Fig. 1.

(A) Rich club curve relative to random model, showing a rich club organization of the human connectome (*P < 0.05, Bonferroni corrected). The selected rich club level of k > 10 is indicated by a red circle. (B) Network representation of local (Left), feeder (Center), and rich club connections (Right). (C) Schematic illustration of local, feeder, and rich club connections.

Physical Length.

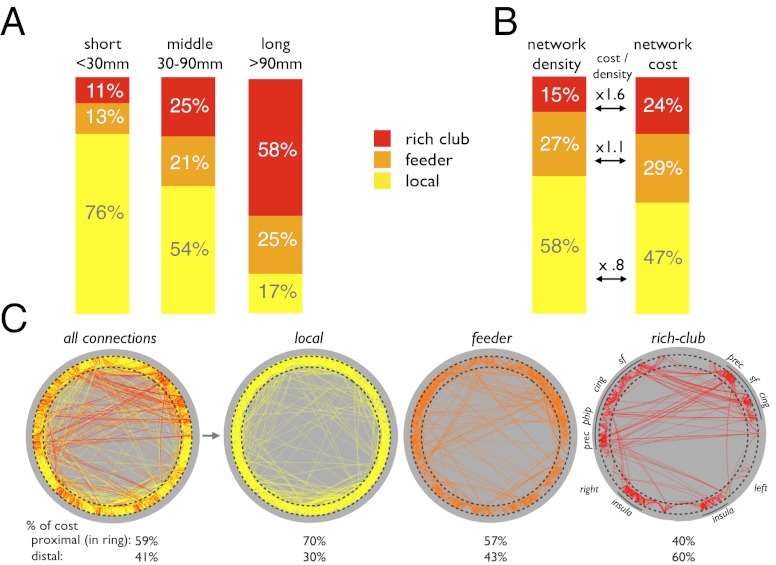
Nodes of the group network were divided into rich club and nonrich club nodes, and edges were divided into three topological categories (Fig. 1C): (i) “rich club connections (R)” linking rich club nodes, (ii) “feeder connections (F)” linking rich club nodes to nonrich club nodes, and (iii) “local connections (L)” linking nonrich club nodes to each other. Statistical analysis revealed differences in connection lengths between topological classes. Rich club connections were found to be significantly longer than feeder and local connections [P = 0.0002 and P = 0.0002 for local and feeder connections, respectively, 10,000 permutations; mean (SD) rich club connections, 37 (38) mm; feeder connections, 26 (23) mm; local connections, 19 (9) mm]. When dividing connections into short (<30 mm, 81% of all connections), medium (30–90 mm, 17%) and long-distance connections (>90 mm, 2%), large proportions of long-distance connections were found to be rich club (48%) and feeder (38%) connections, indicating their strong involvement in long-distance connectivity (Fig. 2A). Examining the weights of the connections in the three distance classes revealed that network density (i.e., streamline count) of long-distance rich club connections was significantly higher than that of long-distance nonrich club connections, underscoring the high-cost aspect of long-distance rich club connections (P = 0.0002 and P = 0.0012 compared with local and feeder connections, respectively; 10,000 permutations).

Fig. 2.

(A) Proportions of short- (<30 mm), medium- (30–90 mm), and long-range (>90 mm) connections belonging to different topological classes. (B) Contributions to network density and network cost of local, feeder, and rich club connections. (C) Nodes are depicted on a ring, organized according to minimization of the inverse of network cost, placing nodes of low connectivity cost in close proximity on the ring (SI Materials and Methods). “% of cost” expresses the proportion of total network cost taken on by connections in close proximity on the ring (proximal) and by connections placed on different parts of the ring (distal connections). cing, posterior and anterior cingulate cortex; insula, insular cortex; phip, parahippocampal; prec, precuneus; sf, superior frontal cortex.

Network Density and Network Cost.

Rich club tractography streamlines were found to include 15% of the total network density, defined as the number of streamlines detected by tractography across the whole brain, but accounted for 24% of the total network cost, defined as the number of streamlines multiplied by their physical length. This percentage results in a cost/density ratio of 1.6 for rich club connections, relative to 1.1 and 0.8 for feeder and local connections, respectively (Fig. 2B).

To visualize the spatial arrangement of rich club, feeder, and local connections, Fig. 2C depicts a graphical representation of the group connectome with brain regions (1,170 nodes) arranged on a circle. The ordering of nodes along the circle’s perimeter was determined by an optimization algorithm based on simulated annealing (SI Materials and Methods). This algorithm attempts to rearrange the nodes of the network such that most of the connections are placed along the circle’s perimeter. Taking the elements of the input matrix as the inverse of network cost (i.e., density times physical distance), this procedure resulted in placing nodes linked by low-cost connections in close proximity on the ring (e.g., nodes linked by short connections representing cortico-cortical U-fibers) and nodes linked by high-cost connections farther apart on the circle’s perimeter. When connections are plotted by topological class, Fig. 2C reveals a strong tendency of rich club connections to span longer distances along the circle, compared with local and feeder connections that are arranged much more densely around the perimeter. Additionally, nodes interlinked by rich club connections aggregate into coherent clusters that correspond to anatomical regions participating in the rich club. Fig. 2C shows that the right and left insula each form a separate community that is distinct from other clusters consisting mainly of regions in or near the brain’s midline (e.g., medial parietal and frontal rich club members).

Communication Cost.

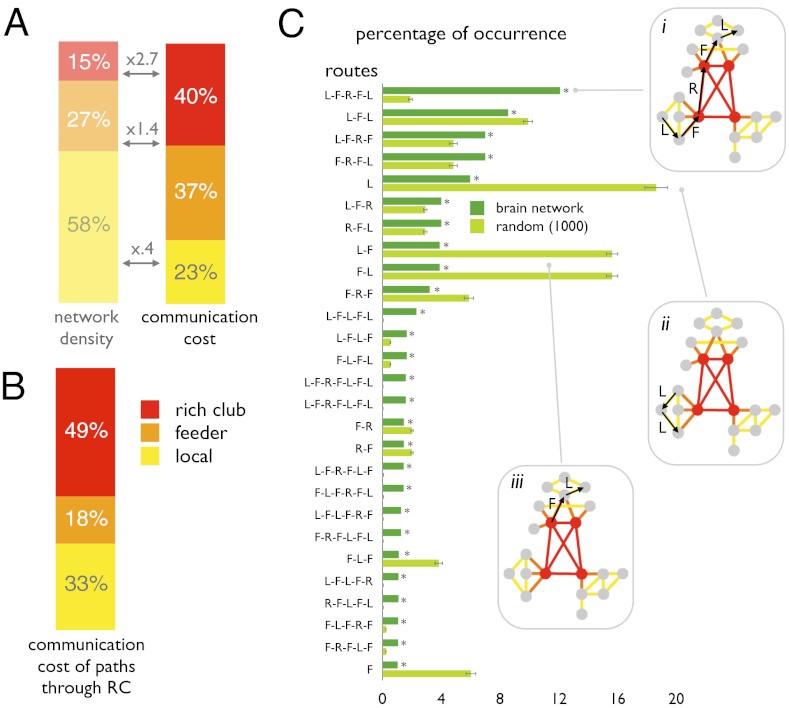
When examining shortest communication paths between all 1,170 parcels regardless of origin or target, 69% of all such paths were found to pass through the rich club; i.e., they traveled across at least one rich club connection and at least two rich club nodes. Along all shortest communication paths (henceforth simply referred to as “paths”), rich club connections accounted for 40% of the total communication cost, defined as the network cost along the edges of paths (Fig. 3A). Feeder connections, directly linked to rich club nodes, accounted for another 37% of the communication cost, and local connections accounted for the remaining 23%. When considering the paths that traveled through the brain’s rich club, the proportion of communication cost spent on rich club connections increased to 49%, whereas 18% and 33% were spent on feeder and local connections, respectively (Fig. 3B).

Fig. 3.

(A) Contributions to communication cost of local feeder and rich club connections. (B) Communication cost of paths that pass through the rich club (69% of all paths). (C) Frequencies of a selection of path motifs in the brain network (main text), all occurring with a frequency greater than 1%, and their corresponding frequencies in a set of a 1,000 random networks, preserving degree sequence. L-F-R-F-L was the most common path motif in the brain network (*P < 0.05, Bonferroni corrected; SI Materials and Methods).

Path Motifs.

Each path consists of an ordered sequence of edges, each belonging to one of three topological classes: local, feeder, and rich club. The order in which these classes are traversed defines classes of paths, or “path motifs,” to which each communication route can be uniquely assigned. The most abundant communication routes found in the human brain followed a “local to feeder to rich club to feeder to local” (L-F-R-F-L) path motif (Fig. 3 C–I). Statistical comparison of frequencies of path motifs was carried out relative to distributions of path motifs obtained from a population of 1,000 equivalent random networks, preserving the original degree sequence and thus an identical number of high-degree nodes but without a coherent rich club. The comparison showed that paths in random networks involved nonrich club connections in much greater proportion, including highly abundant “local to local” and “local to feeder” path motifs (Fig. 3C, ii and iii). In contrast, the L-F-R-F-L path motif was found to be significantly overrepresented in the human brain, relative to randomized networks. The tendency of communication paths in the brain to use rich club connections (Fig. 3 C–I) rather than to remain on local or feeder connections underscores the central role of rich club connections in brain communication.

Degree Dependence of Paths.

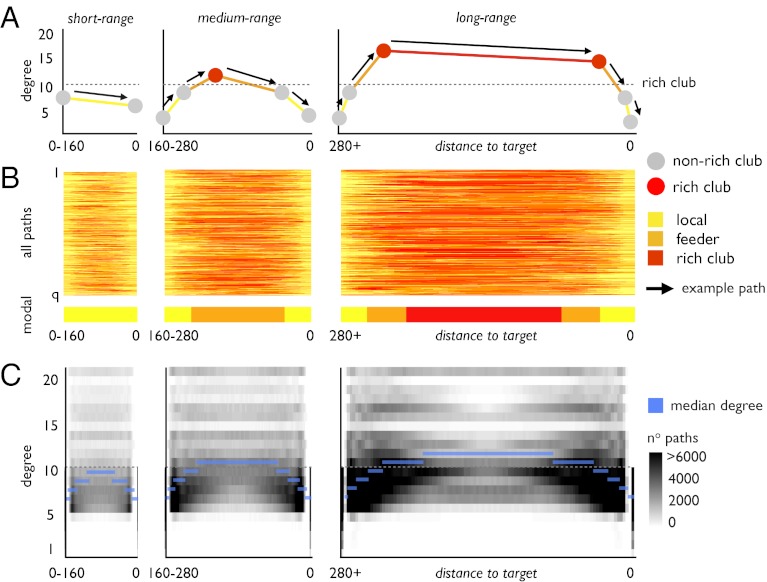
The sequential organization of paths and the preponderance of long-distance connections among rich club nodes suggest a relationship between topology and spatial embedding. To reveal this relationship, all paths joining nonrich club nodes were divided into terciles (bottom, middle, and top 33% of all paths) according to the total physical distance traveled along the edges of the network, resulting in “short-range,” medium-range,” and “long-range” paths. Within each class, all path distances were rescaled to uniform lengths so that the paths could be mutually aligned. As schematically indicated in Fig. 4A, we examined these three classes of paths in terms of the topological class of connections (Fig. 4B) and the degree of nodes (Fig. 4C) encountered along their traveled route. Fig. 4B depicts the short-, medium-, and long-range paths, with the class of connection (i.e., local, feeder, rich club) color coded along the path’s scaled physical length. Fig. 4B again reveals a major contribution of rich club connections, particularly to paths supporting medium-range and long-range communication. Whereas all paths begin and end on nonrich club nodes and thus on local or feeder connections, a large proportion of the distance traveled along medium or long paths is spent on rich club connections. In contrast, short-range paths travel mostly through local and feeder connections and avoid the rich club altogether. Fig. 4C shows three diagrams expressing the frequency with which a short, medium, or long path travels through a node of a specific degree (depicted on the y axis) located at a specific scaled distance from the destination node (depicted on the x axis). Fig. 4C shows that short-range connections mostly pass through nodes with low degree (Fig. 4C, Left), consistent with the finding that short paths mostly travel through local connections. In contrast, medium-range and long-range paths use low-degree nodes near their origin and destination and high-degree nodes, including those forming the rich club, near the middle. Hence, longer paths tend to organize according to a “zooming-out/zooming-in” principle, going from low- to high- to low-degree nodes. Fig. 4C shows that paths originating at a low-degree source node tend to quickly ascend to higher-degree nodes as they travel through local and feeder connections. Along these paths the majority of the total distance traveled is spent between high-degree nodes using rich club connections. When reaching their destination, paths quickly descend across nodes of decreasing degree, finally terminating at a low-degree target node (Fig. 4C, Right). This pattern is in contrast to that in short-range paths, which mostly consist of direct connections or paths that stay on edges between nodes of low degree (Fig. 4C, Left).

Fig. 4.

Paths and their dependence on node degree. (A) Schematic diagram illustrating the relation of node degrees and edge type along communication paths between nonrich club nodes, further grouped into short range, medium range, and long range. (B) Edge type traveled along each path (rows) as a function of rescaled distance between origin and target (x axis). The colored bar shows the modal edge type as a function of distance, taken as the modus over all paths. (C) Distance/degree frequency map for each of the three distance classes. Maps depict the number of times a node of degree k (y axis) is crossed along each path as a function of the distance traveled from source node to destination node (x axis). Maps show that short-range paths mostly use nodes with low degree (i.e., below rich club threshold of k > 10), whereas medium-range and long-range paths tend to follow a “zooming-out/zooming-in pattern.”

Replication Dataset.

All findings regarding rich club organization, regional composition, network density, network cost, communication cost, and path motifs were consistent with those obtained from a second n = 40 replication dataset (Fig. S1).

Discussion

Our findings suggest that rich club connections form a backbone for global brain communication, a coherent set of connections extending over long distances (high cost) and participating in a large proportion of short paths across the network (high capacity). Our analysis confirmed a rich club organization of the human connectome (7), with a cortical rich club that included portions of the precuneus, superior frontal cortex, superior parietal cortex, anterior and posterior cingulate cortex, and the insula (Fig. 1). These findings reinforce rich club observations in nonhuman species, reporting on the tendency of distributed brain regions to form a densely interconnected “hub complex” or “top hierarchical module,” as reported for macaque and cat cortex (17, 18). Extending previous findings, we examined the topological and spatial organization of rich club connections, revealing aspects of their cost, as indexed by their volume, and their capacity, as indexed by their contribution to short communication paths between different parts of the network.

The rich club was found to constitute a high-cost, high-capacity feature of brain connectivity. Rich club tractography streamlines composed a relatively small proportion (15%) of the total network density, but consumed a disproportionately large share (24%) of the total network cost (Fig. 2B). Concordantly, rich club connections were found to span larger physical distances than feeder connections and local edges (Fig. 2 A and C), interconnecting the spatially distributed members of the rich club. Sixty-nine percent of all communication paths were found to pass through the rich club, and rich club connections together with connections feeding pathways into the rich club accounted for 77% of the total communication cost between all brain regions (Fig. 3A). The central role of rich club connections in global brain communication is further underscored by their high prevalence in communication paths (Fig. 3B), in particular those paths that span medium and long distances (Fig. 4). All metrics related to network density and network cost are greatly reduced in random networks that preserve node degrees but degrade global topology. Hence, the topology of the brain’s network appears to be organized to create a focal network through which most of the brain’s long-distance signal traffic must pass.

Importantly, signal traffic in brain networks goes beyond relaying and switching of messages. Instead neuronal information is integrated and elaborated as it is exchanged between regions. Intracortical and short-range axonal connections play a crucial role in this process and account for a large proportion of all cortical wiring (4, 5, 19, 20), but are not captured in diffusion MR imaging. The cortical rich club may therefore constitute a central network that not only attracts and propagates, but also transforms and integrates global signal traffic. The present structural study does not directly address functional aspects of rich club organization, but on the basis of their known physiological properties, most members of the rich club can be characterized as multimodal or “high-order” regions, receiving and integrating information from functionally diverse (nonrich club) brain regions (7, 17, 21). With rich club connections forming a backbone for global signal traffic, the rich club as a whole (i.e., its regions and connections) may thus be seen not only as a central attractor but also as an integrator of neuronal information. Future studies examining the intrinsic connectivity of rich club regions will therefore be of particular importance to fully characterize the role of the rich club in the integration of information across functional subdivisions of the human brain (7, 21).

Our findings support the idea that neural architecture is organized to achieve a high level of global information integration along short communication paths (14, 15), while at the same time conserving material resources such as metabolic energy and wiring volume (22–25). Previous analyses of connectivity in nonhuman primates suggested that long-distance projections, although violating strict minimization of wiring volume, act as long-distance shortcuts, ensuring high levels of global information integration while lowering the number of processing steps during communication (26). These shortcuts may confer important advantages, as a lower number of communication steps shortens transmission delays, facilitates synchronous information processing, and reduces noise during communication, which apparently offsets their higher network cost. Classic “small-world” models (27) incorporate random shortcuts to achieve high efficiency while maintaining high local clustering and thus conserving cost. Elaborating on this, our findings now suggest that the brain is organized as a “rich-world” network with high-degree nodes that support a coherent and interconnected system of long-distance projections whose cost is offset by attracting a high volume of interregional signal traffic.

In our analysis, network cost and communication cost of connections and paths were defined as the number of streamlines multiplied by their physical length, thus representing an aspect of cost related to the network’s spatial embedding (26, 28, 29). This definition of cost assumes that cost is proportional to axonal volume (24, 26), here estimated as the product of streamline density and length. Although neurobiological interpretations of streamline density remain uncertain (30), several studies combining diffusion MRI and histology have demonstrated good overlap between pathways identified by tractography and tract tracing (31–33), as well as an association between streamline density and tract volume (34, 35). More specific estimates of axonal volume may become possible with more sophisticated measurements of axonal microstructure, including variations in the diameter of myelinated axons (36). Future enhancements of high-resolution diffusion imaging may thus allow further refinement of cost-based analyses of brain connectivity.

Methodological limitations inherent to computational streamline tractography likely lead to an underestimation of the density of long-range connections, because longer tractography streamlines are more difficult to complete (37). This underestimation can result in missing connections, for example interhemispheric pathways interconnecting homotopic regions, which are generally underrepresented in diffusion imaging, including in our study (Figs. 1B and 2C). With respect to our analysis, this underestimation of long-distance tracts likely leads to an underestimation of the contribution of rich club connections to network cost and, given their physical length, an underestimation of their cost/density ratio and overall contribution to global brain communication. Indeed, recomputing streamline density favoring longer streamlines (by linearly adjusting the density of a fiber streamline according to its length) further increased the contribution of rich club connections to overall communication cost (communication cost/density ratio: rich club, 2.58; feeder, 1.12; local, 0.13). Eliminating streamline density altogether, we also examined a binary representation of the brain network by using only information on the presence or absence of pathways. The analysis again resulted in a disproportionately high contribution of rich club and feeder connections to global communication cost (communication cost/density ratio: rich club, 2.44; feeder, 1.44; local, 0.53). Considering that intracortical and very short-range connectivities were not measured with DTI, future studies examining the local connectivity profile of rich club regions may be of particular interest, by clarifying their contribution to overall network and communication cost.

The global structure of brain communication showed a prevalence for shortest communication paths to follow an ordered sequence of nodes that fed into, then traversed, and finally exited the rich club (following an “L-F-R-F-L” path motif; Fig. 3C), while passing through nodes of increasing and then decreasing degree (Fig. 4C). Our observation of a “zooming-out/zooming-in” structure of shortest paths suggests a role for the high-degree rich club to facilitate neural communication, as it allows distant brain regions to take advantage of degree-based “greedy routing” strategies. In technological and transportation networks greedy routing refers to a strategy for efficient navigation where steps along a path are selected on the basis of local information only, without knowledge of the global structure of the network (38, 39). The brain likely represents another example of a system where individual elements, be they regions or neurons, can access only local information about connectivity and hence cannot select shortest communication paths on the basis of global knowledge about the brain’s topology. Each minimally short communication path represents a unique and optimally efficient sequence of nodes and edges that is vastly outnumbered by longer alternative routes between source and target. Hence discovering optimally short paths in the absence of global knowledge is a demanding task and constitutes a key problem for navigation and routing in many complex networks. Selecting paths through means of local information, such as through means of greedy routing (38) and/or through means of a mixture of degree-based and similarity-based routing (39), has been shown to be a fruitful strategy for navigation in these systems. Our findings show that a large proportion of the most efficient communication paths, particularly those crossing long distances in the brain, appear to be routed toward and through the rich club along ordered sequences of nodes and edges. In this context, we propose the hypothesis that the brain’s connectivity structure, and in particular its central rich club, is organized to facilitate or promote a variant of degree-based routing of neuronal information. Future studies examining in more detail which strategies drive communication in the brain are of fundamental interest to understand how neurons and brain regions can exchange signals efficiently, in the absence of global knowledge of the brain’s structural connectivity.

Taken together, examining the topology and spatial embedding of the rich club, our findings suggest that rich club connections constitute a feature of human brain connectivity that results from a trade-off between conserving material resources and boosting dynamic performance. Because rich club connections link spatially distributed and remote hub nodes, their overall network cost is high, but this high cost is offset by their disproportionately large contribution to efficient communication. Rich club connections compose a densely interconnected backbone whose central position in the network suggests that it attracts, transforms, and disseminates a large proportion of signal traffic among remote brain regions. Disruption of this “rich club backbone system” may have significant impact on the brain’s functional integrity.

Materials and Methods

A detailed description of the included subject data and the diffusion data preprocessing steps is provided in SI Materials and Methods.

Rich Club Detection.

The so-called rich club phenomenon in networks is said to be present when the high-degree nodes of a network tend to be more densely connected among themselves than expected by chance (12). The rich club was identified by comparing the density of connections among nodes with a minimum degree k to the density found in randomized networks preserving degree sequence. Formally, the rich club coefficient Φ^w(k) is given by (13)

with E_>k denoting the subset of edges between the nodes with a degree >k, W_>k denoting the total sum weights of this subset, and W^ranked denoting the ranked collection of weights in the network, with weights W representing the number of streamlines (network density) of the edges (7). Φ(k) was normalized relative to the rich club coefficient Φ^w_random of a set of comparable random networks (n = 10,000) of equal size and degree sequence, giving a normalized rich club coefficient Φ_norm (12) (SI Materials and Methods).

Connection Metrics.

Network density was defined as the number of tractography streamlines and thus captured an aspect of network topology. Network cost was defined as the number of streamlines multiplied by their physical length, thus representing an aspect of cost related to the network’s spatial embedding (26, 28, 29).

Path Metrics.

Communication cost was based on the path length (topological distance) between any node i and any node j in the network. First, all unique shortest paths between all n = 1,170 nodes in the network were traced. Second, the total communication cost of the shortest path between nodes i and j was computed as the sum of the product of the physical lengths and density (i.e., number of streamlines) of the edges that were used while traveling from node i to j in the network. Subsequently, for each path, the proportion of the total communication cost spent on rich club, feeder, and local connections was computed. Once aggregated across all paths, the communication cost expresses the total amount of signal traffic carried along each edge of the network, taking into account its density, its length, and the number of short paths it supports.

Path Motifs.

All shortest communication paths were classified according to the type (R, F, and L) and sequence of connections passed. We refer to each class as a path motif due to its conceptual resemblance to motifs in graph theory (40). A path motif reflects a specific sequence of edge types that a path crosses when traveling between the source and the target node. For example, the motif R-F-L represents paths that sequentially pass edges of type R, type F, and finally type L, including paths consisting of three edges (RFL), paths consisting of four edges (RRFL or RFLL), paths consisting of five edges (RRRFL, RRFLL, etc.), and so on (see Fig. S2 for examples of path motifs). Note that some sequences of edges are impossible due to the definition of edge types (e.g., RL or RFFL). Path motifs with a frequency exceeding 1% were compared with a population of 1,000 random networks. This population of random networks yielded a null distribution of the number of times a path motif occurs in a network with a random topology. Using this null distribution, each path motif was assigned a P value, expressing the percentage of random values that were found to be more extreme.