Conformational Sampling of Peptides in the Presence of Protein Crowders from AA/CG-Multiscale Simulations

Abstract

Macromolecular crowding is recognized as an important factor influencing folding and conformational dynamics of proteins and nucleic acids. Previous views of crowding have focused on the mostly entropic volume exclusion effect of crowding but recent studies are indicating the importance of enthalpic effects, in particular changes in electrostatic interactions due to crowding. Here, temperature replica exchange molecular dynamics simulations of trp-cage and melittin in the presence of explicit protein crowders are presented to further examine the effect of protein crowders on peptide dynamics. The simulations involve a three-component multiscale modeling scheme where the peptides are represented at atomistic level, the crowder proteins at a coarse-grained level, and the surrounding aqueous solvent as implicit solvent. This scheme optimally balances a physically realistic description for the peptide with computational efficiency. The multiscale simulations were compared with simulations of the same peptides in different dielectric environments with dielectric constants ranging from 5 to 80. It is found that the sampling in the presence of the crowders resembles sampling with reduced dielectric constants between 10 and 40. Furthermore, diverse conformational ensembles are generated in the presence of crowders including partially unfolded states for trp-cage. These findings emphasize the importance of enthalpic interactions over volume exclusion effects in describing the effects of cellular crowding.

INTRODUCTION

It is often assumed that structural and physicochemical properties of biological macromolecules observed in the test tube will also remain similar in living cells. However, the presence of high concentrations of proteins, nucleic acids, and various co-solvents in the cellular environment creates a highly crowded and dense media that likely impacts physicochemical properties compared to the dilute buffer solutions commonly used in vitro^1–3. The macromolecules existing in the cellular milieu occupy the significant amount of the cell volume, hence available volume for the other molecules is restricted, which is known as the excluded volume effect⁴. Furthermore, there is also a confinement effect due to membrane boundaries, the DNA nucleoid, and cytoskeletal elements^5,6. The restricted volume and dense environment are expected to have consequences for the macromolecules in terms of their energetics, transport properties, and reactivity. In particular, there is evidence that molecular crowding and confinement can significantly change the sampling and dynamics of proteins and nucleic acids, and thus possibly influencing biological roles of macromolecules in the cell^7–9. It has been shown on numerous occasions that protein conformation^10,11, folding^12–15, association^16–18, dynamics^19,20, and aggregation^21,22 are highly affected by the excluded volume effect. These results can be interpreted as entropic effects because of the confinement^23–25 and as thermodynamic effects as a result of deviations from ideal solution behavior^26,27. Although disregarded by most in vitro studies, it has also been shown that the presence of crowding is essential for DNA transcription and replication to correlate the in vitro results to in vivo counterparts²⁸.

In most experimental and theoretical studies of crowding and confinement, the focus has been only on the entropic changes caused by the excluded volume. The focus on excluded volume effects is a result of the experimental and theoretical studies of crowding that have been carried out in the past. Typically, inert, polar and non-interacting polymers such as Ficoll 70 and Dextran 70 (in the experiments) and their theoretical counterparts (via hard sphere approximation) have been used as the crowding agents^29–31. These agents have very poor attractive interactions with the proteins, with some exceptions such as in the case of polyethylene glycol (PEG)^32,33. Hence, the main conclusion is that a decrease in available volume limits the existence of high-entropy expanded states vs. more compact states, which suggests that protein-protein binding is favored over dissociated states and that folded protein conformations are stabilized relative to unfolded states under crowded conditions^{10,15,23,29,34–36}. Further analysis of computer simulations employing spherical crowders suggests that crowding may significantly expand the ensemble of sampled structures to include significant populations of non-native compact structures^37,38, but these studies also indicate a destabilization of extended and unfolded conformations in the presence of crowders.

In addition to the excluded volume effect, it is expected that there are also significant enthalpic changes associated with crowding. Because a significant part of the aqueous solvent is displaced by other molecules in crowded cellular environments, changes in intermolecular interactions, such as electrostatic interactions, van der Waals interactions, hydrophobic interactions, and hydrogen bonding, should also be included when considering the effect of crowding. Recent theoretical studies have shown that depending on the strength of attractive force between crowding agents and the protein, or surfaceprotein interaction in a confined area, stabilizing excluded volume effect can be eliminated during the protein binding and folding process^17,39. Furthermore, there are an increasing number of recent reports suggesting that purely entropic volume exclusion effects are not sufficient to account fully for the effect of crowders. For example, in-cell NMR studies of ubiquitin⁴⁰ show that its amide hydrogen exchange rate in the cell is significantly higher than in vitro, possibly because of destabilizing interactions with other proteins. Similarly, NMR-measured hydrogen exchange rates of chymotrypsin inhibitor 2 (CI2) in the presence of high concentrations of bovine serum albumin (BSA) or lysozyme show destabilization of parts of the CI2 structure⁴¹. These findings were in part confirmed by recent all-atom molecular dynamics simulations⁴² where CI2-crowder interactions were found to directly destabilize the structure of the protein. Furthermore, a comparison of in vitro and in vivo stabilities of a β-rich model protein, cellular retinoic acid binding protein (CRABP), using a fluorescence approach as well as urea titrations have indicated reduced stability of CRABP in vivo⁴³. Finally, a study of amide hydrogen exchange rates by MALDI mass spectrometry⁴⁴ showed that at pH = 7 the thermodynamic stability of monomeric λ repressor is higher in vitro than in the intact cell. Together, these studies strongly suggest that a complete understanding of crowding needs to go beyond a purely entropic view stemming from the volume exclusion effect.

Electrostatic interactions are hypothesized to contribute most significantly to the enthalpic component of the crowding free energy^19,45,46. Based on the electrostatic theory, altered electrostatic interactions with a given environment can be modeled in a mean-field manner as an altered dielectric response of the environment⁴⁶. In particular, because proteins, co-solvents, lipids and other macromolecules are generally less polar than water, one may assume that high concentrations of such crowders cause a decrease in the overall dielectric strength of the environment compared to that of bulk water. In an average cell, 20 to 30% of volume is occupied by proteins⁴⁷ . Protein dielectric constants have been investigated by many theoretical studies, and they were found to be in a range between 2 and 20^48–52. Furthermore, high concentrations of carbohydrates, one type of common biological co-solvents, can also decrease the dielectric constant of aqueous solvent to as low as 30⁵³. Finally, even the water itself has been suggested to have a reduced dielectric constant in crowded environments due to confinement effects⁴⁵. Taken together, this suggests that the dielectric strength of a crowded cellular environment is significantly lower than that of dilute aqueous solutions. A decrease in the dielectric constant would reduce the interactions between the solvent and charged residues, decrease the penalty for exposing hydrophobic residues to solvent, and increase the strength of salt bridges and hydrogen bonds because of reduced screening. One consequence would be protein destabilization because of an effective reduction of the hydrophobic effect, but this effect would be counteracted by a stabilization of regular secondary structure elements that involve extensive hydrogen bonding.

These ideas are supported by experimental studies of how the conformational sampling of biomolecules, especially proteins, is altered in the presence of organic co-solvents such as trifluoroethanol (TFE) ^54–56, 1,1,1,3,3,3-hexafluoro-2-propanol (HFIP)^57–59, hexafluoroacetone hydrate (HFA)⁶⁰, methanol, ethanol, propanol, and butanol⁵⁴, all of which lead to a decrease in dielectric response. Consistently, all of these studies demonstrate that the α-helical structure of peptides is stabilized in the presence of these alcohols. A similar stabilizing effect of the alcohols is also observed on β-sheet structures^61,62. On the other hand, it was found that the α-helical B. burgdorferi VlsE protein and the β-sheet human mitochondrial co-chaperonin protein 10 (cpn10) can switch between α-helix or β-sheet structures depending on the amount of alcohol in the media. This suggests that co-solvents may affect the thermodynamic stability of proteins and peptides in more subtle ways than a simple dielectric picture would suggest⁶³.

Computer simulations have further addressed these questions. Dielectric continuum models are easily incorporated into molecular dynamics simulations via implicit solvent models such as the Generalized Born (GB) method⁶⁴. This methodology allows the dielectric constant to be specified directly and can be applied to a wide range of low and high dielectric environments⁶⁵. Our group has previously reported simulations of alanine oligopeptides and bee venom melittin in different dielectric environments using such an approach⁴⁶. The change in the dielectric constant had a profound effect on the conformational sampling of these peptides. In the case of poly-alanine, helical conformations were stabilized at lower dielectric environments. For melittin, a high dielectric environment favored ‘folded’ conformations for monomeric melittin in contrast to low dielectric values where more extended helical structures were favored because they maximized hydrogen bonding. Assuming that lower dielectric constants are reflective of cellular environments these results suggest that crowding may actually induce less compact conformations rather than the more compact conformations predicted by the volume exclusion effect.

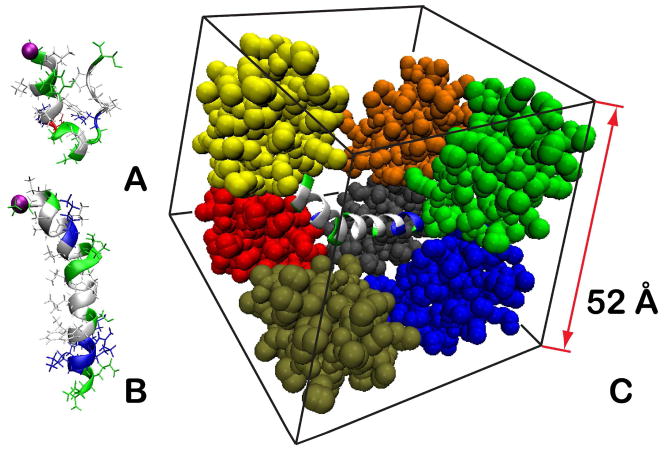
The dielectric view of crowded environments emphasizes the enthalpic effect of crowding but remains a crude approximation of real cellular environments. It is lacking specific interactions with crowders, and in particular electrostatic and van der Waals interactions between individual residues of a given peptide and the surrounding crowder proteins. A more realistic approach involves explicit inclusion of crowder proteins. Full atomistic simulations of such systems with explicit solvent are possible but limited to relatively short simulation times on sub-μs scales because of the large system sizes⁴². Here, we follow a novel multiscale modeling approach where peptides of interest are represented in atomistic detail, crowder proteins are represented with the PRIMO coarse-grained model^66,67, and aqueous solvent is modeled with a GB-type implicit solvent model (see Fig. 1). The combination of this AA/CG-model with replica exchange sampling allows access to relatively long time scales, well into the μs range, in order to examine how the conformational sampling of peptides is altered in the presence of protein crowders in comparison with simple dielectric models. In particular, we focus on two well-known peptides, melittin and trp-cage in the presence of high (~ 40% by volume) concentration of protein crowders. Protein G was chosen as the crowder molecule because it is relatively small and known to be well-behaved in simulation studies.

Figure 1.

Simulated systems: trp-cage (A), melittin (B), and melittin surrounded by 8 protein G crowders in PRIMO representation (C). One of the crowders in C is omitted for clarity. Peptides are colored as follows: hydrophobic residues are shown in white, polar residues in green, basic residues in blue, and acidic residues in red, and the N-terminus is indicated with a purple bead. Crowder proteins are colored by chain.

In the following, we will first describe the computational methodology followed by a presentation and discussion of the simulation results.

METHODS

The dynamics of two peptides, bee venom melittin and trp-cage, in crowded environments was studied here via computer simulations. Previously we simulated melittin in different dielectric environments (ε=5, 20, 40, and 80)⁴⁶. Here, we repeated those simulations for trp-cage, also at ε=5, 20, 40, and 80. In addition, both, melittin and trp-cage, were simulated in the presence of eight protein G molecules embedded in implicit solvent with a dielectric constant of 80.

The melittin structure was obtained from X-Ray analysis (PDB ID: 2MLT⁶⁸). As in the experimental structure, the termini were protected with acetyl (N-terminus) and methyl (C-terminus) groups to maintain electroneutrality. For trp-cage, we used the solution NMR structure (PDB ID: 1L2Y⁶⁹) with unmodified charged termini. Both peptides were modeled in atomistic detail using the CHARMM22 protein force field⁷⁰ with the CMAP dihedral correction term⁷¹. In the simulations with the protein G crowders, the protein G molecules were represented at a coarse-grained (CG) level using the PRIMO (Protein Intermediate MOdel) model developed in our group⁶⁶. PRIMO is a fully transferable CG model designed to be compatible with atomistic models. In PRIMO, there are three interaction sites on the backbone and one to five sites for the side chains of amino acids. The CG sites are systematically chosen to ensure an accurate reconstruction of all-atom representations from PRIMO models⁶⁶. This then allows the use of an interaction potential that is similar to that of a standard molecular dynamics (MD) force field, but with some additional terms⁶⁷. The bonded interactions in PRIMO are based on data from long atomistic explicit solvent simulation of dipeptides with the CHARMM22/CMAP force field and are modeled with either harmonic terms or distance dependent non-harmonic spline-interpolated functions. The 1–4 interactions are modeled with Fourier series torsional terms, spline-interpolated functions and a reduced Lennard-Jones potential. The backbone 1–4 interactions are further augmented by a dihedral dependent two-dimensional cross-correlation term similar to that used in the CHARMM/CMAP model⁷². The initial CMAP potential was obtained from alanine dipeptide sampling and later corrected to reproduce the sampling observed in larger alanine based short peptides. The non-bonded terms in PRIMO include standard Lennard-Jones (LJ) terms, Coulombic electrostatic interactions, and an explicit angle and distance dependent hydrogen bonding potential. The hydrogen bonding term is introduced to counter the weakened electrostatic interactions due to reduced partial charges. PRIMO is combined with implicit solvent using the generalized Born with molecular volume model (GBMV) and augmented with an atomic solvation term (ASP)⁷³. The parameters for the LJ, electrostatics and ASP potentials were adjusted by matching PRIMO energies to that of atomistic CHARMM energies for model peptides and protein decoy sets. Further optimization of the LJ terms was done based on distance-dependent protein-protein interaction energy profiles to match atomistic profiles (see Figure S1 in supporting information). This optimization was carried out for a pure PRIMO model, where both proteins were represented at the CG level, as well as for a mixed setup where one protein was modeled at the CG level but the other one at the atomistic level to reproduce the conditions of the multiscale simulation presented here. Although the full PRIMO model allows stable MD simulations of proteins⁶⁷, we weakly restrained the crowder molecules here to their experimental structures in order to focus the conformational sampling on the peptide systems. We used harmonic constraints of 2 kcal/mol·Å² for Cα sites of every residue of the crowder proteins. However, crowder molecules were free to translate and rotate within the simulation box. Instead of using periodic boundaries, which are not implemented with the GBMV model, we used a quartic repulsive wall potential to maintain crowder molecules and the peptide between +26 and −26 Å in each direction. The resulting protein concentration was therefore about ~ 40% by volume. Because we used implicit solvent, there are no solvent boundary effects with this approach.

In the constant dielectric simulations, non-bonded interactions were cut off at 18 Å, with the potential being smoothly switched to zero starting from 16 Å; the non-bonded interaction list was maintained up to 20 Å. The GBMV implicit solvent model was used with standard parameters as described previously^46,65,74,75. The non-polar part of the solvation energy was estimated using the solvent accessible surface area (SASA) formalism⁷⁶ with a surface tension factor γ of 5.0 cal/mol·Å² for the atomistic model and varying values for the PRIMO model.

An integration time step of 2.0 fs was used with the leapfrog integrator. The SHAKE algorithm⁷⁷ was used to constrain bonds involving hydrogen atoms. In the multiscale simulations, non-bonded interactions were cut off at 16 Å, with smooth switching to zero starting at 14 Å. Albeit the PRIMO coarse-grained model allows longer integration time steps, multiple time stepping is not implemented in CHARMM and we ran the multiscale simulations with a 2.0 fs integration time step as well. For all simulations, we controlled the temperature of the system using a Langevin thermostat with a uniform friction coefficient of 10 ps⁻¹ that was applied to all non-hydrogen atoms.

In order to improve the conformational sampling, temperature replica exchange (TREX) simulations⁷⁸ with temperatures exponentially spaced between 300–400K (homogeneous dielectric simulations), 300–450K (trp-cage multiscale simulations), and 300–500K (melittin multiscale simulations) were performed instead of standard molecular dynamics. Eight replicas were used for the homogeneous dielectric simulations (each run for at least 100 ns, see Table 1). The first 10 ns of each simulation were discarded from the subsequent analysis. The multiscale simulations were run in triplicate, each from different initial structures to improve sampling convergence, each with 24 or 20 replicas, for melittin and trp-cage, respectively, run for 20ns each (see Table 1). Replica exchange simulations had exchange probabilities of about 45% for different dielectric simulations, and 25% for multiscale simulations. From the resulting data, only the data at 300K were analyzed.

Table 1.

Simulated systems

#	Peptide	Crowders	Implicit solvent ε	Temperature range [K]	Replicas	Exchange probability [%]	Length [ns]	Analysis [ns]
1	trp-cage	none	5	300–400	8	53.6	100	10–100
2	trp-cage	none	20	300–400	8	50.5	100	10–100
3	trp-cage	none	40	300–400	8	46.7	100	10–100
4	trp-cage	none	80	300–400	8	47.4	100	10–100
5	trp-cage	8 x protein G	80	300–450	20	27.4	20	5–20
6	trp-cage	8 x protein G	80	300–450	20	28.3	20	5–20
7	trp-cage	8 x protein G	80	300–450	20	27.5	20	5–20
8	melittin	8 x protein G	80	300–500	24	24.4	20	5–20
9	melittin	8 x protein G	80	300–500	24	24.5	20	5–20
10	melittin	8 x protein G	80	300–500	24	24.2	20	5–20

All simulations use temperature replica exchange methodology.

Analysis included calculations of root mean square deviations (RMSD) from the respective native structures, radius of gyration, and internal bending angles. The bending angle was defined as the angle between the N- and C-terminal helices of melittin obtained from the average O(i) – H-N(i+4) vectors for residue indices i, 2–5 and 16–20. A similar angle between the N-terminal helix and the C-terminal loop was defined for trp-cage as the vector between an average of O(i) – H-N(i+4) vectors for residues 1 through 9, and a vector connecting amide N of residue 15 and carbonyl carbon of residue 20.

All simulations were performed using version c36a5 of the CHARMM program package⁷⁹. Replica exchange simulations and the following analysis were done using the Multiscale Modeling Tools for Structural Biology (MMTSB) Tool Set⁸⁰ in conjunction with CHARMM. VMD⁸¹ and POV-Ray were used to visualize the biomolecules and to render the images.

RESULTS

Multiscale simulations of two model peptides, trp-cage and melittin, were carried out in the presence of protein crowders and implicit solvent with ε=80. The resulting conformational ensembles were compared with results from implicit solvent simulations using different dielectric constants but without crowders. The melittin reference simulations are available from a previous study⁴⁶. The trp-cage reference simulations were carried out as part of this study. In the following, the results for trp-cage and melittin are presented in more detail.

Trp-cage

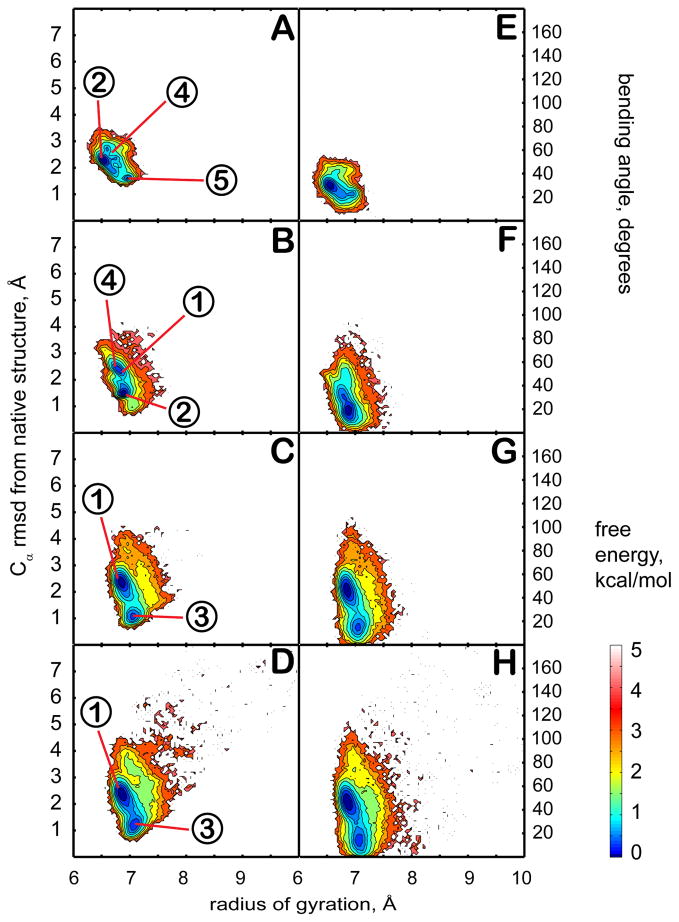
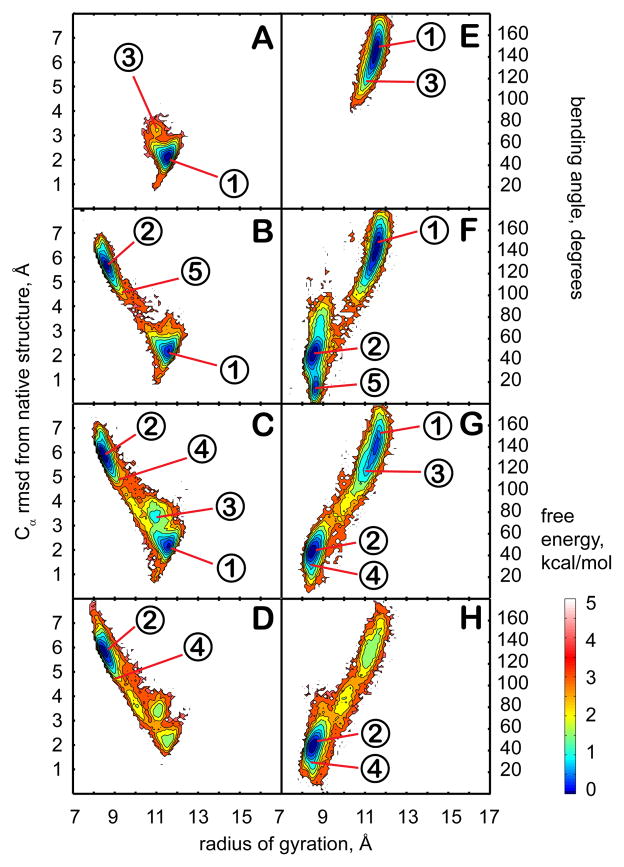
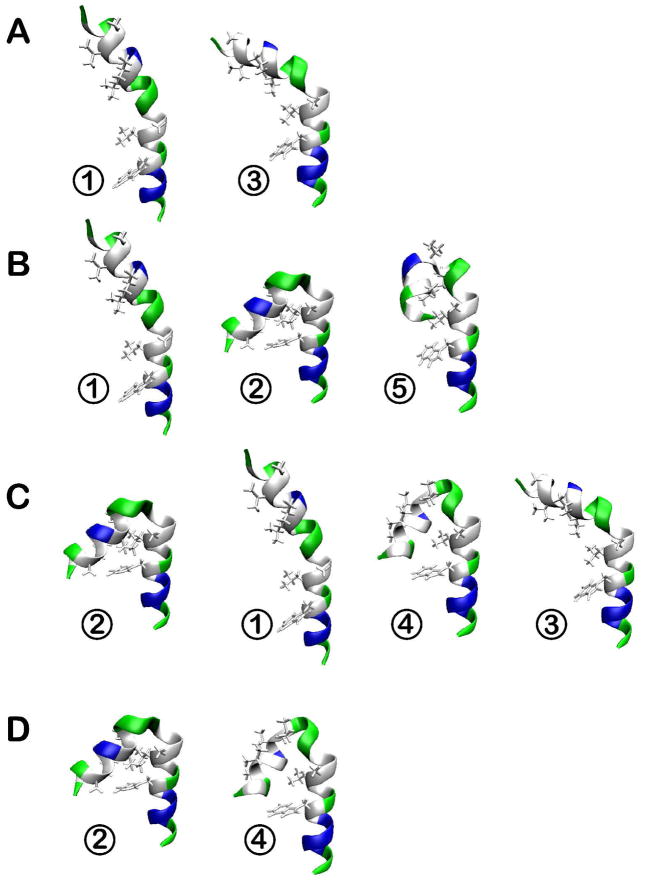
Reference simulations of trp-cage in different dielectric environments (simulations 1–4, Table 1) were carried out following a similar protocol as for earlier melittin simulations in different dielectric environments⁴⁶. Analysis results from the last 90 ns of each simulation are presented in Fig. 2 in the form of potentials of mean force (PMFs) at 300K as a function of the RMSD from the native state or the internal bending angle and the radius of gyration. Furthermore, representative structures obtained from clustering are shown in Fig. 3. The clustering was performed by combining all of the sampled structures (including those from the simulations with the crowders) into a common ensemble. The populations of the resulting clusters in different simulations are given in Table 2.

Figure 2.

Conformational sampling of trp-cage in different dielectric environments with ε = 5 (A,E), ε = 20 (B,F), ε = 40 (C,G), and ε = 80 (D,H). Plots on the left (A–D) show the potential of mean force (PMF) at 300 K as a function of the radius of gyration and the Cα RMSD from the minimized native structure. Right plots (E–H) show the PMF at 300K as a function of the radius of gyration and the bending angle between N- and C-terminal parts of the structure. Contour levels are shown at increments of 0.25 kcal/mol from 0 to 1 kcal/mol, at increments of 0.5 kcal/mol from 1 to 3 kcal/mol, and at increments of 1 kcal/mol from 3 to 5 kcal/mol. The numbers in circles indicate approximate positions of representative structures near cluster centers (see Figure 3 for corresponding structures).

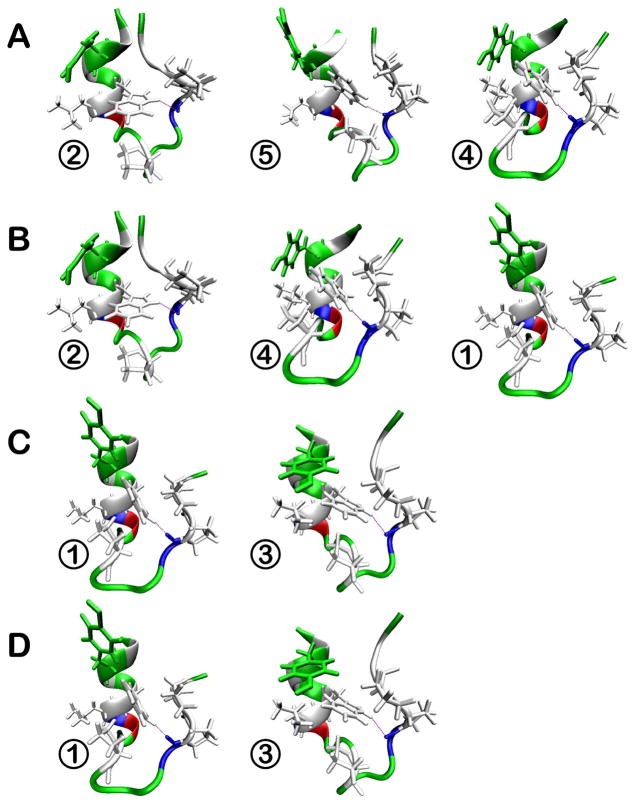
Figure 3.

Representative conformations of trp-cage from clustering (see Table 2) in different dielectric environments with ε = 5 (A), ε = 20 (B), ε = 40 (C), and ε = 80 (D). Hydrophobic residues are shown in white, polar residues in green, basic residues in blue, and acidic residues in red. The structures are placed in order of decreasing relative weight from left to right at each condition (see Table 2) with coloring as in Fig. 1.

Table 2.

Clustering of sampled trp-cage conformations

#1	Cluster populations					Representative structure2
	ε = 5 [%]	ε = 20 [%]	ε = 40 [%]	ε = 80 [%]	ε=80 + crowders [%]	Cα RMSD [Å]	Radius of gyration [Å]	Bending angle [°]
1	0	13.0 (3.2)	58.6 (7.2)	53.9 (3.3)	21.9 (6.2)	2.25	7.25	45.9
2	63.0 (16.5)	40.7 (13.4)	4.2 (1.8)	2.7 (0.9)	16.0 (1.6)	1.56	7.09	18.5
3	1.3 (1.1)	7.6 (1.7)	30.5 (6.0)	32.3 (4.4)	35.8 (4.1)	1.1	7.4	9.5
4	13.9 (4.5)	34.5 (11.4)	2.0 (0.7)	1.8 (0.5)	11.0 (3.5)	2.37	7.14	43.9
5	21.8 (12.7)	3.8 (0.3)	0.2 (0.1)	0	0.4 (0.4)	1.75	7.1	13.9
6	0	0	0	0	6.0 (1.8)	6.53	9.54	118.1
7	0	0	0	0.4 (0.2)	5.0 (0.7)	3.26	7.79	57.9
8	0	0	0	0	3.2 (0.4)	3.59	8.04	36.6

K-means clustering of a combined ensemble based on the mutual structural similarity, using Cα RMSD and a 3.0 Å clustering radius. 9000 structures were selected each from simulations 1 through 4 and another 9000 structures were taken from simulations 5 through 7 to yield a total of 45000 structures that were clustered together. Populations of >10% are indicated in bold face. Uncertainties given in parentheses are estimated from block analysis according to $\sigma /\sqrt{N}$, where σ is the standard deviation and N = 3 since 3 blocks of data were used (see individual block averages in Tables S1 and S2 of supporting information).

¹Cluster number.

²Structure nearest to the respective cluster centroid.

The sampled conformations of trp-cage remain overall near the native structure across the entire range of dielectric constants. However, closer inspection reveals subtle differences between the structures that are sampled at higher and lower dielectric constants. In simulations performed at higher dielectric constants (ε = 40 and 80) there are two main clusters (1 and 3) that account for more than 80% of the sampled states. Structures belonging to cluster 3 are very close to the native state, and retain all its folding features. Cluster 1 is a result of a conformational rearrangement, where the C-terminal coil region is tilted relative to the N-terminal helix with a bending angle in the 40 to 60° range. In this structure, the key hydrogen bond between W6 and R16 is left intact but the C-terminal coil comes closer to the helix thereby minimizing solvent exposure of the hydrophobic P19 residue. Populations between clusters 1 and 3 are similar with a negligible difference in stability. The presence of two near-native conformations at ε=80 agrees with previous simulations of trp-cage in both explicit^82–86 and implicit^87,88 solvents. Most of those simulations show a second minimum within 2.5 Å RMSD of the native state. The radius of gyration of the second state is sometimes less^83,87 and sometimes more^82,86 than the native state depending on the solvation model that was used. In our case, the radius of gyration of the second state (cluster 1) is slightly less than the native state in agreement with previous implicit and explicit solvent simulations^83,87.

At lower dielectric constants, sampling shifts to clusters 2, 4, and 5. In the corresponding structures, the charged C- and N-termini are near each other. In addition, the hydrophobic core is partially disrupted and the non-polar residues P18, L2 and L7 are exposed to the solvent. The stabilization of salt bridges and increased exposure of hydrophobic residues are expected in environments with reduced polarity⁴⁶. The attraction between the oppositely charged termini further causes a partial loss of helicity at the N-terminus by breaking one and two i to i+4 hydrogen bonds at the N-end in clusters 2 and 4, respectively. Structures belonging to cluster 5 feature the formation of a single 3₁₀ helix loop between L2 and Q5 instead. In the least polar environment (ε = 5), cluster 2 is dominant with a significant population of cluster 5, while at ε = 20 clusters 2 and 4 are equally weighted, cluster 5 is not sampled to a significant extent, but sampling of clusters 1 and 3 begins to emerge.

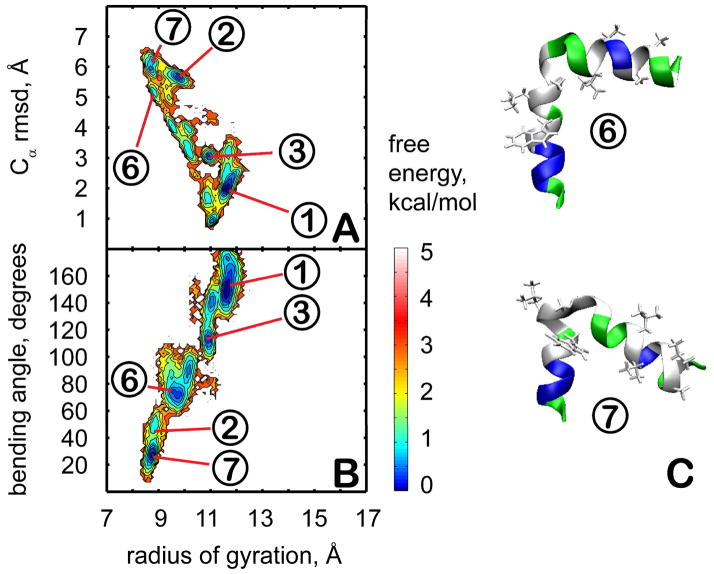
In the presence of the crowders, the PMF changes significantly (see Fig. 4). The sampled conformations are more diverse and consist of structures in clusters in 1, 2, 3, and 4 as well as significant sampling (14% in total) of partially unfolded structures (clusters 6, 7, and 8) that are not seen in the absence of the crowders. In clusters 6 and 8, the hydrogen bond between the indole NH of W6 and the carbonyl group of R16 at the folding core is missing. Structures in cluster 7 maintain the W6-R16 interaction, but the hydrophobic core is disrupted. The partially unfolded conformations are stabilized by attractive interactions with residues on the surface of the crowder molecules. These results suggest that the presence of the protein crowders effectively corresponds to an intermediate dielectric constant in the 20–40 range since structures from clusters 1 and 3 (seen at ε=40) as well as from clusters 2 and 4 (seen at ε=20) are sampled with equal weight. In addition, the presence of the crowder appears to have a destabilizing effect shifting the equilibrium towards unfolded conformations.

Figure 4.

Conformational sampling of trp-cage in the presence of explicit crowders. Plots on the left (A,B) show the PMF at 300 K as a function of the radius of gyration and the Cα RMSD from the minimized native structure (A) or the bending angle between N-terminal and C-terminal parts (B). Contour levels are shown at increments of 0.25 kcal/mol from 0 to 1 kcal/mol, at increments of 0.5 kcal/mol from 1 to 3 kcal/mol, and at increments of 1 kcal/mol from 3 to 5 kcal/mol. Representative structures from clusters unique to the crowder simulations (6,7, and 8) are shown in C with coloring as in Fig. 1.

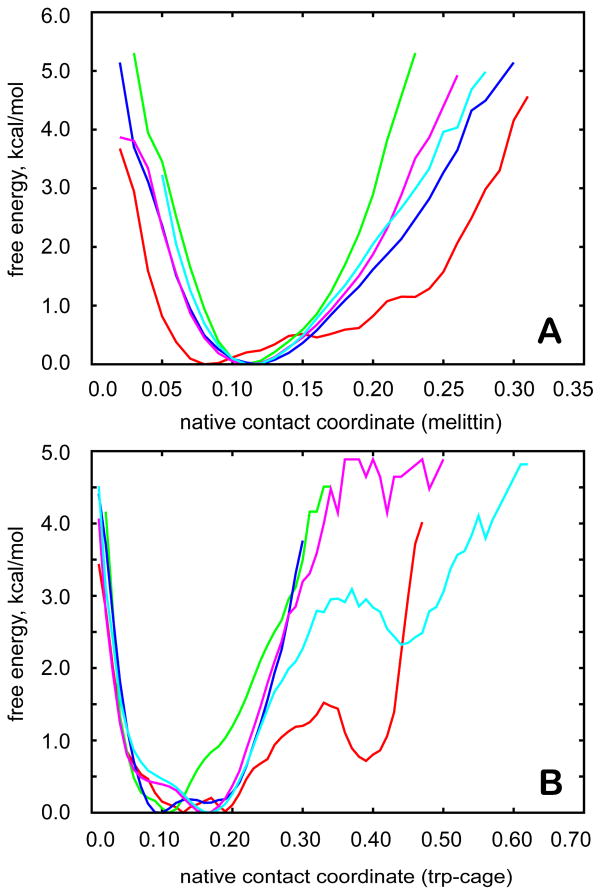
To characterize the thermodynamics of partial unfolding further, we have analyzed the free energy as a function of the fraction of native contacts, with a definition similar to the one used by Sheinerman and Brooks⁸⁹ (see Supporting Information for the exact definition used here). The results shown in Fig. 5 indicate that partially non-native conformations are stabilized in the presence of the explicit crowders. At a native contact coordinate value of 0.4 the stabilization amounts to about 2 kcal/mol over the simulation with ε=80 and to >5 kcal/mol compared to simulations with lower dielectric constants.

Figure 5.

Free energy profile of melittin (A) and trp-cage (B) along the reaction coordinate based on the fraction of native contacts, for which a value of 0.0 means fully native state and a value of 1.0 implies that there are no native contacts in the structure (see Supporting Information for an exact definition). Distributions are given for multiscale simulations (red) as well as for different dielectric environments with ε = 5 (green), ε = 20 (blue), ε = 40 (purple), and ε = 80 (cyan).

Melittin

Simulations of bee venom melittin were reported by our laboratory earlier⁴⁶. Fig. 6 recapitulates PMF analysis of the 300K replicas while Fig. 7 and Table 3 show results from clustering. As described earlier⁴⁶, melittin sampling at different dielectric constants consists of two major states: mostly extended helices (clusters 1 and 3) with bending angles of 110–150° and highly bent, V-shaped structures (clusters 2 and 4) with bending angles of 30–45°. The extended helices maximize backbone hydrogen bonding while exposing hydrophobic residues to solvent. They are dominant at ε=5. The V-shaped structures, in contrast, form a mini hydrophobic core at the expense of breaking backbone hydrogen bonding. These structures are preferred in a high dielectric environment. At intermediate dielectric constants (ε=20 and ε=40) there is an equilibrium between both states. In addition, there is a fifth cluster at ε=20 that contains compact structures with small bending angles.

Figure 6.

Conformational sampling of melittin in different dielectric environments with ε = 5 (A,E), ε = 20 (B,F), ε = 40 (C,G), and ε = 80 (D,H). The underlying data was published earlier⁴⁶. The analysis shown here is based on the replicas at 300K during the interval of 7.5 to 75 ns. Plots on the left (A–D) show the PMF at 300 K as a function of the radius of gyration and the Cα RMSD from the minimized native structure. Right plots (E–H) show the PMF at 300K as a function of the radius of gyration and the bending angle between N- and C-terminal parts of the structure. Contour levels and cluster centers are as in Fig. 2.

Figure 7.

Representative conformations of melittin from clustering (see Table 3) in different dielectric environments with ε = 5 (A), ε = 20 (B), ε = 40 (C), and ε = 80 (D). Coloring is as in Fig.1 and structures are ordered according to relative populations as in Fig. 3.

Table 3.

Clustering of sampled melittin conformations.

#1	Cluster populations					Representative structure2
	ε = 5 [%]	ε = 20 [%]	ε = 40 [%]	ε = 80 [%]	ε=80 + crowders [%]	Cα RMSD [Å]	Radius of gyration [Å]	Bending angle [°]
1	88.5 (1.5)	39.0 (10.0)	31.4 (4.2)	5.3 (5.1)	49.3 (6.1)	1.95	12.03	150.6
2	0	26.3 (4.9)	37.2 (7.2)	69.6 (8.5)	9.9 (1.7)	5.73	9.07	44.1
3	10.0 (0.5)	8.4 (1.5)	9.5 (0.8)	1.6 (1.5)	13.3 (5.1)	2.37	11.39	109.8
4	0	7.7 (2.5)	10.4 (1.5)	10.9 (1.2)	0	5.99	9.27	32.1
5	0	18.0 (6.4)	0.1 (0.0)	1.7 (1.5)	0	5.45	9.53	32.8
6	0	0.1 (0.0)	0.3 (0.1)	0	14.4 (1.2)	5.63	10.2	70.4
7	0	0	0	0	4.0 (2.9)	6.31	9.32	27.9

Clustering of a combined ensemble as for trp-cage but using a radius of 4.0 Å for a total of 45,000 structures. Populations of >10% are indicated in bold face. Uncertainties are given in parentheses.

¹Cluster number.

²Structure nearest to the respective cluster centroid.

In the simulations of melittin in the presence of the crowder molecules, both extended and V-shaped conformations are sampled (see Fig. 8) but there are additional structures at intermediate bending angles between 80 and 100° (cluster 6) that are not sampled significantly with the homogeneous dielectric environments. There is also additional sampling of a more compact conformation (cluster 7) that differs from clusters 2 and 4. In this structure, the regular C-terminal α-helix is disrupted at residue I17 and a single loop of 3₁₀ helix is formed in the middle of the melittin molecule. The result is a loss of three backbone hydrogen bonds that are compensated for by interactions with protein crowder residues. We note that the bending angle for this structure using the standard definition across residues 2–9 and 16–24 appears to be rather small (Fig. 8) considering its three-dimensional structure. An alternate definition of the bending angle involving residues 2–13 and 17–25 better matches the shifted break in the helix and results in a more representative angle of 54°.

Figure 8.

Conformational sampling of melittin in the presence of explicit crowders. Plots on the left (A,B) show the PMF at 300 K as a function of the radius of gyration and the Cα RMSD from the minimized native structure (A) or the bending angle between N-terminal and C-terminal parts (B). Contour levels are shown as in Fig. 4. Representative structures from clusters unique to the crowder simulations (6 and 7) are shown in C with coloring as in Fig. 1.

As in the case of trp-cage, the overall effect of the crowder molecules is similar to an intermediate dielectric environment, but there are again additional effects of the protein crowders that increase the structural diversity of the conformational ensemble. As in the case of trp-cage, the presence of explicit crowders results in more extensive sampling of states with reduced native contacts (Fig. 5). However, we did not observe a significant fraction of unfolded conformations of melittin in the presence of the crowders. Instead, there is extensive sampling of less compact extended helical states.

DISCUSSION

Earlier studies of crowding and confinement have focused on volume exclusion effects and concluded that the primary effect of crowding is a stabilization of compact, native states⁴. Recent experimental studies have suggested that the presence of protein crowders may in fact have a weakly destabilizing effect^40,41, but only few theoretical studies have attempted to explain these observations^18,19,42,46. A particular issue is the computational challenge of developing realistic models of cellular environments that are efficient enough to allow extensive sampling of test molecules. An approach taken by us earlier was to model cellular environments through an effectively reduced dielectric environment⁴⁶. While a reduction of the dielectric response in dense cellular environments seems to be justifiable, it has been unclear what dielectric constant would correspond best to cellular environments and whether a purely mean-field model of crowded environments is sufficiently realistic. Here, we have gone one step further and included explicit protein crowders using a multiscale modeling approach.

We found that for the model peptides trp-cage and melittin studied here the inclusion of protein crowders significantly altered the conformational sampling compared to implicit aqueous solvent with ε=80. There were two main effects: extensive sampling of conformations that were also seen in reduced dielectric environments and sampling of a more diverse set of structures than with homogeneous dielectric environments including partially unfolded states for trp-cage. Comparing the simulations with crowders and the simulations in different dielectric environments can be used to establish what dielectric environment may approximate cellular environments in a mean-field model. Such an analysis can be done based on the relative populations of different clusters as a function of the dielectric constant. From the data in Tables 2 and 3 it can be seen that in the presence of the crowders the populations of the major clusters match the populations of simple dielectric environments with dielectric constants between about 10 and 40. A similar range seems to apply for both trp-cage and melittin suggesting that a value in this range is uniformly valid for modeling crowded cellular environments. The estimate obtained here is for approximately. 40%vol. protein crowders. For lower concentrations of crowding agents, we would expect a higher effective dielectric constant because the reduction of the dielectric response should be less pronounced. On the other hand, we are likely overestimating the effective dielectric response of cellular environments because water itself has likely a reduced dielectric response in crowded environments⁴⁵. This effect would further lower the overall effective polarity of the environment. Hence, the estimate of ε=10–40 obtained here is likely valid for typical cellular environments with volume fractions between 20 and 40%.

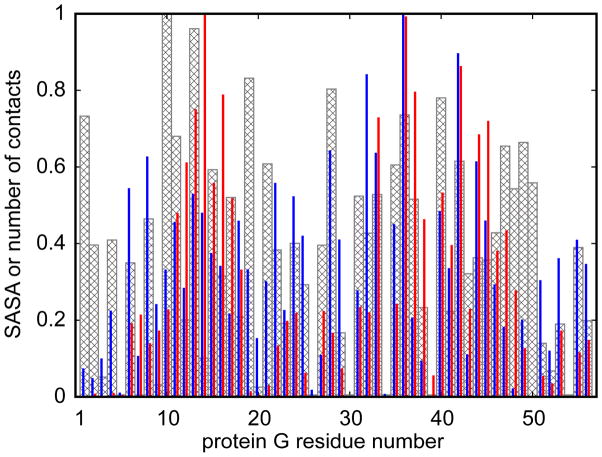
The sampling of more diverse conformational ensembles in the presence of the crowders is presumed to be a consequence of direct interactions between the peptides and the crowder proteins. The importance of peptide-crowder interactions becomes clear from an analysis of the average number of crowders that were in contact with either peptide during the simulation. If a crowder is classified as being in contact with the peptide based on a minimum distance between any pair of heavy atoms of less than 4.0 Å, an average of 3.72 crowders was in contact with trp-cage and 5.42 crowders were in contact with melittin at 300K. Given such extensive protein-protein contacts it may not be surprising that the peptide conformations are perturbed significantly. Especially interesting is the emergence of partially unfolded states for trp-cage that would be entirely unexpected if only the simple volume exclusion effect is considered because of significantly larger radii of gyration compared to the native state. Because we only studied one type of crowder protein here, one concern is whether the findings reported here are sufficiently general to be valid at least qualitatively in arbitrary cellular environments with many different types of proteins. In order to check whether the interactions between the peptides and protein crowder atoms are highly specific, i.e. limited to certain binding sites, we compared the distribution of peptide-crowder contacts with the degree of solvent exposure as a function of crowder residues (see Fig. 9). We find that there is only a weak preference for certain residues and that there is little difference between melittin or trp-cage. This suggests that the nature of peptide-crowder interactions is mostly generic and is not dominated by specific binding interactions. Hence, we assume that other protein crowders would have a similar effect as the protein G crowders studied here in inducing the sampling of more diverse conformational states, including partially unfolded states, compared to aqueous solvent and homogeneous reduced dielectric environments. However, because there is evidence from recent experimental and theoretical studies that different crowder proteins may further modulate the conformational sampling of peptides^41,42 future studies should explore a more diverse set of crowder proteins.

Figure 9.

Normalized number of melittin contacts (blue lines), trp-cage contacts (red lines), and solvent accessible surface area (SASA) estimated by GBMV module (grey bars) for each residue of protein G crowder. Two residues were considered to be in contact if the distance between centers of geometry of all the side chain heavy atoms (Cα atom in case of glycine) was less than 6.5 Å. If at least one peptide residue was found in contact with a crowder residue, the whole peptide was considered to be in contact with that residue.

The simulations presented here represent a novel multiscale simulation approach where an atomistic representation of the peptides is combined with a coarse-grained model of the crowder proteins and an implicit model of the surrounding solvent. The combined AA/CG simulation is facilitated by the newly developed PRIMO CG model that is designed to be compatible with atomistic force fields by following a similar functional form and including charges and Lennard-Jones terms for the CG particles that can directly interact with the atomistic particles. Because explicit solvent is not used and the protein crowders at CG level have reduced degrees of freedom, the resulting system is especially well-suited for replica exchange simulations. Hence, we were able to generate extensive conformational sampling of the peptides of interest with relatively moderate computational resources that would otherwise be difficult to achieve with conventional, fully atomistic, explicit solvent simulations. Furthermore, maintaining the peptides at atomistic level allows us to provide detailed insight into the conformational sampling of peptides in crowded environments that we could not have obtained from fully coarse-grained simulations.

While the use of atomistic force fields with implicit solvent is well-established⁶⁴, the combination with PRIMO is new and has not been tested as extensively. As a result, the exact physics of specific peptide-protein interactions may not be optimally represented yet. However, the purpose of this study was to obtain a mostly qualitative view of how the inclusion of (any) explicit protein crowder affects the conformational sampling of peptides relative to aqueous solvent and reduced dielectric environments. We believe that our current model is already sufficiently realistic to address these questions, but we also continue to optimize PRIMO and its ability to interact with atomistic representations to allow for a broader range of AA/CG simulations.

CONCLUSIONS

The multiscale simulations presented here provide further insight into the macroscopic behavior of biological macromolecules in crowded cellular environments. The simulations confirm our previous assumption that dense cellular environments can be effectively modeled as media with reduced dielectric constants. Based on this work, we estimate that values between 10 and 40 may be good approximations of cellular environments. Furthermore, we also see significant populations of partially unfolded structures in the presence of explicit protein crowders consistent with recent experimental data that suggests a slightly destabilizing effect of dense cellular environments^40,41. The observations presented here cannot be explained by a simple volume exclusion model of crowding. Instead, it appears that electrostatic interactions, both in terms of a general reduction in environmental dielectric response and direct interactions with protein crowders are the key to a complete understanding of the effects of molecular crowding.

The simulations presented here also offer a new paradigm for multiscale simulations where different parts of the system are represented at different levels of detail to balance computational efficiency with the physical realism that can be obtained. In particular, the direct combination of all-atom and coarse-grained levels of representations appears to be a promising approach that we will explore further in future studies.

ABBREVIATIONS

AA

all-atom

CG

coarse-grained

CHARMM

Chemistry at Harvard molecular mechanics program

CMAP

cross-correlation map for torsion angles

GBMV

generalized Born with molecular volume

LJ

Lennard-Jones

MD

molecular dynamics

NMR

nuclear magnetic resonance

PMF

potential of mean force

RMSD

root mean square deviation

SASA

solvent-accessible surface area

TREX

temperature replica exchange