Cell signaling pathways as control modules: Complexity for simplicity?

As biology begins to move into the “postgenomic” era, a key emerging question is how to approach the understanding of how complex biomolecular networks function as dynamical systems. Prominent examples include multimolecular protein “machines,” intracellular signal transduction cascades, and cell–cell communication mechanisms. As the proportion of identified components involved in any of these networks continues to increase, in certain instances already asymptotically, the daunting challenge of developing useful models—mathematical as well as conceptual—for how they work is drawing interest. At one extreme is the hope that fundamental relationships will emerge from essentially statistical analyses of large genomic and proteomic databases enumerating correlations among gene expression, protein level/state/location, and cell behavior. At another extreme is a view that sheer computational power can be harnessed to create comprehensive simulations of the full set of fundamental physicochemical molecular interactions. Recently, an intermediate concept suggests a “modular” framework, treating subsystems of complex molecular networks as functional units that perform identifiable tasks—perhaps even able to be characterized in familiar engineering terms (1). The idea of functional modules as an effective approach to modeling biomolecular systems is quite appealing, because, even in nonbiological applications, engineering design is generally carried out in hierarchical or “nested” fashion. That is, the behavior of a system at the highest (i.e., largest space scale and/or longest time scale) level is typically analyzed and predicted with a model involving properties of the next-lower space/time scales; these properties are then analyzed and predicted with another set of models involving further subdivided space and/or time scales and so forth to a most detailed level as limited by current data.

Despite its intuitive appeal, however, support for the concept of modular cell biology will demand that actual manifestations be identified that can lead to advances in understanding of cell function in molecular terms. Thus, the contribution by Yi et al. (2) is important in providing a compelling example, based on analysis of adaptation in bacterial chemotaxis (3) as a dynamical systems control process. Chemotaxis, most simply defined as a phenomenon in which cells can bias their locomotion along gradients in concentration of a chemical stimulus, has a well characterized foundation of molecular components involved in its signal transduction cascade in the case of the flagellar bacterium Escherichia coli (4). Indeed, the completeness of its component identification has permitted it to be unusually amenable to full computational simulation (5–7). Accordingly, the molecular network of signaling in bacterial chemotaxis offers a timely test bed for elucidating modular representation.

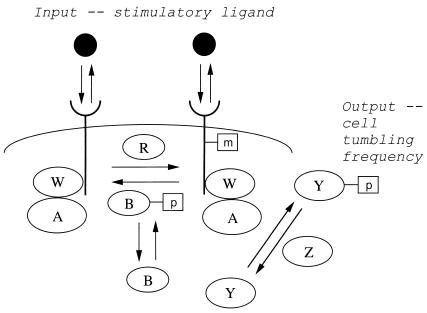
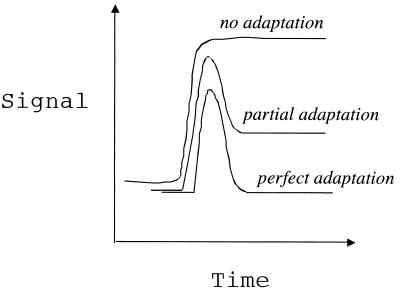
As illustrated schematically in Fig. 1 and outlined by Yi et al. (2), this network comprises six intracellular proteins (designated A, B, R, W, Y, and Z) along with the transmembrane receptor that binds the stimulatory chemotactic ligand. Biologically, the input is the stimulatory ligand concentration, and the output is the frequency of tumbling (the process by which the cell stops swimming in a particular direction and reorients randomly). Because ligand concentration is perceived by receptor binding and the tumbling frequency is governed by the level of phosphorylated Y, a dynamical systems representation can use receptor occupancy and phosphorylated Y as surrogate input and output. A striking previous finding (3) had been that this system of molecular interactions possesses the characteristic of robustness, meaning that the input/output relationship is relatively insensitive to variations in parameter values across a wide range. Robustness is an important property of an engineered system when functional behavior needs to be reliable in the face of external and internal uncertainties and heterogeneities. In the context of bacterial chemotaxis, the input/output property found to be robust is that of perfect adaptation (8). That is, the output (tumbling frequency) attained at steady state after the transient after a change in input (stimulus concentration) is exactly equal to the prestimulus level regardless of the input value (see Fig. 2). This behavior seems to be necessary for bacteria to respond to stimulus concentration gradients (9).

Figure 1.

Schematic illustration of bacterial chemotaxis signaling pathway, adapted from Alon et al. (3) and analyzed by Yi et al. (2) as a feedback control module. The output, cell tumbling frequency, is determined from the input, a stimulatory ligand that binds to cell membrane receptors, by the dynamics of the depicted cascade of interactions between intracellular proteins termed A, B, R, W, Y, and Z. Proteins R and B enzymatically add and remove, respectively, methyl groups (designated by m) on the ligand/receptor complex; the removal activity of B depends on its level of phosphorylation (designated by p), which in turn is mediated by protein A that is coupled to the receptor via protein W. Protein A also adds phosphate groups (which are removed by protein Z) to protein Y; the cell tumbling frequency, which affects the direction of cell locomotion, is governed by the level of protein Y phosphorylation. Adaptation of the output (as illustrated in Fig. 2) after initial response to a change in input is accomplished by the methylation of receptor, which influences the rate at which protein A phosphorylates protein Y.

Figure 2.

Illustration of dynamic responses of a system to a change in input. In the total absence of adaptation, a new steady-state output is attained; partial adaptation reduces the “off-set” of the new steady-state output value compared with the original prestimulus value, whereas perfect adaptation brings the output back to the original value. Alon et al. (3) previously found that the bacterial chemotaxis system shown in Fig. 1 adapts perfectly, and Yi et al. (2) now demonstrate that this pathway possesses characteristic features of an integral feedback control module.

How is this crucial behavior accomplished by the biochemical signaling network of Fig. 1? What Yi et al. (2) have determined is that this network possesses the central characteristics of a process control strategy termed integral feedback control. Process control refers to an engineering operation by which a system makes decisions about how to best manipulate available variables to obtain a desired output. Feedback means that the information on which the decision is based derives from measurement of the output. Diverse types of feedback control are possible, including proportional (P), differential (D), and integral (I) as well as various combinations such as PI, PID, etc. (10). Integral feedback control bases decisions about manipulating system variables on the disparity between the desired output and the actual output integrated over time. A critical feature of integral feedback control, as outlined explicitly by Yi et al. (2), is that the steady-state value ultimately reached after a changed input is indeed the original prestimulus value—i.e., perfect adaptation. Control schemes lacking integral feedback, such as P or PD, in general yield new steady-state values after a changed input that are different from the prestimulus value; in process control parlance, the deviation is known as off-set. In many engineering applications, nonzero off-set is tolerable, but when it is not, implementation of an integral feedback control scheme is required.

Hence, in considering models for bacterial chemotaxis, continuing our example, alternative options are available depending on the goal of the modeling effort. One can employ a full computational simulation of the complete set of physicochemical molecular events, as did Bray et al. (5), Bray and Bourrett (6), and Spiro et al. (7). This approach yields direct prediction of effects of molecular-level alterations on the overall cell behavior, a very useful capability. At the same time, full simulations of this sort may not easily lead to elucidation of central system operating characteristics, as evidenced by the chronology of the integral feedback control representation after initial simulations by over nearly a half decade. If one needs to incorporate the chemotaxis signaling pathway as merely one of perhaps dozens of physiological regulatory processes in the bacterium, profit might be gained from modeling it as a simple input/output module (see figure 2 of Yi et al.; ref. 2), possessing measurable quantitative properties (ultimately predictable from the physicochemical model underneath), alongside analogous modules representing the dynamical characteristics of the other dozens of pathways. This type of framework has been suggested recently for modeling cell-signaling pathways (11).

The question is thus begged as to whether this bacterial chemotaxis signaling pathway is essentially singular in permitting representation as an operational module. Although effort dedicated along these lines is only in a nascent stage, additional examples can in fact be noted. One is the mitogen-activated protein kinase (MAP kinase) pathway, which is found almost universally in eukaryotic cells as a series of at least three protein kinases: a MAP kinase that is phosphorylated by a MAP kinase kinase that has been phosphorylated by a MAP kinase kinase kinase. Such a sequential cascade of reactions was initially speculated to serve as an amplifier of an upstream receptor/ligand binding event. More recent analysis indicates that, in many cases, it acts as a switch providing an almost threshold-like input/output response to receptor activation, with a new steady-state level of MAP kinase activity that is substantially higher than the original baseline level, if the input stimulus is sufficiently great (12). Operation as a switch in this manner could be useful for regulating gene expression events required for a cell decision to divide or differentiate, and this operation can be obtained as a module representing a proportional control scheme in which variables are modulated in response to the immediate difference between a desired output and current output. Interestingly, however, in other situations, this same class of molecular network undergoes exact adaptation or integral feedback control, behavior similar to that of the bacterial chemotaxis pathway, with MAP kinase activity proceeding through a transient peak back to its original baseline level in response to continuous ligand/receptor occupancy (13). The significance of this transient peak for cell behavioral responses, such as migration and proliferation, merits investigation, as does the mechanism in terms of molecular interactions for how this generic MAP kinase pathway can seem to be represented by diverse types of modules. Crosstalk from other signaling pathways is among the likely explanations for the apparent interconversion of a given module from one category of behavior to another.

It is important to appreciate that often the machinery assembled to implement control and safety schemes for operation of a core function is more complicated than the machinery of the core itself (14). As a crude example, consider a liquid-holding tank possessing input and output pipes. This operating system is indeed quite simple. Yet its operating behavior, if uncontrolled, can be quite problematic: for instance, if the input is not properly regulated, a sudden surge may cause the tank to overflow, and if the output is not properly regulated a slow leak may cause the tank to drain dry. Therefore, if one desires to maintain a constant liquid flow reliably in the face of unpredictable surges and leaks, a control system involving valves, flow-rate measurement devices, measurement transducers, and mechanical valve regulators must be built around the tank and pipes—not to mention the computational algorithm required to generate the correct control strategy for the valve regulators derived from the flow-rate measurements. Clearly, most of the complexity of this example system is in the elements that implement the control scheme rather than in the core function. Moreover, the objective of this complexity is to guarantee that the core function will generate reliable output. In a nutshell, the system complexity is built in to provide for simple behavior. This type of complexity is, in many ways, quite the opposite of much of current “complexity theory” in which diverse behaviors are sought from simple systems. This point along with deeper insights have been forwarded more powerfully and elegantly elsewhere (15). Information concerning the molecular makeup of cells, as is emerging from genomic studies, indicates that the proportion of components devoted to regulatory networks as opposed to core functions such as metabolism and energy generation is dominant (16). If this information proves to be general, we can speculate that the compositional complexity of cells is designed chiefly for the purpose of enabling reliable cell decisions concerning simple behavioral functions in uncertain and variable environments. Consequently, a hierarchical framework involving modular control elements—in turn comprised of underlying physicochemical molecular interactions—could be useful for both conceptual and quantitative models of cell function.