CellSeT: Novel Software to Extract and Analyze Structured Networks of Plant Cells from Confocal Images

This article presents a tool to aid researchers in the analysis of confocal images. Tissue-scale structure is used to aid the segmentation of any number of cells. Additional techniques are described that can quantify the fluorescence of nuclear reporters, determine membrane protein polarity, and take many additional biologically relevant measurements.

Abstract

It is increasingly important in life sciences that many cell-scale and tissue-scale measurements are quantified from confocal microscope images. However, extracting and analyzing large-scale confocal image data sets represents a major bottleneck for researchers. To aid this process, CellSeT software has been developed, which utilizes tissue-scale structure to help segment individual cells. We provide examples of how the CellSeT software can be used to quantify fluorescence of hormone-responsive nuclear reporters, determine membrane protein polarity, extract cell and tissue geometry for use in later modeling, and take many additional biologically relevant measures using an extensible plug-in toolset. Application of CellSeT promises to remove subjectivity from the resulting data sets and facilitate higher-throughput, quantitative approaches to plant cell research.

INTRODUCTION

Confocal laser scanning microscopy (CLSM) has become a major source of cellular- and subcellular-scale image data. Many fluorescent probes and dyes are now available to allow the observation of various features of specimens, such as cell walls, organelles, and numerous proteins (Cutler et al., 2000; Pawley, 2006). The challenge has shifted from image acquisition to image analysis and is compounded by the automation of the acquisition process via time-series or automated, feature-driven image capture (Conrad et al., 2011).

To address the emerging bottleneck in data analysis, a number of automated image analysis methods have been developed to extract information from cell-scale data, the most successful requiring special data acquisition techniques to improve data quality (Fernandez et al., 2010) or preprocessing of the image data to ease the segmentation problem (Santuari et al., 2011). In plant science, CLSM images of living tissues reveal individual cells embedded in the implicit network-like structure of the plant tissue. An approach that utilizes this structure to guide further cellular and subcellular segmentation and analysis would make the most use of the implicit structural information available within these plant images.

To this end, the CellSeT software has been developed, which takes advantage of the surrounding cells within a network to extract more reliably individual cell geometry. After segmentation, cells can be semantically tagged from a custom extensible library of biological terms. Further automated analysis can be developed by the user via a plug-in interface. We will describe and demonstrate three plug-ins that can measure fluorescence intensity in cell walls and nuclei and resolve with subpixel accuracy an asymmetrically localized plasma membrane-bound protein.

RESULTS AND DISCUSSION

Overview of CellSeT Software

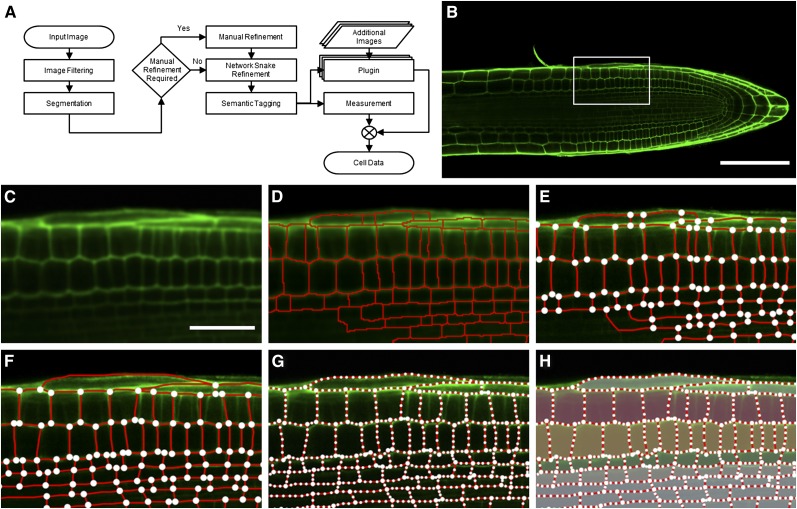
CellSeT provides an automated cell segmentation stage that identifies cell boundaries in cell wall/plasma membrane–marked two-dimensional confocal images through a series of image-processing routines (Figure 1; see Supplemental Movie 1 online). An image (Figure 1B) is first filtered to reduce noise (Figure 1C) and is then segmented into regions representing each cell using a variant of the watershed (Beucher and Lantuejoul, 1979) approach (Figure 1D). In many cases, automatic segmentation is sufficient to correctly identify the structure of all cells of interest. Where image quality is poor (e.g., where some cells are poorly focused), manual user adjustment can correct segmentation in these regions. This manual refinement stage is often brief, with most of the cells of interest having been correctly identified automatically (Figures 1E and 1F).

Figure 1.

The CellSeT Processing Pipeline.

(A) The steps involved in confocal image analysis using CellSeT.

(B) A typical input CLSM image. Cell walls have been stained with propidium iodide (green) to reveal their cellular organization.

(C) A zoomed portion of the input image after filtering.

(D) Two-level watershed segmentation is used to initially distinguish cells. In cases where cell walls are poorly defined, this may lead to under- or oversegmentation.

(E) The refinement graph structure generated using the segmented image.

(F) Manual refinement of the graph structure; oversegmentation in the epidermal cells has been removed, and undersegmentation in the stele cells has been corrected.

(G) CellSeT uses a network snake algorithm to refine the results of manual segmentation.

(H) Cells can be semantically tagged by the user to provide additional information during the output stage (see also Supplemental Movie 1 online).

Bar in (B) = 100 μm; bar in (C) = 30 μm.

Allowing user interaction during segmentation is a trade-off between fully automated and fully manual approaches. The manual adjustment of the results should be viewed as an optional, additional step in the segmentation process, rather than as an alternative to automatic segmentation. Automated segmentation is significantly faster and will successfully identify most cells. Fully manual segmentation, with the aid of a users’ domain knowledge, will produce highly subjective results and should not be relied upon beyond correcting a small number of cells after automatic segmentation; additionally, the manual approach is very labor intensive. The combination of manual and automated approaches is integrated seamlessly by CellSeT, resulting in an efficient and precise cell identification process.

The resulting network of cells is refined using network snake techniques (Butenuth and Heipke, 2010; Sethuraman et al., 2011) that act to pull each cell wall into the optimum location on the image (Figure 1G). Network snakes consist of a set of active contours or “snakes” (Kass et al., 1988) connected together at node points, which mimic the junctions present in plant cell wall images. Each snake has internal parameters, which control its shape (e.g., how much it is permitted to deform or stretch), and external parameters related to image features, which pull the snake toward points on the image. Optimizing these internal and external parameters on all snakes in the network produces a model-driven best local fit of the snake network onto the image data, in this case the network of cell walls. The network snakes improve accuracy and help reduce any subjectivity introduced by the user during manual refinement. Technical details about the network snake implementation are available in previous work (Sethuraman et al., 2011).

CellSeT can perform quantitative analysis of the resulting cellular geometry data quickly, converting the two-dimensional positions of all cell walls into biologically relevant measurements, including cell area and wall length. CellSeT can be easily extended using plug-ins to perform almost any additional measurement required. These plug-ins may utilize markers in additional image channels or additional parameters from the user. The plug-in system is designed to be highly modular; each plug-in can be added, removed, or altered as necessary, and creation of additional plug-ins is straightforward. When the CellSeT software is run, existing and new plug-ins are loaded automatically, and the user interface is altered to accommodate any additional features the plug-ins request. Diagrams showing the data flow for each plug-in can be found in Supplemental Figure 1 online. A library of plug-ins will be maintained alongside the main project release. CellSeT’s geometrical representations can also be exported for use in other modeling packages, such as OpenAlea (Pradal et al., 2008)

To demonstrate how CellSeT exploits the wealth of information associated with networks of cells, we have applied the software to three common image analysis challenges presented by confocal images of plant roots: (1) the automatic detection and quantification of a nuclear reporter, (2) quantification of fluorescently tagged cell membranes and walls, and (3) determining the subpixel location of asymmetrically localized membrane proteins. In the following three sections, a description of the plug-in-based processing within CellSeT is presented. Details of the technical implementation of the approaches can be found in the Methods.

Quantifying the Fluorescence of Nuclear Reporters

Quantification of fluorescence-based measures is a frequently used technique within biological science. Nuclear-localized reporters are widely used to generate spatiotemporal maps of responses to signals, such as hormones (Heisler et al., 2005). However, quantification of such nuclear-localized reporters at a cellular resolution has proved challenging to date. This is typically performed in a low-throughput manner, at best using semiautomatic segmentation to define cells, followed by manual selection of individual nuclei from image stacks (Brunoud et al., 2012). For larger data sets, the time required to process the images becomes prohibitive. The CellSeT nuclei plug-in is capable of quickly detecting nuclei in any number of presegmented cells. CellSeT allows image processing to be targeted on a per-cell basis; this local processing vastly decreases the complexity of the required image analysis implementations. Previous work (Vylder et al., 2010) has shown that restricting nuclei detection to each cell individually can improve detection accuracy; in a scenario where nuclear intensity varies greatly over the image, with some nuclei almost indistinguishable from background, a targeted thresholding approach will outperform a global one. The nuclei plug-in uses targeted Otsu thresholding on each cell individually, distinguishing nuclei from background where a human observer might fail to see a nucleus at all because of low intensity of signal, leading to missing or biased data. Segmentation is further improved through noise-reduction using a connected component algorithm. The size, position, and mean intensity of each nucleus is calculated and combined into the CellSeT output.

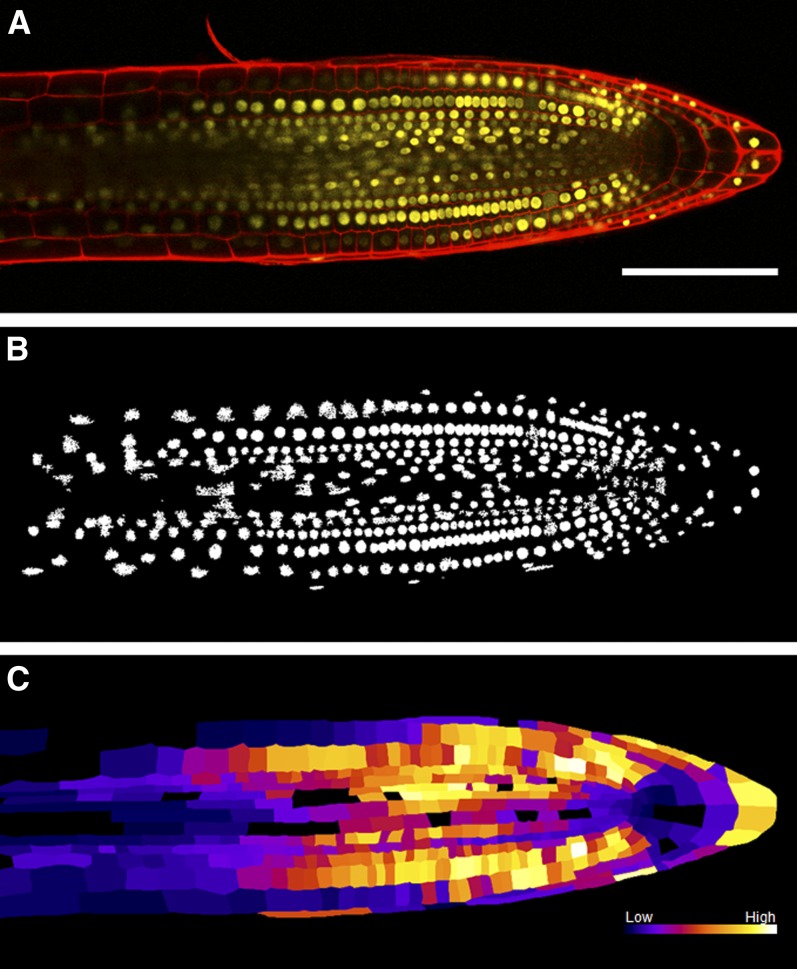
We have validated our nuclei detection plug-in on an image of a root tip of Arabidopsis thaliana expressing the nuclear-localized auxin response reporter DII-VENUS (Figure 2; see Supplemental Movie 2 online) (Brunoud et al., 2012). The key challenges of this image are a wide variation in nuclear intensity between cells and some nuclei fluorescing too dimly for visual recognition. Figure 2B shows the results of nuclei detection after connected component noise removal. Supplemental Figure 2 online shows the improved nuclei detection rate for Figure 2A using local thresholding. Local thresholding identified 94% of cells when compared with a user-defined ground truth; a similar global approach identified only 62%. The nuclei intensity information is then combined with the geometry provided during the CellSeT segmentation stage to produce a heat map representing the nuclei intensity of all cells in the image (Figure 2C). CellSeT software reveals that the DII-VENUS auxin-responsive reporter (whose stability is inversely proportionate to cellular auxin levels) is low in the quiescent center, initial, and columella cells, whereas its signal is much higher in root initial daughter cells (Figure 2C). These results are in good agreement with the published maps (Brunoud et al., 2012) generated manually from the same image sets. CellSeT promises to remove subjectivity and facilitate the use of DII-VENUS and other hormone-responsive reporters in a more quantitative manner.

Figure 2.

Output of the CellSeT Nuclei Plug-in.

(A) The root previously segmented in Figure 1. Red channel: cell walls stained with propidium iodide. Yellow channel: DII-VENUS nuclear marker.

(B) Local Otsu thresholding of the nuclei followed by noise removal using a connected-component algorithm.

(C) A heat map generated using the intensities of each nucleus combined with cell geometry. Brighter colors represent higher levels of DII-VENUS detected in the nuclei of each cell. This reporter is inversely proportionate to the level of auxin; thus, darker regions represent cells containing a higher concentration of auxin (see also Supplemental Movie 2 online).

Bar in (A) = 100 μm.

Quantifying Fluorescence of Membrane Reporters

Because the positions of cells and their walls have been determined by CellSeT, this information can be exploited to evaluate fluorescence levels within cells quickly and with minimal user interaction. Although care is required when quantifying fluorescence levels in confocal images (Pawley, 2000; French et al., 2008), changes in fluorescence are increasingly being used as a form of quantitative measure, and if interpreted conservatively, can yield useful data. The CellSeT intensity plug-in quantifies the mean and integrated intensities of cells and walls in any selected image channels. For walls, the plug-in traverses each segment using a line-drawing algorithm, ensuring that pixels are sampled at regular intervals and are never sampled twice. The mean and total intensities of highlighted walls and cell areas are calculated, with the results combined into the standard CellSeT output. The plug-in can also output a heat map showing the average intensity for highlighted cells overlaid with text giving individual wall intensities.

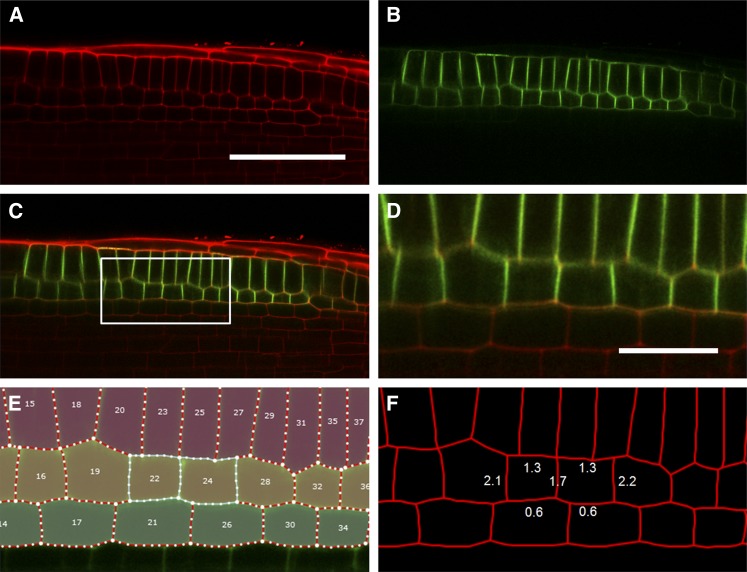
To demonstrate the application of this plug-in, we have evaluated it on images of Arabidopsis roots expressing a green fluorescent protein (GFP) tagged to the auxin efflux carrier PIN2 expressed in root epidermal and cortical tissues (Xu and Scheres, 2005). Quantification of the wall intensities of PIN2-GFP–expressing cortical cells gives information about the reporter’s localization within a cell. Expressing fluorescence as a ratio between the intensity of the reporter channel and the channel used to define the cell wall geometry (in this case propidium iodide staining) allows normalization of the reporter signal to an independent signal located in the same position. This ratiometric approach corrects for any differences in signal caused by walls across the image not lying in the same focal plane. As can be seen from Figure 3F, the normalized fluorescence of anticlinal walls shared between cortical cells within a file are approximately two times greater than the periclinal walls abutting epidermal or endodermal tissues, suggesting a polar spread of the PIN2-GFP signal. The intensity of the outer periclinal walls is approximately double that of the inner walls, presumably because the fluorescence of the former is composed of contributions from the plasma membranes of both cortical and epidermal cells, whereas the latter only represents cortical cell membranes (see PIN2-GFP expression profile in Figure 3B).

Figure 3.

Output of the CellSeT Fluorescence Plug-in.

(A) and (B) Confocal images used to evaluate the plug-in. Red channel: cell walls stained with propidium iodide. Green channel: PIN2-GFP.

(C) Merged image.

(D) A zoomed portion of the input image marked in (C).

(E) CellSeT cell map showing two selected cortical cells.

(F) Average normalized intensities for the cell walls of selected cortical cells expressing PIN2-GFP; fluorescence of the anticlinal walls is approximately twice that of periclinal walls.

Bar in (A) = 50 μm; bar in (D) = 15 μm.

Although this plug-in is able to measure the integrated intensity of shared boundaries between cells, we may wish to locate the peak in intensity of the component membrane markers at a finer resolution (e.g., to determine the polarity of a membrane-bound marker). To address this, the following super-resolution plug-in was developed.

Super-Resolution Localization of Membrane Markers

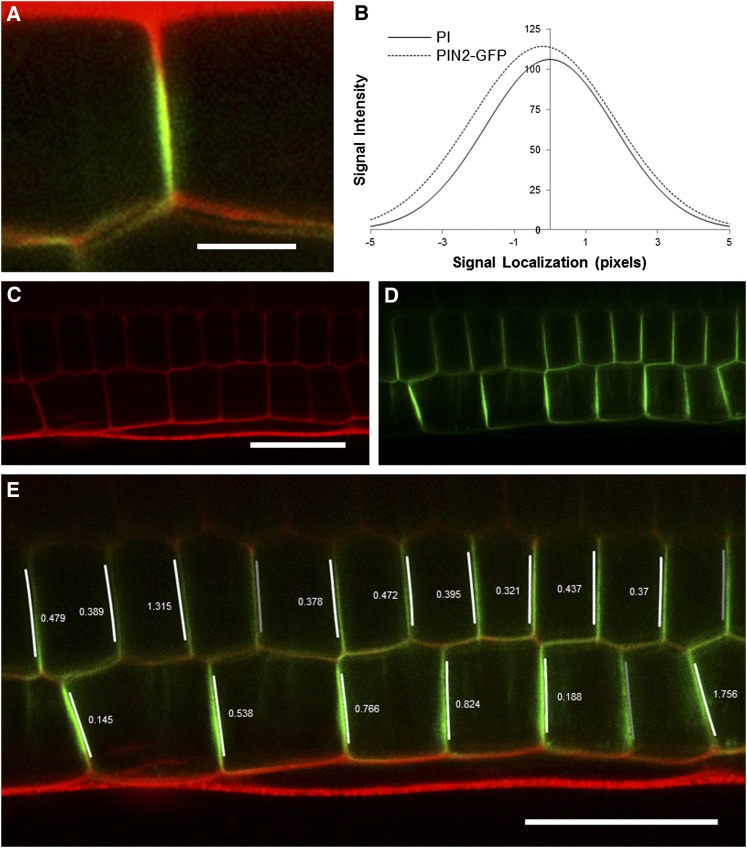
Asymmetric localization of membrane proteins within a cell allows transport of signals and nutrients and the establishment of hormone gradients. The close proximity of adjacent plasma membranes makes the determination of the polarity of proteins such as PIN2 problematic within the given pixel resolution of confocal microscopy. We created a plug-in that provides super-resolution localization of a protein marker relative to a cell wall (Figure 4; see Supplemental Movie 3 online). Super-resolution in this sense relates to an estimate of location at a higher resolution than the native hardware of the imaging system can provide and is possible by fitting models to the raw data and using these models to make predictions.

Figure 4.

Output of the Super-Resolution Plug-in.

(A) A zoomed section of a confocal image showing the PIN2-GFP protein residing on one side of an epidermal anticlinal cell wall. Red channel: cell walls stained with propidium iodide. Green channel: PIN2-GFP.

(B) Example plot of two normal distributions fitted to the wall and PIN2-GFP channels of (A). The offset (0.195 pixels; 0.04 μm) of the means of these two distributions reveals which side of the wall the protein resides.

(C) and (D) Input image of epidermal and cortical cells files of a root expressing PIN2-GFP.

(E) Output of protein localization plug-in with the direction and size of the offset (in pixels) of the PIN2-GFP channel overlaid in epidermal and cortical cell files. Overlaid arrows indicate rootward and shootward polarities. In three locations, no value is shown where this offset is below the detection limit set at 0.1 pixels, and so would not be used for further analysis. PIN2-GFP polarity is correctly detected as shootward in all epidermal cells and rootward in the majority of cortical cells. See also Supplemental Movie 3 online.

Bar in (A) = 5 μm; bar in (C) = 30 μm; bar in (E) = 30 μm.

The CellSeT protein localization plug-in can estimate the offset of a fluorescent membrane marker from the cell wall (assuming the wall is marked with a different fluorophore) to subpixel accuracy and can identify the direction of this offset. Regression is used to fit one-dimensional Gaussian distributions to the point-spread function-derived “blur” present orthogonally to the wall in both marker signals along the length of each wall (Figure 4B). Gaussian distributions are commonly used to model point-spread functions from confocal microscopes (Santos and Young, 2000; Betzig et al., 2006). The offset of these distributions represents the relative position of the protein with respect to the wall. Figure 4B shows the fits to the data in Figure 4A; the signal channel is offset by −0.195 pixels (~0.04 μm). The plug-in uses this information to produce an image detailing the offset direction and magnitude for each selected wall (Figure 4C). This is an important result, because this is traditionally a very subjective process that is hard to verify independently because of the limited resolution of the images available.

The auxin efflux carrier PIN2 is localized to the shootward face of epidermal cells in Arabidopsis root apices (Müller et al., 1998). The results of the plug-in shown in Figure 4E show PIN2-GFP polarity correctly detected as shootward in all epidermal cells and rootward in the majority of cortical cells (15 out of 18). In three cases, shown as darker gray bars, the offset has been calculated to be >0.1 pixels, which represents a distance of 0.02 μm. Empirical observation suggests that offsets of this size are often too small to be measured reliably and so are marked as unreliable (see Supplemental Figure 3 online).

Further testing of this plug-in was conducted on artificial data sets, in which the exact offset of the membrane protein could be adjusted. Supplemental Figure 4A online shows a section of root stained with propidium iodide. An artificial protein channel was generated by duplicating the cell walls into a separate channel and then translating the pixel values by a specified amount. A range of distances was tested, from 0.1 pixels to 1.0 pixels. The results, shown in Supplemental Figure 4C online, show that the plug-in correctly observed the direction of the offset in all tests. We define a successful test as one in which the direction of the offset determined by the plug-in was identical to the direction of the artificially produced offset. Success in this instance was not defined in terms of a match in magnitude, because the plug-in is primarily concerned with direction. Supplemental Figure 4C online reveals that the magnitude of the offset values are in fact often slightly lower than those in the ground truth data, causing if anything an excess of data to be rejected as unconfident (i.e., below the minimum offset threshold). This is preferable to accepting more offsets as being above threshold when they are in fact not. However, it does suggest that although the direction of offset is reliable, the magnitude should not be used as a quantitative measure at this time.

Conclusions

In summary, we have described a novel software tool for the segmentation, tagging, and analysis of network-structured images of plant cells. The tool assists users in the measurement of both geometry and fluorescence levels, providing a streamlined process that is more repeatable and efficient than the laborious manual alternative. The resulting cellular geometry information can be exported for use in multiscale modeling packages, such as OpenAlea (Pradal et al., 2008). Multiscale models that integrate realistic cell and tissue geometries with key subcellular processes, such as auxin transport, are set to become increasingly important in plant developmental biology research. CellSeT software will greatly facilitate such efforts.

The ability to create plug-ins for customized image analysis applications is an important feature of other popular programs, such as ImageJ (Abràmoff et al., 2004). Cell wall and nuclei fluorescence measurements are presented as examples of the further processing made possible by CellSeT’s plug-in architecture. The CellSeT nuclei plug-in is capable of quickly detecting nuclei in any number of presegmented cells and will greatly aid efforts to quantify nuclear-localized reporters (Figure 2). Such reporters are increasingly being used to generate spatiotemporal maps of responses to signals, such as auxin in confocal images of plant tissues (Heisler et al., 2005; Vernoux et al., 2011; Brunoud et al., 2012). Further uses of the nuclei plug-in can include the calculation of ratios between different fluorescent markers (such as a constitutive reporter versus a response marker) in the same nuclei to quantify responsiveness on a per cell basis.

A more complex plug-in, using super-resolution techniques that estimate the offset of fluorescent markers in the membrane versus cell wall to identify the direction of this offset, is also described (Figure 4). This represents an important step forward in objectively measuring the polarity of cell membrane proteins from images taken on a conventional confocal microscope. Such subcellular-scale data sets will greatly aid populating multiscale models with information about the direction of flux of signals such as auxin. Creation of a CellSeT plug-in is simple, and users are encouraged to write and distribute their own plug-ins to enhance the capability of the tool, providing a future-proof and flexible analysis pipeline for biologists wishing to analyze similar confocal images of cellular structures. Further detailed information on the CellSeT plug-ins and the basics of creating customized plug-ins is available, along with the CellSeT software, at www.cellset.net.

METHODS

Plant Material and Growth Conditions

Seedlings were grown vertically on one-half-strength Murashige and Skoog media (Murashige and Skoog, 1962) supplemented with 1% (w/v) agarose (Type PGP, Park Scientific) for 6 d in controlled environmental conditions of 24°C and continuous light of 150 μmol m⁻² s⁻¹ (Holman et al., 2010). Plants were imaged at 6 d after germination.

Confocal Microscopy

Live imaging was performed using an SP5 spectral detection confocal microscope (Leica). All images were taken with an HCX PL APO CS 20×0.7 numerical aperture air objective. Roots were stained by incubating for 1 min in 5 μg/mL propidium iodide solution (Sigma-Aldrich) to visualize cell wall organization. Images were acquired using a 514-nm argon laser line for yellow fluorescent protein (acousto-optical beam splitter [AOBS] setting, 520 to 548 nm) and a 488-nm argon laser line for GFP (AOBS settings, 493 to 551 nm). Propidium iodide staining was imaged using either the 514-nm or 488-nm lines, depending on the other fluorophore present (AOBS settings for each case, 609 to 727 nm).

CellSeT Image Analysis Implementation Details

The CellSeT software uses a specific chain of procedures to generate networks of cells from confocal images. First, the images are processed using a variety of common image filtering techniques. Commonly, a median filter is used to remove speckle noise, followed by a Gaussian blur to remove any larger artifacts. The size of the filter can be changed at the user’s discretion, depending on the levels of noise in the input images. Once filtered, the input image is segmented using the two-level watershed segmentation algorithm (Vincent and Soille, 1991; Sethuraman et al., 2011).

Watershed segmentation is a common approach used to segment images with clear intensity peaks at edges within the image; these peaks are interpreted as peaks in a physical landscape, which determines the boundaries of different catchment basins; hence, “watersheds.” A flooding of the landscape is simulated, and where different pools meet as the water rises, boundaries are determined. Here, an extension of the traditional approach means the water always floods over boundaries within a threshold of the current limit, which helps prevent oversegmentation, a common problem with the watershed approach. The difference between the lower water level and the upper threshold can be set by the user and will generally affect the amount of oversegmentation that occurs. This process can be performed iteratively by the user, quickly producing a sufficient segmentation. The advantage of watersheds is that the approach runs quickly and without user interaction, can segment any number of regions, and provides continuous region segments. Here it performs better than other common approaches, such as global thresholding, because it does not rely on a small number of fixed intensity values to identify the boundaries. It is also simpler to initialize than other more advanced techniques, such as level set methods (Sethian, 1999), and is easier to control than graph-cut methods (Shi and Malik, 2000).

Once initial segmentation is complete, region information is used to generate a graph structure that represents the cell walls. Each wall is represented by a series of interconnected node points, with wall end points connected to others via junction nodes. Where cell boundaries cross the edge of the image, walls are anchored to the image edge by another junction node. If necessary, the user can enter a manual segmentation procedure at this point, removing or adding walls to correct any errors in segmentation. Once manual refinement has been completed, or if it was not necessary, CellSeT uses the cell network to initialize a network snake algorithm (Sethuraman et al., 2011). A network snake is a series of interconnected active contours, similar in structure to the refinement graph. Active contours, or snakes, bend and move to position themselves toward image features while also adhering to other physical constraints about their shape. Each active contour has an associated energy function that is minimized to achieve this. Each node is moved to an optimal position near to its current location, whereby the overall energy of the snake is reduced. Once the majority of nodes have settled in optimum locations, the process is complete. The result of minimizing the energy terms is that snakes will attempt to stay straight and evenly distributed, but will also bend and move slightly to fit onto the underlying image. The energy function becomes more complex where junctions join multiple snake nodes.

A number of alternative extensions to the snakes technique exist, including the ability to model the snakes as an expanding balloon to aid segmentation (Cohen, 1991). In this case, the structured nature of the cells in a plant root makes treating individual snakes as a network an appropriate assumption. Full details of the implementation of the network snakes are provided in previous work (Sethuraman et al., 2011).

The resulting network snake structure does not make the structure of cells themselves explicit. Instead, it consists of a series of interconnected walls, which together mark cells’ boundaries. A right-hand–rule maze-solving algorithm is used to extract the locations and walls associated with any cells in the graph and proceeds as follows. For each junction node, the algorithm searches for a cell by traversing the graph, turning right at each junction. Where a cell exists, this right-hand walk will return to the original junction after a few steps. More formally, this algorithm returns all chordless cycles in the graph structure. Each unique cell is then recorded along with the list of junction nodes associated with it. From this, information on the locations of any intermediate contour nodes can be extracted.

Cellular Analysis

CellSeT provides an interface whereby users can semantically tag cells of various types and highlight walls as candidates for further analysis. CellSeT itself performs a number of direct measurements on the cell network, such as cell area and perimeter, wall length, and wall junction locations. Geometry and numerical data can be exported via XML or plain text files, and imported into modeling software, such as OpenAlea (Pradal et al., 2008). Powerful further analysis can be easily achieved using the plug-in interface, which provides a means of executing custom image analysis and statistical analysis routines on individual cells or groups of cells. In this article, we have detailed the results of three separate plug-ins. In this section, we provide an overview of the image and statistical analysis techniques required for each plug-in.

The wall intensity plug-in has been designed to calculate the mean and total integrated intensities of each individual wall segment and for each cell. Information on any cell or wall highlighted by the user is passed to the plug-in, which uses Bresenham’s line-drawing algorithm (Bresenham, 1965) to sample intensities at each pixel along each wall. Using a raster line-drawing algorithm ensures that each pixel is only sampled once, with no pixels being omitted between samples. Bresenham’s algorithm is also extremely fast, which ensures that hundreds of walls can be analyzed with no noticeable delay. The plug-in will also sample from identical positions in other image channels depending on the requirements of the user.

The nuclei analysis plug-in first detects and then analyzes the mean intensity of a single nuclei in any cell highlighted by the user. A targeted Otsu thresholding (Otsu, 1979) algorithm is used on each cell independently to calculate the optimum threshold for that region. The image is then segmented, and a connected component flood fill is performed on the foreground region to distinguish between the nucleus and any remaining noise. The position of the nucleus is then recorded for output by CellSeT, and the mean intensity of the nucleus is calculated. This information is combined with the existing cell geometry from CellSeT and used to produce the heat map, which is also output by the plug-in.

The protein localization plug-in is aimed at analyzing the offset of an asymmetric transporter protein signal from a cell wall signal. This is achieved by sampling a large number of pixels orthogonal to the cell wall on either side and then fitting one-dimensional Gaussian models to the data (Santos and Young, 2000), modeling the blur present in the signal localization. From these, the model’s mean values can be calculated, locating the peak of the curve, and hence protein location can be predicted to subpixel accuracy. This process begins by traversing the snake wall using Bresenham’s algorithm, and then, at each pixel, additional line-drawing routines are started perpendicular to the direction of travel. The result is the sampling of the majority of pixels traveling outward from the snake line up to a fixed distance away, which is specified by the user. Not every pixel visited will lie an exact pixel distance away from the snake wall when measured as a straight line to the nearest wall element. When a pixel is sampled, the Euclidean distance between it and the nearest point on the snake wall is calculated. This effectively allows sampling of continuous rather than discrete distances, which provides interpolated data to the model-fitting algorithm. At each pixel, the cell wall image and the signal image are both sampled, separate Gaussian distributions are fitted to each set of data, and thus the positions of the signal means can be compared. A least squares approach is taken to fit the Gaussian distributions, after which the offset is calculated as the positive or negative distance between the two peaks. Using real data with an artificial offset, we have evaluated the sensitivity of the offset size prediction (see Supplemental Figure 4 online). Using artificial data following a Gaussian distribution with a known offset, and with added noise components resembling those found in confocal data (Roberts et al., 2009), the success of predicting an offset direction was tested. With this data, at 0.1 pixel offset, the modeled offset predicted the correct offset direction ~75% of the time (see Supplemental Figure 3 online), with the success rate increasing quickly up to 100% at a distance of 0.4 pixels. Whether the offset is positive or negative indicates on which side of the centerline of the walls the signal resides. This directional value is resolved with the direction of travel of the algorithm along the snake wall and is used to calculate the angle of offset. Finally, every offset is combined with the original confocal image to produce a map detailing the offset sizes and directions for each highlighted wall.

Software Availability

The software is open source with a Berkeley Software Distribution license and will be distributed on SourceForge (http://sourceforge.net), along with Visual Studio project files. A link to the SourceForge distribution page is available via www.cellset.net. CellSeT is written in C# utilizing the Windows Presentation Foundation and .NET frameworks and so is available only for Windows operating systems.

Supplemental Data

The following materials are available in the online version of this article.

• Supplemental Figure 1. Flow Diagrams for Each Existing CellSeT Plug-in.

• Supplemental Figure 2. Evaluation of Local Otsu Thresholding against Global Otsu Thresholding.

• Supplemental Figure 3. Quantitative Analysis of the CellSeT Protein Localization Plug-in Using Artificial Data.

• Supplemental Figure 4. Quantitative Analysis of the CellSeT Protein Localization Plug-in.

• Supplemental Movie 1. An Overview of the CellSeT Processing Pipeline.

• Supplemental Movie 2. An Overview of the CellSeT Nuclei Detection Plug-in.

• Supplemental Movie 3. An Overview of the CellSeT Protein Localization Plug-in.

Glossary

CLSM

confocal laser scanning microscopy

GFP

green fluorescent protein

AOBS

acousto-optical beam splitter