New paradigm for drug therapies of cardiac fibrillation

Ventricular fibrillation (VF) is a fatal cardiac arrhythmia during which different parts of the heart do not beat together, and the heart cannot pump. There are about 300,000 sudden cardiac deaths associated with VF alone in the United States each year. On a wider scale, VF remains the leading cause of death among industrialized nations. The implantation of an automatic cardioverter-defibrillator is presently the most successful treatment of patients with uncontrollable VF. Such a device is designed to restore the heart to its normal rhythm via a large electrical shock that terminates any turbulent electrical activity. Drug therapies, in contrast, are aimed to control fibrillation in a less invasive and more cost-effective way by preventing its occurrence. They are thus in principle more desirable if they can be made equally effective as implantable devices. Antifibrillatory drugs, however, have so far remained largely unreliable and unsuccessful. Clinical trials to date, such as the Cardiac Arrhythmia Suppression Trial (1) where the death rate was higher among treated patients than those given placebo, have epitomized the danger of empirical drug therapies.

The experimental findings of Garfinkel et al. (2) in this issue of PNAS point to a promising new direction for antifibrillatory drug development that is based on recent advances in our understanding of cardiac fibrillation. Those authors demonstrate that VF can be suppressed by pharmacologically altering the electrophysiology of cardiac cells in a specific way that prevents wave-breaking instabilities, namely by flattening the action potential duration restitution curve discussed below. The stabilizing effect of flattening restitution has been predicted on the basis of computer simulations of cardiac activation (3, 4). Experimental findings in support of this prediction were recently reported by Riccio et al. (5) who showed that the calcium channel blocker verapamil, observed previously to have an antifibrillatory effect (6), and the electro-mechanical uncoupler diacetyl monoxime, both of which flatten dynamic restitution, also prevented VF induction or converted VF to a periodic rhythm in canine ventricle. The study of Garfinkel et al. (2) brings an important new piece of supporting evidence for the restitution hypothesis (3, 7), which states that flattening restitution inhibits wave breaks that drive VF. Those authors use optical mapping of epicardial electrical activity to explicitly demonstrate that wave breaks are suppressed when a drug (bretylium) is used to flatten restitution. They demonstrate that flattening of restitution by bretylium also prevents the induction of VF and converts VF to either a periodic rhythm or a quiescent but excitable state.

Rotating waves of electrical activity—the so-called rotors—have become the main paradigm for understanding cardiac fibrillation (8, 9). The existence of rotors that emit spiral and scroll waves in two and three dimensions, respectively, is by now well established both theoretically and experimentally. These waves are life-threatening because their 5- to 10-Hz rotation frequency drives an abnormally rapid contraction known as ventricular tachycardia (VT). Moreover, VT is typically unstable and decays reproducibly into VF after a few rotations in healthy tissue. In damaged hearts, such as in patients who suffered a myocardial infarction, slower forms of VT associated with the circulation of electrical impulse around scar tissue are sometimes sustained, but more often than not VT is a dangerous precursor to VF.

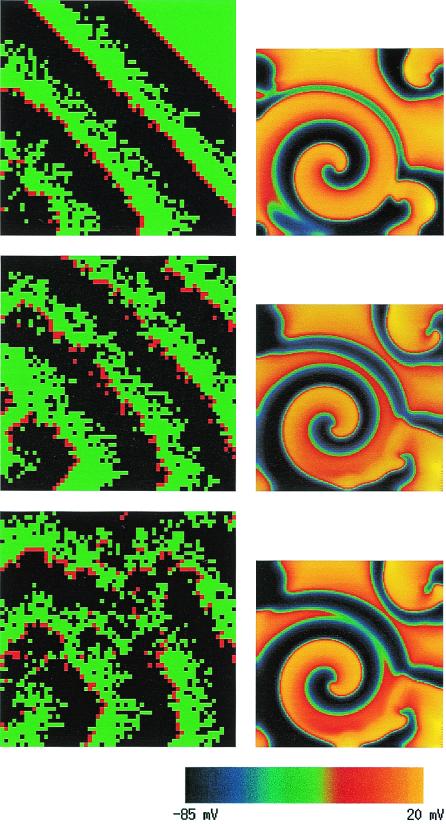
The classic mechanism that has been hypothesized to explain the transition from VT to VF is the fragmentation of activation wave fronts emitted by rotors that leads to the production of new rotors and a turbulent activity. In this picture, wave breaks are the key events that give rise to the repeated birth of new daughter rotors. In general, a wave front will fragment when it encounters patches of refractory (i.e., nonexcitable) tissue. These patches form when cells lack sufficient time to return to an excitable state after a previous excitation, and propagation fails locally on a given patch. Traditionally, the existence of such patches has been attributed to dispersion of refractoriness, i.e., to the fact that not all cells are identical and that some cells have longer refractory periods than others. In this interpretation, the heterogeneity is pre-existent and fixed in space. In a pioneering computer modeling study, Moe et al. (10) simulated a simple cellular-automata model of atrial fibrillation that incorporated a random dispersion of refractory periods. This model produced, remarkably, a fibrillatory-like activity with multiple wandering wavelets that is illustrated here in the left column of Fig. 1. Over the last decade, however, a fundamentally different view of the origin of wave breaks has emerged from simulations of more realistic propagation models governed by nonlinear partial differential equations. The main lesson has been that dynamical wave instabilities already suffice to generate spatial variations of refractoriness that produce wave breaks, even in a spatially homogeneous tissue where all cells have identical properties (3, 4, 7, 11). One essential wave-breaking instability that has been pinpointed (3, 4, 7) is linked to the so-called restitution property of cardiac action potential. Restitution is the relationship between the action potential duration (APD)—essentially the refractory period—and the diastolic interval (DI), which is the time interval between the end of the preceding action potential and the start of the next one. A short (long) DI is typically followed by a short (long) APD. More than three decades ago, Nolasco and Dahlen (12) demonstrated that if the restitution curve APD = f(DI) is sufficiently steep, the APD will spontaneously start to oscillate from beat to beat when a tissue is periodically paced at high frequency. As later shown by Guevara et al. (13), the geometrical construct used by Nolasco and Dahlen to prove this point is equivalent to iterating the one-dimensional map APD_n+1 = f(PCL − APD_n), where APD_n denotes the APD at the nth beat and the pacing cycle length (PCL) is the fixed interval between successive stimuli. It is simple to show that this map undergoes a classic period doubling bifurcation if the PCL is such that the slope S of the restitution curve, evaluated at the fixed point of this map is larger than unity. Consequently, for S>1 the dynamics consists of an alternation of long and short APD, the so-called electrical alternans observed by Mines in the early part of the last century (14). In a one-dimensional ring of tissue, the same instability manifests itself as quasiperiodic oscillations (15) (as opposed to a pure period doubling behavior), and moreover, sufficiently large amplitude oscillations of APD can cause propagation to fail when the excitation wave front re-enters refractory tissue.

Figure 1.

Illustration of wave breaks occurring by two fundamentally distinct mechanisms: fixed heterogeneity corresponding to dispersion of refractoriness (Left) and restitution-driven dynamic heterogeneity (Right). (Left) Three snapshots of a computer simulation of the cellular automaton model of Moe et al. (10) on a 2.4-cm × 2.4-cm square tissue made up of 60 × 60 square patches that are each 4 mm × 4 mm. Refractory periods vary randomly from patch to patch following the rules prescribed in ref. 10. Green (black) squares correspond to excitable (refractory) tissue and red squares correspond to the activation wave front (i.e., squares that were just excited). Ten successive stimuli were applied at the left-hand bottom corner of the tissue and time increases from top to bottom. (Right) Three snapshots of a computer simulation of a two-variable partial differential equation ionic model that incorporates restitution (3), for a 3.4-cm × 3.4-cm spatially homogeneous tissue without any fixed heterogeneity. Time increases from top to bottom with the middle and bottom frames being closely spaced in time. The transmembrane voltage for the right column is color coded according to the right bottom scale from −85 mV to +20 mV.

The manifestation of this instability most relevant for VF is in higher dimensions where propagation failure is nonspatially uniform along the wave front, and thus produces wave breaks. The right column of Fig. 1 illustrates this critical event in a simple two-variable ionic model that incorporates restitution properties (3). Subsequent to breakup, the wave dynamics can either consist of a periodic state with a small number of slowly moving rotors or a spatiotemporally chaotic state with a fluctuating number of closely packed rotors. The latter VF-like state occurs in this simple model for more steeply sloped restitution where wave breaks penetrate closer to the spiral tip. In more complex ionic models, the meandering motion of this tip interacts in a complex way with wave-breaking instabilities (4, 11), and only the latter state appears to be present. Moreover, a precise criterion for the onset of wave breaks is harder to formulate (4). In three dimensions the intramural stretching of scroll vortex filaments complicates the dynamics even further (2). In all cases studied so far, however, flattening restitution tends to prevent wave breaks and fibrillation, consistent with the findings of Riccio et al. (5) and Garfinkel et al. (2).

Not all computer modeling studies and experiments to date support the restitution hypothesis (16). One issue is whether the wave instability that causes VF is fundamentally three-dimensional in nature. Certain ventricular wall-thinning experiments, where rotors are induced in a tissue of variable thickness, have indicated that a minimum thickness is required to sustain VF. On this basis, Winfree (17) has hypothesized that some vortex filament instability may be involved in VF. Computer modeling studies have indeed revealed that a turbulent activity can result from instabilities that elongate filaments and makes them wiggly, either because of a negative filament tension in a tissue of reduced excitability (18) or to fiber twist in normal tissue when the spiral tip meanders wildly (19, 20). In these simulations, wave breaks are either absent or secondary actors. Zaitsev et al. (21) recently have argued for yet a different scenario that is based on new experimental findings. In their picture, the motor of VF may be an invisible rotor hidden inside the ventricular wall, consistent with the theoretical finding that vortex filaments tend to align themselves parallel to the fiber axis (22). These experiments used diacetyl monoxime that flattens restitution (5), and thus the hypothesized existence of stable rotors is not inconsistent, per se, with the restitution hypothesis. The main difference is the role attributed to fixed tissue heterogeneities that appeared to be the main source of asynchronous electrical activity. In contrast, one must conclude that in the experiments of Grafinkel et al. (2) and Riccio et al. (5), dynamic heterogeneity caused by restitution properties is more important.

Clearly, one of the main future challenges, from both theoretical and experimental standpoints, is to sort out the relative importance of fixed and dynamic heterogeneities in the genesis and maintenance of VF, as well as to elucidate further the nature of the electrical activity inside the ventricular wall. Whether antifibrillatory drug therapies developed within the new paradigm of the restitution hypothesis ultimately can be successful in controlling VF will depend largely on the results of this quest. The new findings of Garfinkel et al. (2) give us good reason to be hopeful.