Magnitude and sign epistasis among deleterious mutations in a positive-sense plant RNA virus

Abstract

How epistatic interactions between mutations determine the genetic architecture of fitness is of central importance in evolution. The study of epistasis is particularly interesting for RNA viruses because of their genomic compactness, lack of genetic redundancy, and apparent low complexity. Moreover, interactions between mutations in viral genomes determine traits such as resistance to antiviral drugs, virulence and host range. In this study we generated 53 Tobacco etch potyvirus genotypes carrying pairs of single-nucleotide substitutions and measured their separated and combined deleterious fitness effects. We found that up to 38% of pairs had significant epistasis for fitness, including both positive and negative deviations from the null hypothesis of multiplicative effects. Interestingly, the sign of epistasis was correlated with viral protein–protein interactions in a model network, being predominantly positive between linked pairs of proteins and negative between unlinked ones. Furthermore, 55% of significant interactions were cases of reciprocal sign epistasis (RSE), indicating that adaptive landscapes for RNA viruses maybe highly rugged. Finally, we found that the magnitude of epistasis correlated negatively with the average effect of mutations. Overall, our results are in good agreement to those previously reported for other viruses and further consolidate the view that positive epistasis is the norm for small and compact genomes that lack genetic robustness.

Introduction

Epistasis has been the focus of intensive research since the beginning of genetics as a scientific discipline (Phillips, 2008). In general, epistasis is the interaction between genes or mutations in determining phenotypes. The direction, magnitude and prevalence of epistasis is central to theories seeking to explain the origin of characteristics of genetic systems, such as sex and recombination (De Visser and Elena, 2007), dominance (Bagheri and Wagner, 2004), ploidy (Kondrashov and Crow, 1991), phenotypic plasticity (Remold and Lenski, 2004), robustness (De Visser et al., 2003), the ruggedness of adaptive landscapes (Weinreich et al., 2006; Poelwijk et al., 2007), or attempting to mechanistically explain dynamic biological processes such as the accumulation of mutations in finite populations (Kondrashov, 1994), and speciation by reproductive isolation (Coyne, 1992). Very recently, the evolutionary causes of epistasis, and not only their evolutionary consequences, have also attracted attention (Sanjuán and Nebot, 2008; De Visser et al., 2011; Macía et al., 2012).

Broadly speaking, epistatic interactions can be classified as uni- or multi-dimensional (Kondrashov and Kondrashov, 2001). Uni-dimensional epistasis is defined as deviations from a linear relationship between mean multiplicative fitness and the number of mutations affecting fitness. By contrast, multi-dimensional epistasis includes all the possible individual interactions among a set of mutations. Multi-dimensional epistasis provides a more complete description of the interactions within the fitness landscape defined by a set of mutations. Interactions can be further classified as magnitude or as sign epistasis. Magnitude epistasis (ME) occurs when that the fitness value associated to a mutation, but not its sign, changes upon the genetic background wherein it appears (Weinreich et al., 2005; Poelwijk et al., 2007). Moreover, ME can be positive or negative, depending on whether the fitness of the double mutant is larger or smaller than expected under the multiplicative null model, respectively. ME is a widespread phenomenon observed in organisms of different complexity (Sanjuán and Elena, 2006). Sign epistasis (SE) refers to cases in which the sign of the fitness effect of a mutation is under epistatic control; thus, such a mutation is beneficial in some genetic backgrounds and deleterious in others (Weinreich et al., 2005; Poelwijk et al., 2007). In few instances where it has been sought, SE seems to be quite common, although perhaps not as ubiquitous as ME (Weinreich et al., 2006 Poelwijk et al., 2007; Franke et al., 2011; Kvitek and Sherlock, 2011).

Epistasis is particularly relevant for our understanding of adaptive evolution, as it determines the ruggedness of the adaptive landscape (Withlock et al., 1995; Poelwijk et al., 2011) as well as the accessibility of adaptive pathways throughout the landscape (Weinreich, 2005 Welch and Waxman, 2005; Franke et al., 2011). Evolutionary trajectories may end at suboptimal fitness peaks due to the ruggedness of the fitness landscape. Epistasis can therefore hamper the efficiency of natural selection and thus slow down the rate of adaptation (Withlock et al., 1995). Moreover, epistasis can make certain evolutionary pathways towards higher fitness genotypes selectively inaccessible because of troughs and valleys in the fitness landscape: intermediate genotypes have reduced fitness compared with surrounding genotypes. Weinreich et al. (2005) were the first to notice this evolutionary constraint and to postulate that such limitation would arise only as a consequence of SE. Indeed, a particular type of SE known as RSE, that is, the sign of the fitness effect of a mutation is conditional upon the state of another locus and vice versa, has been shown to be a necessary condition for an adaptive landscape to be rugged (Poelwijk et al., 2011).

RNA viruses are ideal experimental systems for exploring the nature of epistatic interactions: their compact genomes often code for overlapping reading frames, contain functional RNA secondary structures and encode for multi-functional proteins. Altogether, these properties are expected to lead to strong epistasis. Indeed, recent studies exploring uni- and multi-dimensional epistasis have provided empirical evidences that ME is common for RNA viruses such as Foot-and-mouth disease virus (Elena, 1999), bacteriophage φ6 (Burch and Chao, 2004), Vesicular stomatitis virus (VSV, Sanjuán et al., 2004), Human immunodeficiency virus type 1 (Bonhoeffer et al., 2004; Van Opijnen et al., 2006; Parera et al., 2009; Da Silva et al., 2010; Martínez et al., 2011), Rous sarcoma virus (Sanjuán, 2006), or Tobacco etch virus (TEV; De la Iglesia and Elena, 2007b), among others, as well as for ssDNA bacteriophages such as ID11 (Rokyta et al., 2011) or φX174 (Pepin and Wichman, 2007). Furthermore, in most of these studies positive epistasis is more abundant than negative epistasis, although variability exists within each virus. Positive epistasis may appear as a consequence of individual mutations having a large negative impact on fitness such that any additional mutation that still produces a viable virus must necessarily exert a minor impact (Elena et al., 2010). SE, by contrast, has been detected only among compensatory mutations for φX174 (Poon and Chao, 2006) and among pairs of beneficial mutations for ID11 (Rokyta et al., 2011). By contrast, no evidence of SE was found for combinations of beneficial mutations in the RNA bacteriophage MS2 (Betancourt, 2010).

In this study we sought to characterize the patterns of multi-dimensional epistasis for the RNA plant virus TEV (genus Potyvirus, family Potyviridae). TEV has a single-stranded positive-sense RNA genome of ca. 9.5 Kb that encodes for a single polyprotein that self-processes into 10 mature peptides. An additional peptide is translated from an overlapping ORF after +2 frameshifting. To this end, we generated a collection of 53 double mutants by randomly combining 20 individual mutations whose deleterious fitness effect had been previously quantified (Carrasco et al., 2007b). The fitness of all single and double mutants was evaluated in the primary host Nicotiana tabacum. We characterized the statistical properties of the distribution of epistatic interactions and found a mixture of positive and negative effects (including some examples of synthetic lethals (SLs)). Next, we found that RSE was the most common type of epistasis. We also explored the negative association between the average fitness effect of deleterious mutations and the strength of the epistastic interaction in which they were involved. Finally, we tried to frame the observed epistatic effects within a model of the protein–protein interaction network (PPIN) formed by all 11 TEV proteins.

There are many novelties within our study. First, this is the first description of extensive SE, particularly of the reciprocal type, contributing to the architecture of fitness of an RNA virus. Second, we contextualize epistasis in the network of interactions among viral proteins. Third, it is the first report of epistasis for a eukaryotic virus in its natural host rather than in in vitro cell cultures, which represent an artificial and oversimplified environment. Last, but not least, this is the first analysis of multidimensional epistasis for any plant pathogen.

Materials and methods

Virus genotypes

A subset of 20 mutants non-lethal in N. tabacum (Supplementary Table 1) was randomly chosen from a larger collection generated in a previous study (Carrasco et al., 2007b). Six were synonymous mutations, whereas the rest were nonsynonymous. Plasmid pMTEV (Bedoya and Daròs, 2010) was used to reconstitute the wild-type TEV and to generate the mutant genotypes. These 20 mutations were randomly combined to generate a set of 53 double mutants (Supplementary Table 2) by site-directed mutagenesis using the QuikChange II XL Site-Directed Mutagenesis Kit (Stratagene, Santa Clara, CA, USA) as described by Carrasco et al. (2007a). The kit incorporates PfuUltra high fidelity DNA polymerase that minimizes the introduction of undesired mutations. The uniqueness of each mutation was confirmed by sequencing an 800-bp fragment encompassing the mutated nucleotide.

Infectious RNA of each genotype was obtained by in vitro transcription after BglII linearization of the corresponding plasmid as described in Carrasco et al. (2007a).

Inoculation experiments

All N. tabacum plants were inoculated at an identical growth stage to minimize variations in defense response to infection with developmental stage. All inoculations were done in a single experimental block. Nine plants per TEV genotype were inoculated by rubbing the first true leaf with 5 μl containing 5 μg RNA in vitro transcript of the virus and 10% Carborundum (100 mg ml⁻¹).

Ten days post-inoculation, the whole infected plant, except the inoculated leaf, was collected. The collected tissue was frozen in liquid nitrogen and grounded with mortar and pestle.

RNA purification and virus quantification

An aliquot of approximately 100 mg of grounded tissue was taken and mixed with 200 μl of extraction buffer (0.2 ℳ Tris, 0.2 ℳ NaCl, 50 mℳ EDTA, 2% SDS; pH 8). An equal volume of phenol:chloroform:isoamylic alcohol (25:25:1) was added, thoroughly vortexed and centrifuged at 14 000 g for 5 min at 25 °C. Ca. 160 μl of the upper aqueous phase was mixed with 80 μl of a solution containing 7.5 ℳ LiCl and 50 mℳ EDTA and incubated overnight on ice at 4 °C. The precipitated RNA was centrifuged at 14000, g for 15 min at 4 °C, washed once with 70% ice-cold ethanol, dried in a SpeedVac (Thermo Fisher Scientific, Waltham, MA, USA) and resuspended in 30 μl of DEPC-treated ultrapure water. RNA concentration was measured spectrophotometrically and the samples were diluted to a final concentration of 50 ng μl⁻¹.

Within-plant virus accumulation was measured by absolute RT−qPCR using an external standard (Pfaffl, 2004). Standard curves were constructed using five serial dilutions of TEV RNA produced by in vitro transcription and diluted in RNA obtained from the host plant.

RT−qPCR reactions were performed in 20 μl volume using One Step SYBR PrimeScript RT−PCR Kit II (TaKaRa, Bio Inc, Otsu, Japan) following the instructions provided by the manufacturer. The forward TEV−CP 5′-TTGGTCTTGATGGCAACGTG and reverse TEV−CP 5′-TGTGCCGTTCAGTGTCTTCCT primers amplify a 71 nt fragment within the TEV CP cistron. CP was chosen because it is located in the 3′ end of TEV genome and hence would only quantify complete genomes. Each RNA sample was quantified three times in independent experiments. Amplifications were done using the ABI PRISM Sequence Analyzer 7000 (Applied Biosystems, Carlsbad, CA, USA). The thermal profile was: RT phase consisted of 5 min at 42 °C followed by 10 s at 95 °C; and PCR phase of 40 cycles of 5 s at 95 °C and 31 s at 60 °C. Quantification results were examined using SDS7000 software v. 1.2.3 (Applied Biosystems).

For each genotype, a Malthusian growth rate per day was computed as m=(1/t)log(Q_t), where Q_t are the pg of TEV RNA per 100 ng of total plant RNA quantified at t=10 days post-inoculation. Absolute fitness was then defined as W=e^m (Crow and Kimura, 1970).

Estimation of epistasis among pairs of mutations

Epistasis among pair of mutations x and y, ɛ_xy, was calculated as ɛ_xy=W₀₀W_xy−W_x0W_0y (Kouyos et al., 2007), where W₀₀, W_xy, W_x0, and W_0y correspond to the absolute fitness of the wild-type, the double mutant and each single mutant, respectively. A value of ɛ_xy>0 corresponds to the case of positive (antagonistic) epistasis, whereas a value of ɛ_xy<0 is indicative of negative (synergistic) epistasis. Values of ɛ_xy not significantly deviating from zero were qualified as multiplicative (that is, non-epistatic) mutational effects.

In all cases, reported error intervals correspond to ±1 s.e.m. All statistical analyses were performed using IBM SPSS v. 19 (Armonk, NY, USA).

Results

Epistasis among pairs of deleterious mutations

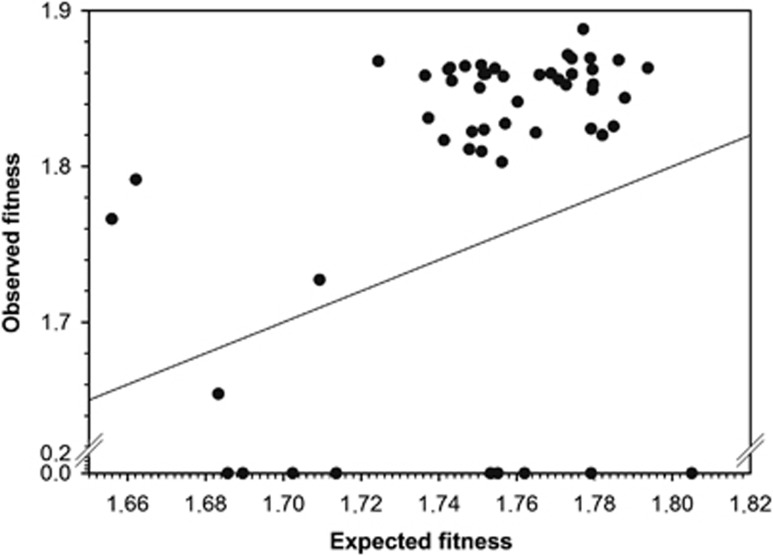
Figure 1 shows the relationship between observed and expected fitness values for the set of 53 double mutant genotypes synthetized for this study (Supplementary Table 2). The solid line represents the null hypothesis of non-epistatic fitness effects. The observed fitness values of 20 double mutant genotypes significantly departed from this null expectation (Supplementary Table 2; t-tests, in all cases P⩽0.049). Nine of these cases were SLs, which means that two mutations that were viable by themselves become lethal when combined. These SLs represent an extreme case of negative epistasis. All other significant cases corresponded to positive epistasis. Therefore, we found variability in the sign and strength of epistasis. However, only the nine SLs remained significant after applying the more stringent sequential Bonferroni correction for multiple tests of the same hypothesis (Rice, 1989). Nonetheless, for all analyses presented below, we used all 20 significant cases, unless otherwise indicated. This decision represents a compromise between reducing the data set to only the nine SLs (which precludes running any additional analysis) and using the whole data set irrespective of the significance of observed fitness values.

Figure 1.

Relationship between observed and expected multiplicative fitness for 53 TEV genotypes carrying pairs of nucleotide substitutions. The solid line represents the null hypothesis of multiplicative fitness effects. Deviations from this line arise as a consequence of the existence of epistatic fitness effects.

Three double mutants contained two synonymous mutations, 22 combined one synonymous and one nonsynonymous mutation and 28 carried two nonsynonymous mutations. No differences existed, however, in the magnitude of epistasis among these genotypic classes (Kruskal–Wallis test: χ²=0.405, 2 df, P=0.817).

Using the whole data set, we sought to test whether the distribution of SL and viable mutations were homogeneous among pairs of mutations within the same cistron or among affecting different cistrons. In two out of nine SLs both mutations were at the same cistron (22.2%), whereas in the case of viable double mutant genotypes, only one genotype out of 44 had both mutations in the same cistron (2.3%), a significant difference (χ²=5.569, 1 df, P=0.018) despite the small sample size. Furthermore, the average epistasis coefficient computed for mutations within the same cistron was −1.142±0.617, whereas it was reduced to −0.171±0.090 for pairs of mutations affecting different cistrons. This 85.1% relaxation in the strength of epistasis was also significant (t₅₁=2.477, P=0.017). Therefore, we can conclude that a tendency exists for mutations affecting the same cistron to generate a SL phenotype and to interact in a stronger and more negative manner, whereas mutations affecting different viral proteins presented weaker interactions.

Statistical properties of the epistasis distribution

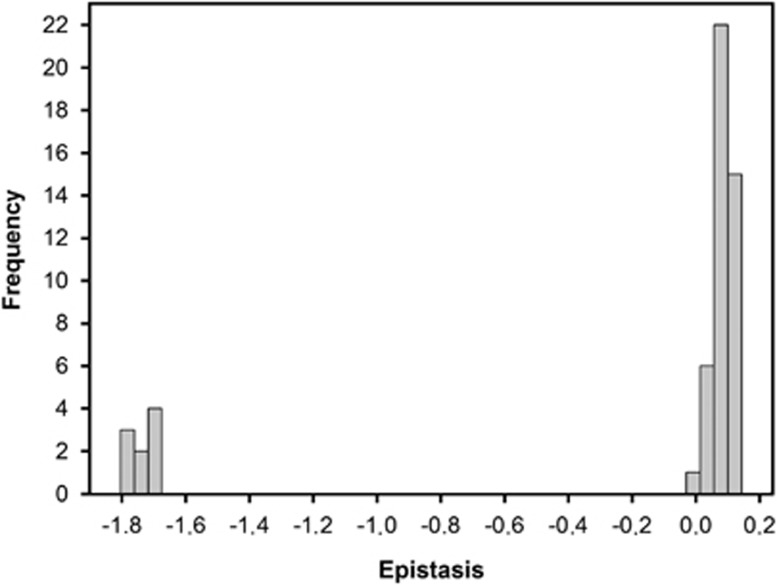
Figure 2 illustrates the distribution of epistasis parameters for all pairs of point mutations analyzed. The distribution had a bimodal shape, with SLs representing the left probability mass and the viable genotypes being on the right side of the distribution. The average epistasis was 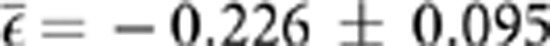, a value that departs from the null hypothesis of multiplicative effects (t₅₂=2.376, P=0.021). Furthermore, the distribution had a significant negative skewness (g₁=−1.806±0.327; t₅₂=5.515, P<0.001), that is, the tail containing negative epistasis is heavier than the Gaussian and thus asymmetric. Similarly, the distribution was significantly leptokurtic (g₂=1.326±0.644, t₅₂=2.058, P=0.045), indicating that it had a more acute peak around the mean value compared with the Gaussian.

Figure 2.

Distribution of epistasis. Epistasis, ɛ, was computed as the difference between the observed fitness of the double mutant (W₀₀W_xy) and the value expected from subtracting the effects of each single mutant from the wild-type value (W_x0W_0y).

Given that lethal mutations are largely irrelevant for evolutionary dynamics, we sought to reanalyze the epistasis distribution after removing SLs. The main consequence of this removal was that the average epistasis then becomes significantly positive (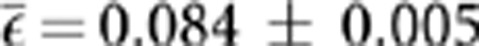; t₄₃=17.438, P<0.001). Regarding the shape of the distribution, it still remained asymmetric with significant negative skewness (g₁=−1.050±0.358; t₄₃=2.936, P=0.005), although the skewness parameter was 41.9% smaller than when SLs were included in the data set. In contrast, the distribution became 77.1% more leptokurtic (g₂=2.348±0.702, t₄₃=3.346, P=0.002), as a consequence of the removing the cases from the left tail extreme.

Pervasive RSE

We were interested in evaluating the extent to which SE was present in our data set. Poelwijk et al. (2011) defined mathematically the condition for SE as

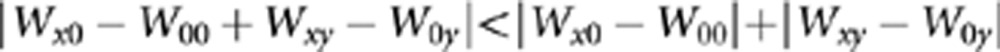Twelve out of the twenty TEV double-mutant genotypes for which we had detected significant epistasis (Supplementary Table 2) fulfilled this condition and thus can be classified as cases of SE. The other eight, hence, correspond to cases of ME. Is this 3:2 proportion expected given the observed fitness values of individual mutations and of the double mutants? To tackle this question we applied the above inequality to the 33 non-epistatic pairs of mutations, founding that 26 fulfilled it, despite not being significant. A Fisher's exact test failed to detect significant differences among epistatic and non-epistatic pairs fulfilling the inequality (1-tailed P=0.124), thus confirming that the observed proportion of ME and of SE was not significantly enriched in the later class. Therefore, we conclude that SE makes a major contribution (60%) to all cases of significant epistasis.

Next, we specifically evaluated the contribution of RSE to the observed pattern of SE. According to Poelwijk et al. (2011) the following additional condition must be met by a pair of mutations showing SE in order to be considered as cases of RSE:

Herewith, this condition was fulfilled by 11 out of 12 cases of SE (91.7%). Indeed, only synthetic lethal PC6/PC76 did not match it. As before, given the fitness of single and double mutants, we tested whether this extremely high prevalence of RSE among cases of SE is to be expected. We counted the number of cases that fulfilled this second inequality (25) among the 26 non-epistatic cases that matched the first one. A Fisher's exact test also showed no significant enrichment in cases of RSE among cases of SE (1-tailed P=0.538). Therefore, we conclude that RSE is common in TEV genome.

Correlation between fitness effects and epistasis

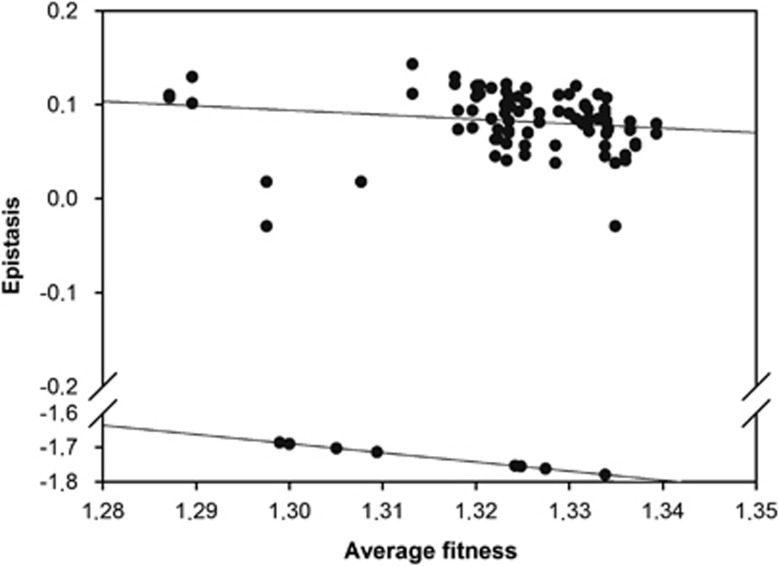
It has been observed that average deleterious mutational effects and the strength of positive epistasis are not independent parameters but, instead, are negatively correlated (Wilke and Adami, 2001 You and Yin, 2002; Wilke et al., 2003; Bershtein et al., 2006; Sanjuán et al., 2006; De la Iglesia and Elena, 2007). We sought to investigate if this negative relationship holds for TEV. Figure 3 shows the relationship between the mean fitness of the two mutations combined and the estimated epistasis for all 53 double mutants. A first observation is that two different and significant relationships exist in correspondence to different phenotypic classes: one for the nine SLs (Spearman's r_S=−1.000, 7 df, P<0.001) and another one for the viable genotypes (r_S=−0.416, 42 df, P=0.005). However, overall a significant negative correlation existed after controlling for the difference within two phenotypic classes (partial r=−0.331, 50 df, P=0.017). The slope for the viable genotypes was significantly smaller than the slope for the SLs (analysis of covariance test for the homogeneity of slopes in Figure 3: F_1,49=9.212, P=0.004), suggesting that the underlying mechanisms for the observed relationships were different for each phenotypic class. Indeed, the correlation observed for the SLs is trivial because it is expected based on the definition of epistasis used here. If the observed fitness of the double mutant is W_xy=0, then 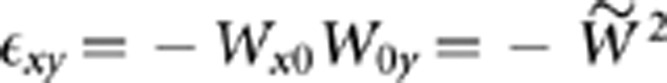, where 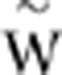is the geometric mean fitness of mutations x and y. The validity of this explanation was confirmed by the fact that linear regression throughout the origin of epistasis on 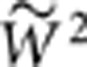for the SLs data rendered the expected slope of −1.000±0.000.

Figure 3.

Association between average mutational effects and the magnitude of epistasis. Two apparent relationships exist: one for pairs of mutations generating viable genotypes (upper cloud) and a different one associated to the SLs (lower cloud). The regression lines are included to illustrate the difference in the underlying relationship between epistasis and average mutational effects between both types of phenotypes.

These correlations suggest that mutational effects and epistasis are not independent traits, but instead, they may evolve hand in hand. Stronger mutational effects are associated with more positive interactions, whereas milder effects are associated with more relaxed positive interactions. Therefore, a reduction in the magnitude of mutational effects translates into a relaxation of the positive epistasis.

Epistasis in the context of TEV PPIN

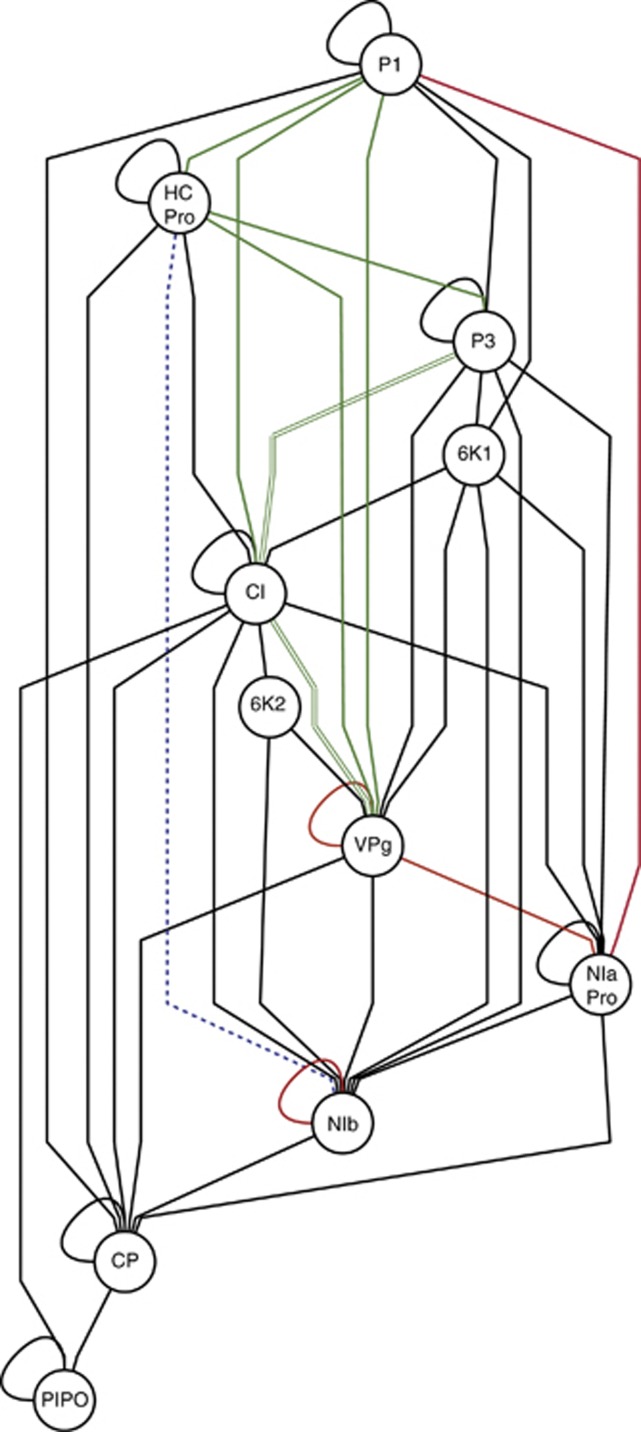
Mutations were grouped according to the mature protein they affect. By doing so, we focused on the analyses of interaction among proteins rather than among individual nucleotide residues. Rodrigo et al. (2011) inferred the undirected PPIN shown in Figure 4 using a compendium of physical interactions experimentally determined by the yeast two-hybrid method. We were interested in correlating the network properties with the characteristics of the distribution of epistasis inferred in this study.

Figure 4.

TEV PPIN inferred from yeast two-hybrid data published elsewhere. The 11 mature peptides are indicated as nodes. Black edges correspond to interactions for which we did not detect significant epistasis. Red edges correspond to cases of negative epistasis and green edges correspond to cases of positive epistasis. Double green lines correspond to two pairs of mutations affecting the same proteins. The dashed blue line corresponds to a case in which a first pair of mutations showed positive epistasis (PC19/PC95) but a second pair had negative epistasis (PC22/PC95). The PPIN was drawn using Cytoscape (Killcoyne et al., 2009).

First, we sought to test whether the number of significant epistatic and non-epistatic interactions was homogeneously distributed among pairs of proteins directly linked in the PPIN graph or unlinked (Figure 4). A Fisher's exact test failed to reveal a significant association (P=0.151), thus rejecting the hypothesis that a direct interaction between two proteins is a necessary condition to generate significant epistasis.

Second, we explored whether the number of pairs of proteins involved in positive and negative epistatic interactions was evenly distributed among pairs directly connected in the PPIN and those that are not (Figure 4). It has been argued for modularly organized PPINs that mutations affecting independent modules would show a pattern of positive epistasis, although PPINs organized as a single-functional module would be more sensitive to the effect of mutations and show a pattern of negative epistasis (Sanjuán and Elena, 2006; Sanjuán and Nebot, 2008; Macía et al., 2012). In agreement to this expectation, we found that nine out of fourteen (64.3%) positive interactions between linked elements, whereas only two out of six (33.3%) interactions between unlinked elements were positive. Thus, we conclude that mutations affecting connected elements in the PPIN tend to be involved in more positive epistatic interactions than those affecting non-connected components.

Finally, we hypothesized that highly linked nodes would have a stronger tendency to be epistatic, whereas less connected nodes will be less so. To test this hypothesis, we first computed the tendency of a protein to be involved in significant epistasis interactions (that is, epistasiness) for each protein as the absolute value of the average epistasis coefficient computed across all interactions in which this protein was involved and using the whole data set. Absolute values were used because we tested for the tendency for involvement in significant interactions regardless of their sign. Then, we computed the connectivity of each node as the number of links it has in Figure 4. A non-parametric correlation coefficient failed to detect a significant association between these two variables (r_S=−0.221, 6 df, P=0.599). Therefore, we conclude that the tendency of a protein to be involved in epistatic interactions is not a necessary consequence of the amount of interactions itself.

Discussion

In this study, the distribution of epistatic interactions on fitness for a plant RNA virus has been evaluated by constructing genotypes carrying pairs of single-nucleotide substitutions, each having a deleterious fitness effect. We detected cases of both positive and negative epistasis, although positive epistases were significantly more abundant than negative ones, such that the combined effect of mutations is significantly less harmful than expected under the null multiplicative model. This dominance of positive epistasis is particularly frequent among mutations affecting two different proteins, whereas, on average, mutations affecting the same protein interact in a negative manner. These findings are in good agreement with observations accumulated in recent years for other RNA viruses, including retroviruses, and small ssDNA viruses (reviewed by Elena et al., 2010), both using experimental approaches to characterize uni- and multi-dimensional epistasis. Given this heterogeneity in viral systems, it thus seems highly likely that positive epistasis among deleterious mutations is a general feature of most small viruses. What may be the mechanistic reason for this excess of positive epistasis? Several reasons can be brought forward. First, the compactness of viral genomes, many of which even had adopted the strategy of overlapping genes and multifunctional proteins, necessarily implies that the deleterious effects of different mutations can partially overlap, hence producing positive epistasis. Indeed, this expectation is well fulfilled by our finding that interactions are, on average, more positive when mutations occur in two different proteins than when they both occur in the same one. Second, positive epistasis can also be a consequence of the existence of elements of RNA secondary structure. Indeed, it was shown by computer simulations of RNA folding that mutations affecting the same structural element may restore it and thus generate positive epistasis (Wilke et al., 2003 Sanjuán et al., 2006). Another observation that seems to be common among experiments of multi-dimensional epistasis in RNA viruses is the existence of frequent cases of synthetic lethality, for example, for the mammalian rhabdovirus VSV (Sanjuán et al., 2004).

The dominance of positive epistasis among deleterious mutations and the existence of frequent cases of synthetic lethality are both fingerprints of another phenomenon: the low genetic robustness of viral genomes. It has been postulated that epistasis and robustness are two sides of the same coin and that negative epistasis must be a hallmark for genetic robustness (De Visser et al., 2003, 2011; Proulx and Phillips, 2005; Desai et al., 2007). Indeed, the observed negative correlation between epistasis and mutational effects shown in Figure 3 provides additional support for this hypothesis and is consistent with observations made in systems as diverse as artificial life (Wilke and Adami, 2001; Edlund and Adami, 2004), computer simulations of genetic systems (You and Yin, 2002; Macía et al., 2012), RNA (Wilke et al., 2003; Sanjuán et al., 2006) and protein folding (Bershtein et al., 2006), and in a mutation–accumulation experiment done with TEV (De la Iglesia and Elena, 2007). The negative correlation between epistasis and mutational effects means that the milder the average mutational effect is, the more negative the epistatic interactions between mutations will be. This results in a genotype that is more mutationally robust against genetic perturbations. In contrast, positive epistasis reflects strong mutational effects and, therefore, low genetic robustness. Sanjuán and Elena (2006) postulated that robustness would scale up with genetic complexity and that it may result from the fact that more complex genetic systems may contain more redundant structures capable of buffering the effect of mutations. Very recently, Macía et al. (2012) tested this hypothesis by simulating the evolution of genetic circuits under variable selection for robustness. They found that, as predicted, negative epistasis was caused by the existence of genetic redundancy in complex networks and not due to complexity itself, as the correlation disappeared when the formation of redundant structures was not allowed during the evolution of complex networks. In this sense, RNA viruses will occupy the lower side of the complexity spectrum and, therefore, would be highly sensitive (that is, non-robust) to mutations.

Within cases of significant epistatic interactions, we found a large contribution of SE relative to the contribution of ME. This represents the first description of SE for an RNA virus, as previous studies of multi-dimensional epistasis in RNA viruses did not explicitly look for SE (for example, Bonhoeffer et al., 2004; Sanjuán et al., 2004; Sanjuán, 2006; Van Opijnen et al., 2006) or simply failed to find them (Betancourt, 2010). In contrast, SE has been shown to be common during adaptation of β-lactamase to cefotaxime (Weinreich et al., 2006; Salverda et al., 2011), in evolution experiments compensating for the cost of antibiotic resistance in bacteria (Schrag et al., 1997; Maisnier-Patin et al., 2002) and viruses (Molla et al., 1996; Cong et al., 2007; Martínez-Picado and Martínez, 2009), in experimental evolution of asexual Saccharomyces cerevisiae (Kvitek and Sherlock, 2011), and in multi-dimensional tests of epistasis in Aspergillus niger (Franke et al., 2011). All but one cases of SE detected in TEV corresponded to RSE, perhaps making this observation even more interesting. This type of epistasis is particularly relevant from the perspective of describing fitness landscapes. Poelwijk et al. (2011) have shown that the existence of multiple adaptive peaks in a fitness landscape, that is, ruggedness, requires RSE. Furthermore, Kwitek and Sherlock (2011) experimentally confirmed that RSE caused the ruggedness of a fitness landscape. The ruggedness of adaptive landscapes is critical to predict whether evolving populations may reach the global optima or may get stuck into suboptimal peaks (Weinreich, 2005; Withlock et al., 1995). Our finding of a predominance of RSE suggests that the fitness landscape for TEV, and maybe for other RNA viruses, must be highly rugged.

In conclusion, the results reported here, together with previous findings, contribute to the perspective that viral genomes are dominated by positive epistasis, which may result from their compactness and lack of genetic redundancy. In addition, we provide the first direct proof that SE, in particular RSE, contributes in a large extent to the architecture of viral fitness. The high frequency of RSE suggests that adaptive landscapes for RNA viruses maybe highly rugged. This ruggedness may impose harsh constraints on the often-invoked but not empirically grounded limitless adaptability of RNA viruses.

Data archiving

Data have been archived at Dryad: doi: 10.5061/dryad.bq4pp7f9.

The authors declare no conflict of interest.