Trapping DNA near a Solid-State Nanopore

Abstract

We demonstrate that voltage-biased solid-state nanopores can transiently localize DNA in an electrolyte solution. A double-stranded DNA (dsDNA) molecule is trapped when the electric field near the nanopore attracts and immobilizes a nonend segment of the molecule across the nanopore orifice without inducing a folded molecule translocation. In this demonstration of the phenomenon, the ionic current through the nanopore decreases when the dsDNA molecule is trapped by the nanopore. By contrast, a translocating dsDNA molecule under the same conditions causes an ionic current increase. We also present finite-element modeling results that predict this behavior for the conditions of the experiment.

Introduction

It is now well established that single molecules of DNA can be induced to pass (translocate) through a voltage-biased nanopore in a thin insulating membrane, and detected electronically. Detection is achieved by monitoring the changes in the nanopore ionic conductivity induced by the molecule's transient presence inside the nanopore. This effect has been observed in protein nanopores embedded in lipid membranes (1), and in solid-state nanopores fashioned in thin insulating silicon nitride and oxide membranes (2,3). Recent progress with these systems has shown that biological pores in lipid membranes are capable of identifying individual bases along a single-stranded DNA molecule (4,5). Nanopores in single-layer graphene membranes, geometrically capable of single-base resolution, have also recently been demonstrated in Garaj et al. (6). DNA translocating nanopores in thicker graphene-based membranes have also been reported in Schneider et al. (7) and Merchant et al. (8).

In this article, we show that a voltage bias across a solid-state nanopore can cause dsDNA molecules to become trapped at the orifice of a nanopore under suitable conditions. dsDNA trapping at a nanopore requires that the molecule be attracted toward the nanopore and ultimately lay immobilized across its input orifice (Fig. 1). Both attraction and trapping are induced by an electric field that results from the voltage bias applied across the nanopore. For this kind of trapping to be realized, it is necessary that the molecule be stiff enough, the nanopore small enough, and the local electric field weak enough to prevent buckling that allows a folded molecule to translocate through the nanopore. On the other hand, the local electric field must be strong enough to actually immobilize and trap the molecule at the orifice of the nanopore.

Figure 1.

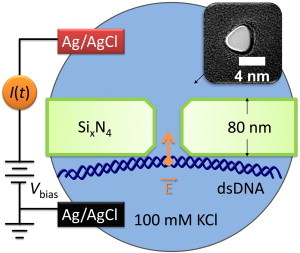
Schematic of the experimental setup. (Orange arrow) Electric-field-induced trapping force. (Inset, top right) Transmission electron micrograph of a typical nanopore.

We have been able to realize and observe this new (to our knowledge) phenomenon because the modification of the nanopore conductivity can be made remarkably different for a molecule trapped across a nanopore compared to when it is translocating through it. In fact, we shall show that the trapped molecule can decrease the conductivity under conditions where the translocating molecule increases it. We anticipate that this new nanopore-trapping phenomenon will be relevant to a number of single-molecule applications.

Materials and Methods

Two reservoirs of electrolyte solution are separated by an ion impermeable nonconductive low-stress silicon nitride (Si_xN₄) membrane. A single 4–5-nm pore in the membrane provides the only fluidic and ionic conductive path between the two chambers (Fig. 1). Externally applied voltage bias (V_bias), through Ag/AgCl electrodes in the fluid on each side of the membrane, induces charged potassium and chlorine ions, as well as double-stranded (dsDNA) molecules, to pass through the nanopore (9). The resulting current can be recorded as a function of time and reveals the state of individual dsDNA molecules inside and near the pore.

Nanopores with 4-nm diameter (Fig. 1) were drilled in 80-nm-thick freestanding Si_xN₄ membranes on silicon chips, with a 200 keV model No. 2010F transmission electron microscope (JEOL USA, Peabody, MA). The 80-nm-thick Si_xN₄ membrane forms a 2.5-μm square, centered in a thicker and approximately tenfold larger square membrane consisting of the same 80 nm of Si_xN₄ above 2 μm of SiO₂. This geometry reduces preamplifier-induced capacitive noise in the ionic current measurements and provides mechanical support (10).

The nanopore chip is mounted in the flow cell chamber. An electrolyte solution is admitted into the reservoirs on both sides of the membrane. This solution consists of KCl salt in deionized water, buffered with 10 mM TRIS and 1 mM EDTA. A quantity of 10-kilobase (kb) dsDNA (obtained from New England Biolabs, Ipswich, MA) molecules was added to the solution on the negative side of the membrane at a concentration of 1 μg/30 μL.

Ag/AgCl electrodes immersed in the electrolyte on each side of the nanopore are connected to an Axopatch 200B patch-clamp amplifier (Molecular Devices, Sunnyvale, CA). This instrument both sets the voltage bias on the two sides of the nanopore and measures the resulting current through the pore. The ionic current signal is filtered through an eight-pole 60 kHz low-pass Bessel filter and digitized at a rate of 250 kilosamples/s. A search and fitting algorithm, implemented in the software MATLAB (The MathWorks, Natick, MA), locates and least-square-fits dsDNA modulations in the current, taking into consideration the filter effect.

Results

Fig. 2 shows a segment of an ionic current trace through a nanopore, during a time interval that includes the new (to our knowledge) kind of molecular 10-kb dsDNA event that this article presents. The electrolyte was 100 mM pH 9.1 KCl and the nanopore diameter was 5 nm. The applied voltage bias was 350 mV and resulted in an open pore current of 2.36 nA, as seen in regions A and E of Fig. 2. The full event consists of an ∼900-μs-long, ∼180-pA decrease in the ionic current (region B of Fig. 2), followed by a brief ∼100-μs return to the open-pore current (region C of Fig. 2) and then a transient current enhancement in region D of Fig. 2. The enhancement is consistent with a single unfolded molecule of dsDNA translocating through the nanopore (11).

Figure 2.

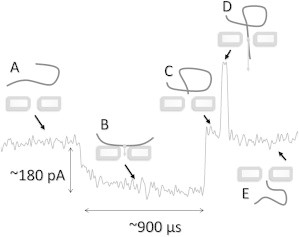
Current trace of a trapping event followed by translocation. The current in region B decreases from the open pore level in regions A and E. Briefly, the current returns to the open pore level, in region C, before the translocating dsDNA molecule increases the current, transiently, in region D.

The decrease in current shown in region B of Fig. 2 contrasts with the enhancement expected from a dsDNA translocation and has not been previously reported in the literature. All 10 nanopores having diameters ranging from 3.2 to 5.3 nm displayed the new feature in region B, typically at a voltage bias above 300 mV. The current decrease shown in region B of Fig. 2 relative to open pore current ranged from 55 pA to 342 pA at 600 mV and varied in duration from several μs to several seconds.

Fig. 3 a shows the results of a particular experiment conducted at a 600-mV bias, where multiple events were recorded and displayed as a scatter plot. Each point in the scatter plot represents a single event, indicating the observed average current increase and its duration. Average duration was 57.0 ± 17.5 μs equivalent to a mean dsDNA translocation speed of 6.0 ± 1.8 cm/s. All the translocation events observed at 100 mM were unfolded. Out of the 86 translocation events plotted in Fig. 3 a, 17 exhibited a decrease in the nanopore current similar to that seen in region B of Fig. 2. The duration of this new feature ranged from 70 μs to 2550 μs. The latter is more than an order-of-magnitude longer than dsDNA translocation times at the same bias. In most cases, the return to the open pore current displayed in region C of Fig. 2 was shorter than 8 μs and remained unresolved.

Figure 3.

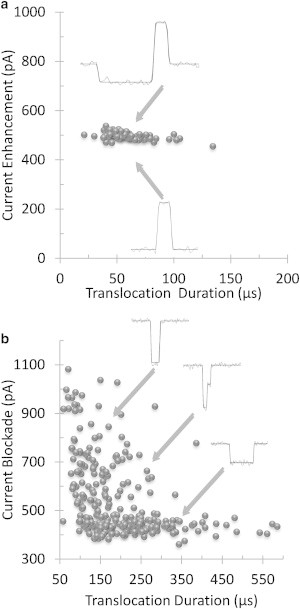
(a) Scatter plot of 86 10-kb dsDNA events at 600 mV in 100 mM KCl. Seventeen of the 86 events show a decrease in the ionic current before translocation (top trace). The remaining events exhibit only the typical translocation induced increase in the ionic current (bottom trace). (b) 285 10-kb dsDNA translocation events through the same nanopore as in panel a, at 500 mV in 1 M KCl. Current traces show representative events from different areas of the scatter plot.

Fig. 3 b shows that when the electrolyte molarity is raised to 1 M KCl, typical dsDNA translocation events that now decrease the nanopore current are observed (2). This control experiment did not reveal depressed currents preceding the translocations like those in region B of Fig. 2. Consistent with previous reports from Li et al. (9), several types of translocation events were recorded (Fig. 3 b). These were unfolded events in which one end of the dsDNA molecule enters the nanopore, and several types of folded events in which two strands of the same dsDNA enter the pore simultaneously. During folding, translocation events displayed a current blockage that is approximately twice that of unfolded events. Fig. 3 b presents a scatter plot of 285 blockade events at 500 mV bias. Out of the 285 events, 237 were unfolded, with average translocation duration of 166 ± 61 μs.

For use in modeling the results above, we also measured room temperature electrolyte conductivity of the 100 mM and the 1 M KCl solutions to be 13.22 ± 0.06 mS/cm and 106.63 ± 0.51 mS/cm, respectively.

Discussion and Analysis

We posit that trapping of the dsDNA molecule across the orifice of the nanopore is responsible for the decreased current observed in Figs. 2 and 3 a. In region B of Fig. 2, the applied voltage bias establishes a strong electric field near the nanopore, which traps the molecule against the nanopore but is insufficient to fold and translocate it through the nanopore. The decrease in current is associated with the trapped dsDNA molecule blocking some of the ionic current flow thorough the nanopore. This effect is dominant when the molecule is oriented (Fig. 4) perpendicular to the nanopore axis at its orifice and leads to a drop in the recorded current. Brownian fluctuation forces continuously counter the trapping force and can eventually dislodge the dsDNA molecule to a sufficient degree to restore the open pore current (region C of Fig. 2). Within a short time, one of the molecule's ends enters the nanopore and normal translocation ensues (region D of Fig. 2). Here the ionic current increases because mobile counterions are brought into the nanopore along its whole length by the translocating dsDNA molecule. The possibility that trapping and translocation events can lead to opposite sign current modulation is supported by the modeling presented below.

Figure 4.

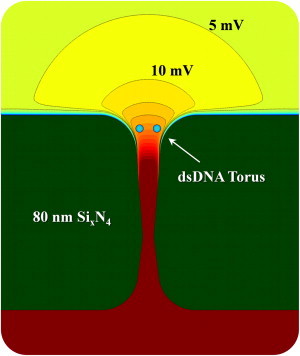
Profile of the nanopore geometry used in the finite element calculations along with potential contours at 600-mV applied bias.

Fig. 4 shows a section of the nanopore geometry used in finite element calculations incorporating Maxwell, Navier-Stokes, and Nernst-Plank physics. The narrowest constriction (apex) of the nanopore has a 4.5-nm diameter and is located 30.4 nm and 49.6 nm away from the surfaces of the membrane. Translocating dsDNA is represented by a 2.2-nm diameter cylinder coaxial with the nanopore. Trapped dsDNA is modeled as a ring torus with a 25.1-nm circumference and the same 2.2-nm molecular diameter. The cylindrical symmetry of the torus makes calculations with that geometry practical. This torus is located 9 nm into the nanopore orifice to account for dsDNA bending, which results from the electric field near the nanopore. The axis of the dsDNA molecule is, in this case, perpendicular to the nanopore axis.

The ionic current through the nanopore is calculated by solving the coupled electrostatics, fluid dynamics, and drift-diffusion equations on a triangular grid with the software package Comsol (Comsol AB, Stockholm, Sweden). The applied bias voltage creates a strong electric field near and inside the nanopore. This electric field induces ions to move electrophoretically through the fluid. Negative charge of the dsDNA molecule and the Si_xN₄ nanopore surface leads to an enhanced potassium ion concentration inside the nanopore and electroosmotic flow of the fluid. Concentration gradients lead to diffusive ion flow. These ion-flow mechanisms account for the nanopore currents calculated.

Two parameters used in the model presented require derivation.

The first is ionic mobility. Invoking Kohlrausch's law of independent migration of ions, we can express the electrolyte conductivity κ in terms of the potassium ${\mu }_{K^{+}}$ and chlorine ${\mu }_{C{l}^{-}}$ mobilities, the KCl concentration c, the elementary charge e, and Avogadro's number N_a, as

$$\kappa =\left({\mu }_{K^{+}}+{\mu }_{C{l}^{-}}\right)c{N}_{a}e.$$ (1)

The ratio of the potassium ion mobility to that of the chlorine ion can be obtained from the transference numbers for 100 mM and 1 M KCl solutions in Currie and Gordon (12). Table 1 presents the calculated effective ionic mobilities from Eq. 1. These values are calculated from the measured electrolyte conductivity and thus account for small pH and buffer perturbations.

Table 1.

Calculated effective mobilities and surface charge for the two electrolyte solutions used

Parameter	0.1 M KCl	1 M KCl	Units
${\mu }_{K^{+}}$	6.10	5.34	$\frac{m^2}{Vs}{10}^{-8}$
${\mu }_{C{l}^{-}}$	6.36	5.60	$\frac{m^2}{Vs}{10}^{-8}$
σ	140.2	69.8	$\frac{mC}{m^2}$

The second important modeling parameter is the nanopore surface charge. Electrolyte pH and ionic concentration determine the Si_xN₄ nanopore surface charge. The oxygen-plasma-treated, low-stress silicon-nitride used in this work has zero surface charge at pH 4.1 (10). Using the two-site theory in Harame et al. (13) predicts that only 4% of the surface groups are amines. Deprotonated silanol groups establish a negative surface charge on the surface under the experimental conditions in this work (14). The mass action law for the deprotonation reaction of the silanol groups, considering surface activity states that

$$\sigma e^{-\beta e({\psi }_d+\sigma /C)}+{10}^{pH-pK}\left(e\Gamma +\sigma \right)=0,$$ (2)

where σ is the Si_xN₄ surface charge, β⁻¹ = kT, ψ_d is the diffusive layer potential, Γ is the total silanol surface density, and pK is the deprotonation logarithmic rate constant. The Stern capacity C relates the diffusive potential to the surface potential ψ₀,

$$C=\frac{\sigma }{{\psi }_0-{\psi }_d}.$$ (3)

The Grahame equation relates the surface charge and the diffusive potential,

$$\sigma =\frac{2\epsilon {\epsilon }_0{\lambda }_d}{\beta e}\text{sinh}\left(\frac{\beta e{\psi }_d}{2}\right),$$ (4)

where λ_d is the Debye screening length. Equations 2–4 can be solved self-consistently. We calculate and present the Si_xN₄ surface charge (Table 1) for C = 2.9 F/m², Γ = 2.33 nm⁻², and pK = 6.75. The C, Γ, and pK values are consistent with what others have measured (13,14).

Simulations of the translocating and the trapped dsDNA molecule geometries predict the experimentally observed opposite sign ionic current modulations (ΔI) at low salt (Fig. 5). When negatively charged dsDNA is translocating it increases the K⁺ concentration inside the nanopore. Despite obstructing part of the nanopore, the total ionic charge inside the nanopore is increased by 17% compared to the open-pore case. The additional free charge along the length of the nanopore increases both the electroosmotic and the drift-diffusion currents when the dsDNA molecule is translocating. Calculations predict a 22% current enhancement at 600 mV bias, compared to 21% measured experimentally.

Figure 5.

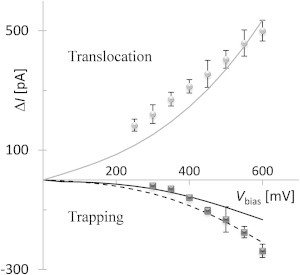
Translocation experimental data (gray circles) and simulation prediction (gray solid line). Trapping experimental data (black squares) and simulation prediction (black lines). The dashed and solid lines represent 2.8 nm and 2.2 nm diameter dsDNA trapping models, respectively.

When dsDNA is trapped, the total ionic charge inside the nanopore is increased by only 5%. The additional charge in this case is localized to a small section perpendicular to the nanopore axis. Electroosmotic current near the dsDNA molecule is increased due to the additional charge despite the obstruction. The trapped dsDNA molecule blocks some of the drift-diffusion current both near the center of the nanopore and near the walls. The decrease in the drift-diffusion current is larger than the increase in the electroosmotic current and the overall ionic current is lower when dsDNA is trapped compared to the open pore case. Because the additional charge is concentrated near the orifice, the total current at 600 mV bias is predicted to decrease by 6% for a trapped molecule compared to a decrease of 10% measured experimentally. The torus model likely overestimates the interactions of the trapped dsDNA with the nanopore wall. An alternative calculation for a 2.2-nm diameter sphere, matching the surface charge of dsDNA and centered at the orifice of the nanopore, also predicts a reduction in the ionic current relative to the open pore current. In the case of the sphere, there is no interaction between the sphere and the nanopore's walls.

The applied voltage-induced electric field creates a strong trapping potential near the nanopore (Fig. 4). The maximum restoring force necessary to free the dsDNA molecule at a 600-mV applied voltage bias is 5.4 pN. This is significantly larger than the ∼74-fN average entropic force resulting from the reduced availability of conformation states with trapping. The entropic force is, however, sufficient to displace the molecule laterally ∼1 nm away from the axis of the nanopore, eventually allowing capture of one of the molecule's free ends. Once translocation begins, the charge along the translocating strands pushes the trapped segment an additional 3 nm away from the axis laterally, and the 129.7 pN translocation force overwhelms any residual trapping potential. Trapping forces presented include the dsDNA molecule's drag due to electroosmotic fluid flow and are roughly linear with applied bias. At the lower 350-mV bias, a fluctuation of the entropic force may displace the trapped segment of the dsDNA molecule briefly before translocation (region C of Fig. 2).

Conclusion

Under the right experimental conditions, a negatively charged dsDNA molecule can become trapped at the orifice of a nanopore. The size of the nanopore and the strength of the electric field have to be within a narrow range so that the molecule becomes trapped but does not buckle and translocate. The trapped molecule decreases the current through the nanopore in contrast to the current enhancement observed during translocation at low molarities. This phenomenon will affect capture statistics in nanopores too small to allow folded events and may remain undetected at high molarities. It would be interesting to explore the trapping phenomenon for dsDNA molecules with length on the order of, or less than, a few persistence lengths. However, the translocation history of such short molecules is difficult to record.

The possibility of trapping a charged molecule at the orifice of a solid-state nanopore suggests some interesting applications. If a transition from trapping a charged polymer to its folded translocation occurs at a certain applied voltage, the persistence length of the molecule can be calculated. Charged molecules that are too stiff to buckle for any reasonable applied voltage can be precisely positioned over the nanopore and permanently immobilized through nonspecific binding to the membrane. For example, a single-walled carbon nanotube decorated with a single-stranded DNA molecule can be electrophoretically aligned with a nanopore. Fabricating an array of nanopores can result in precise alignment and control surface mobility of a trapped molecule through the trapping force. Through controlling the surface mobility of a DNA molecule that is translocating through a larger nanopore, one can control its translocation speed.