Bovine β-Lactoglobulin Is Dimeric Under Imitative Physiological Conditions: Dissociation Equilibrium and Rate Constants over the pH Range of 2.5–7.5

Abstract

The oligomerization of β-lactoglobulin (βLg) has been studied extensively, but with somewhat contradictory results. Using analytical ultracentrifugation in both sedimentation equilibrium and sedimentation velocity modes, we studied the oligomerization of βLg variants A and B over a pH range of 2.5–7.5 in 100 mM NaCl at 25°C. For the first time, to our knowledge, we were able to estimate rate constants (k_off) for βLg dimer dissociation. At pH 2.5 k_off is low (0.008 and 0.009 s⁻¹), but at higher pH (6.5 and 7.5) k_off is considerably greater (>0.1 s⁻¹). We analyzed the sedimentation velocity data using the van Holde-Weischet method, and the results were consistent with a monomer-dimer reversible self-association at pH 2.5, 3.5, 6.5, and 7.5. Dimer dissociation constants K_D^2-1 fell close to or within the protein concentration range of ∼5 to ∼45 μM, and at ∼45 μM the dimer predominated. No species larger than the dimer could be detected. The K_D^2-1 increased as |pH-pI| increased, indicating that the hydrophobic effect is the major factor stabilizing the dimer, and suggesting that, especially at low pH, electrostatic repulsion destabilizes the dimer. Therefore, through Poisson-Boltzmann calculations, we determined the electrostatic dimerization energy and the ionic charge distribution as a function of ionic strength at pH above (pH 7.5) and below (pH 2.5) the isoelectric point (pI∼5.3). We propose a mechanism for dimer stabilization whereby the added ionic species screen and neutralize charges in the vicinity of the dimer interface. The electrostatic forces of the ion cloud surrounding βLg play a key role in the thermodynamics and kinetics of dimer association/dissociation.

Introduction

β-Lactoglobulin (βLg) is the most abundant protein in the whey of cow's milk, although its function remains unknown. Investigators have intensely studied βLg using almost every conceivable biophysical technique because of its ready accessibility, intrinsically interesting biophysical properties, wide-ranging applications in the food and nutraceutical industries (1–8), and the significant allergenic reaction it causes in some humans (this protein is lacking in human milk) (9–11).

A member of the lipocalin family, βLg is a small protein of 162 amino acids with a molecular mass of ∼18,400 Da, featuring an eight-stranded β-barrel (strands A–H) succeeded by a three-turn α-helix and a final β-strand (strand I) that forms part of the dimerization interface (Fig. 1). The secondary and tertiary structures of bovine βLg are largely preserved from below pH < 2 to higher than pH 8 (12–14). The quaternary structure over this pH range is reported to be predominantly dimeric at moderate ionic strength (e.g., 100 mM NaCl) and temperatures above 20°C (12,15), whereas at low pH and very low ionic strength (pH < 3.0 and I < 10 mM), bovine βLg is predominantly monomeric (12,16).

Figure 1.

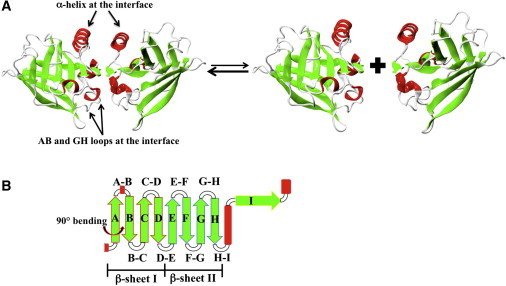
(A) Cartoon representation of the dimeric and monomeric βLg structures (PDB code 1BEB, chains A and B). The α-helices are colored red, the β-strands are green, and loops and turns are white. (B) Schematic representation of βLg topology (color code as in panel A). The I strand is involved in the dimer formation, whereas strands A–H fold into two β-sheets (strands A_N-D and E-H-A_C, where A_N and A_C respectively denote the N- and C-terminal portions of strand A, which suffers a 90° bend).

Bovine βLg has two common variants, denoted A and B, that differ by only two residues: Asp-64 and Val-118 in βLg A are replaced by glycine and alanine, respectively, in βLg B (17,18). Native or heterologously expressed wild-type βLg A and B have been structurally characterized to high resolution in both a monomeric state (by NMR methods (19–21)) at pH ∼2.5, very low ionic strength and moderate protein concentrations of ∼10−20 mg mL⁻¹, and a dimeric state (by x-ray diffraction methods over the pH range ∼5.5–8.2, and low to high ionic strengths and high concentrations of >400 mg cm⁻³ in a crystal (22–26)). For variant A, at low temperatures (<10°C) and moderate ionic strength (∼0.1 M), near the isoelectric point (pH ∼5.3), there is low-resolution structural evidence for an octameric form (∼144 kDa) (27–30) that so far has not succumbed to detailed structural characterization. This higher-order oligomerization is not observed for βLg B (29,31) or for the rarer variant, βLg C (29,32,33), where Glu-59 of variant B is replaced by histidine (34).

The main contributing force to βLg oligomerization (keeping in mind the effects of varying pH and ionic strength on dimerization) is the hydrophobic effect (35). However, polar peptide-peptide interactions in the antiparallel pairing of the I strands, and, especially at pH above the isoelectric point, salt bridges between residues on a long loop between strands A and B (the AB loop) are clearly significant (36,37). Recent theoretical calculations suggest that the hydrophobic effect is driven by a decrease of the water-accessible surface area upon dimer formation (38).

Investigators have determined the dimer dissociation constant (K_D^2-1) using a variety of techniques, including analytical ultracentrifugation (AUC) (15,16,37,39–47), isothermal titration calorimetry (48,49), small-angle x-ray scattering (SAXS) (50), and light scattering (16,31,50,51). For βLg A and B, the experimentally determined K_D^2-1 values fall within the 1–300 μM range at an ionic strength of ∼100 mM and over a wide pH range either side of the isoelectric point of ∼5.2 (16,17,52,53) (see Table S1 in the Supporting Material). In addition, dimer formation can be slightly enhanced by nonpolar mutations in the AB loops, which form part of the dimer interface (37). On the other hand, disruption of the intermolecular Asp-33…Arg-40 salt bridge by mutation of Asp-33 to Arg, or by mutation of Arg-40 to Asp or Glu, substantially weakens the dimer. The heterodimer, featuring a single mutation Arg-33 or Asp-40 to one or another subunit, has a K_D^2-1 similar to that of the wild-type (37). Mutations of I-strand residues to Pro were shown to be deleterious to dimer stability, but mutation of the I-strand Arg-148 to Ala had little effect on dimer stability (37). However, complementary studies on equine and porcine βLg, which are monomeric where bovine βLg is dimeric (54,55), failed to create dimeric species when mutations were made in an attempt to recreate the salt bridges observed in the dimer interface of bovine βLg (37,56). Thus, because the I-strand and the AB loop constitute a necessary, but not sufficient, criterion for dimerization, the structural determinants and the mechanism of dimer stabilization remain somewhat uncertain.

NMR studies of native or wild-type bovine βLg have generally been performed at low pH (∼2.5), very low ionic strength, protein concentrations of ∼1 mM (∼18 mg mL⁻¹), and temperatures of ∼37°C (19–21). In these studies, researchers tended to assume that the protein is rigorously monomeric. However, very few quantitative data are available regarding the degree of association into a dimeric species under these conditions. SAXS and light-scattering data obtained at 20°C, pH 2.3, and ionic strength of 7 mM indicate >90% monomer (50). Variable-temperature studies point generally to an endothermic enthalpic contribution to the free energy of the dissociation (31,36,41,42,44–46,48,49), and isothermal titration calorimetry, AUC, and light-scattering measurements point to highly nonideal solutions at concentrations > ∼2 mg mL⁻¹ (∼0.1 mM) (16,31,40,57). However, at pH ∼7, the pH near which almost all x-ray crystallographic structural studies have been conducted, native or wild-type bovine βLg gives poorly resolved NMR spectra. In an Ala34Cys mutant that forms a covalently linked disulfide-bridged dimer (58), NMR studies at pH ∼7 were unable to detect the conformational changes associated with the Tanford transition, a pH-gated movement of an external loop bearing Glu-89 that at pH above its pK_a of ∼7.3 exposes its buried side chain (23,59–61). Most probably, the timescale in which such conformational changes develop is too slow to be detected.

The accurate measurement of the association-dissociation process, and especially of the kinetics of this process, is a necessary prerequisite to understanding the kinetics of folding and unfolding of oligomeric proteins, for which bovine βLg has long been a paradigm of study (62–66). As yet, an in-depth study of the kinetics of βLg oligomerization with respect to variant and pH has not been performed. In the work presented here, we employed AUC to compare the dimer dissociation constant (K_D^2-1) and the kinetics of oligomerization of the βLg A and B variants over a wide pH range at a fixed ionic strength of 100 mM NaCl. We complemented these studies with electrostatic calculations to derive information on the stabilization of the βLg dimer over the monomer as a function of ionic strength.

Materials and Methods

A full description of the protein expression and purification processes (67,68), AUC experiments (36,69), and continuum electrostatic calculations (23,70–76) is provided in the Supporting Material, together with the accompanying Fig. S1, Fig. S2, Fig. S3, Fig. S4, Fig. S5, Fig. S6, Fig. S7, Fig. S8, Fig. S9, Fig. S10, Fig. S11, Fig. S12, Fig. S13, Fig. S14, Fig. S15, Fig. S16, Fig. S17, Fig. S18, Fig. S19, Fig. S20, and Fig. S21, and Table S2, Table S3, Table S4, Table S5, Table S6, and Table S7.

Results

We used AUC in both sedimentation velocity (SV) and sedimentation equilibrium (SE) modes (77–79) to characterize the oligomerization (80) of two βLg variants in solution. In our initial work, we conducted SV experiments to assess the oligomeric state of the βLg A and B variants over a broad pH range (pH = 2.5, 3.5, 4.5, 5.5, 6.5, and 7.5), for which two different buffers (20 mM citrate and 20 mM MOPS) were required. Essentially, constant ionic strength was maintained by 100 mM NaCl as the background electrolyte in all solutions. SV data for each variant at three concentrations (see Fig. S1, Fig. S2, Fig. S3, Fig. S4, Fig. S5, Fig. S6, Fig. S7, Fig. S11, Fig. S12, Fig. S13, Fig. S14, Fig. S15, Fig. S16, and Fig. S17) were collected at each pH value. Summaries of weight-averaged s_20,w coefficients, along with the hydrodynamic properties and fit statistics, are provided in Table S4 (βLg A) and Table S5 (βLg B). SE data, collected under the same conditions, were used separately and in conjunction with SV data to determine the equilibrium constants for dimer dissociation (K_D^2-1). Rate constants (k_off) for the dimer-monomer reaction at different pH values could also be estimated from the SV data (81,82). The pH-dependent behavior of βLg B paralleled that of βLg A. To ensure that our thermodynamic and kinetic parameters would be responsive to changes in the AUC data, we modeled the sensitivity of a parameter of interest to variations in other variables used to fit the SV and SE data, and thus were able to derive realistic estimates of the errors in our results. The Supporting Material shows the SV and SE data, and fits to these data for βLg A (Fig. S1, Fig. S2, Fig. S3, Fig. S4, Fig. S5, Fig. S6, and Fig. S7) and βLg B (Fig. S11, Fig. S12, Fig. S13, Fig. S14, Fig. S15, Fig. S16, and Fig. S17). The measured βLg concentrations are provided in the figure captions and Table S2. Table 1 summarizes the K_D^2-1 and k_off values.

Table 1.

Equilibrium^∗ and rate^† constants calculated for βLg A and βLg B dimer dissociation at different pH values and buffer solutions, and an ionic strength of 100 mM NaCl from global fits^‡ of SE and SV data

	KD2-1 (/μM)		koff (/s−1)		kon (calc.) (/M−1 s−1)
	βLg A	βLg B	βLg A	βLg B	βLg A	βLg B
pH 2.5	14.8	8.2	0.008	0.009	540	1100
Citrate	(11.2–18.4)	(5.8–11.1)	(0.002–0.019)	(0.003–0.029)
pH 3.5	4.0	1.4	[0.007]§	[0.041]§	—§	—§
Citrate	(2.3–6.0)	(1.1–4.5)
pH 6.5	4.0	2.5	Fast (> 0.1)	Fast (> 0.1)	>25,000	>40,000
MOPS	(2.7–5.6)	(1.0–7.1)
pH 7.5	10.8	8.6	Fast (> 0.1)	Fast (> 0.1)	>9,200	>12,000
MOPS	(7.6–15.8)	(6.3–10.9)

^∗Calculated from global fitting of SV and SE data. Values calculated from global fitting of SE or SV data are provided in Table S7.

^†Calculated from global fitting of SV data (SE data contain no kinetic signal). Values calculated from global fitting of SE and SV data are provided in Table S7.

^‡Calculated error ranges representing an estimated 69% confidence interval are reported in parentheses.

^§Indicative value, because no error range could be determined; k_on not calculated.

Characterizing the oligomeric state of βLg A and βLg B in SV experiments

Continuous size distribution and mass analyses

We first fitted the SV data for βLg A and βLg B to a continuous c(s) distribution using the program SEDFIT (83). Representative fits of the data for βLg A and βLg B at pH 2.5 and at three protein concentrations of ∼5, ∼15, and ∼45 μM (Fig. 2 and Fig. S8) suggest that under these conditions, both βLg variants self-associate with a dissociation constant (K_D^2-1) close to or in the range of the concentrations investigated (84). At the ∼5 μM concentration of βLg A (Fig. 2 A, solid line), the continuous c(s) distribution as a function of the standardized sedimentation coefficient at 20°C in water (s_20,w) shows an asymmetric shape with a maximum at 2.1 S that tails to higher sedimentation coefficients. In contrast, at ∼45 μM (Fig. 2 A, dotted line) the maximum is at 2.6 S and tails to lower sedimentation coefficients, whereas at ∼15 μM (Fig. 2 A, dashed line) the c(s) distribution is more symmetrical with a maximum at an intermediate value of 2.4 S. βLg B at pH 2.5 displays similar behavior (Fig. S8). For both βLg A and βLg B, the c(s) model gave a good fit to the data, as judged by the low root mean-square deviation (RMSD), runs test-Z scores, and random distribution of residuals, as shown in the top panels of frames B, C, and D in Fig. 2 and Fig. S8. Similar asymmetric distributions in c(s) versus s_20,w plots were also apparent at pH 6.5 and 7.5 for βLg A and βLg B, indicating similar self-association behavior (Fig. 3 and Fig. S9, E and F, derived from SV data depicted in Fig. S6, Fig. S7, Fig. S16, and Fig. S17, E and F).

Figure 2.

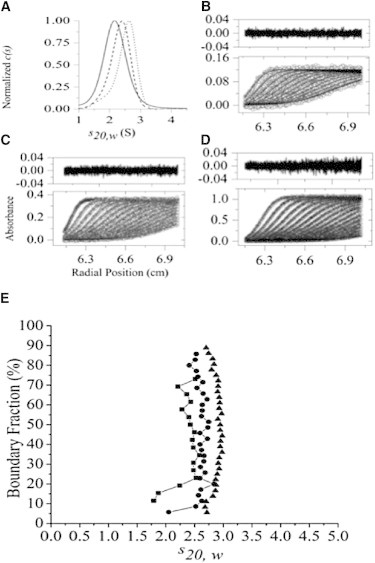
SV data for βLg A at pH 2.5 in 20 mM citric acid, 100 mM NaCl, and at 25°C. (A) Continuous c(s) analysis derived from SV data for βLg A at concentrations of (B) 5.3 μM (solid line), (C) 15.7 μM (dashed line), and (D) 33.4 μM (dotted line). The SV data and least-squares fits are shown in the bottom panels and the residuals in the top panels of B, C, and D. Statistics for the nonlinear least-squares fits: (B) RMSD = 0.005, runs test-Z score = 7.6; (C) RMSD = 0.006, runs test-Z score = 13; (D) RMSD = 0.005, runs test-Z score = 12. (E) van Holde-Weischet integral distribution plot for βLg A at pH 2.5 and concentrations of ∼5 μM (squares), 15 μM (circles), and 45 μM (triangles).

Figure 3.

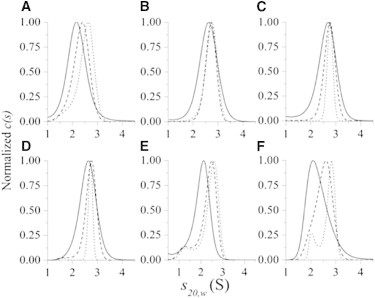
Normalized c(s20,w) distribution plots for βLg A over a pH range of 2.5–7.5. The figure shows the distribution plots for βLg A obtained from the fitting of SV data using a continuous c(s) distribution model. The three protein concentrations explored were ∼5 μM (solid line), 15 μM (dashed line), and 45 μM (dotted line); actual concentrations are given in parentheses. In 20 mM citrate and 100 mM NaCl: (A) pH 2.5 (5.3, 15.7, 33.4 μM), (B) pH 3.5 (4.8, 15.8, 26.7 μM), (C) pH 4.5 (2.5, 14.5, 43.9 μM), and (D) pH 5.5 (6.5, 16.8, 47.3 μM). In 20 mM MOPS and 100 mM NaCl: (E) pH 6.5 (3.5, 11.0, 33.0 μM) and (F) pH 7.5 (5.15, 22.6, 36.5 μM). Statistics for the fits can be found in Fig. S1, Fig. S2, Fig. S3, Fig. S4, Fig. S5, Fig. S6, and Fig. S7.

Weight-averaged s_20,w values were derived at each concentration from the continuous c(s) distribution versus s_20,w. (Table S4 (βLg A) and Table S5 (βLg B)). At pH 2.5, 3.5, 6.5, and 7.5, an increase in the weight-averaged s_20,w with increasing protein concentration was observed for both βLg A and βLg B, confirming the concentration-dependent change in the oligomeric state indicated in the continuous c(s) distribution plots.

At pH 4.5 and 5.5, however, the symmetrical c(s) distributions and near-constant weight-averaged s_20,w values for βLg A and βLg are consistent with a single species predominating at all concentrations (Fig. 3 and Fig. S9, C and D). At ∼45 μM, where the c(s) distributions presented the sharpest and most symmetrical peaks, the SV data were fitted to a continuous mass distribution model (Fig. S10), leading to a molar mass of ∼33,000 Da, which is close to that expected for a βLg dimer of ∼36,700 Da. When the data at pH 5.5 were fitted to a single discrete species model, the mass was estimated to be 34,000 ± 1200 Da (see also Fig. S3, Fig. S4, and Fig. S5 for βLg A, and Fig. S13, Fig. S14, and Fig. S15 for βLg B). There is no evidence in any of the SV data to suggest the presence of a larger oligomeric species (i.e., trimer, tetramer, octamer, etc.) in solution.

van Holde-Weischet analyses

We analyzed the SV boundary shapes as a function of loading concentrations and pH using the van Holde-Weischet method (85). The G(s) plots are shown in Fig. S18 and Fig. S19 for βLg A and βLg B. At pH 2.5 and at the lowest concentration (squares), the curves systematically show a half-parabolic shape (Fig. 2 E (=S18 A) and Fig. S8 E (=S19 A)), indicating, in this case, a reversible monomer-dimer equilibrium (86). However, increasing the loading concentrations leads to a shift of the curve to higher sedimentation coefficients and a change in shape of the curve toward linearity (Fig. 2 E and Fig. S19 A, circles and triangles). Similar behavior is also seen at pH 3.5, 6.5, and 7.5 (Fig. S18 and Fig. S19, B, E, and F). However, at pH 4.5 and 5.5, which lie near the protein isoelectric point (pI = 5.1–5.3) (16,17,52,53), for both βLg A and βLg B, the van Holde-Weischet plots show a more pronounced linearity even at the middle concentrations explored (Fig. S18 and Fig. S19, C and D), indicating a more strongly associated dimer. At the highest concentrations, the near-linear and vertical curves provide evidence for the almost-exclusive presence of βLg A and βLg B dimers. Thus, K_D^2-1 near the pI must be far below 5 μM.

Thermodynamic and kinetic parameters for the monomer-dimer self-association of βLg

We performed multispeed SE experiments to further investigate the self-association of βLg. At pH 4.5 and 5.5, SE data were fitted to a single-species model, which gave molecular masses close to that calculated for the βLg dimer (see Fig. S3, Fig. S4, and Fig. S5 for βLg A, and Fig. S13, Fig. S14, and Fig. S15 for βLg B), confirming SV data indicating that K_D^2-1 in these conditions has submicromolar values, which would be outside our instrument's sensitivity in absorbance mode. At pH 2.5, 3.5, 6.5, and 7.5, we calculated the equilibrium constants for βLg A and B dimer dissociation (K_D^2-1) from SE data and further optimized them by integrating SV data into the fit using the monomer-dimer self-association model implemented in SEDPHAT. Other models (e.g., monomer-trimer and monomer-tetramer) yielded worse fits. Global fitting of SE and SV data yielded more precise but insignificantly different values for K_D^2-1 compared with those determined through individual SE or SV fitting (Table S7). The globally fitted SE and SV data at each pH, along with the fit statistics, are provided in the Supporting Material (Fig. S1, Fig. S2, Fig. S6 and Fig. S7 for βLg A, and Fig. S11, Fig. S12, Fig. S16, and Fig. S17 for βLg B). As can be seen from Table S6, the s-values for the dimer (s2) are closely matched (2.76−2.92 S) across the pH range for βLg A and βLg B. There is somewhat more variability in the s-value for the monomer (s1; 1.40−2.26 S) over the pH range studied, but at a given pH, βLg A and βLg B share similar values. This variability may reflect pH-dependent changes in the size, shape, and/or dynamics of the monomer.

For both βLg variants, the globally fitted K_D^2-1 values at pH 3.5 and 6.5 are smaller than those observed at pH 2.5 and 7.5. These trends are consistent with the continuous c(s) distribution analyses shown in Fig. 2 and Fig. S8. Across the full pH range, the K_D^2-1 parameters for βLg A are systematically larger than those for βLg B, although in each pairwise comparison at a given pH, the differences are only marginally significant.

Finally, the rate constants calculated using the SV data (Table 1) for the dimer dissociation, k_off, reveal a significant difference at acidic pH when compared with near-neutral pH. At pH 2.5, k_off = 0.008 s⁻¹ for βLg A (range: 0.002−0.019) s⁻¹ and 0.009 s⁻¹ for βLg B (range: 0.003−0.029). In contrast, at pH 6.5 and 7.5, the dimer dissociation occurs on a timescale faster than can be measured using AUC techniques (k_off > 0.1 s⁻¹). Because these remarkable kinetic results cannot easily be rationalized by the extra carboxylic acid/carboxylate group that βLg A has on an external loop (Asp-64) in comparison with βLg B (Gly-64), we turned to continuum electrostatic energy calculations to gain insight into the role that ionic strength may play in the association processes of βLg.

A mechanism for stabilizing the βLg dimer revealed by continuum electrostatic calculations

The sensitivity of the dimer-dissociation equilibrium constant to ionic strength at low pH (pH < 3.5) is well documented (36). However, the stabilizing interactions for the dimer (Fig. S20) have only been broadly commented on. Thus, we sought to perform some calculations of the electrostatic binding energy for dimer formation as a function of ionic strength, as outlined in Materials and Methods.

The results are shown in Fig. S21 A, and although the calculated values overestimate the experimental dimerization free energy determined in similar conditions of pH and ionic strength, the calculated trend reveals clearly that an increase in ionic strength strongly favors the formation of a dimer. The relationship between binding energy and ionic strength of the solution is well described by an extended Debye-Hückel model, and a plot of binding energy versus ln(I^1/2/(1+I^1/2)) shows linearity to ∼25 mM (Fig. S21 B). The ion density around the protein in the low ionic strength range (5−20 mM NaCl) is represented in Fig. 4, A–D. With increasing ionic strength, the ion distribution around the protein covers wider patches, particularly in the vicinity of the dimer interface (Fig. 4, A and B).

Figure 4.

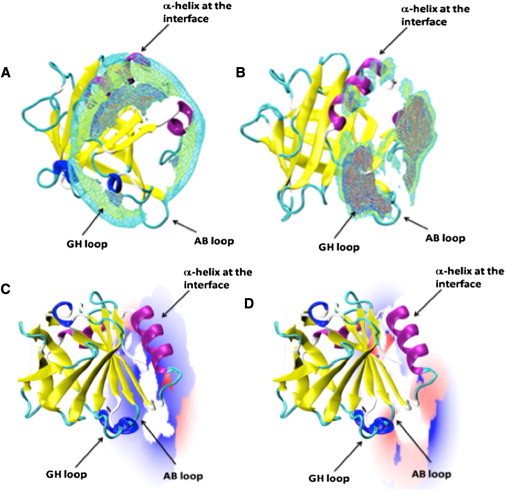
Top panels: Wireframe mesh representation of the ion charge-density maps calculated around the βLg A dimer in different NaCl concentrations at pH 2.5 (A) and pH 7.5 (B), and represented around a single monomer for clarity. The ion charge density is shown at ion concentrations of 5 mM (red), 10 mM (blue), 15 mM (yellow), and 20 mM (cyan). βLg A is represented in cartoon mode and colored by secondary structure elements (cyan, loops; blue, turns; violet, α-helices; yellow, β-strands). Bottom panels: Ionic atmosphere calculated around a βLg A dimer at pH 2.5 (C) and 7.5 (D) and projected onto a plane parallel to the dimer interface. For clarity, only one monomer of the protein is shown. Positive and negative ion atmospheres are colored in red and blue, respectively, at ±0.1 kT/e- contour levels.

At pH 2.5 and in 5 mM NaCl, negative ion density is shown to be in proximity to Arg-148 on dimer-interface strand I. At higher ionic strength (10−20 mM), the ion density covers a wider region around the protein. Indeed, negative-ion charge density is mainly localized around the protein α-helix and surrounds the positively charged Lys-135, Lys-138, and Lys-141 (Fig. 4 A). At pH 7.5, on the other hand, the ion distribution is mainly concentrated in proximity to the negatively charged AB and GH loops, whereas the α-helix and Arg-148 show only a relatively sparse distribution compared with pH 2.5, because the positively charged residues on the α-helix (Lys-135, Lys-138, and Lys-141) are in part neutralized by nearby negatively charged residues (Asp-129, Asp-130, Glu-131, Glu-134, and Asp-137; Fig. 4, B and D). Overall, at pH 7.5, the surrounding charge cloud has a net positive value, because at pH 7.5 the protein electrostatic potential is overall negative (∼−9). Two different regions of positive and negative ion density appear to influence dimer formation for βLg A at pH 7.5. The positive region is associated with the dimer-interface loop AB, especially in the vicinity of Asp-28 and dimer-bridging Asp-33, and the negative region is associated with the main α-helix and Arg-148, as at pH 2.5 but with lessened charge density. Loop GH bearing residues Glu-108, Glu-112, and Glu-114 is surrounded by strong positive ion density, but of these residues only Glu-114 projects toward the dimer interface (Fig. 4 D). Note, however, that although residues Asp-130, Glu-134, and Asp-137 on the main α-helix are not involved directly in the dimer interface, they do project toward the dimer interface (Fig. 4, B and D).

Overall, the data suggest that at pH 2.5 the dimer is stabilized by a relatively high density of anions spanning the dimer interface that militate against charge repulsion of the positively charged protein subunits. However, at pH 7.5, dimer formation is stabilized by a relatively low density of cations in the region of the AB loop and GH loops.

Discussion

A considerable body of work, as discussed in the Introduction, shows that bovine βLg experiences a variety of conformational states and quaternary associations as a function of pH, temperature, ionic strength, and genetic variant. In particular, extensive studies by different groups using different techniques have focused on the dimer-monomer equilibrium, as summarized in Table S1 (12,15,16,30,32,36–42,44–50,53,87). In addition, there is copious literature on the structure, dynamics, and folding-unfolding processes of bovine βLg (58,63,88–91,92). However, to the best of our knowledge, no studies have reported on the rate constants for the dissociation of the dimer.

At pH more than one pH unit away from the isoelectric point of bovine βLg, this dimer is less strongly associated, with the dimer dissociation constant K_D^2-1 ranging from ∼5 to 500 μM. At low pH, K_D^2-1 is extraordinarily sensitive to ionic strength. This dissociation is the key first step of physical denaturation, and the association is the final step of folding. In the course of obtaining these rate constants by AUC methods, we obtained the equilibrium constants for dimer dissociation over the pH range of 2.5–7.5.

Although different research groups using different techniques and sources of protein have reported similar values for the equilibrium constant K_D^2-1 for the dimer-monomer equilibrium at near-neutral pH, a very considerable range of values have been obtained at low pH, where the effects of ionic strength (36,46,50), and indeed of the ion pair used (36), on the dimer-monomer equilibrium are substantial. There is also persistent evidence that when variants A and B of bovine βLg were measured in the same laboratory by the same technique, the variant B dimer was the more stable by a factor of 2−3 in K_D^2-1 values (corresponding to ∼2−3 kJ mol⁻¹ in Gibbs free energy at 25°C) (12,15,48,49,53). However, this difference is swamped by the different values for K_D^2-1 reported by different techniques, such as light-scattering versus AUC versus isothermal dilution calorimetry, such that, at pH 2.46−2.7, 100 mM ionic strength and 20−25°C, values for K_D^2-1 for βLg A span the range of 130 μM (53) to 310 μM (44), whereas βLg B spans the range of 32 μM (46) to 159 μM (40). At pH 6.5–7.0, values for K_D^2-1 for βLg A span the range of 4.9 μM (37) to 24 μM (44,48), whereas βLg B spans the range of 7.0 μM (15) to 14 μM (49). Notwithstanding the variability in values, the farther from the isoelectric point (pH ∼5.3) the measurements are made, in both acidic and basic directions, the less stable is the dimer (i.e., increased K_D^2-1). The effect of ionic strength on the K_D^2-1 at near-neutral pH is less pronounced than at acidic pH, consistent with the smaller magnitude of charge on the protein (−9 at pH ∼7.5 and +20 at pH ∼2.5).

The values of K_D^2-1 observed here for recombinant βLg A (and also βLg B) are all smaller than the corresponding values observed for the same variant at comparable pH and concentration of NaCl, especially at pH 3.5 and 2.5. For example, at pH 2.5, our measured K_D^2-1 for βLg A is 15 μM, a value substantially smaller than that reported for native βLg A (62.5 μM) at the same ionic strength and temperature (but at pH 3) by Sakurai et al. (36). Their value obtained at 200 mM NaCl is not significantly different from ours, suggesting that at low pH citrate and ClO₄⁻, anions exert a similar effect on dimer stability (36). At pH 6.5 and 7.5, our values for K_D^2-1 approach those reported by others, but they still remain slightly smaller. The difference in dimer-dissociation constants K_D^2-1 invariably observed between variants A and B under identical conditions is noticeably less pronounced for our measurements. Indeed, for a given pH, the difference we observe is of marginal significance, but collectively over four pH values, K_D^2-1 for βLg A is always greater (i.e., the dimer is less stable) than that for βLg B, indicating that there is a real difference in dimer stability. Our recombinant βLg differs from native βLg only in the presence of a neutral methionine at the N-terminus, but in all other respects it resembles the wild-type (93). The stability of bovine βLg is known to be sensitive to site-directed mutations in unexpected ways (63,91,92,94).

βLg A and βLg B differ at two sites, one involving Asp for Gly at position 64 on an exposed external loop, and the other involving Val for Ala in a buried site at position 118. At low pH, then, both variants bear the same charge, and thus the similarity in rate constants for dissociation, k_off, is not surprising. Dissociation appears to be remarkably slow, but when k_on is calculated from k_off/K_D^2-1, association is also slow, being far from diffusion-controlled association, consistent with the high charge and the requirement to organize electrostatic shielding in the dimer. On the other hand, at near-neutral pH, dissociation is too fast to be measured by AUC (i.e., k_off > 0.1 s⁻¹). Using this as an estimated lower bound leads to values for k_on that are nearly two orders of magnitude higher than those found at acidic pH, a result that is consistent with the greatly reduced charge on the protein subunits. Such findings confirm the well-established role of charge-charge interactions in the definition of the rate constants for protein association, as reported in many previous studies (95). Furthermore, considering the importance of electrostatic interactions and diffusion rates of the interacting partners, ionic strength has a high influence on protein association kinetics (96,97). Indeed, the somewhat sluggish dissociation rate at pH 2.5 compared with pH 7.5 may be correlated with the greater disruption of the denser ion cloud that surrounds the dimer at pH 2.5 compared with the more diffuse cloud at pH 7.5.

The remarkable shielding effect produced by anions allows the highly charged βLg molecules to form a dimer at acidic pH that is only slightly less stable than that formed at near-neutral pH, where the protein charge is much smaller. Continuum electrostatic calculations show where neutralizing charges congregate on the surface of the protein. These calculations reveal that upon dimer formation at pH 2.5, there is an increased negative charge at the dimer interface around the side chains of Arg-148. Arg-148 sits at the middle of the β strand I that forms the extended antiparallel β-sheet on dimer formation. Thus, by bridging repelling charges at the dimer interface, the anions can actively stabilize the dimer, as shown by changes in ion distribution at the dimer interface at different pH values (Fig. 4).

A covalent disulfide-bridged dimer (Ala34Cys) linking the AB loops makes it possible to conduct NMR studies at pH > 5. Interestingly, higher dynamics have been observed in the proximity of charged residues of βLg, especially Asp-64 (61). Thus, the substitution of Asp-64 in βLg A by an apolar Gly amino acid in βLg B appears to favor a higher stability for the latter dimer due to reduced protein dynamics at site on a loop adjacent to the AB loop that forms part of the dimer interface. Moreover, for both variants, changes in ion charge distribution upon dimer formation are also concentrated in those regions that have been shown to have the highest dynamics (98), the negatively charged AB and GH loops. Thus, dimer association appears to be driven, at least in part, by neutralization of charge with resultant loss of conformational flexibility.

Conclusions

In this work, we characterized the dimer-monomer equilibria of bovine βLg variants A and B over a wide pH range and at a fixed ionic strength of 100 mM NaCl and temperature of 25°C. By using a common protein source, common experimental conditions, common instrumentation, and a rigorous procedure for data and error analysis, we were able to obtain both new (to our knowledge) and reliable quantitative information about the monomer-dimer equilibrium of bovine βLg. Furthermore, global fitting of both SV and SE isotherms improved the characterization of the thermodynamics of βLg A and B dimer dissociation. The rate constants for dimer dissociation, calculated for the first time to our knowledge, are markedly smaller for both βLg A and B at pH 2.5 compared with pH 7.5. In addition, we investigated the contribution of the ionic strength to stabilization of the dimer using electrostatic calculations, which revealed that patches on the protein surface are involved in ion binding, particularly at the dimer interface. These electrostatic calculations trace the relationship between the electrostatic energy of binding and the effect of ions at the dimer interface. The calculations reinforce NMR data showing that the electrostatic properties of the molecule are directly correlated to protein dynamics, and that specific binding of counterions facilitates dimer association. Finally, under conditions typically associated with milk and its processing, β-lactoglobulin is mostly dimeric but in a dynamic equilibrium with its monomer.