A review of statistical methods for protein identification using tandem mass spectrometry

Abstract

Tandem mass spectrometry has emerged as a powerful tool for the characterization of complex protein samples, an increasingly important problem in biology. The effort to efficiently and accurately perform inference on data from tandem mass spectrometry experiments has resulted in several statistical methods. We use a common framework to describe the predominant methods and discuss them in detail. These methods are classified using the following categories: set cover methods, iterative methods, and Bayesian methods. For each method, we analyze and evaluate the outcome and methodology of published comparisons to other methods; we use this comparison to comment on the qualities and weaknesses, as well as the overall utility, of all methods. We discuss the similarities between these methods and suggest directions for the field that would help unify these similar assumptions in a more rigorous manner and help enable efficient and reliable protein inference.

1. INTRODUCTION

Recent advances in DNA sequencing and genomics have made it possible to reconstruct and study the 1918 influenza virus [35], increase the visible color spectrum of mice using human genes [13], and elucidate the process by which some bacteria can reassemble their shattered genomes after exposure to extremely high levels of radiation [37]. But DNA sequencing has its limits; for instance, all cells in the human body are genetically identical despite their vast and observable functional differences. Finding the proteins, which have functional importance, in a group of cells can be much more informative. High-throughput sequencing methods have been applied to RNA [24], an intermediate between DNA and protein, but RNA transcript is often a poor surrogate for protein expression; not all of the transcribed RNA is translated, and once translated, the half-lives of different proteins vary widely [2, 11].

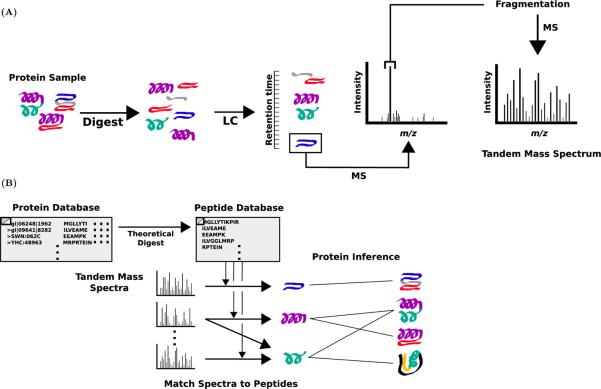
Tandem mass spectrometry has emerged as the most powerful tool for analysis of proteins in complex mixtures [22, 32]. Figure 1A displays the process by which data is acquired in tandem mass spectrometry-based proteomics. A protein sample is first subjected to enzymatic digestion which breaks the protein into peptides; if a protein is represented as a string of its amino acids, then the peptides produced by digestion will be a set of substrings. Certain digestive enzymes, for example trypsin or chymotrypsin, cut only at specific amino acids, resulting in a reduced number of possible peptides for each protein. After digestion, the peptide mixture is separated using liquid chromatography (LC), which sequentially elutes peptides according to their hydrophobicity. Subsequently, the population of peptides eluted at a particular retention time are further separated by their precursor mass to charge ratio (m/z) using mass spectrometry; this is accomplished by selecting high intensity peaks from the precursor scan. The population of peptides with a particular retention time and m/z value is then fragmented at certain chemical bonds, producing several fragments for each peptide [32]. Ideally, the population of peptides fragmented is homogenous. The m/z of each fragment in this population is then measured using mass spectrometry to produce a tandem mass spectrum, a collection of summary statistics about that population of fragments. This process is repeated for different LC retention times and m/z values, resulting in several thousand tandem mass spectra from a single experiment.

Figure 1. Protein identification using tandem mass spectrometry.

(A) In the tandem mass spectrometry-based proteomics experiment, a collection of proteins is digested into peptides. The peptides are separated by their LC retention time and then by separated by precursor m/z using mass spectrometry (MS). The resulting peptide population is fragmented and subject to a second round of mass spectrometry to produce a tandem mass spectrum. This process is repeated for different LC elution times and precursor m/z values to produce several thousand tandem mass spectra. (B) The observed tandem mass spectra are matched to peptides using a search database. In the graphical view of the inference problem, proteins are adjacent to their constituent peptides (i.e. an edge connects proteins to the peptides they would produce in the proteomics experiment).

The problem of tandem mass spectrometry-based protein identification is to identify the proteins in the original sample from the observed tandem mass spectra (Figure 1B). By using existing knowledge from classical genetics, biochemistry and genomics, it is possible to create a database containing an approximate superset of all possible proteins of interest for a given sample. The proteins in this database can be associated with the peptides they would be expected to produce when subject to digestion, creating a peptide database; these peptides may consist of only those that result from a perfect digestion, or may include peptides lacking certain cleavages. Each observed spectrum is mapped to one or several peptides by comparing it to the predicted theoretical tandem mass spectrum for each peptide in the peptide database [8, 25]. These peptide-spectrum matches (PSMs) are imperfect: error may result from several sources. For instance, matching the spectra to peptides in the peptide database implicitly makes the incorrect assumption that the population of peptides at each hydrophobicity and m/z value is homogeneous. Errors can also result from an oversimplified model of how peptides generate theoretical spectra. Furthermore, it is well-established that some peptides, for instance those with extreme m/z values, are infrequently observed, even when they are present [21, 34].

PSMs are scored by the quality of the match between the observed and theoretical tandem mass spectra [14, 16, 17] and associated with the proteins that would theoretically produce them when digested. These associations between proteins, peptides, and spectra can be represented graphically to form a tripartite graph on proteins, peptides, and spectra by placing edges between proteins and their constituent peptides and between peptides and spectra that match them (Figure 1B). All protein identification algorithms start with this tripartite graph and the PSM scores, and then compute either a predicted set of present proteins or a ranking of proteins based on the belief that they are present in the sample.

An ideal protein identification method would maximize sensitivity, the proportion of truly present proteins that are identified, while simultaneously minimizing the false discovery rate (FDR) [3] of identified proteins. The FDR measures the proportion of identified proteins that are not truly in the sample. The FDR is a useful measure because it quantifies the proportion of protein identifications that would be biologically meaningless in a follow-up experiment. Evaluating a method by estimating the sensitivity and FDR of a method is not trivial, because it is difficult to develop gold standards for complex protein mixtures, which are the most interesting application for tandem mass spectrometry-based protein identification.

Notation

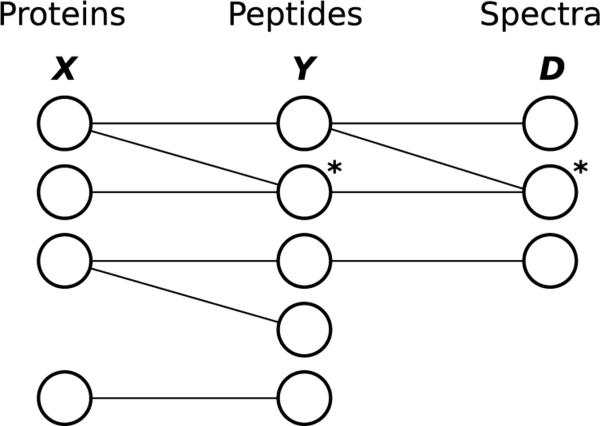
We describe existing methods using a common framework. Figure 2 presents a graphical view of well-established dependencies in protein inference; these dependencies clearly reflect dependencies inherent in the mass spectrometry process and are used by every protein identification method. We denote the proteins using a collection of random indicator variables X. Similarly, we denote the set of peptides using a collection of random indicator variables Y. The collection of observed spectra and any other associated evidence (for instance, the precursor m/z associated with the spectrum) are encapsulated in a collection D. For simplicity, we call the objects in the collection D “spectra,” even though they may be spectra paired with precursor masses or other information. Also, we don't discuss the different assumed peptide charge states used for PSM matches; a peptide identified at multiple charge states can either be treated as a single peptide or treated as several unique peptides (one for each charge state). Every method discussed can be approached in one of these ways without making specific note of a charge state. We will use i, j, k to respectively index the collection of proteins, peptides, and spectra. Table 1 provides a quick reference for this notation.

Figure 2. The general graphical view of dependencies in protein inference.

Proteins (X), peptides (Y), and spectra (D) form a tripartite graphGwith edges indicating well-established dependencies motivated by the mass spectrometry process. Examples of a degenerate peptide and a degenerate spectrum are labeled with asterisks. It is important to note that in the graphG, all proteins, peptides, and spectra are included, even those that are not connected to observed spectra.

Table 1.

Notation reference. Here we define each variable from our notation. We also present the variables used to index each collection. Because the notation for indices is consistent, the type of variable accessed in the graph G is known by the name of the variable: i ∈ V, i′ ∈ V, are proteins in G, j ∈ V, i′ ∈ V are peptides in G, and k ∈ V, k′ ∈ V are observed spectra. Similarly, (i, j) ∈ E denotes an edge between protein i and peptide j and (j, k) ∈ E denotes an edge between peptide j and spectrum k

Name	Meaning	Indexed by
X	Collection of indicator variables for the proteins	i, i′ ,…
Y	Collection of indicator variables for the peptides	j, j′ ,…
D	Collection of observed spectra and precursor masses	k, k′ ,…
s	Collection of PSM scores	(j, k)
G = (E, V)	The graph containing all proteins, peptides, and observed data	–
G′ = (E′, V′)	The graph containing all observed data, peptides adjacent to the observed spectra, and proteins adjacent to those peptides	–
x*	Collection of indicator variables for the proteins identified by a method	i, i′ ,…
y*	Collection of indicator variables for the peptides identified by a method	j, j′ ,…

Denote the tripartite graph on all proteins in the protein database, all peptides in the peptide database, and all observed spectra as G = (E, V ). We say that two nodes (e.g. a protein and a peptide) are “adjacent” in the graph if there is an edge between them. Let G′ = (E′, V′) denote the “observed graph,” a subgraph of G containing only the peptides in G adjacent to observed spectra and only the proteins in G adjacent to those peptides. The edges in G depict dependencies inherent in the mass spectrometry process. Note that these edges depict a subset of possible dependencies in the general inference problem; a specific model may introduce further dependencies by tying parameters that model the processes depicted in this graph. For instance, a method may exclude peptides with masses exceeding some threshold; in that example, the mass threshold used would introduce dependencies not depicted in G (i.e. if a peptide with a particular mass is deemed present, then a peptide with the same mass will not be excluded by the mass threshold). Conversely, some approaches approximate the known dependencies by removing edges from or altering G. Unless otherwise stated, all models assume that proteins and peptides not included in the observed graph are absent.

Of particular interest are peptides and spectra like those labeled with an asterisk in Figure 2. Peptides in G adjacent to multiple proteins are called “degenerate peptides”; likewise, spectra that match multiple peptides are known as “degenerate spectra.” Peptide and spectrum degeneracy are noteworthy because without degenerate peptides and degenerate spectra, G is a tree; inference on that tree can be performed efficiently (unless further dependencies are introduced by tying parameters). Because the proteins and peptides are represented by boolean random variables, the computational cost of a generic naive approach to inference on a general graph may be exponential in both the number of peptides and proteins queried; in practice the number of peptides and proteins of interest is often on the order of ten thousand, making such a naive approach to protein inference practically infeasible.

We let s_j,k denote the PSM score for a paired peptide j and spectrum k. s_j,k is a rough estimate of Pr(Y_j|D_k) for (j, k) ∈ E. This likelihood is estimated empirically using distributions of features of example PSMs where Y is known. Peptide scoring procedures assume that the spectrum D_k is not degenerate and thus cannot arise from any other peptide; degenerate spectra are eliminated by keeping only the edge to the peptide with the highest likelihood score. By also estimating the prior probability Pr(Y_j = y_j), these methods then use Bayes rule to estimate:

$$s_{j,k}=\mathrm{Pr}(Y_j\mid D_k)=\frac{\mathrm{Pr}(D_k\mid Y_j)\mathrm{Pr}\left(Y_j\right)}{{\sum }_{y_j}\mathrm{Pr}(D_k\mid Y_j=y_j)\mathrm{Pr}(Y_j=y_j)}$$

In general, s_j,k is not a good approximation for Pr(Y_j|D) for two reasons. First, a peptide may be included in several PSMs with different scores. Second, s_j,k does not incorporate protein-level information, which causes covariance in peptides adjacent to the same protein.

Protein grouping

Many of the methods presented below perform some form of protein grouping; that is, they merge multiple proteins together into a single graph node before or during inference. These nodes are then treated as a single protein. Afterward, some methods even use the graph connectivity to remove certain proteins before inference is performed.

A “protein group” refers to a set of proteins which are adjacent to identical peptide sets (using either G or G′, depending on the graph used by a particular method). After they are merged, these protein groups are treated as any other protein; therefore, for simplicity we will refer to both proteins and protein groups as proteins. In addition, some methods remove a protein if it is adjacent to a set of peptides that is a subset of the peptides adjacent to another protein. We denote this as the “Occam's razor principle.”

Protein grouping makes evaluation of protein identication methods more difficult because identification of a protein group does not imply that all proteins in the group are present. Instead, a present protein group indicates that at least one protein contained in the group is present. For this reason, it is nontrivial to compare two methods if one performs protein grouping and one does not. In contrast, the Occam's razor principle does not merge nodes in the graph and does not influence the way in which the results should be interpreted; however, the Occam's razor principle operates imperatively without a supporting model, and can make it more difficult to intuitively understand methods that employ it. Methods that use the Occam's razor principle, even those that are numerical and probabilistic, are colored by a heuristic behavior.

2. EXISTING APPROACHES

Several computationally feasible approaches have emerged for performing protein inference from G and the PSM scores. Here we classify these methods as belonging to one of the following categories: set cover methods, iterative methods, and Bayesian methods. Set cover methods approach the problem by accepting a set of peptides based on their associated PSM scores and then accepting a set of proteins based on their adjacency to the accepted PSMs. Iterative methods employ numeric heuristics, which are often probabilistically motivated, to iteratively compute protein scores until convergence is reached. Lastly, Bayesian methods generatively model the mass spectrometry process and then attempt to compute or approximate marginals or a maximum a posteriori (MAP) set for the proteins.

Set cover methods

One- and two-peptide rules

The one- and two-peptide rules are the simplest methods for protein identification. First, peptides are thresholded so that only peptides paired in a PSM with a score at least τ are present. Second, proteins are similarly thresholded to keep only proteins adjacent to at least one (or at least two when using the two-peptide rule) present peptides. Formally, the N-peptide rule can be stated as follows:

$$y_j^{\ast }=\exists k:(j,k)\in E,s_{j,k}\ge \tau$$

$$x_i^{\ast }=\mid \{y_j^{\ast }:(i,j)\in E\}\mid \ge N$$

Usually, degenerate spectra are eliminated by keeping only the edge pairing a spectrum with its highest-scoring peptide match; although this step is not necessary, it prevents an individual spectrum from matching several peptides. Note that using the one-peptide rule by itself, a single degenerate peptide may force several proteins to be present (for the N-peptide rule, N peptides would be required).

DTASelect

DTASelect [33] is a more sophisticated version of the one- and two-peptide rules. First, protein grouping may be performed. Then, DTASelect lets the user select from several criteria to determine which peptides are present, for example, peptides contained in a PSM with a score greater than a threshold or peptides matching at least a certain number of spectra. Similarly, the user manually creates a rule for what proteins are present. Formally, DTASelect allows users to define pairs of scoring functions and thresholds f_Y, τ_Y and f_X, τ_X for peptides and proteins, respectively:

$$y_j^{\ast }=f_Y(G,s)\ge {\tau }_Y$$

$$x_i^{\ast }=f_X(G,s,y\ast )\ge {\tau }_X$$

DTASelect can also determine which proteins are similar to a given protein by comparing their sets of adjacent peptides; this similarity measure can be useful to determine situations when a set of peptides can originate from many possible sets of proteins that contain similar sets of adjacent peptides.

IDPicker

Frequently, one present protein will produce a handful of degenerate peptides associated with high-scoring PSMs. In such a situation, the one- and two-peptide rules and DTASelect may not only infer that the present protein was in the sample, they may also infer that many other proteins adjacent to these peptides were in the sample. Consequently, degenerate peptides may lead to a high FDR with these approaches. IDPicker [38] addresses this problem by finding the smallest set of proteins to explain the present peptide set. This smallest protein set defines the “minimum set cover” of the present peptides. Formally, if y is the set of peptides adjacent to the present set of proteins y, IDPicker performs the following optimization:

$$\begin{array}{cc}\hfill y_j^{\ast }& =f_Y(G,s)\ge {\tau }_Y\hfill \\ \hfill y_j& =\{\begin{array}{cc}1,\hfill & \exists i:(i,j)\in E,x_i\hfill \\ 0,\hfill & \text{else}\hfill \end{array}\phantom{\}}\hfill \\ \hfill x\ast & =\underset{x:y\ast \subset y}{\text{argmin}}\mid x\mid \hfill \end{array}$$

Because it defines the present peptides conditional on the present proteins, and then optimizes a constrained set of these proteins, IDPicker models the mass spectrometry process from left to right in the graph in Figure 2. In contrast, the one- and two-peptide rules and DTASelect define the peptide and protein relationship conditionally from right to left on the graph in Figure 2, despite the fact that the processes underlying mass spectrometry conditional dependency are oriented from left to right.

Like the one- and two-peptide rules, IDPicker is not a probabilistic approach; however, the two objectives it jointly optimizes (maximize the identified peptides explained and minimize the number of proteins to explain them) can be through a probabilistic lens. When approached in this manner, there is an inherently Bayesian flavor to IDPicker. Recognizing the similarity to Bayesian methods is important because it explains similar behavior between IDPicker and Bayesian methods with a very strict prior on the number of present proteins; the fact that IDPicker most closely resembles Bayesian methods with strict priors provides understanding for why IDPicker is widely regarded as conservative compared to probabilistic methods.

IDPicker can be reconstructed probabilistically by separating the optimization into the product of likelihood and a prior. The necessity that all threshold-passing peptides must be explained can be enforced by using a likelihood that is nonzero only when each of those peptides is adjacent to a present protein. Furthermore, large protein sets can be penalized by placing a prior on X that decreases with the cardinality of X (via an arbitrary strictly decreasing positive function h). The MAP estimate of the resulting model will be identical to the minimum set cover found by ID-Picker; of the protein sets that result in nonzero likelihood, the smallest will have the highest prior and will therefore be the MAP estimate (at least one nonzero likelihood is guaranteed because each peptide in the graph must be adjacent to at least one protein, by definition).

$$\begin{array}{cc}\hfill y_j^{\ast }& =f_Y(G,s)\ge {\tau }_Y\hfill \\ \hfill \mathrm{Pr}(D\mid Y)& =\{\begin{array}{cc}1,\hfill & y\ast \subset y\hfill \\ 0,\hfill & \text{else}\hfill \end{array}\phantom{\}}\hfill \\ \hfill Y_j\mid X& =\{\begin{array}{cc}1,\hfill & \exists i:(i,j)\in E,X_i\hfill \\ 0,\hfill & \text{else}\hfill \end{array}\phantom{\}}\hfill \\ \hfill \mathrm{Pr}\left(X\right)& \propto h\left(\mid X\mid \right)\hfill \\ \hfill D& ╨X\mid Y\hfill \end{array}$$

IDPicker performs protein grouping; this operation resolves some possible ambiguities where two sets of proteins would both be candidates for the MAP estimate. Note that, in this context, the Occam's razor principle would be redundant, because any protein set containing a protein adjacent in G to a subset of the peptides from another protein could be reduced to explain the same peptides without including the former protein.

Iterative methods

ProteinProphet

ProteinProphet [23] is one of the first probabilistically motivated methods for protein identification, and is still one of the most popular and highly regarded. We will first describe a simplified version of their procedure and then use that to motivate the additional complexity used in ProteinProphet.

ProteinProphet operates on G′, the graph of observed data and the adjacent peptides and proteins; proteins not in G′ are given posteriors of zero. First, ProteinProphet performs protein grouping using this graph and eliminates proteins by the Occam's razor principle. Then, ProteinProphet eliminates degenerate spectra by removing all but the highest scoring PSM containing each spectrum. Then ProteinProphet computes peptide scores from the remaining connected PSMs; these scores are treated as approximate peptide probabilities:

$$\begin{array}{cc}\hfill s_j^{\prime }& =\underset{k}{\max }{s}_{j,k}\hfill \\ \hfill & =s_{j,k\left(j\right)},k\left(j\right)=\underset{k}{\text{argmax}}{s}_{j,k}\hfill \\ \hfill & \le 1-\prod _k(1-s_{j,k})\hfill \end{array}$$

First, consider a graph with no degenerate peptides. In this case, a simplified version of ProteinProphet assumes that each peptide contributes independent evidence to the protein adjacent to that peptide:

$$\mathrm{Pr}(X_i\mid D)=1-\prod _{j:(i,j)\in E\prime }(1-s_j^{\prime })$$

When degenerate peptides are encountered, ProteinProphet partitions each peptide score s′_j among its adjacent proteins:

$$\begin{array}{cc}\hfill s_{i,j}^{″}& =w_{i,j}{s}_j^{\prime }\hfill \\ \hfill \sum _{i:(i,j)\in E\prime }{w}_{i,j}& =1\hfill \end{array}$$

Then these partitioned peptide scores s″ are used as if there is no degeneracy:

$$\mathrm{Pr}(X_i\mid D)=1-\prod _{j:(i,j)\in E\prime }(1-s_{i,j}^{″})$$

Given the protein posteriors, the peptide scores are partitioned so that the size of the partition associated with each protein is proportional to that protein's posterior:

$$w_{i,j}\propto \mathrm{Pr}(X_i\mid D)$$

Because the sum of weights for each peptide must sum to unity, the proportion constant can be removed thus:

$$w_{i,j}=\frac{\mathrm{Pr}(X_i\mid D)}{{\sum }_{i\prime :(i\prime ,j)\in E\prime }\mathrm{Pr}(X_{i\prime }\mid D)}$$

Finally, the protein posterior estimates ∀i, Pr(X_i|D) and the partition weights ∀(i, j) ∈ E′, w_i,j are iteratively updated in a batch-wise manner, until convergence is reached:

$$\forall (i,j)\in E\prime ,w_{i,j}\leftarrow 1$$

while convergence is not reached do

$$\begin{array}{cc}\hfill & \forall j,s_{i,j}^{″}\leftarrow w_{i,j}{s}_j^{\prime }\hfill \\ \hfill & \forall i,\mathrm{Pr}(X_i\mid D)\leftarrow 1-{\prod }_{j:(i,j)\in E\prime }(1-s_{i,j}^{″})\hfill \\ \hfill & \forall (i,j)\in E^{\prime },w_{i,j}\leftarrow \mathrm{Pr}(X_i\mid D)∕{\sum }_{i\prime :(i\prime ,j)\in E\prime }\mathrm{Pr}(X_i^{\prime }\mid D)\hfill \end{array}$$

end while

As described, this scheme treats each partitioned peptide score as exact independent evidence to an adjacent protein. For this reason, a single high-scoring non-degenerate peptide j may single-handedly result in a prediction that the adjacent protein i is present. This protein would be given the same posterior as a protein with several high-scoring peptides:

$$\begin{array}{cc}\hfill s_j^{\prime }& \approx 1\hfill \\ \hfill \{i\prime :(i\prime ,j)\in E\prime \}& =\left\{i\right\}\hfill \\ \hfill \mathrm{Pr}(x_i\mid D)& =1-\prod _{j\prime :(i,j)\in E\prime }(1-s_{i,j\prime }^{″})\hfill \\ \hfill & =1-(1-s_j^{\prime })\hfill \\ \hfill & \approx 1\hfill \end{array}$$

The creators of ProteinProphet make a useful observation: among high-scoring peptides, there are fewer incorrect peptide identifications for peptides associated with proteins that have evidence from several other peptides. ProteinProphet therefore computes a score called “NSP” (“number of sibling peptides”) that summarizes other peptide evidence for a particular protein i adjacent to peptide j:

$$NS{P}_j=\sum _{j\prime \ne j:\exists i,(i,j\prime )\in E\prime }{s}_j^{\prime }$$

These NSP values are binned to estimate a new peptide score conditional on the NSP bin:

$$\mathrm{Pr}(Y_j\mid D_{k\left(j\right)},bin\left(NS{P}_j\right)=a)\approx s_j^{‴}=\frac{\mathrm{Pr}(Y_j\mid D_{k\left(j\right)})\mathrm{Pr}(bin\left(NS{P}_j\right)=a\mid Y_j)}{{\sum }_{y_j}\mathrm{Pr}(Y_j=y_j\mid D_{k\left(j\right)}\mathrm{Pr}(bin\left(NS{P}_j\right)=a\mid Y_j=y_j)}$$

where ProteinProphet approximates the true peptide posteriors with the peptide score: $\mathrm{Pr}(Y_j\mid D_{k\left(j\right)})\approx s_j^{\prime }$. The NSP probabilities are estimated by taking the ratio of expected numbers of present peptides in each NSP bin.

$$\mathrm{Pr}(bin\left(NS{P}_j\right)=a\mid Y_j)\approx \frac{{\sum }_{j:bin\left(NS{P}_j\right)=a}{s}_j^{‴}}{{\sum }_j{s}_j^{‴}}$$

Finally, the use of NSP is extended to treat each degenerate peptide as several partitionied peptides, one for each adjacent protein. The peptide scores conditioning on this new NSP score NSP′ for each protein and peptide will be denoted $s_{i,j}^{\left(IV\right)}=\mathrm{Pr}(Y_j\mid D_{k\left(j\right)},NS{P}_j^{i^{\prime }})$

$$\begin{array}{cc}\hfill NS{P}_j^{i\prime }& =\sum _{j\prime \ne j:(i,j\prime )\in E\prime }{s}_{i,j}^{″}\hfill \\ \hfill \mathrm{Pr}(bin\left(NS{P}_j^{i\prime }\right)=a\mid Y_j)& \approx \frac{{\sum }_i{\sum }_{j:bin\left(NS{P}_j^{i\prime }\right)=a}{w}_{i,j}{s}_{i,j}^{\left(IV\right)}}{{\sum }_i{\sum }_j{w}_{i,j}{s}_{i,j}^{\left(IV\right)}}\hfill \end{array}$$

The final algorithm is as follows:

$$\forall (i,j)\in E\prime ,w_{i,j}\leftarrow 1$$

while convergence is not reached do

$$\begin{array}{cc}\hfill & \forall (i,j)\in E\prime ,\text{computer}{s}_{i,j}^{\left(IV\right)}\hfill \\ \hfill & {\forall }_i,\mathrm{Pr}(X_i\mid D)\leftarrow 1-{\prod }_{j:(i,j)\in E\prime }(1-w_{i,j}{s}_{i,j}^{\left(IV\right)})\hfill \\ \hfill & \forall (i,j)\in E\prime ,w_{i,j}\leftarrow \mathrm{Pr}(X_i\mid D)∕{\sum }_{i\prime :(i\prime ,j)\in E\prime }\mathrm{Pr}(X_i^{\prime }\mid D)\hfill \end{array}$$

end while

When posterior protein estimates Pr(X_i|D) are given by any method, some threshold τ_X is used to choose the final set of accepted proteins:

$$x\ast =\{i:\mathrm{Pr}(X_i\mid D)>{\tau }_X\}$$

Scaffold

Scaffold [29] first aggregates PSM scores from multiple search engines (e.g. Mascot [26], Sequest [8], X!Tandem [5]) are aggregated to form a single score these aggregated peptide scores are then used for protein identification.

Scaffold employs a novel approach to the problem of spectral degeneracy to perform inference on the observed graph G′. When a spectrum matches multiple peptides, then only the peptides with scores approximately equal to the top-scoring peptide are kept. These remaining peptides are grouped together for that spectrum, creating a “peptide group” with a score equal to the scores of the approximately equal scores of the PSMs from that spectrum and the peptides it contains.

Scaffold resolves peptide degeneracy using a greedy method. Proteins are assigned peptide groups that are not adjacent to any other proteins. The protein scores are equal to the sum of the scores of the assigned peptide groups. Then, degenerate peptide groups (i.e. peptide groups containing peptides ajdacent to multiple proteins) are assigned to the protein with the highest protein score. This process is repeated until no more peptide groups can be assigned, and these ranks are used to represent the belief that a protein is present. The resulting graph with edges connecting proteins to their assigned peptide groups is processed using ProteinProphet, but with no weighting of peptide groups.

In Scaffold, proteins are first grouped using standard protein grouping, but proteins may also be grouped if the sum of the scores of the peptides they do not share is lower than 0.95. The Occam's razor principle is used to discard proteins that don't have unique peptide evidence. In an identical manner to ProteinProphet, the present set of proteins x* is found by applying some threshold to the sorted list of protein posteriors.

EBP

The EBP method [27] is another probabilistically phrased and motivated method, but is ultimately a complex numerical heuristic similar to ProteinProphet. Like ProteinProphet, EBP operates on the observed graph G′. Initially, the EBP method removes spectra degneracy using the same method as ProteinProphet, and computing $\mathrm{Pr}(Y_j\mid D_{k\left(j\right)})\approx s_j^{\prime }={\max }_k{s}_{j,k}$. EBP partitions the problem of protein identification into two parts. First, the set H consists of proteins that are either present or homologous to a present protein. Second, the set X ⊂ H consists of proteins that are present in the sample.

Proteins in H must be adjacent to at least one present peptide. Membership in H is calculated using a Poisson distribution to estimate the probability complement to the event that peptide adjacent to the protein is truly present. Membership in X is calculated conditional on membership in H using a weighting scheme similar to ProteinProphet; each weight, where Σ_i w_i,j = 1, represents the probability that a present peptide j originated from protein i.

In a manner very siminProphet's NSP score, EBP computes an approximate abundance estimate v_i for each protein. The abundance estimates are computed as the total sum of weighted peptide scores associated with a protein:

$$v_i=\sum _{j:(i,j)\in E\prime }{w}_{i,j}{s}_j^{\prime }$$

The abundance estimates are thresholded into abundance class bins a_i = bin(v_i). For each abundance class bin, there is a corresponding set of parameters θ_a = (N_a, τ_a, n_a, γ_a, κ_a, λ_a) with the following meanings:

Variable	Meaning
Na	Number of proteins in bin a
τ a	Total length of proteins in bin a
na	Number of peptide matches to proteins in bin a
γ a	Proportion of proteins in bin a that are in H
κ a	Total length of proteins in bin a and in H
λ a	Number of peptide matches in bin a that are correct

These parameters, along with w, are used to sequentially compute estimates of the following:

$$\begin{array}{cc}\hfill a\mid w,{\forall }_j{s}_j^{\prime }& \hfill \\ \hfill \mathrm{Pr}(H_i\mid D,\theta ,a)& \hfill \\ \hfill \mathrm{Pr}(X_i\mid H_i,D,\theta ,a,w)& \hfill \\ \hfill \theta \mid \forall i\mathrm{Pr}(H_i\mid D,\theta ,a)& \hfill \\ \hfill w\mid \forall i,\mathrm{Pr}(X_i\mid D)& \hfill \end{array}$$

The value a is updated as stated above by first computing v_i|w and then thresholding it into the appropriate bin. The probability Pr(H_i|D, θ, a) is estimated by modeling the number of correct peptide identifications matching a protein i ∈ H as a Poisson process. The parameters of this Poisson process are defined by the parameters in the appropriate bin θ_ai, and by a heuristic value $e\sqrt{\log \left(\mid \{j:(i,j)\in E\}\mid \right)}$, an estimate of the proportional probability that the highest-scoring random match is to one of the peptides adjacent to i. A value proportional to the conditional probability that i ∉ H is estimated using the estimated prior probability that i ∉ H, the product of probabilities that all peptides observed are incorrect identifications and the probability that the observed number of peptides would be produced by the Poisson distribution:

$$\mathrm{Pr}(\neg H_i\mid D,\theta ,a)\propto (1-{\gamma }_{a_i})\prod _{j:(i,j)\in E\prime }(1-s_j^{\prime })\times \mathrm{Pr}\left(\mid \{Y_j:(i,j)\in E\}\mid =\mid \{j:(i,j)\in E\prime \}\mid \Vert \{Y_j:(i,j)\in E\}\mid ~Poisson\left(\frac{e\sqrt{\log \left(\mid \{j:(i,j)\in E\}\mid \right)}{\lambda }_{a_i}}{{\kappa }_{a_i}}\right)\right)$$

Similarly, a value proportional to the probability that i ∉ H can be estimated by summing over outcomes with a nonzero quantity m of correct peptides identifications. The resulting summation terms will consist of two Poisson probabilities (one for the correct peptide identifications, and the other for the incorrect peptide identifications) multiplied by the probability that exactly that many peptides are correct matches. The latter probability is estimated by summing over all possible subsets of exactly m present peptides adjacent in G′ to i:

$$\begin{array}{cc}\hfill \text{Pr}& (\mid \{j:(i,j)\in E\prime \}\mid =m\mid D)\hfill \\ \hfill & =\sum _{\mid \{y_j:(i,j)\in E\prime \}\mid =m}\prod _{j:(i,j)\in E\prime }{s}_j^{\prime }{y}_j+(1-s_j^{\prime })(1-y_j)\hfill \end{array}$$

The probability that a protein is truly present in the sample given that it is adjacent to a truly present peptide is computed by marginalizing out the variable H_i; this marginalization only takes one step because the set X ⊂ H:

$$\begin{array}{cc}\hfill \text{Pr}& (X_i\mid D,\theta ,a)\hfill \\ \hfill & =\sum _{h_i}\text{Pr}(X_i\mid H_i=h_i,D,\theta ,a)\text{Pr}(H_i=h_i\mid D,\theta ,a)\hfill \\ \hfill & =\text{Pr}(X_i\mid H_i,D,\theta ,a)\text{Pr}(H_i=h_i\mid D,\theta ,a)\hfill \end{array}$$

When computing Pr(X_i|H_i, D, θ, a), the method used is nearly identical to the method used to compute Pr(X_i|H_i, D, θ, a); the difference is that in computing Pr(X_i|H_i, D, θ, a) the weighted value s″ is used in place of all instances of s′.

The entire iterative estimation process is repeated until the estimated values appear to converge. The EBP method is not demonstrated to be a true expectation-maximization (EM) [4] method, despite its probabilistic motivation and description; iterative estimation of posteriors, weights, and other parameters is not equivalent to iteratively maximizing the expectation of the full protein configuration likelihood.

The authors don't state an explicit procedure used for updating w; instead, they indicate that the greatest weight must be given to the protein with the highest current posterior estimate. Presumably, the authors use the same procedure as ProteinProphet for updating w. The present set of proteins x* is found by applying some threshold to the sorted list of protein posteriors. It is suggested that a combinatorial function would allow extension to replicate experiments by requiring that the protein be present in a certain number of those experiments.

PANORAMICS

The PANORAMICS method [9] similarly uses the observed graph G′. First, peptide scores are normalized using parameters that must be established from a known data set. Then, proteins are grouped and peptides that produce indistinguishable theoretical spectra are merged. After that, spectral degeneracy is removed by keeping only the edge to the highest-scoring peptide. Peptide probabilities are estimated by estimating the probability that a peptide is absent; the chances a peptide is absent are computed by computing the probability that all PSMs containing that peptide are absent by taking the product over the complements of their scores:

$$s_j^{\prime }=1-\prod _{k}1-s_{j,k}$$

If $X_i^{j^{\prime }}$ denotes the event that peptide j is present as a result of the present protein i, then the probability that protein i is present and the probability that peptide j is present is given using a formula similar to the unweighted formulation of ProteinProphet:

$$\begin{array}{cc}\hfill \text{Pr}(X_i\mid D)& =1-\prod _{j:(i,j)\in E\prime }1-\text{Pr}(X_i^{j\prime }\mid D)\hfill \\ \hfill s_j^{\prime }\approx \text{Pr}(Y_j\mid D)& =1-\prod _{i:(i,j)\in E\prime }1-\text{Pr}(X_i^{j\prime }\mid D)\hfill \end{array}$$

Finally, by assuming that the probability of observing any peptide given that an adjacent protein is present depends only on the peptide, the probability of the event $X_i^{j^{\prime }}$ can be rewritten:

$$\text{Pr}(X_i^{j\prime }\mid D)=\text{Pr}(X_i\mid D)\text{Pr}(Y_j\mid \exists i:(i,j)\in E\prime )$$

By rephrasing $X_i^{j^{\prime }}$ in this way, it is possible to redefine the posterior protein and peptide probabilities:

$$\begin{array}{cc}\hfill \text{Pr}(X_i\mid D)& =1-\prod _{j:(i,j)\in E\prime }1-\text{Pr}(X_i\mid D)\text{Pr}(Y_j\mid \exists i:(i,j)\in E\prime )\hfill \\ \hfill s_j^{\prime }& =1-\prod _{j:(i,j)\in E\prime }1-\text{Pr}(X_i\mid D)\text{Pr}(Y_j\mid \exists i:(i,j)\in E\prime )\hfill \end{array}$$

Values of Pr(X_i|D) and Pr(Y_j|∃i : (i, j) ∈ E′) that are consistent with these equations are found using the Newton-Raphson method. A present set of proteins x* is found by applying some threshold to the sorted list of protein posteriors.

Bayesian methods

Hierarchical statistical model

The hierarchical statistical model [31] assumes that D ⫫ X|Y and generatively models the process by which proteins create spectra to perform inference on G′. Spectral degeneracy is eliminated by keeping only the edge incident to the peptide with the highest PSM score for any spectrum.

First, the model assumes an independent and identically distributed (i.i.d) prior for all proteins: Pr(X_i) = γ. Next, the authors model the process by which a known set of proteins creates a set of peptides as independent processes from each adjacent protein in G′. Their model uses different parameters to model the emission of peptides resulting from different cleavages of that protein; a specific cleavage indicates that the enzyme cut where expected, while a nonspecific cleavage indicates that the enzyme would have to cut at an unexpected location.

$$\text{Pr}(Y_j\mid X)=1-\prod _{i:(i,j)\in E\prime }1-{\alpha }_{i,j}$$

where

$${\alpha }_{i,j}=\{\begin{array}{cc}{\alpha }_N^{\prime }\hfill & \text{one nonspecific cleavage}\hfill \\ {\alpha }_S^{\prime }\hfill & \text{one specific cleavage}\hfill \\ {\alpha }_{NN}^{\prime }\hfill & \text{two nonspecific cleavage}\hfill \\ {\alpha }_{NS}^{\prime }\hfill & \text{one specific and one nonspecific cleavage}\hfill \\ {\alpha }_{SS}^{\prime }\hfill & \text{two specific cleavage}\hfill \end{array}\phantom{\}}$$

The probability of a correct PSM match given the associated peptides is likewise calculated using Z as a random variable that indicates whether a PSM match is correct:

$$\text{Pr}(Z_{j,k\left(j\right)}\mid Y_j=y_j)=\{\begin{array}{cc}\delta \hfill & y_j=1\hfill \\ 0\hfill & \text{else}\hfill \end{array}\phantom{\}}$$

The authors also model the distribution of PSM scores as a mixture of the PSM score distributions from correct and incorrect PSM matches with mixing proportion λ, where q are factors that influence the score:

$$a~\mathit{Mixture}\left(\{f_{\mathit{correct}}\left(q\right),f_{\mathit{incorrect}}\left(q\right)\},\lambda \right)$$

These likelihoods must be defined in order to perform protein inference. In practice, they are defined as parameterized distributions, and the parameter estimates are made using a separate data set.

Lastly, the probability that the number of peptide hits for present proteins is greater than some threshold m is modeled using parameters ρ₁ and ρ₀:

$$\text{Pr}(\mid \{i:(i,j)\in E\prime \}\mid >m\mid X_i=x_i)={\rho }_1^{x_i}{\rho }_0^{\neg x_i}$$

Then, approximate maximum likelihood estimates (MLEs) of the parameters θ = (γ, α, δ, λ, ρ₁, ρ₀) are computed using EM with hidden variables X, Y, and Z. Finally, using the estimated θ values, the posterior probabilities are estimated for proteins:

$$\text{Pr}(X_i\mid D)\approx \text{Pr}(X_i\mid \theta ,s,G)$$

These posteriors are thresholded to produce a present set of proteins x*.

Nested mixture model

The nested mixture model approach [19] to protein identification transforms G′ into a tree. This transformation is accomplished by copying each degenerate peptide (and the spectra it matches) so that each copy is adjacent to only one protein. Spectral degeneracy is also removed by keeping only the highest-scoring edges for each spectrum. This transformation ensures the graph G′ is a tree. Because each peptide can only be associated with a single protein, let i(j) denote the protein associated with peptide j.

The model assumes an i.i.d prior for all proteins: Pr(X_i) = γ. All peptides adjacent to absent proteins are assumed to be absent, and the peptides adjacent to present proteins are drawn from a mixture model of present and absent peptides:

$$\text{Pr}(Y_j\mid X_{i\left(j\right)}=x_{i\left(j\right)})=\{\begin{array}{cc}\alpha \hfill & x_{i\left(j\right)}=1\hfill \\ 0\hfill & \text{else}\hfill \end{array}\phantom{\}}$$

The number of peptides adjacent to present and absent proteins are of known distributions f₁ and f₀, respectively:

$$\begin{array}{cc}\hfill \mid \{j:(i,j)\in E\prime \}\mid & \mid X_i=x_i~f(x_i\mid {\theta }_f)\hfill \\ \hfill f\left(x_i\right)& =\{\begin{array}{cc}{f}_1\left({\theta }_f\right)\hfill & x_i=1\hfill \\ f_0\left({\theta }_f\right)\hfill & \text{else}\hfill \end{array}\phantom{\}}\hfill \end{array}$$

In a similar manner, the distributions of PSM scores containing present and absent peptides are also modeled using distributions g₁ and g₀, respectively:

$$\begin{array}{cc}\hfill S_{j\left(k\right),k}\mid Y_{j\left(k\right)}& =y_{j\left(k\right)}~g(y_{j\left(k\right)}\mid {\theta }_g)\hfill \\ \hfill g\left(y_{j\left(k\right)}\right)& =\{\begin{array}{cc}{g}_1\left({\theta }_g\right)\hfill & y_{j\left(k\right)}=1\hfill \\ g_0\left({\theta }_g\right)\hfill & \text{else}\hfill \end{array}\phantom{\}}\hfill \end{array}$$

The distributions f and g are parameterized by θ_f and θ_g, respectively. Because the transformed graph G′ is a tree, the peptides are conditionally independent of one another given the associated protein. In a similar manner, the scores are conditionally independent of one another given the associated peptide. The likelihood can then be computed:

$$\begin{array}{cc}\hfill \text{Pr}(D\mid X=x,\theta )& =\prod _i\left[\text{Pr}(m=\mid \{j:(i,j)\in E\prime \}\mid \mid m~f(x_i,{\theta }_f))\sum _y\prod _{j:i=i\left(j\right)}\left[\text{Pr}(Y_j=y_j\mid X_i=x_i)\prod _{k:j=j\left(k\right)}\text{Pr}(S_{j,k}=s_{j,k}\mid S_{j,k}~g(y_j\mid {\theta }_g))\right]\right]\hfill \\ \hfill & =\prod _i\left[\text{Pr}(m=\mid \{j:(i,j)\in E\prime \}\mid \mid m~f(x_i,{\theta }_f))\prod _{j:i=i\left(j\right)}\left[\sum _{y_j}\text{Pr}(Y_j=y_j\mid X_i=x_i)\prod _{k:j=j\left(k\right)}\text{Pr}(S_{j,k}=s_{j,k}\mid S_{j,k}~g(y_j\mid {\theta }_g))\right]\right]\hfill \end{array}$$

Similarly, the likelihood constant can be computed and normalized out by summing over all protein states in the joint probability:

$$\sum _x\text{Pr}(D\mid X=x,\theta )\text{Pr}(X=x)=\prod _i\left[\sum _{x_i}\text{Pr}(X_i=x_i)\text{Pr}(m=\mid \{j:(i,j)\in E\prime \}\mid \mid m~f(x_i,{\theta }_f))\prod _{j:i=i\left(j\right)}\left[\sum _{y_j}\text{Pr}(Y_j=y_i\mid X_i=x_i)\prod _{k:j=j\left(k\right)}\text{Pr}(S_{j,k}=s_{j,k}\mid S_{j,k}~g(y_i\mid {\theta }_g))\right]\right]$$

The EM algorithm is used to compute approximate MLE estimates of the parameters θ = (γ, α, θ_f, θ_g). Posteriors for each protein are computed and these posteriors are thresholded to compute the set of present proteins x*.

MSBayes

MSBayes [20] takes a novel approach to protein inference; a complex, static model of peptide detectability [10, 21, 34] is used to model the mass spectrometry process for the entire graph G, rather than for the observed graph. The best peptide match for each spectrum determines the peptide score s_j; peptides that are not in the observed graph are given scores of zero.

In MSBayes, each protein has an independent prior Pr(X_i|D) = γ; the value of γ is either 0.5 (a uniform prior), or chosen using prior information about the number of proteins in the data set. The peptide scores are assumed to comprise the data, which are conditionally independent of the proteins given the peptides. Each peptide is assumed conditionally independent of other peptides given the proteins. Likewise, scores are assumed to be conditionally independent of each other given the peptide set:

$$\begin{array}{cc}\hfill \text{Pr}(D\mid X=x)& =\text{Pr}(S=s\mid X=x)\hfill \\ \hfill & =\sum _y\text{Pr}(S=s\mid Y=y)\text{Pr}(Y=y\mid X=x)\hfill \\ \hfill & =\sum _y\prod _j\text{Pr}(S_{k\left(j\right)}=s_{k\left(j\right)}\mid Y_j=y_j)\text{Pr}(Y_j=y_j\mid X=x)\hfill \\ \hfill & =\sum _y\prod _j\text{Pr}(S_{k\left(j\right)}=s_{k\left(j\right)}\mid Y_j=y_j)\text{Pr}(Y_j=y_j\mid X=x)\text{Pr}(Y_j=y_j\mid X=x)=1-\prod _{i:(i,j)\in E}1-x_i{\alpha }_{i,j}\text{Pr}(S_{k\left(j\right)}=s_{k\left(j\right)}\mid Y_j=y_j)\hfill \\ \hfill & =\frac{\text{Pr}(Y_j=y_i\mid S_{k\left(j\right)}=s_{k\left(j\right)})\text{Pr}(S_{k\left(j\right)}=s_{k\left(j\right)})}{\text{Pr}(Y_j=y_j)}\hfill \end{array}$$

where Pr(Y_j = y_j|S_k(j) = s_k(j)) is estimated by Peptide-Prophet [16]. The peptide emission probabilities α_i,j are estimated using a static predictor of peptide detectability. This detectability predictor [34] is composed of a neural network that uses 175 features of each protein-peptide pair to predict whether a peptide will be observed given that an adjacent protein is present. The parameters of this model are trained using a “protein standard,” a small data set composed of a known set of proteins that have been biochemically purified.

Lastly, Markov chain Monte Carlo (MCMC) is used to jointly sample from the space of proteins and peptides and compute protein posteriors and a MAP protein set as follows:

x, y ← some configuration : Pr(D, X = x, Y = y) > 0

while convergence is not reached do

• b_x ← random({i₁, i₂, …} : |b_x| = u

• b_y ← random({j₁, j₂, …} : |b_y| = v

• Denote X′ = {X_i : i ∈ b_x}

• Denote Y′ = {Y_j : j ∈ b_y}

• ∀x′∀y′, p_x′,y′ ← ∝ Pr(X′ = x′, Y′ = y′|∀_i ∉ b_xX_i = x_i, ∀j ∉ b_yY_j = y_j, D)

• Sample an x′, y′ proportional to p_x′,y′

• ∀_i ∈ b_xx_i ← $x_i^{\prime }$

• ∀_j ∈ b_yy_j ← $y_j^{\prime }$

end while

The posterior of each protein can be estimated by computing the frequency of iterations for which that protein is present in the configuration x. These posteriors are thresholded to estimate the present set of proteins x*. Alternatively, the MAP protein and peptide set can be computed by storing the joint configuration that results in the highest proportional posterior. This MAP protein set can be treated as the set of present proteins:

$$x\ast =x_{\mathit{MAP}}$$

Fido

Fido [30] first removes spectral degeneracy by keeping only the edge to the highest-scoring peptide for each spectrum. Peptides with identical theoretical spectra are merged so that they are treated as the same peptide. Then, protein posteriors are computed using a graphical model similar to MSBayes. The Fido model is different in that it does not use a static detectability model; peptide detectabilities are estimated using a fixed parameter α that is shared among all peptides. Fido can operate on the observed graph G′ or on the full graph G, by using zero or near-zero scores for unobserved peptides. A noise model is used to account for the chance that a peptide is observed incorrectly; the parameter β is used to model the probability that a peptide will be observed even though it is absent.

The data are assumed conditionally independent of the proteins given the peptides. Furthermore, the process by which a peptide is emitted from an adjacent protein is assumed to be independent of other peptides being emitted. Likewise, the process by which absent peptides are incorrectly observed is assumed to be independent of the process by which proteins emit peptides. Together, these assumptions allow the peptide set to be marginalized out given the protein set:

$$\begin{array}{cc}\hfill \text{Pr}(D\mid X=x)& =\sum _y\text{Pr}(D\mid Y=y)\text{Pr}(Y=y\mid X=x)\hfill \\ \hfill & =\sum _y\prod _j\text{Pr}(D_{k:j\left(k\right)=j}\mid Y_j=y_j)\text{Pr}(Y_j=y_j\mid X=x)\hfill \\ \hfill & =\prod _j\sum _{y_i}\text{Pr}(D_{k:j\left(k\right)=j}\mid Y_j=y_j)\text{Pr}(Y_j=y_j\mid X=x)\text{Pr}(Y_j\mid X=x)=1-(1-\beta )\prod _{i:x_i,(i,j)\in E}1-\alpha \hfill \\ \hfill & =1-(1-\beta ){(1-\alpha )}^{\mid \{i:x_i,(i,j)\in E\}\mid }\hfill \end{array}$$

A value proportional to the probability of observing a spectrum given the adjacent peptide state is calculated directly using the original likelihood Pr(D_k|Y_j = y_j); this score is estimated empirically by PeptideProphet and is used, along with an estimate of Pr(Y_j = y_j), to compute S_j,k. By using the PeptideProphet estimate for the peptide prior Pr(Y_j = y_j) and the score S_j,k, a value proportional to the original likelihood can be computed:

$$\text{Pr}(D_k\mid Y_j=y_j)\propto \frac{y_j{S}_{j,k}+(1-y_i)(1-S_{j,k})}{\text{Pr}(Y_j=y_j)}$$

Disjoint subgraphs are independent; therefore, posteriors are computed by marginalizing the set of proteins in each connected subgraph of G. Because the cost of this marginalization is exponential in the number of proteins in the connected subgraph, graph transformations are used to reduce the number of proteins in a connected subgraph, and then exact or approximate posteriors are computed using the transformed subgraph.

The first graph transforming method clusters proteins using the same procedure for protein grouping; however, rather than treat each cluster as present or absent, a cluster is represented by the number of present proteins it contains. Because computation of Pr(Y_j = y_j|X = x) only depends on the number of present proteins adjacent to peptide j, and because all proteins adjacent to peptide j must be in the same cluster, then it is sufficient to condition on the number of proteins in the adjacent clusters. Let N_v represent the number of present proteins in protein cluster v, where v indexes the protein clusters and X^(v) represents the set of proteins in cluster v. Finally, let the size of cluster N_v be written len(N_v), while denoting the number of present proteins in the cluster with |N_v|. Marginalizing over all protein configurations can then be performed by marginalizing over all cluster configurations and accounting for the number of unique protein configurations that could result in an identical cluster configuration:

$$\text{Pr}(Y=y\mid X=x)=\prod _j\text{Pr}(Y_j\mid X=x)=\prod _j\text{Pr}(Y_j\mid N=n)$$

$$\text{Pr}(N_{\upsilon }=n_{\upsilon }\mid X^{\left(\upsilon \right)}=x^{\left(\upsilon \right)})=\{\begin{array}{cc}1\hfill & n_{\upsilon }=\mid x^{\left(\upsilon \right)}\mid \hfill \\ 0\hfill & \text{else}\hfill \end{array}\phantom{\}}$$

$$\text{Pr}(X^{\left(\upsilon \right)}=x^{\left(\upsilon \right)}\mid N_{\upsilon }=n_{\upsilon })=\frac{\text{Pr}(N_{\upsilon }=n_{\upsilon }\mid X^{\left(\upsilon \right)}=x^{\left(\upsilon \right)}=)\text{Pr}(X^{\left(\upsilon \right)}=x^{\left(\upsilon \right)})}{\text{Pr}(N_{\upsilon }=n_{\upsilon })}$$

$$\text{Pr}(N_{\upsilon }=n_{\upsilon })={\gamma }^{n_{\upsilon }}{(1-\gamma )}^{\mathit{len}\left(N_{\upsilon }\right)-n_{\upsilon }}\left(\begin{array}{c}\hfill \mathit{len}\left(N_{\upsilon }\right)\hfill \\ \hfill n_{\upsilon }\hfill \end{array}\right)$$

Effectively, considering the clusters rather than the proteins exploits symmetry that results in an identical likelihood from multiple protein configurations. Marginalizing over all cluster configurations can be performed much more efficiently than marginalizing over all protein configurations:

$$\begin{array}{cc}\hfill \text{Pr}(X_i\mid D)& =\frac{{\sum }_n\text{Pr}(D\mid N=n)\text{Pr}(N=n\mid X_i)}{\text{Pr}\left(D\right)}\hfill \\ \hfill \text{Pr}(N=n)& =\prod _{\upsilon }\text{Pr}(N_{\upsilon }=n_{\upsilon })\hfill \\ \hfill \text{Pr}(N_{\upsilon }=n_{\upsilon }\mid X_i^{\left(\upsilon \right)})& =\frac{\text{Pr}(X_i^{\left(\upsilon \right)}\mid N_{\upsilon }=n_{\upsilon })\text{Pr}(N_{\upsilon }=n_{\upsilon })}{\gamma }\hfill \\ \hfill \text{Pr}(X_i^{\left(\upsilon \right)}\mid N_{\upsilon }=n_{\upsilon })& =\frac{n_{\upsilon }}{\mathit{len}\left(N_{\upsilon }\right)}\hfill \end{array}$$

The second graph transformation graphically exploits the fact that proteins will not co-vary due to a shared peptide if the peptide has a score equal to zero. A peptide j with a zero score $S_j^{\prime }=0$ must be absent; therefore, it cannot be emitted by any adjacent protein and cannot be the result of the noise model. Consider a graph with that peptide duplicated so that a unique copy exists for each adjacent protein, and these peptides are now only adjacent to one protein each. The set of necessary events likewise states that each adjacent protein cannot emit the peptide, and that the peptide cannot be created by the noise model. The only difference introduced is that the noise model is counted once for each protein in the transformed graph, rather than once overall. This effect is therefore removed by dividing the original likelihood by (1 − β) for each duplicate peptide added (aside from the original).

This second transformation substantially decreases the number of proteins in each connected subgraph, which makes marginalization more efficient. Furthermore, because the peptide scores are not sacrosanct, small scores can be treated as zero for the purposes of this operation. Thus, in the cases when the marginalization would be too computationally expensive, the graph transformation can be relaxed to duplicate peptides with larger scores. In this way, approximate posteriors can be computed to meet a desired time constraint specified by the user. These posteriors can be thresholded to produce a present set of proteins x*; the same graph transformations can be used to find the MAP protein set, which will be composed of the MAP protein set in each connected subgraph.

COMPARISON OF EXISTING APPROACHES

In the publications originally presenting these methods, some are compared against other existing approaches. In this section, we analyze each comparison and evaluate the methods relative to each other. Table 2 depicts our analysis of each published comparison between a pair of methods. For each method, we consider the accuracy demonstrated in the original publication, as well as the computational cost required to apply it to large, biologically interesting data sets.

Table 2.

Published method comparisons. We analyze published comparisons between methods and evaluate them. The entries in a row depict our evaluations of the labeled method relative to other methods from each column. For each cell, we categorize the outcome of a comparison between two methods. The various symbols indicate whether the row method performed much worse (□□□□), slightly worse (■□□□), essentially the same (■■□□), slightly better (■■■□) or significantly better (■■■■) than the column method. For each pair of methods, we compare the accuracy and the scalability. Accuracy evaluates the ability of a method to identify many present proteins at a low FDR when applied to an unseen data set. Scalability evaluates the computational efficiency of a method and whether it can be applied to large, biologically interesting data sets

		One- and two-peptide	IDPicker	Protein-Prophet	EBP	PANORAMICS	Hierarchical	Nested Mixture	MSBayes	Fido
One- and two-peptide	Accuracy		■ □ □ □
	Scalability		■ ■ ■ □
IDPicker	Accuracy	■ ■ ■ □
	Scalability	■ □ □ □
ProteinProphet	Accuracy				■ ■ □ □	■ ■ ■ □	■ ■ □ □	■ ■ ■ □	■ ■ □ □	■ □ □ □
	Scalability				■ ■ ■ □	■ □ □ □	■ ■ ■ ■	■ ■ □ □	■ ■ □ □	■ ■ □ □
EBP	Accuracy			■ ■ □ □
	Scalability			■ □ □ □
PANORAMICS	Accuracy			■ □ □ □
	Scalability			■ ■ ■ □
Hierarchical	Accuracy			■ ■ □ □				–
	Scalability			□ □ □ □				□ □ □ □
Nested Mixture	Accuracy			■ □ □ □			–
	Scalability			■ ■ □ □			■ ■ ■ ■
MSBayes	Accuracy			■ ■ □ □						■ ■ □ □
	Scalability			■ ■ □ □						■ ■ □ □
Fido	Accuracy			■ ■ ■ □					■ ■ □ □
	Scalability			■ ■ □ □					■ ■ □ □

We also consider the validity of the published evaluation of each pair of methods. Traditionally, decoy database methods have been used to evaluate mass spectrometry-based protein identifications [7]. This approach introduces proteins into the protein database that are known to be absent; these absent proteins, known as “decoys,” may come from a species known not to contribute to the sample, or may be generated by shuffling or reversing the original protein database. The proteins comprising the original protein database (before decoys are introduced) are called “target” proteins. The decoy proteins can be used to estimate the FDR of a given set of protein identifications; if decoy proteins are favored no more and no less than absent targets, and if the number of decoys and targets are equal, then for each decoy protein found in a predicted present protein set x*, it is expected that one incorrect target protein in x* is also present. This target-decoy approach makes assumptions that are known to be incorrect regarding the target and decoy databases, which result in several caveats to using it to estimate the FDR.

Below, we describe the caveats to the published comparisons between pairs of methods, as well as the outcome of the competition to produce an analysis of each method's accuracy. Overall, we use this analysis of a method's accuracy, along with the method's efficiency and computational scalability, as criteria to predict and evaluate its utility for identifying proteins in large data sets from complex protein mixtures. Each method is evaluated against the other methods and assigned a score: performed much worse (□□□□), slightly worse (■□□□), essentially the same (■■□□), slightly better (■■■□) or significantly better (■■■■). Relative scores indicating that a method performed significantly worse than other methods suggest serious drawbacks to using that method that will frequently come up in common practice. Relative scores indicating that a method performed slightly worse than another method suggest a significant drawback to using the method, but not so significant that it prevents the method from being useful in certain settings. In the following discussion of these comparisons, we justify each evaluation.

In [38], IDPicker is compared to the one- and two-peptide rules using replicate experiments from a protein standard containing 49 proteins, proteins from yeast cells, and proteins from human. For each data set, the authors choose a peptide threshold τ_Y by controlling the peptide FDR estimated using a decoy database. The IDPicker method substantially increases the specificity of the method, while slightly lowering the sensitivity. It is trivial to observe that IDPicker will always select a subset of the proteins chosen by the one- or two-peptide rule when using the same peptide threshold for both methods; therefore, IDPicker can never have superior sensitivity, and so it is appropriate to use a more lax peptide threshold for IDPicker in order to compare it to the one- and two-peptide rules. Even so, it is practically and theoretically clear that IDPicker will result in substantially greater specificity, especially in instances where there are many degenerate peptides. Each degenerate peptide adjacent to a present protein has a large chance of receiving a high score; using the one- and two- peptide rules, all proteins adjacent to that degenerate peptide will be included in x*, even if only one of them was present.

Furthermore, degenerate target peptides are much more likely to be adjacent to target proteins; the expected scores of target peptides, which consist of a mixture of present and absent proteins, will be higher than the expected score of decoy peptides, which are necessarily absent. Target protein identifications are often used as a surrogate for true positive protein identifications when there is no ground truth regarding the set of present proteins. Therefore, methods like the one- and two-peptide rules are more likely to include absent target proteins rather than decoy proteins, resulting in an overestimated sensitivity and underestimated FDR.

Understandably, the IDPicker method is less efficient than the computationally trivial one- and two-peptide rules. Solving minimum set cover is NP-complete [15]; however, like many NP-complete problems, it can often be solved efficiently in practice, and when an exact solution is inefficient, it can be approximated using established approaches.

ProteinProphet is one of the most popular and seminal protein identification methods, and so many methods have been compared to it. In [27], the EBP method is compared to ProteinProphet using several replicate experiments on a protein standard consisting of 18 purified proteins [18]. Using two protein thresholds τ_X ∈ {0.9, 0.7, EBP achieves a greater specificity (one fewer decoy protein identified), but a lower sensitivity (one and two fewer present proteins identified, respectively). Furthermore, EBP is shown to be conservative; the FDR estimated computing the expected value of the complement of the posterior probabilities of proteins included in x* [6] is substantially higher than the true FDR. For this reason, a fairly high protein threshold would be required to achieve greater sensitivity. This higher protein threshold is likely to increase the FDR. For this reason, we conclude that the method has not been demonstrated to be superior to ProteinProphet. EBP may even lower the interpretability of the protein posteriors due to its conservative estimates.

The iterative procedures underpinning EBP are very similar to ProteinProphet and are mostly very efficient; however, when estimating the probabilities Pr(H_i|D, θ_ai) and Pr(T_i|D, θ_ai, w), there is a sum over all subsets of observed peptides adjacent to a protein. This term requires summing over the power set, which grows exponentially with the number of observed peptides adjacent to any protein. Unless this sum of products can be transformed into a product of sums using dynamic programming or some other procedure, it will become prohibitively inefficient to perform on data sets from complex organisms like humans, where the number of peptides adjacent to a protein can be very large.

In [9], ProteinProphet is compared with PANORAMICS on a data set from the plant Arabidopsis thaliana. The authors calibrated parameters for their peptide score in a rigorous manner using a protein standard; the protein standard is different enough from the A. thaliana data set that these parameter estimates are unlikely to provide an unfair advantage to their method. The authors then search the data against two different databases. The first database is the A. thaliana proteome (targets) combined with reversed copies of every target protein. The second database is the NCBI NR database, which contains over 3.1 million proteins. For both searches, the protein threshold τ_X was varied to produce a receiver operating characteristic (ROC) curve, which plots the number of true positive protein identifications against the number of false positive protein identifications. When the spectra were searched against the A. thaliana data set, ProteinProphet identifies more target proteins from the A. thaliana proteome in the low FDR region. In general, ProteinProphet performs very well at low FDR thresholds, and it is common to see comparisons in which competing methods outperform ProteinProphet only once the FDR becomes higher.

When these spectra are searched against the combined NCBI NR (target) and NCBI NR reversed (decoy) database, PANORAMICS identifies many more targets than Protein-Prophet in the moderate FDR region. The authors suggest that this increased number of identified targets indicates an increased sensitivity compared to ProteinProphet; however, the paper does not indicate whether these NCBI NR proteins are actually from A. thaliana. The demonstrated tendency to distinguish targets from decoys, regardless of species, is actually quite detrimental; in practice, the organisms producing the sample data are almost always known, and the challenge is to separate and distinguish the present target proteins from the absent target proteins. A preference for target proteins, regardless of species, can be the result of degenerate peptides from a single present protein that allow several other adjacent proteins to be included in the set x*. For this reason, PANORAMICS appears to be slightly less reliable than ProteinProphet, which includes fewer and fewer target proteins as the protein threshold τ_X is lowered.

The principle strength of the PANORAMICS method is its elegant simplicity, which casts the protein identification problem as a numeric equation; approaches to numerically solve such equations are extremely efficient. Their numeric solution is not demonstrated to be unique, but it is an appealing heuristic.

In [31], ProteinProphet is again compared, this time to the hierarchical model. The two methods are both used to analyze a data set consisting of 23 peptides together with 12 purified proteins. The proteins are enzymatically digested, and the resulting peptide mixture is treated as containing 35 present “proteins”; the 23 peptides are treated as single-peptide proteins. The authors use the two methods to identify peptides at different peptide thresholds, and they demonstrate that ProteinProphet has a slightly greater sensitivity at a low FDR and a lower sensitivity at a higher FDR. They do not perform a similar comparison for proteins; instead, they choose a single cutoff at τ_X = 0.8 and show that ProteinProphet and the hierarchical model identify the same number of present proteins and decoy proteins. The ad hoc choice of protein threshold is uninformative, especially given the tendency of ProteinProphet to outperform other methods in the low FDR region.

Unfortunately, the hierarchical model computes a sum over all peptide and protein configurations, and the paper does not discuss the resulting computational cost. Depending on the implementation, the cost of computing posteriors will grow with either the exponential or the factorial of the number of variables (or the number of proteins, if the sum of products over peptides is transformed into a product of sums) in a connected subgraph; in practice, this poor scalability makes the hierarchical model computationally prohibitive for so many data sets that the method is not practically useful.

In [19] the nested mixture model is compared to ProteinProphet on a yeast data set using an unspecified decoy database of artificial proteins. The nested mixture model has slightly higher sensitivity than ProteinProphet at low FDR, which is fairly impressive. Overall, the method performs similarly to ProteinProphet; however, the utility of the nested mixture model is low, because the treatment of degenerate peptides (essentially assuming that no peptides are degenerate) will cause the model to perform poorly on data sets from complex organisms such as human, whose graphs feature substantial peptide degeneracy. Furthermore, the treatment of degenerate peptides resembles the one- and two-peptide rules, and may result in an overestimate of sensitivity, because target peptides are more likely to have higher scores and target proteins are more likely to share degenerate peptides with other target proteins. Also, like the one- and two-peptide rules, the independent treatment of peptides makes this method very computationally efficient.

In [20], ProteinProphet is compared to MSBayes on a protein standard composed of 49 proteins [38] using a detectability model with hundreds of parameters chosen from another replicate of the same data set. MSBayes is shown to have a higher specificity but a lower sensitivity using a protein threshold of τ_X = 0.5. Considering that the threshold is so lax, the fact that ProteinProphet is still more specific indicates that the MAP protein set is very permissive. Furthermore, the fact that so many parameters for the detectability model are estimated on essentially the same data set makes the results less meaningful; even though the detectability model is shown to perform fairly well using parameters estimated from other data sets [34], it is highly probable that even fairly small changes in the quality of the peptide detectability estimates may result in large changes in the set of identified proteins.

MSBayes is not as efficient as ProteinProphet, but this may be because MSBayes is implemented in an interpreted language. The underlying MCMC procedure could be reimplemented in a more efficient, compiled language to be roughly the same speed as ProteinProphet. The MCMC procedure jointly samples protein and peptide states, despite the fact that the model permits peptides to be conditionally independent of each other given the protein set. Using this conditional independence would permit the peptides to be marginalized out in linear time given a sampled protein state, dramatically reducing the space that needs to be sampled. Furthermore, d-separation can be exploited to ensure that a block sampling chooses protein blocks so that every protein in the block shares a peptide with another protein in the block. Otherwise, a block will be d-separated by proteins whose states have been sampled, and can be sampled independently, rather than jointly.

In [30] ProteinProphet is compared to Fido on a protein standard of several replicate experiments performed using 18 purified proteins [18], a data set from the bacterium Haemophilus influenza set, a yeast data set [14], and a data set from the worm Caenorhabditis elegans [12] using a variety of decoy databases. The model parameters α, β, and γ are estimated using a low-resolution (about 10 points per variable) grid search to choose the values that simultaneously maximize the accuracy (as measured by target decoy distrimination) and minimize the error between the empirical FDR (using the decoy database) and the estimated FDR (using the computed posterior probabilities). Using these parameters, Fido performs slightly better for the low FDR regions of the yeast, H. influenza, and C. elegans data sets and substantially better on the protein standard. On the protein standard, which consisted of hundreds of replicate experiments, ProteinProphet gives many proteins posteriors of 1.0, including some decoy proteins. Fido does not give these proteins such high posteriors, and is substantially more accurate and better calibrated, partly due to the noise model, which can account for large numbers of spectra yielding higher average PeptideProphet scores, even for decoy peptides. The small improvement on three of the data sets must be measured against the fact that Fido estimates some parameters using the target and decoy database specifically for each set. Although estimating parameters on each data set using the target and decoy labels makes the small improvements less meaningful, it is unlikely that this parameter estimation results in substantial overfitting; the parameters are shown to be relatively robust between data sets, and it would be surprising if a low-resolution optimization of three jointly related parameters could simultaneously result in an accurate and well-calibrated model due to overfitting alone. Furthermore, the improvement on the protein standard data set is so substantial that it is nearly impossible that it is due to overfitting.

Fido is just as efficient as ProteinProphet. In practice, some data sets may respond less to the graph transformations, but large connected subgraphs can still be separated by duplicating peptides even when they have nonzero scores. If protein grouping is used, Fido's clustering transformation will provide no speedup; however, posteriors assigned to protein groups are not as informative as posteriors assigned to individual proteins. For this reason, it is necessary to use a prior or rephrase the likelihood if inference on protein groups is to be reinterpreted as posteriors on individual proteins. The speedup introduced by protein clustering may allow more realistic protein priors to be efficiently applied.

In [30] Fido is also compared to MSBayes on a protein standard composed of 49 purified proteins [38]. Fido performs slightly better in the low FDR region, but both methods basically perform the same. Furthermore, there is the possibility that a very small number of human contaminant proteins may bias the evaluation slightly because they will be treated as absent even though they're present.

Fido is more efficient than MSBayes, which is written in an interpreted language. However, a python reimplementation of Fido makes the runtime comparable to MSBayes; therefore, it is reasonable to assume that an efficient reimplementation of MSBayes in a compiled language could be scaled to very large data sets.

DISCUSSION

Quantitative methods, which estimate numeric protein scores instead of simply imperatively computing the protein set x*, have a distinct advantage over nonquantitative methods, because quantitative methods offer information regarding the confidence of the proteins identified. Furthermore, among quantitative methods, probabilistic methods offer easily interpreted scores; marginal protein posterior probabilities indicate the chances that a certain protein is present in the sample. In contrast, with nonprobabilistic quantitative methods, a score threshold of τ_X may be appropriate for one data set, but on another larger data set, the protein threshold should be stricter ${\tau }_X^{\prime }>{\tau }_X$. This property leads to a method that must be run and adjusted manually to achieve satisfactory results.

Probabilistically motivated heuristics, like the iterative methods presented in this review, often provide very useful and satisfying ways to approach a problem initially, but these methods do not provide an intuitive understanding of the inference problem itself; therefore, numeric heuristics can be very difficult to improve and extend. Furthermore, because these methods are defined procedurally, rather than derived from clearly stated assumptions, they can be brittle. For example, ProteinProphet is often extremely accurate and efficient; however, for some large data sets, like the combined replicates from the protein standard of 18 proteins, ProteinProphet becomes inaccurate and unreliable. Post-processing methods like MAYU [28] attempt to compute more rigorous FDR estimates after ProteinProphet is run, but the entire approach of “fixing” the results after the fact, rather than improving the gestalt process of identification, is reminiscient of the very approach that sometimes makes ProteinProphet unreliable.

Several assumptions stated or implicit in these various approaches are quite similar. For instance, the one- and two-peptide rules, DTASelect, ProteinProphet, EBP, Scaffold, PANORAMICS, and the nested mixture model all make assumptions that make the graph into a tree by somehow partitioning peptides among their adjacent proteins. This shared assumption is no coincidence: inference on a tree is substantially easier than inference on a general graph. Thus, rather than starting with a formal and rigorous formulation of the protein identification problem and then making it more efficient, these methods change the question they ask so that it becomes easier to answer. Likewise, every method presented makes assumptions to remove spectral degeneracy, which results in a subgraph on peptides and spectra composed of disjoint trees.

Rather than making assumptions that make the graph (or a snapshot of the graph in one iteration) into a tree, the hierarchical model, MSBayes, and Fido attempt to solve the actual problem by modeling the mass spectrometry process generatively and then taking steps to compute protein posteriors or the MAP protein set. In the case of the hierarchical statistical model, a naive treatment of inference on the non-tree topology of the graph results in a runtime exponential in the number of connected proteins in a subgraph; this runtime makes the procedure of little use in practice. MSBayes, on the other hand, avoids an exponential runtime by using MCMC. Fido uses graph transformations so that the cost of marginalization or approximate marginalization is not prohibitively large.

Because the Bayesian methods approach protein inference by modeling the mass spectrometry process and then taking the necessary steps to make inference feasible, they have a convenient modularity that allows the models to be easily improved; for instance, prior information regarding the number of present proteins or prior information regarding peptide detectability can be easily integrated into these models. In contrast, iterative methods are much more difficult to improve in this way. For instance, it would be quite difficult to come up with a way to correctly adjust ProteinProphet's protein-peptide weights to account for prior information on the number of present proteins. Bayesian approaches, on the other hand, don't partition the peptides among adjacent proteins; instead, they take into account the fact that shared peptides may only be present in a single protein by “explaining away” the shared peptide when an adjacent protein is present. Because Bayesian methods model mass spectrometry in an intuitive way, it is trivial to see how these methods could incorporate prior information into the protein prior for a model.

It is easy to see that much more accurate and sophisticated models of the mass spectrometry process are possible. For example, peptide detectability is best modeled in a sample-specific way, not statically. Although some of the factors that determine peptide detectability are invariant between experiments, others will depend on the experiment and on the specific proteins present. For instance, a highly abundant protein can result in highly abundant adjacent peptides, some of which may outcompete other less-abundant present peptides with similar mass and retention time; these less abundant peptides will not be selected during the precursor scan, and will not be detectable. Bayesian methods are very well-suited to incorporate more complex models of peptide detectability, which could easily model experiment-specific peptide detectability trends. Similarly, Bayesian methods can be easily extended to the full tripartite graph. The spectral degeneracy removed by all methods offers a great deal of unused information: for example, a spectrum with a spurious highest scoring peptide match is likely to have a lower ranked peptide match from a present peptide. Using protein-level information, the present peptide may have other evidence, which could upweight the chances it produced the degenerate spectrum, and subsequently downweight the effect of the spurious PSM.

These more complex models of mass spectrometry will introduce greater computational burden; however, that must not dissuade us from modeling the process as accurately as possible. First of all, there is a wealth of information on efficient graphical inference, for instance tree decomposition [1] and loopy belief propagation [36], that could substantially improve the efficiency of inference even with accurate models.

Furthermore, even if the cost of inference using a more accurate model were prohibitive, a better generative model of the mass spectrometry process could be applied to evaluation. The target-decoy strategy is so flawed that it makes rigorous comparison of methods very difficult. On one hand, degenerate peptides may increase the probability estimates of absent target proteins more than decoy proteins, yielding an incorrectly optimistic estimate of sensitivity and FDR. On the other hand, because high-scoring decoy peptides are going to stratify uniformly over the decoy proteins, whereas high-scoring target peptides are more likely to cluster to fewer present target proteins, target-decoy databases may overestimate the number of absent targets and yield overly pessimistic FDR estimates [28]. Robust generative models could supplement or replace the target-decoy strategy, and be used to evaluate the protein sets proposed by different methods.

Models of the mass spectrometry process and inference techniques are not the only facets of protein inference that could benefit from increased formality and attention. The problems of evaluating methods and reporting results are also ripe for fundamental improvements and novel approaches. For instance, posterior-based rankings on proteins don't account for non-independence between the included proteins: if a higher-scoring protein is chosen, that choice should decrease the rank of another protein that is adjacent to an overlapping set of peptides. Furthermore, the MAP approach does not adequately illustrate the relative advantage of the MAP set compared to the protein set yielding the second highest posterior. Often this leads to biologists interpreting results themselves, even after substantial statistical inference is performed: it is common to ask, “Are there any other sets of proteins that might result in the identified set x* using this method?” Ideally, rigorous statistical procedures should evaluate methods by mapping all possible sets of present proteins to all possible sets of identified proteins and estimating the probability that a method would make each identification from each present set. If such an approach could be made computationally efficient, then it could dramatically improve the utility of mass spectrometry and substantially improve the confidence with which protein samples can be analyzed.

Above all, it is important to recognize that a number of very similar approaches to protein identification have been repeatedly applied in different packaging. When a field is in its infancy, heuristics are the natural approach to take; heuristics are fast sketches of our qualitative goals, and they are often easy to implement. Nevertheless, as a field grows into maturity, it is increasingly important to approach problems formally. Mass spectrometry is currently experiencing an exciting watershed moment reminiscient of the early ages of the genomics era, where formal approaches to open problems promise to not only substantially improve our understanding of the processes that drive life, but also to propose questions that may result in novel statistical concepts and methods with myriad of other applications.