Rate constants and mechanisms of intrinsically disordered proteins binding to structured targets

Abstract

The binding of intrinsically disordered proteins (IDPs) to structured targets is gaining increasing attention. Here we review experimental and computational studies on the binding kinetics of IDPs. Experiments have yielded both the binding rate constants and the binding mechanisms, the latter via mutation and deletion studies and NMR techniques. Most computational studies have aimed at qualitative understanding of the binding rate constants or at mapping the free energy surfaces after the IDPs are engaged with their targets. The experiments and computation show that IDPs generally gain structures after they are engaged with their targets; that is, interactions with the targets facilitate the IDPs’ folding. It also seems clear that the initial contact of an IDP with the target is formed by just a segment, not the entire IDP. The docking of one segment to its sub-site followed by coalescing of other segments around the corresponding sub-sites emerges as a recurring feature in the binding of IDPs. Such a dock-and-coalesce model forms the basis for quantitative calculation of binding rate constants. For both disordered and ordered proteins, strong electrostatic attraction with their targets can enhance the binding rate constants by several orders of magnitude. There are now tremendous opportunities in narrowing the gap in our understanding of IDPs relative to ordered proteins with regard to binding kinetics.

1. Introduction

Essentially all cellular functions involve the binding of proteins to their macromolecular targets, which can be other proteins, nucleic acids, or their complexes. Much of the focus of protein binding studies is on structures of the resulting complexes and binding affinities. An underlying assumption is that cellular processes are under thermodynamic control, i.e., dictated by the relative stability of unbound and bound species at thermal equilibrium. However, numerous examples demonstrate that the rates of binding reactions are essential to cellular functions.^1–3 Indeed, given that cellular processes invariably involve competing pathways and any particular reaction may not have time to reach thermal equilibrium, it can be argued that kinetic control, rather than thermodynamic control, is the norm (i.e., the dominant species produced are determined by rate constants, not just binding affinities).⁴ Elucidating the pathways of protein binding processes and understanding how the magnitudes of binding rate constants relate to physical properties of proteins are thus of fundamental importance.

The binding of relatively rigid, globular proteins tends to be limited by the diffusional approach toward their targets, and has been the subject of many experimental and computational studies.^{2, 5} For these cases, it has recently become possible to robustly predict the binding rate constants by modeling the diffusional approach and accounting for biasing effects of long-range electrostatic interactions between the binding molecules.⁶ For flexible proteins, the binding mechanisms become much more complicated, presenting challenges to mechanistic interpretation of experimental observations and to computational studies aimed at quantitative predictions of binding rate constants.

This Perspective article concerns an extreme form of flexible proteins, i.e., proteins that are disordered in the unbound state and become ordered in the bound state. These so-called intrinsically disordered proteins (IDPs) have received wide attention in recent years,^7–9 though most of it not on binding kinetics.¹⁰ (Not all IDPs become ordered upon binding.) Nevertheless the binding kinetics of a growing list of IDPs has now been subjected to experimental and computational studies. Here we review these studies, paying particular attention to four IDPs, on which the integration of experiment and computation has been especially useful for elucidating the binding mechanisms and rationalizing the magnitudes of the binding rate constants. Dock-and-coalesce emerges as an unifying mechanistic model, and forms the basis for quantitative calculation of binding rate constants. There are now tremendous opportunities in narrowing the gap in our understanding of IDPs relative to ordered proteins with regard to binding kinetics.

2. Extended interaction surfaces of IDP-target complexes

Many (though not all) IDPs gain structures upon binding their cellular targets, and the complexes formed typically feature extended interaction surfaces.¹¹ Below we summarize the structures of four systems, to illustrate the structural and functional diversities of IDPs.

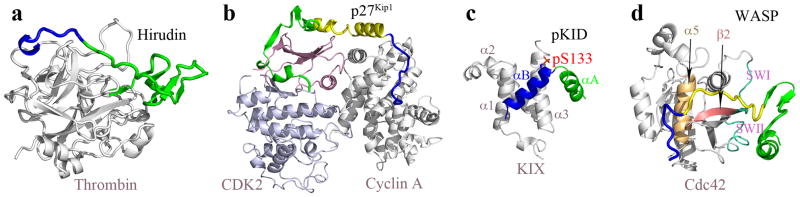
Hirudin is a potent thrombin inhibitor isolated from the bloodsucking leech Hirudo medicinalis. Thrombin is the key enzyme in the blood coagulation cascade. Inhibiting the coagulation system of the victim is obviously to the advantage of the producing animal, but hirudin can also be useful as an anticoagulation agent. Its 65 residues form a tadpole-like conformation, with a compact N-terminal head domain and a highly acidic, disordered C-terminal tail.¹² The N-terminal domain binds to the active site of thrombin, whereas the C-terminal tail binds to a basic exosite, the fibrinogen recognition site (Protein Data Bank (PDB) entry 4HTC; Fig. 1a).¹³ Such an extended binding interface results in the tight and specific complex of hirudin and thrombin. The N-terminal fragment (residues 1-53) and C-terminal fragment (residues 54-65) of hirudin can separately bind to their respective sub-sites on thrombin.^14–16

Fig. 1.

Native complexes of four intrinsically disordered proteins with their targets. (a) Hirudin bound to thrombin. The N-terminal domain (residues 1-53) and C-terminal tail (residues 54-65) of hirudin are shown in blue and green, respectively; thrombin is in gray. (b) The p27^Kip1 N-terminal region bound to the cyclin A-CDK2 complex. The rigid coil (residues 25-37), the linker helix (residues 38-59), and α-helix/β-strand/3₁₀ helix (residues 60-93) are shown in blue, yellow, and green, respectively; cyclin A is in gray; and the N- and C-terminal lobes of CKD2 are in pink and light blue, respectively. (c) pKID bound to KIX. αB and αA of pKID are shown in blue and green, respectively; KIX is in gray. (d) WASP GTPase binding domain bound to Cdc42. The N-terminal basic region (residues 230-237), the CRIB motif (residues 238-249), and the C-terminal β-hairpin and α-helix (residues 250-277) of the GBD are shown in blue, yellow, and green, respectively; Cdc42 is in gray, but its switch I (SWI) and switch II (SWII) regions, β2, and α5 are highlighted in magenta, red, and orange, respectively.

p27^Kip1 belongs to a family of proteins that inhibit the kinase activity of cyclin-dependent kinases (CDKs), by binding, via an N-terminal 65-residue region, to the complexes between the CDKs and their activating cyclins. In the unbound state, this N-terminal region is disordered.¹⁷ Upon binding to the CDK2-cyclin A complex, the p27^Kip1 N-terminal region forms an extended structure, consisting sequentially of a rigid coil (residues 25-37), an α-helix (residues 38-59), a β-haipin, a β-strand, and a 3₁₀ helix (residues 60-93) (PDB entry 1JSU; Fig. 1b).¹⁸ The two end segments of the p27^Kip1 N-terminal region contact cyclin A and CDK2, respectively, with the α-helix serving as a rigid linker. Specifically, the rigid coil is bound to the peptide-binding groove in the conserved cyclin box of cyclin A; and the β-hairpin, β-strand, and 3₁₀ helix clamp around the β-sheet of the CDK2 N-terminal lobe. In the interactions with CDK2, the β-hairpin forms a sandwich with the CDK2 β-sheet; the β-strand displaces (and thereby disorders) the first strand and significantly shifts the second strand of the CDK2 β-sheet; and the 3₁₀ helix inserts into the catalytic cleft beneath the CDK2 β-sheet.

CREB is a transcriptional activator whose activity is mediated by binding with the co-activator paralogs P300 and the CREB binding protein (CBP). The binding requires phosphorylation of CREB Ser133, located in the kinase-inducible domain (KID; residues 88-160). Phosphorylated KID (pKID) interacts with a conserved domain, referred to as KIX, of P300/CBP. The KIX domain is a 3-helix bundle (with helices α1, α2 and α3); bound pKID forms two α-helices, αA and αB (PDB entry 1KDX; Fig. 1c).¹⁹ Free pKID is disordered; the sequence corresponding to αA populates the helical conformation to a significant extent (>50%), but the αB sequence has low (10–15%) helical content.²⁰ In the complex with KIX, αB and αA are arranged at a 90° angle and wrap around the KIX α3 helix, with αB docking to a shallow groove over KIX α3 and α1, while αA latching to another face of KIX α3.

The Wiskott-Aldrich syndrome protein (WASP), upon binding Cdc42, a Rho-family GTPase, stimulates the initiation of actin polymerization. The GTPase binding domain (GBD) of WASP is intrinsically disordered.^{21, 22} In the free form, the GBD is bound to the C-terminal actin regulatory region of WASP, resulting in an auto-inhibited state.²³ Cdc42 binding releases the C-terminal actin regulatory region, allowing the latter to bind G-actin and the actin nucleating Arp2/3 complex. In the complex with Cdc42, WASP GDB adopts an extended conformation (PDB entry 1CEE; Fig. 1d).²² The N-terminal basic region (residues 230-237) of the GBD contacts helix α5 and the tip of the β2- β3 hairpin of Cdc42; the CRIB motif (residues 238-249) of the GBD aligns with strand β2 and the preceding switch I region of Cdc42; and the C-terminal β-hairpin and α-helix of the GBD pack against the switch II region of Cdc42.

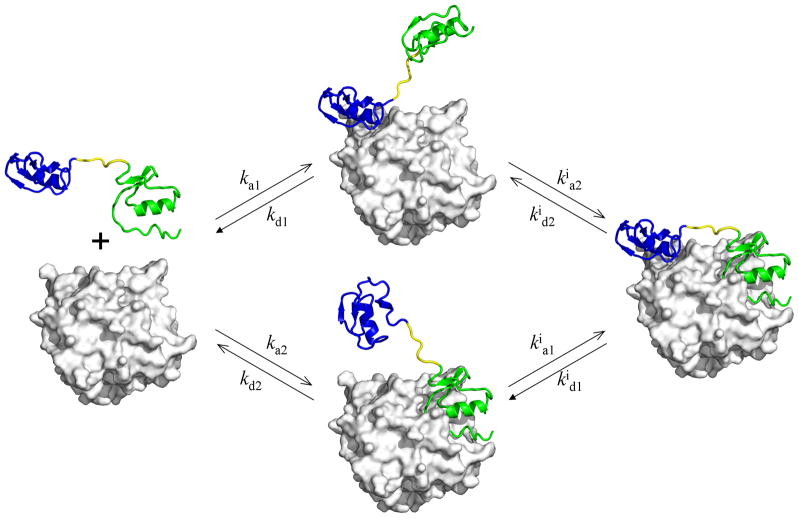
An extended interaction surface provides a simple way to increase the binding affinity, by accumulating the contributions of the different segments. This accumulation can be illustrated by a simple model (Fig. 2), in which a ligand is comprised of two linked segments which bind to separate sub-sites on the receptor. If the two isolated segments have dissociation constants K_d1 and K_d2 for their respective sub-sites, then the dissociation constant for the full ligand binding to the two sub-sites simultaneously can be written as

Fig. 2.

Bimolecular and intramolecular steps in a model IDP consisting of two folded domains connected by a linker. In blue and green are the N- and C-terminal domains of rhodniin; in gray is the thrombin target.

$$K_{\text{d}}=K_{\text{d}1}{K}_{\text{d}2}/C_{\text{eff}}$$ (1)

The properties of the linker are a main determinant of C_eff (a fact that is often overlooked). Under the simplifying assumption that the linker does not interfere with the interactions of the terminal segments with their sub-sites, it can be shown that²⁴

$$C_{\text{eff}}=p(\mathbf{d})$$ (2)

where p(r) is the probability density of the end-to-end vector r of the linker and d is this vector in the ligand-receptor complex. Note that both C_eff and p(d) have the unit of inverse volume.

A typical C_eff value predicted by Eq. (2) is 1 mM for a flexible linker,²⁴ and can be much higher for a rigid linker.²⁵ If K_d1 = K_d2 = 1 μM and C_eff = 1 mM, then K_d = 1 nM. So linking two fragments with moderate binding affinities can result in a high-affinity ligand. This idea was the basis of a class of designed thrombin inhibitors known as hirulogs, comprised of a tetrapeptide, (D-Phe)-Pro-Arg-Pro, targeting the active site, a flexible oligoglycyl linker, and the C-terminal tail (Asn53-Leu64) of hirudin targeting the fibrinogen recognition site.²⁶ While the two terminal fragments each have micromolar dissociation constants, hirulogs with four or more glycine residues as linkers have K_d between 2–3 nM. With a two-glycine linker, K_d increases to 64 nM. Both the magnitude of K_d and the dependence on linker length are consistent with C_eff expected of a flexible linker.²⁴ The increase in K_d in the case of a two-glycine linker can be attributed to the fact that the intervening residues between Arg in the N-terminal fragment and Asp55 in the C-terminal fragment have to be stretched to nearly a straight line in order to span the distance in between (at 20.9 Å according to the structure of a hirulog-thrombin complex¹⁵).

In the unbound state, an IDP is more stable than a hypothetic rigid protein adopting the bound structure. This stabilization of the unbound state allows the IDP to achieve a relatively low apparent affinity without sacrificing the specificity of the complex with its cellular target. The low apparent affinity is compatible with a high dissociation rate constant, meaning that the IDP-target complex rapidly dissociates. It was noted that rapid dissociation is essential for the many IDPs involved in signaling or regulation.¹⁰ The rest of the article is devoted to the association rate constant.

3. Experimental studies of IDP binding kinetics

An extended binding interface not only affects the binding thermodynamics but also the binding kinetics. For a globular folded protein, binding to a structured target occurs by reaching an intermediate complex (known as a transient complex) by diffusion and thereafter making nearly at once all its interactions with the target.²⁷ For an IDP, such a scenario corresponds to conformational selection, and is unlikely for two reasons. First, in this hypothesized intermediate complex, the conformation of the IDP is already near-native but is largely formed without the aid of interactions with the target, contrary to expectations. Moreover, this intermediate complex, with the extended conformation of the IDP all at once poised for close contact with the target, would have exceedingly severe orientational restraints in aligning to the target surface; reaching this intermediate complex by diffusional encounter in a single step would have an excessively low rate constant.^{6, 10} Instead the binding of an IDP will likely involve intermediate complexes in which only one segment of the IDP is bound to the target while the remaining segments undergo conformational search in a pseudo intramolecular context (Fig. 2). Such sequential or multiple-pathway mechanisms involving binding-induced protein folding have been invoked in a number of experimental studies of IDP binding kinetics.^28–31

3.1 Binding of hirudin to thrombin

By measuring the time dependence of thromobin-catalyzed product formation in the presence of hirudin, Stone and Hofsteenge²⁸ obtained the hirudin-thromobin association rate constant. The rate constant is independent of substrate binding at the active site, and is highly dependent on ionic strength.³² They proposed a two-step binding mechanism. The first step is rate-limiting and involves the ionic interactions between the acidic C-terminal tail of hirudin with a basic region of thrombin, which based on the structure of the hirudin-thromobin complex¹³ can now be identified as the fibrinogen recognition site. The second step results in the tight binding between hirudin and thrombin.

This mechanism was supported by subsequent observations that neutralization of hirudin C-terminal acidic residues significantly reduced the association rate constant³³ whereas N-terminal charge mutations had little effect on k_a.³⁴ As further support, neutralization of basic residues around the thrombin fibrinogen recognition site also significantly reduced k_a.³⁵ The high value of k_a, 1.3 × 10⁸ M⁻¹s⁻¹ at an ionic strength of 0.125 M,³³ along with the strong ionic-strength dependence, clearly suggests that the rate-limiting step of hirudin-thrombin association is an electrostatically enhanced diffusion-controlled process.²

Stopped-flow fluorescence measurements by Jackman et al.¹⁶ have further shown that the binding of the hirudin C-terminal tail induces thrombin conformational changes that are propagated to the active site and facilitate the binding of the N-terminal domain. The N-terminal fragment has a rate constant of 8.7 × 10⁵ M⁻¹s⁻¹ binding to the thrombin active site. When thrombin is pre-bound with the C-terminal fragment (which presumably pre-organizes the active site), the association rate constant increases by 1.7-fold to 15 × 10⁵ M⁻¹s⁻¹.

Like hirudin, a number of other thrombin inhibitors are found to occupy both the active site and the fibrinogen recognition site, and are thus likely to follow a similar two-step binding mechanism. A highly specific thrombin inhibitor, rhodniin, isolated from the assassin bug Rhodnius prolixus, consists of two Kazal-type domains connected by a 6-residue acidic linker (Fig. 2). The N- and C-terminal domains bind to the thrombin active site and fibrinogen recognition site, respectively; the linker is displaced from the thrombin surface.³⁶ Like the hirudin C-terminal tail, the rhodniin C-terminal domain is highly acidic. The rhodniin-thrombin association rate constant is also high, with a value of 7.6 × 10⁸ M⁻¹s⁻¹ at ionic strength = 0.250 M.³⁷ Again, it seems likely that the rate-limiting step here is the electrostatically enhanced diffusion-controlled binding of the C-terminal domain to the fibrinogen recognition site on thrombin.

Dipetalogastin II, isolated from the blood-sucking insect Dipetalogaster maximus, is homologous to rhodniin and an equally potent thrombin inhibitor.³⁸ Lepez and Nowak³⁹ designed a chimera comprised of the active-site binding domain (residues 1-48) of dipetalogastin II and the C-terminal tail (residues 55-65) of hirudin, linked by a five-glycine linker. The chimera binds to thrombin with a rate constant of 8.4 × 10⁸ M⁻¹s⁻¹ (at ionic strength = 0.125 M), similar to that for hirudin. When the Dipetalogastin II and hirudin fragments are connected directly (i.e., without the five-glycine linker), the binding rate constant is reduced to 0.14 × 10⁸ M⁻¹s⁻¹. The decrease in k_a suggests that, after binding of the hirudin fragment at the fibrinogen recognition site, strain at the fragment interface slows down the binding of dipetalogastin II fragment to the active site, such that the initial binding step becomes only partially rate-limiting.

3.2 Binding of p27^Kip1 N-terminal region to cyclin A-CDK2 complex

Kriwacki and co-workers²⁹ used surface plasmon resonance measurements to characterize the binding kinetics of the p27^Kip1 N-terminal region with the cyclin A-CDK2 binary complex. They found that the p27^Kip1 N-terminal region can bind to cyclin A and CDK2 separately, with a much higher rate constant to the former than to the latter (2.9 × 10⁶ versus 5.1 × 10³ M⁻¹s⁻¹). The binding to the cyclin A-CDK2 complex is dominated by a rate constant, 1.6 × 10⁶ M⁻¹s⁻¹, similar to that for binding to cyclin A; an additional minor phase has a rate constant of 5.6 × 10³ M⁻¹s⁻¹. Kriwacki and co-workers proposed that the binding process of the p27^Kip1 N-terminal region to the cyclin A-CDK2 complex proceeds in a sequential manner. It starts with the binding of the p27^Kip1 N-terminal segment (residues 25-37) to cyclin A, followed by the folding of the linker helix and finally by the binding of the C-terminal segment (residues 60-93) to CDK2. This binding mechanism further implies that removing the C-terminal segment would not affect the overall binding rate constant whereas removing the N-terminal segment would slow the binding to the rate constant for binding to CDK2 alone. These were precisely the outcome observed with p27^Kip1 deletion mutants, providing strong support for the sequential binding mechanism. While binding could in principle proceed with the C-terminal segment binding first, such a pathway would lose out in the kinetic competition against the pathway with the N-terminal segment binding first, due to the latter’s much higher rate constant.

A rate constant at k_a = 1.6 × 10⁶ M⁻¹s⁻¹ for the binding of the p27^Kip1 N-terminal region to the cyclin A-CDK2 complex is consistent with the data of Bienkiewicz et al.¹⁷ for the time course of reaching binding equilibrium (as measured by inhibition of cyclin A-CDK2 activity). In this experiment, the cyclin A-CDK2 complex was present at a concentration of C = 50 nM. The calculated time constant for binding equilibrium would be 1/k_aC = 0.2 min; the observed time constant is under a few minutes. Interestingly, Bienkiewicz et al. found that stabilizing the linker helix by alanine mutations slowed down the formation of the inhibited ternary complex, suggesting that the flexibility of the linker helix might have been evolutionarily tuned to optimize the overall binding rate constant.

3.3 Binding of pKID to KIX

Sugase et al.³⁰ recently used ¹H-¹⁵N single quantum correlation (HSQC) titrations and ¹⁵N relaxation dispersion measurements to identify intermediates along the pathway to form the pKID-KIX native complex. The HSQC titrations detected an early encounter complex, which is in fast exchange with the unbound state and has the KIX-facing residues of αB forming transient contacts with KIX. The ¹⁵N relaxation dispersion data further indicated a late intermediate, in fast exchange with the bound state. In this late intermediate, αB is incompletely folded but αA is nearly fully folded.

Fitting the relaxation dispersion data to a 3-state model (consisting of the free, late intermediate, and bound states), Sugase et al. found the bimolecular rate constant for forming the late intermediate to be 6.3 × 10⁶ M⁻¹s⁻¹. From the late intermediate, the rate constant for transition to the native complex is at least 20-fold higher than that for dissociation. So forming the late intermediate is rate-limiting for the overall process of reaching the native complex.

3.4 Binding of WASP GBD to Cdc42

By stopped-flow fluorescence measurements, Hemsath et al.³¹ obtained the rate constant for WASP GBD and Cdc42 association. The value of k_a is highly dependent on ionic strength, and equals 2.2 × 10⁷ M⁻¹s⁻¹ at ionic strength = 0.08 M. In addition, mutations of basic residues in the WASP N-terminal basic region and Cdc42 acidic residues (Glu49 and Glu178) around the binding site for the basic region lead to significant decreases in k_a. These results suggest that binding of the basic region is rate-limiting, and this step is an electrostatically enhanced diffusion-controlled process.

Interestingly, WASP GBD binds to another Rho GTPase, TC10, that shares 70% sequence identity with Cdc42 at a 1000-fold lower k_a. Part of the k_a decrease can be attributed to the substitutions of Cdc42 Glu49 and Glu178, to a oppositely charged lysine and a neutral threonine, respectively. Mutation of these TC10 residues to glutamate (the resulting mutant is referred to as TC10_EE) increases k_a by 10-fold. These results suggest that WASP GBD binding to TC10 may still start from the binding of the N-terminal basic region, but the subsequent step may be slowed down to make the latter rate-limiting.

Hemsath et al. proposed that, to stimulate actin polymerization, the basic region of WASP GBD is the initial recognition site of Cdc42. Anchoring to the basic region and the CRIB motif enables Cdc42 to displace the actin regulatory region from the rest of the WASP GBD. So in this biological context it is the initial recognition step, not necessarily the full process of forming the Cdc42-WASP GBD complex, that is key to the initiation of actin polymerization. The rate of the initial recognition step is biologically important, as TC10, in contrast to Cdc42, fails to stimulate actin polymerization; this activity is restored in the TC10_EE mutant.

As noted previously,² compared to methods such as stopped-flow spectrometry that operate in solution, surface plasmon resonance has confounding effects such as mass transport and surface immobilization. These effects could be especially problematic for the binding kinetics of IDPs.

4. Computation on IDP binding mechanisms and rate constants

A number of recent computational studies concerned the mechanisms and rate constants for IDPs binding to their structured targets. Some of these studies^{4, 40, 41} aimed at elucidating the differences, from a conceptual point of view, between binding of IDPs and binding of ordered proteins. Others focused on the late stage of binding processes, after the IDPs are already engaged with the targets.^42–45 There is promise that a method developed for the binding of ordered proteins, when applied to segments of an IDP, can yield the binding mechanism of the IDP and quantitatively predict the binding rate constant.⁶

4.1 Conceptual framework for k_a calculation

Wolynes et al.⁴⁰ made the insightful observation that an IDP, by virtue of its extended conformations, can engage with the target when their centers of mass are still far apart, and coined the term flycasting to describe this situation. They proposed that flycasting can enhance the association rate constant. Their calculation, based on the Smoluchowky-Debye model for diffusion-controlled bimolecular reaction, predicted a modest 1.6-fold increase in k_a for an IDP over a fully folded protein. It should be noted that rate enhancement produced by the Smoluchowky-Debye model, due to its reduction to a single reaction coordinate (i.e., the separation between centers of mass), is inherently small.⁴ More realistic models, accounting for the stereospecificity of the native complex, can produce orders-of-magnitude rate enhancement, e.g., by relaxing orientational restraints between the binding partners^{6, 10} or by long-range attraction.²

Huang and Liu⁴¹ assessed the flycasting concept within a Go-like coarse-grained model for the pKID-KIX system. The strength of interactions within the pKID molecule was varied to tune its flexibility. Langevin dynamics simulations were carried out to produce thermodynamic and kinetic information on the binding process. These simulations showed that, not surprisingly, the distance at which pKID first becomes engaged with KIX increases with increasing flexibility of pKID. However, the rate constant for forming such an initial complex actually decreases modestly with increasing flexibility of pKID, due to the decrease in diffusion constant (or equivalently, the increase in hydrodynamic radius). On the other hand, the energy barrier separating the initial complex and the native complex decreases with increasing flexibility of pKID, and correspondingly, from the initial complex, the commitment to forming the native complex, as opposed to dissociating, increases. As a result the overall binding rate constant is higher (by 2.5-fold) for a flexible pKID than for a rigid pKID. The rate enhancement due to molecule flexibility is again modest, perhaps due to the native-centric nature of the Go model used in the simulations.

A toy model for IDPs consists of two folded domains connected by a linker (Fig. 2). Binding will start with one domain docking to its cognate sub-site, followed by pseudo intramolecular search of the second domain for the latter’s cognate sub-site. The overall process can be described by the kinetic scheme

$$\text{A}+\text{B}\underset{k_{\text{d}1}}{\overset{k_{\text{a}1}}{\rightleftarrows }}\text{A}·\text{B}\underset{k_{\text{d}2}^{\text{i}}}{\overset{k_{\text{a}2}^{\text{i}}}{\rightleftarrows }}\text{C}$$ (3)

where A and B represent the IDP and the target, respectively; A·B is the intermediate with the first domain bound but the second domain is still unbound; and C is the native complex with both domains bound. Provided that the intermediate does not accumulate significantly, the overall association rate constant is

$$k_{\text{a}}=\frac{k_{\text{a}1}{k}_{\text{a}2}^{\text{i}}}{k_{\text{d}1}+k_{\text{a}2}^{\text{i}}}$$ (4)

Note that the rate constant, k_a1, for binding the first domain is always an upper bound of the overall rate constant k_a. This upper bound is approached, i.e., the binding of the first domain becomes rate-limiting, when the dissociation rate constant, k_d1, for the first domain from its sub-site is much lower than the intramolecular association rate constant, $k_{\text{a}2}^{\text{i}}$, for the second domain. The latter can be related to the bimolecular association rate constant k_a2 for the isolated second domain binding to the target via⁴

$$k_{\text{a}2}^{\text{i}}=k_{\text{a}2}p(\mathbf{d})$$ (5)

where p(d) gives the effective concentration for intramolecular binding [Eq. (2)].

A competing pathway will have the order of binding the two domains reversed. If both pathways contribute to the binding, then the overall association rate constant will be the sum of the rate constants of the two pathways. It is possible that the overall k_a is dominated by the contribution from one pathway. In any event, the toy model described here suggests that the rate constant for binding an IDP can be calculated by treating the IDP as folded segments connected by linkers. Development along this line will be further discussed below.

4.2 Energy landscape near the native complex

A number of recent studies focused on the late stage of the binding process, by calculating the free energy surface in the region where internal degrees of freedom of the IDP are coupled with the separation from the target. For example, using a Go-like coarse-grained model for the pKID-KIX system, Turjanski et al.⁴² carried out Langevin dynamics simulations to obtain the free energy surface as a function of the native contacts formed by the αA and αB helices of pKID with KIX. They identified a major intermediate, with αB bound but αA unbound. This intermediate is similar to the late intermediate detected by Sugase et al.³⁰ using ¹⁵N relaxation dispersion (see Sect. 3.3). Turjanski et al. pointed out that it is not surprising that the pathway involving initial binding of αB dominates the pKID-KIX binding process, given that αB makes the dominant contribution to the native contacts between pKID and KIX (see Fig. 1c).

Chen⁴³ carried out all-atom molecular dynamics simulations of a bimolecular system, comprised of the C-terminal peptide (residues 376-387) of the tumor repressor p53 and monomeric S110B(ββ), in implicit solvent. In these simulations the separation between the centers of mass of the two molecules was constrained to various values. The simulations suggested that the p53 peptide first contacts S110B(ββ) while unfolded; both the N-and C-termini can form the initial contact, and long-range electrostatic interactions may play a role in the initial contact formation. No experimental data on the binding pathway seemed available, since no comparison was made.

Wang et al.⁴⁴ carried out simulations of a Go-like coarse-grained model for the WASP GBD-Cdc42 system, with constrained separation between centers of mass. An intermediate displayed in a figure of this study appears to have both the N-terminus and the C-terminus of WASP GBD contacting Cdc42. This contradicts the experimental data of Hemsath et al.³¹ indicating the N-terminus alone in the initial contact (see Sect. 3.4). Wang et al.⁴⁵ also carried out a similar study for the binding of a peptide (residues 2-32 of a 68-residue inihibitor called IA₃) to the yeast aspartic proteinase A (YPrA). IA₃ is disordered in the unbound state and its residues 2-32 fold into a long helix in the bound state.⁴⁶ The simulations showed that the peptide folded into the helical conformation only after extensive (nonnative) contacts with YPrA were made. An earlier experimental study⁴⁷ using temperature jump detected a fast process (with ~80 ns relaxation time), which was interpreted as folding of IA₃ while bound to YPrA. While there was general agreement in this regard, neither the simulations nor the experiment suggested a specific pathway for the coupled binding and folding.

4.3 Segment-based calculation of k_a

None of the computational studies discussed above was designed to make k_a predictions that can be directly compared against experimental values. Given the significant successes in predicting the association rate constants of ordered proteins,^{2, 5} we applied the TransComp method developed for ordered proteins to segments of hirudin in order to predict its binding rate constant with thrombin.⁶ This was based on the observation that IDPs usually adopt extended conformations in the bound state, and it is likely that the different segments of an IDP sequentially bind to respective sub-sites. TransComp would predict the binding rate constant of the initial segment, which as noted above provides an upper bound to the overall association rate constant of the IDP. If the subsequent intramolecular binding is fast, such that the initial binding becomes rate-limiting, the TransComp result can actually be taken as the overall association rate constant. The intramolecular step is facilitated by the interactions between the IDP and the target, and thus has a good likelihood of being fast. In the case of pKID binding to KIX, the rate constant for the transition from a late intermediate to the native complex³⁰ points to this scenario (see Sect. 3.3). The interpretation of the experimental data for the binding of IA₃ to YPrA⁴⁷ is also consistent with scenario.

TransComp is based on the idea that relative translational and diffusional diffusion of the two binding molecules brings them to the rim of the bound-state energy well; the rim defines the transient complex. An automated procedure identifies the transient complex by mapping the energy surface in the six-dimensional space of relative translation and rotation, after freezing the binding molecules in their respective native conformations. The rate constant is then calculated as

$$k_{\text{a}}=k_{\text{a}0}exp(-\mathrm{\Delta }{G}_{\text{el}}^{\ast }/k_{\text{B}}T)$$ (6)

where k_a0 is the basal rate constant, i.e., the rate constant for reaching the transient complex by unbiased random diffusion; and the Boltzmann factor, in which $\mathrm{\Delta }{G}_{\text{el}}^{\ast }$ is the intermolecular electrostatic interaction energy in the transient complex, captures the biasing effect of long-range electrostatic interactions.

The application of TransComp to the initial binding of a segment of an IDP to its sub-site on the target raises two technical issues. The first is that TransComp treats both binding molecules as rigid, whereas the IDP segment of course undergoes a disorder-to-order transition. If the disorder-to-order transition of the segment is fast on the timescale of the diffusional approach to the transient complex, then this transition does not slow down the binding⁴⁸ and hence the rigid treatment is justified.

The second issue is how to identify the first segment that binds to the target. This can be addressed by doing TranComp calculations for different segments of the IDP and proposing the segment with the highest rate constant as the first binding segment. As noted above, competing pathways starting from the binding of different segments may coexist, but the pathway with the highest rate constant will dominate the binding process.

5. Dock-and-coalesce: a unifying mechanism?

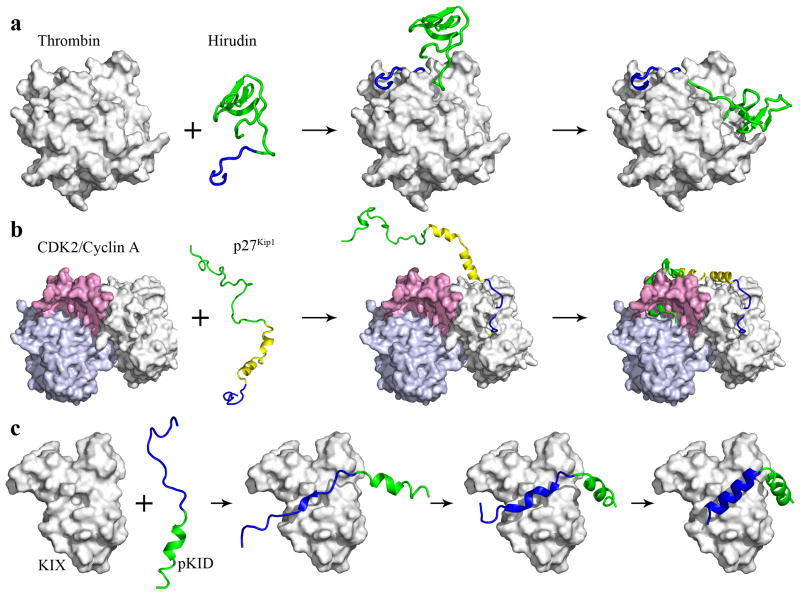
As mentioned, the segment-based TransComp approach was applied to the binding of hirudin to thrombin.⁶ The predicted binding rate constant is in quantitative agreement with experimental data,³³ and the calculation suggests a dock-and-coalesce binding mechanism: the binding starts with the docking of the C-terminal tail of hirudin to the fibrinogen recognition site; subsequently the N-terminal domain coalsces around the active site. Dock-and-coalesce is a recurring feature in the binding of other IDPs as well (Fig. 3).

Fig. 3.

The dock-and-coalesce mechanism for the binding of IDPs to their structured targets. The docking step is followed by one or more coalescing steps. The coalescing steps are fast for (a) hirudin binding to thrombin and (b) p27^Kip1 N-terminal region binding to the cyclin A-CDK2 complex. In (c) pKID binding to KIX, the second coalescing step is fast but it is unclear whether the first coalescing step is also fast.

5.1 Hirudin

Applying TransComp to the binding of the C-terminal tail (residues 54-65) to the fibrinogen recognition site of thrombin, we obtained a rate constant of 2.5 × 10⁸ M⁻¹s⁻¹ at an ionic strength of 0.125 M. This is ~2000-fold higher than the rate constant, 1.2 × 10⁵ M⁻¹s⁻¹, calculated for binding of the N-terminal domain (residues 1-46) binding to the active site of thrombin. The rate constant for binding the C-terminal tail is in close agreement with the experimental value, 1.3 × 10⁸ M⁻¹s⁻¹, for binding the entire hirudin.³³ Our calculations and the experimental data thus strongly indicate that the dominant pathway for hirudin binding consists of docking of the C-terminal tail to the fibrinogen recognition site of thrombin and subsequent fast coalescing of the N-terminal domain around the active site (Fig. 3a). The calculated rate constant for binding the N-terminal domain is also in reasonable agreement with the measured value (8.7 × 10⁵ M⁻¹s⁻¹) for binding the isolated N-terminal domain.¹⁶

TransComp decomposes the association rate constant into the basal rate constant k_a0, which is determined by the orientational restraints between the binding molecules, as reflected by the shape of the binding interface; and the electrostatic contribution, as captured by the electrostatic interaction energy $\mathrm{\Delta }{G}_{\text{el}}^{\ast }$. The decomposition shows that the high k_a for binding the C-terminal tail is due to strong electrostatic attraction. The basal rate constant is at 3.9 × 10⁵ M⁻¹s⁻¹, and the electrostatic interaction energy is −3.9 kcal/mol, which corresponds to a 650-fold rate enhancement. In comparison, for binding the N-terminal domain, the basal rate constant is at 0.7 × 10⁵ M⁻¹s⁻¹, and the electrostatic interaction energy, −0.3 kcal/mol, is minuscule.

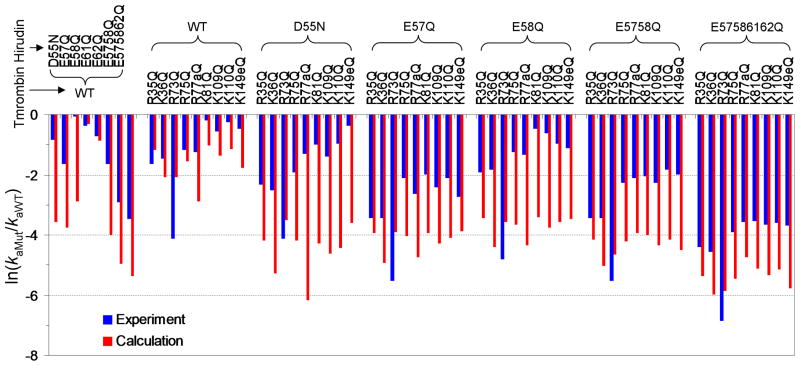
As further support of the dock-and-coalesce mechanism emerging from the segment-based TransComp approach, here we carry out k_a calculations for 62 hirudin and thrombin mutants previously studied experimentally by Stone et al.³³ and Myles et al.³⁵ In these mutants, either acidic residues in the C-terminal tail of hiruin, or basic residues around the fibrinogen recognition site of thrombin, or both are neutralized. For most of these mutants, the resulting reductions in k_a are well reproduced by the TransComp calculations for docking the C-terminal tail of hirudin (Fig. 4). However, the calculations have a tendency of overestimating the reductions in k_a (in particular, for cases involving the thrombin R77aQ mutation). A number of factors, including reorganization of charged sidechains and repositioning of the transient complex for the docking step, could mitigate some of the effects of the charge-neutralization mutations on k_a.

Fig. 4.

Comparison of calculated and experimental results for the changes in hirudin-thrombin association rate constants for 62 mutants. The experimental data are from Stone et al.³² and Myles et al.³⁴ The calculated results are from applying TransComp to the binding of the hirudin C-terminal fragment (residues 54-65) to thrombin.

5.2 p27^Kip1 N-terminal region

Encouraged by the success in establishing the binding mechanism of hirudin and in predicting the binding rate constant, we now extend the segment-based TransComp approach to the binding of the p27^Kip1 N-terminal region to the cyclin A-CDK2 complex. The predicted rate constant for binding the rigid coil (residues 25-37) is at 12 × 10⁶ M⁻¹s⁻¹ at an ionic strength of 0.3 M., when the target is either the cyclin A-CDK2 complex or cyclin A alone. This result only slightly overestimates the experimental values for the entire p27^Kip1 N-terminal region binding to the two targets (~2 × 10⁶ M⁻¹s⁻¹).²⁹ The calculation implicates significant electrostatic rate enhancement; the predicted k_a increases by 9-fold when the ionic strength is lowered to 0.05 M and decreases by 2-fold when the ionic strength is raised to 0.6 M. On the other hand, TransComp calculation for binding the α-helix/β-strand/3₁₀ helix (residues 60-93) to either the cyclin A-CDK2 complex or CDK2 alone failed, meaning that the binding cannot proceed with the molecules treated as rigid. Indeed, rigid docking of the α-helix/β-strand/3₁₀ helix to the binding site on CDK2 encounters severe steric clashes; that significant conformational rearrangements are necessary for the binding of the α-helix/β-strand/3₁₀ helix may be the reason of the low binding rate constant (~5 × 10³ M⁻¹s⁻¹).²⁹

Combining these segment-based TransComp calculations with the experimental results of Lacy et al.²⁹ leads to the dominant pathway for the binding of the p27^Kip1 N-terminal region to the cyclin A-CDK2 complex (Fig. 3b). The binding starts with the docking of the rigid coil (residues 25-37) to cyclin A; subsequently the linker helix latches across the cyclin A-CDK2 complex and the α-helix/β-strand/3₁₀ helix coalesce around the β-sheet of the CDK2 N-terminal lobe.

5.3 pKID

The NMR experiments of Sugase et al.³⁰ identified an early intermediate in which the αB sequence, presumably largely unfolded, is engaged with KIX (Fig. 3c). This then evolves into a late intermediate in which the αB sequence becomes more folded and the αA sequence is nearly fully folded. Finally the late intermediate rapidly converts to the native complex. This binding pathway is in line with the dock-and-coalesce model.

5.4 Other IDPs

We have applied the segment-based TransComp approach to the binding of several other IDPs, including WASP GBD binding to Cdc42 (X. Pang and H.-X. Zhou to be published), and WASP actin regulatory region binding to actin (X. Pang, K. H. Zhou, S. Qin, and H.-X. Zhou, to be published). The calculations all suggest a dock-and-coalesce mechanism and yield binding rate constants in agreement with experimental values.

6. Rate constant of the coalescing step: influence of linker length and flexibility

Our rate calculations following the dock-and-coalesce mechanism have so far relied on the assumption that the docking step is rate-limiting, so that the precise value of the rate constant of the coalescing step does not affect the overall binding rate constant. In some cases the coalescing step may be slowed sufficiently to make it rate-limiting instead. To gain a basic understanding of the coalescing step, here we idealize the coalescing segment as a spherical domain connected to the docking segment by a linker modeled as a worm-like chain. The docking segment is already bound to its sub-site; the coalescing segment, under the restraint of the linker, searches for its sub-site, which is a circular patch on an infinite reflecting plane. We focus on the question of how the physical properties of the linker, i.e., contour length and chain flexibility, affect the rate constant, $k_{\text{a}2}^{\text{i}}$, of the coalescing step.

We find $k_{\text{a}2}^{\text{i}}$ in two ways. The first is by using Eq. (5). The bimolecular rate constant k_a2 in that expression, for the binding of the isolated coalescing segment, in our idealized model is⁴⁹

$$\frac{1}{k_{\text{a}2}}=\frac{1}{\pi a^2\kappa }+\frac{1}{4Da}$$ (7)

where a is the radius of the circular binding site, κ is the reactivity at the binding site, and D is the diffusion constant of coalescing segment. The second factor in Eq. (5) is the probability density for the linker end-to-end vector r, when r is set to the displacement vector from the attachment point on the docking segment to the center of the binding site for the coalescing segment. Let the magnitude of this displacment vector be d. In addition to d, the contour length (l_c) and the persistence length (l_p) of the linker affect the value of the probability density.

The second way of finding $k_{\text{a}2}^{\text{i}}$ is by Brownian dynamics simulations of the intramolecular binding of the coalescing segment. The restraint of the coalescing segment by the linker is equivalent to an effective potential

$$U_{\text{eff}}(\mathbf{r})=-k_{\text{B}}\mathit{T}lnp(\mathbf{r})$$ (8)

We calculate $k_{\text{a}2}^{\text{i}}$ as the inverse of the mean first passage time to react (with rate constant γ) in a “reaction” region (cylinder with very small height ε; κ = γε) over the binding site. The initial positions of the coalescing segment are distributed in the space outside the reaction region according to p(r). Each trajectory is propagated until reaction occurs; the total length of the trajectory is the first passage time. This algorithm for calculating the intramolecular binding rate constant is adapted from a previous algorithm for calculating bimolecular binding rate constants.⁵⁰ Details on treating reaction in the reaction region and the reflecting boundaries can also be found in that work.

We fix κ at 10D/a and d at 5a, and vary l_c and l_p. Fig. 5a displays the inverse of $k_{\text{a}2}^{\text{i}}$, in units of D/a², as a function of the contour length l_c when the persistence length is fixed at l_p/a = 1.2. There is good agreement between the results calculated according to Eq. (5) and those obtained from Brownian dynamics simulations, except in the limit l_c → d. [Eq. (5) is valid when p(r) is smooth around r = d; however, p(r) always has considerable variation around r = l_c. So as l_c → d Eq. (5) is no longer valid.] Note that $k_{\text{a}2}^{\text{i}}$ has a maximum at l_c/a ~ 8, which can be attributed to the fact that there is an optimal contour length in order to span a given end-to-end distance. A very short linker has to be stretched to nearly a straight line in order to span the distance, whereas a very long linker has to curl up to bring its ends together; both of these have low probability.

Fig. 5.

Effects of (a) linker length and (b) linker flexibility on the rate constant of the coalescing step. In (a), l_p/a = 1.2; in (b), l_c/a = 8. The theory curves are from using Eq. (5). For the simulations, the height ε of the reaction region is set to 0.01a and the rate constant γ is chosen to make κ = γε = 10D/a. p(r) is calculated from 500,000 worm-like chain conformations, each generated as a freely rotating chain with a bond length approaching zero and a bond angle approaching 180°. p(r) and the derivative of lnp(r) with respect to r at 100 even intervals in 0 < r < l_c are stored. Each simulated $k_{\text{a}2}^{\text{i}}$ value is by averaging the first passage times of 5,000 trajectories.

Fig. 5b displays $k_{\text{a}2}^{\text{i}}$ as a function of the persistence length l_p for a fixed contour length l_c/a = 8. Eq. (5) is seen to work well, except for large l_p/d. A $k_{\text{a}2}^{\text{i}}$ maximum is again present, occurring at l_p/a ~ 1.5. The results of Fig. 5 thus show that, for each l_p, there is an l_c at which $k_{\text{a}2}^{\text{i}}$ is maximal; conversely, for each l_c, there is an l_p at which $k_{\text{a}2}^{\text{i}}$is maximal. The implication is that IDPs can vary linker length and flexibility to tune their binding rate constants.

There is experimental evidence for the influence of both linker length and linker flexibility on intramolecular binding rates. When designing chimeras of dipetalogastin II and hirudin as thrombin inhibitors, Lepez and Nowak³⁹ introduced a five-glycine linker. When this linker sequence was eliminated (so that the dipetalogastin II and hirudin fragments were directly connected), the overall binding rate constant was reduced by 60-fold. The reduction can be attributed to a slowing down of the coalescing step, caused in part by an overly tight connection between the dipetalogastin II and hirudin fragments.

In the case of the p27^Kip1 N-terminal region binding to the cyclin A-CDK2 complex, Bienkiewicz et al.¹⁷ found that stabilizing the linker helix by alanine mutations slowed down the formation of the inhibited ternary complex. We interpret this observation as indicating that optimal binding requires a certain degree of flexibility in the linker helix; rigidifying the linker helix can slow down the intramolecular rate and hence the overall binding rate constant.

7. Concluding remarks

Recent years have seen significant progress in understanding the mechanism governing the binding of folded proteins to their macromolecular targets and in predicting their binding rate constants.^{2, 5} In contrast, our understanding on the binding kinetics of intrinsically disordered proteins to their targets is far from complete. The problem is receiving increasing attention, both experimentally and computationally. Of obvious interest is how the molecular flexibility inherent in IDPs affects binding mechanisms and binding rates.

Experimental and computational studies have now laid the groundwork for understanding the binding kinetics of IDPs. It seems clear that, at least for the many IDPs that adopt extended conformations on their targets, they gain the structures after engagement with their targets. Interactions with the targets facilitate the folding of the IDPs. The initial contact of an IDP with the target is usually formed by just a segment, not the entire IDP. The docking of one segment to its sub-site followed by coalescing of other segments around the corresponding sub-sites emerges as a recurring feature in the binding of IDPs.

The observed rate constants of IDP binding show that intrinsic disorder does not boost rate constants beyond what can be achieved by ordered proteins. Instead, intrinsic disorder is a very effective way to avoid excessively low rate constants that would result from severe orientational restraints in aligning IDPs to the targets to form extended interaction surfaces.¹⁰ For both disordered and ordered proteins, strong electrostatic attraction with their targets can enhance the binding rate constants by several orders of magnitude.^{2, 6, 51}

There are now tremendous opportunities in narrowing the gap in our understanding of IDPs relative to ordered proteins with regard to binding kinetics. NMR techniques such as HSQC titration and relaxation dispersion, along with traditional mutation and deletion studies, provide probes for binding mechanisms. On the computational side, the dock-and-coalesce model forms the basis for identifying binding pathways and quantitative calculation of binding rate constants. Mapping of free energy surfaces at the late stage of binding processes will continue to be useful for elucidating binding mechanisms. It can be anticipated that the binding of many more IDPs will be subjected to detailed kinetic interrogation.