Ratcheting up protein translocation with anthrax toxin

Abstract

Energy-consuming nanomachines catalyze the directed movement of biopolymers in the cell. They are found both dissolved in the aqueous cytosol as well as embedded in lipid bilayers. Inquiries into the molecular mechanism of nanomachine-catalyzed biopolymer transport have revealed that these machines are equipped with molecular parts, including adjustable clamps, levers, and adaptors, which interact favorably with substrate polypeptides. Biological nanomachines that catalyze protein transport, known as translocases, often require that their substrate proteins unfold before translocation. An unstructured protein chain is likely entropically challenging to bind, push, or pull in a directional manner, especially in a way that produces an unfolding force. A number of ingenious solutions to this problem are now evident in the anthrax toxin system, a model used to study protein translocation. Here we highlight molecular ratchets and current research on anthrax toxin translocation. A picture is emerging of proton-gradient-driven anthrax toxin translocation, and its associated ratchet mechanism likely applies broadly to other systems. We suggest a cyclical thermodynamic order-to-disorder mechanism (akin to a heat-engine cycle) is central to underlying protein translocation: peptide substrates nonspecifically bind to molecular clamps, which possess adjustable affinities; polypeptide substrates compress into helical structures; these clamps undergo proton-gated switching; and the substrate subsequently expands regaining its unfolded state conformational entropy upon translocation.

Introduction

Proteins, organelles, metabolites, and various cargos are continuously transported into, out of, and around cellular compartments. Generally, these movements are catalyzed by macromolecular machines, which consume energy and directionally translocate along specific polymeric tracks. These polymer tracks come in various forms, including microtubules, nucleic acids, and polypeptides. While it is consistently observed that chemical energy is consumed to do mechanical work, the underlying molecular mechanisms of energy transduction and directed movement at the nanoscale level are poorly understood and remain intense areas of research.^1–7

Biological processes occur on the nanoscale under ambient chemical and temperature conditions. Scientists have long mused about the ability of nanoscopic power devices to harness energy from their environments. The most famous thermodynamic trick of the 19th century is credited to Maxwell, who proposed in Theory of Heat how energy is statistically distributed in a population of gas molecules.⁸ When Maxwell began to imagine the molecular world, he expressed a most remarkable “contradiction” by the conclusion of his manuscript, which he subtitled, “Limitation of the Second Law of Thermodynamics.” To illustrate, he proposed a Gedankenexperiment (thought experiment) [Fig. 1(A)] involving a vessel divided into two sections, A and B. Each side contains a similar proportion of gas molecules with a similar distribution of velocities and temperature. The division between the two sections contains a hole with a trap door operated by a “being” who only permits the movement of the faster molecules from A to B, and concurrently the movement of slower molecules from B to A. The being, coined “Maxwell's demon” by Lord Kelvin⁹ would “thus, without expenditure of work, raise the temperature of B and lower that of A, in contradiction to the Second Law of Thermodynamics.”⁸ Later, it was reasoned that because the demon would need precise information on each gas molecule to sort them by velocity, the entropy change of the system and surroundings upon creating a thermal gradient would not be less than zero. Obtaining and consuming that information came at a price, and Maxwell's Gedankenexperiment, in fact, obeyed the Second Law of Thermodynamics. The device is, therefore, an information-powered heat pump.

Figure 1.

Real and imagined heat engines and pumps. (A) Maxwell's demon is an example of an information-powered heat pump. Left, two compartments are divided by a partition with a trap door operated by the demon. Hot (red) and cold (blue) gas atoms are shown evenly divided into each compartment. Middle and right, in order to obey the second law, the demon must consume stored information (“101101011…”) on the individual atoms' velocities and positions, to properly sort the hot ones to the right and the cool ones to the left. (B) Thermodynamic cycle of Sullivan's drinking bird exemplifies a basic heat engine. Inertial movements of the bird are linked to the establishment and dissipation of ΔT gradients across the glass vessel body, which contains MeCl₂ (purple fluid). Left, when the bird dips its beak into the shot glass, MeCl₂ leaks from the opposite end of the tube into the reservoir, acting to ratchet the bird upward. Middle, evaporative cooling leads to MeCl₂ condensation. Right, MeCl₂ in the reservoir travels up the neck, shifting the center of mass. The bird lurches forward to complete the thermodynamic cycle.

The drinking bird novelty device [Fig. 1(B)] patented by Sullivan in 1946 is now a famous staple demonstration in science classrooms all over the world.¹⁰ Deliberately flirting with one's disbelief in perpetual-motion machines, the happy-go-lucky device teeters relentlessly, dipping its beak into a glass of water. At first glance, one may think the bird is a “free” energy device. Of course, there is a man behind the curtain: the drinking bird, like a Stirling heat engine, functions by means of a required thermal gradient (ΔT). [Evaporative cooling on the wetted bird beak creates the ΔT; see Fig. 1(B) for details.] As noted by Carnot, “the motive power undoubtedly increases with difference in temperature between the warm and cold bodies.”¹¹ Thus a nonzero ΔT is the driving force that powers the heat engine to produce spontaneous motion.

Nanomachines as Ratchets

Further adoption of Maxwell's demon led Smoluchowski¹² and later Feynman¹³ to propose a nanoscale heat-engine device in related Gedankenexperiments. Imagine a system with two thermal reservoirs; across the two reservoirs is a drive shaft containing a pulley, a rope, and a weight. Gas molecules in the hotter reservoir transfer random thermal energy to large vanes, albeit the applied forces are random in direction. An anisotropic sawtooth-patterned ratchet wheel resides within the cooler reservoir. The ratchet wheel engages a pawl that effectively biases rotation of the wheel in one direction. Therefore, while Brownian motion of particles contained within the hotter reservoir pushes the vaned wheel randomly in either direction, the pawl-and-ratchet device in the colder reservoir rectifies these random fluctuations, biasing net motion in the allowed direction; and hence the pulley and rope turn, lifting the weight.

The ΔT energy gradient across the reservoirs is an essential feature of the ratcheting nanodevice.¹³ If stochastic motion within the pawl in the colder reservoir were on the order of that on the hotter vaned-wheel reservoir (i.e., the condition of thermal equilibrium), then the system could not possibly do useful work, and the weight could not be lifted. Thus the Smoluchowski-Feynman ratchet is a nanomechanical heat engine (analogous to Sullivan's drinking bird). In addition to a nonzero thermal gradient, the machine operates on the principle that the mean displacement of random motion is on the order of the period, L, of the spatially periodic potential function during the time in which the barrier is switched to its minimized state [Fig. 2(A)]. A diode represents an analogous ratchet-like component for an electrical circuit. A four-diode bridge device can rectify an oscillating electrical current produced by a magnet displaced at random through a coil of wire; however, the diode bridge cannot use Nyquist noise (random equilibrium thermal fluctuations of electrons in the electrical circuit) to do work. Thus the pawl in Feynman's ratchet, the one-way valve in Smoluchowski's ratchet, and the demon-operated trap door in Maxwell's Gedankenexperiment can be thought of as mechanical diodes; however, each is only capable of using nonequilibrium energy fluctuations, energy gradients (e.g. ΔT), or stores of ordered information to do useful work.

Figure 2.

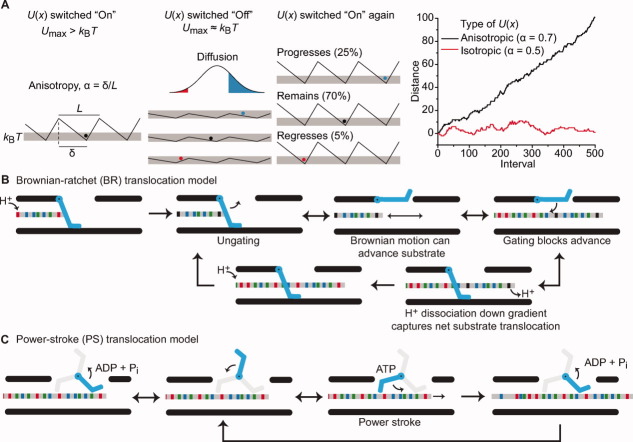
Molecular mechanisms of nanomachines. (A) Flashing BR model. Far left, a saw-tooth potential function, U(x), with respect to distance, x, is depicted, where the positional anisotropy, α, of U(x) is related to the distance between the maximum and minimum, δ, of each period, L, such that α = δ/L. When U(x) is switched on, the particle is trapped in a well, since U_max > k_BT. Middle left, when the potential is switched off, the particles diffuse freely according to Einstein's relation. (middle right) When U(x) is switched back on, one interval is completed and the particle is trapped again. Thus the probability of progressing is greater than regressing. Far right, a Monte Carlo simulation of the flashing BR model plotting x versus the number of switching intervals for an anisotropic (black, α = 0.7) and an isotropic (red, α = 0.5) U(x). (B) A ΔpH-dependent BR mechanism for protein translocation. The substrate polypeptide chain is depicted as a simplistic gray rod with different functional groups colored as follows acidic (red), basic (blue), and nonpolar (green). A gate (cyan) electrostatically excludes anionic charges on deprotonated acidic residues. In this cyclical mechanism, substrate acidic residues are protonated (black); the gate opens, allowing for Brownian motion to take place. The peptide can only advance up to the point where deprotonated acidic residues enter the channel. Closing of the gate traps the peptide in the channel, as the dissipation of H⁺ ions down the gradient upon deprotonation prevents retrograde movements. Further protonation then allows the cycle to repeat. (C) An ATP-dependent PS mechanism for protein translocation. The substrate chain is colored as in (B) while in this case, the gate acts more like a paddle with active (cyan) and inactive (gray) states. In the ADP-bound state, the paddle has low affinity for peptide; the paddle exchanges ADP for ATP, and subsequent ATP hydrolysis triggers a conformational change, allowing the paddle to push the polypeptide chain forward (power stroke). Cycles of ADP release and ATP hydrolysis allow the mechanism to continue.

We can simulate net motion in the Smoluchowski-Feynman ratchet using a spatially anisotropic potential but not an isotropic one [Fig. 2(A)]. Here we depict the ratchet wheel as a linearized repeating anisotropic potential and the pawl as a movable particle. To keep the model simple, the pawl (particle) can move relative to a stationary ratchet wheel in effect. When the potential is momentarily flashed off, the ratchet particle can freely diffuse. In principle, these energy barriers can be modulated on or off by any number of means, as long as the barriers are approximately k_BT, when switched off. (T is the temperature, and k_B is the Boltzmann constant.) When the energy well is offset and anisotropic, the particle is more likely to cross a closer peak, rather than a more distant peak. When the potential is flashed on, the particle will have a significantly higher probability of progressing rather than regressing. Directional flux is, therefore, supported by anisotropy. A perfectly symmetrical energy potential cannot support net movement in any particular direction [Fig. 2(A)]. Energy input into such a system is required in order to flash, rock, or alter the potential function. Of course, the energy input may also be used to more directly push or drive the particle (via a power stroke). However, because of the significance of diffusion and random motion at the molecular level, the ratchet-like property of the flashing asymmetrical energy potential is critical to net directional translocation. Therefore, a minimal structural feature for net motion is a physically periodic substrate and a modulated clamping interaction with the nanomachine.

Because ΔT at the required nanometer length scale is impossible to achieve inside of cells, biological nanomachines must use other kinds of energy gradients to do work. Hence the interconversion of chemical- or electrical-potential energy to mechanical kinetic energy is ubiquitous in biological molecular motors, switches, pumps, and transporters. How do nature's molecular machines perform their necessary work? As we learned from Sullivan's drinking bird [Fig. 1(B)], defining the problem facing a nanomechanical system, its environment, parts, and energy source are essential to elucidating its mechanism.

The physical environment of the cell

The environment of the cell is extraordinarily violent, where molecular movements carried out by nanomachines would be akin to sailing in a hurricane. Robert Brown initially observed the chaotic motion of pollen grains in solution; and these motions are referred to as Brownian motion. For the erratic path an individual pollen grain travels, its Brownian motion emerges statistically from the unequal number of collisions between the larger particle with many more numerous solvent molecules (having a large distribution of velocities).¹⁴ Einstein described the average diffusion of particles of radius, r, in a solution of viscosity, η, as the mean square displacement, <Δx²>, where <Δx²> = 2Dt: t is the time; the diffusion constant, D, is k_BT/β; and β, the frictional coefficient, is 6πηr.¹⁵ Thus given equal thermal energy inputs, larger objects diffuse slower than smaller ones. While macroscopic forces, F, are largely inertial and depend heavily upon mass, m, and acceleration, a, (i.e. F = ma), Langevin noted that microscopic Brownian particles experience a noisy, fluctuating force, ζ, which he called the “complementary force.”^{16, 17} The fluctuating force arises from a barrage of solvent molecules colliding with the Brownian particle, and it allows an instantaneous force to be assessed for a single particle. Langevin hypothesized forces are related to velocity, v, the frictional coefficient, and fluctuating force by F = −βv + ζ. For nanomachines, forces scale to surface area and not volume. For any single molecule, ζ can be quite significant, hence the random, unpredictable nature of any individual Brownian walk.

The behavior of polymers in solution is especially relevant for nanomachines that unfold and translocate proteins. From statistical mechanics, an unstructured protein has many more degrees of freedom than a simple, rigid Brownian particle. A peptide backbone in the unfolded state can be assumed to have 3 degrees of freedom per amino acid, considering relevant ϕ/ψ-angle conformations. The multiplicity, W, of this peptide system, given as W = 3^N, translates into a configurational entropy, S, of Nk_B ln 3. Therefore, a polypeptide with N = 50 residues has a thermal energy of ∼33 kcal mol⁻¹ (∼140 kJ mol⁻¹). These energies are much more significant for the polymer relative to a simple, rigid Brownian particle, which experiences only three translational degrees of freedom.

Molecular mechanisms of biological nanomachines

Generally, two competing mechanisms describing the functionality of nanoscale molecular machines have been presented¹⁸ [Fig. 2(B,C)]. On one hand, nanomachines falling into the Brownian-ratchet (BR) classification do work by using external energy sources to harness Brownian thermal energy [Fig. 2(B)].^{13, 19–21} A Brownian ratchet on the biological scale is analogous to a Smoluchowski-Feynman ratchet and requires an external gradient as an energy source. Imagine a nanomachine acting on an unfolded polypeptide chain with sites that can be modified to be in permissive and nonpermissive states [Fig 2(B)]. The ratchet can switch between the permissive on and nonpermissive off states through the modification of the substrate, in this case by protonation. Analogously, a gate in the transporter switches to a permissive open or nonpermissive closed state, depending on the protonation state of the polymer. Under the influence of a chemical gradient (e.g. a proton gradient, ΔpH) residues may be more likely to be in a permissive state on one side of the membrane than on the other. Thus translocation can proceed in the direction of nonpermissive modification, since nonpermissively modified substrate will be unable to retrotranslocate. A number of chemical modifications have been suggested to follow such a mechanism. Protonation,^{21, 22} chaperone binding,^{23, 24} glycosylation, disulfide bonding, and conditions that promote protein folding¹⁹ are all capable of biasing movement through a translocase channel.

On the other hand, the power-stroke (PS) classification suggests that molecular machines use external energy sources to directly drive motion without the need for harnessing Brownian thermal fluctuations [Fig. 2(C)].²⁵ The binding of ATP, for example, induces a conformational change in the protein machine that performs useful work such as pulling or pushing a substrate through the translocase. The machine engages with the translocating polypeptide chain via a polypeptide clamp or other active site loop structure. ATP hydrolysis and release of ADP and inorganic phosphate (P_i) allows the machine to return to its original conformation. However, the resetting of the polypeptide clamp or other active-site structure must occur via a different path back to the initial state, else it would essentially undo the work done in the ATP binding step.

The major difference between the BR and PS models is that the latter does not consider Brownian thermal fluctuations (or Langevin's random force, ζ) to be part of the mechanism. However, BR and PS mechanisms should not be held as mutually exclusive models. Instead, these two types of mechanisms may occur at distinct junctures in the transport cycle. For example, the two-headed motor, kinesin, uses an ATP-driven PS to nudge the trailing leg forward; however, this push provided by ATP binding is far too small to drive the leg the 8 nm span between binding sites on the microtubule, and a BR phase is required to bridge the remaining distance by allowing the head to diffuse and seek its next binding site, thus completing the transport cycle.²⁶ Furthermore, as operating on polymers in a cell is akin to sailing in a hurricane, consider two readily available types of machinery for hoisting up a sail: a simple hand crank and a hand crank with a ratchet. Under ideal conditions, the crank driven by a PS may suffice in performing the task. However, under tropical cyclone conditions, a system that includes both a PS-driven crank and a ratchet may become necessary. While extremely windy and diffusive weather likely makes it difficult for the sailor to turn the simple hand crank in the proper direction, the ratchet ensures that substeps of a crank cycle are not lost to diffusive backsliding.

Anthrax Toxin as a Protein Translocation Model System

In this review, we focus on protein pumps or translocases that move proteins within the cell. These nanomachines consume energy in order to disassemble and translocate folded polypeptide substrates. They are found both in solution and in lipid bilayer membranes. The former serve the cell as disaggregases, protein complex disassembly machines, and unfoldases that aid in intracellular protein degradation.^27–29 The latter allow proteins to be transported either across or into lipid bilayers.^{1, 2, 4} The binary A/B bacterial toxins³⁰—including diphtheria, botulinum, and anthrax toxin—are a widely studied class of membrane transport systems, which use their own transport machinery to enter cells.^31–33 These A/B toxins assemble into complexes on cell surfaces and then utilize host cell chemical potentials to unfold and translocate enzymatic factors into the host cell.

Anthrax toxin, the binary A₂B toxin³¹ produced by Bacillus anthracis,^{1, 34} [Fig. 3(A)], represents an attractive model system for probing the molecular mechanism of protein translocation across membrane bilayers for a variety of reasons. First, its three protein components can be expressed recombinantly and studied independently. Second, the protein translocase and the individual steps of substrate translocation can be readily reconstituted from purified proteins and studied using planar bilayer electrophysiology at the ensemble^{21, 22, 38, 49, 50–58} and single-molecule level.^{22, 40, 49, 51, 59} Critical to this electrophysiological approach (also used in other systems^60–67) is the ability to precisely control the driving force and solution conditions on either side of the membrane. Third, for a membrane-protein system, structural studies using X-ray crystallography are tractable, because the translocase also exists in a soluble state.^{38, 40, 42, 68} In this manner, researchers have been able to obtain structural information^{35, 36, 38–40, 42, 68–70} and distinguish possible translocation models using a wide variety of functional assays.^{21, 22, 38, 49–58, 71}

Figure 3.

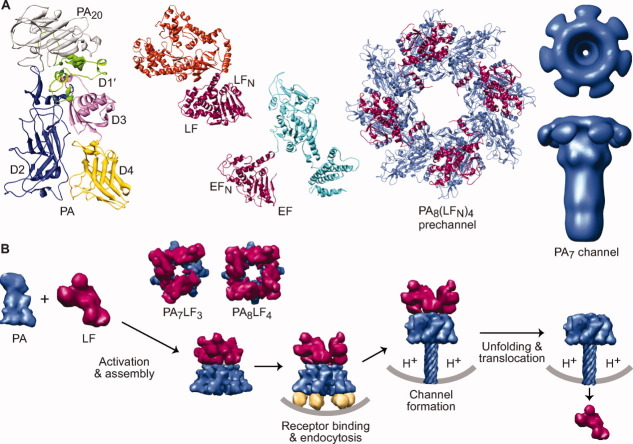
An overview of the anthrax toxin protein translocation system. (A) Components of anthrax toxin (left to right). Ribbons depiction of PA (3TEW³⁵) colored by domain: PA₂₀ (gray), D1′ (green), Ca²⁺ ions (dark green), D2 (blue), D3 (magenta), and D4 (yellow). The enzymes, LF (1J7N³⁶) and EF (1YOV³⁷); their amino-terminal PA binding domains (LF_N and EF_N, respectively) are colored red-violet and their catalytic domains colored orange and cyan, respectively. A representative PA prechannel complex, PA₈(LF_N)₄, (3KWV³⁸); the PA oligomer and LF_N colored denim and red-violet, respectively. Axial view (above) and sideview (below) of a three-dimensional EM reconstruction of the PA₇ channel³⁹ (colored denim) (Prof. Mark Fisher graciously provided the EM density map). (B) Anthrax toxin assembly and transport. PA (denim) is proteolytically nicked and assembles with LF (red-violet) and forms PA₈LF₄ and PA₇LF₃ prechannel complexes^{40, 41} (based on 3KWV³⁸ and 1TZO,⁴² respectively). Prechannel complexes bind cellular receptors (gold; 1T6B⁴³ and 1TZN⁴⁴) triggering endocytosis; acidic pH conditions in the endosome induce PA to form a transmembrane channel^{39, 45, 46} (atomic model 1V36⁴⁷); the pH gradient that develops across the endosomal membrane destabilizes LF,⁴⁸ drives LF unfolding^{22, 49} and translocation^{21, 22} through the PA channel.

The structures of the three anthrax toxin components are known [Fig. 3(A)]. The protective antigen (PA) component, which forms the translocase channel, is secreted as an 83 kDa proprotein.⁶⁸ The other two components that are transported by PA are ∼90 kDa enzymes, lethal factor (LF),³⁶ and edema factor (EF).⁷⁰ In order for the toxin to function, PA must first be proteolytically nicked by a furin-family protease,^{72, 73} releasing an amino-terminal 20 kDa fragment, PA₂₀. The resulting 63 kDa fragment can assemble into an active holotoxin complex comprised of multiple copies of LF and EF bound to a ring-shaped PA oligomer [Fig. 3(B)]. There are two known PA “prechannel” oligomeric architectures, a homoheptamer (PA₇)^{42, 68, 74} and a homooctamer (PA₈).^{38, 40, 75} The assembly and binding interactions between the PA oligomer and its substrates are well characterized.^{38, 76–81} Currently only one crystal structure is known of a prechannel core complex, PA₈(LF_N)₄, where LF_N is the PA-binding domain of LF [Fig. 3(A)].³⁸ These prechannel complexes either assemble on cells by binding a specific protein receptor^{82, 83} or localize to cells after assembling in the plasma.⁷⁵ Internalization and subsequent acidification within the endosomal compartment converts PA prechannels into membrane-embedded channels,^{45, 84, 85} which are strongly cation-selective.⁴⁶

The acidic environment of the endosome is required for the action of the toxin,⁸⁶ and it generates a proton motive force (PMF) comprised of both a chemical potential (ΔpH) and an electrical potential (Δψ) capable of driving LF/EF unfolding^{22, 48, 49} and translocation.^{21, 22, 48, 49, 52} Translocation initiates from the amino terminus of LF,⁸⁷ albeit a cationic unstructured amino terminus is sufficient for initiating translocation.^{38, 88} The ΔpH component of the PMF is sufficient to unfold and translocate proteins.²² Moreover, while either the ΔpH or Δψ is sufficient to translocate both LF_N and the amino-terminal PA binding domain of EF (EF_N) the translocation of the physiological full-length LF and EF substrates requires the ΔpH more so than the Δψ.²¹ The molecular mechanism of ΔpH-driven translocation is believed to be consistent with a charge-state BR model,^{21, 22, 53, 54, 89} where differential protonation of anionic charges in the substrate polypeptide are essential for transport^{21, 22} [Fig. 2(B)]. In support of the charge-state BR model, ΔpH-driven translocation depends upon charged residues^{53, 54} and, more precisely, acidic residues²² in the translocating protein sequence.

PA Channel

Recent reports have provided insights into the structure of the PA translocase both in its soluble prechannel state and its membrane-inserted channel state. Many studies have shown that PA forms PA₇ oligomers, mostly due to the nature of the preparation used.^{42, 68, 74} When PA co-assembles with either of its substrate proteins, PA oligomerization turns out to be much more complex and heterogeneous. Under these conditions, PA forms mixtures of PA₇ and PA₈ oligomers in solution and on cell surfaces.⁴⁰ The PA₈ oligomer can carry a maximum payload of four LF or EF molecules, while the PA₇ oligomer can carry a maximum payload of three substrates [Fig. 3(B)].^{38, 40, 41} Despite a slight increase in the internal diameter of the oligomeric ring and a corresponding increase in the single-channel ion conductance of the PA₈ oligomer relative to the PA₇ oligomer, the change in channel diameter appears to have a very subtle impact on the translocation mechanism.⁴⁰ The PA₈ oligomer, however, has the advantage of increased thermostability relative to the PA₇ oligomer, where the added interdomain contacts and surface burial in PA₈ oligomer provide additional stabilizing contacts.^{40, 75} Thus the more stable PA₈ oligomer is less sensitive to premature channel formation under physiological temperature and pH conditions.⁷⁵ This stability difference, however, is not observed when either PA oligomer is bound to the extracellular domain of its host cell receptor, and the receptor domain effectively stabilizes PA₇ and PA₈ oligomers through a similar mechanism.^{42, 45, 90} A recent study described a molecular mechanism for PA oligomer stoichiometry.³⁵ The interface between PAs domain 2 and domain 4 (D2-D4) controls the relative proportions of the PA₇ and PA₈ complexes that form as PA assembles, and the D4 domain natively adopts pro-PA₇ and a pro-PA₈ conformations in ∼3:1 ratio.³⁵ The octamer has also been exploited as structural tool for crystallographic studies due in part to the architecture's increased thermostability and internal symmetry.^{38, 40}

Using electron microscopy (EM), the structure of the PA₇ channel has been recently imaged [Fig. 3(A)].³⁹ The PA channel is mushroom-shaped and approximately 170 Å tall × 125 Å wide at its maximum dimensions. The wider, cap-shaped part of the structure is about 70 Å long and likely contains the LF/EF binding sites. Beneath the cap is a 100 Å long stem, which is likely a 14-strand β-barrel structure; the stem ultimately inserts into and spans the membrane bilayer.⁶⁹ Earlier electrophysiology studies suggested the stem is an extended β-barrel structure.⁹¹ From basic modeling studies,⁴⁸ the β-barrel stem is likely only able to accommodate structures as wide as an α helix (10–15 Å wide); therefore, LF and EF must unfold during translocation.

The PA translocase channel can be divided into three sections (Fig. 4): the substrate docking surface in the cap (called the α-clamp site), a critical hydrophobic constriction point about one-third of the distance into the translocase (called the ϕ-clamp site), and the highly charged solvophilic β-barrel stem portion, which comprises the bottom two-thirds of the translocase. Interestingly, there appears to be separate polypeptide interaction sites, or clamps, associated with these different points in the PA translocase channel. These clamps also allow the channel to interact with the substrate nonspecifically. We consider the notion of a clamp to more closely resemble a dynamic binding site for polypeptide, where, for example, a clamp site can be modulated from a higher-affinity binding mode to a lower-affinity binding mode. This dynamic is critical to allowing the translocase to both favor unfolding and translocation while preventing tight binding interactions from occurring that would otherwise impede transport. In the following sections, we will summarize these clamp structures and their associated activities.

Figure 4.

Peptide clamps in the PA channel. The PA channel (denim) contains clamping sites (green) and a β-barrel tube with positively (blue) and negatively (red) charged patches. Partially unfolded substrates (red-violet) first bind to the α-clamp site.³⁸ Subsequently, the peptide threads into the ϕ clamp, which is comprised of a ring of F427 residues.⁵² Finally, the substrate polypeptide chain encounters the β-barrel tube,^{91, 92} which may act as a putative charge clamp, attracting cationic sequence and preventing the retrotranslocation of deprotonated acidic residues.

The α clamp

Recently, the structure of PA₈(LF_N)₄ was reported, providing a molecular description of the interaction between the PA oligomer and LF_N.³⁸ LF binds to PA in two distinct subsites: a carboxy-terminal subsite comprised of specific interactions and an unconventional binding cleft formed at the interface of adjacent PA subunits, called the “α clamp.” Interestingly, in the complex, LF_N α1 and β1 unfold from their native conformation and dock into the α-clamp subsite on the surface of the PA₈ oligomer [Figs. 4 and 5(A)]. PA R178 forms contacts with LFs α1 and suggests an electrostatic capping interaction with the negative dipole of the carboxy-terminal end of α1. The interaction has been extensively verified to occur in the prechannel and channel configuration of PA.^{38, 71} Furthermore, the partial unfolding of LF_N upon binding PA is relevant to toxin assembly, as PA prechannels are produced less efficiently when co-assembled with an LF_N construct lacking its α1/β1 structures.³⁸

Figure 5.

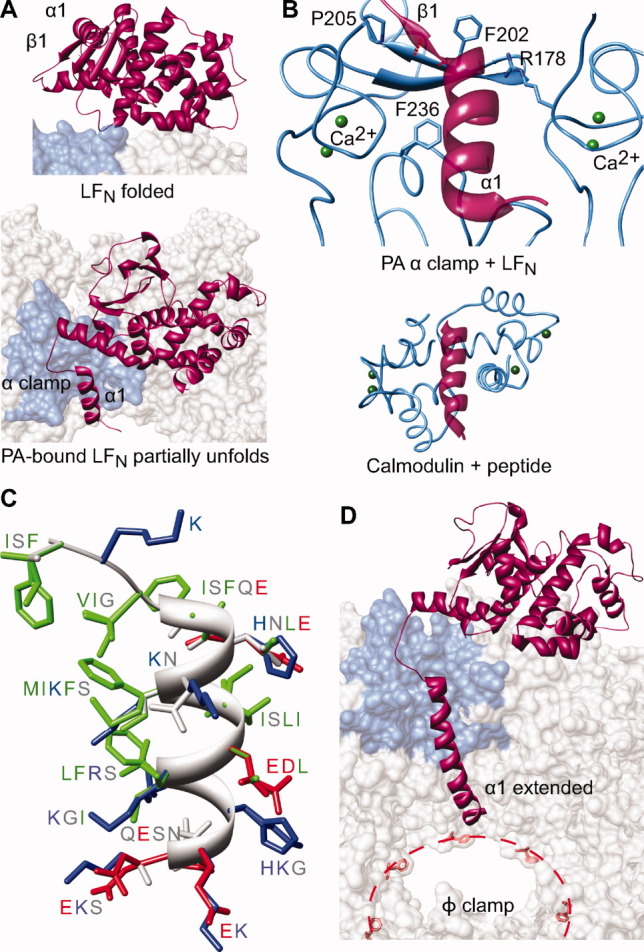
The α clamp. (A) LF_N (red-violet) changes conformations from (top) a folded (1J7N³⁶) to (bottom) a partially unfolded (3KWV³⁸) state, such that LF α1/β1 unfurl and bind into PA's α clamp (denim surface). (B) Top, a detailed view of the α clamp (denim ribbon) in complex with LF's α1 (red-violet ribbon) indicating the structural calcium ions (green) scaffolding the site. Bottom, calmodulin in complex with a peptide helix (1CDM⁹³), where the latter is colored analogously to the α-clamp structure. (C) The α clamp can bind nonspecifically to and translocate a variety of sequences illustrated in a helical structural alignment, which is colored by residue chemistry: basic (blue), acidic (red), polar (gray), and hydrophobic (green).³⁸ (D) Considering the Zimm-Bragg formalism,⁹⁴ the α clamp may act as an α-helix nucleation site. Elongated helical structure can then be fed into the ϕ clamp (red dotted line and F427 residues).

The manner in which the α clamp interacts with LF_N's α1/β1 explains why the site is well equipped to recognize protein sequence in a nonspecific manner.³⁸ Structurally, PA's EF-hand-type twin Ca²⁺-binding sites frame the cleft and provide a structural scaffold consistent with how calmodulin complexes bind to peptide helix substrates [Fig. 5(B)].^{93, 95} In this manner, the residues lining the site coordinate the Ca²⁺ ions, leaving their backbone atoms to form much of the interacting surface with the unfolded structure. Overall, LF_N α1/β1 excludes 1000 Ų of solvent accessible surface area (SASA) on PA. Functional studies show the α-clamp-LF_N interaction is worth ∼2.5 kcal mol⁻¹, and this thermodynamic stability is largely invariant with sequence.³⁸ Interestingly, PA α-clamp residue L203 forms two parallel β sheet-like hydrogen bonds with LF_N β1 residues. The parallel β-sheet interaction is effectively limited to two hydrogen bonds, as PA P205 prevents further β-sheet like bonds from forming. Extensive mutagenesis in LF failed to identify specific side chain interactions in the α clamp. In fact, the α1 sequence in LF can be essentially replaced with other sequences in LF and EF and still maintain essentially wild-type binding and translocation activity [Fig. 5(C)].³⁸ Aromatic residues F202 and F236 were found to be important for full-length LF translocation; however, neither residue plays a role in initial binding to LF_N.³⁸ Thus, the α-clamp site can garner significant nonspecific polypeptide binding activity using a general shape-complementarity binding mechanism, leading to the exciting prospect that helical structure in the substrate represents a key handle for the translocase to grip its substrate during translocation.

The co-crystal structure of PA₈(LF_N)₄ provides a first-time look at the process of protein unfolding on the surface of an unfolding machine [Fig. 5(A)].³⁸ Since more than half of the total binding interface is attributed to recognizing LF_N's unfolded α1/β1 structure, it would appear that substrate unfolding is required to obtain tight binding to the PA oligomer. This unfolding requirement is indeed the case, as the substrate's affinity for channels is reduced 10⁴-fold when unfolding is prohibited by covalently linking α1 to the main body of LF_N with a disulfide bond.³⁸ Furthermore, solution studies probing the degree of LF_N unfolding revealed that the substrate is effectively destabilized by ∼1 kcal mol⁻¹ upon binding to PA. It is still unclear to what degree the protein becomes destabilized on the surface of the PA oligomer; however, decreases in fluorescence anisotropy and inversely proportional increases in atomic displacement parameters (B factors) have been observed in the substrate when it binds the PA oligomer. Thus, while 2.5 kcal mol⁻¹ of binding stabilization is derived from the docking of LF_N into the α clamp, the remaining folded protein is destabilized by at least 1 kcal mol⁻¹. This value potentially represents a destabilization minimum, given the degree of disorder introduced into the body of the protein. The nonspecific binding activity of the α-clamp site is likely critical to the channel's ability to unfold and translocate multidomain substrates, like full-length LF.

The ϕ clamp

The acidified endosomal trafficking route produces conditions that thermodynamically destabilize the substrates, LF and EF, causing them to populate molten-globule intermediates.⁴⁸ To determine how LF and EF are linearized and fully unfolded during translocation, a series of experiments were performed to identify potential active-site residues lining the PA channel.⁵² An interesting conserved residue, F427, was identified in an otherwise hydrophilic PA loop, N⁴²²AQDDFSSTP. As most of the channel-lining residues are hydrophilic and/or anionic,^{89, 91} this aromatic site is unusual in terms of its chemistry and prominence in the interior of the PA channel. Structurally, each PA subunit contributes one F427 residue, and the collective ring of aromatic rings forms a hydrophobic bottleneck in the PA channel. The site, dubbed the “ϕ clamp,” is critical for translocase function (Fig 4).⁵² Analogous ϕ-clamp sites have been identified in numerous protein translocases, including soluble ones that hydrolyze ATP,⁹⁶ revealing the general importance of the site to the mechanism of translocation.

PAs ϕ clamp has been characterized extensively by numerous biophysical techniques to better understand the molecular mechanism of translocation. The F427 residues radially converge within the channel, forming a symmetric ring of rings, which is very narrow. Single-channel electrophysiology studies confirmed that the ϕ clamp forms a conductance bottleneck (or constriction point) within the channel. As the ion conductance path and the protein translocation path are the same, it is unsurprising that defects arising from mutations to the ϕ clamp manifest in increased substrate diffusion, backsliding, and retrotranslocation. The retrotranslocation phenotype of these ϕ-clamp mutants likely explains their >1000-fold losses in translocation activity;⁵² moreover, the ratchet-like behavior of the ϕ clamp indicates it is a dynamic clamping site, allowing translocation to proceed in one direction but opposing backsliding in the opposite.

The ϕ clamp has broad substrate specificity with preference for hydrophobic aromatic compounds.⁵² The broad specificity is consistent with the π-cloud electrons of the Phe residues making cation-π, π-π, and π-dipole interactions. Recent reports⁵⁷ indicate substitution of a single Phe residue in the ϕ clamp with a charged residue fully inactivates the translocase, which is consistent with a cooperative site. Since the hydrophobic effect generally exhibits a high degree of cooperativity in protein folding studies,^97–99 it is reasonable to hypothesize that the ϕ clamp is a hydrophobic interaction site, operating similar to a protein chaperone, where the site interacts with a broad spectrum of peptide chemistries during translocation.

An analysis of known prechannel oligomeric crystal structures reveals that the ϕ-clamp loop is quite flexible and exists in two different conformations.^{38, 40, 44} In the ligand-free structure of PA₈ (Protein Data Bank 3HVD),⁴⁰ both the ϕ-clamp loop and the hydrophilic loop containing K397, located directly above the ϕ-clamp loop, are tilted upward, relative to the PA₈(LF_N)₄ structure (3KWV)³⁸ and the PA₇ structure (1TZO).⁴² Interestingly, it appears as if the conformations of the two loops are coordinated, since a K397 loop in the down conformation would sterically clash with a ϕ-clamp loop in the up conformation. While these structures are of PA prechannels, some evidence supports the functional implications of coordinated loop movement.¹⁰⁰ A mutagenesis study of K397 and D426 found that these residues may make a salt bridge upon channel formation.¹⁰⁰ This salt bridge linking these two flexible loops may position the ϕ clamp in an active conformation,^{100, 101} or the different configurations observed may be alternative binding modes of the ϕ clamp, that is, a high affinity and a lower affinity state of the site. Proton binding may be able to modulate the salt-bridge interaction, altering the substrate affinity of the ϕ clamp site.

The β barrel

The length, diameter, and electrostatic composition of the PA channel and its extended β-barrel stem likely play a key role in the molecular mechanism of translocation (Fig. 4). While an atomic-resolution structure of the PA channel is currently unavailable, a β-barrel model⁴⁷ has been proposed.^{91, 92} EM studies also show a tube-like stem consistent with a β-barrel architecture.^{39, 69} The β barrel's inner diameter is no wider than the width of an α helix⁴⁸ and may stabilize helical structure due to favorable van der Waals contacts and backbone desolvation. A number of charged residues populate both the inside and outside of the β barrel. These charges create patches of alternating electrostatic potential within the barrel (Fig. 4). The precise role of the charged groups in the barrel is unknown; however, the charge-state BR mechanism [Fig. 2(B)] proposes that differential electrostatic repulsion between the channel and substrate polypeptide is critical to the overall mechanism of ΔpH-driven translocation.

Translocation Powered by a ΔpH

The PA translocase machine is powered by the chemical potential component, ΔpH, of the PMF.^{21, 22} While a pure Δψ can drive the translocation of LF's amino-terminal domain, LF_N,⁵⁰ the ΔpH is required for the translocation of the full-length substrates, LF and EF,²¹ and a ΔpH alone is sufficient for translocation.²² A charge-state BR model was initially proposed for the molecular mechanism of ΔpH-driven translocation [Fig. 2(B)].²¹ The model is based on the fact that the PA channel itself is cation-selective (or anion-repulsive),⁴⁶ and yet LF and EF are anionic substrates with isoelectric points of 5.4 and 6.6, respectively (more importantly, their amino-terminal domains, LF_N and EF_N, have pI values of 4.9). Krantz et al. proposed that this paradox is resolved if acidic residues can be protonated during their translocation through the PA channel, thereby allowing their anionic charges to be neutralized.²¹ The ΔpH naturally favors substrate protonation on the endosomal side of the membrane, where the pH is ∼5.5, but once the substrate reaches the higher pH side of the membrane (neutral cytosolic pH), these acidic residues would spontaneously deprotonate. Thus, while these protonated acidic residues could pass through the channel's cation-selective filter, they would be trapped on the opposite side of the membrane upon substrate deprotonation. In this mechanism, substrate motion is largely explained by Brownian motion, and the ratchet is an electrostatic trap created via cycles of acidic residue protonation and deprotonation on either side of the channel's charge-selectivity filter.

Several recent studies support the charge-state BR model of translocation. In one study, it was shown that sulfate groups attached to LF_N via cysteine linkage inhibited Δψ-mediated translocation.⁵⁶ Since the sulfate moiety essentially cannot be protonated under the experimental conditions, the authors concluded that only titratable negative charges could pass through the cation-selective channel. Another study reached a similar conclusion by incorporating cysteic acid residues in a semisynthetic LF_N construct.⁵⁴ Furthermore, semisynthetic LF_N constructs lacking titratable acidic residues in the amino-terminal presequence display significant translocation defects.⁵⁴ A recent report extensively probed the role of both positively and negatively charged residues in LF_N's presequence.²² Interestingly, substrates lacking acidic residues could be translocated by a Δψ alone, yet they do not display ΔpH-dependent translocation. This evidence strongly supports the model that the ΔpH drives translocation by protonating acidic residues and is consistent with the charge-state BR model. Furthermore, it was demonstrated that basic residues likely act as chaperones for deprotonated acidic residues. That is, segments of sequence containing high densities of negative charge will not enter the PA channel as efficiently as those containing positively-charged residues nearby.

The ΔpH plays a role not only in translocation but also in the unfolding of the substrate. As discussed above, the thermal energy of even a small polypeptide is quite large (over 100 kJ mol⁻¹) and, if properly rectified, can lead to significant force generation (tens of piconewtons), which is sufficient to accelerate the protein unfolding process. The most ΔpH-dependent step of translocation is associated with the protein folding barrier,⁴⁹ which is consistent with the observation that a ΔpH alone is sufficient to unfold and translocate a fully folded substrate.²² Furthermore, acidic residues in LF_N are naturally concentrated in an optimal position immediately before the substrate's folded domain and separating this region of optimal charge density from the folded domain greatly inhibits translocation.²² Taken together, these results imply a model for ΔpH-dependent unfolding. As the substrate presequence is translocated and captured on the high pH side of the membrane, the remainder of the polypeptide is caught in an extended state with more limited conformational options. This results in entropic tension that is only relieved via substrate unfolding.

Translocation-Coupled Unfolding

The narrow architecture of the PA translocase channel necessitates that substrates must unfold before translocation. Critical to understanding protein translocation is determining how driving forces are coupled to substrate unfolding. Thoren et al. probed the folding step by site-directed mutagenesis, thermodynamic stability studies, and planar lipid bilayer electrophysiology.⁴⁹ The ΔpH- or Δψ-driving-force dependencies of the activation energy of translocation (ΔG‡) revealed a boomerang-shaped curve with two distinct limiting slopes. At low driving force, the ΔG‡ is 10-fold more force dependent than at high driving forces. Thus two major barriers are crossed during translocation: one that is strongly force-dependent and one that is largely force-independent. Thoren et al. were then able to show that substrate unfolding occurs at the more force-dependent barrier and little unfolding occurs at the more force-independent barrier.⁴⁹

By examining destabilizing mutations throughout the substrate protein's structure, the location of the folded substructure that is rate-limiting to the unfolding step of translocation was identified. For LF_N, the substrate's β-sheet subdomain corresponds to this “mechanical breakpoint” region. β-sheet regions often represent the rate-limiting mechanical breakpoint in a force-dependent unfolding mechanism, as probed by optical force microscopy; and the orientation and topology of β-sheet substructures are key determinants of the forces required for unfolding.¹⁰² Interestingly, the β-sheet substructure region is less ordered for PA-bound LF_N relative to unbound LF_N.³⁸ Thus, the unfolding of LF α1/β1 upon binding essentially lowers the activation energy required to unfold the substrate, as strain and disorder is pinpointed at the mechanical breakpoint site.

Finally, because so little unfolding appears to occur in the less force-dependent step, it has been proposed that this step is limited by the translocation of the unfolded chain.⁴⁹ The translocation barrier by its nature of having a shallow force dependence cannot be reduced significantly and places an overall speed limit on the rate of protein translocation for anthrax toxin^{21, 49} and other systems.^103–105 Despite the fact that other translocases use ATP as their source of free energy, it appears the translocation step is bottlenecked in the range of ∼1 to 10 s for protein substrates that range in size from 100 to 800 residues in length. Most likely, this bottlenecking limits the ultimate rate of translocation and reflects that the overall force-independence of the postunfolding event is a general feature in many systems.

A different model proposed by Basilio et al. proposes that translocation is not a barrier-limited process but rather an electrodiffusive movement of a “charged rod” through the channel.⁵¹ By definition, this particular model does not consider unfolding during LF translocation to be rate-limiting. It is difficult to reconcile this model with the majority of published studies on protein unfolding, which show, in fact, that unfolding is barrier limited¹⁰⁶ and force-dependent.^{102, 107–109} Force along the translocation axis of a membrane-embedded translocase are readily achieved for charged ions, q, in an electric field, E, by F = Eq. Similarly, optical force-microscopy measurements of substrate proteins being pulled through ATP-dependent unfolding machines show significant barriers to unfolding, where the most force-dependent step is related to unfolding.¹¹⁰ Thus studies of soluble ATP-dependent unfolding machines agree more closely with the conclusions of Thoren et al.⁴⁰ and are less consistent with the charged-rod hypothesis proposed by Basilio et al.⁵¹

Processing Unfolded Protein: Challenges and Solutions

The nature of unfolded polypeptide presents significant complexities and challenges for the nanomachine, including: (i) chemical complexity;^{38, 52, 111} and (ii) configurational complexity, diffusion, and orientation.^{38, 49} By contrast, the nanomachine kinesin moves along a very specific polymer track, a microtubule. The regular chemical periodicity of microtubule tracks provides convenient, highly organized highways for kinesin to transverse.⁷ Dealing with the chemical and configurational complexity of an unfolded protein polymer implies that the fundamental challenge the translocase faces is entropic in nature. In order to do work on a reasonable timescale, protein translocases must contend with entropy.

The catalytic power of orienting substrates in an enzyme reaction was initially described by Page and Jencks, where enzyme catalyzed rates are accelerated by the appropriate orientation of reactive chemical groups.¹¹² This orientation effect, referred to as an “entropy trap,” was considered to be critical to the observed rate accelerations of enzyme-catalyzed reactions. The entropy trap results from the exchange of enthalpic interactions in an enzyme's active site binding pockets with the substrates; these binding interactions can reduce the overall rotational and translational degrees of freedom and accelerate the chemical reaction. The individual chemical steps of anthrax toxin translocation are protonation, deprotonation, and translocation [Fig. 2(B)]. It is likely these steps require oriented and somewhat ordered substrates, thereby reducing the conformational search and subsequently lowering the ΔG^‡ for each reaction. Efficient, well-designed protein translocases are enzyme catalysts, and as such, they would tend to maximize ordered motion, and minimize heat dissipation, to the greatest extent possible and within the limits of the Second Law. As concluded by Jencks, the more an enzyme minimizes counterproductive motions of its substrate, the more significant acceleration in catalysis is realized.

Chemical complexity

Imagine a protein channel that is 50 to 150 Å long; during translocation, a frame of 15 to 50 residues is contained in the channel. The possible chemical complexity (considering the 20 natural amino acids) is enormous, ranging from 15²⁰ to 50²⁰ depending on channel length and polypeptide conformation. Therefore, it is reasonable to assume that protein translocases are not designed to specifically recognize each and every type of possible amino acid sequence. This type of design principle would be impossible to encode into the machine. Instead, the translocase may recognize broad structural or chemical properties of peptides. This type of sequence recognition is often called “nonspecific binding,” and it refers to the ability of a binding site to recognize substrates using general features of the polymer. Even in the case of anthrax toxin—which only has two known natural substrates, LF and EF—the PA translocase is highly nonspecific and capable of translocating heterologous sequences.^{38, 88, 113, 114} This nonspecificity comes as no surprise, given that the frame of sequence within the machine is continuously changing during translocation. Here we consider two classes of mechanisms that the anthrax toxin protein transporter system exploits in addressing the issue of nonspecificity:

• Class I: Hone in on general sequence properties, namely patches of sequence dense in hydrophobicity (i.e. sequence hydropathy) and/or a particular type of charge.

• Class II: Bind nonspecifically to sequences with similar steric shape, without regard to sequence chemistry.

For the Class I mechanism, we hypothesize that the machine can effectively average diverse residue chemistries into mean sequence properties for a given segment of peptide, thereby minimizing chemical complexity. The likely rational behind the ϕ-clamp site is its preference for hydrophobic and aromatic groups with little or no specificity for the precise geometrical arrangements of such groups.⁵² Crude estimates of polypeptide binding attribute ∼1.5 kcal mol⁻¹ of binding free energy to the ϕ clamp.³⁸ Additionally, the cation selectivity of PA implies that an anion-repulsion site resides within the channel, which repels negatively charged sequences and attracts positively charged sequences. Acidic residues in the translocating chain are responsible for ΔpH-driven translocation; however, the specific location and identity of these charges are much less critical.²²

By contrast, the α-clamp site is structurally designed to complement α-helical shape, rather than particular residue chemistries. Only one α-clamp residue, R178, makes any significant van der Waals contacts with LF_N α1 residues; the rest of the interaction is dominated by backbone contacts. Additional backbone interactions independent of side chain chemistry include two parallel β-sheet hydrogen bonds with LF_N β1. Thus the α clamp employs a Class II mechanism of highly nonspecific binding, providing ∼2.5 kcal mol⁻¹ of binding free energy.³⁸ Furthermore, this binding energy was achieved independently of the sequence composition [Fig. 5(C)]. The α clamp is capable of binding a wide variety of sequences, including nonamphipathic ones. Also the α clamp may take advantage of the intrinsic polarity of an α helix, given that the positive polarity at the amino end of the helix is oriented towards the cation-selective channel, and the negative polarity at the carboxy end is capped by the guanadino group of R178.³⁸ Therefore, the α clamp derives its binding affinity from shape complementarity and a pair of backbone hydrogen bonding interactions, rather than sequence-specific polar, charged, or hydrophobic contacts.

Configurational entropy, diffusion, and substrate orientation

Assume a 10-residue peptide is recognized during a cycle of translocation, and each residue can be in the α, β, or left-hand turn conformation. Such a peptide could effectively occupy ∼10⁵ possible conformations. Selecting specific subsets of possible conformations to bind and forcibly move during protein translocation would require work. For example, to select 10 conformations out of 10⁵ would require ∼4 kcal mol⁻¹ of work, independent of operating under a load. Adding chemical complexity to the system further increases the entropic penalty. Assuming the translocase requires a binary pattern of hydrophobic and hydrophilic sites within the polypeptide sequence, and as there are 10³ possible binary patterns in a decamer, selecting 10 of these configurations would increase the required amount of work to 7 to 8 kcal mol⁻¹.

A translocase thus has two mechanisms available to offset the entropic costs of binding the decamer segment: (i) making specific enthalpic interactions and/or (ii) through the dissociation of ordered solvent. The former is a mechanism of specificity and is unlikely. Specific interactions are often weak, as they can be offset by losses of peptide-solvent hydrogen bonds or ionic interactions. For the latter, many^{97, 98, 115} have considered that the hydrophobic effect is dominant in biomolecular interactions and is due to changes in solvation of the interacting groups. The effect is related to SASA displaced upon binding. For PA, the α clamp provides 2.5 to 4 kcal mol⁻¹ of binding free energy through nonspecific binding.³⁸ Given the SASA apparent in the structure is 1000 Ų, we can estimate that the free energy gain per unit surface area is 2 to 4 cal mol⁻¹ Å⁻². This value is 5- to 10-fold less than the 20 cal mol⁻¹ Å⁻² calculated from a 1023-protein metaanalysis.¹¹⁶ The disparity from the observed value for PA's α clamp may be due to changes in backbone configurational entropy, lower levels of ordered solvent are released upon binding, the introduction of strain and disorder elsewhere into the system, or simply a limitation inherent to the metaanalysis calculation. In any case, we may presume that nonspecific binding interactions stabilized through a general desolvation strategy can be used to do work, namely by ordering the translocating chain for further processing and/or by reducing the stability of the substrate protein. In order to achieve these aims, ∼1000 to 2000 Ų of SASA was excluded upon binding. We contend that such interactions in a translocase would benefit from a uniform substructure, such as an α helix.

Even if we assume that the thermodynamic penalty is satisfied by some other means, the kinetic search process may limit translocation. Experimentally, protein substrates with ∼250 to 750 residues can translocate in ∼1 to 10 s,^{21, 103–105, 117} and thus an interesting question is whether the translocase facilitates this search process. To speed up the search, the translocase may limit the conformational space of the translocating chain to a particular structure most suitable for its active site to bind. Assume the translocase engages more or less a helical structure to produce maximum force during translocation. A Class II-type structure may be able to facilitate the formation of helical structure during translocation. According to the Zimm–Bragg model for helix formation, α-helix stability, K_N, of an N-residue peptide is given as K_N = σs^N.⁹⁴ The initiation of α-helical structure, which is described by the factor, σ, is the limiting step. The equilibrium constant, K_N, increases with each additional residue added to the nascent helix. Thus helix formation is a nucleation process, where the equilibrium stability of a helical substrate would be greatly enhanced by the presence of a Class II structure, in the spirit of PA's α clamp (Fig. 5). Helical structure has an additional advantage of possessing reduced conformational entropy relative to unstructured peptide, minimizing the potential for dissipative losses and allowing for a more efficient utilization of the available electrical/chemical free energy source. We conclude that helix-nucleation machinery in translocases (if oriented properly along the axis of the translocase) would provide a significant kinetic benefit to the translocation mechanism.

A Proton-Engine Mechanism for Translocation

Protons are dissipated by the PA translocase during translocation by means of the protonation and deprotonation of acidic residues in the substrate chain.^{21, 22} Similar to the Cl⁻/H⁺ antiporter, which exchanges two Cl⁻ ions for one H⁺ ion,¹¹⁸ protons are consumed by the PA translocase as a fuel to drive protein flux. How are directionality and force derived from the dissipation of H⁺ ions down their gradient? In prior models, Brownian motion in the translocating protein is effectively biased by changes in protonation state of acidic residues in the protein substrate. We propose that sites like the ϕ clamp may switch conformation during the substrate protonation/deprotonation cycle and that this action plays a key role in governing the process of translocation. Given that a salt bridge likely positions the ϕ-clamp loop in an active conformation,¹⁰⁰ protonation could switch the interaction between on and off states. We envision that the necessary force is generated in this mechanism through biasing of Brownian motion, electrostatic repulsion, and the release of unfolded-state conformational entropy, ΔS_config, upon substrate extrusion from the channel.

In this model, the α-clamp site not only facilitates protein unfolding but also stabilizes and templates the formation of α-helical structure inside the PA channel [Fig. 5(D)]. Furthermore, the internal diameter observed and predicted for 14- to 16-stranded β barrels is a suitable steric fit for peptide helices and likely favorable to helix initiation. For example, crystal structures of protein autotransporters are comprised of a β barrel, which contain α helices from the translocating chain within the lumen of the barrel.^{119, 120} Why may this be important? We propose that ΔS_config will be much greater for a helix-to-coil transition. Thus during particular cycles of the transport pathway, the channel may maximize the amount of compact structures that form, including helical conformations. The activity of the α clamp supports this hypothesis,³⁸ as well as recent work measuring the minimal length of polypeptide spanning the PA channel.⁵⁵ In the latter study, it was suggested using a streptavidin-biotin intermediate-capture approach that peptide chain spans the PA channel in an entirely nonhelical, fully-extended conformation. Thus, the authors conclude that the substrate translocates in a fully-extended conformation devoid of helical structure. The streptavidin-capture data show that the rate of capture for the shortest, 33-residue probe is on the order of 1000 s, which is extremely slow, considering the 260-residue substrate, LF_N, translocates in ∼10 s. The kinetics, however, suggest the opposite conclusion that the substrate is in a more compact structure >99% of the time, where the extended state is rare (i.e., <1%). The authors further argue that longer-length substrates are less accessible to streptavidin capture because the chain will spend more time retracted in the channel. This explanation is in fact consistent with the chain experiencing a more compacted state. The compacted/coiled state is likely helical based on the Zimm–Bragg formalism,⁹⁴ the substrate desolvation activity of the upstream ϕ-clamp site,⁵² the structure of the LF_N-liganded α clamp,³⁸ and the known Ramachandran preferences¹²¹ for polypeptides (i.e., anything less than an extended β conformation likely resides in the α-helical Ramachandran well, as the left-hand turn conformation is rare).

We suggest the translocating chain can fluctuate between more extended and more condensed states. The only requirement of our model is that during translocation the structure of polypeptide in the channel must be more compact than that immediately following extrusion from the channel; the absolute degree of helicity is not critical, as the peptide will be confined within the channel, regardless. When the polypeptide transitions from a more constrained helical state to a less constrained state, the realized increase in ΔS_config is significant. We propose a proton-engine mechanism, whereby the ΔpH, ϕ clamp, α clamp, and anionic-charge repulsion site in the PA channel coordinate protein translocation (Fig. 6):

1. Step 1. Anionic/deprotonated polypeptide loads into the upper vestibule of the PA channel by means of Brownian motion, binding into the α-clamp site as helix. The α clamp acts as a helix nucleating binding site, orienting, and feeding the growing helical chain toward the channel lumen.

2. Step 2. The ϕ clamp switches to a closed position, tightly gripping the substrate polypeptide. Binding of unfolded chain at the ϕ clamp prevents backsliding.⁵² The ϕ clamp impedes H⁺ flow, reducing [H⁺] below the ϕ clamp. Acidic substrate residues above the clamp are subsequently protonated, and consequently less anionic in charge. The stability of the interaction at the ϕ clamp site may be further strengthened by the reduction in negative charge of the substrate.

3. Step 3. While the substrate polypeptide is tightly engaged at the ϕ clamp, the amino-terminal end of the peptide eventually begins to extrude from the end of the channel, where conformational space of the chain is less restricted. Translocation is thus thermodynamically favorable in the direction out of the channel due to the gain in TΔS_config. Importantly, the peptide can bypass the anionic charge repulsion site in the channel, since the peptide is now protonated at its Asp and Glu sites.

4. Step 4. The ΔpH at the ϕ clamp weakens as the substrate in the β barrel loses structure, solvent penetrates up the barrel, and H⁺ dissipate out of the channel. The ϕ clamp switches to the open state, releasing bound peptide. Due to the charge selectivity of the channel, the peptide may only proceed through the channel until peptide and channel are no longer electrostatically compatible. At this point, translocation pauses until peptide recompresses into helix, the ϕ-clamp site can reset, and the deprotonated section of chain is protonated. The cycle will repeat in a fashion analogous to the thermodynamic cycles of a heat engine.

Figure 6.

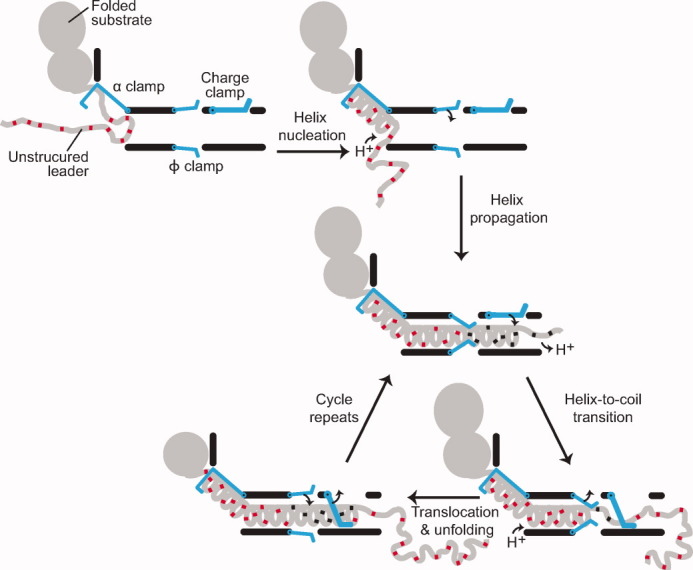
Translocation by a proton-driven engine. Folded substrate and unstructured leader sequence (gray) bind and dock to the PA channel. The α clamp nucleates and subsequently propagates helix formation. The ϕ clamp engages the compact translocating chain; deprotonated acidic residues (red) are then protonated (black). An increase in TΔS_config outside the channel favors the transition of helix to unstructured random coil; acidic residues deprotonate in the higher pH of the cytosol. The charge clamp engages, permitting the passage of protonated acidic residues while preventing the retrotranslocation of deprotonated ones. Ungating of the ϕ clamp allows the chain to translocate, while the α clamp continues to stabilize and template unfolded polypeptide into helix. The cycle repeats until the substrate is fully unfolded and translocated.

An entropic force generation mechanism

How much force may be generated during this proton engine's power stroke? In this mechanism, the power stroke is defined by the distance over which potential energy, stored in the form of compressed and ordered substrate polypeptide conformations, is released into relaxed and disordered conformations. Assuming an α-helical compressed state, which has threefold fewer degrees of freedom per residue than the fully random coil state, the mechanochemistry of this process is: F = TΔS_config/d, where d is the difference in length of peptide undergoing a α-helix-to-coil transition (2.2 Å per residue). F works out to ∼20 pN—enough force to greatly accelerate protein unfolding reactions.^{102, 107–109} This calculation is an upper-limit. These forces are significant and higher than those estimated for BR models, where the substrate is a simple Brownian particle with only three translational degrees of freedom. The step size of the anthrax toxin translocase has yet to be reported; however, the ∼10-nm long β barrel likely places an order of magnitude limit on the power stroke length. Interestingly, the productive force generated over the range of the step as helix melts into random coil would not decrease over distance translocated. Conversely, the electrostatic force arising from the developing charge repulsion between the channel and peptide would decrease inversely as the square of the distance translocated. Here, we do not assume that the power stroke is largely dependent on the electrostatic repulsion between the substrate chain and the channel. Such an electrostatic force should not be ignored, although it would tend to occur over shorter distances.

The electrostatic repulsion may be considered the trigger that switches the translocase-substrate interaction between high-affinity and low-affinity modes, preventing unproductive motions. This electrostatic switch is akin to Maxwell's demon-operated trapdoor or any directionally biased ratchet. Conformational switching is generally what is observed for many ATPases and GTPases, and we expect switching to be a possible means by which both proton and ATP power sources are utilized. The available free energy dissipated by the pH gradient itself is more than adequate to supply the switch with the necessary power to drive the system and rectify the expansion direction of a more compacted α-helical peptide conformation to a more disordered state.