Abstract
The adherence of patients to therapy is a crucial factor for successful HIV anti-retroviral therapy. Imperfect adherence may lead to treatment failure, which can cause the emergence of resistance within viral populations. We have developed a stochastic model that incorporates compartments of latently infected cells and virus genotypes with different susceptibilities to three simultaneously used drugs. With this model, we study the impact of several key parameters on the probability of treatment failure, i.e. insufficient viral suppression, and the emergence of resistance. Specifically, we consider the impact of drug dosage, drug half-lives, fitness costs for resistance, different basic reproductive numbers of the virus and the influence of pre-existing mutations under various levels of adherence. Furthermore, we also investigate the influence of different temporal distributions of non-adherent days (drug holidays) during a treatment. Factors that promote resistance evolution include a high reproductive number, extended drug holidays and poor adherence. Pre-existing mutations only have a substantial effect if they confer resistance against more than one drug. Overall, our study highlights the importance of the interactions between imperfect adherence, pharmacodynamics, pharmacokinetics and latently infected cells for our understanding of drug resistance and therapy failure in HIV anti-retroviral therapy.
Keywords: HIV, mathematical model, adherence, treatment failure, resistance
1. Introduction
In the last decade, there has been a steady progress towards an increasing number of new anti-retroviral drugs which often show increased efficacy or reduced side effects. Especially since the introduction of highly active anti-retroviral therapy (HAART), HIV has become a manageable chronic disease. Nonetheless, despite even the most recent advances in the development of new drug classes, such as integrase inhibitors, HIV has proved to be able to adapt and evolve resistance [1]. Resistance mutations may accumulate in the viral genome and lead to multi-resistant genotypes. This might eventually result in complete treatment failure and therefore reduce the choice for a follow-up treatment regimen.
Adherence, i.e. the probability that a patient takes the drugs at the prescribed time-points, plays a key role in the prevention of resistance. Although present-day drug regimens facilitate adherence by increasing the interval between drug administrations and lowering the pill burden, poor adherence is still a major cause for treatment failures [2]. Different factors such as young age, basic education, current drug abuse and psychiatric disorders are often associated with poor adherence [3].
The different drugs used in HAART affect different stages in the life cycle of virions. Therefore, the number of RNA copies per millilitre rapidly declines after the onset of therapy. Productively infected cells have a short half-life, which also results in a decreasing prevalence of these cells. However, HIV may integrate its DNA copy into the DNA of a host cell which produces only little or no virus. Because these latently infected cells are not actively producing virions, their number does not quickly decline owing to a shortened half-life. The occasional re-activation of these cells makes them serve as a reservoir for the virus. Furthermore, tissues that exhibit poor drug penetration may serve as sanctuaries for infected cells [4]. The presence of these protected and latent reservoirs renders HIV eradication virtually unachievable [5] and therefore makes lifelong treatment necessary. The possible reactivation of latently infected cells and the short generation time of HIV also imply that treatment interruptions will eventually lead to a quick rebound of the viral load. Because of its slow turnover, the latent reservoir may also serve as an archive for genotypes carrying resistance mutations. These genotypes get a head-start when drug concentrations reach insufficient suppressive levels and spread through the population. This mechanism further increases the likelihood of the emergence of multi-resistant genotypes that arise owing to suboptimal adherence.
Several clinical studies focused on inferring the effect of adherence on treatment success as well as the factors determining the level of adherence [3,6,7]. However, while these studies clearly show that adherence affects treatment outcome, we still lack a theoretical understanding of the impact of imperfect adherence, especially of how adherence interacts with other parameters. The few theoretical studies that have assessed the impact of adherence were restricted to mono-therapy [8] or neglected latently infected cells [9]. Thus, these studies do not adequately capture the effect of adherence on resistance in the context relevant for currently practised HAART.
The present study integrates these previous attempts to gain an insight into the role of adherence in the emergence of resistance. Specifically, we developed a model that incorporates the key aspects that affect the success of therapy: pharmacodynamics, pharmacokinetics, multiple drugs and latently infected cells. With this model, we investigate a broad range of adherence scenarios covering the large variability in patient behaviour.
2. Methods
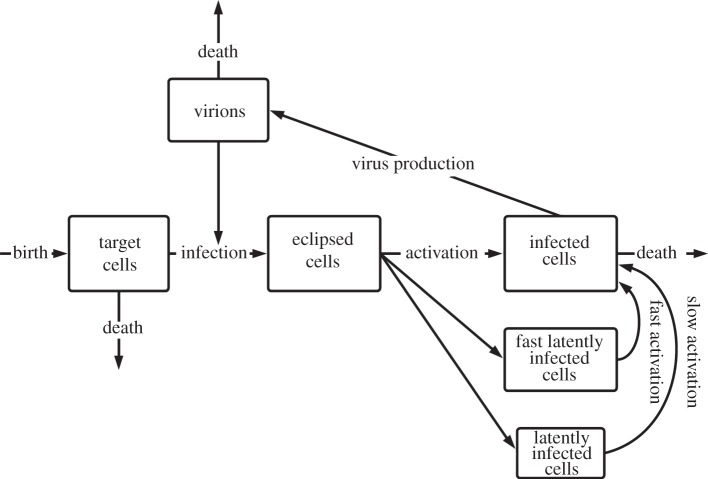
The model that has been developed for this article is based on a stochastic version of the standard virus dynamics model [10]. It incorporates the discrete change of target cells, infected cells and virions over time. The stochasticity was implemented by using the τ-leap method [11]. Newly infected cells first enter the compartment of eclipsed cells. These target cells have incorporated viral DNA, but they are still in the viral eclipse phase and have not become productive yet. This enables the model to capture the population dynamics more realistically [12]. Furthermore, the model has been modified to include two compartments of latently infected cells to account for the tri-phasic decay of plasma HIV RNA that is reported to occur under ongoing HAART therapy [13]. A schematic overview of the model is shown in figure 1. After the initiation of anti-HIV therapy, the virus load typically declines with a decay half-life in the order of days. Thereafter follows a phase with a lower virus decay and a half-life of several weeks. This second phase is mainly represented by the compartment of latently infected cells. During the last phase, the decay of plasma RNA copies decreases even more, leading to an estimated half-life of several years. The compartment of slow latently infected cells reflects this third phase in the course of HIV therapy. In our model, we assume that these compartments do not contribute directly to virus proliferation by means of bystander production, but instead they constantly replenish the compartment of infected cells by reactivation. We make the assumption that self-proliferation and cell death of latently infected cells are negligible compared with the reactivation of these cells.
Figure 1.
Flow diagram of the extended virus dynamics model. It incorporates compartments of eclipsed, fast and slow latently infected cells. The box sizes roughly correspond to the relative abundance of each cell type. The different genotypes of the virions and infected cells are not indicated.
In order to simulate the well-established standard of combination therapy in HIV, we consider a treatment that includes three anti-retroviral drugs. Furthermore, we implement multiple genotypes (gt) that have three loci each with two alleles, a susceptible and a resistant allele. Thus, the model contains eight genotypes that have different resistance patterns for three different drugs. Every resistance allele adds a cost that decreases the reproductive success of its genotype. If not stated otherwise, we assume a fitness cost of 20 per cent for every mutation [14]. For simplicity, we assume that the acquisition of the resistant allele confers complete resistance to the corresponding drug. This assumption does not reflect the full spectrum of clinical observations, because resistance mutations often just decrease susceptibility. We generally decided to assume cautious (i.e. worst-case) parameter estimates that would favour the emergence of resistance.
Besides the pharmacokinetics, the model also contains pharmacodynamics that describe the accumulation and excretion of the administered drugs. Each drug is defined by its IC50 concentration, its half-life, the dosage interval and the dose that is chosen relative to the IC50 value. If not stated otherwise, we set every drug half-life to 12 h and administered 10 units once a day (qd), when the IC50 concentration is defined as 1 unit (see appendix A for the action of drug concentration).
Every run starts with a population of target cells at the carrying capacity and with an inoculum of 1000 wild-type virions if not further specified. The simulation is being run for 360 days without any treatment. Within these 360 days, the infection reaches a stable steady state, and the treatment starts afterwards with all three drugs at the same time. If adherence is less than perfect, all three drugs are missed simultaneously with a probability of (1 − p) per day, where p corresponds to the adherence level. There are two different criteria for a treatment failure. The first criterion depends on the overall viral load: under good adherence, the viral load usually drops very quickly within the first days of treatment. If the viral load peaks over 106 virions in two tests, the treatment is considered a failure. The second criterion checks whether a fully resistant triple mutant that produces at least 10 slow latently infected cells is present during any test. In accordance with the recommendations of the International AIDS Society USA Panel [15], these criteria are tested every 120 days. The emergence of a fully resistant strain and its following spread through the population always implies a treatment failure but the opposite is not necessarily valid. Therefore, we decided to record and show the two events independently. Every run simulates a total of 1080 days and for every parameter set, at least 1000 simulations were run. The adherence parameter has a resolution of 10−2 and the temporal resolution corresponds to 10−2d. We used a specified standard set of parameters (see appendix A for detailed information about parameters and model equations).
3. Results
In the following, we will consider the impact of different key parameters on the outcome of HAART. These key parameters cover drug dosage, drug half-lives, fitness costs for resistance, the basic reproductive number, pre-existence of resistance, drug holidays and adherence. Non-compliance with medical advice is a major obstacle to the delivery of healthcare. A suboptimal adherence extends the phases of intermediate drug concentrations that preferentially select resistance mutations. Because poor adherence is a regular challenge to treatment effectiveness, we tested all other parameters in combination with a continuous gradient of adherence.
Owing to the high number of virions in an untreated patient at the steady state and the relatively high mutation rate, we can expect every possible single point mutation to be already present at the beginning of a treatment course. Therefore, we monitored only the emergence of a fully resistant triple mutant strain.
We monitor three different treatment outcomes: the emergence of the fully resistant mutant, the treatment failure due to an elevated viral load but without the triple mutant, or none of the aforementioned events occurs within two years. We show the probability of treatment failure and the risk for the emergence of the fully resistant strain as a function of adherence to the treatment. The probability of treatment failure or the risk of the emergence of a resistant strain is given by the proportion of simulation runs in which such an event has occurred.
3.1. Drug dosage
The dosage of a specific drug may vary greatly because physicians want to minimize negative side-effects while at the same time administer enough to achieve optimal viral suppression. Typical clinical drug concentrations range from 10 to 100 times the IC50 concentration [16]. Intuitively, we would expect the probability of treatment failure and resistance to decline with increasing dose. This is only true if the drug concentrations in the patient are constantly high enough to reduce the basic reproductive number of the wild-type and the present resistant strains below unity. Otherwise, the drug concentration might fall to intermediate concentrations where the wild-type is still under control but mutant strains may propagate. Therefore, intermediate drug concentrations promote the selection of resistant genotypes. If drug concentrations continue to fall below this mutation selection window, even the wild-type may begin to increase its numbers and would outcompete the mutants as a result of its higher fitness [17]. Since drug half-lives and drug dosage have a major influence on the drug concentration levels and the rate of its decline, we looked at the potential of both parameters.
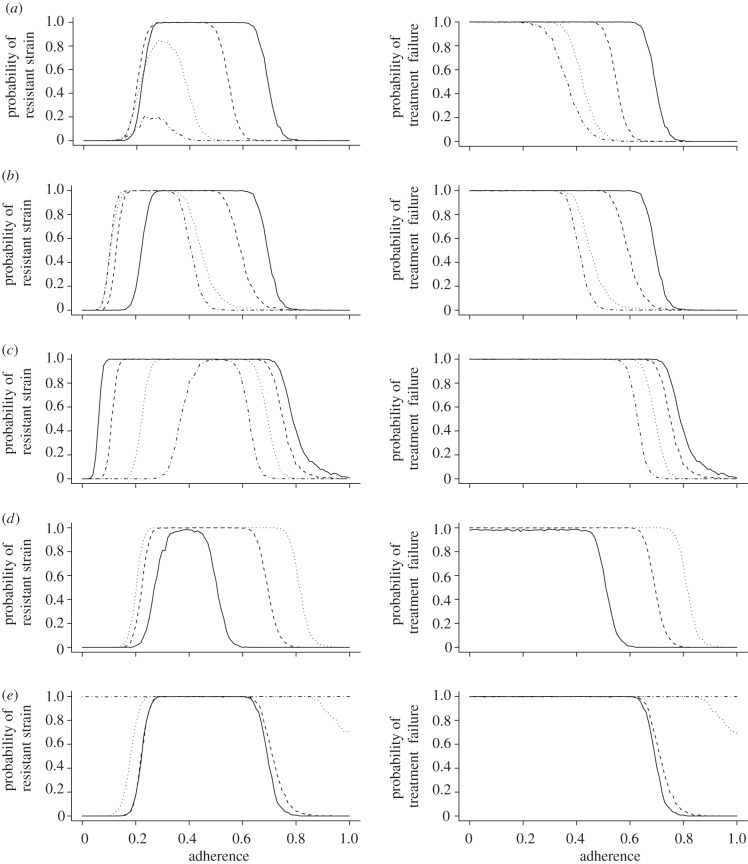
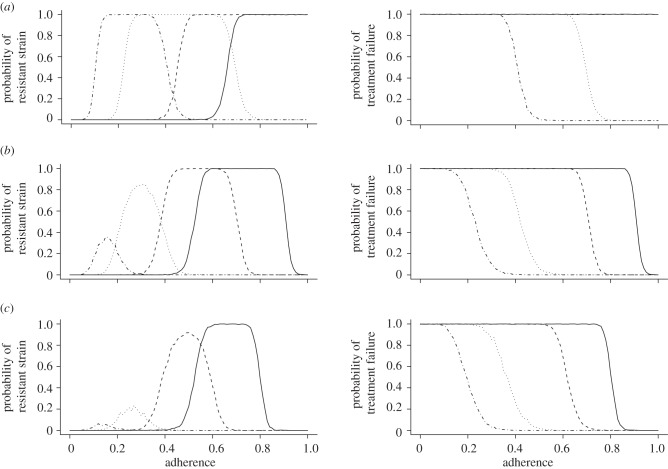
We find in figure 2a that higher drug doses consistently decrease the probability of treatment failure and the emergence of a resistant strain. However, this decrease saturates at higher doses. This is mostly due to the involved pharmacodynamics which cause the inhibitory effect to level out at increasingly higher concentrations. Assuming that side-effects become increasingly severe at high concentrations, it might therefore be more advisable to switch to another drug regimen with different pharmacokinetic properties rather than to simply increase the dosage in order to increase the efficacy.
Figure 2.
The plots in the left column show the probability of the emergence of a fully resistant strain over the level of adherence. The plots in the right column show the probability of treatment failure due to insufficient viral suppression over the level of adherence. (a) Effect of different dosing regimens (solid lines, 10; dashed lines, 20; dotted lines, 50; dashed-dotted lines, 100). (b) Effect of different drug half-lives. (Left panel: solid lines, 3 short; dashed lines, 2 short; dotted lines, 1 short; dashed-dotted lines, 3 long; right panel: solid lines, 3 short; dashed lines, 2 short, 1 long; dotted lines, 1 short, 2 long; dashed-dotted lines, 3 long). (c) Effect of different fitness costs per resistance mutation (solid lines, 0.05; dashed lines, 0.1; dotted lines, 0.2; dashed-dotted lines, 0.3). (d) Effect of different basic reproductive numbers (solid lines, R0 = 5; dashed lines, R0 = 8; dotted lines, R0 = 11). (e) Effect of pre-existing resistance mutations in the inoculum (solid lines, wild-type; dashed lines, single mutant; dotted lines, double mutant; dashed-dotted lines, triple mutant). Please refer to the appendix A for the standard set of parameters which are kept constant.
3.2. Drug half-lives
Drugs with lower decay characteristics increase the minimal and the maximal drug concentrations during perfect adherence to the regimen because these concentrations do not drop to such low concentrations before the next dose is administered (see figure 6). Therefore, they help in maintaining suppressive drug concentrations over a longer time period and decrease the risk of viral blips. Viral blips are bursts of virion production that elevate the viral load for a short time above the limit of detection. On the other hand, if several subsequent doses are missed, longer half-lives can contribute to longer intervals of intermediate drug concentrations, which may favour the selection of resistant mutants. The half-lives of anti-retroviral drugs vary extensively between classes. Protease inhibitors generally exhibit rather short half-lives of 2–6 h, whereas some non-nucleoside reverse transcriptase inhibitors may have half-lives of up to two days. Another complication results from the fact that most half-lives are only known for plasma concentrations. The few established examples of intracellular half-lives indicate that they may be 4–10 times higher than their corresponding plasma half-lives [18].
In our model, we tested the interplay of various combinations of short (12 h) and long (24 h) half-lives. Figure 2b shows that longer drug half-lives significantly decrease the risk of the emergence of the fully resistant strain and the risk of treatment failure. In particular, the usage of two long-lasting drugs compared with one long-lasting drug grants a substantial advantage when preventing the emergence of resistance. The effect is very similar in preventing treatment failure.
3.3. Fitness costs for resistance
Mutations that grant the carrier a resistance to a drug also usually entail a fitness cost relative to the susceptible wild-type. These fitness costs may greatly impair the reproductive success of the virus. In order to study the effect of different fitness costs on therapy outcome, we ran several simulations with 5, 10, 20 or 30 per cent fitness reduction per mutation.
Figure 2c shows that, in the range from 70 to 100 per cent adherence, the probability of the emergence of the fully resistant strain is almost identical to the probability of treatment failure. This suggests that for this range of adherence frequencies, almost every treatment failure occurred owing to the emergence of the fully resistant strain. With an increase in fitness cost, the probability of treatment failure and drug resistance decrease in parallel for this range of adherences. For adherence frequencies below 60 per cent, treatment failure occurs almost always irrespective of the fitness cost.
3.4. Basic reproductive number
Here, the basic reproductive number refers to the absolute fitness of the wild-type at the within-host level. It is defined as the expected number of infected cells produced by a single infected cell in the target cell population of an uninfected host. Extensive studies estimating the basic reproductive number of HIV have been conducted. Previous studies postulated an R0 between 5 and 68 in macaques [19]. A more recent article has found an R0 for humans of about 8 with an interquartile range of 4.9–11 [20].
In figure 2d, we tested basic reproductive numbers of 5, 8 and 11. Because of its short generation time, the virus suffers significantly from a low reproductive number. Accordingly, a relatively small increase can escalate the risk of both treatment failure and the emergence of resistance. This can be especially dramatic as there are individuals that exhibit basic reproductive numbers of 20 and higher [20].
3.5. Pre-existence of resistance
Individuals may get infected by a virus strain that is already treatment-experienced and that therefore already carries one or several resistance mutations. The prevalence of transmitted drug resistance in Europe and the United States usually varies in the range of 7–21% [21–24]. In these cases, the virus is at least partially resistant to the treatment and is expected to develop full resistance faster. We tested this possibility by replacing our original wild-type inoculum with either a single, double or a triple mutant that carries all three resistance alleles. It has to be considered that this model also incorporates the reversion of mutations. Therefore, in a population of single mutants, a wild-type is likely to occur that is more competitive in the absence of treatment.
While an infection with the single-resistant strain only very slightly increases the risk of either treatment failure or triple mutant emergence, the infection with a double or triple mutant leads under almost all levels of adherence to certain treatment failure (figure 2e). It is plausible that a random single mutant inoculum does not lead to a substantially different rehabilitation outcome also because with the wild-type inoculum every possible single mutant is present at the steady state. Double mutants, on the other hand, usually do not occur at such high relative frequencies as is the case with a double mutant infection. Furthermore, they maintain the large frequencies in the slow latent reservoir even after they may have been outcompeted by the wild-type in the acutely infected compartment. This may be particularly important because the slow compartment can restore the general population during treatment interruptions. The double mutant infection also usually leads to the random generation of a few triple mutants that outrun the double mutants as soon as treatment starts. Thus, double and triple mutant infections almost always lead to imminent treatment failure and the emergence of full resistance.
3.6. Drug holidays
Drug Holidays are periods during which a patient does not take his drug on several subsequent days. Such phases pose a special threat to successful treatment because the drug concentration is systematically allowed to decline to sub-inhibitory levels. In order to make the results of these simulations comparable to our previous results, we adapt the previously established scale of adherence by measuring the fraction of days on which the drugs are not taken.
| 3.1 |
where dd is the number of days during which the drugs are taken, and dt is the total number of days on the treatment regardless of whether the drugs are taken or not. This ensures that we can compare scenarios with the same number of days off the treatment. Only the distribution of these days will differ. We tested drug holidays with preset lengths between 1 and 5 days. The onset of a drug holiday was chosen stochastically. Drug holidays are allowed to overlap; therefore, the potential length of a single drug holiday may be much longer than the preset duration, i.e. before a drug holiday ends, another drug holiday may have already started which prolongs the original drug holiday by a certain number of non-adherent days.
We ran two sets of simulations: in the first set, the effect of drug holidays was assessed involving the standard drug regimen. In the second set, we replaced one drug with the standard half-life of 12 h with another that had a half-life of 24 h.
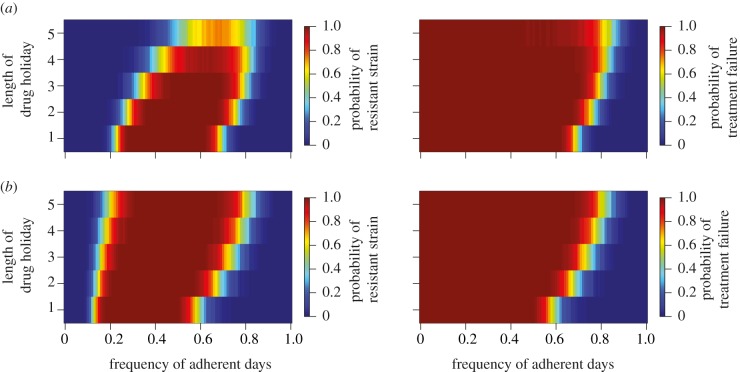
The results in figure 3a indicate a strong impact of the length of the drug holidays on the probability of treatment failure and resistance emergence. Therefore, not only the total number but also the temporal distribution of days off the regimen plays a key role in preventing treatment failure and drug resistance. Specifically, drug holidays longer than 4 days show a very low risk of promoting resistance because intermediate drug concentrations occur too rarely. Either the drugs are being taken and the viraemia gets suppressed or the treatment interruptions are so long that the drug concentrations drop to a level where there is not enough selective pressure to favour the resistant mutant over the wild-type.
Figure 3.
The plots show the length of a drug holiday over the frequency of adherent days. For the plots in the left column, red indicates a high probability of the emergence of a fully resistant strain. In the right column, red indicates a higher probability of treatment failure due to insufficient viral suppression. (a) Effect of drug holidays on treatment outcome under the standard parameters and drug half-lives of 12 h each. (b) Effect of drug holidays with a treatment regimen replacing one drug with another which has a half-life of 24 h.
Replacing one of the involved drugs with a drug with a long-half-life changes the picture (figure 3b). For drug holidays up to 3 days, the risk of treatment failure due to the emergence of a fully resistant strain or insufficient viral suppression decreases marginally, similar to the effect in figure 2b. However, combining a long-half-life drug with two short-half-life drugs may be detrimental (compared with three short-half-life drugs) because it can select the fully resistant mutant at prolonged drug holidays. Also, the risk of insufficient viral suppression at less than perfect adherence increases steadily for drug holidays of 4 or 5 days. This demonstrates that drug regimens involving drugs with longer half-lives are not in every case the more successful treatment options. Longer half-lives increase the time during which the drug concentration remains in the mutation selection window while the patient is on a drug holiday. Concentrations of drugs with a shorter half-life decrease more rapidly, and quickly leave the range in which the wild-type is inferior to the resistant strain.
Additional simulations, figures and results have been performed to allow a more detailed insight into single patient infections, and can be found in §§A.2 and A.3.
4. Discussion
In this article, we compared the relative impact of different parameters on therapy failure and drug resistance under various levels of adherence. In general, most of our results suggest that treatment failure due to insufficient suppression or the emergence of a resistant mutant is a considerable risk because it seems to arise even at slightly less than perfect adherence levels. But it should be noted that our model parameters, especially those regarding the drug properties, favour a negative treatment outcome. In particular, many drugs have higher genetic barriers and therefore the virus requires multiple mutations to become significantly resistant. Furthermore, there is uncertainty concerning the actual costs of resistance mutations, detection intervals between viral assessments and the values of f1 and f2. In order to capture the consequences of this uncertainties, we repeated our simulations with modified ranges of these parameters and show the results in §A.2. For these reasons, our model results should not be considered as quantitative predictions of the risk of treatment failure and resistance evolution but rather as a qualitative assessment of the main factors that determine treatment outcome.
Our results show that all tested parameters significantly change the probability of the emergence of a fully resistant strain and the probability of treatment failure. Particularly, the influence of the basic reproductive number is rather surprising, especially compared with the influence of the fitness costs per mutation. Both parameters directly affect the reproductive fitness of mutant strains. But decreasing the costs per mutation from 30 to 20 per cent only moderately increases the risk of a triple mutant, raising the basic reproductive number from 5 to 8, which has about the same affect as that of a 15 per cent reduced adherence level.
Also, the clinically relevant case of pre-existent mutations deserves further notice. An inoculum consisting of single mutant virions poses about the same threat as the standard wild-type inoculum. An infection with a strain that carries mutations to two or even three drugs on the other hand is almost guaranteed to spawn a fully resistant strain. This effect would not be visible without the introduction of latently infected cells. Because, even though we allow for reversion of mutations, the (in the absence of treatment) more competitive single mutants or wild-type strains are not able to drive the less fit strains to extinction. The resistant strains will still prevail in considerable abundance in the latently infected compartment, which has a slower turnover than the productively infected compartment. This is why the latent compartment serves as a kind of archive for every strain that was at some point sufficiently frequent.
Drug holidays represent a special scenario of adherence. The patient does not take his medication for a certain number of subsequent days. With our parameters, these treatment interruptions repetitively allow drug concentrations to fall within the mutation selection window or to sub-inhibitory levels where even the wild-type can proliferate. These phases of intermediate drug concentrations are responsible for the selection of drug-resistant strains. Interestingly, we observed a rather sharp boundary in the length of drug holidays beyond which the fully resistant strain is not selected anymore; if drug holidays are too long, the relative amount of time during which resistant strains are favoured is not large enough. The same holds true for extremely low adherence levels in other simulations. In these cases, treatment failure will occur mostly just because of the insufficient suppression of wild-type viraemia but the emergence of a fully resistant mutant will not contribute. Therefore, it is possible that longer drug holidays even slightly decrease the risk of detecting treatment failure.
Combination therapy with at least three drugs has become standard in treating HIV patients. The concept of latently infected cells is well established in the literature, but models that consider these slow turnover cells are still rare. In order to capture this situation, we have developed a within-host model of combination therapy in HIV that incorporates latently infected cells, pharmacokinetics, pharmacodynamics and imperfect adherence. Many of our observations would not have been visible, or at least not to the same extent, if our model had not included these aspects of infection and therapy. Especially when studying the mechanisms that lead to the emergence of resistance, the latent compartment becomes almost indispensable. Our results suggest that taking these complexities into account is crucial for the understanding of resistance evolution in HIV.
Acknowledgements
We thank Pia Schulz zur Wiesch, Jan Engelstädter, Huldrych Günthard, Helen Kirsty Alexander, Laurence Läser and Pleuni Pennings for their valuable comments.
Appendix A
A.1. Model equations
The change of target cells T as well as the different genotypes of eclipsed infected cells Egt, productive infected cells Igt, slow and fast latently infected cells Lgt and Lgt* and virions Vgt over time is given by the following set of equations:
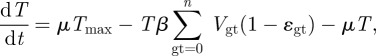 |
A1 |
| A2 |
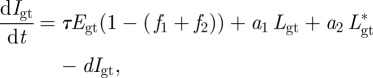 |
A3 |
| A4 |
| A5 |
| A6 |
where μ is the death rate of target cells and Tmax is the carrying capacity of the target cells. n is the number of genotypes which is 2 to the power of l, where l is the number of loci, which in our case was three. With three loci and two alleles each, we defined eight different genotypes: a wild-type, three single mutants, three double mutants and a fully resistant triple mutant. τ is the rate at which the incubated infected cells become productively infected cells [12]. f1 and f2 represent the fraction of infected cells that remain in the fast or slow latently infected compartment while a1 and a2 are the activation rates of the two types of latently infected cells. The infection rate of target cells β is determined by the basic reproductive number R0,
| A7 |
where c is the death rate of virions, d is the death rate of infected cells and N is the viral production rate. This formula assumes that infected cells that are not yet productive have the same death rate as uninfected target cells [20].
The inhibitory effect of a drug acts solely on the infectivity of the virus but does not affect their production. This assumption was made for mathematical convenience. In our model, we implemented two drugs, A and B, belonging to the same class and therefore having an additive effect, while the third drug C is from another class and has an auxiliary multiplicative effect. This combination reflects the widespread use of two reverse transcriptase inhibitors, together with a protease inhibitor [15]. The inhibitory effect on a specific genotype ɛgt was calculated using a formulation for multiple synergistically and non-synergistically acting drugs [25].
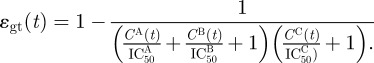 |
A8 |
Here CA(t), for example, is the concentration of drug A at time t. The IC50 value is a specific concentration of a drug at which 50 per cent inhibition is achieved. If a specific genotype carries a resistance allele then the corresponding drug is assumed to have no effect at all. For simulation, the IC50 values of all drugs were set to 1 unit.
The force of infection per genotype Λgt corresponds to the rate with which an infected cell of type gt contributes to the population of virions of every other genotype gt′ and its own genotype gt.
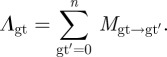 |
A9 |
The mutation matrix Mgt→gt′ is given by the per-locus mutation rate m. For the three-loci/two-alleles case considered here, no mutation occurs with a probability (1 − m)3, one mutation mutation occurs with probability m(1 − m)2, two mutations occur with probability m2(1 − m) and all three mutations occur with probability m3.
When the drugs are taken, the concentrations of all three drugs are assumed to increase instantaneously by 10 units, if not stated otherwise. The drug concentrations decay afterwards according to the following function:
| A10 |
where t1/2A is the half-life of drug A within the patient, and t0 is the last time point where the drugs have been taken.
We decided to modify the reproductive success of a specific genotype by implementing a suppressive force on the virus production. Possible fitness effects that would affect the infectivity of a virion were neglected for mathematical convenience. The replicative fitness of every genotype ωgt is influenced by the cost ql that each of the three loci being considered may exert. In the case of the wild-type allele, ql would be 0.
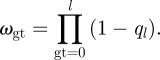 |
A11 |
If not stated otherwise, we choose ql to be 0.2 for every loci with the resistance allele [14].
A.2. Additional results
Besides the results presented in the main article, we also ran some additional simulations to look at the effect of random distribution of resistance costs as well as different detection intervals. In the first simulation, the costs for any resistance in any run of the simulation were randomly assigned to a value between 0 and 0.5. This was compared with the standard case where every resistance mutation always exerts a cost of 0.2. For the second simulation, we changed the interval between the tests where the viral load or a fully resistant strain could be detected. As mentioned earlier, two positive tests above 106 virions are necessary to suggest insufficient viral suppression. To conclude the emergence of a triple mutant, only one positive test is sufficient.
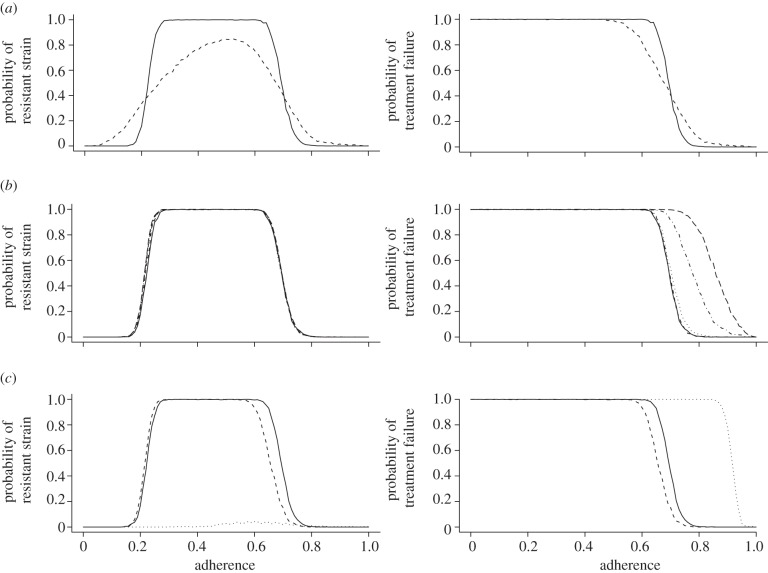
The results in figure 4a show that a random distribution of resistance costs may result in extreme cases where the costs for the three resistance alleles are accidentally all very low or very high. Accordingly, the probability of a resistant strain or a treatment failure already begins to increase for slightly less than perfect adherence levels. On the other hand, the probability for the emergence of a resistant strain is lowered at intermediate adherence levels because random combinations of very high costs render the triple mutant almost non-competitive. This effect is less visible when looking at the probability of a treatment failure because the normal wild-type strain that does not suffer from resistance costs can also cause treatment failure.
Figure 4.
The plots in the left column show the probability of the emergence of a fully resistant strain over the level of adherence. The plots in the right column show the probability of treatment failure due to insufficient viral suppression over the level of adherence. (a) Effect of the random assignment of resistance costs (solid lines, 0.2; dashed lines, random 0–0.5). (b) Effect of different detection intervals between viral assessments (solid lines, 120 days; short dashed lines, 60 days; dotted lines, 30 days; dashed-dotted lines, 7 days; long dashed lines, 1 day). (c) Effect of different fractions of latently infected cells. The standard values for f1 and f2 are 10−2 and 10−4, respectively (solid lines, standard; dashed lines, fn × 0.1; dotted lines, fn × 10).
As can be seen in figure 4b, a shorter detection interval between examinations can increase the likelihood of discovering a treatment failure. However, it has no influence on the detection of a fully resistant strain. Therefore, the earlier mentioned increase is based solely on the enhanced detection of insufficient viral suppression. Although this enhancement is very minimal, above a 30 day interval and below that it is either impractical or misleading because a single viral blip might get scored twice. Detection intervals should not be longer than 120 days because they increase the time a patient is on a failed regimen and should probably receive second-line treatment.
The f1 and f2 parameters in our standard set are only known approximately. To assess their influence on treatment outcome, we decided to change them by one order of magnitude in either direction. This should allow to evaluate whether the actual fraction of cells that remain latently infected is of major importance or whether a large deviation would be misleading.
We find that a 10-fold increase of f1 and f2 causes almost always treatment failure owing to insufficient viral suppression (figure 4c). The comparison of the two plots suggests that the emergence of a fully resistant strain does not account for this outcome. Instead, the results indicate that (for these values of f1 and f2) the higher prevalence of latently infected cells does serve as a reservoir that is almost able to supply enough reactivated cells and indirectly virions that it can cause on its own detectable viral loads. A 10-fold change in the other direction does not have such a major impact. The risk of treatment failure due to the emergence of a fully resistant strain or insufficient viral suppression decreases only marginally. As long as the latent reservoir is able to maintain a chronic infection that prevents the eradication of infected cells and provides an archive for a substantial number of mutants, its function is retained. Therefore, we can conclude that as long as the fraction of latently infected cells is not largely overestimated, the standard parameter choice for f1 and f2 (table 1) remains a reasonable approximation. Most importantly, the fact that full virus suppression is achieved during therapy of most patients indicates that this is indeed the case (i.e. the reservoir is not substantially larger than assumed in the standard parameter values).
Table 1.
Model parameters. The provided references support the order of magnitude of the parameters, not the exact value.
| parameter | value | description/explanation |
|---|---|---|
| Tmax | 107 [26] | carrying capacity of target cells |
| μ | 0.1d−1 [27] | death rate of target cells |
| τ | 1d−1 [28] | activation rate of non-productive infected cells |
| d | 1d−1 [13] | death rate of infected cells |
| N | 1000d−1 [29] | viral production rate |
| c | 10d−1 [30] | death rate of virions |
| β | determined by R0 | infection rate of target cells |
| a1 | determined by t1/2,a1 | activation rate of fast latently infected cells |
| a2 | determined by t1/2,a2 | activation rate of slow latently infected cells |
| t1/2,a1 | 30d [31] | half-life of fast latently infected cells |
| t1/2,a2 | 360d [31] | half-life of fast latently infected cells |
| f1 | 10−2 | fraction of cells going to the fast latently infected cells |
| f2 | 10−4 | fraction of cells going to the slow latently infected cells |
| m | 3.5 × 10−5 [32] | mutation rate |
| R0 | 8, if not stated otherwise [20] | basic reproductive number |
Besides the changes of viral parameters and treatment monitoring, we also further examined substantial pharmacokinetic deviations. The concentration measurements of protease inhibitors in the plasma indicate half-lives in the order of a few hours. Our standard value of 12 h is based on the fact that other classes of anti-retroviral drugs have higher half-lives and on the assumption that the intracellular half-life is much higher than the one in the blood plasma [18]. Nonetheless, we tested a combination therapy with sets of drugs that each have half-lives of 6 h or 4 h. Because such short half-life leads (with the standard dosage) almost always to therapy failure, which is clearly not observed, we counterbalance the shorter half-lives with higher dosage regimens of 50 or 100 units.
Figure 5a shows that half-lives which are much lower than 12 h always lead to the emergence of a fully resistant strain, even if the patient is highly adherent. With such low half-lives, the drug concentrations rapidly enter the mutation selection window, which increases the frequency of resistant genotypes. Not surprisingly, in those cases, the treatment fails independent of the level of adherence—either due to the selection of the fully resistant mutant or due to insufficient suppression of the wild-type. If higher drug doses are given (figure 5b,c) these negative effects are reduced. At perfect adherence, the patient is now again able to avoid the selection of a fully resistant strain and also to suppress the wild-type. However, with half-lives of 4 h and doses 100 times above the IC50, the patient is still likely to have treatment failure at slightly less than perfect adherence.
Figure 5.
The plots in the left column show the probability of the emergence of a fully resistant strain over the level of adherence. The plots in the right column show the probability of treatment failure due to insufficient viral suppression over the level of adherence. (a) Effect of drug regimens involving drugs with short half-lives and doses 10 times above the IC50. (b) Effect of drug regimens involving drugs with short half-lives and doses 50 times above the IC50. (c) Effect of drug regimens involving drugs with short half-lives and doses 100 times above the IC50. Solid lines, 4 h; dashed lines, 6 h; dotted lines, 12 h; dashed-dotted lines, 24 h.
A.3. Examples
The plots in figures 6 and 7 represent single runs of individual patients visualizing different aspects of the model. Figure 6 shows the time course of the drug concentration, while figure 7 depicts the population dynamics of infected CD4+ cells. All parameters correspond to the standard case as described earlier.
Figure 6.
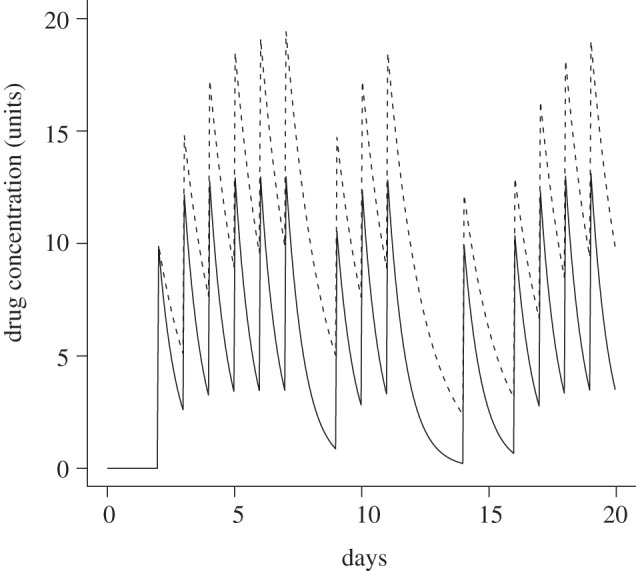
A typical time course of the drug concentrations for two different drugs at the begin of the treatment. The patient is 80% adherent. Drugs are taken or missed simultaneously. Each dose corresponds to 10 units. The first drug has a 12 h half-life (solid line); the other drug has a 24 h half-life (dashed line).
Figure 7.
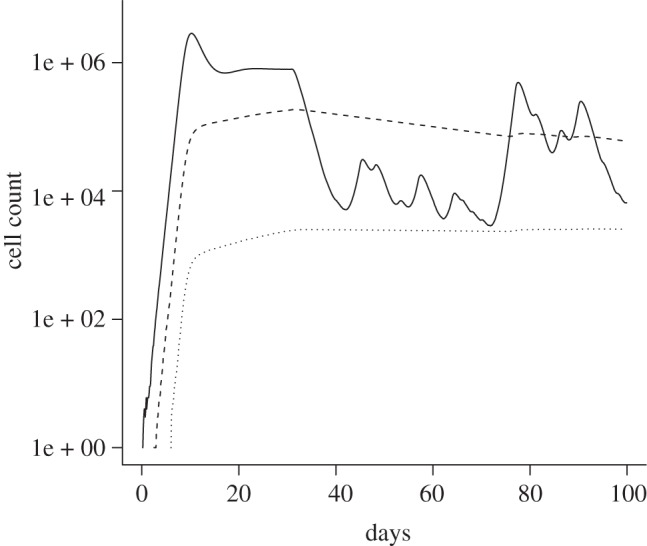
Cell populations (solid lines, infected cells; dashed lines, latently infected cells; dotted lines, slow latently infected cells) in an example patient, which is 60% adherent. The treatment starts at day 30. No discrimination is being made between genotypes. All other parameters are as described in table 1.
References
- 1.Baldanti F., Paolucci S., Gulminetti R., Brandolini M., Barbarini G., Maserati R. 2010. Early emergence of raltegravir resistance mutations in patients receiving HAART salvage regimens. J. Med. Virol. 82, 116–122 10.1002/jmv.21651 (doi:10.1002/jmv.21651) [DOI] [PubMed] [Google Scholar]
- 2.Robbins G. K., Daniels B., Zheng H., Chueh H., Meigs J. B., Freedberg K. A. 2007. Predictors of antiretroviral treatment failure in an urban HIV clinic. J. Acquir. Immune Defic. Syndr. 44, 30–37 10.1016/j.bbi.2008.05.010 (doi:10.1016/j.bbi.2008.05.010) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Glass T. R., et al. 2010. Longitudinal analysis of patterns and predictors of changes in self-reported adherence to antiretroviral therapy: Swiss HIV cohort study. J. Acquir. Immune Defic. Syndr. 54, 197–203 10.1097/QAI.0b013e3181ca48bf (doi:10.1097/QAI.0b013e3181ca48bf) [DOI] [PubMed] [Google Scholar]
- 4.Pomerantz R. J. 2003. Reservoirs, sanctuaries, and residual disease: the hiding spots of HIV-1. HIV Clin. Trials 4, 137–143 10.1310/80JH-148K-NADQ-U927 (doi:10.1310/80JH-148K-NADQ-U927) [DOI] [PubMed] [Google Scholar]
- 5.Chun T. W., Stuyver L., Mizell S. B., Ehler L. A., Mican J. A., Baseler M., Lloyd A. L., Nowak M. A., Fauci A. S. 1997. Presence of an inducible HIV-1 latent reservoir during highly active antiretroviral therapy. Proc. Natl Acad. Sci. USA 94, 13 193–13 197 10.1073/pnas.94.24.13193 (doi:10.1073/pnas.94.24.13193) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Sethi A. K., Celentano D. D., Gange S. J., Moore R. D., Gallant J. E. 2003. Association between adherence to antiretroviral therapy and human immunodeficiency virus drug resistance. Clin. Infect. Dis. 37, 1112–1118 10.1086/378301 (doi:10.1086/378301). [DOI] [PubMed] [Google Scholar]
- 7.Harrigan P. R., et al. 2005. Predictors of HIV drug-resistance mutations in a large antiretroviral-naive cohort initiating triple antiretroviral therapy. J. Infect. Dis. 191, 339–347 10.1086/427192 (doi:10.1086/427192). [DOI] [PubMed] [Google Scholar]
- 8.Miron R. E., Smith? R. J. 2010. Modelling imperfect adherence to HIV induction therapy. BMC Infect. Dis. 10, 1–16 10.1186/1471-2334-10-6 (doi:10.1186/1471-2334-10-6) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Wahl L. M., Nowak M. A. 2000. Adherence and drug resistance: predictions for therapy outcome. Proc. R. Soc. Lond. B 267, 835–843 10.1098/rspb.2000.1079 (doi:10.1098/rspb.2000.1079) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 10.Wei X. et al. 1995. Viral dynamics in human immunodeficiency virus type 1 infection. Nature 373, 117–122 10.1038/373117a0 (doi:10.1038/373117a0). [DOI] [PubMed] [Google Scholar]
- 11.Gillespie D. T. 2001. Approximate accelerated stochastic simulation of chemically reacting systems. J. Chem. Phys. 115, 1716–1733 10.1063/1.1378322 (doi:10.1063/1.1378322). [DOI] [Google Scholar]
- 12.Althaus C. L., De Vos A. S., De Boer R. J. 2009. Reassessing the human immunodeficiency virus type 1 life cycle through age-structured modeling: life span of infected cells, viral generation time, and basic reproductive number, R0. J. Virol. 83, 7659–7667 10.1128/JVI.01799-08 (doi:10.1128/JVI.01799-08). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Perelson A. S., Essunger P., Cao Y., Vesanen M., Hurley A., Saksela K., Markowitz M., Ho D. D. 1997. Decay characteristics of HIV-1-infected compartments during combination therapy. Nature 387, 188–191 10.1038/387188a0 (doi:10.1038/387188a0). [DOI] [PubMed] [Google Scholar]
- 14.Martinez-Picado J., Martínez M. A. 2008. HIV-1 reverse transcriptase inhibitor resistance mutations and fitness: a view from the clinic and ex vivo. Vir. Res. 134, 104–123 10.1016/j.virusres.2007.12.021 (doi:10.1016/j.virusres.2007.12.021) [DOI] [PubMed] [Google Scholar]
- 15.Thompson M. A. et al. 2010. Antiretroviral treatment of adult HIV infection: 2010 recommendations of the International AIDS Society–USA Panel. JAMA 304, 321–333 10.1001/jama.2010.1004 (doi:10.1001/jama.2010.1004) [DOI] [PubMed] [Google Scholar]
- 16.Shen L. et al. 2008. Dose-response curve slope sets class-specific limits on inhibitory potential of anti-HIV drugs. Nat. Med. 14, 762–766 10.1038/nm1777.Dose-response (doi:10.1038/nm1777.Dose-response). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 17.Kepler T. B., Perelson A. S. 1998. Drug concentration heterogeneity facilitates the evolution of drug resistance. Proc. Natl Acad. Sci. USA 95, 11 514–11 519 10.1073/pnas.95.20.11514 (doi:10.1073/pnas.95.20.11514) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 18.Bazzoli C., Jullien V., Le Tiec C., Rey E., Mentré F., Taburet A. M. 2010. Intracellular pharmacokinetics of antiretroviral drugs in HIV-infected patients, and their correlation with drug action. Clin. Pharmacokinet. 49, 17–45 10.2165/11318110-000000000-00000 (doi:10.2165/11318110-000000000-00000). [DOI] [PubMed] [Google Scholar]
- 19.Nowak M. A. et al. 1997. Viral dynamics of primary viremia and antiretroviral therapy in simian immunodeficiency virus infection. J. Virol. 71, 7518–7525 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Ribeiro R. M., Qin L., Chavez L. L., Li D., Self S. G., Perelson A. S. 2010. Estimation of the initial viral growth rate and basic reproductive number during acute HIV-1 infection. J. Virol. 84, 6096–6102 10.1128/JVI.00127-10 (doi:10.1128/JVI.00127-10) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Yerly S., et al. 2007. Transmission of HIV-1 drug resistance in Switzerland: a 10-year molecular epidemiology survey. AIDS 21, 2223–2229 10.1097/QAD.0b013e3282f0b685 (doi:10.1097/QAD.0b013e3282f0b685) [DOI] [PubMed] [Google Scholar]
- 22.Vercauteren J., et al. 2009. Transmission of drug-resistant HIV-1 is stabilizing in Europe. J. Infect. Dis. 200, 1503–1508 10.1086/644505 (doi:10.1086/644505) [DOI] [PubMed] [Google Scholar]
- 23.Bartmeyer B., et al. 2010. Prevalence of transmitted drug resistance and impact of transmitted resistance on treatment success in the German HIV-1 seroconverter cohort. PLoS ONE 5, e12718. 10.1371/journal.pone.0012718 (doi:10.1371/journal.pone.0012718) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 24.Jain V., et al. 2010. Transmitted drug resistance in persons with acute/early HIV-1 in San Francisco, 2002–2009. PLoS ONE 5, e15510. 10.1371/journal.pone.0015510 (doi:10.1371/journal.pone.0015510). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Ferguson N. M., et al. 2005. Adherence to antiretroviral therapy and its impact on clinical outcome in HIV-infected patients. J. R. Soc. Interface 2, 349–363 10.1098/rsif.2005.0037 (doi:10.1098/rsif.2005.0037) [DOI] [PMC free article] [PubMed] [Google Scholar]
- 26.Kouyos R. D., Althaus C. L., Bonhoeffer S. 2006. Stochastic or deterministic: what is the effective population size of HIV-1? Trends Microbiol. 14, 507–511 10.1016/j.tim.2006.10.001 (doi:10.1016/j.tim.2006.10.001) [DOI] [PubMed] [Google Scholar]
- 27.Perelson A. S., Kirschner D. E., De Boer R. J. 1993. Dynamics of HIV infection of CD4+ T cells. Math. Biosci. 114, 81–125 10.1016/0025-5564(93)90043-A (doi:10.1016/0025-5564(93)90043-A) [DOI] [PubMed] [Google Scholar]
- 28.Dixit N. M., Markowitz M., Ho D. D., Perelson A. S. 2004. Estimates of intracellular delay and average drug efficacy from viral load data of HIV-infected individuals under antiretroviral therapy. Antivir. Ther. 9, 237–246 [PubMed] [Google Scholar]
- 29.Stafford M. A., Corey L., Cao Y., Daar E. S., Ho D. D., Perelson A. S. 2000. Modeling plasma virus concentration during primary HIV infection. J. Theor. Biol. 203, 285–301 10.1006/jtbi.2000.1076 (doi:10.1006/jtbi.2000.1076). [DOI] [PubMed] [Google Scholar]
- 30.Ramratnam B., et al. 1999. Rapid production and clearance of HIV-1 and hepatitis C virus assessed by large volume plasma apheresis. Lancet 354, 1782–1785 10.1016/S0140-6736(99)02035-8 (doi:10.1016/S0140-6736(99)02035-8) [DOI] [PubMed] [Google Scholar]
- 31.Strain M. C., et al. 2005. Effect of treatment, during primary infection, on establishment and clearance of cellular reservoirs of HIV-1. J. Infect. Dis. 191, 1410–1418 10.1086/428777 (doi:10.1086/428777). [DOI] [PubMed] [Google Scholar]
- 32.Mansky L. M., Temin H. M. 1995. Lower in vivo mutation rate of human immunodeficiency virus type 1 than that predicted from the fidelity of purified reverse transcriptase. J. Virol. 69, 5087–5094 [DOI] [PMC free article] [PubMed] [Google Scholar]