Fitting a Bivariate Measurement Error Model for Episodically Consumed Dietary Components

Abstract

There has been great public health interest in estimating usual, i.e., long-term average, intake of episodically consumed dietary components that are not consumed daily by everyone, e.g., fish, red meat and whole grains. Short-term measurements of episodically consumed dietary components have zero-inflated skewed distributions. So-called two-part models have been developed for such data in order to correct for measurement error due to within-person variation and to estimate the distribution of usual intake of the dietary component in the univariate case. However, there is arguably much greater public health interest in the usual intake of an episodically consumed dietary component adjusted for energy (caloric) intake, e.g., ounces of whole grains per 1000 kilo-calories, which reflects usual dietary composition and adjusts for different total amounts of caloric intake. Because of this public health interest, it is important to have models to fit such data, and it is important that the model-fitting methods can be applied to all episodically consumed dietary components.

We have recently developed a nonlinear mixed effects model (Kipnis, et al., 2010), and have fit it by maximum likelihood using nonlinear mixed effects programs and methodology (the SAS NLMIXED procedure). Maximum likelihood fitting of such a nonlinear mixed model is generally slow because of 3-dimensional adaptive Gaussian quadrature, and there are times when the programs either fail to converge or converge to models with a singular covariance matrix. For these reasons, we develop a Monte-Carlo (MCMC) computation of fitting this model, which allows for both frequentist and Bayesian inference. There are technical challenges to developing this solution because one of the covariance matrices in the model is patterned. Our main application is to the National Institutes of Health (NIH)-AARP Diet and Health Study, where we illustrate our methods for modeling the energy-adjusted usual intake of fish and whole grains. We demonstrate numerically that our methods lead to increased speed of computation, converge to reasonable solutions, and have the flexibility to be used in either a frequentist or a Bayesian manner.

1. INTRODUCTION

This paper is about the important public health problem of understanding the distribution of episodically consumed dietary component intakes in terms of their energy-adjusted amounts, and relating this to diet-disease relationships. Before commenting in more detail, we first discuss the literature for simpler problems that are also of interest.

In nutritional surveillance and nutritional epidemiology, there is considerable interest in understanding the distribution of usual dietary intake, which is defined as long-term daily average intake. In addition, of interest is the regression of this intake on measured covariates, which is needed to correct diet-disease relationships for measurement error in assessing diet. If the dietary component of interest is ubiquitously consumed, as most nutrients are, the data are continuously distributed and methods are well-established for solving both problems. See for example Nusser, et al. (1997) for surveillance and Carroll, et al. (2006) for measurement error modeling.

Another class of dietary components is those which are episodically consumed, as is true of most foods, e.g., fish, red meat, dark green vegetables, whole grains. When consumption is measured by a short-term instrument such as a 24 hour recall, hereafter denoted by 24hr, the episodic nature of these dietary components means that their reported intake may either equal zero on a non-consumption day, or is positive on a day the component is consumed. In many studies, non-consumption days predominate for several episodically consumed foods of interest. For example, in our data example, for fish and whole grains, 65% and 12% reported no consumption on both of two administrations of the 24hr, respectively. Thus, data on episodically consumed dietary components are zero-inflated data with measurement error. Recently, Tooze, et al. (2006) for nutritional surveillance and Kipnis, et al. (2009) for nutritional epidemiology have reported so-called two-part methods, which are actually nonlinear mixed effects models, for analyzing episodically consumed dietary components in the univariate case. These methods are known commonly as the “NCI method” because many of the co-authors of these papers are members of the National Cancer Institute (NCI), and because SAS routines based upon the NLMIXED procedure are available at http://riskfactor.cancer.gov/diet/usualintakes/, an NCI web site. Other two-part models in different contexts are described for example in Olsen and Schafer (2001), Tooze, et al. (2002) and Li, et al. (2005).

We are interested in the more complex public health problem of understanding the usual intake of an episodically consumed dietary component adjusted for energy intake (caloric intake), along with the distribution of usual intake of energy. This is critical because it addresses the issue of dietary component composition, and makes comparable diets of individuals whose usual intakes of energy are very different. As an example, the U.S. Department of Agriculture’s Healthy Eating Index-2005 (www.cnpp.usda.gov/HealthyEatingIndex.htm) is a measure of diet quality that assesses conformance to Federal dietary guidance. One component of that index is the number of ounces of whole grains consumed per 1000 kilocalories: there are other items in the HEI-2005 that deal with episodically consumed dietary components, and all of them are adjusted for energy intake. The data needed to compute such variables are thus the usual intake of the dietary component consumed and the usual amount of calories consumed, and (possibly normalized) ratios of them.

Recently, Kipnis, et al. (2010) have developed a model for an episodically consumed dietary component and energy, see Section 2. They fit this model using nonlinear mixed effects models with likelihoods computed by adaptive Gaussian quadrature using the SAS procedure NLMIXED. However, as described in Section 2 and documented in Section 4, this form of computation can be slow, and can have serious convergence issues. This is extremely problematic, because of the importance of the problem and the fact that solutions will find wide use in the nutrition community, but only if they are numerically stable.

In this paper, we take an alternative Markov Chain Monte Carlo (MCMC) approach to computation, which is faster and numerically more stable. There are many good introductory papers reviewing MCMC, such as Casella, et al. (1992), Chib, et al. (1995) and Kass, et al. (1998). Effectively, we exploit the well-known fact (Lehmann and Casella, 1998, Chapter 6.8) that in fully parametric regular models of the type we study, Bayesian posterior means of parameters are asymptotically equivalent to their corresponding maximum likelihood estimators. To implement an MCMC approach in our problem, there are technical issues that have to be overcome, including the fact that one of the covariance matrices in the model of Kipnis, et al. (2010) is patterned. Besides fitting the model, our main focus in this paper is to discuss how to use the parameter estimates to then estimate the distributions of the usual intake of energy and energy-adjusted usual intake of dietary components.

In Section 2, we describe the model of Kipnis, et al. (2010). In Section 2, we also briefly outline some of the details of our implementation, although the technical details are given in the Appendix. In Sections 3 and 4, we take up the analysis of the NIH-AARP Study of Diet and Health (http://dietandhealth.cancer.gov/) as an illustration of our model and method. Section 5 gives concluding remarks.

2. Data and Model

2.1. The Data

In practice, the response data often come from repeated 24hr. Necessarily, due to cost and logistical reasons, the number of recalls is limited, and is rarely greater than 2. In a 24hr, what is observed is whether a dietary component is consumed, and if it is consumed, the reported amount. In addition, the amount of energy reported to be consumed is also available. Thus, for person i = 1, ..., n, and for the k = 1, ..., m_i repeats of the 24hr, the data are Ỹ_ik = (Y_i1k, Y_i2k, Y_i3k)^T, where

• Y_i1k = Indicator of whether the episodically consumed dietary component is consumed.

• Y_i2k = Amount of the dietary component consumed as reported by the 24hr, which equals zero if the dietary component is not consumed.

• Y_i3k = Amount of energy consumed as reported by the 24hr.

There are also generally covariates such as age category, ethnic status and in many cases the results of reported intakes from a food frequency questionnaire. We will generically call these covariates X.

2.2. The Model

Here we describe the nonlinear mixed effects latent variable model of Kipnis, et al. (2010). There are i = 1, ..., n individuals and k = 1, ...,m_i repeats of the 24hr. Also, the observed data have three parts, relating to whether the episodically consumed dietary component is consumed, the amount if it is consumed, and the amount of energy. Also with the observed data, we will have covariates for the individual, generically called X, see below for more precise notation. Finally, Kipnis, et al. (2010) use what are called in nutritional epidemiology “person-specific random effects” which are generically denoted by U, so that individuals actually differ from one another in usual intake when they have the same values of the covariates.

To be more precise, for the i^th individual there are covariates (X_i1, X_i2, X_i3): X_i1 are the covariates for the indicator of consumption, X_i2 are the covariates for the consumption amount of the dietary component of interest, and X_i3 are the covariates for the consumption of energy. Often, in practice, the covariates for each observed data component are the same, so that X_i1 = X_i2 = X_i3. Along with the covariates, there are corresponding person specific random effects (U_i1, U_i2, U_i3), the role of which is to allow different people who share the same covariates to have different amounts of usual intakes. As we will see shortly, there are also errors accounting for day-to-day variation. Only the covariates, the person-specific random effects, and, because of transformations, the variances of the random errors are relevant to the definitions of usual intake, which are given below at equations (6)–(7).

The model of Kipnis, et al. (2010) uses a latent variable approach. Let (W_i1k, W_i2k, W_i3k) be latent variables that are assumed to follow the linear mixed effects model

$$W_{\mathit{\text{ijk}}}={\text{X}}_{\mathit{\text{ij}}}^{\text{T}}{\mathit{\text{β}}}_j+U_{\mathit{\text{ij}}}+{\epsilon }_{\mathit{\text{ijk}}}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{for}\hspace{0.17em}\hspace{0.17em}j=1,\hspace{0.17em}2,\hspace{0.17em}3,$$ (1)

where (U_i1, U_i2, U_i3) = Normal(0, Σ_u) are the person-specific random effects, while the within-person errors that account for day-to-day variation (ε_i1k, ε_i2k, ε_i3k) = Normal(0, Σ_ε). The (U_i1, U_i2, U_i3) and (ε_i1k, ε_i2k, ε_i3k) are mutually independent.

The observed data are related to the latent variables as follows:

$$Y_{i1k}=I(W_{i1k}>0);$$ (2)

$$Y_{i2k}=Y_{i1k}{g}^{-1}(W_{i2k},\hspace{0.17em}{\lambda }_F);$$ (3)

$$Y_{i3k}=g^{-1}(W_{i3k},\hspace{0.17em}{\lambda }_E),$$ (4)

where I(·) is the indicator function and g⁻¹(x, λ) is the inverse of the Box-Cox transformation g(x, λ) = (x^λ − 1)/λ for λ ≠ 0 and g(x, 0) = log(x) if λ = 0. We used the same Box-Cox transformations as Kipnis, et al. (2009, 2010). Under the model defined by (1)–(4), the probability to consume follows the probit model

$$\text{pr}(Y_{i1k}=1|{\text{X}}_{i1},\hspace{0.17em}{U}_{i1},\hspace{0.17em}{U}_{i2},\hspace{0.17em}{U}_{i3})=\Phi ({\text{X}}_{i1}^{\text{T}}{\mathit{\text{β}}}_1+U_{i1}),$$ (5)

where Φ(·) is the standard normal distribution function. The probit model is commonly used to model a relationship between a binary dependent variable and one or more independent variables. The probit link was used in Kipnis, et al. (2010) to allow the day-to-day variation in whether a food is consumed to be correlated with the amount of energy consumed, and in such a way that the day-to-day variation random variables (ε_i1k, ε_i2k, ε_i3k) are jointly normal, thus facilitating both nonlinear mixed effects software and the MCMC. The Box-Cox transformations in (3)–(4) allow for skewed distributions typically seen with dietary data. Of course, the notation in (5) means that consumption depends on (U_i1, U_i2, U_i3) only through U_i1.

Under the assumption that the 24hr is unbiased for usual (mean) intake, the usual intake of the dietary component and energy are given as T_Fi = E(Y_i2k|X_i1, X_i2, U_i1, U_i2) and T_Ei = E(Y_i3k|X_i3, U_i3). Kipnis, et al. (2009, 2010) use a Taylor series approximation E{g⁻¹(v + ε)|v) ≈ g⁻¹(v, λ) + (1/2)var(ε){∂²g⁻¹(v, λ)/∂v²}. Using this approximation, see equation (19) of Kipnis, et al. (2009), and under the covariance matrix restriction described below in Section 2.3, they show that the usual intake T_Fi of the dietary component and the usual intake T_Ei of energy for individual i are given as

$$T_{Fi}=\Phi ({\text{X}}_{i1}^{\text{T}}{\mathit{\text{β}}}_1+U_{i1})g_{*}\{{\text{X}}_{i2}^{\text{T}}{\mathit{\text{β}}}_2+U_{i2},\hspace{0.17em}{\lambda }_F,\hspace{0.17em}{\sum }_{\epsilon }(2,\hspace{0.17em}2)\},$$ (6)

$$T_{Ei}=g_{*}\{{\text{X}}_{i3}^{\text{T}}{\mathit{\text{β}}}_3+U_{i3},\hspace{0.17em}{\lambda }_E,\hspace{0.17em}{\sum }_{\epsilon }(3,\hspace{0.17em}3)\},$$ (7)

where the (j, k) element of Σ_ε is denoted as Σ_ε(j, k) and $g_{*}(v,\hspace{0.17em}\lambda ,\hspace{0.17em}{\sigma }_{\epsilon }^{*})=g^{-1}(v,\hspace{0.17em}\lambda )+(1/2){\sigma }_{\epsilon }^2\{{\partial }^2{g}^{-1}(v,\hspace{0.17em}\lambda )/\partial v^2\}$. Of course, (6)–(7) are approximations because g_*(·) is an approximate inverse of g(·). We can combine the usual intakes of dietary component and energy in various ways, e.g., the number of ounces of whole grains per 1000 kilo-calories, i.e., 1000 × T_Fi/T_Ei.

Remark 1

The Taylor series approximation to computing expectations of inverses of the Box-Cox transformation is used here because it was used by Kipnis, et al. (2009, 2010). More precise quadrature formulae can be used, and we have done so, finding almost no numerical changes. The computational convenience of the approximation makes it attractive.

2.3. Restriction on the Covariance Matrix

There are two restrictions necessary in the specification of Σ_ε. First, following Kipnis, et al. (2009, 2010), we set ε_i1k and ε_i2k to be independent. The intuitive way to think about the independence between the first two is that whether the dietary component is consumed or not and the amount consumed are assumed to be independent. This actually makes sense because a dietary component being consumed cannot indicate how much was consumed. Second, for identifiability of β₁ and the distribution of U_i1, we require that var(ε_i1k) = 1, because otherwise the marginal probability of consumption is $\Phi \{({\mathbf{\text{X}}}_{i1}^{\text{T}}{\mathit{\text{β}}}_1+U_{i1})/{\mathit{\text{var}}}^{1/2}({\epsilon }_{i1k})\}$. Without this second restriction, β₁, var(U_i1), cov(U_i1, U_i2) and cov(U_i1, U_i3) are identified only up to scale factors. Hence we have that

$${\sum }_{\epsilon }=\left[\begin{array}{ccc}1& 0& s_{13}\\ 0& s_{22}& s_{23}\\ s_{13}& s_{23}& s_{33}\end{array}\right].$$ (8)

The difficulty with parameterizations such as (8) is that (s₁₃, s₂₃, s₂₂, s₃₃) cannot be left unconstrained, or else (8) need not be a covariance matrix. Define $s_{13}={\rho }_{13}{s}_{33}^{1/2}$ and s₂₃ = ρ₂₃(s₂₂s₃₃)^1/2. Then the determinant $|{\sum }_{\epsilon }|=s_{22}{s}_{33}(1-{\rho }_{13}^2-{\rho }_{23}^2)$. Since Σ_ε is a covariance matrix, its determinant must be non-negative, and hence we cannot allow the correlations (ρ₁₃, ρ₂₃) to vary freely. There are many ways to parameterize Σ_ε in an unrestricted way that forces it to be positive semi-definite. Here we use a polar coordinate representation, ρ₁₃ = γ cos(θ) while ρ₂₃ = γ sin(θ), with γ ∈ (−1, 1) and θ ∈ (−π, π).

The zero entries in (8) are not required, although they are implicit in the two part model used in the original papers involving only the episodically consumed dietary component and not energy (Tooze, et al., 2006; Kipnis, et al., 2009) and they make intuitive sense in our context. We have chosen to use this restriction for these reasons and especially so that the marginal model for the episodically consumed dietary component is the same as that in the literature.

Kipnis, et al. (2010) explore a sample selection model (Heckman, 1976, 1979; Leung and Yu, 1996; Kyriazidou, 1997; Min and Agresti, 2002) that does not have this restriction. They found that such a sample selection model can be very unstable in our context, with the components of Σ_u and Σ_ε varying wildly. Although it is possible to use MCMC computations to fit the sample selection model, given the acceptance of the restriction in nutritional epidemiology and of the NCI method, we focus on the covariance model (8).

Remark 2

It is very important to allow for Σ_ε being non-diagonal. The term s₂₃ ≠ 0 simply reflects the reality that, within a person and hence conditional on (U_i1, U_i2, U_i3), the amount of food reported consumed and the amount of energy consumed are sometimes highly correlated. The reason we allow s₁₃ ≠ 0 is to account for the very real possibility that, again within a person, the very fact that one consumes a food leads to a higher or lower reported energy (caloric) intake.

2.4. Model Fitting and Computation

It is possible in principle to fit model (1)–(8) using nonlinear mixed effects software. Kipnis, et al. (2010) use the SAS procedure PROC NLMIXED. However, we have found that such implementation is slow and not very stable, with many issues of convergence. NLMIXED uses adaptive Gaussian quadrature to integrate the likelihood over the distribution of random effects. NLMIXED can have convergence problems, especially when there are too many, or too few, zeros. What typically happens is that corr(U_i1, U_i2) tries to go to 1.00 or sometimes even −1.00, or that var(U_i1) or var(U_i2) tries to go to 0.00. When one of these things happens, the model usually converges, according to the change-in-likelihood criterion, but the Hessian is not positive definite. Occasionally, NLMIXED fails to converge at all. In general, we have found that when NLMIXED does not have such numerical problems, its results and ours are in reasonable agreement. These issues are described in more detail in Section 4.2.

Hence, for stability and speed, we have turned to a Bayesian approach for fitting the model described by equations (1)–(8). We emphasize that the Markov Chain Monte Carlo computation can either be thought of as a strictly Bayesian computation with ordinary Bayesian inference, or as a means of developing frequentist estimators of the crucial parameters, based on the well-known fact that in parametric models such as ours, the posterior mean of the parameters is a consistent and asymptotically normally distributed frequentist estimator, see for example Lehmann and Casella (1998, Chapter 6.8).

Our computational algorithm, described in detail in the appendix, uses Gibbs sampling with some Metropolis-Hastings steps. We have implemented this approach in both Matlab and R, and it is fast enough for practical use. In the NIH-AARP Diet and Health Study described in Section 3, with a sample size of 899, for a burn-in of 1, 000 steps followed by 10, 000 MCMC iterations, our Matlab and R programs take approximately 2 minutes and 11.7 minutes on an Intel(R) Xeon(TM) CPU with 3.73GHz and 7.8GB of RAM in a Linux system, respectively. For a burn-in of 5, 000 steps followed by 15, 000 MCMC iterations, our Matlab and R programs take approximately 3 minutes and 17.5 minutes, respectively. Both programs are available from the first author.

We have also developed an implementation in WinBUGS with a BUGS model called from R by using the package R2WinBUGS. Details are available from the third author. As to be expected, the WinBUGS code is much slower than the custom programs, taking approximately 5 hours (Pentium computer with 3.5GHz CPU and 1.99GB of RAM in a Windows system) for a burn-in of 1, 000 steps followed by 10, 000 MCMC samples. We are also currently developing a SAS macro for use by the nutritional community. On various test data sets, the WinBUGS, R, SAS and Matlab code gave very similar answers. In our empirical work, we use the Matlab code.

Remark 3

There are important data conventions that we use. These are described in detail in the Appendix. For example, in Section A.1, we mention that covariates are always standardized to have sample mean zero and sample variance one. The reason is a matter of scaling: energy intake is in terms of calories, which are typically in the 1,000’s, so that the corresponding regression parameters, without standardization, with the FFQ energy as a covariate, would necessarily be tiny, making it hard to develop a plausible prior distribution. As described in Section A.1, we also standardize the responses for numerical stability and weaken dependence upon the prior distributions, and in Section A.2 we describe why this standardization makes sense. We have fit our method with various different prior distributions, and there is very little sensitivity to prior specification.

2.5. The Role of Covariates

Covariates are important for estimating the distribution of usual intakes, for at least three reasons.

• First, as a matter of model specification. Consider abstractly the simple linear regression model Y = β₀ + β₁ X + ε: given X, ε might be normally distributed, but if X is not simultaneously normally distributed, then removing it from the model would give a model Y = κ₀ + ξ, and ξ would not be normally distributed, and our model assumptions would be violated.

• Subar, et al. (2006) studied using food frequency questionnaire (FFQ) data as covariates to estimate the distributions of individual usual intakes of episodically consumed dietary components. They found strong and consistent relationships between FFQ and 24hr. This supports the postulate that FFQ data may provide important covariate information in supplementing 24hr for estimating usual intake of dietary components. Besides FFQ, there are some other clinical covariates such as gender, age, body mass index (BMI), etc. that may be associated with usual intake. Thus, our covariates included an intercept, age, BMI, the FFQ for energy intake and the FFQ for the dietary component of interest. They are used to reduce the error with which the usual intake is estimated, and to make more plausible our distributional assumptions.

• Kipnis, et al. (2009) state in their abstract “One feature of the proposed method is that additional covariates potentially related to usual intake may be used to increase the precision of estimates of usual intake and of diet-health outcome associations”. In their introduction they state “In Section 3, using data from the Eating at Americas Table Study (EATS), we quantify the increased precision obtained from including a FFQ report as a covariate”.

A referee has asked whether the β-coefficients for the covariates are interpretable, and whether it would be of interest to make inferences about whether the covariates are associated with usual intake. Because energy adjusted usual intakes involve three β-coefficients for each covariates, interpretation of any one of them is difficult. Whether a particular covariate is associated with usual intake is a mildly interesting question, but if far less important than estimating distributions of energy-adjusted usual intakes.

2.6. Simulation Study

We performed a simulation study that was based upon our empirical study given in Section 3, in order to ascertain whether the methodology results in reasonably unbiased estimates of (β₁, β₂, β₃, Σ_u, Σ_ε). To test whether our algorithm can produce non-near-zero correlations when the true correlations are actually far from zero, we simulated 200 data sets, each of size n = 1, 000, roughly the size of the NIH-AARP calibration cohort in Section 3. In this simulation, we used the same covariates for each of the three outcomes, i.e., we set X_i1 = X_i2 = X_i3. The covariate vectors had three components, the first equal to 1.0 for an intercept, and the other two generated as Normal(0, 1). The parameters (β₁, β₂, β₃) were generated as Uniform(0, 1) for each simulated data set. We used

$${\sum }_u=\left[\begin{array}{ccc}0.50& 0.24& 0.24\\ 0.24& 0.70& 0.35\\ 0.24& 0.35& 0.70\end{array}\right];\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\sum }_{\epsilon }=\left[\begin{array}{ccc}1.00& 0.00& 0.47\\ 0.00& 1.20& 0.78\\ 0.47& 0.78& 1.40\end{array}\right].$$

The mean of the posterior means of (β₁, β₂, β₃) was unbiased overall and are not reported here. The mean of the posterior means of (Σ_u, Σ_ε) were

$${\widehat{\sum }}_u=\left[\begin{array}{ccc}0.51& 0.27& 0.27\\ 0.27& 0.68& 0.33\\ 0.27& 0.33& 0.67\end{array}\right];\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{\widehat{\sum }}_{\epsilon }=\left[\begin{array}{ccc}1.00& 0.00& 0.39\\ 0.00& 1.23& 0.80\\ 0.39& 0.80& 1.43\end{array}\right].$$

Crucially, for the main purposes of estimating the distribution of usual intakes, the posterior means were essentially unbiased for estimating Σ_u. As seen in the Appendix, Σ_ε also has a role in the definition of usual intake, and it too was essentially unbiased except for a small bias of size 0.08 in estimating cov(ε_i1k, ε_i3k), a term that does not appear in the definitions of usual intake.

Remark 4

We give here only the results of a single simulation because what we have shown above are representative of other simulations we have done. For example, we have simulated cases where the off-diagonal elements of Σ_u were zero and cases where some of them were negative. We have also simulated cases that the diagonal elements of Σ_u were smaller and somewhat larger. In none of the cases did we see any significant bias in the estimates.

Remark 5

We have not displayed the simulation results for the Proc NLMIXED procedure because in those cases that it converges, it is very nearly unbiased, just like our method.

3. Empirical Analysis: Methods

3.1. Introduction to the NIH-AARP Diet and Health Study

The NIH-AARP Diet and Health Study, see http://dietandhealth.cancer.gov/ and Schatzkin, et al. (2001), has two components, the main study with diet assessed by a Food Frequency Questionnaire (FFQ) and a calibration substudy with additional diet assessment by two 24hr. We considered a part of the main study that consists of n_p = 142, 364 women, who contributed an FFQ as well as relevant demographic characteristics. The data used were the same as in Sinha, et al. (2010). The covariates X used included an intercept, age, body mass index, the FFQ for energy intake and the FFQ for the dietary component in question. The 24hr was not available for these subjects. Thus, the primary sample represents data on X_i = X_i1 = X_i2 = X_i3 for i = 1, ..., n_p.

In addition to the primary sample, there was a subsample of n_v = 899 women in the calibration sub-study who completed an FFQ and demographic characteristics, so that there are X_i = X_i1 = X_i2 = X_i3 for = n_p + 1, ..., n_v + n_p. In addition, these women completed two 24hr. Hence we observed (Y_i1k, Y_i2k, Y_i3k) for k = 1, 2 and for i = n_p + 1, ..., n_v + n_p.

We illustrate our computational algorithm using data from both the two 24hr and the FFQ for whole grains, fish and energy intake, along with covariates. Following Kipnis, et al. (2009, 2010), the FFQ values for fish, whole grain and energy intake were transformed using λ = 0.25, λ = 0.33 and λ = 0.00, respectively. The 24hr used λ = 0.50, λ = 0.33 and λ = 0.33, respectively.

The MCMC calculations result in samples from the posterior distribution of $\text{𝓑}={({\mathit{\text{β}}}_1^{\text{T}},\hspace{0.17em}{\mathit{\text{β}}}_2^{\text{T}},\hspace{0.17em}{\mathit{\text{β}}}_3^{\text{T}})}^{\text{T}}$, Σ_u, Σ_ε and (U_i1, U_i2, U_i3), the latter only for i = n_p + 1, ..., n_v + n_p. The means of the samples for (𝓑, Σ_u, Σ_ε) can be taken as frequentist point estimates of these quantities, and are denoted here as (β̂₁, β̂₂, β̂₃, Σ̂_u, Σ̂_ε). We will use shorthand notation for usual intake:

• Usual dietary component intake is T_Fi

  $$={\text{𝓖}}_1\{{\mathbf{\text{X}}}_{i1},\hspace{0.17em}{\mathbf{\text{X}}}_{i2},\hspace{0.17em}{\mathit{\text{β}}}_1,\hspace{0.17em}{\mathit{\text{β}}}_2,\hspace{0.17em}{U}_{i1},\hspace{0.17em}{U}_{i2},\hspace{0.17em}{\sum }_{\epsilon }(2,2)\},\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\text{see}\hspace{0.17em}(6);$$

• Usual energy intake is T_Ei = 𝓖₂{X_i3, β₃, U_i3, ∑_ε(3, 3)}, see (7).

For both usual dietary component intake and usual energy intake, 24hr samples are available for i = n_p + 1, ..., n_v + n_p.

3.2. Frequentist Analysis

We are going to write the variable of interest as 𝓗(T_Fi, T_Ei). Thus, (a) the dietary component is 𝓗(T_Fi, T_Ei) = T_Fi; (b) energy is 𝓗(T_Fi, T_Ei) = T_Ei; and (c) the energy adjusted dietary component is 𝓗(T_Fi, T_Ei) = 1000 × T_Fi/T_Ei. In general then, the usual intake variable of interest for person i can be written as

$${\text{𝓠}}_i=\text{𝓗}[{\text{𝓖}}_1\{{\mathbf{\text{X}}}_{i1},\hspace{0.17em}{\mathbf{\text{X}}}_{i2},\hspace{0.17em}{\mathit{\text{β}}}_1,\hspace{0.17em}{\mathit{\text{β}}}_2,\hspace{0.17em}{U}_{i1},\hspace{0.17em}{U}_{i2},\hspace{0.17em}{\sum }_{\epsilon }(2,\hspace{0.17em}2)\},\hspace{0.17em}{\text{𝓖}}_2\{{\mathbf{\text{X}}}_{i3},\hspace{0.17em}{\mathit{\text{β}}}_3,\hspace{0.17em}{U}_{i3},\hspace{0.17em}{\sum }_{\epsilon }(3,\hspace{0.17em}3)\}],$$

for i = 1, ..., n_p + n_v, where we have that (U_i1, U_i2, U_i3) = Normal(0, Σ_u).

Estimation of the distribution of 𝓠 across the population is easily accomplished by a Monte-Carlo computation. This is a different Monte-Carlo computation than the MCMC, and is performed after the MCMC has been done. Specifically, for a large B, where we took B = 5, 000, and for b = 1, ..., B generate (U_bi1, U_bi2, U_bi3) = Normal(0, Σ̂_u). Here B is not the number of burn-in steps, but simply a large enough number to do numerical integration. Then the distribution of usual intake can be estimated as the empirical distribution of the values

$${\text{𝓠}}_{bi}=\text{𝓗}[{\text{𝓖}}_1\{{\mathbf{\text{X}}}_{i1},\hspace{0.17em}{\mathbf{\text{X}}}_{i2},\hspace{0.17em}{\widehat{\mathit{\text{β}}}}_1,\hspace{0.17em}{\widehat{\mathit{\text{β}}}}_2,\hspace{0.17em}{U}_{bi1},\hspace{0.17em}{U}_{bi2},\hspace{0.17em}{\widehat{\sum }}_{\epsilon }(2,\hspace{0.17em}2)\},\hspace{0.17em}{\text{𝓖}}_2\{{\mathbf{\text{X}}}_{i3},\hspace{0.17em}{\widehat{\mathit{\text{β}}}}_3,\hspace{0.17em}{U}_{bi3},\hspace{0.17em}{\widehat{\sum }}_{\epsilon }(3,\hspace{0.17em}3)\}],$$

taken across i = 1, ..., n_v + n_p and b = 1, ..., B.

Standard errors and confidence intervals for the distribution of usual intake can be formed easily by bootstrapping. We used 400 bootstrap samples in our numerical work.

Remark 6

For bootstrap confidence intervals, it is often recommended to use at least 399 bootstrap samples, as we have done, see for example Davidson and MacKinnon (1999). We have experimented with using up to 1, 000 bootstrap samples, but this significantly increases computing time without changing the basic results in any material way.

3.3. Bayesian Analysis

As described below, Bayesian inference on the distribution of usual intake depends on estimating the distribution of the covariates. The distribution of usual intake 𝓗(T_F, T_E) in a population can be described as follows. Let 𝓧 = (X₁, X₂, X₃) and let f_X(𝓧|ζ) = f_X(X₁, X₂, X₃, ζ) be the distribution of 𝓧 in the population, based on a parameter ζ. Write 𝓤 = (U₁, U₂, U₃)^T. Use the shorthand notation

$$\begin{array}{l}\text{𝓚}(\text{𝓧},\hspace{0.17em}\text{𝓑},\hspace{0.17em}\text{𝓤},\hspace{0.17em}{\sum }_{\epsilon })\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\text{𝓗}[{\text{𝓖}}_1\{{\mathbf{\text{X}}}_1,\hspace{0.17em}{\mathbf{\text{X}}}_2,\hspace{0.17em}{\mathit{\text{β}}}_1,\hspace{0.17em}{\mathit{\text{β}}}_2,\hspace{0.17em}{U}_1,\hspace{0.17em}{U}_2,\hspace{0.17em}{\sum }_{\epsilon }(2,\hspace{0.17em}2)\},\hspace{0.17em}{\text{𝓖}}_2\{{\mathbf{\text{X}}}_3,\hspace{0.17em}{\mathit{\text{β}}}_3,\hspace{0.17em}{U}_3,\hspace{0.17em}{\sum }_{\epsilon }(3,\hspace{0.17em}3)\}].\end{array}$$

Then the distribution of usual intake is

$$\begin{array}{l}F(v|\text{𝓑},\hspace{0.17em}{\sum }_u,\hspace{0.17em}\mathit{\text{ζ}},\hspace{0.17em}{\sum }_{\epsilon })=\text{pr}\{\text{𝓚}(\text{𝓧},\hspace{0.17em}\text{𝓑},\hspace{0.17em}\text{𝓤},\hspace{0.17em}{\sum }_{\epsilon })\le v|\text{𝓑},\hspace{0.17em}{\sum }_u,\hspace{0.17em}{\sum }_{\epsilon },\hspace{0.17em}\mathit{\text{ζ}}\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=\int I\{\text{𝓚}(\text{𝓧},\hspace{0.17em}\text{𝓑},\hspace{0.17em}\text{𝓤},\hspace{0.17em}{\sum }_{\epsilon })\le v\}{f}_{\text{𝓤}}(\text{𝓤}|{\sum }_u)f_X(\text{𝓧}|\mathit{\text{ζ}})d\text{𝓤}d\text{𝓧}.\end{array}$$

We suggest approximating this using Monte-Carlo integration, as follows. Again, let B be large where we took B = 1, 000, and for b = 1, ...B, let u_b = Normal(0, I₃). Let ${\sum }_u^{1/2}$ be the symmetric square root of Σ_u. Then

$$F(v|\text{𝓑},\hspace{0.17em}{\sum }_u,\hspace{0.17em}\mathit{\text{ζ}},\hspace{0.17em}{\sum }_{\epsilon })\approx B^{-1}{\sum }_{b=1}^B\int I\{\text{𝓚}(\text{𝓧},\hspace{0.17em}\text{𝓑},\hspace{0.17em}{\sum }_u^{1/2}{\mathbf{\text{u}}}_b,\hspace{0.17em}{\sum }_{\epsilon })\le v\}\hspace{0.17em}{f}_X(\text{𝓧}|\mathit{\text{ζ}})d\text{𝓧}.$$

The posterior distribution of F(v|𝓑, Σ_u, ζ, Σ_ε) is then calculated from the MCMC samples: our methods in the Appendix are easily generalized to sample from the posterior distribution of ζ.

In the NIH-AARP Diet and Health Study, with a sample size of n_p + n_v > 140, 000, we effectively know the distribution of 𝓧. Let the values in the data be 𝓧_i for i = 1, ..., n_v + n_p. Then we have

$$\begin{array}{l}F(v|\text{𝓑},\hspace{0.17em}{\sum }_u,\hspace{0.17em}\mathit{\text{ζ}},\hspace{0.17em}{\sum }_{\epsilon })\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\approx {\{(n_v+n_p)B\}}^{-1}{\sum }_{b=1}^B{\sum }_{i=1}^{n_v+n_p}I\{\text{𝓚}({\text{𝓧}}_i,\hspace{0.17em}\text{𝓑},\hspace{0.17em}{\sum }_u^{1/2}{\mathbf{\text{u}}}_b,\hspace{0.17em}{\sum }_{\epsilon })\le v\}.\end{array}$$

The posterior distribution of F(v|𝓑, Σ_u, ζ, Σ_ε) can then be calculated from the MCMC samples.

4. Results

Along with illustrating the distributions of usual intakes of the dietary components adjusted for energy, we also compared our results with NLMIXED.

4.1. Analysis

We used a burn-in of 5,000 steps followed by 15,000 MCMC samples. We saved every 10^th sample to reduce autocorrelation.

4.1.1. Frequentist Analysis

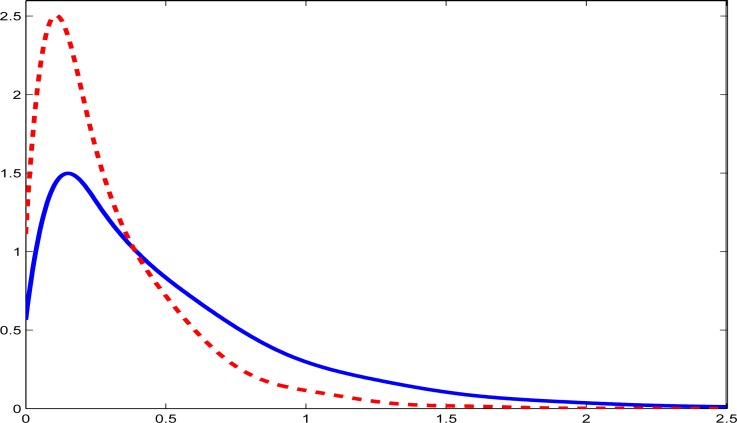
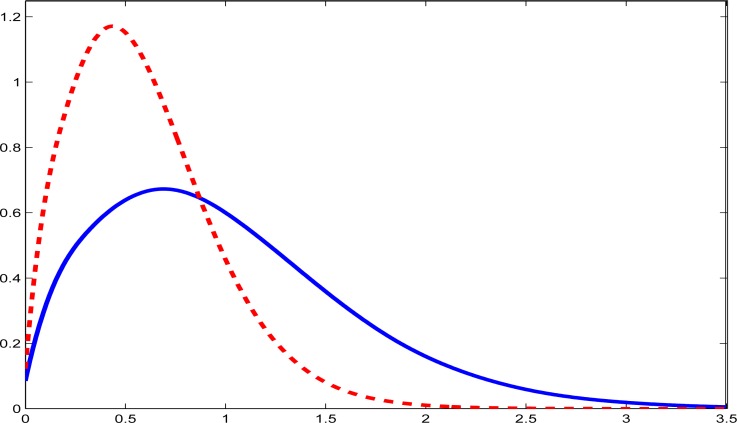
In Table 1 we present summary statistics (mean, standard deviation and selected percentiles) of the usual intakes as well as the usual intakes adjusted for energy. Figures 1 and 2 give density estimates for usual intake and energy adjusted intake of fish and whole grains, respectively: a similar plot for usual energy intake was also produced but not displayed here. The evident skewness of the usual intakes of fish and whole grains is expected, as are the somewhat less skewed nature of the energy adjusted intakes.

Table 1:

Estimated distributions of the usual intake for Whole Grains, Fish and Energy and the estimated distributions of energy-adjusted usual intake for Whole Grains and Fish, for women. The 5^th percentile of the distribution is labeled as 5^th, etc. For energy-adjusted fish intake, we give the results for both the frequentist (“Freq”) and the Bayesian (“Bayes”) fits. Estimates were very similar for both Freq and Bayes fits and thus we have only displayed results for fish.

	Whole Grains		Fish			Energy
	Usual Intake (Unit: cup)	per 1000 kcals	Usual Intake (Unit: oz.)	per 1000 kcals	Bayes, per 1000 kcals	Usual Intake (Unit: kcal)
Mean	1.013	0.625	0.539	0.338	0.339	1631.77
s.d.	0.631	0.375	0.486	0.309	0.315	369.16
5th	0.181	0.121	0.053	0.033	0.028	1075.70
10th	0.287	0.189	0.089	0.057	0.057	1180.37
25th	0.536	0.345	0.193	0.122	0.122	1370.29
50th	0.911	0.569	0.399	0.249	0.249	1604.04
75th	1.375	0.841	0.736	0.456	0.456	1863.01
90th	1.867	1.127	1.176	0.731	0.731	2118.74
95th	2.195	1.320	1.508	0.945	0.951	2282.50

Figure 1:

Density estimates for fish. The solid line is the density estimate for usual intake in the unit of oz. The dashed line is the density estimate for usual intake per 1000 kilo-calories.

Figure 2:

Density estimates for whole grains. The solid line is the density estimate for usual intake in the unit of cups. The dashed line is the density estimate for usual intake per 1000 kilo-calories.

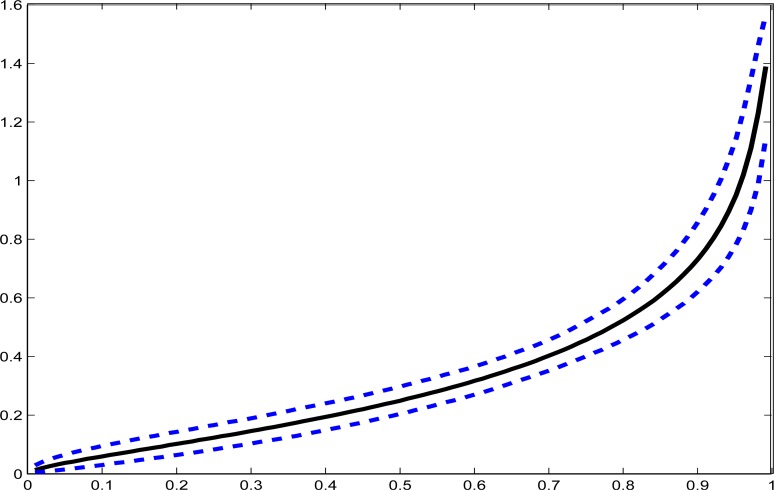
We bootstrapped the validation and primary data sets separately 400 times, see Remark 6, reran the analysis, and formed bootstrap confidence intervals. Since the distribution of the covariates X is essentially known because of the size of the primary study, this bootstrap simply reflects the uncertainty in the parameter estimates as they propagate through to usual intakes. To give a graphical summary including uncertainty, in Figure 3 we plot the actual estimated percentiles of the distribution of adjusted fish intake against the percentile number, as well as the 95% pointwise bootstrap confidence interval for these percentiles.

Figure 3:

Quantile functions for usual fish intake per 1000 kilo-calories. Horizontal axis is the relative percentile, e.g., the value at 50 is the median. The vertical axis is the estimated percentile (solid line) in the unit of oz./(1000 kcal). Dashed lines are the pointwise 95% bootstrap confidence intervals.

4.1.2. Bayesian Analysis

In Table 1 we also give the Bayesian analysis for energy-adjusted fish intake. As seen there, the Bayesian analysis posterior means of the distribution of energy-adjusted fish intake is nearly identical to the frequentist analysis. The same thing was found for all the columns in Table 1.

In addition, posterior credible interval lengths were almost equivalent to those of the frequentist method and are not displayed here.

4.2. Comparison With Proc NLMIXED

We described in Section 2.4 some of the motivation for our computational approach. In this section, we show documentation of those claims.

First, in Table 2, we describe aspects of the analysis for women of whole grains, fish and dark-green vegetables, using the AARP data set. The first line in the table is the number of minutes of computation for the nonlinear mixed effects program and our MCMC approach. It can be seen that the MCMC approach is considerably faster. While not displayed here, for Milk for men, which had only 12% reported non-consumption on the 24hr, the nonlinear mixed effects program took 200 minutes, while ours took only 4 minutes. This illustrates our claim concerning speed of computation.

Table 2:

Comparison between two computational methods, “NLMIXED” and “MCMC”, to fit the bivariate nonlinear mixed effects model, for whole grains, fish and dark-green vegetables. Displayed are the estimates of correlations among the components of (U_i1, U_i2, U_i3), the estimates for the MCMC approach being posterior means. The numbers displayed in parentheses are the standard errors from the inverse of the Hessian matrix (“NLMIXED”) and from MCMC samples (“MCMC”). Here “Dark Green” refers to Dark-Green vegetables, where the nonlinear mixed effects analysis converged but to a singular covariance matrix for Σ_u. The phrase “Time in Minutes” refers to computation time to complete the analysis. The overall % of zeros from the 24hr are also displayed.

	Whole Grains		Fish		Dark Green
	NLMIXED	MCMC	NLMIXED	MCMC	NLMIXED	MCMC
Time in Minutes	20	3	12	3	12	4
% zeros on 24hr	32%		77%		73%
Correlations
corr(Ui1, Ui2)	0.65 (0.17)	0.48 (0.09)	−0.39 (0.44)	0.08 (0.07)	1.00 (N/A)	0.48 (0.06)
corr(Ui1, Ui3)	0.20 (0.08)	0.18 (0.07)	0.28 (0.14)	0.26 (0.07)	0.27 (N/A)	0.24 (0.06)
corr(Ui2, Ui3)	0.37 (0.10)	0.40 (0.07)	0.02 (0.16)	0.02 (0.09)	0.27 (N/A)	0.28 (0.06)

A second aspect is that we claimed that sometimes the nonlinear mixed effects analysis of Kipnis, et al. (2010) suffered from convergence to a singular covariance matrix estimate for Σ_u. This occurred for dark-green vegetables, see Table 2, where it was estimated that the correlation between (U_i1, U_i2), corr(U_i1, U_i2), was equal to 1.00. This seemingly ridiculous result is in marked contrast to the much more sensible posterior mean of 0.48.

A third aspect of the comparison is that we claimed that when the method of Kipnis, et al. (2010) converged to a reasonable answer, our results were in general agreement with theirs. This is borne out in Table 2, where we have listed the standard errors of the estimates using the Hessian for the nonlinear mixed effects analysis, and using the MCMC samples for our method. The estimates are quite similar with the exception of corr(U_i1, U_i2) for fish, which can be explained as follows. We performed a separate bootstrap calculation for this correlation with our method and the nonlinear mixed effects analysis, which suggested a standard error as large as the difference between the two. The other standard errors are also different, but this may well reflect imprecision in the former caused by using a Hessian in a nonlinear mixed effects model instead of a bootstrap.

Remark 7

While it may seem obvious, it is useful to clarify what we mean by the term “convergence”. We are not meaning asymptotic rates of convergence, because these are the standard n^1/2-type one sees in parametric models. We are also not talking about theoretical rates of numerical convergence, e.g., how fast is convergence of the Proc NLMIXED procedure in terms of number of iterations. Instead, for us the term convergence has the meaning that Proc NLMIXED announces that it has converged to a solution with a nonsingular Hessian. Of course, our method, being based on proper priors, converges in the usual MCMC sense.

5. Discussion

Understanding the distribution of energy-adjusted usual intake of episodically consumed dietary components is of considerable public health importance, having implications for basic understanding of both dietary component composition and policy. Being able to correct for measurement error due to within-person variation in short-term assessment of intake, when investigating diet-disease relationships in cohort studies, is equally important. Because of the importance of these problems, models and fitting methods for addressing them will find wide use in the nutrition community. Thus, it is not only important that the models are reasonable, but that the fitting methods be reasonably fast, that they converge, and that the answers from the fitting methods usually make sense. The main point of this paper has been to show that an MCMC approach satisfies these criteria, and has the potential to be used widely in the nutrition community. The fact that the MCMC approach can be used in a frequentist sense is a new insight for nutritional epidemiology, which is decidedly frequentist in orientation, although the MCMC model fitting can also allow Bayesian inference.

There is an enormous literature on measurement error models, both parametric and nonparametric, for estimating distributions (e.g., Fan, 1991; Wand, 1998; Johnson, et al., 2007; Staudenmeyer, et al., 2008; Delaigle, et al, 2008 among many others) and in regression (Ferrari, et al., 2004, e.g., Liang and Wang, 2005 among many others). Many more references are given in Carroll, et al. (2006). However, none of these papers deal with our topic of episodically consumed and hence zero-inflated dietary components along with continuous components that involve skewness, a structured covariance matrix, correlations of random effects, and usual intakes on the original data scale.

An issue of practically much less importance is that the model of Kipnis, et al. (2010) in equation (6) assumes that each food is consumed by all individuals. Kipnis, et al. (2009) address this issue, by adding a fixed effect regression so as to model never-consumers. They show that even without energy in the model, and with only two 24hr as is standard for such data, their method was numerically very unstable. Our method easily handles such an extension, but its practical implications are not particularly clear when, for example, in other studies, less than 0.5% of subjects claimed on the FFQ never to eat fish or whole grains.

User-friendly SAS macros are being written for distribution to the nutrition community. These programs will also allow sampling weights, so that they can be used in population-based survey samples, and will thus be of interest both nationally and internationally. We are presently working on extending the methods to analyze multiple foods and nutrients simultaneously, with allowance for survey weights, so that analysis of dietary patterns and dietary composite scores can be undertaken.

Supplementary Materials

food.and.energy.paper.preprint.vk.doc

This preprint was requested by reviewer #3

food.and.energy.paper.figure1.pdf

Fig. 1 for the requested preprint.

Appendix: Details of the MCMC

A.1. Notational Convention

Standardization is important in MCMC applications both for numerical stability and to allow fairly off-the-shelf prior distributions to make sense. Prior to analysis, we standardized the covariates to have mean 0.0 and variance 1.0. The observed, transformed non-zero 24hr were standardized to have mean 0.0 and variance 2.0. More precisely, we first transformed the non-zero dietary component data as Z_i2k = g(Y_i2k, λ_F), and then we standardized these data as $Q_{i2k}=\sqrt{2}(Z_{i2k}-a_F)/s_F$. Similarly, for energy we transformed to Z_i3k = g(Y_i3k, λ_E) and then standardized to $Q_{i3k}=\sqrt{2}(Z_{i3k}-a_E)/s_E$. Of course, whether the dietary component is consumed or not is Q_i1k = Y_i1k. Collected, the data are Q̃_ik = (Q_i1k, Q_i2k, Q_i3k)^T. The terms (a_F, s_F, a_E, s_E) are not random variables but are merely constants used for standardization, and we need not consider inference for them.

We will first describe the algorithm used in terms of the Q_ijk, and then in Section A.11, we describe the back-transformation method that we used to obtain estimation and inference for usual intake.

Remark 8

Having the total variability of the non-zero transformed responses equal to 2.0 is extraordinarily convenient. Effectively, this means that var(U_ij) + var(ε_ij) ≈ 2.0 for j = 1, 2. Thus, neither component of this sum is at all likely to be large. Hence, a prior mean for the diagonal elements of Σ_u all equalling 1.0, while too large in our examples, is at least relatively near a reasonable answer. Having priors for var(ε_ij) for j = 1, 2 that are Uniform[0, 3] is flexible and does not allow ridiculous answers.

A.2. Prior Distributions

Because the data were standardized, following the discussion of Remark 8, we used the following conventions.

• The priors for all β_j were normal with mean zero and variance 100.

• The prior for Σ_u was exchangeable with diagonal entries all equal to 1.0 and correlations 0.50. There was 5 degrees of freedom in the inverse Wishart prior, i.e., m_u = 5. Thus, the prior is IW{(m_u − 3 − 1)Ω_u, m_u}.

• The priors for s₂₂ and s₃₃ were Uniform[0,3]. This range is reasonable because of the standardization.

• The priors for (γ, θ) were uniform on their range.

We experimented with different priors for Σ_u, e.g., setting the correlations equal to 0.0, setting the diagonal elements equal to 0.5, etc. The results were essentially unchanged when these were done.

A.3. Generating Starting Values for the Latent Variables

While we observe Q̃_ik, in the MCMC we need to generate the latent variables W̃_ik to initiate the MCMC.

• For energy, Q_i3k = W_i3k, no data need to be generated.

• For the amounts, Q_i2k, we just simply set W_i2k = Q_i2k.

• For consumption, we generate 𝓤_i = (U_i1, U_i2, U_i3)^T as normally distribution with mean zero and covariance matrix given as the prior covariance matrix for Σ_u. We then also compute $z_{\mathit{\text{ik}}}=|{\mathbf{\text{X}}}_{i1}^{\text{T}}{\mathit{\text{β}}}_{1,\hspace{0.17em}\text{prior}}+U_{i1}+Z_{\mathit{\text{ik}}}|$, where Z_ik = Normal(0, 1) are generated independently. We then set W_i1k = z_ikQ_i1k − z_ik(1 − Q_i1k).

• We then updated W̃_ik by a single application of the updates given in Section A.9.

A.4. Complete Data Loglikelihood

The loglikelihood of the complete data is

$$\begin{array}{l}{\sum }_{i=1}^n{\sum }_{k=1}^2\text{log}\{Q_{i1k}I(W_{i1k}>0)+(1-Q_{i1k})I(W_{i1k}<0)\}\\ +(n/2)\text{log}(|{\sum }_u^{-1}|)-(1/2){\sum }_{i=1}^n{\text{𝓤}}_i^{\text{T}}{\sum }_u^{-1}{\text{𝓤}}_i\\ -(1/2){\sum }_{j=1}^3{({\mathit{\text{β}}}_j-{\mathit{\text{β}}}_{j,\hspace{0.17em}\text{prior}})}^{\text{T}}{\Omega }_{\beta ,j}^{-1}({\mathit{\text{β}}}_j-{\mathit{\text{β}}}_{j,\text{prior}})\\ +\{(m_u+3+1)/2\}\text{log}(|{\sum }_u^{-1}|)-(1/2)\text{trace}({\Omega }_u{\sum }_u^{-1})\\ -(1/2)(2n)\text{log}\{s_{22}{s}_{33}(1-{\gamma }^2)\}\\ -(1/2){\sum }_{i=1}^n{\sum }_{k=1}^2{\{{\widetilde{\mathbf{\text{W}}}}_{\mathit{\text{ik}}}-{({\mathbf{\text{X}}}_{i1}^{\text{T}}{\mathit{\text{β}}}_1,\hspace{0.17em}\dots ,\hspace{0.17em}{\mathbf{\text{X}}}_{i3}^{\text{T}}{\mathit{\text{β}}}_3)}^{\text{T}}-{\text{𝓤}}_i\}}^{\text{T}}{\sum }_{\epsilon }^{-1}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times \{{\widetilde{\mathbf{\text{W}}}}_{\mathit{\text{ik}}}-{({\mathbf{\text{X}}}_{i1}^{\text{T}}{\mathit{\text{β}}}_1,\hspace{0.17em}\dots ,\hspace{0.17em}{\mathbf{\text{X}}}_{i3}^{\text{T}}{\mathit{\text{β}}}_3)}^{\text{T}}-{\text{𝓤}}_i\}.\end{array}$$

A.5. Complete Conditionals for (γ, θ, s₂₂, s₃₃)

The complete conditionals for (γ, θ, s₂₂, s₃₃) do not have an explicit form, so we use a Metropolis-Hastings within Gibbs sampler to generate them in turn. Since Σ_ε is determined by γ, θ, s₂₂ and s₃₃, we write it as ${\sum }_{\epsilon }^{-1}$ ≡ f(γ, θ, s₂₂, s₃₃). Also, current values are γ_t, θ_t, s_{22, t} and s_{33, t}.

Generation of γ

For convenience, we set γ to be discrete with 41 equally-spaced values on its range. Let γ_t be the current value. The candidate value y is selected randomly from γ_t and its two nearest neighbors. The candidate value y is accepted with probability α(γ_t, y), α(γ_t, y) = min{1, g(y)/g(γ_t)}, where

$$\begin{array}{l}g(y)\hspace{0.17em}\hspace{0.17em}\propto \hspace{0.17em}\hspace{0.17em}{(1-y^2)}^{-n}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times \text{exp}[-(1/2){\sum }_{i=1}^n{\sum }_{k=1}^2{\{{\widetilde{\mathbf{\text{W}}}}_{\mathit{\text{ik}}}-{({\mathbf{\text{X}}}_{i1}^{\text{T}}{\mathit{\text{β}}}_1,\hspace{0.17em}\dots ,\hspace{0.17em}{\mathbf{\text{X}}}_{i3}^{\text{T}}{\mathit{\text{β}}}_3)}^{\text{T}}-{\text{𝓤}}_i\}}^{\text{T}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times f(y,\hspace{0.17em}{\theta }_t,\hspace{0.17em}{s}_{22,t},\hspace{0.17em}{s}_{33,t})\{•\}],\end{array}$$

where {•} means that the term before f(·) is transposed and substituted. If the candidate y is accepted, then γ_t+1 = y. Otherwise, γ_t+1 = γ_t.

Generation of θ

This is done exactly as for γ, except now

$$\begin{array}{c}g(y)\propto \text{exp}[-(1/2){\sum }_{i=1}^n{\sum }_{k=1}^2{\{{\widetilde{\mathbf{\text{W}}}}_{\mathit{\text{ik}}}-{({\mathbf{\text{X}}}_{i1}^{\text{T}}{\mathit{\text{β}}}_1,\hspace{0.17em}\dots ,\hspace{0.17em}{\mathbf{\text{X}}}_{i3}^{\text{T}}{\mathit{\text{β}}}_3)}^{\text{T}}-{\text{𝓤}}_i\}}^{\text{T}}\\ \times f({\gamma }_{t+1},\hspace{0.17em}y,\hspace{0.17em}{s}_{22,t},\hspace{0.17em}{s}_{33,t})\{•\}].\end{array}$$

If the candidate y is accepted, then θ_t+1 = y. Otherwise, θ_t+1 = θ_t.

Generation of s₂₂

Suppose the current value of s₂₂ is s_{22, t}. A candidate value y is generated from the Uniform distribution of length 0.4 with mean s_{22, t}: y ∼ Uniform [s_{22, t} − 0.2, s_{22, t} + 0.2]. The candidate value y is accepted with probability α(s_{22, t}, y), where

$$\begin{array}{l}\alpha (s_{22,t},\hspace{0.17em}y)=\text{min}\{(1,\hspace{0.17em}g(y)I_{[0,3]}(y)/g(s_{22,t})\};\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}g(y)\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\propto \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}{y}^{-n}\text{exp}[-(1/2){\sum }_{i=1}^n{\sum }_{i=1}^2{\{{\widetilde{\mathbf{\text{W}}}}_{\mathit{\text{ik}}}-{({\mathbf{\text{X}}}_{i1}^{\text{T}}{\mathit{\text{β}}}_1,\hspace{0.17em}\dots ,\hspace{0.17em}{\mathbf{\text{X}}}_{i3}^{\text{T}}{\mathit{\text{β}}}_3)}^{\text{T}}-{\text{𝓤}}_i\}}^{\text{T}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times f({\gamma }_{t+1},\hspace{0.17em}{\theta }_{t+1},\hspace{0.17em}y,\hspace{0.17em}{s}_{33,t})\{•\}]\end{array}$$

If the candidate is accepted, then s_{22, t+1} = y. Otherwise, s_{22, t+1} = s_{22, t}.

Generation of s₃₃

This is the same as that for s₂₂, except now

$$\begin{array}{l}\alpha (s_{33,\hspace{0.17em}t},\hspace{0.17em}y)\hspace{0.17em}=\hspace{0.17em}\text{min}\{1,\hspace{0.17em}g(y)I_{[0,3]}(y)/g(s_{33},\hspace{0.17em}t)\};\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}g(y)\hspace{0.17em}\propto \hspace{0.17em}{y}^{-n}\text{exp}[-\frac{1}{2}{\sum }_{i=1}^n{\sum }_{k=1}^2{\{{\widetilde{\mathbf{\text{W}}}}_{\mathit{\text{ik}}}-{({\mathbf{\text{X}}}_{i1}^{\text{T}}{\mathit{\text{β}}}_1,\hspace{0.17em}\dots \hspace{0.17em},\hspace{0.17em}{\mathbf{\text{X}}}_{i3}^{\text{T}}{\mathit{\text{β}}}_3)}^{\text{T}}-{\text{𝓤}}_i\}}^{\text{T}}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times f({\gamma }_{t+1},\hspace{0.17em}{\theta }_{t+1},\hspace{0.17em}{s}_{22,t+1},\hspace{0.17em}y)\{•\}].\end{array}$$

If the candidate is accepted, then s_{33, t+1} = y. Otherwise, s_{33, t+1} = s_{33, t}.

A.6. Complete Conditional for Σ_u

By “rest”, we mean all the observable data, latent variables and parameters other than the one in question. By inspection, the complete conditional for Σ_u is

$$[{\sum }_u|\text{rest}]=\text{IW}\{(m_u-K-1){\Omega }_u+{\sum }_{i=1}^n{\text{𝓤}}_i{\text{𝓤}}_i^{\text{T}},\hspace{0.17em}n+m_u\}.$$

A.7. Complete Conditionals for β

Let the elements of ${\sum }_{\epsilon }^{-1}$ be ${\sigma }_{\epsilon }^{j\ell }$. For any j, except for irrelevant constants,

$$\begin{array}{lll}\text{log}\left[{\mathit{\text{β}}}_j|\text{rest}\right]\hfill & =\hfill & -(1/2){({\mathit{\text{β}}}_j-{\mathit{\text{β}}}_{j,\text{prior}})}^{\text{T}}{\Omega }_{\beta ,j}^{-1}({\mathit{\text{β}}}_j-{\mathit{\text{β}}}_{j,\text{prior}})\hfill \\ \hfill & \hfill & -(1/2){\sum }_{i=1}^n{\sum }_{k=1}^2{(W_{\mathit{\text{ijk}}}-{\mathbf{\text{X}}}_{\mathit{\text{ij}}}^{\text{T}}{\mathit{\text{β}}}_j-U_{\mathit{\text{ij}}})}^2{\sigma }_{\epsilon }^{jj}\hfill \\ \hfill & \hfill & -{\sum }_{i=1}^n{\sum }_{k=1}^2{\sum }_{\ell \ne j}{\sigma }_{\epsilon }^{j\ell }(W_{\mathit{\text{ijk}}}-{\mathbf{\text{X}}}_{\mathit{\text{ij}}}^{\text{T}}{\mathit{\text{β}}}_j-U_{\mathit{\text{ij}}})(W_{i\ell k}-{\mathbf{\text{X}}}_{i\ell }^{\text{T}}{\mathit{\text{β}}}_{\ell }-U_{i\ell })\hfill \\ \hfill & =\hfill & {\text{𝓒}}_1^{\text{T}}{\mathit{\text{β}}}_j-(1/2){\mathit{\text{β}}}_j^{\text{T}}{\text{𝓒}}_2^{-1}{\mathit{\text{β}}}_j\hfill \end{array}$$

which implies [β_j |rest] ∼ Normal(𝓒₂𝓒₁, 𝓒₂), where

$$\begin{array}{lll}{\text{𝓒}}_2\hfill & =\hfill & {({\Omega }_{\beta ,j}^{-1}+2{\sum }_{i=1}^n{\sigma }_{\epsilon }^{jj}{\mathbf{\text{X}}}_{\mathit{\text{ij}}}{\mathbf{\text{X}}}_{\mathit{\text{ij}}}^{\text{T}})}^{-1};\hfill \\ {\text{𝓒}}_1\hfill & =\hfill & {\Omega }_{\beta ,j}^{-1}{\beta }_{j,\text{prior}}+{\sum }_{i=1}^n{\sum }_{k=1}^2{\sigma }_{\epsilon }^{jj}{\mathbf{\text{X}}}_{\mathit{\text{ij}}}(W_{\mathit{\text{ijk}}}-U_{\mathit{\text{ij}}})\hfill \\ \hfill & \hfill & +{\sum }_{i=1}^n{\sum }_{k=1}^2{\sum }_{\ell \ne j}{\sigma }_{\epsilon }^{j\ell }(W_{i\ell k}-{\mathbf{\text{X}}}_{i\ell }^{\text{T}}{\mathit{\text{β}}}_{\ell }-U_{i\ell }){\mathbf{\text{X}}}_{\mathit{\text{ij}}}.\hfill \end{array}$$

A.8. Complete Conditionals for 𝓤_i

Except for irrelevant constants, and remembering that j = 1, ..., 3,

$$\begin{array}{lll}\text{log}\left[{\widetilde{\mathbf{\text{U}}}}_{\mathbf{\text{i}}}|\text{rest}\right]\hfill & =\hfill & -(1/2){\text{𝓤}}_i^{\text{T}}{\sum }_{\mathbf{\text{u}}}^{-1}{\text{𝓤}}_i\hfill \\ \hfill & \hfill & \begin{array}{l}-(1/2){\sum }_{k=1}^2{\{{\widetilde{\mathbf{\text{W}}}}_{\mathit{\text{ik}}}-{({\mathbf{\text{X}}}_{i1}^{\text{T}}{\mathit{\text{β}}}_1,\hspace{0.17em}\dots \hspace{0.17em},\hspace{0.17em}{\mathbf{\text{X}}}_{i3}^{\text{T}}{\mathit{\text{β}}}_3)}^{\text{T}}-{\text{𝓤}}_i\}}^{\text{T}}{\sum }_{\epsilon }^{-1}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\times \{{\widetilde{\mathbf{\text{W}}}}_{\mathit{\text{ik}}}-{({\mathbf{\text{X}}}_{i1}^{\text{T}}{\mathit{\text{β}}}_1,\hspace{0.17em}\dots \hspace{0.17em},\hspace{0.17em}{\mathbf{\text{X}}}_{i3}^{\text{T}}{\mathit{\text{β}}}_3)}^{\text{T}}-{\text{𝓤}}_i\}\end{array}\hfill \\ \hfill & =\hfill & {\text{𝓒}}_1^{\text{T}}{\text{𝓤}}_i-(1/2){\text{𝓤}}_i^{\text{T}}{\text{𝓒}}_2^{-1}{\text{𝓤}}_i\hfill \end{array}$$

which implies [𝓤_i|rest] ∼ Normal(𝓒₂𝓒₁, 𝓒₂), where

$$\begin{array}{l}{\text{𝓒}}_2\hspace{0.17em}=\hspace{0.17em}{({\sum }_u^{-1}+2{\sum }_{\epsilon }^{-1})}^{-1};\\ {\text{𝓒}}_1\hspace{0.17em}=\hspace{0.17em}{\sum }_{k=1}^2{\sum }_{\epsilon }^{-1}\{{\widetilde{\mathbf{\text{W}}}}_{\mathit{\text{ik}}}-{({\mathbf{\text{X}}}_{i1}^{\text{T}}{\mathit{\text{β}}}_1,\hspace{0.17em}\dots \hspace{0.17em},\hspace{0.17em}{\mathbf{\text{X}}}_{i3}^{\text{T}}{\mathit{\text{β}}}_3)}^{\text{T}}\}.\end{array}$$

A.9. Complete Conditionals for W_i1k

Here we do the complete conditional for W_iℓk with ℓ = 1. Except for irrelevant constants,

$$\begin{array}{lll}\text{log}[W_{i\ell k}|\text{rest}]\hfill & =\hfill & \text{log}\{Q_{i\ell k}I(W_{i\ell k}>0)+(1-Q_{i\ell k})I(W_{i\ell k}<0)\}\hfill \\ \hfill & \hfill & -(1/2)(W_{i1k}-{\mathbf{\text{X}}}_{i1}^{\text{T}}{\mathit{\text{β}}}_1-U_{i1},\hspace{0.17em}\dots \hspace{0.17em},\hspace{0.17em}{W}_{i3k}-{\mathbf{\text{X}}}_{i3}^{\text{T}}{\mathit{\text{β}}}_3-U_{i3}){\sum }_{\epsilon }^{-1}(•)\hfill \\ \hfill & =\hfill & \text{log}\{Q_{i\ell k}I(W_{i\ell k}>0)+(1-Q_{i\ell k})I(W_{i\ell k}<0)\}\hfill \\ \hfill & \hfill & -(1/2){\sigma }_{\epsilon }^{\ell \ell }{(W_{i\ell k}-{\mathbf{\text{X}}}_{i\ell }^{\text{T}}{\mathit{\text{β}}}_{\ell }-U_{i\ell })}^2\hfill \\ \hfill & \hfill & -{\sum }_{j\ne \ell }{\sigma }_{\epsilon }^{\ell j}(W_{i\ell k}-{\mathbf{\text{X}}}_{i\ell }^{\text{T}}{\mathit{\text{β}}}_{\ell }-U_{i\ell })(W_{\mathit{\text{ijk}}}-{\mathbf{\text{X}}}_{\mathit{\text{ij}}}^{\text{T}}{\mathit{\text{β}}}_j-U_{\mathit{\text{ij}}})\hfill \\ \hfill & =\hfill & \text{log}\{Q_{i\ell k}I(W_{i\ell k}>0)+(1-Q_{i\ell k})I(W_{i\ell k}<0)\}\hfill \\ \hfill & \hfill & +{\text{𝓒}}_1{W}_{i\ell k}-(1/2)W_{i\ell k}^2{\text{𝓒}}_2^{-1},\hfill \end{array}$$

where

$$\begin{array}{l}{\text{𝓒}}_2=1/({\sigma }_{\epsilon }^{\ell \ell })\\ {\text{𝓒}}_1={\sigma }_{\epsilon }^{\ell \ell }({\mathbf{\text{X}}}_{i\ell }^{\text{T}}{\beta }_{\ell }+U_{i\ell })-{\sum }_{j\ne \ell }{\sigma }_{\epsilon }^{\ell j}(W_{\mathit{\text{ijk}}}-{\mathbf{\text{X}}}_{\mathit{\text{ij}}}^{\text{T}}{\mathit{\text{β}}}_j-U_{\mathit{\text{ij}}}).\end{array}$$

If we use the notation TN₊(μ, σ, c) for a normal random variable with mean μ, standard deviation σ is truncated from the left at c, and TN₋(μ, σ, c) is truncated from the right at c, then it follows that with μ = 𝓒₂𝓒₁ and $\sigma ={\text{𝓒}}_2^{1/2}$,

$$\begin{array}{lll}[W_{i\ell k}|\text{rest}]\hfill & =\hfill & Q_{i\ell k}{\text{TN}}_{+}(\mu ,\hspace{0.17em}\sigma ,\hspace{0.17em}0)+(1-Q_{i\ell k}){\text{TN}}_{-}(\mu ,\hspace{0.17em}\sigma ,\hspace{0.17em}0)\hfill \\ \hfill & =\hfill & \mu +Q_{i\ell k}{\text{TN}}_{+}(0,\hspace{0.17em}\sigma ,\hspace{0.17em}-\mu )+(1-Q_{i\ell k}){\text{TN}}_{-}(0,\hspace{0.17em}\sigma ,\hspace{0.17em}-\mu )\hfill \\ \hfill & =\hfill & \mu +Q_{i\ell k}{\text{TN}}_{+}(0,\hspace{0.17em}\sigma ,\hspace{0.17em}-\mu )-(1-Q_{i\ell k}){\text{TN}}_{+}(0,\hspace{0.17em}\sigma ,\hspace{0.17em}\mu )\hfill \\ \hfill & =\hfill & \mu +\sigma \{Q_{i\ell k}{\text{TN}}_{+}(0,\hspace{0.17em}1,\hspace{0.17em}-\mu /\sigma )-(1-Q_{i\ell k}){\text{TN}}_{+}(0,\hspace{0.17em}1,\hspace{0.17em}\mu /\sigma )\}.\hfill \end{array}$$

Generating TN₊(0, 1, c) is easy: if c < 0, simply do rejection sampling of a Normal(0, 1) until you get one that is > c. If c > 0, there is an adaptive rejection scheme (Robert, 1995). The “truncated normal” was used because the latent variable W_i1k is associated with Y_i1k which indicates whether the dietary component is consumed or not. If the dietary component is indeed consumed, then based on our model (2), W_i1k should have a positive value. Similarly, if the dietary component is actually not consumed, then W_i1k should have a negative value. In order to achieve these, we need a truncated distribution. Besides, the conditional distribution of W_i1k proportional to a normal distribution, thus we chose truncated normal.

A.10. Complete Conditionals for W_i2k When it is Not Observed

For p = 2, the variable W_ipk is not observed when Q_{i, p−1, k} = 0, or, equivalently, when W_{i, p−1, k} < 0. Except for irrelevant constants,

$$\begin{array}{lll}\text{log}[W_{\mathit{\text{ipk}}}|\text{rest}]\hfill & =\hfill & -(1/2)\sum _j\sum _{\ell }{\sigma }_{\epsilon }^{j\ell }(W_{\mathit{\text{ijk}}}-{\mathbf{\text{X}}}_{\mathit{\text{ij}}}^{\text{T}}{\mathit{\text{β}}}_j-U_{\mathit{\text{ij}}})(W_{i\ell k}-{\mathbf{\text{X}}}_{i\ell }^{\text{T}}{\mathit{\text{β}}}_{\ell }-U_{i\ell })\hfill \\ \hfill & =\hfill & -(1/2)W_{\mathit{\text{ipk}}}^2{\text{𝓒}}_2^{-1}+{\text{𝓒}}_1{W}_{\mathit{\text{ipk}}}\hfill \end{array}$$

where

$$\begin{array}{l}{\text{𝓒}}_2=1/({\sigma }_{\epsilon }^{pp});\\ {\text{𝓒}}_1={\sigma }_{\epsilon }^{pp}({\mathbf{\text{X}}}_{ip}^{\text{T}}{\mathit{\text{β}}}_p+U_{ip})-\sum _{\ell \ne p}{\sigma }_{\epsilon }^{p\ell }(W_{i\ell k}-{\mathbf{\text{X}}}_{i\ell }^{\text{T}}{\mathit{\text{β}}}_{\ell }-U_{i\ell }).\end{array}$$

Therefore,

$$[W_{\mathit{\text{ipk}}}|\text{rest}]=Q_{\mathit{\text{ipk}}}{Q}_{i,p-1,k}+(1-Q_{i,p-1,k})\text{Normal}({\text{𝓒}}_2{\text{𝓒}}_1,\hspace{0.17em}{\text{𝓒}}_2).$$

A.11. Usual Intake, Standardization and Transformation

Here we show how to go from the transformed and standardized data to usual intakes. We first consider energy, where we used the transformation

$$Q_{i3k}=\sqrt{2}\{g(Y_{i3k},\hspace{0.17em}{\lambda }_E)-a_E\}/s_E=g_{\text{tr}}(Y_{i3k},\hspace{0.17em}{\lambda }_E,\hspace{0.17em}{a}_E,\hspace{0.17em}{s}_E)={\mathbf{\text{X}}}_{i3}^{\text{T}}{\mathit{\text{β}}}_3+U_{i3}+{\epsilon }_{i3k}.$$

When λ_E = 0, the back-transformation is

$$\begin{array}{ccc}\hfill g_{\text{tr}}^{-1}(z,\hspace{0.17em}0,\hspace{0.17em}{a}_E,\hspace{0.17em}{s}_E)& =& \text{exp}\{a_E+s_{E}z/\sqrt{2}\};\hfill \\ \hfill {\partial }^2{g}_{\text{tr}}^{-1}(z,\hspace{0.17em}0,\hspace{0.17em}{a}_E,\hspace{0.17em}{s}_E)/\partial z^2& =& \frac{s_E^2}{2}{g}_{\text{tr}}^{-1}(z,\hspace{0.17em}0).\hfill \end{array}$$

When λ_E ≠ 0, the back-transformation is

$$g_{\text{tr}}^{-1}(z,\hspace{0.17em}{\lambda }_E,\hspace{0.17em}{a}_E,\hspace{0.17em}{s}_E)={\left[1+{\lambda }_E\{a_E+s_{E}z/\sqrt{2}\}\right]}^{1/{\lambda }_E};$$ (A.1)

$${\partial }^2{g}_{\text{tr}}^{-1}(z,\hspace{0.17em}{\lambda }_E,\hspace{0.17em}{a}_E,\hspace{0.17em}{s}_E)/\partial z^2=\frac{s_E^2}{2}(1-{\lambda }_E){\left[1+{\lambda }_E\{a_E+s_{E}z/\sqrt{2}\}\right]}^{-2+1/{\lambda }_E}$$ (A.2)

Define

$$\begin{array}{l}{g}_{\text{tr}}^{*}\{v,\hspace{0.17em}{\lambda }_E,\hspace{0.17em}{a}_E,s_E,\hspace{0.17em}{\sum }_{\epsilon }(3,\hspace{0.17em}3)\}\\ \hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}=g_{\text{tr}}^{-1}(v,\hspace{0.17em}{\lambda }_E,\hspace{0.17em}{a}_E,\hspace{0.17em}{s}_E)+(1/2){\sum }_{\epsilon }(3,\hspace{0.17em}3)\frac{{\partial }^2{g}_{\text{tr}}^{-1}(v,\hspace{0.17em}{\lambda }_E,\hspace{0.17em}{a}_E,\hspace{0.17em}{s}_E)}{\partial v^2}.\end{array}$$

As in Kipnis, et al. (2009), the usual intake of energy for person i is

$$\begin{array}{lll}{T}_{Ei}\hfill & =\hfill & E\{g_{\text{tr}}^{-1}({\mathbf{\text{X}}}_{i3}^{\text{T}}{\mathit{\text{β}}}_3+U_{i3}+{\epsilon }_{i3},\hspace{0.17em}{\lambda }_E,\hspace{0.17em}{a}_E,\hspace{0.17em}{s}_E)|{\mathbf{\text{X}}}_{i3},\hspace{0.17em}{U}_{i3}\}\hfill \\ \hfill & \approx \hfill & g_{\text{tr}}^{*}\{{\mathbf{\text{X}}}_{i3}^{\text{T}}{\mathit{\text{β}}}_3+U_{i3},\hspace{0.17em}{\lambda }_E,\hspace{0.17em}{a}_E,\hspace{0.17em}{s}_E,\hspace{0.17em}{\sum }_{\epsilon }(3,\hspace{0.17em}3)\}.\hfill \end{array}$$

Similarly, a person’s usual intake of the dietary component on the original scale is defined as

$$T_{Fi}=\Phi ({\mathbf{\text{X}}}_{i1}^{\text{T}}{\mathit{\text{β}}}_1+U_{i1})g_{\text{tr}}^{*}\{{\mathbf{\text{X}}}_{i2}^{\text{T}}{\mathit{\text{β}}}_2+U_{i2},\hspace{0.17em}{\lambda }_F,\hspace{0.17em}{a}_F,\hspace{0.17em}{s}_F,\hspace{0.17em}{\sum }_{\epsilon }(2,\hspace{0.17em}2)\}.$$