Abstract
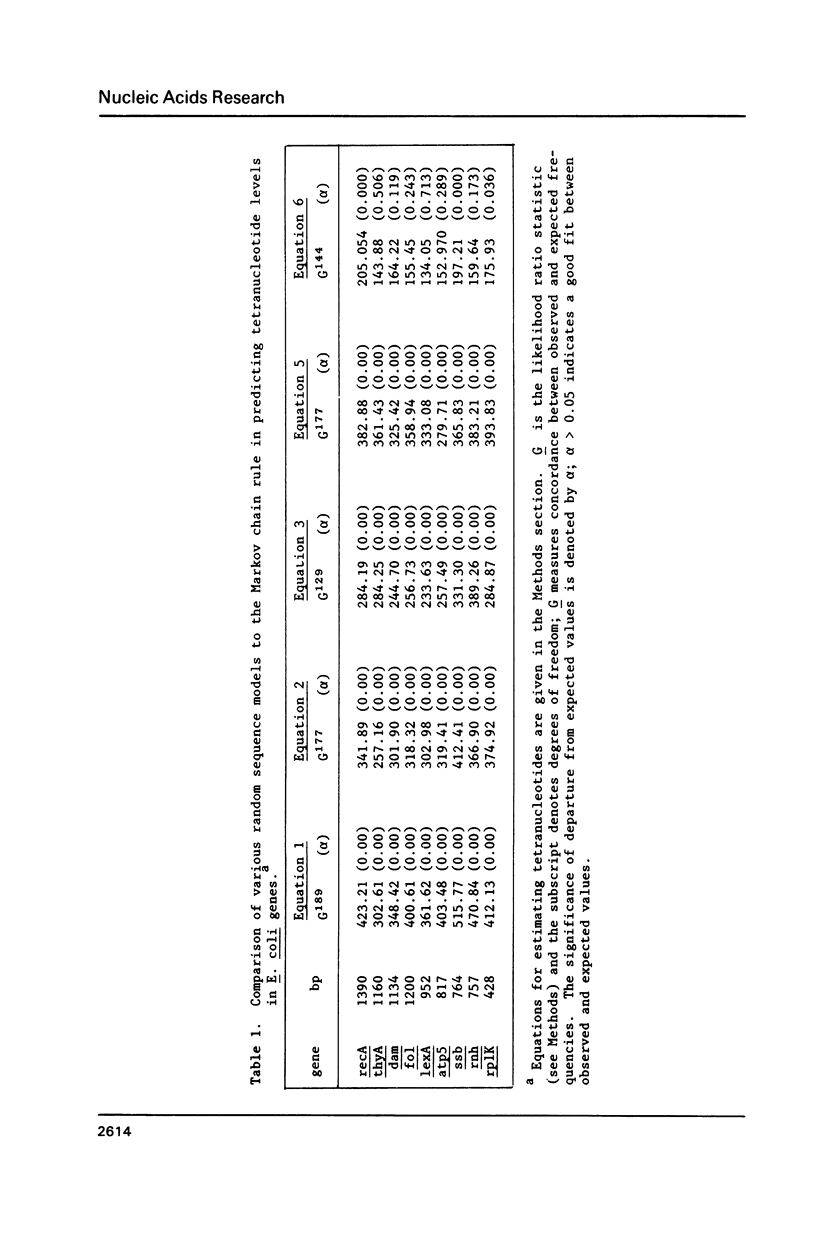
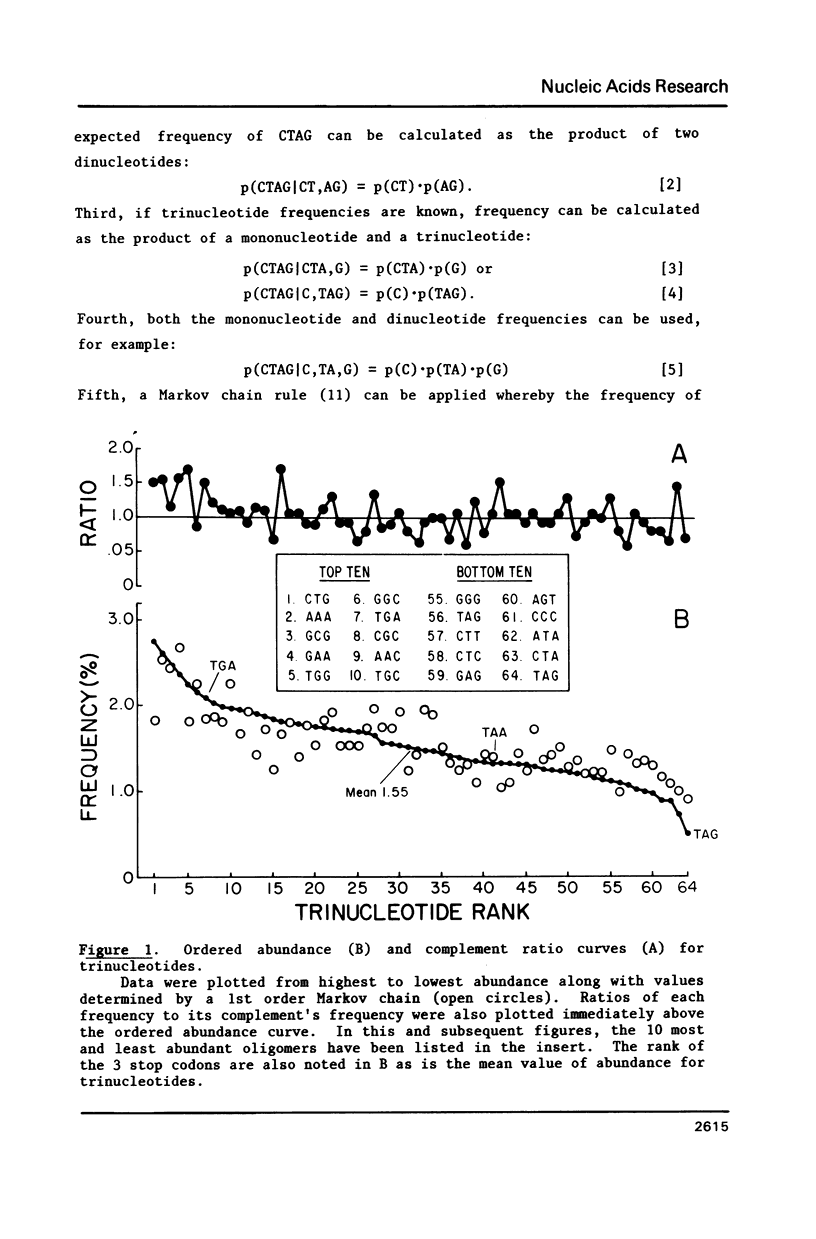
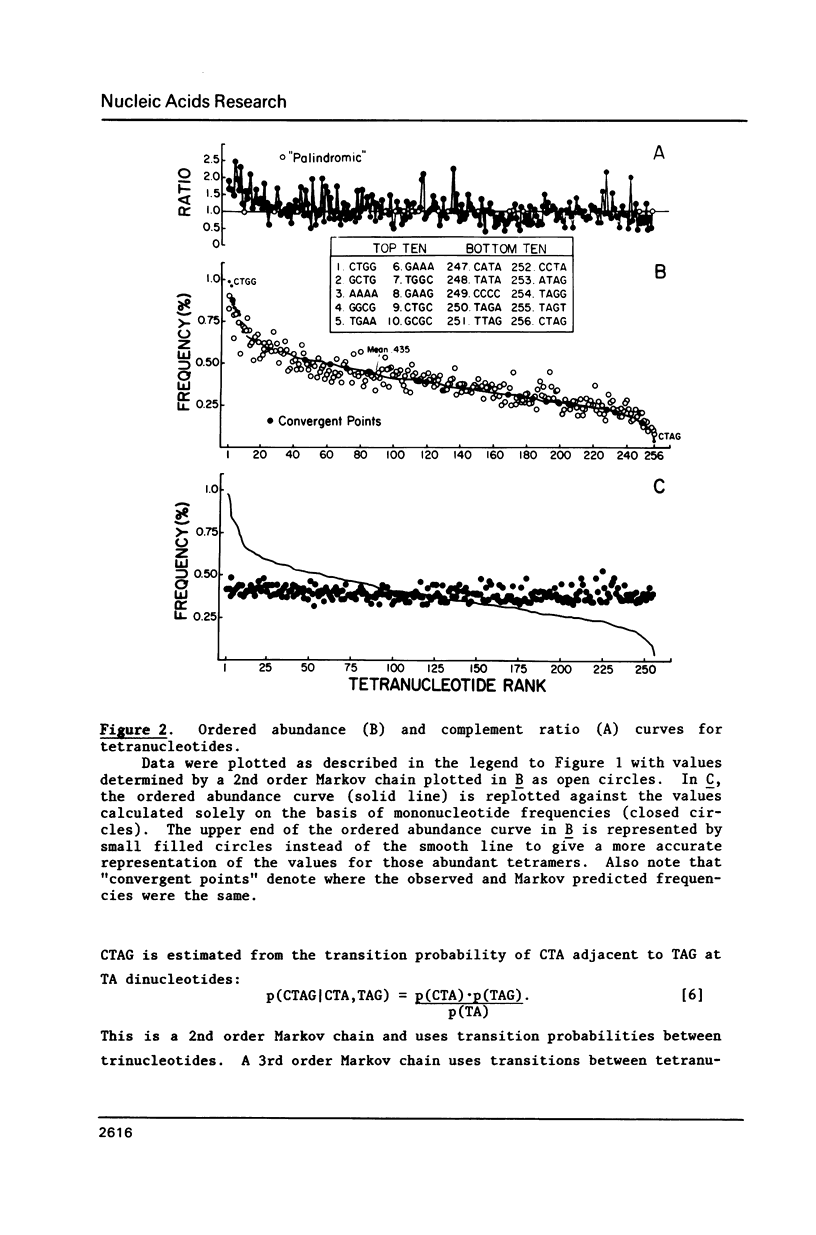
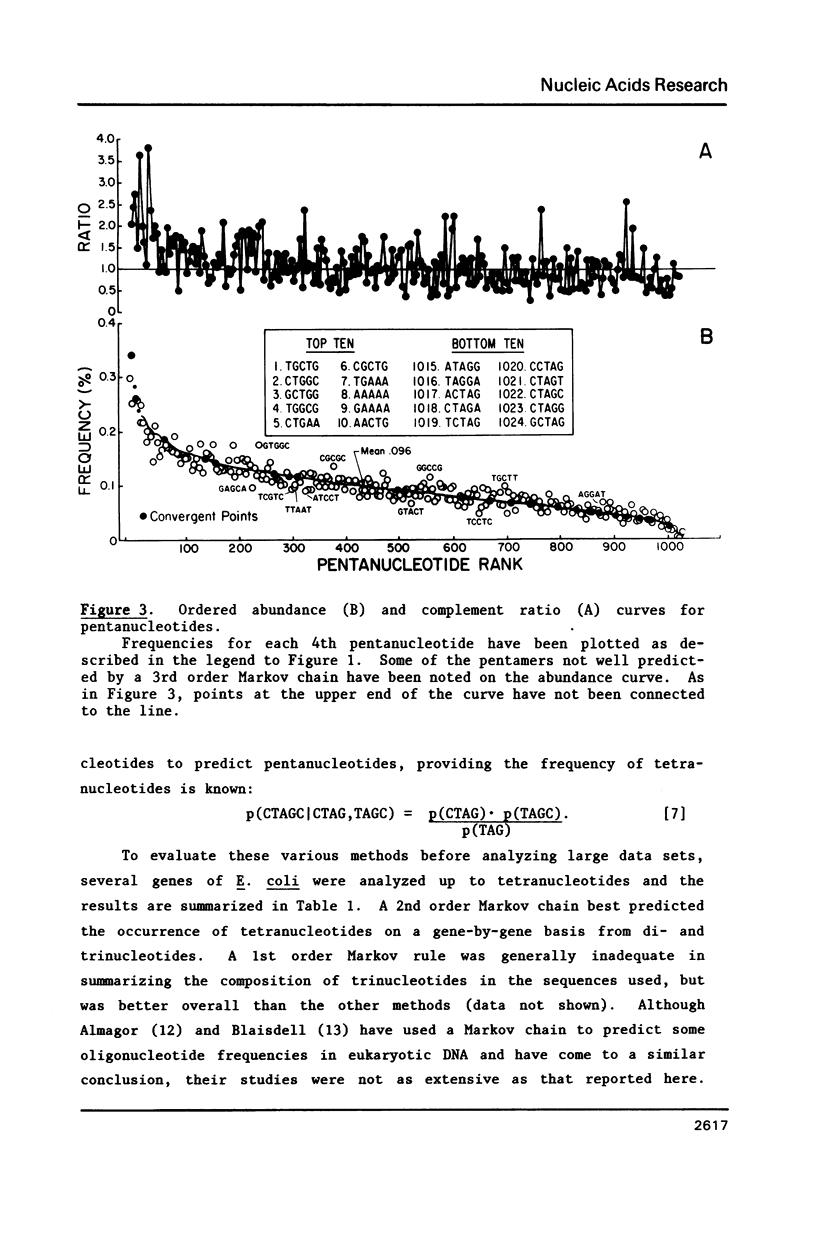
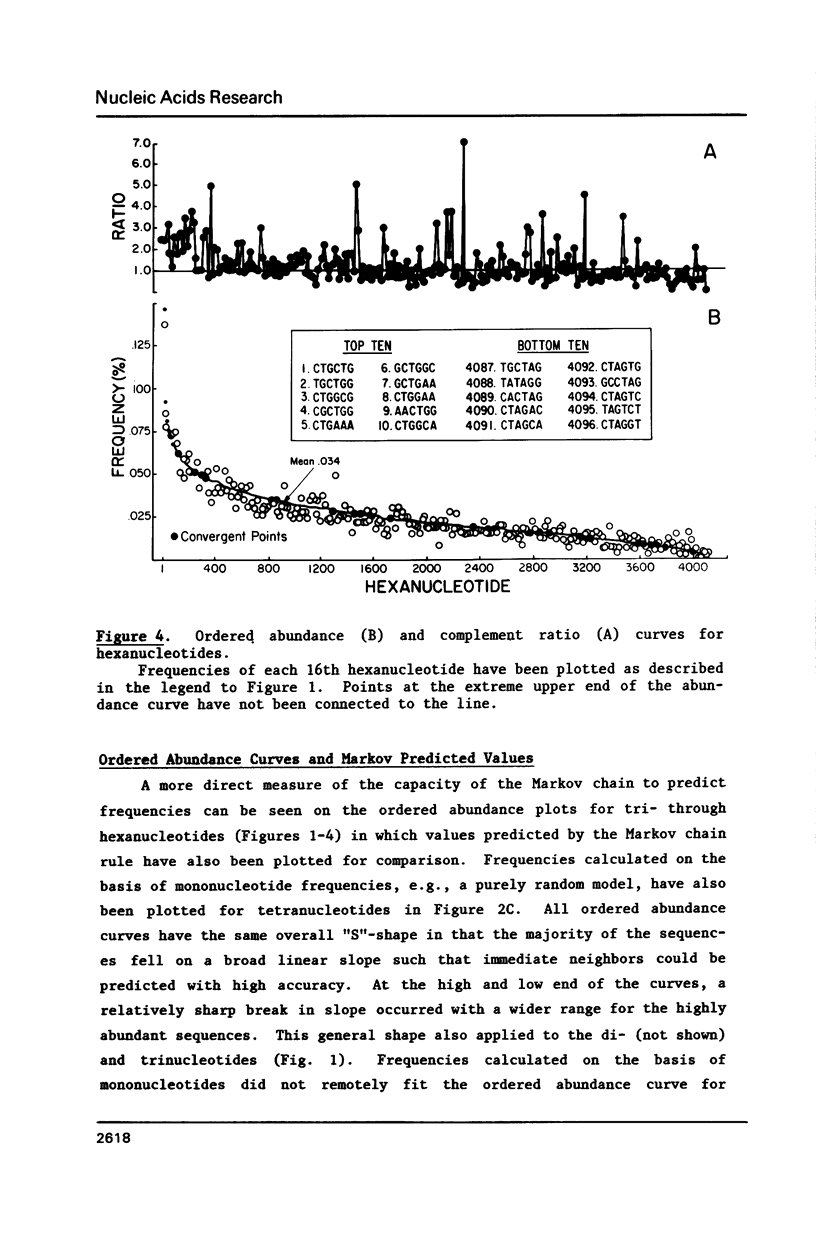
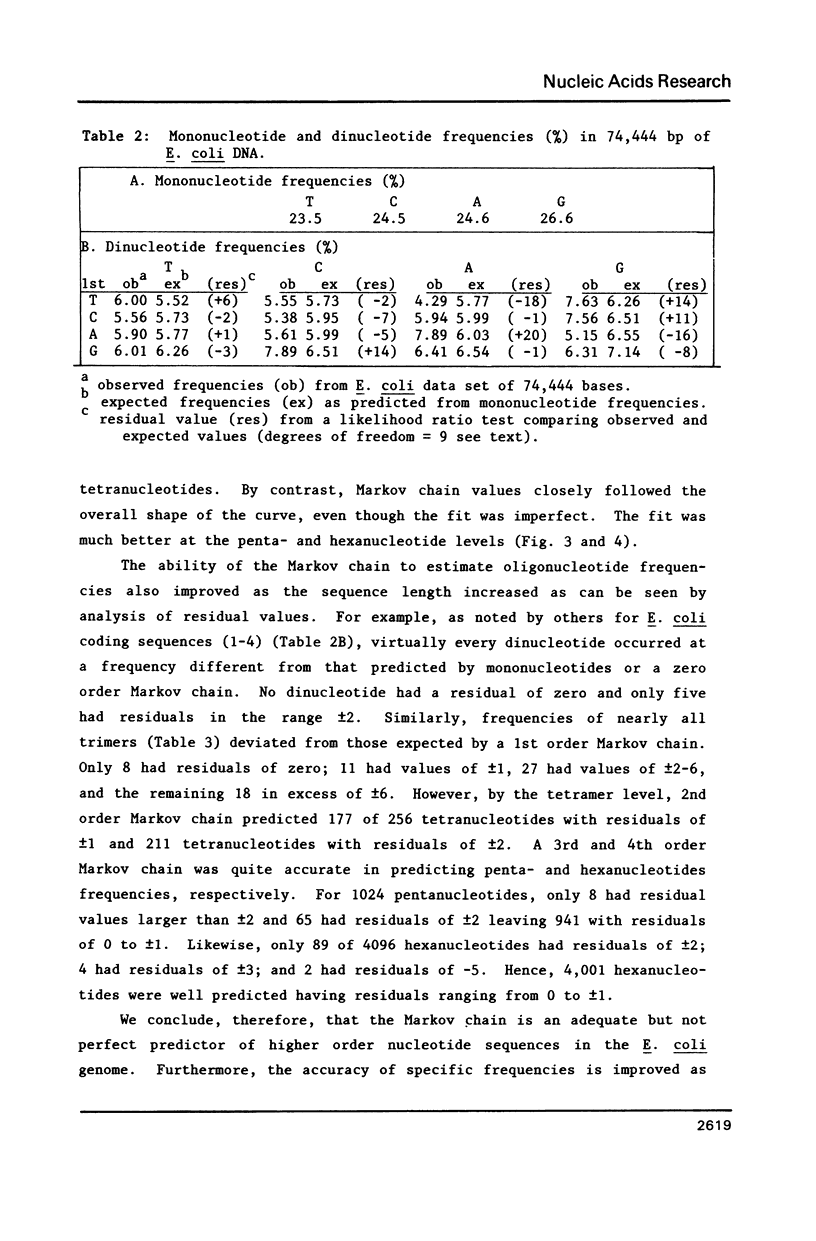
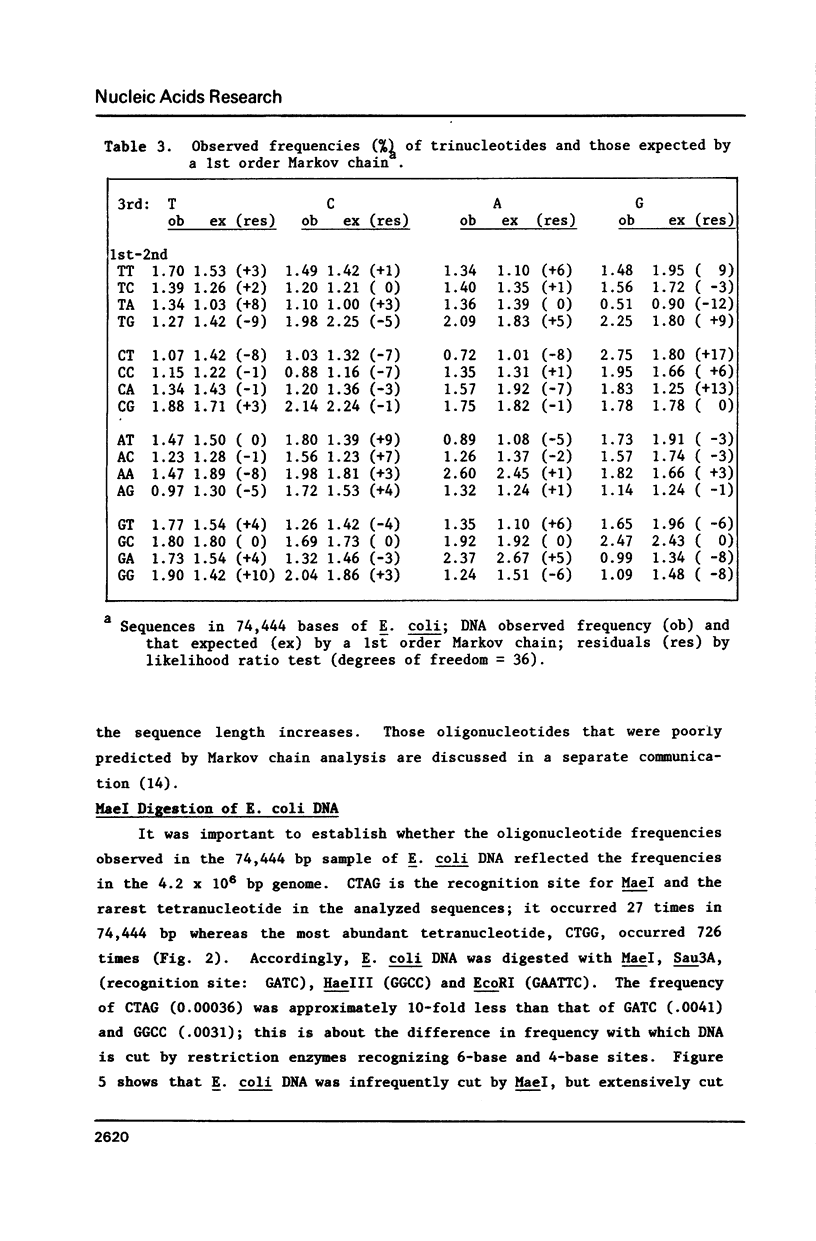
Several statistical methods were tested for accuracy in predicting observed frequencies of di- through hexanucleotides in 74,444 bp of E. coli DNA. A Markov chain was most accurate overall, whereas other methods, including a random model based on mononucleotide frequencies, were very inaccurate. When ranked highest to lowest abundance, the observed frequencies of oligonucleotides up to six bases in length in E. coli DNA were highly asymmetric. All ordered abundance plots had a wide linear range containing the majority of the oligomers which deviated sharply at the high and low ends of the curves. In general, values predicted by a Markov chain closely followed the overall shape of the ordered abundance curves. A simple equation was derived by which the frequency of any nucleotide longer than four bases in the E. coli genome (or any genome) can be relatively accurately estimated from the nested set of component tri- and tetranucleotides by serial application of a 3rd order Markov chain. The equation yielded a mean ratio of 1.03 +/- 0.94 for the observed-to-expected frequencies of the 4,096 hexanucleotides. Hence, the method is a relatively accurate but not perfect predictor of the length in nucleotides between hexanucleotide sites. Higher accuracy can be achieved using a 4th order Markov chain and larger data sets. The high asymmetry in oligonucleotide abundance means that in the E. coli genome of 4.2 X 10(6) bp many relatively short sequences of 7-9 bp are very rare or absent.
Full text
PDF








Images in this article
Selected References
These references are in PubMed. This may not be the complete list of references from this article.
- Almagor H. A Markov analysis of DNA sequences. J Theor Biol. 1983 Oct 21;104(4):633–645. doi: 10.1016/0022-5193(83)90251-5. [DOI] [PubMed] [Google Scholar]
- Arnold J., Eckenrode V. K., Lemke K., Phillips G. J., Schaeffer S. W. A comprehensive package for DNA sequence analysis in FORTRAN IV for the PDP-11. Nucleic Acids Res. 1986 Jan 10;14(1):239–254. doi: 10.1093/nar/14.1.239. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blaisdell B. E. A measure of the similarity of sets of sequences not requiring sequence alignment. Proc Natl Acad Sci U S A. 1986 Jul;83(14):5155–5159. doi: 10.1073/pnas.83.14.5155. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Blaisdell B. E. Markov chain analysis finds a significant influence of neighboring bases on the occurrence of a base in eucaryotic nuclear DNA sequences both protein-coding and noncoding. J Mol Evol. 1984;21(3):278–288. doi: 10.1007/BF02102360. [DOI] [PubMed] [Google Scholar]
- Elleman T. C. A method for detecting distant evolutionary relationships between protein or nucleic acid sequences in the presence of deletions or insertions. J Mol Evol. 1978 Jun 20;11(2):143–161. doi: 10.1007/BF01733890. [DOI] [PubMed] [Google Scholar]
- Nussinov R. Nearest neighbor nucleotide patterns. Structural and biological implications. J Biol Chem. 1981 Aug 25;256(16):8458–8462. [PubMed] [Google Scholar]
- Nussinov R. Some rules in the ordering of nucleotides in the DNA. Nucleic Acids Res. 1980 Oct 10;8(19):4545–4562. doi: 10.1093/nar/8.19.4545. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nussinov R. Strong doublet preferences in nucleotide sequences and DNA geometry. J Mol Evol. 1984;20(2):111–119. doi: 10.1007/BF02257371. [DOI] [PubMed] [Google Scholar]
- Nussinov R. The universal dinucleotide asymmetry rules in DNA and the amino acid codon choice. J Mol Evol. 1981;17(4):237–244. doi: 10.1007/BF01732761. [DOI] [PubMed] [Google Scholar]
- Sankoff D., Cedergren R. J. A test for nucleotide sequence homology. J Mol Biol. 1973 Jun 15;77(1):169–164. doi: 10.1016/0022-2836(73)90369-0. [DOI] [PubMed] [Google Scholar]
- Smith T. F., Waterman M. S., Burks C. The statistical distribution of nucleic acid similarities. Nucleic Acids Res. 1985 Jan 25;13(2):645–656. doi: 10.1093/nar/13.2.645. [DOI] [PMC free article] [PubMed] [Google Scholar]




