Competing mechanisms and scaling laws for carbon nanotube scission by ultrasonication

Abstract

Dispersion of carbon nanotubes (CNTs) into liquids typically requires ultrasonication to exfoliate individuals CNTs from bundles. Experiments show that CNT length drops with sonication time (or energy) as a power law t^-m. Yet the breakage mechanism is not well understood, and the experimentally reported power law exponent m ranges from approximately 0.2 to 0.5. Here we simulate the motion of CNTs around cavitating bubbles by coupling Brownian dynamics with the Rayleigh–Plesset equation. We observe that, during bubble growth, CNTs align tangentially to the bubble surface. Surprisingly, we find two dynamical regimes during the collapse: shorter CNTs align radially, longer ones buckle. We compute the phase diagram for CNT collapse dynamics as a function of CNT length, stiffness, and initial distance from the bubble nuclei and determine the transition from aligning to buckling. We conclude that, depending on their length, CNTs can break due to either buckling or stretching. These two mechanisms yield different power laws for the length decay (0.25 and 0.5, respectively), reconciling the apparent discrepancy in the experimental data.

The dispersion of carbon nanotubes (CNTs) in liquids is critical for the use of CNTs in applications ranging from biomedical sensors to structural composites (1). However, CNTs form insoluble bundles and ropes during production due to van der Waals attraction. Commonly, CNTs are exfoliated and dispersed in liquids by sonication, where energy is supplied to the system as ultrasonic waves. These waves induce cavitation, which leads to progressive exfoliation of bundles into individual CNTs. Understanding dispersion by sonication is critical for the use of CNTs in biological and materials applications (2).

Prior studies have monitored the effects of sonication on CNT dispersion quality and length (3–7). Most of these studies sonicated a sample under controlled conditions and monitored bundle diameter and length. Although sonication decreases bundle diameter at short times as individual CNTs are exfoliated, it also cuts the CNTs. Shortening has been observed for both single-walled and multiwalled CNTs (SWNTs and MWNTs) (4, 5).

Similar shortening occurs during sonication of polymer solutions (5, 8–12), where the mechanism is well established; cavitation induces high strain rates in the liquid, stretching polymer molecules to failure. Although the mechanism of CNT shortening remains unclear, there are some similarities between sonicated polymers and CNTs. Like polymers, CNTs show a nonrandom cutting pattern; i.e., they break near their center of mass (CoM) (5). Similar to polymers, the kinetics of CNT shortening are length-dependent, and sonicated CNTs approach a limiting length, below which no shortening occurs (6, 13). Evidence suggests that thermal effects (due to local temperature rise during bubble collapse) are negligible and mechanical effects dominate (6, 14, 15).

Experiments consistently report a power law relation between CNTs’ average length and sonication time L ∼ t^-m. This same power law captures the dependence of length on sonication energy, showing that sonication time and power have a combined effect (4). Yet the literature disagrees on the power law exponent m. Various values for this exponent have been reported: m ∼ 0.5 (5) and m ∼ 0.22 (4). Comparing these experimental data is difficult because of differences in CNT diameter, mechanical properties, waviness, surface functions, and wettability; yet the mismatch is surprising, because the scaling of length with time is tied to the underlying physics of scission. Here, we model CNT dynamics during sonication to understand the CNT breaking mechanisms and reconcile the experimental data.

Model

Shortening of CNTs can be treated as a first-order chemical reaction without recombination (4, 5, 11). The kinetics of the system follow dn/dt = kn, where k is the length-dependent scission rate and n is the ensemble-averaged number of CNTs with length L. Assuming an initial population of n₀ CNTs with monodisperse length, L₀ yields n(t) = n₀L₀/L(t) by conservation of CNT mass; i.e., CNT total length. Assuming a power-law dependence k = aL^q, where a is a constant and q is the power law exponent, and integrating in time yields a length-dependent balance

[1]

i.e., a power law relationship between length and time, with m = 1/q. Although simplistic, the assumption of initial monodispersity is a reasonable starting point for analyzing the process.

Hennrich et al. proposed a model which resembles the well-established polymer description (5). The model postulates that CNTs align radially with respect to collapsing bubbles. Because of the radial sink flow, sections of the CNT near the surface of the bubble experience higher drag than farther sections, resulting in a net stretching force on the CNT. The maximum tension occurs at the CNT center and can be calculated by considering the drag exerted on the two halves of the CNT,

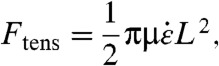[2]

where μ is the liquid viscosity and 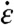is the radial strain rate at the CNT center, which can reach approximately 10⁹ s^-1 near a collapsing cavity.The critical force for cleaving a CNT is

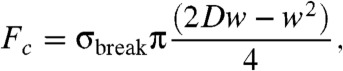[3]

where σ_break is the CNT tensile strength, D is its diameter, and w is its wall thickness (5). Experiments on SWNTs indicate a typical tensile strength of 37 GPa (1). Hence, the critical force is F_c ∼ 20 nN for a CNT with D = 1.2 nm and w = 0.34 nm.

According to Eqs. 2 and 3, SWNTs shorter than approximately 120 nm should not break during sonication, in reasonable agreement with experimental evidence (5). Because the tensile force depends on the length squared, the scission rate should do so too, such that q ∼ 2 and m ∼ 0.5 (5). (We show below that this equivalence between critical force and scission rate is approximately correct). This result is in general agreement with their experimental results, although the length distribution has large error bars that could affect the scaling law.

Recently, we suggested an alternative mechanism of CNT breakage where the CNTs are oriented parallel to the bubble surface at the beginning of the collapse phase, due to the bubble expansion flow (4). The extensional flow during collapse then exerts competing forces that could either rotate the CNT or directly buckle it. Experimental evidence (rings, kinks) suggests the possibility of buckling (16, 17). Cohen and Mahadevan argued that CNTs could be trapped inside a collapsing bubble and buckle due to interfacial forces, yielding rings and kinks (17).

Chew et al. neglected surfactant effects and assumed that CNTs enter the bubble during growth due to hydrophobic effects, and exit the bubble in an orientation tangential to the bubble surface during bubble collapse (14). [This contrasts with the assumption that bubbles would trap CNTs during the collapse (17).] By combining molecular dynamics with experiments, Chew et al. concluded that buckling dominates and stretching is not significant.

Disagreement between experimental studies, combined with the disparate proposed models, raise the question of whether breakage during sonication may follow different routes depending on CNT properties and experimental conditions—and hence yield different power laws. To study breakage under broad conditions, we model the growth of bubbles and compute the dynamics of CNTs in the ensuing flow.

Cavitation Dynamics.

The physics of cavitation is a classical subject, tracing back to the 19th century. Here we summarize the equations that describe cavitating bubbles (18, 19). Acoustic waves traveling in a liquid can be modeled as longitudinal pressure waves. The local acoustic pressure is P_A(t) = P_A0 sin(ωt), where P_A0 is the amplitude.

The frequency ω is usually approximately 20 kHz for laboratory sonicators. The supplied power ranges between 20 and 160 W, yielding pressure peaks up to 7,500 kPa near the sonicator tip. Local pressure changes cause preexisting gaseous nuclei to grow via mass transfer, including diffusion of dissolved gas, liquid evaporation, and coalescence. Bubbles can grow up to thousand-fold their initial radius. The oscillating external pressure then causes a violent bubble collapse, inducing high strain rates in the liquid.

Models of cavitation dynamics trace to Lord Rayleigh (20), who treated the collapse of an empty cavity in an inviscid liquid. Plesset (21) introduced effects of viscosity, surface tension, and variable external pressure. The generalized Rayleigh–Plesset (R–P) equation neglects mass transfer and is derived from the Navier–Stokes equation as (19, 21)

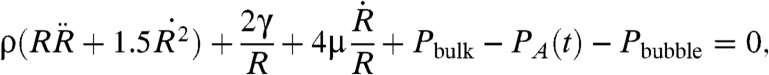[4]

where R is the bubble radius; γ, ρ, and μ are the liquid surface tension, density, and viscosity; P_bulk is pressure of the liquid bulk; and P_bubble is the radius-dependent pressure inside the bubble. Flynn modeled the dependence of P_bubble on r (22). His model neglects mass transfer between the bubble and the bulk; i.e., the mass inside the bubble is constant, and assumes that the bubble is filled with evaporated solvent (vapor), whose partial pressure is the vapor pressure P_v of the liquid, and dissolved air (gas), which behave as an ideal gas mixture. The bubble lifetime is divided into two phases: growth and initial collapse are assumed to be quasistatic and isothermal and are driven by the acoustic pressure in Eq. 4. The final collapse is dominated by inertial terms; hence, it occurs independently of acoustic pressure and violently, and thus is assumed to be adiabatic (15, 23). The pressure inside the bubble is P_bubble = P_v + P_gas, where P_gas is the partial pressure due to the gas. In the isothermal phase, P_gas is P_gas = P_gas,0(R_i/R)^3κ, where κ is the adiabatic index (ratio of isobaric and isochoric heat capacities C_p/C_v, κ = 1.4 for an ideal diatomic gas), R_i is the initial radius of the cavity, and P_gas,0 is the partial pressure due to the gas at the beginning of the process. P_gas,0 is derived assuming nuclei at ambient bulk pressure as P_gas,0 = P_bulk - P_v + (2γ/R_i). The transition to adiabatic dynamics occurs when P_gas = P_v during the collapse phase. The critical radius for this transition is R_crit = R_i(P_gas,0/P_v)^1/3κ. R_crit and R_max (the maximum bubble radius) are not the same. During the collapse, the gas partial pressure is P_gas = 2P_v(R_crit/R)^3κ.

The R–P equation requires the acoustic pressure P_A0, bulk pressure P_bulk, viscosity μ, surface tension γ, density ρ, and acoustic frequency ω. We use the properties of water with sodium dodecyl sulfate above the critical micellar concentration at atmospheric pressure P_bulk = 101 kPa; i.e., μ = 1 mPa s, γ = 40.1 mN m^-1, and ρ = 1000 kg/m³ (24). The model parameters are P_A0, ω, and the initial bubble radius R_i. The bubble velocity is zero at the beginning of the expansion. During collapse, the bubble surface reaches velocities near the speed of sound in the fluid, inducing high liquid strain rates in the order of 10⁹ s^-1 (5). The lifetime of the bubble is typically approximately 100 μs. Interestingly, as the acoustic pressure increases, there is a transition from a single-peak to a double-peak bubble when the radius becomes so large that the bubble cannot collapse completely within one acoustic cycle (18).

Brownian Dynamics Simulation.

Brownian dynamics simulations have been used to study flexible polymer scission in extensional flows (25). Here we combine the flow field around the bubble with a Brownian dynamics algorithm for stiff chains. Our method consists of two steps (see SI Appendix, Fig. S1). We compute the position R(t) and velocity V(t) of the bubble surface by time-integrating Eq. 4 with a 4th order Runge-Kutta method. The flow field v(r,t) in the fluid is simply v(r,t) = V(t)R(t)²/r². We use model paramaters representative of typical sonication conditions (19), R_i = 10 nm, ω = 20 kHz, and P_A0 of 1,500 and 4,500 kPa for single and double-cycles bubbles.

After computing the flow, we simulate the motion of CNTs near the bubble. We model CNTs as semiflexible filaments (26–28), with persistence length L_p between 40 and 175 μm for SWNTs (28). We discretize the semiflexible filament into a chain of N beads and (N─1) rods; we simulate the chain motion by Brownian dynamics, according to the force balance on bead j, (29–33),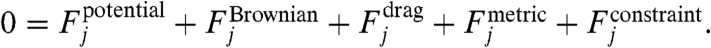

As usual, inertia is neglected and Brownian forces are represented by uncorrelated noise. The bending (potential) forces are computed as a function of angles between neighboring bonds and are parameterized by the bending stiffness L_pk_BT. Metric forces are used to attain the appropriate equilibrium chain configurations (33, 34). The drag force describes the influence of fluid flow v(r,t) on the motion of each bead; a local anisotropic friction (drag) coefficient accounts for the rodlike shape of the chain.

Each simulation requires CNT length L and persistence length L_p, the initial distance d_i of the CNT CoM from the bubble center, and the precomputed flow field v(r,t). The initial CNT orientation is random, and the conformation is selected from the theoretical equilibrium distribution for a chain with a given L_p (29). For each set of inputs (L,L_p, d_i), we run approximately 1,000 independent simulations to sample the behavior of an ensemble of CNTs.

Results

Growth Phase Pathways.

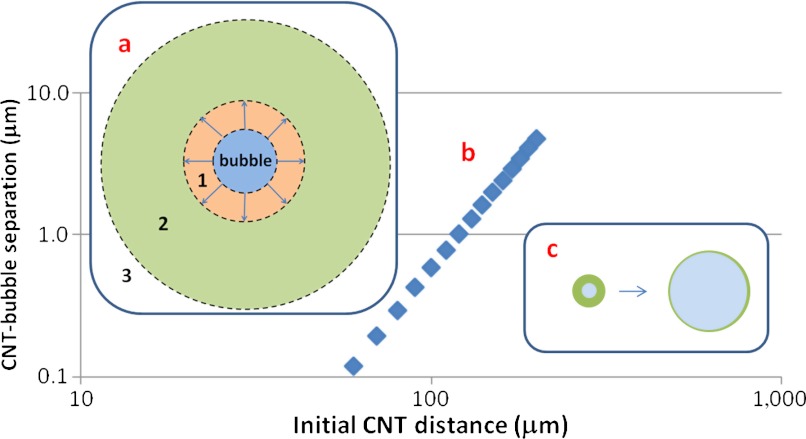
During bubble growth, the distance d(t) of a CNT CoM from the bubble center depends monotonically on its initial distance d_i; i.e., CNTs do not overtake each other. The initial orientation affects the trajectory marginally; therefore, d_i alone captures the CNT state at the beginning of bubble growth. CNT behavior during growth can be classified into three regimes according to d_i (Fig. 1A). The closest CNTs (Region 1) align tangential to the bubble and may be “caught” by the advancing bubble wall during growth; i.e., they approach the surface closely enough that thermal diffusion (approximately 50 nm, see below) may bring them within the range of electrostatic [Debye length below 5 nm (28)] and hydrophobic [shorter range (35)] interactions (not included in our model). CNTs in Region 2 also align tangent to the bubble surface during growth, regardless of their initial orientation, but do not fall within the range of surface forces. In Region 3 (bulk), CNTs are too far to be significantly affected by the bubble. The relative size of these regions depends on the bubble parameters; typical values are approximately 40 μm and approximately 250 μm for the radii of Regions 1 and 2. Fig. 1B and SI Appendix, Fig. S2 show typical monotonic dependence of final CNT-bubble separation (d_max - R_max) on d_i. The minimum separation occurs at the end of the growth phase; this separation is small because the fluid between the CNT and bubble wall is incompressible and stretches into a thin layer during bubble growth (Fig. 1C). This relationship is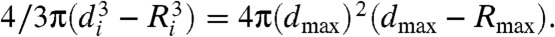

Fig. 1.

(A) Qualitative partition of the surroundings of a growing bubble at the start of sonication. CNTs in Region 1 align tangent to the bubble and could be entrained during growth; CNTs in Region 2 align tangent to the bubble wall; CNTs in the bulk (Region 3) are minimally affected by the bubble’s growth. (B) Representative CNT-bubble separation at the end of growth vs. CNT initial distance from the bubble center (P_A0 = 1500 kPa, L = 1.5 μm, L_p = 20 μm, N = 33). (C) During growth, CNTs approach the bubble surface because of the thinning of the incompressible fluid layer around the bubble.

Fig. 1B confirms this relationship by showing that (d_max - R_max) vs. d_i follows a power law of approximately 3.05. Therefore, CNT thermal diffusion during bubble growth is negligible; the diffusive length scale during growth (D_tt_g)^1/2 ∼ 50 nm is small relative to the motion of the fluid (28) (here, D_t = k_BT/μL is the translational diffusivity and t_g is the bubble growth time). Importantly, Region 1 is less than 1% of the volume of Region 2; therefore, almost all CNTs affected by the flow follow bulk dynamics, independent of potential entrapment into the bubble or on the bubble surface. Hence, whether CNTs enter the bubble [as previously posited (14, 17)] is only relevant to a tiny fraction of the CNT population; therefore, hydrophobic interactions between CNT and bubble surface can be neglected because they affect such few CNTs. Finally, the outward radial extensional flow reorients the CNTs tangentially. This flow also straightens out the CNT thermal curvature (the chain is in tension during growth, hence bending modes are partially suppressed).

Collapse Phase Pathways.

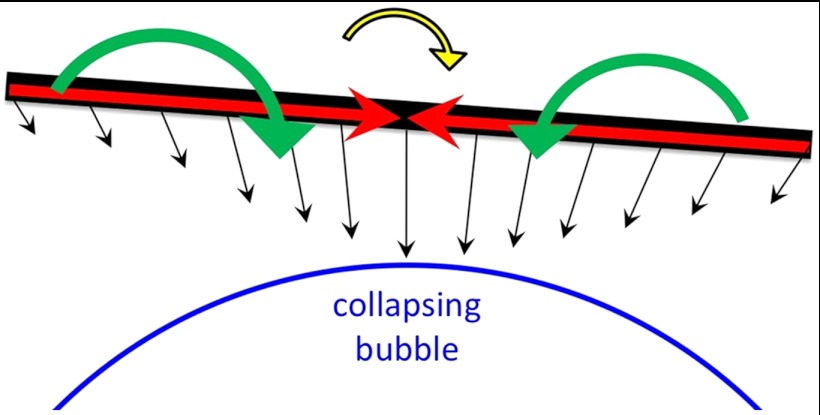
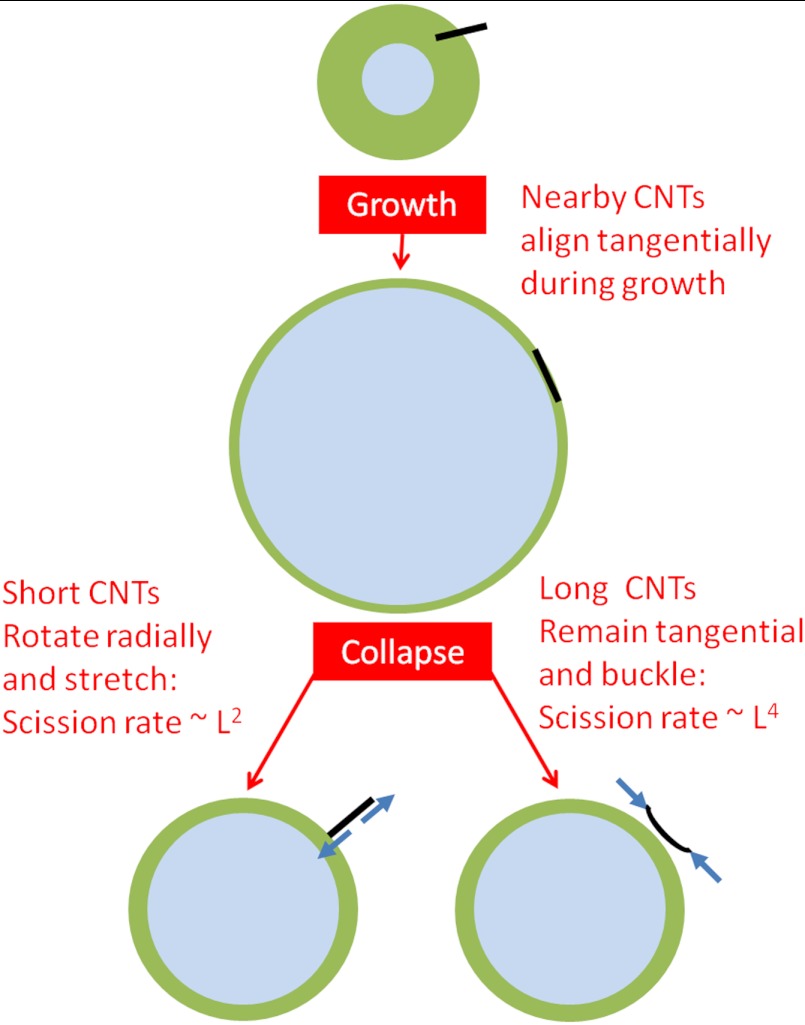
CNTs in Region 2 orient tangentially during bubble growth and are strongly affected by bubble collapse. Depending on L, L_p, and d_i, such CNTs follow either of two main dynamics: rotation into radial orientation or buckling. The tangential configuration is unstable to two modes: overall chain rotation, which is promoted by any slight rotational diffusion due to Brownian forces; and buckling into a U shape (or higher order shapes if the shear rate is high enough). The CNT is subjected to viscous drag along its length (Fig. 2); the local velocity and hence the drag force grows with decreasing distance from the bubble. The component of the drag parallel to the CNT axis induces a compressive axial force on the CNT. The perpendicular component induces an overall inward radial motion of the CoM and opposite torques on the two halves of the CNT. When the CNT is perfectly tangential to the bubble, its two halves experience equal opposing torques that tend to bend the CNT by moving its CoM closer to the bubble and its ends farther from the bubble surface. Any Brownian rotation causes one end of the CNT to be closer to the bubble surface than the other end. Such closer proximity corresponds to larger drag force on one end than on the other, which results in a net torque on the CNT. If the torque imbalance is sufficiently large, the CNT rotates and orients radially, according to the assumption of ref. 5 and in contrast with ref. 14. If the torque imbalance is small, the viscous torques on the two halves combine with the viscous axial compression to buckle the CNT. The torque imbalance scales as L³, whereas propensity to buckling scales as L⁴; therefore, the dominant behavior in a CNT population should be length-dependent. (See below for detail.) Any partial fluid slip on the CNT surface merely rescales the friction factor, independent of CNT length, and does not affect the relative balance between rotation and buckling; prior studies indicate that the assumption of Stokesian drag coefficient ζ_⊥ ∼ 4πη_s/ log(L/D) is accurate (27, 28).

Fig. 2.

Schematic of the forces and torques on a CNT (black) near a collapsing bubble (blue). The flow causes a compressive force (red) on the CNT, as well as inward torques (green), which can combine to buckle the CNT. Brownian torques may slightly rotate the CNT and cause a torque imbalance (yellow) that rotates the CNT radially (clockwise here).

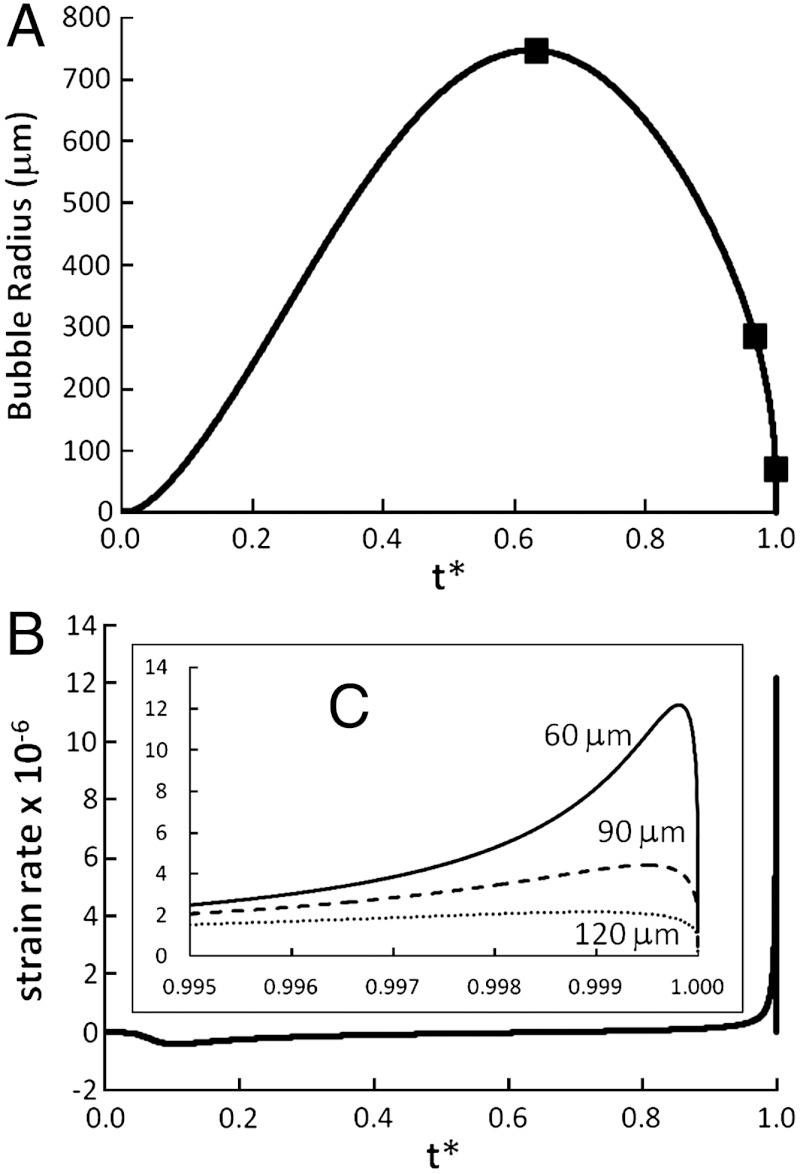
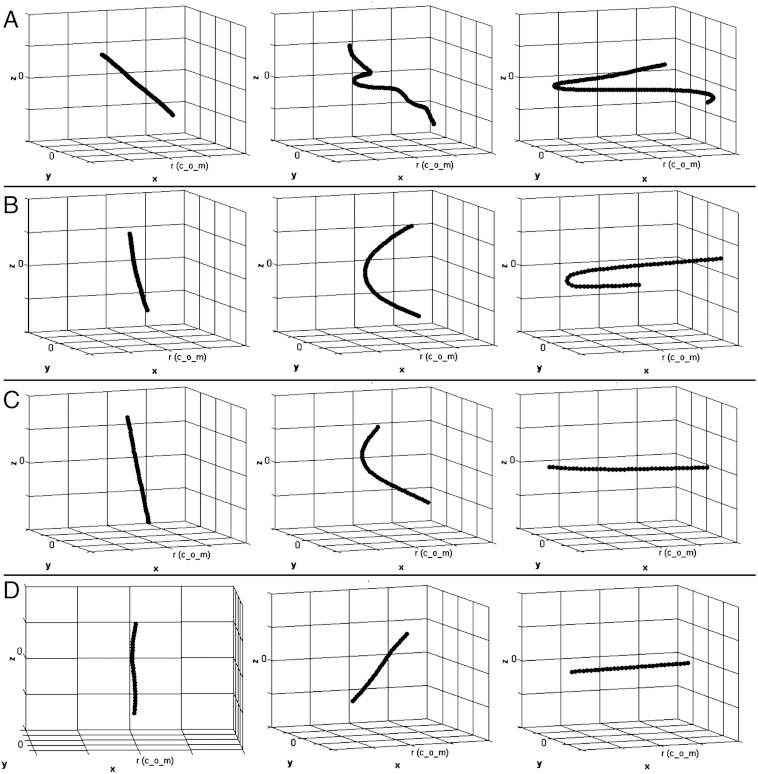
Figs. 3 and 4 and Movie S1 show the dynamics of the bubble radius and the strain rate experienced by the CNT CoM and representative examples of buckling and rotation. Time is rescaled to the total bubble lifetime. Four distinct behaviors are observed. The longest CNTs (Fig. 4A, L = 3 μm) buckle into highly bent shapes. Intermediate CNTs (Fig. 4B, L = 1.5 μm) bend into a U shape, which sharpens in time. Below a certain length (Fig. 4C, L = 1 μm), the CNTs bend but do not develop high curvature; instead, the CNTs straighten out and relieve curvature by snaking into radial orientation. Finally, the shortest CNTs (Fig. 4D, L = 0.75 μm) directly rotate into radial orientation. Similar trends are observed for the double-cycle bubble (SI Appendix, Figs. S3–S6). The dominant behavior (buckling vs. rotation) depends also on persistence length and maximum fluid strain rate (related to d_i). Below, we study this dependence by simulating ensembles of CNTs over a range of parameter sets.

Fig. 3.

(A) Bubble radius vs. dimensionless time t^∗ for P_A0 = 1500 kPa. The snapshots in Fig. 4 are marked. (B) Dimensionless strain rate (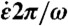) at the CNT CoM as a function of t^∗ (P_A0 = 5000 kPa, L = 1.5 μm, L_p = 20 μm, N = 33, d_i = 60 μm) and (C) near the end of collapse for varying d_i.

Fig. 4.

Snapshots (noted in Fig. 3A) of the collapse process of representative CNTs. The bubble center is in the -x direction. d_i = 50 μm, L_p = 50 μm. (A) L = 3 μm,N = 121, CNT remains tangential and buckles directly. (B) L = 1.5 μm,N = 61, CNT remains tangential until it bends and buckles. (C) L = 1 μm,N = 41 CNT starts tangentially, then rotates radially while bending slightly. (D) L = 0.75 μm,N = 31, CNT starts tangentially then rotates radially without bending.

Conclusion

Breaking Condition for Rotating and Stretching.

The propensity of a CNT to rotate into radial alignment during bubble collapse depends on its length L. The Brownian torque k_BT is independent of L, but the viscous torque is not. The normal velocity v_n of a differential element on the CNT grows linearly with distance s from the CNT CoM as 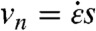. The local perpendicular drag coefficient ζ_⊥ = 4πη_s/ log(L/D) yields a normal drag force ζ_⊥v_n (28). The viscous torque on a differential CNT element is the cross product of the normal drag force with the distance to the CNT CoM, which yields an additional dependence on s; integrating this elemental viscous torque over the entire CNT yields a viscous torque that scales with L³. Thus, the CNT’s propensity to rotate during the collapse is expressed by the rotational Peclet number (ratio of viscous to Brownian torques) as 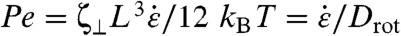, where D_rot is the rotational diffusivity.

A radially aligned CNT can stretch because the end of the CNT nearest the bubble is pulled faster than its far end. As in ref. 5, the breaking condition for stretching are determined by equating the net viscous stretching force (Eq. 2) to the critical scission force (Eq. 3), yielding the critical strain rate

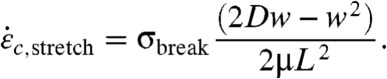[5]

Breaking Condition for Buckling.

Longer CNTs buckle rather than rotating radially during collapse. A tight enough radius of curvature will cause CNT breakage. The net compressive load is the integral of the strain force per unit length rate along the CNT. The net compressive force at the CoM of a tangentially aligned CNT is proportional to 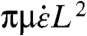as in the stretching case (Eq. 2). CNTs can be modeled as stiff, slender, inextensible beams (27, 36). Thus, the critical compressive force for buckling is defined by Euler’s equation F_c = π²EI_M/L² = π²L_pk_BT/L² where E is the elastic modulus of the beam and I_M is the moment of inertia of the beam and L_p = EI_M/k_BT (27). This axial buckling force is orders of magnitude smaller than the radial shell buckling force described by Chew et al. (14, 37); therefore, axial buckling will dominate. CNT buckling starts when the net compressive load along its body (Eq. 3) exceeds F_c, yielding the critical condition for buckling .

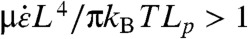However, all buckled CNTs do not necessarily break. To break, a CNT must experience a sufficiently high local curvature stress. From elastic beam theory, the maximum curvature stress in a buckled CNT is |σ| = ED/(2ξ_c), where ξ_c is the minimum radius of curvature of the CNT (38, 39); a buckled CNT breaks if its minimum radius of curvature falls below a critical value ξ_c < ξ_c,crit = ED/2σ_break.

Estimates of σ_break and ξ_c,crit vary based on CNT diameter and number of walls, but the critical radius of curvature ξ_c,crit is independent of L. Breakage due to buckling will occur at higher strain rates; i.e., when 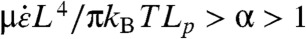, where α is a dimensionless factor that may depend on σ_break and on L_p/ξ_c because the strain rate required to break a point of localized curvature roughly scales with L_p/ξ_c. Eq. 6 yields the critical strain rate for disruptive buckling (breaking due to buckling)

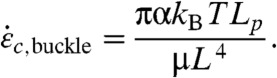[6]

Scission Rate Scaling.

These two mechanisms for stretching and for buckling lead to different scaling for the CNT scission rate. The instantaneous strain rate at a CNT CoM is 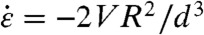; it is highest near the end of bubble collapse (Fig. 3 B and C) and scales as

[7]

The SI Appendix, Fig. S7 shows that β is in the range 0.82 to 1 for CNTs in Region 2. Eqs. 5–7 show that CNTs within a critical d_i,c experience a strain rate 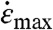higher than the critical strain rate and break. Because the CNT number density is uniform, the number of breaking events per unit time varies linearly with the critical volume, k ∼ (d_i,c)³. Crucially, the rate constant k depends inversely on the critical strain rate, which has a different power-law dependence on L, depending on the mechanism—buckling vs. stretching. The critical strain rate to break depends on L² for stretching (Eq. 5) vs. L⁴ for buckling (Eq. 6). The kinetics of the process depends on the dominant breaking mode. The switch between these modes is length dependent because the CNT propensity to rotate scales as L³ (due to the L³ scaling of Pe), whereas the propensity to buckle scales as L⁴ (Eq. 7). Therefore, as sonication progresses, L decreases, and the dominant breaking mechanism will switch from buckling to stretching.

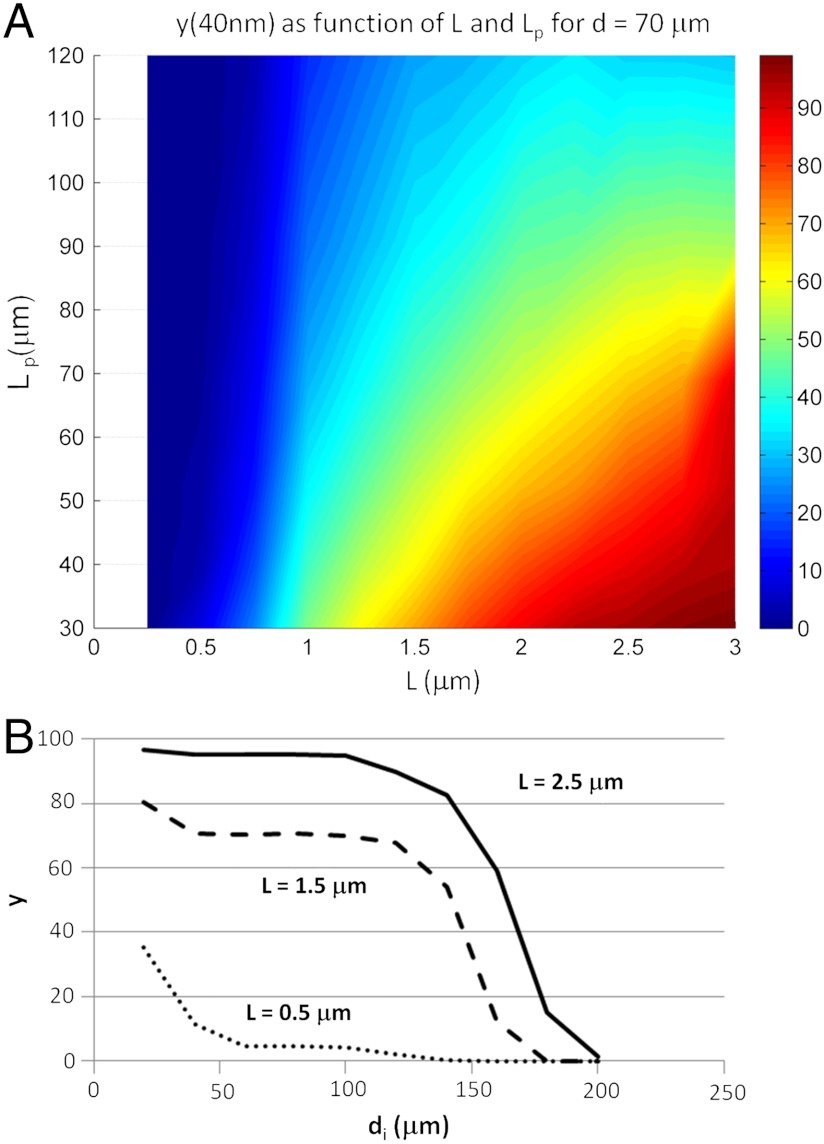
To confirm this hypothesis, simulations are carried out for various parameters in (L, L_p, d_i) space. The maximum strain rate and minimum radius of curvature experienced by each CNT are tracked during the calculations, in order to compute ξ_c,avg, the minimum radius of curvature averaged over all CNTs and y(ξ_c), the fraction of CNTs whose minimum radius of curvature fell below a threshold value ξ_c. We initially choose ξ_c = 40 nm as an upper estimate—thin SWNTs may have ξ_c below 15 nm (39) (Fig. 5 and SI Appendix, Figs. S8 and S9). Fig. 5A reports y(40 nm) vs. L and L_p. Few short CNTs experience high curvature because most of them simply rotate radially; conversely, most of the long CNTs buckle sharply. As L_p increases, CNTs resist bending and buckling (Eq. 6). Fig. 5B shows y(40 nm) as a function of d_i. Recall that d_i is a unique marker of maximum strain rate, and this figure clearly confirms Eq. 7. For high L, there is a plateau in y; below a certain d_i, most chains experience high curvature and hence are expected to break. Above this threshold d_i, the fraction of chains that experience high curvature drops off dramatically because the maximum strain rate is not large enough. In contrast, for low L, most of the chains rotate and avoid compression-induced curvature. These results explain the overall CNT breaking mechanisms (depicted in Fig. 6) according to two regimes: For long CNTs, 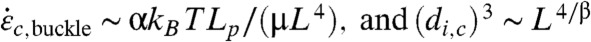. For short CNTs,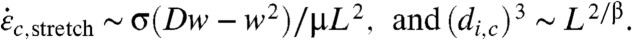

Fig. 5.

(A) y(40 nm); i.e., percentage of CNTs whose minimum radius of curvature falls below 40 nm during bubble collapse, as a function of L and L_p. (d_i = 70 μm, P_A0 = 4500 kPa, 960 CNTs simulated per trial). (B) y(40 nm) vs. d_i. For long CNTs, the probability of buckling catastrophically is roughly independent of initial distance d_i over a broad range of lengths. (L_p = 30 μm).

Fig. 6.

Overall schema for CNT breaking. CNTs near the bubble nucleus (green region) align tangentially during bubble (blue) growth. During collapse, CNTs may rotate radially and stretch or buckle depending on their length.

The scission rate k represents breaking events/time. The number of breaking events per unit time is proportional to the volume of the region around the bubble with CNTs experiencing a strain rate necessary to break (d_i,c)³; i.e., k ∼ L^p/β, with p = 2 for short CNTs that rotate radially and stretch, p = 4 for long CNTs that buckle, and β ≈ 0.82–1 from our simulations. Therefore, the average CNT length decays with a power law m = 1/q = β/p (see Eq. 1), where m ≈ 0.41–0.5 for short CNTs and m ≈ 0.205–0.25 for long CNTs. The crossover between the two behaviors depends on CNT stiffness (persistence length); in polydisperse samples, the two mechanisms can coexist. The prediction for short CNTs compares well with the power-law of 0.5 measured in samples of short SWNTs (5). The prediction for long CNTs captures the power-law of 0.22 measured for long MWNTs (4).

In conclusion, our simulation results and scaling arguments show that for a given population of CNTs of length L, the scission rate scales with L^q, where q depends on the length-dependent mode of deformation during bubble collapse. The model reconciles the apparent contradiction in the experimental data by showing that two separate breaking mechanisms (and two separate scaling laws) are expected because CNTs can rotate radially and stretch or buckle depending on their length and stiffness. Direct comparison between different CNT samples is complicated by other properties; e.g. sidewall defects, which induce permanent bends and kinks and may affect these scaling relationships.

These peculiar dynamics, due to the rapid reversal of the biaxial stretching flow during bubble expansion into uniaxial stretching during collapse, may impact several research areas. Of course, these results generally hold for similar stiff fibrils undergoing ultrasonication, including various interesting systems such as mineral rods and whiskers; e.g., sepiolite and bohemite, metal and metal oxide nanorods and nanowires. These rodlike colloids are normally suspended by sonication, which is likely to cut them, affecting their length-dependent dynamics and liquid crystalline phase behavior. Further experiments should be carried out to explore these mechanisms in more detail, including possibly direct visualization of CNT or fibrils during sonication events, which should be within reach based on recent reports (40). Moreover, it is interesting to speculate on the effect of shape in other deformable particles whose unperturbed shape is platelike or isotropic, such as biological cells, graphene, and clay. Graphene and clay should align parallel to the bubble surface during bubble expansion and may buckle upon sudden flow reversal. Cells are often sonicated to release their DNA or proteins; in this process, they may stretch into disks parallel to the bubble surface and then buckle into parachute shapes during the sudden collapse-induced uniaxial stretching flow. After all, the classical “frangar, non flectar” may not hold at the micro- and nanoscale.