Abstract
We compared image restoration methods [Richardson-Lucy (RL), Wiener, and Next-image] with measured “scatter” point-spread-functions, for removing subsurface fluorescence from section-and-image cryo-image volumes. All methods removed haze, delineated single cells from clusters, and improved visualization, but RL best represented structures. Contrast-to-noise and contrast-to-background improvement from RL and Wiener were comparable and 35% better than Next-image. Concerning detection of labeled cells, ROC analyses showed RL ≈Wiener > Next-image >> no processing. Next-image was faster than other methods and less prone to image processing artifacts. RL is recommended for the best restoration of the shape and size of fluorescent structures.
OCIS codes: (170.0170) Medical optics and biotechnology, (170.3880) Medical and biological imaging, (100.0100) Image processing, (100.1830) Deconvolution, (180.0180) Microscopy, (180.2520) Fluorescence microscopy
Introduction
We are developing cryo-imaging technology and applying it to a very large number of biomedical and biotechnology applications, including stem cell therapy, metastatic cancer, gene expression mapping, mouse phenotyping, imaging agents, etc [1–5]. The Case cryo-imaging system consists of a bright-field/fluorescence microscope, an imaging system positioner, and a customized, motorized cryostat, and significant automation software. By alternately sectioning and imaging, a cryo-imaging system will acquire 3D, high-resolution, large field of view, color, and molecular fluorescence image volumes from sequential images of the tissue block face. Serially acquired images of the sample block face are stacked to create 3D microscopic resolution, brightfield and fluorescence data sets with 15 μm-scale or better resolution. Cryo-imaging can detect even single fluorescently labeled cancer and stem cells throughout a mouse. In the case of bright fluorescent cells and transparent tissues, light scatter and subsurface fluorescence is an issue in block face imaging. In our laboratory, we have noted subsurface fluorescence from a variety of sources, including isolated fluorescently labeled stem cells and cancer cells [1,4]. Spaan et al, observed subsurface fluorescence in a section-and-image system when they imbedded arteries with a fluorescent plastic [6]. One approach to reduce this problem is to incorporate a microscope with optical sectioning capabilities. Tsai et al used laser ablation for removing physical sections of tissue and a two-photon instrument for optical sectioning of the newly exposed volume [7]. Ragan et al. used a fast two-photon imager and serial milling to image an entire fluorescently stained heart embedded in paraffin at microscopic resolution [8]. Although incorporation of confocal or two photon microscopes is a powerful approach, the field of view is necessarily limited by a relatively high numerical aperture. That is, to achieve optical sectioning <10 µm on a “macro” confocal microscope (e.g., Leica LSI), the NA would be 0.31 and the field of view would be only 0.5 mm. With such a microscope, larger fields of view will necessarily require lower NA’s and thicker optical sections. Similar limitations on field of view are found with other optical sectioning approaches such as computational optical sectioning with a high numerical aperture microscope or structured illumination [9,10], although more exotic solutions exist with larger fields of view [11]. With a field of view of 0.5 mm, it would take 80 x 160 = 12800 images for each slice, an impractical approach. Instead, we typically use a field of view of ≈20 mm and use image processing on the physically sectioned data. Steyer et al. [4] developed the “Next-image” processing method wherein the next image in a stack is used to estimate and remove the subsurface contribution in the current image. Results were positive, but this method uses a difference between two images, necessarily a noisy process. Using an imaging cryomicrotome to assess blood flow with microspheres, van Horssen also subtracted a blurred version of the next image to reduce subsurface fluorescence [12].
In this report, we address the problem of subsurface fluorescence using image deconvolution methods which use more than two images, presumably providing improved contrast to noise characteristics as compared to Next-image processing. As reviewed in references [13,14], there are a very large number of deconvolution algorithms which could be applied. We evaluated the Richardson-Lucy (RL) algorithm [15,16], a powerful iterative maximum likelihood image restoration algorithm, and the Wiener filter [17], a single step method that accounts for noise characteristics. Using a variety of test data sets, we qualitatively and quantitatively compare results to our “Next-image” processing method. In the next section, we briefly describe the three image restoration methods.
Image restoration methods
We assume that for fluorescence images in homogeneous tissue, output images o, are obtained by the convolution of the true signal i with the point spread function h as in Eq. (1).
| (1) |
The independent variable X refers to position coordinates in 3D. By convention, the optic axis perpendicular to the imaging plane is the Z axis. Using matrix notation, the image formation model can be written as
| (2) |
where n is a noise random variable. The point spread function (PSF), h, describes the nature of the blur mostly caused by scattering and absorption in the tissue. (Optical blur in our microscope is negligible as described later.)
In the case where the image pixels are modeled as Poisson distributed, the expected value of each pixel is given by Eq. (2).
Wiener Deconvolution
The Wiener filtering method models additive noise. The filter is derived by considering the mean square error between the filtered estimate and the true object. We minimize to solve for the Wiener filtered image:
| (3) |
In Eq. (3) is the power spectrum of the PSF, is the power spectrum of the true image and is the power spectrum of the noise. The ratio is referred to as the noise to signal ratio (NSR). The NSR serves to damp amplification of high frequency noise due to the low amplitude of the PSF power spectrum at high frequencies. Typically the noise and true image power spectra are not known apriori. It is common practice to approximate this ratio by a scalar parameter.
Richardson Lucy (RL) method
The RL algorithm is a non-linear iterative image restoration method obtained by maximizing the log likelihood function assuming Poisson statistics. The likelihood of observing the image voxel is given by Eq. (4).
| (4) |
Here is the likelihood of observing the voxel at X. If we make a large number of observations of the voxel at X, then it would be Poisson distributed with a mean of . The log-likelihood over all voxels given the ideal image can be written as
| (5) |
The dependence of o,i and h on position is implied in Eq. (5). Maximizing this function with respect to i subject to the constraint that i is non-negative yields the desired solution. The necessary condition for the ideal image i to be the maximum of the log likelihood function is given by
| (6) |
| (7) |
Here is the adjoint of h. Combining Eq. (6) and Eq. (7) we get a non linear algebraic equation for i. We can then use the method of successive approximation to set up an iterative scheme for determining i.
| (8) |
It has been shown that the RL solutions converges to the maximum likelihood solution [18]. The non negativity constraint is maintained if the initial guess is non-negative [15] and can be inferred from Eq. (8).
The RL algorithm can amplify noise after a large number of iterations. One recommended approach is to simply stop the algorithm before noise amplification [15]. A modified likelihood function suggested by White [19] uses a damping parameter to control noise amplification. The dampened RL algorithm is obtained by modifying the log likelihood function (Eq. (9)) appropriately.
| (9) |
The functions f and g are given in Eq. (11) and Eq. (10) respectively.
| (10) |
| (11) |
The parameter T in Eq. (10) is the damping factor and is set as a multiple of the background noise in the image to prevent noise amplification. The variable N in Eq. (11) is an integer and the algorithm is insensitive to N as long as it is a large number and is usually set at 10. The variable N determines how flat the function f becomes for small values of y. The damped RL iteration is given by Eq. (12)
| (12) |
where is max( ,1).
Next-image processing
The Next-image processing or subtraction method [4] is derived by considering an elementary model of light propagation in tissue i.e. the exponential decay and scattering of emitted fluorescence as it passes through a finite thickness of tissue. Based on this model the subsurface fluorescence contribution from a slice below the block face is estimated and subtracted from the current image.
The subsurface fluorescence compensated image is given by
| (13) |
where is the ideal image of the kth section that we seek to estimate. The kth section lies just above the k + 1th section and s is the section thickness. The fraction of incident light that goes through the tissue air interface is ; the fraction of emitted light that passes through the air tissue interface is ; is the fraction of emitted epifluorescence intensity; is the total tissue attenuation coefficient; is a two dimensional Gaussian function characterized by variance σ2, that approximates in-plane scattering of light.
The exponential attenuation factor in Eq. (13) is replaced by a scaling factor k and rewritten as Eq. (14).
| (14) |
Parameters k and σ are estimated in a semi-automated fashion as described by Steyer et al [4]. Briefly, individual microspheres are identified in the volume of interest. The image sections lying above the microspheres i.e. the regions containing the out of plane fluorescence are considered. For every image plane or region of interest containing out of plane fluorescence, the successive image is scaled and blurred by k and h respectively and subtracted from it. An objective function Fobj given by Eq. (15) was minimized to estimate k and σ
| (15) |
where the sum is over all the pixels in the subtracted image region; is the subtracted image region and i, k are the subscripts corresponding to a pixel location; is the mean value of the subtracted image region.
Experimental methods
Measurement and processing of PSF
We measured the PSF from cryo-images of a fluorescent point source in phantoms. Green (515 nm) FluoSpheres sulfate microspheres of diameter 0.2 μm (Molecular Probes, Invitrogen, Eugene, OR) were embedded in a freezing compound (O.C.T, Tissue Tek, Ted Pella, Inc., Redding, CA) which when frozen has scatter and attenuation properties similar to frozen brain tissue [4]. Samples were sectioned at 10 μm thickness and imaged at 20x magnification, giving an in-plane pixel size of 5.4 µm. The nature of the image acquisition in cryo-imaging makes the PSF asymmetric along z; i.e., no fluorescence is left once the source is sectioned away. Twenty measured PSF’s were aligned and averaged. There was a constant, low background signal in the averaged PSF arising from the OCT which was estimated from the mean of the local sub-volume devoid of signal. This constant value was subtracted from the averaged PSF. The measured PSF was resampled to lower resolution by box-car averaging. For resampling to higher resolution, tri-linear interpolation was used.
The above PSF depends upon scatter and absorption in the medium rather than optical properties of our microscope. For a 1X objective with 0.11NA, the manufacturer reports a depth of field of 477 μm, a distance much greater than the depth of measured subsurface fluorescence. To measure relative contributions of scatter and absorption versus optical blurring, we compared measurements in OCT or tissue to those in free-space. For 0.2 μm microspheres on a coverless glass slide in free space, digital images had a single bright pixel (5.4 μm pixel size) with no attenuation over a depth of field of ≈500 μm. In OCT gel, the image of the microsphere was typically 3x3 pixels and attenuated to background over a depth of about 100 μm. In free-space, 15 μm diameter microsphere images typically had low intensity, single pixel side lobes along x and y when imaged with a pixel size of 15.4 μm. After background subtraction, the intensity of the side lobes was 1/10 the peak intensity. There was minimal intensity drop over a 500 μm depth of field. As shown in multiple figures, there is significant blurring and attenuation of these microspheres in tissue and OCT.
Biological sample and phantom experiments
We performed a variety of imaging experiments using phantom and animal tissues. First, we created an O.C.T phantom containing 15.4 µm green fluorescent microspheres, mimicking cells. According to the manufacturer, microsphere size was 15.4 ± 1.4 μm (standard deviation) and the total fluorescence intensity varied by less than 4%. Images were acquired with an in-plane resolution of 4 μm and section thickness of 5 µm with a 27x magnification. Second, to test algorithms in autofluorescent tissues, we injected 5 million of the 15.4 µm green fluorescent microspheres through the left ventricle of mouse, providing an elegant test sample with microspheres trapped in small vessels throughout the mouse. After sufficient time to allow for circulation, the mouse was euthanized, embedded in O.C.T, and imaged using the cryo-imaging system [4]. Cryo-imaging was done at 7x magnification (15.6 μm in-plane resolution) and 40μm slice thickness. Third, we also imaged 14 day embryos of a transgenic mouse line expressing green fluorescent protein (EGFP) under the regulatory control of the smooth muscle gamma-actin promoter (SMGA). These SMGA/EGFP mice express fluorescently labeled smooth muscle delineating the vascular, respiratory, and GI systems. In all experiments, a long pass GFP filter cube (Exciter: HQ470/40x, Dichroic: Q495LP, Emitter: HQ500LP, Chroma, Rockingham, VT) was used. The excitation peak was 475nm and the emission peak was 509nm. Animal experiments were covered under an IACUC approved protocol.
Restoration experiments and analyses
All image processing and analysis was done in Matlab using algorithms previously described and PSF measured as above. Unless indicated otherwise, the following parameters were used: Wiener (NSR = 0.01), RL (N = 20, T = 3), and Next-image processing parameters were as follows: μt was, O.C.T. (187 cm-1) heart (267 cm-1), liver (218 cm-1), brain (161 cm-1), and fat (254 cm-1) ; σ was, O.CT.(7.2 μm), heart (9.1 μm), liver(7.5 μm), brain (11.2 μm), and fat (12.2 μm).
We qualitatively and quantitatively evaluated restoration. To compare images qualitatively following restoration, we windowed the images so that the microspheres correspond to the brightest objects in the processed and unprocessed images. Second, to determine the contrast to noise ratio and contrast to background ratio, we used morphological reconstruction to determine the background in the unprocessed and the restored images. The bead locations were determined by hysteresis thresholding. The upper and lower thresholds for hysteresis thresholding were determined manually by inspecting the microsphere intensities and the histogram of the image. The maximum intensities of the microspheres from the bead locations were recorded. We selected regions of interest (4x4 pixels) in sections above the ones containing the bead and measured the noise in that region after verifying that they did not contain any microspheres.
We constructed ROC curves for microsphere detection as a function of processing methods. We used a sub-volume of the brain (401x401x20 voxels) and manually determined microspheres (n = 175) to serve as the gold standard. Using the processed images, we varied the threshold for detection so as to trace out the ROC curve. A connected component analysis was done on the binary image following thresholding to determine the centroid of all connected groups of voxels detected as microspheres. For a detected cluster to be classified as true positive, it had be less than 10 voxels in volume and had to be within 5 voxel Euclidean distance of the manually recorded location. If a cluster was larger than 10 voxels and it contains a manually recorded location, a true positive was recorded and the rest of the pixels in the cluster were assigned as false positives. Clusters which did not meet either of the aforementioned criteria were labeled as false positives. The ROC curve was generated by varying the threshold across the full range of image voxel values.
Results
PSF measurements for 20 Microspheres (0.2 μm diameter) were aligned and averaged. Maximum intensity projections (MIPS) along XY and YZ are shown in Fig. 1 . The subsurface fluorescence artifact, hereafter called the ‘comet’ tail artifact extends to about 100 μm and spreads maximally in the XY plane to ≈15 μm. Region of interest volumes below the beads was used to estimate background intensity, a value which was typically <10% of the maximum value. As argued in Methods, this response is largely due to the scatter/attenuation in the medium rather than optical blurring.
Fig. 1.

Measured scatter PSF of the cryo-imaging system. Twenty measured PSFs were aligned and averaged. A background value was subtracted. Maximum intensity projections in the YZ (a) and XY (b) planes are shown. The comet tail extends approximately 100 µm and the maximal in-plane spread is 15 µm. The PSF was acquired at a resolution of 5.4x5.4x10 µm using microspheres 0.2 μm diameter
Restoration results for larger microspheres (15.4 μm) embedded in O.C.T are shown in Fig. 2 . Comet tail artifacts in the unprocessed image extended to a height of ≈100 μm. All three image restoration methods reduced the comet tail artifacts. Next-image did not affect the in-plane dimension, which was about 30 μm, indicating lateral blur from the microspheres. RL and Wiener narrow the in-plane width to 2-4 pixels (5 μm pixel size), a value corresponding to the actual size of the microspheres. RL restores the shape of the microspheres along Z better than Wiener and Next-image processing. Wiener deconvolution introduces noise compared to RL and Next-image processing.
Fig. 2.
Reduction of comet tail artifacts using image restoration algorithms. Microspheres (15.4 μm diameter) were embedded in O.C.T phantom, imaged, and processed. MIPS of a sub volume are shown. The unprocessed image (a) shows the comet tail artifact extending to a depth of ≈100 μm. RL processing (b) removes comet tail artifacts and restores the shape of the bead both in-plane and along Z. Next-image processing (c) reduces the comet tail artifacts but in-plane spread persists. Wiener deconvolution (d) removes comet tail artifacts but the resultant image suffers from high frequency noise and in-plane restoration is not as effective as in RL. Parameters were: voxel size 4 × 4 × 5µm3, (RL, 20 iterations, damping factor of 3), and Wiener, NSR = 10−4. Scale bar corresponds to 50 µm
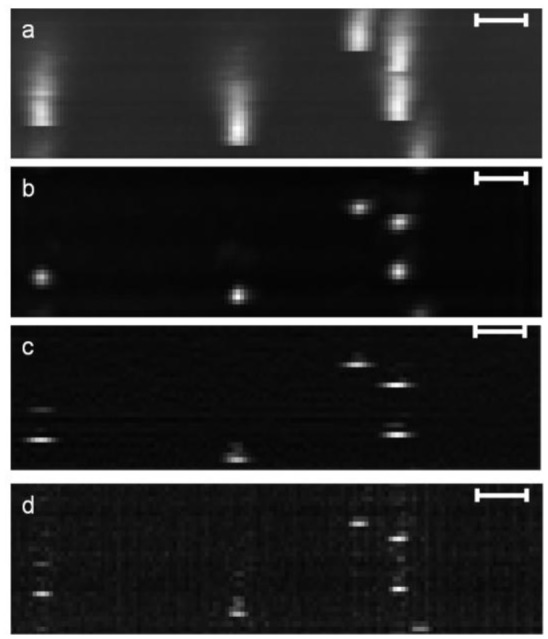
In Fig. 3 , we magnify images to examine the quality of restoration for a single representative microsphere. Subsurface fluorescence is clearly reduced in all methods, although Wiener retains some small noise speckles. We note that this noise with Wiener can be reduced by increasing the NSR parameter, but there is a tradeoff between size restoration and image noise. The shape of the spherical microsphere is clearly evident with RL but not with other methods. The RL deconvolved microsphere occupied 10-15 µm in the Z direction and an estimated 12-16 µm across within the cutting plane.
Fig. 3.

Restoration of a single, representative microsphere from the same volume in Fig. 2. Unprocessed image (a) contains significant subsurface fluorescence artifacts and in-plane spread. RL (b), Wiener (c) and Next-image (d) effectively remove subsurface fluorescence. RL gives a truer spatial representation of the microsphere.
We compared the three restoration methods on a variety of tissues with fluorescent cells or microspheres. In tissue, we use lower resolution cryo-imaging: 40 µm slice thickness and 15.6 µm pixels. Observations were similar to those for the O.C.T. phantom, with RL giving the best result, although all three methods gave significant improvement. Results were surprisingly robust even though we used a scatter PSF from O.C.T. to correct scatter in tissue, and probably this is due to using lower resolution data. In Fig. 4 , we show image results from RL restoration in heart tissues showing some diffuse auto fluorescence. RL removed subsurface fluorescence in the heart tissue as evidenced by the removal of comet tail artifacts, and the results for Wiener and Next-Image (not shown) were comparable.
Fig. 4.
Reduction of subsurface fluorescence in the various tissue types. Subsurface fluorescence is seen in both the axial (a) and (c) side view. The PSF measured in OCT was subsampled to restore the images. The restored images show reduced subsurface fluorescence in the axial view (b) and the comet tail reduction in the side view (d). RL image restoration parameters, N = 20 iterations and a damping factor of 1. The original image size was 1036x1360x20 with pixel size of 15.6x15.6x40 µm.
To quantify restoration results, we estimated the contrast to noise ratio (CNR) and contrast to background ratio (CBR) after processing with the image restoration methods (Table 1 ).
Table 1. CNRs and CBRs for restored and unprocessed images. The average values were obtained over 200 microspheres in the brain after detection and manual verification.
| Algorithm | Mean Peak Value | Background | CNR | CBR |
|---|---|---|---|---|
| Unprocessed | 26 | 1.7 | 27 +/− 5 | 14 +/− 2 |
| RL | 60 | 1.8 | 53 +/− 19 | 32 +/−11 |
| Wiener | 54 | 1.77 | 51 +/− 16 | 29 +/− 9 |
| Next-Image | 18 | 0.72 | 39 +/−15 | 23 +/− 9 |
Image data was mouse brain tissue with 15.4 µm microspheres. CNRs and CBRs were improved by processing. RL and Wiener filter gave comparable results, which were better than Next-image. RL more than doubled the CBR, indicating that it will be much easier to detect cells by thresholding following RL processing. We also compared the integrated intensity of the RL and Wiener deconvolved volumes versus the original volume and found that they varied by less than 3%.
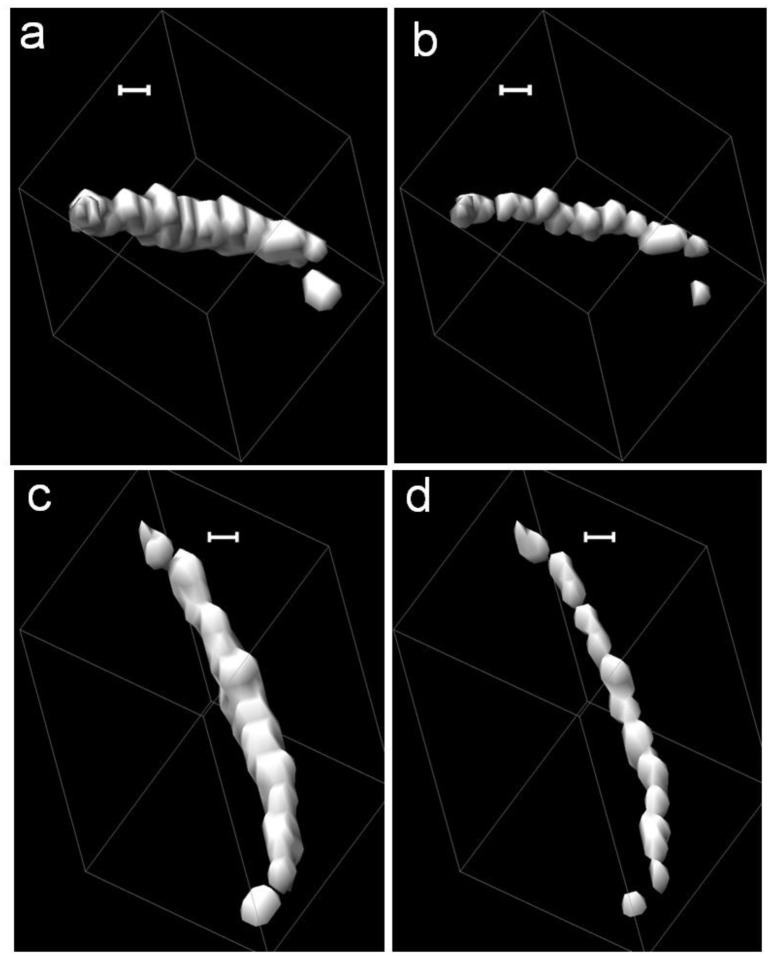
Figure 5 shows the impact of deconvolution on clusters of perfused microspheres in the mouse brain. We present here result of RL (Figs. 5b & 5d). The other two methods provided comparable results. The string of microspheres is oriented at an angle to the z-axis and appears as a single continuous object in the iso-surface rendering of the uprocessed image (Figs. 5a & 5c). Following RL deconvolution, the iso-surface rendering shows better separation of microspheres and clearly delineates 13 microspheres.
Fig. 5.
Isosurface rendering of string of microspheres in the mouse brain trapped in the vasculature. The cluster is oriented along the z-axis of the volume. Two different views of the unprocessed volumes are shown in (a) & (c) and the RL deconvolved volumes are rendered in (b) & (d). Following deconvolution there is better separation between the microspheres along the z-axis. The images were generated from microspheres in the mouse brain. The images were acquired at 15.6x15.6x40 microns. The RL parameters were 20 iterations and a damping factor of 3. The scale bar corresponds to 50 µm.
In addition to microspheres and cells, we assessed restoration on fluorescent anatomical structures. In Fig. 6 , we show results from a transgenic embryo with EGFP under the promoter for smooth muscle gamma actin, the so-called SMGA mouse (kindly provided by J. Lessard, University of Cincinnati [20]). The embryo expresses GFP in the smooth muscle cells lining the GI tract and the esophagus. After RL processing, cross sections are clearly improved as compared to the unprocessed image data. Unprocessed images clearly show subsurface fluorescence in the lumen of the esophagus, which is removed by RL processing, allowing one to clearly see the outline of the esophageal wall. The Next-image processing method has a comparable performance in terms of removing subsurface fluorescence inside the lumen of the esophagus. The Wiener deconvolution method amplifies noise and produced ringing artifacts at the wall of the esophagus and subsurface fluorescence removal wasn’t nearly as effective as the other two methods.
Fig. 6.
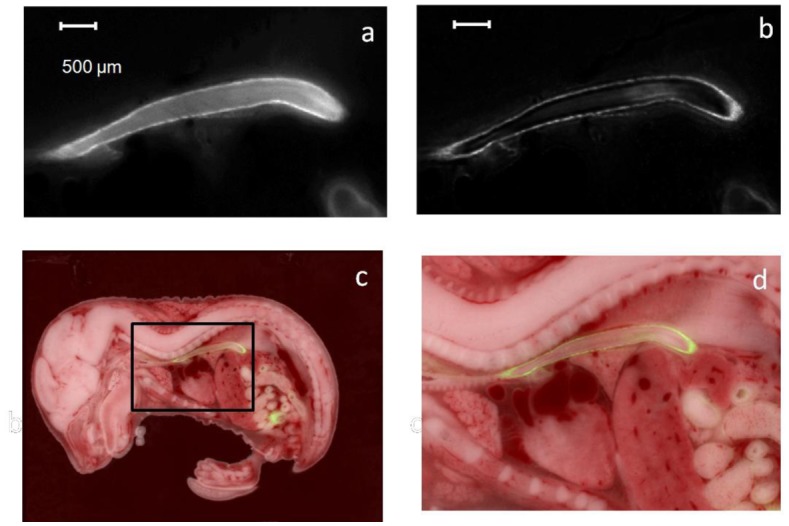
Image restorations by elimination of subsurface fluorescence from fluorescent structures. XY cross sections were obtained from the esophagus of a mouse (a). Unprocessed image shows significance subsurface fluorescence in the lumen of the esophagus. RL image restoration (b) removes the subsurface fluorescence and clearly delineates the esophagus. The brightfield section with the corresponding RL processed fluorescence image is shown in (c) and the region in the box is zoomed in and shown in (d). The images were acquired at a resolution of 15.6x15.6x20 µm. A sub volume of size 337x195x44 containing the esophagus was processed. RL parameters, 20 iterations and 0.3 damping parameter.
We assessed the impact of the restoration algorithms on microsphere detection (Fig. 7 ). ROC curves were generated as described in Methods for the three restoration methods. A statistical comparison of the Area Under the Curves (Az) showed significant difference (P<0.02) between the microsphere detection using unprocessed data and the restored data. In addition, RL and Wiener restoration were significantly better (P<0.05) than Next-image processing.
Fig. 7.
ROC curves for detection of microspheres in tissue. Following restoration, detection was done using a simple thresholding technique. Areas under the curves (Az) were 0.9977, 0.9985, 0.99894, and 0.99892, for unprocessed, Next-image, RL, and Wiener respectively. The inset shows the curve after zooming in on the x-axis between 0 and 0.01 where there are slight but visually perceptible differences between the curves. The image thresholds for two of the data points are marked as T = 0, T = 1 and T = 3(inset).
Discussion
Next-image, Wiener, and RL all greatly reduced the subsurface artifact in both phantom and tissue experiments. RL and Wiener provided very high contrast improvement, shape and size restoration. In addition, deconvolution of clusters of fluorescent microspheres clearly separated it into individual microspheres. Next-image processing provides artifact free images and very fast execution times. Below, we review each of these criteria.
A restoration method should remove subsurface fluorescence, localizes the fluorescence signal to the proper location, and restore shape and size. In Fig. 2, RL clearly restores the shape and size of the microspheres better than either Wiener or Next-image processing. Taking all qualitative observations together, we conclude that RL > Wiener > Next-image.
We determined a variety of quantitative metrics of image quality including CNR, CBR, and ROC. CNR assesses noise as well as the effectiveness of deconvolution in reassigning intensity from neighboring pixels to the source. CBR measures the ability to threshold for detection. As shown in Table 1, RL improved CNR by a factor of 2 and was 35% better than the Next-image processing and marginally better than Wiener filtering. Next-image processing did not improve contrast as much as RL or Wiener because the subtraction step adds to the noise and diminishes the peak intensity of microspheres. The CBR for RL and Wiener were much higher than the Next-image processing for the same reasons. CNR and CBR are indicators of an improved ability to detect cells and microspheres.
Statistical analysis of areas under the ROC curves (Az) indicates that each of the three processing methods is significantly different from the “raw” result without processing (P < 0.02). Wiener and RL are significantly different (P < 0.05) from Next-image processing, but there is no significant difference between Wiener and RL (P > 0.05). Statistically significant results are obtained even when all four methods are nearly identical in the larger graph in Fig. 7. This result is due to the very large number of background pixels, giving a large number of true negatives (NN) and low prevalence (Np) in an ROC. At a threshold of T = 0 (upper right), every pixel will be counted as a detected microsphere and the false positive fraction ( = FP/NN) must be 1.0 and every microsphere will be detected giving a true positive fraction (TP/NP) of 1.0. At a threshold of T = 1, the false positive fraction drops precipitously to a very small number because of the large number of pixels having value 0, and the true positive fraction remains at 1.0. As a result, this gives data points at the upper left corner of the ROC and Az values very near the ideal value of 1.0. Only when we zoom into low values of false positive fraction (inset) do we see a difference in the methods. There are differences among the curves over a limited range of thresholds (inset). This difference gives rise to statistically different Az values. Please note that low prevalence does not impact the accuracy of statistical testing with Az [21].
To examine the ROC in another way, we can examine the sensitivity of the method for a given false positive fraction. At a false positive fraction (1- specificity) of 0.0015, the detection sensitivity jumps from 60% for the unprocessed images to greater than 95% for RL. This almost two-fold increase in sensitivity corresponds to a detection of tens of thousands of microspheres or cells over one of our large volume data sets.
With regards to fluorescent stem and cancer cells, our ultimate goal is quantification. We are creating an evolving analysis pipeline consisting of three steps: (1) Preprocessing to remove subsurface fluorescence and improve contrast to background ratio. (2) Detection of clusters using pattern classification approaches. (3) Enumeration of cells within a cluster using a model-based approach. In this study, we have focused on the first step. Hence, in the ROC analysis, we used a simple thresholding approach to detect clusters.
The restoration methods perform well in various tissue types, despite potential variation in scatter and attenuation (Figs. 4-6). This relative insensitivity to PSF error is probably due to the decreased cryo-image resolution (40 µm slice thickness and 15.4 µm in-plane pixels) when imaging tissue. That is, when the PSF is resampled for the working resolution imaging, its depth extends only about 2 slices and 3 pixels. Any deviation between tissue types would probably be of the order of a pixel. Both Wiener and RL would be relatively insensitive to such variations. We verified this by purposefully making small variations in the PSF decay along the radial or z-directions and found little variation in the output
With these processing methods, cells are more easily quantified but one must be careful about assigning fluorophore concentration values. RL and Wiener reassign intensity values from neighboring pixels to the source. Because of this reassignment, these methods do not necessarily give calibrated results across experiments. For example, if one were to use thinner slices, there would be more sampling of the fluorescent signal and a higher signal value after processing. Although Next-image does not concentrate the fluorescence comet tail into the source, there is a subtraction step which tends to reduce peak signal. In most experiments, such as cell counting, we are not concerned with fluorophore concentration. In those cases where fluorophore concentration is of interest, we will determine calibration methods which account for processing.
Other considerations include computation time and robustness. A potential downside to RL is that it can amplify noise as the number of iterations increase. However, in our hands, when we use a damping factor over a very large range (0.3-3), we have not observed such behavior. With Next-image processing, we are always ensured of getting an improved result closer to the actual input image data. As described previously, computation time gives Next-image a distinct advantage over RL and Wiener. We benchmarked processing times using a work station with a quad-core 3 GHz processor and 32GB of RAM. In order to analyze a stack of images of size 1360x1040x150, it takes 45 minutes for RL, 79 seconds for Wiener and 15 seconds for Next-image method. Another downside of RL is the need for large amounts of memory, requiring one to partition a large mouse volume for processing. This additional complexity is not inherent with Next-image processing where one can simply consider two images at a time. Please note that timing and memory considerations for RL are based on un-optimized Matlab code. Multi-threading, GPU calculations, and C++ implementations might give much different results. In summary, we believe that both RL and Next-image have value for cryo-imaging. On the one hand, in those instances where one wants to process a large volume image data with strong fluorescence signal, one should use Next-image processing. On the other hand, if we want to create the best reconstruction of the distribution of fluorescence such as in the embryo experiment (Fig. 6), RL has clear advantage. In addition, for very dim cells, RL clearly improves detection, an important consideration in many cryo-imaging applications. We conclude that image restoration is a valuable processing step to include in the cryo-imaging pipeline and that multiple algorithms should be included.
Acknowledgment
This investigation was conducted in a facility constructed with support from Research Facilities Improvement Program Grant Number C06 RR12463-01 from the National Center for Research Resources, National Institutes of Health. This research is supported by the Ohio Wright Center of Innovation and Biomedical Research and Technology Transfer award: “The Biomedical Structure, Functional and Molecular Imaging Enterprise,” National Institutes of Health (NIH) R42CA124270, phase I and NIH 1R24 CA110943. GS was partially supported by NIH training grant, NIH T32EB007509. Dr. Wilson has interest in BioInVision, Inc., which intends to commercialize Cryo-imaging technology.
References and links
- 1.Steyer G. J., Roy D., Salvado O., Stone M. E., Wilson D. L., “Cryo-Imaging of Fluorescently-Labeled Single Cells in a Mouse,” Proc. Soc. Photo Opt. Instrum. Eng. 7262, 72620W–, W8. (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Roy D., Steyer G. J., Gargesha M., Stone M. E., Wilson D. L., “3D cryo-imaging: a very high-resolution view of the whole mouse,” Anat. Rec. (Hoboken) 292(3), 342–351 (2009). 10.1002/ar.20849 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Gargesha M., Qutaish M., Roy D., Steyer G., Bartsch H., Wilson D. L., “Enhanced Volume Rendering Techniques for High-Resolution Color Cryo-Imaging Data,” Proc. Soc. Photo Opt. Instrum. Eng. 7262, 72655V (2009). [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Steyer G. J., Roy D., Salvado O., Stone M. E., Wilson D. L., “Removal of out-of-plane fluorescence for single cell visualization and quantification in cryo-imaging,” Ann. Biomed. Eng. 37(8), 1613–1628 (2009). 10.1007/s10439-009-9726-x [DOI] [PMC free article] [PubMed] [Google Scholar]
- 5.Roy D., Gargesha M., Steyer G. J., Hakimi P., Hanson R. W., Wilson D. L., “Multi-scale Characterization of the PEPCK-Cmus Mouse Through 3D Cryo-Imaging,” Int. J. Biomed. Imaging 2010, 1–12 (2010). 10.1155/2010/105984 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 6.Spaan J. A., ter Wee R., van Teeffelen J. W., Streekstra G., Siebes M., Kolyva C., Vink H., Fokkema D. S., VanBavel E., “Visualisation of intramural coronary vasculature by an imaging cryomicrotome suggests compartmentalisation of myocardial perfusion areas,” Med. Biol. Eng. Comput. 43(4), 431–435 (2005). 10.1007/BF02344722 [DOI] [PubMed] [Google Scholar]
- 7.Tsai P. S., Friedman B., Ifarraguerri A. I., Thompson B. D., Lev-Ram V., Schaffer C. B., Xiong Q., Tsien R. Y., Squier J. A., Kleinfeld D., “All-optical histology using ultrashort laser pulses,” Neuron 39(1), 27–41 (2003). 10.1016/S0896-6273(03)00370-2 [DOI] [PubMed] [Google Scholar]
- 8.Ragan T., Sylvan J. D., Kim K. H., Huang H., Bahlmann K., Lee R. T., So P. T., “High-resolution whole organ imaging using two-photon tissue cytometry,” J. Biomed. Opt. 12(1), 014015 (2007). 10.1117/1.2435626 [DOI] [PubMed] [Google Scholar]
- 9.Mitić J., Anhut T., Meier M., Ducros M., Serov A., Lasser T., “Optical sectioning in wide-field microscopy obtained by dynamic structured light illumination and detection based on a smart pixel detector array,” Opt. Lett. 28(9), 698–700 (2003). 10.1364/OL.28.000698 [DOI] [PubMed] [Google Scholar]
- 10.Neil M. A., Juskaitis R., Wilson T., “Method of obtaining optical sectioning by using structured light in a conventional microscope,” Opt. Lett. 22(24), 1905–1907 (1997). 10.1364/OL.22.001905 [DOI] [PubMed] [Google Scholar]
- 11.Li G. D., Savvas D., Arthur E., Lucy E. J., “A new wide field-of-view confocal imaging system and its applications in drug discovery and pathology,” Proc. Soc. Photo Opt. Instrum. Eng. 6009, 1–16 (2005). [Google Scholar]
- 12.van Horssen P., Siebes M., Hoefer I., Spaan J. A., van den Wijngaard J. P., “Improved detection of fluorescently labeled microspheres and vessel architecture with an imaging cryomicrotome,” Med. Biol. Eng. Comput. 48(8), 735–744 (2010). 10.1007/s11517-010-0652-8 [DOI] [PMC free article] [PubMed] [Google Scholar]
- 13.Sarder P., Nehorai A., “Deconvolution methods for 3-D fluorescence microscopy images,” IEEE Signal Process. Mag. 23(3), 32–45 (2006). 10.1109/MSP.2006.1628876 [DOI] [Google Scholar]
- 14.Wallace W., Schaefer L. H., Swedlow J. R., “A workingperson’s guide to deconvolution in light microscopy,” Biotechniques 31(5), 1076–1078, 1080, 1082 passim (2001). [DOI] [PubMed] [Google Scholar]
- 15.Lucy L. B., “An iterative technique for the rectification of observed distributions,” Astron. J. 79, 745–754 (1974). 10.1086/111605 [DOI] [Google Scholar]
- 16.Richardson W. H., “Bayesian-Based Iterative Method of Image Restoration,” J. Opt. Soc. Am. 62(1), 55–59 (1972). 10.1364/JOSA.62.000055 [DOI] [Google Scholar]
- 17.N. Wiener, ed., Extrapolation, Interpolation, and Smoothing of Stationary Time Series (Wiley, New York, 1949). [Google Scholar]
- 18.Shepp L. A., Vardi Y., “Maximum likelihood reconstruction for emission tomography,” IEEE Trans. Med. Imaging 1(2), 113–122 (1982). 10.1109/TMI.1982.4307558 [DOI] [PubMed] [Google Scholar]
- 19.White R. L., “Image restoration using the damped Richardson-Lucy method,” Proc. Soc. Photo Opt. Instrum. Eng. 2198, 1342–1348 (1994). [Google Scholar]
- 20.Szucsik J. C., Lewis A. G., Marmer D. J., Lessard J. L., “Urogenital tract expression of enhanced green fluorescent protein in transgenic mice driven by a smooth muscle gamma-actin promoter,” J. Urol. 171(2), 944–949 (2004). 10.1097/01.ju.0000099168.25976.9a [DOI] [PubMed] [Google Scholar]
- 21.Park S. H., Goo J. M., Jo C. H., “Receiver operating characteristic (ROC) curve: practical review for radiologists,” Korean J. Radiol. 5(1), 11–18 (2004). 10.3348/kjr.2004.5.1.11 [DOI] [PMC free article] [PubMed] [Google Scholar]