Sensing and decision-making in random search

Abstract

Many organisms locate resources in environments in which sensory signals are rare, noisy, and lack directional information. Recent studies of search in such environments model search behavior using random walks (e.g., Lévy walks) that match empirical movement distributions. We extend this modeling approach to include searcher responses to noisy sensory data. We explore the consequences of incorporating such sensory measurements into search behavior using simulations of a visual-olfactory predator in search of prey. Our results show that including even a simple response to noisy sensory data can dominate other features of random search, resulting in lower mean search times and decreased risk of long intervals between target encounters. In particular, we show that a lack of signal is not a lack of information. Searchers that receive no signal can quickly abandon target-poor regions. On the other hand, receiving a strong signal leads a searcher to concentrate search effort near targets. These responses cause simulated searchers to exhibit an emergent area-restricted search behavior similar to that observed of many organisms in nature.

Organisms routinely locate targets in complex environments. Organisms can find targets by following gradients in the strength of sensory signals, provided such gradients are available and reliably lead toward targets (1). But search conditions are not always so favorable. In many natural settings sensory signals are infrequent, noisy, and contain little directional information (2). For example, moths, sharks, and sea birds search environments that contain scent cues emitted by prey or mates, but these cues are often extremely sparse and subject to large fluctuations (3–5). Under such sparse-signal conditions, it is not clear what behaviors allow organisms to efficiently and reliably locate resources.

Researchers have developed much of the theory of sparse-signal search by studying mathematical models of searching organisms (6–11). The dominant paradigm for developing such models emerged from the random foraging hypothesis—the idea that searchers can encounter targets efficiently by adopting statistical movement strategies that can be described as random walks [(6, 7), see refs. 2, 4, 12 for alternative approaches]. This hypothesis, which has been applied to searching organisms ranging from bees (6) to sea turtles (13), is often invoked when it is not possible or practical for searchers to remember explicit spatial locations (7) and the typical distances between targets exceed the searcher’s sensory range (14). This framework has been used to compare the performance of searchers moving according to different kinds of random walk behavior. In particular, many studies have tried to determine whether searchers moving according to Lévy walks outperform searchers that move according to other types of random walk strategies (e.g., refs. 8–11).

If models are to yield insight into the behavior of searching organisms in nature, they must be simple enough to be studied, but should also capture the dominant features of search behavior. Implicit in the random foraging approach is the assumption that changes in a searchers’ movement behavior in response to sensory data are second-order effects, and that search behavior and performance are dominated by the features of the intrinsic (random) search strategy that the searcher employs. Here we explore an alternative hypothesis: that sensory processes can have a dominant effect on search performance, even when sensory signals are rare, noisy, and lack directional information.

Below we develop a general mathematical framework for modeling search decision-making. As in past models, the framework allows a searching organism to make movement decisions based on an intrinsic movement strategy (e.g., Lévy walk), but allows such decisions to be modified based on noisy sensory data. This framework thus provides an explicit way to model changes in behavior in response to sensory measurements. We explore the effect of incorporating sensory data into search decisions using individual-based simulations of searching predators. We compare search times of simulated predators that make search decisions using random strategies alone (Lévy walk and a unique diffusive strategy), to predators that modify their search behavior based on olfactory measurements.

Model Development

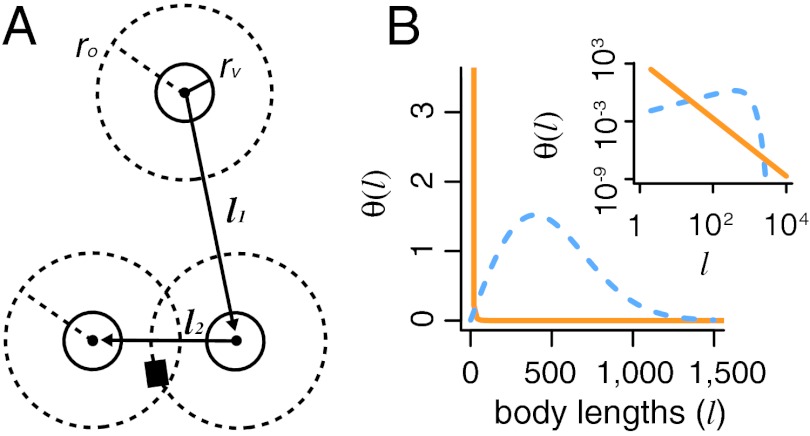
To study search decision-making, we consider an idealized model of a predator in search of prey. We wish to compare the behavior and performance of predators that search using a single intrinsic random strategy to predators that adaptively change their search behavior using the incomplete information gained from sensory measurements. To evoke a strong intuition we consider two types of predator: a visual predator that makes movement decisions based on an intrinsic strategy and locates prey through a short-range, high acuity sense (vision), and a visual-olfactory predator that changes its search behavior based on noisy olfactory data and detects prey at short-range using vision. Predators wander through a large (periodic) two-dimensional habitat in which the mean distance between prey is large. We assume prey emit a scent that can be detected by nearby predators. Similar to previous approaches (e.g., ref. 15), we assume that search is divided into two phases: a local scanning phase and a movement phase [Fig. 1A, (16)].

Fig. 1.

Schematic of predator search. (A) During the scanning phase of the search, a prey encounter occurs if the predator is within a radius of r_v (solid inner circle) of a prey item (black square). The predator also detects scent signals emitted by prey within a radius of r_o (dashed outer circle) at an average rate of ≥1 per τ_o units of time. The predator then turns a random uniform angle between 0 and 2π. During the movement phase, the predator moves a distance of l units determined by its step length distribution. (B) Step length distributions corresponding to visual Lévy (solid curve, α = 3,l_m = 1 body length) and TDD (η = 1/(1,000)² body lengths, dashed curve) strategies. Inset shows distributions on log-log scale.

During the scanning phase, the predator locates any prey within its vision distance r_v (Fig. 1A, solid inner circle) with probability one. This encounter probability reflects the high local acuity of vision. Visual-olfactory predators also scan for olfactory signals. The duration of the scanning phase is denoted τ_v and τ_o for visual and visual-olfactory predators respectively. τ_v includes the time needed to visually search a region of radius r_v and reorient before taking another step. τ_o includes the time taken to collect and process olfactory signals, visually search a region of radius r_v, and reorient before taking another step. We define the olfactory radius r_o (Fig. 1A, dashed outer circle) as the distance where the predator registers an average of one scent signal per scanning period τ_o (see below). We assume that each prey item emits scent at rate λ. During the movement phase, the predator travels in a random uniform direction, a distance of l, at speed v. Visual predators draw the step length l from a prescribed step length distribution θ(l), examples of which are described in the next subsection. Visual-olfactory predators draw from a modified step length distribution defined below by Eq. 1.

During the movement phase, we assume that the predator cannot locate prey or detect scent signals. Additionally, we assume that the predator only responds to the most recent scent signal information and does not store information about the locations it has visited. We study this limiting case where sensory signals are rare, lack directional information, and are not remembered by the predator because this is the scenario in which random search strategies are often invoked. We thus evaluate the scenario in which noisy sensory data are least likely to yield improvement over purely random search. However, we point out that more sophisticated strategies are possible if predators remember past signal encounters or previously visited locations (1, 2, 17).

Searching Without Olfactory Data.

To model predator movements, we begin with a model of decision-making in the absence of any interaction with olfactory data. Researchers typically model the decision process of random searchers by selecting two actions from prescribed probability distributions: a step length l, and a turn angle ϕ. The details of these distributions determine asymptotic properties of the search and strategies are often categorized by this asymptotic behavior: diffusive behavior, in which long-term mean-squared displacement (MSD) scales linearly with time, and superdiffusive behavior in which MSD increases superlinearly with time. An important feature of these strategies is that, unless the searcher encounters a target, the distributions that define how searcher moves (i.e., the distributions of l and ϕ) are fixed. The distributions are not altered in response to sensory measurements.

We model the movements of visual predators using two types of strategies: a Lévy strategy and a unique diffusive strategy. For both, we take the distribution of turn angles between successive steps to be independent and identically distributed ϕ ∼ unif(0,2π) (6). The Lévy strategy draws step lengths from a Pareto distribution, 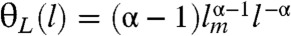, with tail with parameter α and minimum step length l_m [Fig. 1B solid curve, superdiffusive for 1 < α < 3 (6)]. For the second strategy, we introduce a step-length distribution which we call the true distance distribution (TDD) θ_T(l): a greedy strategy wherein the predator selects step lengths from the probability distribution of the distance to the nearest prey item (Fig. 1B dashed curve, see SI Text for further discussion). When prey are distributed according to a Poisson spatial process with intensity η in two dimensions, the TDD is given by the Rayleigh distribution θ_T(l) = 2ηπle^-ηπl2. This strategy is quite distinct from the Lévy strategy (compare curves in Fig. 1B) and later serves to illustrate the strong homogenizing effect of olfactory data on search behavior.

Incorporating Olfactory Data to Make Search Decisions.

The key distinction between visual and olfactory senses in our model is that the visual sense yields perfect information about the location of prey whereas the olfactory sense does not. Thus, including olfactory data allows us to model a predator’s ability to gather and respond to partial information about target positions gleaned from sensory measurements. Below we develop a model for incorporating olfactory signals into search decision-making, but note that this framework could be modified to model responses to other types of sensory cues.

We hypothesize that predators utilize olfactory data through two steps. First, a predator uses a signal observation to estimate the likely distance to the nearest prey. Second, the predator modifies its intrinsic tendency to move in a particular way (represented by θ(l)) based on this information. In keeping with recent models of olfactory search, simulated predators collect olfactory data for τ_o units of time and encounter H∈{0,1,2,…} detectable units of scent (2, 17). In order to act optimally, a predator must make movement decisions based on two distinct uncertainties. First, the predator’s distance to the nearest target is uncertain and is characterized by the probability distribution ν. Second, for a particular ν, the optimal step length distribution θ is also uncertain. Identifying optimal predator behavior requires calculating a Bayesian posterior for the distance distribution ν|_H, and then determining the associated optimal step length distribution θ|_H. This problem remains unsolved and is perhaps intractable. Instead, we approximate this process.

We wish to capture two elements of search decision-making: an intrinsic tendency to move in a particular way θ(l), and a likelihood function P(H = h|l) that translates an observed scent signal h into information about the distance to the nearest prey. A natural model for signal response that incorporates these features is a Bayesian update of the step length distribution θ itself:

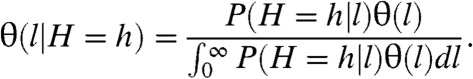[1]

We refer to this as “signal-modulation” of the step length distribution θ(l). This approximation to the optimal strategy yields significant improvement in search performance (see SI Text for further elaboration).

Interpreting Scent Signals.

We assume the predator can estimate or intuit the probability of registering h units of scent in τ_o units of time, as a function of its distance to the nearest prey. This task amounts to being able to estimate the likelihood function P(H = h|l), which depends on the process of scent propagation.

In the complex environments where many species search, turbulent fluctuations in fluid velocity cause large local fluctuations in scent concentration (18). When a prevailing wind or water current is present, predators can gain additional information about the location of a scent source by measuring the velocity of the current (2, 3). We consider the more difficult scenario in which there is no prevailing current. Under these conditions, we model scent arrival as packets that appear at the prey position x₀ according to a Poisson arrival process and then move as a Brownian motion. From the predator’s perspective, this scenario is equivalent to encountering a random number of units of scent, H ∼ Pois(τ_oR(|x - x_o|)), at its location x during a scanning phase of length τ_o, where R is the rate of scent arrival defined by Eq. 3 (see Materials and Methods). Denoting l = |x - x₀|, under these assumptions, the likelihood of h encounters is

[2]

Eq. 2 depends on values of several physical parameters (e.g., the rate at which detectable patches of scent decay) that may be difficult for a predator to infer from measurements of its physical environment. We therefore take a qualitative view in prescribing the parameters of scent propagation. The most important qualitative feature is the length scale r_o, which corresponds to the distance at which a predator will register on average one unit of scent per scanning period τ_o. Heuristically, r_o is the distance at which the predator is likely to detect a faint, yet nontrivial scent. A second qualitative restriction is the expected number of encounters per unit τ_o at a distance of one body length from the prey λ_a. Given these two measurements, the likelihood function can be estimated.

The quantities r_o and λ_a are much more readily measurable by a searching organism than are the explicit parameters in Eq. 3. It thus seems likely that these quantities may constitute part of an organism’s “olfactory search image” (19), and may serve as the direct measurements useful for reinforcement learning.

Results

Visual-Olfactory Predators Find Targets Faster and More Reliably than Visual Predators.

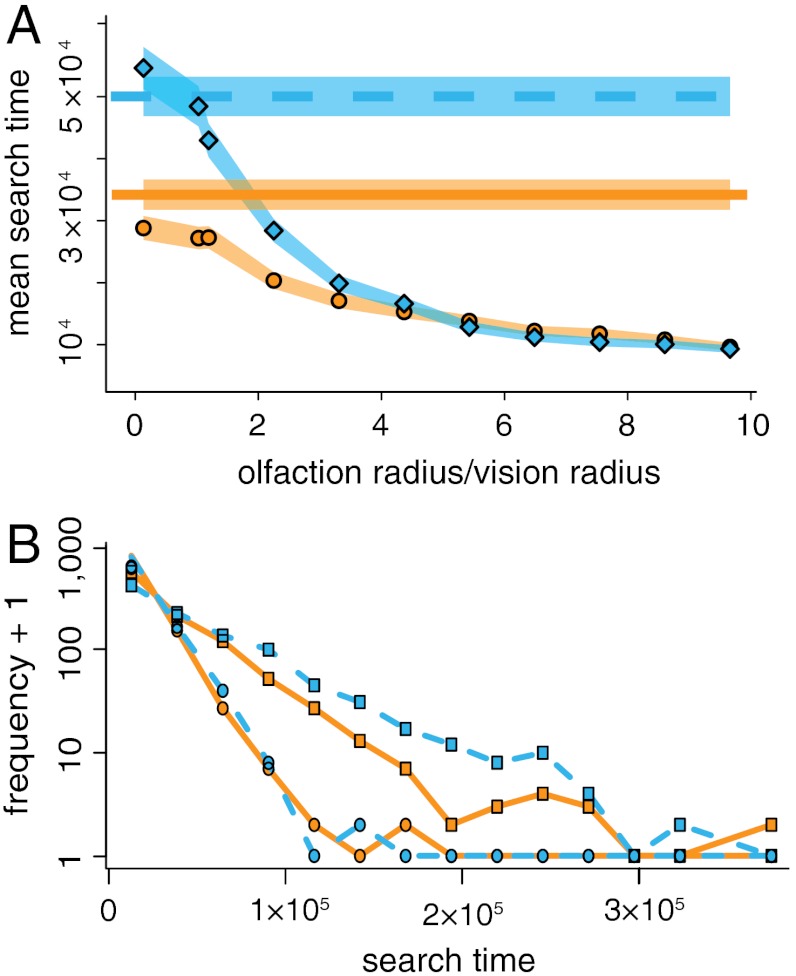
Fig. 2A shows mean search times of simulated visual and visual-olfactory predators (search time = time until first target encounter). Visual predators that use the Lévy strategy (Fig. 2A, solid line, see also Materials and Methods) have lower mean search times than predators that use the TDD strategy (Fig. 3A, dashed line). However, when conditions are such that the olfactory radius r_o is greater than the vision radius r_v, visual-olfactory predators find prey faster than their visual counterparts (Fig. 2A; circles represent results from visual-olfactory Lévy with optimal α, where optimal α was in the range 2.6–3.0 for all r_o/r_v; diamonds represent visual-olfactory TDD strategy; see also Figs. S1–S3). Mean search time of visual-olfactory predators continues to decrease as the distance over which prey scents can be detected increases.

Fig. 2.

Predator search times. (A) Mean search time as a function of the ratio of the olfaction radius (r_o) to vision radius (r_v). Solid orange line (visual Lévy), dashed blue line (visual TDD), orange circles (visual-olfactory Lévy), and blue diamonds (visual-olfactory TDD) each represent mean search time of 1,000 replicate simulations. Confidence bands represent ± 2 SEM. The following parameters values were used: a = 1, r_v = l_m = 50a, τ_v = 1 s, τ_o = 30 s, mean intertarget distance was 1,000a, and λ_a = 100 units of scent per τ_o (see Model Development for description of parameters, also SI Text). (B) Empirical distribution of search times of visual Lévy (orange solid line, squares), visual TDD (blue dashed line, squares), visual-olfactory Lévy (orange solid line, circles), and visual-olfactory TDD (blue dashed line, circles) strategies. In the case of the visual-olfactory strategies, frequencies are shown for r_o/r_v = 4. Note the large number of searches resulting in long search times for visual predators.

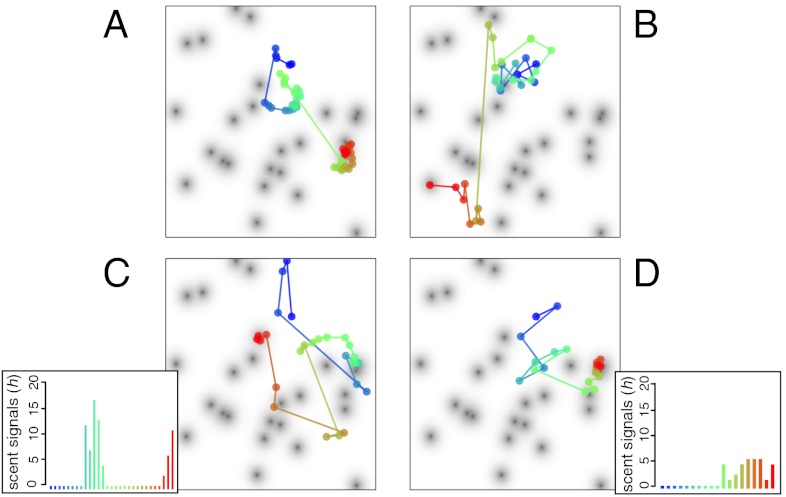
Fig. 3.

Typical search paths through a scent field with log ₁₀(1 + mean number of scent encounters per unit τ_o) indicated by grayscale (darker gray denotes more encounters). In white regions, mean number of encounters is effectively zero. Paths for (A) visual Lévy, (B) visual TDD, (C) visual-olfactory Lévy, and (D) visual-olfactory TDD are shown. Color scale of path changes from blue to red with increasing time. Inset boxes in (C) and (D) show the number of hits received during each scanning period with colors corresponding to colors in search paths. r_o/r_v = 4 in all boxes; all other parameters as in Fig. 2A.

Visual-olfactory predators have lower mean search times than visual predators primarily because they rarely search for long periods of time without finding prey. Fig. 2B shows that the tails of the search time distributions for the visual-olfactory predators (Fig. 2B, circles) decay roughly exponentially at a rate that is much faster than the decay rate of the visual predators (Fig. 2B, squares).

At least two factors contribute to the difference in performance between the two predator types. First, visual-olfactory predators learn from “no-signal” events and respond to these events by leaving regions that do not contain targets. Second, as has been observed in many species in nature (3, 20), visual-olfactory predators perform area-restricted search (21) and concentrate search effort in regions that contain prey. Below we discuss how both of these behaviors emerge naturally through responses to sensory data.

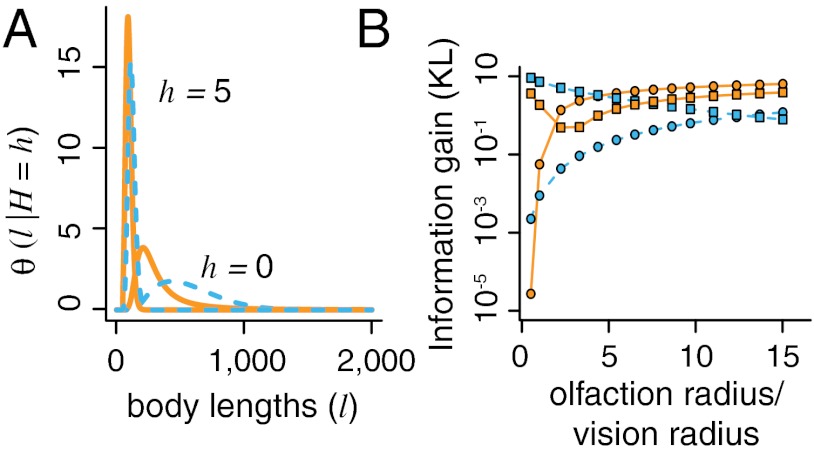
To characterize changes in predator behavior in response to sensory data in the following sections, we use a metric of information gain: the Kullback-Leibler divergence [KL, (22)]. The magnitude of the change in behavior of a visual-olfactory predator when it receives a signal of strength h relative to its intrinsic behavior θ(l), is given by KL = ∫θ(l|h) log(θ(l|h)/θ(l))dl. A literal interpretation of the quantity KL is the following: suppose an observer must decide, based on empirical data, whether a searcher is using olfactory data or not. The KL gives a mean rate of gain of information obtained by observing a visual-olfactory searcher moving in response to a signal of magnitude h. In regimes where the signal contains little useful information (for example when r_o/r_v ≈ 1 and h = 0), the behavior is not modified greatly from θ(l). The resulting KL value is small. However, when information is substantial (say when h = 5, for small r_o/r_v) the KL is larger.

Visual-Olfactory Predators Learn from No-Signal Events.

Fig. 3 shows typical search paths of the four strategies through a target field in the regime where r_o > r_v. When searching such an environment, a predator will frequently be too far from prey to receive scent signals. For example, the inset boxes in Fig. 3 C and D show that the number of signals received in scanning phases is typically zero, with signals of greater than zero only occurring when the predator is close to prey. Intuitively, it may seem that a predator gains little information from these no-signal events. Yet, by not receiving a scent signal, the predator gains a vital piece of information: prey are not likely to be nearby.

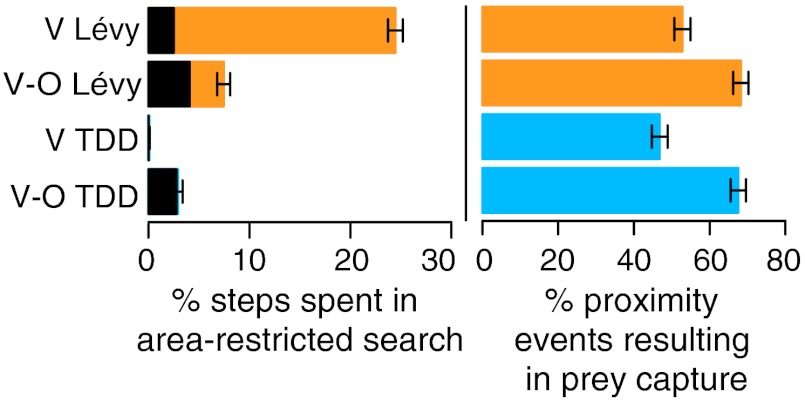
Fig. 4A shows step length distributions of visual-olfactory predators after receiving no signal. Both strategies exhibit a low probability of making small steps. The Lévy strategy in particular, is strongly affected; Fig. 1B shows that this strategy has a high probability of taking small steps between reorientations. Yet, when the visual-olfactory Lévy predator receives no signal, it is unlikely to make a small step (Fig. 4A, Fig. S4). Fig. 4B shows that when h = 0, KL increases as the olfaction radius becomes larger. In fact, as r_o/r_v becomes large, both strategies change more in response to no-signal events than when h = 5 (Fig. 4B, circles (h = 0) cross above squares (h = 5) for both strategies). For r_o/r_v sufficiently large, the change in behavior in response to no-signal events allows visual-olfactory predators to avoid performing area restricted search (ARS) when they are far from prey (Fig. 5). The visual Lévy predator, on the other hand, spends 24% of its steps in ARS but only 2.4% in ARS near targets. Avoiding these wasted steps strongly affects search time. Even by responding only to no-signal events and ignoring cases in which h > 0, a visual-olfactory Lévy predator can find prey much more rapidly than a visual Lévy predator (Fig. S5).

Fig. 4.

Effect of olfactory data on step lengths. (A) Step length distributions after signal modulation when h = 0 and when h = 5. (B) Information gain as measured by the Kullback-Leibler divergence between the visual strategy and the corresponding visual-olfactory strategy when h = 0 (circles) and h = 5 (squares) as a function of r_o/r_v. Dashed curves represent visual-olfactory TDD strategy. Solid curves represent visual-olfactory Lévy strategy. Note the increasing information gain when h = 0. In both boxes a = 3 and r_o/r_v = 4, all other parameters as in Fig. 2A.

Fig. 5.

Effect of olfactory data on area-restricted search (ARS). Left bars show % steps spent performing ARS. Shaded regions show the % steps spent performing ARS searches within 4r_v of prey. For the visual Lévy predator (top bar), contrast the large % of steps spent in ARS, with the small fraction of these steps spent near prey (top bar, shaded region). ARS defined as any period in which predator makes ≥5 consecutive steps within a region of radius 4r_v. Right bars show % of proximity events in which predator locates prey. Bars for visual-olfactory (V-O) predators show that they successfully locate nearby prey more frequently than do visual (V) predators. Proximity events defined to by any period of ≥1 consecutive steps within 2r_v of a target. r_o/r_v = 4; all other parameters as in Fig. 2A.

The observation that no-signal events contain valuable information is qualitatively similar to an observation from optimal foraging theory regarding a forager searching a discrete patch for hidden resources. In that scenario, the more time the forager spends in the patch without encountering resources, the more certain it becomes that the patch does not contain resources (23). Our model extends this idea to searchers moving through continuous spatial environments using two sensory modalities and reveals that the change in a searchers behavior in response to no-signal events depends critically on the length scales of these sensory modalities.

Visual-Olfactory Predators Concentrate Search Effort Near Targets.

From Fig. 3 A and B, it is clear that visual predators behave similarly in regions that are near and far from prey. Visual-olfactory predators, on the other hand, make more short exploratory steps in the vicinity of prey (Fig. 3 C and D). The strong change in strategy that occurs when a visual-olfactory predator receives a nonzero scent signal is reflected in the large value of KL for all values of r_o/r_v (Fig. 4B). Both visual-olfactory strategies increase their probability of making a short step when they encounter a nonzero scent signal (Fig 4A). Because of this behavior, visual-olfactory predators perform ARS near targets and are more likely to encounter nearby prey than are visual predators (Fig. 5).

Discussion

The framework presented here allows one to include responses to partial information gained from noisy sensory measurements when modeling random search. Our results reveal that analysis of the length scales of sensory modalities, in this case r_o and r_v, is crucial to determining whether such a sensory response will dominate search performance. The distinction between different types of intrinsic strategies [e.g., Lévy vs. TDD (8, 10)] is important when it is genuinely not possible to learn about resources from a distance (r_o/r_v ≤ 1). However, when r_o/r_v > 1, searchers that dynamically modify their behavior in response to sensory data experience a qualitative improvement in search performance. This improvement holds over a wide range of the parameters of the scent model and other features of predator behavior (Figs. S1–S3). This finding suggests a connection between sensing, decision-making, and search performance, even under sparse-signal conditions.

Moreover, behaviors such as area-restricted search near prey (20) emerge naturally from responses to sensory information. Visual-olfactory predators perform this behavior in our simulations by turning more frequently when they receive scent cues. Historically, ARS has been explained as a consequence of a predator concentrating search effort in areas where it has previously found prey. This response is beneficial if prey are clustered in space (21). Yet, we show that this behavior can also emerge when prey are not spatially clustered, if predators change their movement behavior in response to noisy sensory data. Recent evidence suggests that some species may initiate area-restricted search in this way. For example, wandering albatrosses appear to alter turning patterns after encountering prey scent, effectively concentrating their search effort in local regions (3). Greater frigatebirds forage primarily in highly productive mesoscale eddies (24). These predators appear to track these eddies, at least in part, using scent cues.

In our simulations Lévy predators intersperse periods of local search with large-scale relocation movements. Movements of many species including foraging marine fish and reptiles (13), and ants in search of colony-mates (25) exhibit this qualitative pattern (7, 13, 25), which is often cited as a feature of Lévy walks that makes them effective strategies for encountering targets. Yet, our results show that Lévy predators spend much of their time searching locally in regions that do not contain prey (Fig. 5). On the other hand, visual-olfactory predators appropriately match their behavior to their proximity to targets, leading to shorter search times. In light of our results, a natural hypothesis is that searching organisms utilize different movement behaviors depending on their perceived distance to targets. It has been shown that strategies that mix movements with different length scales can outperform strategies that draw movements from a single distribution, but that such mixed movement behavior can be difficult to distinguish from a Lévy strategy (11). Indeed, recent analyses have begun to find evidence of mixed behaviors in movement data [e.g., (26)]. Our framework provides a means of studying how such mixed behaviors can emerge through interactions with sensory information.

Materials and Methods

Scent Propagation.

To see how R(l) depends on the distance between predator and prey, let u(x) represent the mean concentration of scent at predator position x emitted by a prey item located at position x₀. An expression for the steady-state diffusion process without advection is given by 0 = DΔu(x) - μu(x) + λδ(x₀), where D represents the combined molecular and turbulent diffusivity (m² s^-1), μ represents the rate of dissolution of scent patches (s^-1), and λ represents the rate of scent emission at the prey (s^-1). In two dimensions, the mean rate of scent patch encounters by a predator of linear size a located at x is given by 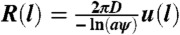where 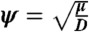(2), which implies

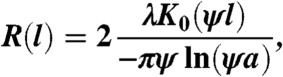[3]

where K₀ represents a modified Bessel function of the second kind.

Simulation Details.

The SI Text shows the robustness of results to changes in model parameters. For each of the four search strategies (visual Lévy, visual TDD, visual-olfactory Lévy, and visual-olfactory TDD), we performed simulations in which predators explored a periodic environment with 100 prey. Prey were positioned according to a Poisson point process with the mean distance between prey chosen to achieve the desired density. In each scanning phase, h was generated as a deviate from a Poisson distribution with mean given by the product of τ_o and Eq. 3 summed over all prey. In each simulation, the searcher was positioned at a random location and allowed to move through the environment until it came within a distance of r_v of a prey item during its scanning phase. For each strategy, we performed 1,000 simulations and recorded the time until first prey encounter in each simulation. Predators were assumed to travel at a constant speed of one body length per unit time. Environments were constructed so that prey density had a mean of one prey per 10⁶ squared body lengths, a realistic low density for prey, but qualitative results hold for lower prey densities (see Fig. S1 and SI Text). In the case of the Lévy strategies, we repeated simulations across a range of α values from α = 1.2 to α = 3. Note that the optimal value of α for the Lévy predator was α = 3 for which the long-term behavior is expected to be Gaussian (6). In all figures, Lévy strategies with the optimal value of α are shown unless otherwise noted.